2. fejezet - ALAPFOGALMAK, DEFINÍCIÓK

A kísérlet a vizsgált folyamat lefolytatása ismert és reprodukálható körülmények között annak érdekében, hogy a folyamat eredményét megismerjük.

Aktív kísérletről beszélünk, ha a folyamat körülményeit (paramétereit) mi állítjuk be. Passzív kísérletről beszélünk, ha a vizsgált jelenségbe nincs módunk beavatkozni.

A továbbiakban az aktív kísérletek megtervezésével fogunk foglalkozni.

A kísérlet sorozat több egymás után megismételt kísérlet halmaza.

A kísérlet sorozat sorrendje lehet időrendi vagy véletlenszerű (randomizált).

A faktorok a folyamatot jelentősen befolyásoló körülmények (paraméterek).

A faktor-szintek a faktorok által felvehető értékek.

Ha egy kísérletben minden faktor ugyanannyi szintet vehet fel, akkor a kísérletben az összes lehetséges faktor-szint száma:

n=pk

ahol p egy-egy faktor szintjeinek száma

k a faktorok száma

na kísérletek száma.

Egy kísérletben célszerűen legfeljebb 15 faktor lehet, és azok legfeljebb 30 szintet vehetnek fel.

A faktorokkal szemben támasztott követelmények:

Ha egy faktort a vizsgálatból kihagyunk, akkor a vizsgált folyamatot általunk nem ismert, véletlen vagy szisztematikus hatások érhetik. Az is lehetséges, hogy a nem vizsgált faktor szintje a kísérletek alatt nem változik, de nem optimális, ebben az esetben a kísérletekkel meghatározott optimum nem a valódi optimum lesz.

Ezért célszerű inkább több faktort vizsgálni, mint kevesebbet.

A kísérleti beállítás a kísérletsorozat-halmaz egyik eleménél a lehetséges faktor-szintek valamelyik kombinációja.

Az optimalizációs paraméter az az ismérv, amelynek alapján a folyamatot optimalizálni akarjuk. Az optimalizációs paraméter a kísérletek célja; a kísérleti eredmény, amelynek a számunkra legkedvezőbb értékét keressük.

Az optimalizációs paraméter lehet egyszerűen maga a kísérleti eredmény, de lehet a kísérlet többféle eredményének valamilyen módon létrehozott kombinációja is.

Az optimalizációs paraméterrel szemben támasztott követelmények:

A vizsgált folyamat megismeréséhez a folyamat matematikai modelljét használjuk fel. A modell az y optimalizációs paraméter és az x1, x2,…xn faktorok közötti függvénykapcsolat, amelynek általános alakja a φ válasz-függvény (2):

y = φ (x1, x2,….,xn)

Az optimalizációs paraméter lehet valamely gyártási folyamatban előállított termék minősége, mennyisége vagy önköltsége; lehet egy mezőgazdasági termék legeredményesebb termelési technológiája, de lehet egy oktatási módszer hatékonysága is.

Az optimalizációs paraméter és a faktorok kapcsolatának ábrázolására a „fekete doboz” hasonlatot szokták alkalmazni (2.1. ábra).

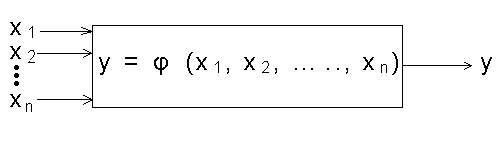
A fekete doboz a vizsgált folyamat vagy objektum, amelyet a bemutatott matematikai modellel kívánunk leírni és helyettesíteni a kísérletezés és a megvalósítás során. A fekete doboz az ismeretlen kapcsolatot szimbolizálja a rá ható 7x1, x2, …, xn faktor, mint bemenet és az y optimalizációs paraméter, mint kimenet között.

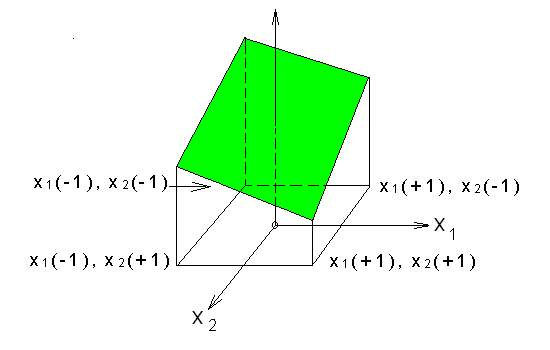
Két faktor esetén a válasz- függvényt szemléletesen, térben is ábrázolhatjuk (2.2. ábra). Itt az x1 és x2 faktor a vízszintes síkon található, míg az y optimalizációs paraméter értékei kirajzolják a válasz-függvény felületét, amelynek legmagasabb pontja a keresett optimális beállítást jelzi. A válasz-függvénynek most csak egy kis négyszögletes darabját látjuk az x1= -1, x1= +1, x2= -1 és x2= +1 pontok felett.

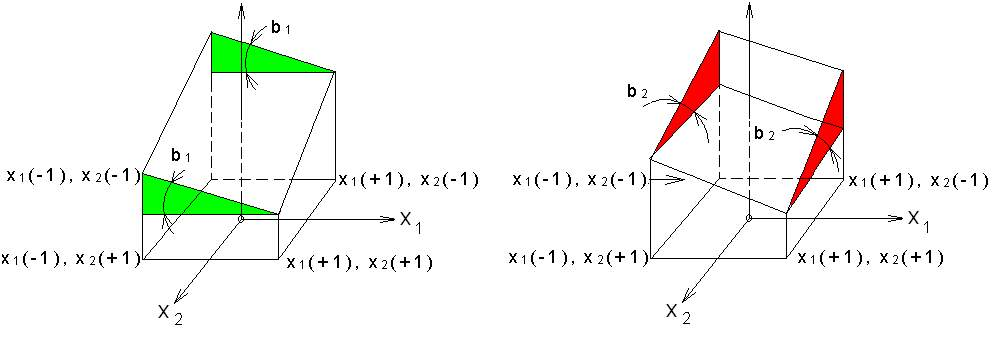
A fő-hatások független hatások, vagyis olyan hatások (faktorok), amelyeknek együttes hatása megegyezik azon hatások összegével, amelyet külön-külön gyakorolnának az optimalizációs paraméterre. A 2.3. ábrán egy kétfaktoros esetben mutatjuk be a lineáris modellt. A 2.3. ábra bal oldalán látható, hogy a válasz-felület x1 irányú b1 meredeksége állandó, különböző x2 értékek mellett. A 2.3. ábra jobb oldalán pedig az látható, hogy az x2 irányban is állandó a b2 meredekség.

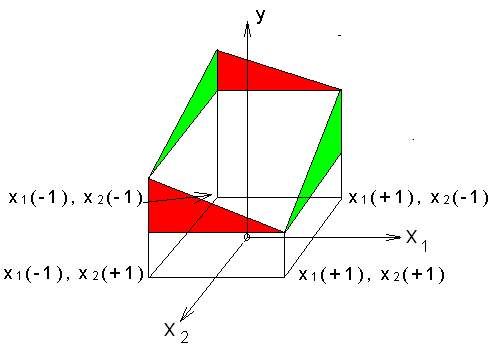
Kereszt-hatásról beszélünk akkor, ha két faktor egyidejű hatása nem ugyanolyan változást hoz létre az optimalizációs paraméteren, mint a két faktor független hatásának az összege. Az 2.4. ábrán olyan kétfaktoros kísérlet válasz-felülete látható, amelynél az x1 faktor és az x2 faktor között kölcsönhatás áll fenn. Az ilyen válasz-felület nem sík, hanem görbült felület, és lineáris modellel nem lehet elegendő pontossággal modellezni.

A folyamat matematikai modellje, azaz az y optimalizációs paraméter és az x1, x2,…xn faktorok közötti függvénykapcsolat elvileg bármilyen lehet. A kísérlettervezésben a kísérleti adatok azonban mindig csak többé-kevésbé pontos közelítést tesznek lehetővé. Matematikai modellként ezért célszerű mindig a lehető legegyszerűbb közelítő függvényt választani. A tapasztalat szerint leginkább az algebrai polinomok felelnek meg, bár bizonyos esetben előnyös lehet a logaritmus függvénnyel történő közelítés is.

y=log x

A logaritmikus közelítést ritkábban szokták alkalmazni. A továbbiakban csak polinomiális közelítéssel fogunk foglalkozni.

lineáris közelítés:y=b0+b1x

másodfokú közelítés:

y=( b0+b1x) (b0+b1x)=b02+2b0b1x+b12x2

ahol az ortogonalitás következtében x2=0, ezért az együtthatók egyszerűbb jelöléseivel írható, hogy a lineáris modell:

y=b0+b1x,

Tehát ortogonális polinomok esetében másodrendű közelítés egy faktor esetén nem lehetséges.

lineáris közelítés (6):

y=b0+b1x+b2x2

másodfokú közelítés (7):

y=( b0+b1x1+b2x2) (b0+b1x1+b2x2)=

b02+b0b1x1+b0b2x2+b0b1x1+b12x12+

+b1b2x1x2+b0b2x2+b1b2x1+b22x22

ahol x12=x22=0, és ha egyszerűsítjük az együtthatókat, írható, hogy a másodrendű modell:

y=b0+b1x1+b2x2+b1b2x1x2

lineáris közelítés:y=b0+b1x+b2x2+b3x3

másodfokú közelítés:

y=( b0+b1x+b2x2+b3x3) (b0+b1x+b2x2+b3x3) (b0+b1x+b2x2+b3x3)=

y=b0+b1x1+b2x2+b3x3+b12x1x2+b13x1x3+b12x1x2

az előzőekhez hasonló módon.

A másodfokú polinomiális közelítésben szereplő b12x1x2, b13x1x3, és b12x1x2 tagok a faktor-hatások keveredését, tehát a faktorok kölcsönhatásait írják le.