4. fejezet - A TAGUCHI-MÓDSZER
- 4.1. A Taguchi-filozófia
- 4.2. A Taguchi kísérlet tervezési módszer
- 4.3. A kísérleti eredmények kiértékelése
- 4.4. Az ortogonális táblázat
- 4.5. A lineáris gráf
- 4.6. A kölcsönhatások háromszög-táblázata
- 4.7. A „jel/zaj” (Signal-to-Noise, S/N) analízis
- 4.8. Három- és négyszintű kísérleti tervek
- 4.9. Taguchi „Szakácskönyve”
- 4.10. A fő-hatások oszlopainak megválasztása
- 4.11. Több lépésben végrehajtott kísérleti terv
- 4.12. Mit tegyünk, ha nincs előzetes információnk arról, hogy vannak-e kölcsönhatások az egyes hatások között?
- 4.13. Szűrő kísérleti tervek
- 4.14. A Taguchi „szakácskönyv” L8 és L16 kísérleti terveinek átalakítása kétszintűről négyszintűvé
4.1. A Taguchi-filozófia
Dr. Genichi Taguchi japán mérnök volt, aki a II. világháború után alapított Electrical Communication Laboratories dolgozójaként úgy találta, hogy a kísérlettervezés és a minőség ellenőrzés hagyományos módszerei már nem felelnek meg a modern kor követelményeinek. Kidolgozta a kísérlettervezés statisztikai módszerét, melyért 1960-ban állami kitüntetést kapott. 1980-ban az amerikai Bell Laboratóriumban ismertette új statisztikai módszereit, amelyek azóta az egész világon elterjedtek.
A Taguchi-filozófia forradalmasította a gyáripar minőségellenőrzési módszerét. Ez a filozófia 3 alapelven alapul:
-
A gyártmány minőségét nem utólag kell ellenőrizni, hanem a gyártmányba bele kell tervezni („quality design”).
-
A minőség akkor lesz a legjobb, ha minimalizáljuk az előirányzattól való eltérést. Úgy kell megtervezni a terméket, hogy érzéketlen legyen az ellenőrizhetetlen környezeti hatásokra („robust design”).
-
Az előírástól való eltérés függvényében definiálni kella minőség előírt „költségét”. Atényleges költséget a teljes termelési folyamat során rendszeresen mérni kell („cost of quality”).
4.2. A Taguchi kísérlet tervezési módszer
A Taguchi módszernem annyira a kísérlettervezés matematikai formuláin, sokkal inkább a kísérleteken, gyakorlati, tapasztalati tervezési módszereken alapul. Ez az új elgondolás tette a Taguchi-módszert egyedülállóan sikeressé a hagyományos módszerekkel szemben.
A korábban alkalmazott, ma már „hagyományos”-nak nevezett módszer, a faktoriális kísérlettervezési módszer segített a kísérletezőnek megtalálni a kísérleti eredményre ható legfontosabb faktorokat, és azok lehetséges összes kombinációját, mindezeknek a hatását a kísérleti eredményre, és megtalálni az optimális eredményt hozó faktorkombinációt.Ezek a faktoriális tervek azonban a nagyon sokfaktoros esetekben túl bonyolultakká váltak, és túl sok kísérlet elvégzését tettek szükségessé (különösen mezőgazdasági, vegyipari és biológiai gyártás illetve tervezés esetén). A részleges faktoriális kísérletek megtervezésénél a feles és negyedes replikációk még jól tervezhetők a kihagyott kölcsönhatások következtében létrejövő hatás-keveredések szempontjából, azonban a nyolcados vagy még magasabb rendű replikációkat már igen nehezen lehet áttekinteni.
Taguchi a faktoriális kísérlettervezési módszert fejlesztette tovább. Oly módon csökkentette az optimum eléréséhez vezető kísérletek számát, illetve oly módon növelte a viszonylag egyszerűen megvizsgálható faktorok és kölcsönhatások számát, hogy rengeteg kísérlet eredménye alapján létrehozott néhány, a gyakorlatbangyakran előforduló feladatra kísérleti terveket. A tervekhez úgynevezett ortogonális táblázatokat dolgozott ki. Ezekben az ortogonális táblázatokban („orthogonal arrays”) kidolgozta a legáltalánosabbnak nevezhető faktor kombinációkat, és meghatározta, hogy hogyan célszerű elhelyezni a fontosabb és kevésbé fontos hatásokat és kölcsönhatásokat azokban. Ezek a táblázatok alkotják Taguchi „szakácskönyvét”.
A szakácskönyv alkalmazójának nem kell végiggondolni minden lehetséges hatás- és kölcsönhatás variációt, csupán jól kell használni a szakácskönyvet. A gyártmány vagy folyamat előzetes ismeretében meg kell határozni azokat a legfontosabb hatásokat és kölcsönhatásokat, amelyek befolyásolhatják a gyártmány vagy folyamat minőségét. Egyetlen befolyásoló faktort sem szabad figyelmen kívül hagyni. Ezután kikeressük a Taguchi-szakácskönyvből azt a kísérleti tervet, amely az adott esetben a legmegfelelőbb, és el kell dönteni, hogy melyik faktor melyik oszlopba kerüljön.
Előzetes információ szükséges annak eldöntéséhez is, hogy az egyes faktoroknak mekkora legyen az alsó és a felső szintje. Ha túl nagy a távolságuk, átléphetjük velük és nem találjuk meg az optimomot, ha túl kicsi, nem lesz a faktor eléggé érzékeny az optimum megtalálására. Ha a szintek túl távol vannak az optimumtól, a kísérleti felület esetleg nem lesz egyértelmű, még az is lehet, hogy egy mellék-optimumot fogunk megtalálni. Gondolni kell arra is, hogy egy-egy kísérlet ne tartalmazzon összeférhetetlen faktorszinteket (pl. túl magas hőmérséklet túl magas nyomással kombinálva robbanáshoz vezethet).
Mindez sok előzetes ismeretet és mérlegelést igényel, de ez az ára annak, hogy nagyságrendekkel kevesebb kísérletet kelljen elvégezni lényegesen kevesebb idő- és költségráfordítással, mint a hagyományos kísérlettervezési módszerek alkalmazásával kellett.
A Taguchi kísérleti terv a lehető legkevesebb kísérlet lebonyolítását teszi lehetővé. Egy kétszintű 15 faktoros teljes faktoriális kísérleti terv 32 768 (215) kísérletből áll. Egy frakcionális kísérleti terv Taguchi ortogonális táblázata alapján 15 kétszintű faktor vizsgálatát 16 kísérlettel teszi lehetővé!
A kísérlet teljes lebonyolítása az alábbi lépésekből áll:
-
Egy „brain storming”-on meg kell határozni a minőség jellemzőit, a kísérletben megvizsgálandó legfontosabb faktorokat és azok szintjeinek szóba jöhető értékeit.
-
Meg kell tervezni és lebonyolítani a kísérleteket a Taguchi-szakácskönyv valamelyik receptje szerint.
-
Analizálni kell az eredményeket, és meg kell határozni az optimális körülményeket.
-
Le kell futtatni egy ellenőrző kísérletet az optimális körülmények mellett.
4.3. A kísérleti eredmények kiértékelése
Három dolgot kell meghatározni a kísérletek alapján.
-
Meg kell határozni a gyártmány vagy folyamat optimális feltételeit
-
Becslést kell adni az egyes faktorok hatásának erősségére
-
Meg kell határozni a kísérleti eredmény nagyságát az optimális paraméterek mellett
Az optimális feltételek meghatározása az összes faktor hatásának kiszámítása alapján történik. Ez a számítás egyszerű aritmetikai műveletek alkalmazásával elvégezhető, akár egy kis kézi kalkulátor segítségével. Ezen hatások ismeretében becslést végezhetünk arra, hogy milyen faktor-beállításokkal érhetünk el optimális eredményt. Ha szükséges, a faktorszintek újabb, kedvező irányú megválasztásával egy további kísérletsorozatot tervezhetünk meg.
A szórás-analizis (Analysis of Variance, ANOVA) az a statisztikai módszer, amelyet leggyakrabban alkalmaznak annak vizsgálatára, hogy mely faktorok szignifikánsak, tehát melyik faktorokat érdemes ellenőrizni a gyártás vagy a folyamat alatt.
Az újabb kísérleti terv elkészítésénél kihagyhatjuk azokat a faktorokat, amelyek hatása elhanyagolhatónak bizonyult. Az elhanyagolhatóságot a Taguchi-féle „jel/zaj” (Signal-to-Noise, S/N) analízis segítségével dönthetjük el.
Taguchi két fontos vizsgálatot javasol a kísérletek után elvégezni:
Először:Az egységes megközelítésegykísérlet eredményének vagy ismételt kísérletek átlagos eredményének feldolgozására a hatások elemzése ANOVA analízissel.
Másrészt:Nagyon hasznos azonos körülmények között megismételt kísérletek végzése. Az S/N analízis alapján meghatározható a faktorok legrobusztusabb kombinációja.
4.4. Az ortogonális táblázat
Az ortogonális táblázatok jellemzői:
- Az ortogonális táblázatok általában 2-szintű változókat tartalmaznak
- Jelölésük L4, L8 vagy L16. Ezek 22, 23 vagy 24 kísérletet tartalmaznak. A sorok száma ezeknél 4, 8 vagy 16.
- Az oszlopok száma mindig 1-gyel kevesebb, mint a soroké.
- Az oszlopok jelentése: „VALAMI amire kíváncsiak vagyunk”. Ez lehet hatás vagy kölcsönhatás, tetszés szerint.
- A sorok az egyes kísérleti beállítások faktorszint-kombinációit tartalmazzák.
- A kísérleti beállítások szintjének jelölése „1” vagy „2”. az „1” az egyik, a „2” a másik szintjét jelenti az adott „valami”-nek.
- A kísérleti beállítások megtervezése a táblázatban a faktoriális kísérleti terveknél alkalmazott módszerrel történik, tehát a főhatás oszlopokban az „1” és „2” szintet négyesével, kettesével, majd egyesével váltogatjuk.
- A kereszthatás oszlopok kísérleti beállításainak szintjeit a hatások oszlopainak szorzásával képezzük, ahol azt a szabályt alkalmazzuk, hogy azonos számok szorzata mindig „1”, különböző számok szorzata mindig „2” lesz.
AVIII. Táblázat egy L8 ortogonális táblázatot mutat be, amelynek oszlopaiban A, B, C, D, E, F, és G-vel jelöltük azt a 7 „VALAMI”-t, amire kíváncsiak vagyunk.Ezek lehetnek főhatások és kölcsönhatások is. A sorokban T-1, T-2, T-3, T-4, T-5, T-6, T-7 és T-8 jelöli a kísérleteket.
AVIII. Táblázatnak egy teljes faktoriális kísérleti terv esetén a IX. Táblázat felelne meg, amelyben feltűntettük a 7 „VALAMI”-nek az alsó és felső szintjeit, és azok lehetséges összes kombinációját. AVIII. Táblázatban szereplő 1 és 2 számok alapján bejelöltük a IX. Táblázatban azokat a cellákat, amelyekben a T1, T2,… T7, T8 kísérlet beállítási kombinációi találhatók.
Látható, hogy a VIII. Táblázat összes lehetséges faktorszint kombinációja közül a IX. Táblázatban nagyon sok kimaradt, de az ortogonalitási feltételek a kitöltött cellák esetén fennmaradtak.
Ha megnézzük a VIII. táblázat faktor-szintjeit, észrevehető, hogy a C oszlop számai az A és B oszlop számainak szorzatai. Tehát írható, hogy C=AB. Hasonlóképpen az is írható, hogy E=AD, F=BD és G=ABD. A C, E, F és Goszlopokba kerülő „VALAMI”-kre gyakorolt többi hatás ezek hatásával keveredni („konfundálódni”) fog. Ezért a kísérletek megtervezése során ezekre a keveredésekre figyelni kell.
Taguchi ezeket a keveredéseket figyelembe véve alkotta meg szakácskönyvét, és ezzel megkönnyíti a kísérletek megtervezését. A szakácskönyv szabályaitól azonban nem célszerű eltérni.
VIII.táblázat Teljes faktoriális kísérleti terv 7 „VALAMI”-nek a vizsgálatára
Teljes faktoriális kísérleti terv 7 „VALAMI”-nek a vizsgálatára
|
A „VALAMI„ neve |
Eredmények |
|||||||||
|
A |
B |
C |
D |
E |
F |
G |
||||
|
A kísérlet sorszáma |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|||
|
T-1 T-2 T-3 T-4 T-5 T-6 T-7 T-8 |
1 1 1 1 2 2 2 2 |
1 1 2 2 1 1 2 2 |
1 1 2 2 2 2 1 1 |
1 2 1 2 1 2 1 2 |
1 2 1 2 2 1 2 1 |
1 2 2 1 1 2 2 1 |
1 2 2 1 2 1 1 2 |
|||
IX.táblázat
A VIII. Táblázat T-1, T-2 , … , T-8 kísérletének beállítási kombinációi
|
A1 |
A2 |
|||||||||||||||||||
|
B1 |
B2 |
B1 |
B2 |
|||||||||||||||||
|
C1 |
C2 |
C1 |
C2 |
C1 |
C2 |
C1 |
C2 |
|||||||||||||
|
D1 |
E1 |
F1 |
G1 |
T-1 |
||||||||||||||||
|
G2 |
||||||||||||||||||||
|
F2 |
G1 |
|||||||||||||||||||
|
G2 |
T-3 |
|||||||||||||||||||
|
E2 |
F1 |
G1 |
||||||||||||||||||
|
G2 |
T-5 |
|||||||||||||||||||
|
F2 |
G1 |
T-7 |
||||||||||||||||||
|
G2 |
||||||||||||||||||||
|
D2 |
E1 |
F1 |
G1 |
|||||||||||||||||
|
G2 |
T-8 |
|||||||||||||||||||
|
F2 |
G1 |
T-6 |
||||||||||||||||||
|
G2 |
||||||||||||||||||||
|
E2 |
F1 |
G1 |
T-4 |
|||||||||||||||||
|
G2 |
||||||||||||||||||||
|
F2 |
G1 |
|||||||||||||||||||
|
G2 |
T-2 |
|||||||||||||||||||
Taguchi az ortogonális táblázatokban nem tűnteti fel sem az A, B, stb. jelölést, sem a T-1, T-2, stb. jelölést, hanem teljesen általános alakban, sorszámozással jelöli a sorok és oszlopok mentén a beállítási szinteket (X. Táblázat).
Tehát aX. Táblázatban az 1, 2, 3, 4, 5, 6 és 7. oszlopban azok a „dolgok” (faktorok) helyezkednek el, amelyeknek a hatását vizsgálni akarjuk. A sorok az egyes kísérleteket jelentik. Tehát összesen 8 kísérletet kell elvégezni ahhoz, hogy 7 dologhatását megvizsgálhassuk. A cellákban a faktorok beállítandó szintjei találhatók egy-egy kísérlet során.
X.táblázat Kísérleti terv 7 hatás vizsgálatára
Kísérleti terv 7 hatás vizsgálatára
|
Oszlopok Kísérlet |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
Eredmények |
|
1 2 3 4 5 6 7 8 |
1 1 1 1 2 2 2 2 |
1 1 2 2 1 1 2 2 |
1 1 2 2 2 2 1 1 |
1 2 1 2 1 2 1 2 |
1 2 1 2 2 1 2 1 |
1 2 2 1 1 2 2 1 |
1 2 2 1 2 1 1 2 |
A faktoriális kísérleti terv módszernél más jelöléseket alkalmaztunk: a hatásokat x1, x2, x3, stb jelölte, míg a kölcsönhatásokat x1x2 vagy x2x3, stb. Ezekkel a jelölésekkel talán szemléletesebben tudnánk követni az összefüggéseket a hatások és kölcsönhatások között. Például a X. Táblázat a faktoriális kísérleti terveknél alkalmazott jelölésekkel a XI. Táblázatban látható módon alakulna.
XI. táblázat
A X. táblázat a faktoriális kísérleti terveknél alkalmazott jelölésekkel
|
Oszlopok Kísérlet |
x1 |
x2 |
x1x2 |
x3 |
x1x3 |
x2x3 |
x1x2x3 |
Eredmények |
|
1 2 3 4 5 6 7 8 |
1 1 1 1 2 2 2 2 |
1 1 2 2 1 1 2 2 |
1 1 2 2 2 2 1 1 |
1 2 1 2 1 2 1 2 |
1 2 1 2 2 1 2 1 |
1 2 2 1 1 2 2 1 |
1 2 2 1 2 1 1 2 |
Azonban Taguchi tudatosan alkalmaz más jelöléseket, mert a kísérletek számának csökkentését azáltal kívánta elérni, hogy a lehetséges teljes, vagy feles, negyedes, nyolcados faktoriális kísérleti terv kötöttségeitől is megszabadul. Ezért bizonyos, gyakorlatban gyakran előforduló sémáknak megfelelően választotta meg azokat a kölcsönhatásokat, amelyeket érdemesnek tart vizsgálni. Ezt az általa bevezetett sémát a lineáris gráfok és a kölcsönhatás-táblázatok segítségével ismerteti.
4.5. A lineáris gráf
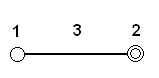
Az egyes faktorok és kölcsönhatások kapcsolatát Taguchi egy „lineáris gráf” formájában ábrázolja. A gráf csomópontjai a hatások (faktorok), és a csomópontok közötti gráf-ágak az adott csomóponti hatások kölcsönhatásai (4.1. ábra).
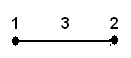
A 4.1. ábrán 1 és 2 tehát az x1 és x2 faktort jelenti, míg a 3 jelű vonal az x1x2 kölcsönhatást. A számozás pedig megegyezik a faktor vagy a kölcsönhatás oszlop-számával az ortogonális táblázatban.
Ha megnézzük a X. Táblázat L8 szintű ortogonális táblázatát, akkor azt látjuk, hogy az 1. oszlopban lévő faktor szintjét a kísérleti terv lebonyolítása során csak egyszer kell megváltoztatni (a 4. kísérlet után). A 2. oszlopban lévő faktor szintjeit a kísérleti terv lebonyolítása során háromszor kell megváltoztatni (a 2., 4. és 6. kísérlet után). A 4. számú oszlopban lévő faktor szintjeit pedig minden egyes kísérlet után meg kell változtatni. Ez pedig a gyakorlatban lehet, hogy nem is olyan egyszerű feladat. Például nézzünk meg egy olyan kísérletsorozatot, ahol az üveg fújás optimális beállításait keressük, és a vizsgált három faktor az üveg olvadék hőmérséklete, az üvegfújó eszköz típusa, és az üveg olvadék összetétele. Az üvegfújó eszköz megváltoztatása egyszerűen keresztül vihető, a hőmérséklet megváltoztatása már elég körülményes,és az összetétel megváltoztatásához ki kell üríteni, le kell hűteni, ki kell tisztítani, újra kell tölteni és fel kell fűteni a kemencét. Tehát célszerű a faktorokat úgy helyezni el az egyes oszlopokban, hogy az 1. oszlopba kerüljön az üveg összetétele, a 2. oszlopba a hőmérséklet és a 4. számú oszlopba az üvegfújó eszköz típusa.
A lineáris gráfokban az ilyen típusú mérlegelésre Taguchi egy újabb jelölést vezetett be. A csomópontokat négy féle ponttal jelölte (4.2. ábra).

Az ortogonális táblázat megtervezésekor a jobb áttekinthetőség kedvéért az egyes oszlopokat csoportosíthatjuk a szükséges beállítások (faktor-szint változtatások) gyakorisága szerint, (például a XVI. vagy a XVII. táblázatban a Group 1-ben csak egyszer kell változtatni a faktor-szintet az egész kísérletsorozat elvégzése közben, míg a Group 2-ben három-négyszer és a Group 3-banmég többször).
Ennek a kísérletnek a lineáris gráfja ezekkel a jelölésekkel a 4-3. ábrán látható. Ez a lineáris gráf 3 hatás és 3 kölcsönhatás vizsgálatára alkalmas. Az L8 szintű ortogonális mátrixnak viszont 7 oszlopa van. Lehetőség van ennek a 7 oszlopnak a segítségével a háromszoros kölcsönhatásra következtetni, de ha a szórás analízissel történő vizsgálat azt mutatja, hogy ennek az oszlopnak a hatása nem szignifikáns (ez valószínű, mert ebben a hatások már erősen keverednek), akkor ez az oszlop a „zaj”-ra lesz jellemző. Így feleslegessé válhat ismételt kísérletek végzése, amelyeknek szintén a zaj meghatározása a fő célja.
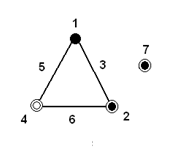
Amint látjuk, Taguchi csak a kettős kölcsönhatásokat vizsgálja, a faktoriális kísérleti terveknél megismert többszörös (több faktor közötti egyidejű) kölcsönhatásokat nem. Vagyis csak arra kíváncsi, hogy két faktor között van vagy nincs kölcsönhatás.
4.6. A kölcsönhatások háromszög-táblázata
A kölcsönhatások háromszög-táblázatai az ortogonális táblázatok összes lehetséges kölcsönhatásának információit tartalmazzák. A XIV. Táblázat egy háromszög-táblázatot mutat be. A táblázat a XIII. Táblázat L8 szintű ortogonális táblázatához és a 4.3. ábra lineáris gráfjához tartozik.
XIII. táblázat
8 kísérletből álló kísérleti terv 7 hatás vizsgálatára
|
Oszlopok Kísérlet |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
Eredmények |
|
1 2 3 4 5 6 7 8 |
1 1 1 1 2 2 2 2 |
1 1 2 2 1 1 2 2 |
1 1 2 2 2 2 1 1 |
1 2 1 2 1 2 1 2 |
1 2 1 2 2 1 2 1 |
1 2 2 1 1 2 2 1 |
1 2 2 1 2 1 1 2 |
A XIII. táblázat kölcsönhatásait mutatja be az alábbi háromszög-, vagy kölcsönhatás táblázat (XIV. táblázat).
XIV.táblázat A XIII. táblázat kölcsönhatásai
A XIII. táblázat kölcsönhatásait bemutató háromszög táblázat
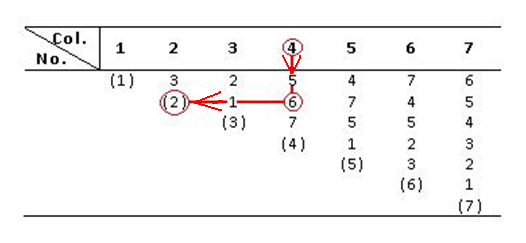
A háromszög táblázat minden oszlopa megfelel az ortogonális táblázat azonos számú oszlopának. Ha most azt szeretnénk megtudni, hogy az ortogonális táblázat 4. és 2. oszlopa közötti kölcsönhatás melyik oszlopban található, akkor induljunk el a 4. oszloptól lefelé, majd onnan ahonnan lehetséges, egy irány-töréssel vízszintesen a (2) pont irányába. Ha a töréspont a „6”-nál volt, akkor ez lesz a kölcsönhatás oszlopa.
A háromszög táblázat alkalmazása rendkívül lerövidíti a kísérlet megtervezésének idejét, és csökkenti a tévedések lehetőségét.
4.7. A „jel/zaj” (Signal-to-Noise, S/N) analízis
Egy olyan kísérleti program, amely ismételt kísérleteket tartalmaz, sokkal több információt eredményez a kísérleti eredmény hibáiról, mint ha minden kísérletet csak egyszer végeznénk el. Az egyetlen kísérlet „indulás a semmiből”, az ismétlés, ha teljesen az előbbivel azonos körülmények között végezzük, megmutatja azokat a hibákat, amelyeket a mérőműszerek és a mérési módszerek hibája okoz, sőt egyéb hibák is felléphetnek, mivel lehet, hogy nem sikerül még egyszer teljesen az előzőhöz hasonló körülményeket elő állítani.
Taguchi kidolgozott egy formulát ismételt kísérletek S/N analízise céljára:
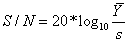
Vagy másképpen:
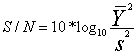
ahol
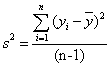
Az S/N érték fenti formulája akkor igaz, ha a szórás függ az átlagtól.
Ha a szórás független az átlagtól, akkor az S/N értéket a következőképpen alkalmazhatjuk. Vezessük be a következő jelölést:
S/N= z
Amennyiben a kísérletek eredményét úgy értékeljük, hogy a legjobb a tervezett nominális érték, akkor
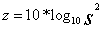
Ha pedig az a véleményünk, hogy a nominálishoz képest „a kisebb eredmény még jobb”, akkor alkalmazzuk a (34)-et:
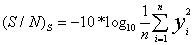
Végül abban az esetben, ha „a nagyobb eredmény még jobb” a (35) szerint
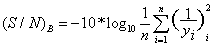
A S/N analízis megértésére egy elméleti példát mutatunk be a XV. Táblázatban:
XV. táblázat
kétszer elvégzett, 8 kísérletből álló kísérleti terv ortogonális mátrixa,
2-2 y eredménnyel
|
RUN NO. |
C 1 |
B 2 |
3 |
A 4 |
5 |
6 |
7 |
RESULTS Y |
AVG.
|
STD. DEV. S |
z = 10logs2 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
35, 37 |
36 |
1.41 |
3.0103 |
|
2 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
34, 40 |
37 |
4.24 |
12.5527 |
|
3 |
1 |
2 |
2 |
1 |
1 |
2 |
2 |
41, 43 |
42 |
1.41 |
3.0103 |
|
4 |
1 |
2 |
2 |
2 |
2 |
1 |
1 |
40, 46 |
43 |
4.24 |
12.5527 |
|
5 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
42, 44 |
43 |
1.41 |
3.0103 |
|
6 |
2 |
1 |
2 |
2 |
1 |
2 |
1 |
39, 45 |
42 |
4.24 |
12.5527 |
|
7 |
2 |
2 |
1 |
1 |
2 |
2 |
1 |
36, 38 |
37 |
1.41 |
3.0103 |
|
8 |
2 |
2 |
1 |
2 |
1 |
1 |
2 |
33, 39 |
36 |
4.24 |
12.5527 |
Ha a táblázatban megnézzük az átlagos Y értékeket, felfedezhetjük, hogy a számértékek körülbelüli nagysága ugyanolyan sorrendben váltakozik, mint a 3 oszlopban. Minthogy a 3 oszlop az 1 és 2 oszlop kölcsönhatásait tartalmazza, arra következtethetünk, hogy a mi átlagos kísérleti eredményeinket a C és B faktor hatása befolyásolja.
Ha megfigyeljük a szórás (s) oszlopot, azt vehetjük észre, hogy a számértékek körülbelüli nagyságának sorrendje a 4 oszlopéhoz hasonlít. Minthogy a 4 oszlop az A faktor hatását tartalmazza, ebből arra következtethetünk, hogy a cellán belüli szórás (az egyes kísérletek ismételt eredményeinek szórása) az A faktor hatása alatt áll.
A „z” oszlop hasonló gondolatot sugall. A „z” oszlop éppen azért került ide, hogy bizonyítsuk, hogy ha ANOVA analízissel akarjuk statisztikailag igazolni az egyes faktorok szignifikáns voltát, akkor nem a szórást, hanem a z értéket kell alkalmazni.
Összefoglalva az eddigieket, azt látjuk, hogy az A faktor hatással van a szórásra, vagyis az ismétlőképességre, de nincs hatással a kísérletek abszolút értékére. Viszont a B és a C faktor a kísérletek abszolút értékére van hatással, miközben nem befolyásolja a cellán belüli szórást.
Kezünkben van tehát annak a kulcsa, hogy a fenti faktorok megválasztásával csökkentsük a cellán belüli szórást (anélkül, hogy rontanánk az átlagot), illetve javítsuk az átlagot anélkül, hogy rontanánk a szórást.
Vagyis lehetőségünk van javítani a rendszerünk minden fontos jellemzőjét.
4.8. Három- és négyszintű kísérleti tervek
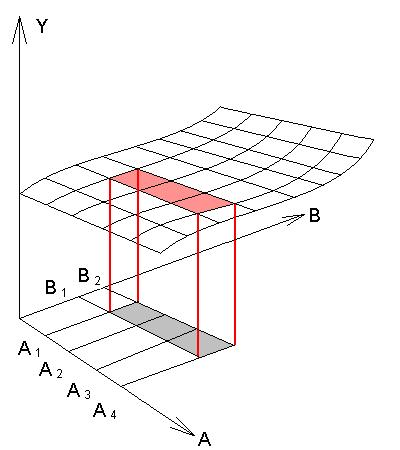
Eddig csak kétszintű Taguchi kísérletekről van szó. Lehetőség van azonban három- és négyszintű faktorokkal is dolgozni. Ekkor az ortogonális táblázat egyik, vagy több oszlopában a faktorok szintjét 3 vagy 4 értéken váltogatjuk. A szinteknek természetesen nagyság szerint kell követni egymást. Az eredmény pedig az adott faktor hatását a faktor 3 vagy 4 szintjén mutatja meg, tehát olyan, mintha a többdimenziós eredményfelületen az adott faktor tengelye irányában több lépést tettünk volna meg. Az adott faktor irányában tehát az eredményfelületnek egy síkmetszetét kapjuk meg, és az eredmény változását függvényszerűen ábrázolhatjuk (4.4. ábra)
4.9. Taguchi „Szakácskönyve”
4.9.1. Jelölések
A következőkben bemutatjuk a 7 alapvető kísérleti tervet Taguchi szakácskönyvéből. A tervekhez megadjuk az ortogonális táblázatot, a lineáris gráfokat és esetenként a kölcsönhatás táblázatokat (háromszög táblázatokat) is.
A kísérleti tervek jelölése a következő:
La(bc)a a kísérletek száma
ba faktor-szintek száma
ca vizsgálható hatások („dolgok”) száma
Például:
L9(34) egy 9 kísérletből álló, négy 3 szintű faktor hatásának vizsgálatára kidolgozott kísérletsorozat tervét jelenti.
Vannak olyan kísérleti tervek is, amelyben kétszintű és többszintű faktorok is vannak (kevert kísérleti tervek). Ezek jelölése például:
L18(21 x 37)Ez egy kétszintű és hét háromszintű, összesen 18 kísérletből álló kísérletsorozatot jelent.
A továbbiakban ismertetjük Taguchi „receptjeit” az ortogonális táblázattal, a kölcsönhatások
háromszög táblázatával és a lineáris gráfokkal.
4.9.2. L4 (23) kísérleti terv
XVI.Táblázat
L4 (23) kísérleti terv ortogonális táblázata
|
Col. No. |
1 |
2 |
3 |
|
1 |
1 |
1 |
1 |
|
2 |
1 |
2 |
2 |
|
3 |
2 |
1 |
2 |
|
4 |
2 |
2 |
1 |
|
Group 1 |
Group 2 |
||
Az L4(23) terv lineáris gráfja a 4.5. ábrán látható.
4.9.3. L8 (27) kísérleti terv
XVII.Táblázat
L8 (27) kísérleti terv Ortogonális táblázata
|
Col. No. |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
2 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
|
3 |
1 |
2 |
2 |
1 |
1 |
2 |
2 |
|
4 |
1 |
2 |
2 |
2 |
2 |
1 |
1 |
|
5 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
|
6 |
2 |
1 |
2 |
2 |
1 |
2 |
1 |
|
7 |
2 |
2 |
1 |
1 |
2 |
2 |
1 |
|
8 |
2 |
2 |
1 |
2 |
1 |
1 |
2 |
|
Group 1 |
Group 2 |
Group 3 |
|||||
XVIII.táblázat
L8 (27) kísérleti terv Kölcsönhatás táblázata
|
Col. No. |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
(1) |
3 |
2 |
5 |
4 |
7 |
6 |
|
|
(2) |
1 |
6 |
7 |
4 |
5 |
||
|
(3) |
7 |
5 |
5 |
4 |
|||
|
(4) |
1 |
2 |
3 |
||||
|
(5) |
3 |
2 |
|||||
|
(6) |
1 |
||||||
|
(7) |
A lineáris gráfok a 4.6. ábrán láthatók:
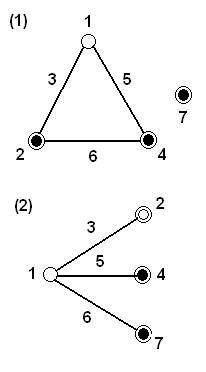
4.9.4. L16 (215) kísérleti terv
Az L16 (215) kísérleti terv sokféle kísérleti sorrendben megtervezhető attól függően, hogy hány hatást és hány kölcsönhatást akarunk megvizsgálni a 16 kísérletből álló kísérletsorozat során.
A lehetőségek sokaságát mutatják a 4.7., 4.8., 4.9., 4.10. és 4.11.ábrán bemutatott lineáris gráfok. Az ortogonális táblázat minden esetben azonos (XIX.táblázat), csak a hatásokat és kölcsönhatásokat más-más oszlopba helyezzük el attól függően, hogy melyik főhatást milyen komplikált beállítani.
XIX. táblázat
L16 (215) kísérleti terv Ortogonális táblázata
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
2 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
|
3 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
|
4 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
1 |
1 |
1 |
1 |
|
5 |
1 |
2 |
2 |
1 |
1 |
2 |
2 |
1 |
1 |
2 |
2 |
1 |
1 |
2 |
2 |
|
6 |
1 |
2 |
2 |
1 |
1 |
2 |
2 |
2 |
2 |
1 |
1 |
2 |
2 |
1 |
1 |
|
7 |
1 |
2 |
2 |
2 |
2 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
1 |
1 |
|
8 |
1 |
2 |
2 |
2 |
2 |
1 |
1 |
2 |
2 |
1 |
1 |
1 |
1 |
2 |
2 |
|
9 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
|
10 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
1 |
|
11 |
2 |
1 |
2 |
2 |
1 |
2 |
1 |
1 |
2 |
1 |
2 |
2 |
1 |
2 |
1 |
|
12 |
2 |
1 |
2 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
1 |
1 |
2 |
1 |
2 |
|
13 |
2 |
2 |
1 |
1 |
2 |
2 |
1 |
1 |
2 |
2 |
1 |
1 |
2 |
2 |
1 |
|
14 |
2 |
2 |
1 |
1 |
2 |
2 |
1 |
2 |
1 |
1 |
2 |
2 |
1 |
1 |
2 |
|
15 |
2 |
2 |
1 |
2 |
1 |
1 |
2 |
1 |
2 |
2 |
1 |
2 |
1 |
1 |
2 |
|
16 |
2 |
2 |
1 |
2 |
1 |
1 |
2 |
2 |
1 |
1 |
2 |
1 |
2 |
2 |
1 |
|
Group 1 |
Group 2 |
Group 3 |
Group 4 |
||||||||||||
XX. táblázat
L16 (215) kísérleti terv Kölcsönhatás táblázata
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
(1) |
3 |
2 |
5 |
4 |
7 |
6 |
9 |
8 |
11 |
10 |
13 |
12 |
15 |
14 |
|
(2) |
1 |
6 |
7 |
4 |
5 |
10 |
11 |
8 |
9 |
14 |
15 |
12 |
13 |
|
|
(3) |
7 |
6 |
5 |
4 |
11 |
10 |
9 |
8 |
15 |
14 |
13 |
12 |
||
|
(4) |
1 |
2 |
3 |
12 |
13 |
14 |
15 |
8 |
9 |
10 |
11 |
|||
|
(5) |
3 |
2 |
13 |
12 |
15 |
14 |
9 |
8 |
11 |
10 |
||||
|
(6) |
1 |
14 |
15 |
12 |
13 |
10 |
11 |
8 |
9 |
|||||
|
(7) |
15 |
14 |
13 |
12 |
11 |
10 |
9 |
8 |
||||||
|
(8) |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|||||||
|
(9) |
3 |
2 |
5 |
4 |
7 |
6 |
||||||||
|
(10) |
1 |
6 |
7 |
4 |
5 |
|||||||||
|
(11) |
7 |
6 |
5 |
4 |
||||||||||
|
(12) |
1 |
2 |
3 |
|||||||||||
|
(13) |
3 |
2 |
||||||||||||
|
(14) |
1 |
A lineáris gráfok 5 hatás és 10 kölcsönhatás vizsgálatára a 4.7. ábrán láthatók:
Tegyük fel, hogy most csak 5 hatásra és azok kétszeres kölcsönhatásaira (összesen 10 kölcsönhatás) vagyunk kíváncsiak. Ha nem akarjuk vizsgálni az összes kölcsönhatást, a kísérlet fölösleges oszlopait nem használjuk fel, de a teljes 16 kísérletet el kell végezni. Fel is használhatjuk a felmaradt 5 oszlopot a kísérlettel kapcsolatos egyéb hatások egymástól független vizsgálatára; ekkor ezeknek a vizsgált faktoroknak a szintjeit variáljuk a kísérleti tervnek megfelelően.
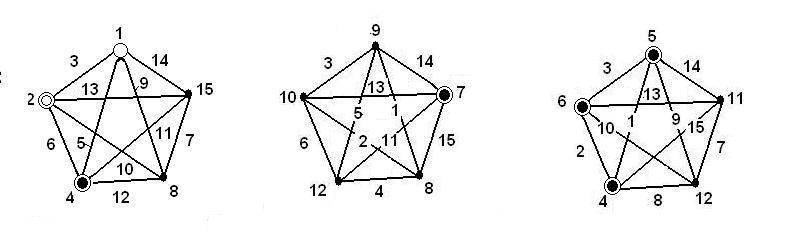
A lineáris gráfok 7 hatás és 8 kölcsönhatás vizsgálatára a 4.8. ábrán láthatók:
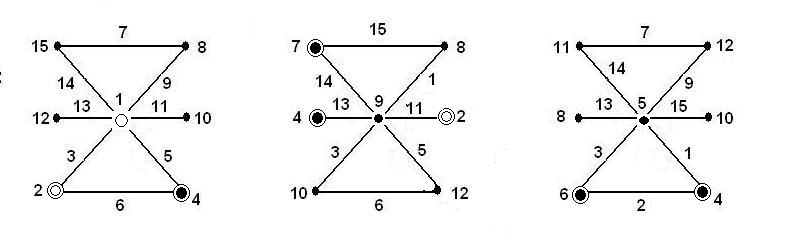
A lineáris gráfok 5 hatás és kölcsönhatásainak, továbbá másik 3 hatás és azok kölcsönhatásainak vizsgálatára a 4.9. ábrán láthatók:
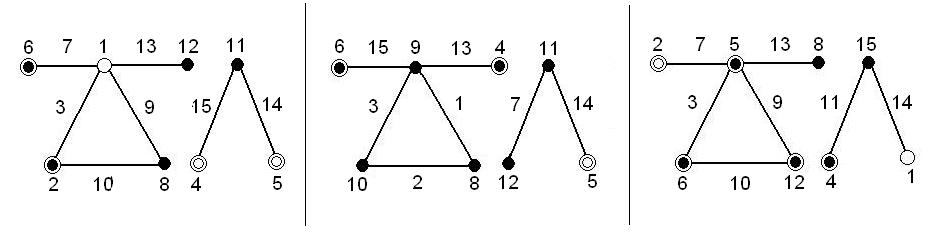
A lineáris gráfok 8 hatás és 7 kölcsönhatás vizsgálatára a 4.10. ábrán láthatók:
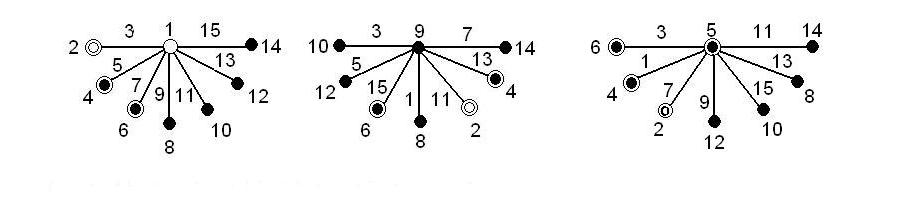
A lineáris gráfok 10 hatás és 5 kölcsönhatás vizsgálatára a 4.11. ábrán láthatók:
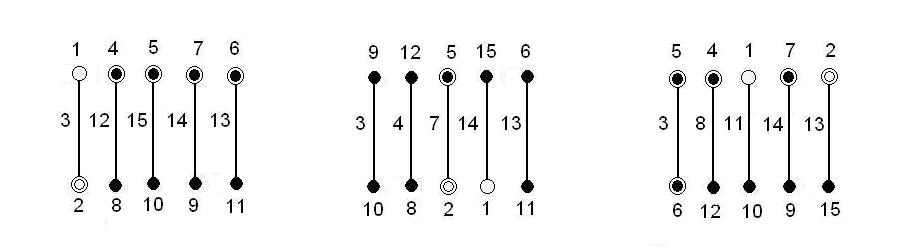
4.9.5. L12(211) kísérleti terv
XXI. táblázat
L12(211) kísérleti terv Ortogonális táblázata
|
Col. No. |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
||||
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
||||
|
2 |
1 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
2 |
2 |
||||
|
3 |
1 |
1 |
2 |
2 |
2 |
1 |
1 |
1 |
2 |
2 |
2 |
||||
|
4 |
1 |
2 |
1 |
2 |
2 |
1 |
2 |
2 |
1 |
1 |
2 |
||||
|
5 |
1 |
2 |
2 |
1 |
2 |
2 |
1 |
2 |
1 |
2 |
1 |
||||
|
6 |
1 |
2 |
2 |
2 |
1 |
2 |
2 |
1 |
2 |
1 |
1 |
||||
|
7 |
2 |
1 |
2 |
2 |
1 |
1 |
2 |
2 |
1 |
2 |
1 |
||||
|
8 |
2 |
1 |
2 |
1 |
2 |
2 |
2 |
1 |
1 |
1 |
2 |
||||
|
9 |
2 |
1 |
1 |
2 |
2 |
2 |
1 |
2 |
2 |
1 |
1 |
||||
|
10 |
2 |
2 |
2 |
1 |
1 |
1 |
1 |
2 |
2 |
1 |
2 |
||||
|
11 |
2 |
2 |
1 |
2 |
1 |
2 |
1 |
1 |
1 |
2 |
2 |
||||
|
12 |
2 |
2 |
1 |
1 |
2 |
1 |
2 |
1 |
2 |
2 |
1 |
||||
|
Group 1 |
Group 2 |
||||||||||||||
Megjegyzés:
Ezt a tervet „szűrő terv”-nek nevezik, mert akkor célszerű alkalmazni, ha sok hatás van, és azt szeretnénk tudni, melyik szignifikáns, melyik nem, miközben a kölcsönhatásokkal még nem kívánunk foglalkozni. Két-két oszlop kölcsönhatása ugyanis az L12(211) kísérleti tervnél konfundálódik a többi kilenc oszlophatással. Csak szekvenciál analizissel lehet felderíteni a kölcsönhatásokat. Ezért ez a kísérleti terv nem alkalmazható akkor, ha kölcsönhatásokat is akarunk vizsgálni.
4.9.6. L9 (34) kísérleti terv
XXII. táblázat
L9 (34) kísérleti terv Ortogonális táblázata
|
1 2 3 4 |
|
|
1 2 3 4 5 6 7 8 9 |
1 1 1 1 1 2 2 2 2 3 3 3 2 1 2 3 2 2 3 1 2 3 1 2 3 1 3 2 3 2 1 3 3 3 2 1 |
A lineáris gráf az 1 és 2 főhatás és kölcsönhatás között a 4.12. ábrán látható:

Megjegyzés:
A kölcsönhatásokat elhelyezhetjük anélkül, hogy oszlopokat (fő-hatásokat) kellene feláldozni, ha az 1 és 2 oszlop kétszintű tervét használjuk fel. Viszont így a háromszintű oszlopok kölcsönhatásai bizonyos mértékig keveredni (konfundálódni) fognak a többi háromszintű oszlop hatásaival.
4.9.7. L18(21 x 37) kísérleti terv
XXIII.táblázat
L18(21 x 37) kísérleti terv Ortogonális táblázata
|
C ol. No. |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|||||||
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|||||||
|
2 |
1 |
1 |
2 |
2 |
2 |
2 |
2 |
2 |
|||||||
|
3 |
1 |
1 |
3 |
3 |
3 |
3 |
3 |
3 |
|||||||
|
4 |
1 |
2 |
1 |
1 |
2 |
2 |
3 |
3 |
|||||||
|
5 |
1 |
2 |
2 |
2 |
3 |
3 |
1 |
1 |
|||||||
|
6 |
1 |
2 |
3 |
3 |
1 |
1 |
2 |
2 |
|||||||
|
7 |
1 |
3 |
1 |
2 |
1 |
3 |
2 |
3 |
|||||||
|
8 |
1 |
3 |
2 |
3 |
2 |
1 |
3 |
1 |
|||||||
|
9 |
1 |
3 |
3 |
1 |
3 |
2 |
1 |
2 |
|||||||
|
10 |
2 |
1 |
1 |
3 |
3 |
2 |
2 |
1 |
|||||||
|
11 |
2 |
1 |
2 |
1 |
1 |
3 |
3 |
2 |
|||||||
|
12 |
2 |
1 |
3 |
2 |
2 |
1 |
1 |
3 |
|||||||
|
13 |
2 |
2 |
1 |
2 |
3 |
1 |
3 |
2 |
|||||||
|
14 |
2 |
2 |
2 |
3 |
1 |
2 |
1 |
3 |
|||||||
|
15 |
2 |
2 |
3 |
1 |
2 |
3 |
2 |
1 |
|||||||
|
16 |
2 |
3 |
1 |
3 |
2 |
3 |
1 |
2 |
|||||||
|
17 |
2 |
3 |
2 |
1 |
3 |
1 |
2 |
3 |
|||||||
|
18 |
2 |
3 |
3 |
2 |
1 |
2 |
3 |
1 |
|||||||
|
Group 1 |
Group 2 |
Group 3 |
|||||||||||||
A lineáris gráf a 4.13. ábrán látható:

Megjegyzés:
A kölcsönhatásokat most is elhelyezhetjük anélkül, hogy oszlopokat (fő-hatásokat) kellene feláldozni, ha az 1 és 2 oszlop kétszintű tervét használjuk fel. Viszont így a háromszintű oszlopok kölcsönhatásai bizonyos mértékig itt is keveredni (konfundálódni) fognak a többi háromszintű oszlop hatásaival.
|
C ol. No. |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|||||||
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|||||||
|
2 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
|||||||
|
3 |
1 |
1 |
1 |
1 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
|||||||
|
4 |
1 |
2 |
2 |
2 |
1 |
1 |
1 |
2 |
2 |
2 |
3 |
3 |
3 |
|||||||
|
5 |
1 |
2 |
2 |
2 |
2 |
2 |
2 |
3 |
3 |
3 |
1 |
1 |
1 |
|||||||
|
6 |
1 |
2 |
2 |
2 |
3 |
3 |
3 |
1 |
1 |
1 |
2 |
2 |
2 |
|||||||
|
7 |
1 |
3 |
3 |
3 |
1 |
1 |
1 |
3 |
3 |
3 |
2 |
2 |
2 |
|||||||
|
8 |
1 |
3 |
3 |
3 |
2 |
2 |
2 |
1 |
1 |
1 |
3 |
3 |
3 |
|||||||
|
9 |
1 |
3 |
3 |
3 |
3 |
3 |
3 |
2 |
2 |
2 |
1 |
1 |
1 |
|||||||
|
10 |
2 |
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
|||||||
|
11 |
2 |
1 |
2 |
3 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
1 |
|||||||
|
12 |
2 |
1 |
2 |
3 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
|||||||
|
13 |
2 |
2 |
3 |
1 |
1 |
2 |
3 |
2 |
3 |
1 |
3 |
1 |
2 |
|||||||
|
14 |
2 |
2 |
3 |
1 |
2 |
3 |
1 |
3 |
1 |
2 |
1 |
2 |
3 |
|||||||
|
15 |
2 |
2 |
3 |
1 |
3 |
1 |
2 |
1 |
2 |
3 |
2 |
3 |
1 |
|||||||
|
16 |
2 |
3 |
1 |
2 |
1 |
2 |
3 |
3 |
1 |
2 |
2 |
3 |
1 |
|||||||
|
17 |
2 |
3 |
1 |
2 |
2 |
3 |
1 |
1 |
2 |
3 |
3 |
1 |
2 |
|||||||
|
18 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
2 |
3 |
1 |
1 |
2 |
3 |
|||||||
|
19 |
3 |
1 |
3 |
2 |
1 |
3 |
2 |
1 |
3 |
2 |
1 |
3 |
2 |
|||||||
|
20 |
3 |
1 |
3 |
2 |
2 |
1 |
3 |
2 |
1 |
3 |
2 |
1 |
3 |
|||||||
|
21 |
3 |
1 |
3 |
2 |
3 |
2 |
1 |
3 |
2 |
1 |
3 |
2 |
1 |
|||||||
|
22 |
3 |
2 |
1 |
3 |
1 |
3 |
2 |
2 |
1 |
3 |
3 |
2 |
1 |
|||||||
|
23 |
3 |
2 |
1 |
3 |
2 |
1 |
3 |
3 |
2 |
1 |
1 |
3 |
2 |
|||||||
|
24 |
3 |
2 |
1 |
3 |
3 |
2 |
1 |
1 |
3 |
2 |
2 |
1 |
3 |
|||||||
|
25 |
3 |
3 |
2 |
1 |
1 |
3 |
2 |
3 |
2 |
1 |
2 |
1 |
3 |
|||||||
|
26 |
3 |
3 |
2 |
1 |
2 |
1 |
3 |
1 |
3 |
2 |
3 |
2 |
1 |
|||||||
|
27 |
3 |
3 |
2 |
1 |
3 |
2 |
1 |
2 |
1 |
3 |
1 |
3 |
2 |
|||||||
|
Group 1 |
Group 2 |
Group 3 |
||||||||||||||||||
4.9.8. L27(313) kísérleti terv
XXIV. táblázat
L27(313) kísérleti terv Ortogonális táblázata
XXV. táblázat
L27(313) kísérleti terv kölcsönhatás táblázata
|
Col. No. |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
|
(1) |
3 |
2 |
2 |
6 |
5 |
5 |
9 |
8 |
8 |
12 |
11 |
11 |
||
|
4 |
4 |
3 |
7 |
7 |
6 |
10 |
10 |
9 |
13 |
13 |
12 |
|||
|
(2) |
1 |
1 |
8 |
9 |
10 |
5 |
6 |
7 |
5 |
6 |
7 |
|||
|
4 |
3 |
11 |
12 |
13 |
11 |
12 |
13 |
8 |
9 |
10 |
||||
|
(3) |
1 |
9 |
10 |
8 |
7 |
5 |
6 |
6 |
7 |
5 |
||||
|
2 |
13 |
11 |
12 |
12 |
13 |
11 |
10 |
8 |
9 |
|||||
|
(4) |
10 |
8 |
9 |
6 |
7 |
5 |
7 |
5 |
6 |
|||||
|
12 |
13 |
11 |
13 |
11 |
12 |
9 |
10 |
8 |
||||||
|
(5) |
1 |
1 |
2 |
3 |
4 |
2 |
4 |
3 |
||||||
|
7 |
6 |
11 |
13 |
12 |
8 |
10 |
9 |
|||||||
|
(6) |
1 |
4 |
2 |
3 |
3 |
2 |
4 |
|||||||
|
5 |
13 |
12 |
11 |
10 |
9 |
8 |
||||||||
|
(7) |
3 |
4 |
2 |
4 |
3 |
2 |
||||||||
|
12 |
11 |
13 |
9 |
8 |
10 |
|||||||||
|
(8) |
1 |
1 |
2 |
3 |
4 |
|||||||||
|
10 |
9 |
5 |
7 |
6 |
||||||||||
|
(9) |
1 |
4 |
2 |
3 |
||||||||||
|
8 |
7 |
6 |
5 |
|||||||||||
|
(10) |
3 |
4 |
2 |
|||||||||||
|
6 |
5 |
7 |
||||||||||||
|
(11) |
1 |
1 |
||||||||||||
|
13 |
12 |
|||||||||||||
|
(12) |
1 |
|||||||||||||
|
11 |
||||||||||||||
A lineáris gráfok a 4.14. ábrán láthatók:
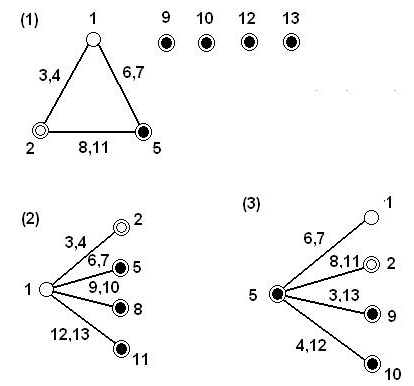
4.10. A fő-hatások oszlopainak megválasztása
A fenti kísérleti tervekben csoportosítva látjuk az oszlopokat (Group 1, Group 2, Group +).
A Grup1 oszlopaiba helyezzük azokat a faktorokat, amelyek szintjeit bonyolult váltogatni, mert a kísérletek során ebben az oszlopban csak egyszer kell szintet változtatni. A Group 2 oszlopaiba kerülhetnek a könnyebben változtatható, és a későbbiekben a Group 3-ba a legkönnyebben változtatható faktorok.
4.11. Több lépésben végrehajtott kísérleti terv
Előfordulhat, hogy a kísérleteket nem akarjuk gyors egymásutánban lebonyolítani, hanem kisebb sorozatokba (blokkokban fogjuk elvégezni. Nem oszthatjuk ötlet szerűen blokkokra a kísérleti tervet.
Tegyük fel, hogy egy L16 kísérleti tervet két napon akarunk végrehajtani, nyolc kísérletet az egyik napon és nyolcat a másikon. Ha az L16 ortogonális mátrix első nyolc kísérletét végezzük el az első napon és a másodi nyolcat a második napon, akkor nem lehetünk biztosak abban, hogy az 1. faktor kimutatható hatása valóban az 1. faktor hatása, vagy a két nap különböző körülményeiből ered. Ezért az 1. oszlop nem használható egyik faktor hatásának vizsgálatára sem, hanem ez lesz a „felosztási változó” (blocking variable”).
Ha az L16 kísérleti tervet 4 alkalommal akarjuk végrehajtani, akkor a 2. és 3. oszlopot is fel kell áldozni, mert ezekben a négy blokkon belül a faktorok szintjei azonosak.
4.12. Mit tegyünk, ha nincs előzetes információnk arról, hogy vannak-e kölcsönhatások az egyes hatások között?
Taguchi a következőket tanácsolja:
-
Ha csak 2 faktorunk van, alkalmazzuk az L4 tervet, és helyezzük a főhatásokat az 1. és a 2. oszlopba.
-
Ha 3 faktorunk van, alkalmazzuk az L8 tervet, és helyezzük a főhatásokat az 1. , a 2. és a 4. oszlopba.
-
Ha 4 vagy 5 faktorunk van, alkalmazzuk az L16 tervet, és helyezzük a főhatásokat az 1. , a 2., a 4. és a 8. oszlopba, végül 5 faktor esetén a 15. oszlopba.
4.13. Szűrő kísérleti tervek
Ezek a kísérleti tervek arra szolgálnak, hogy kiszűrjük velük a nem szignifikáns faktorokat, és a továbbiakban részletesen vizsgálhassuk a szignifikánsakat.
Tegyük fel, hogy egy L16 kísérleti tervben 15 faktor közül akarjuk kiszűrni a nem szignifikánsakat. Ezért mind a 15 oszlopban elhelyezünk egy-egy faktort (ezt akísérleti tervet „telített” kísérleti tervnek nevezik). Az egyes oszlopok viszont továbbra is részben fő-hatásokra, részben kölcsönhatásokra utalnak, ezért lehet, hogy némelyik a 15 faktor közül a kölcsönhatás miatt tűnik szignifikánsnak, vagy éppen nem szignifikánsnak.
Az L12 kísérleti terv viszont alkalmas a faktorok szűrő vizsgálatára, mert ez éppen a kölcsönhatások vizsgálatára nem alkalmas.
Ha igen sok lehetséges faktorunk van (ez a gyakorlati feladatoknál igen gyakori helyzet), akkor inkább végezzük a szűrést több részletben. Ne akarjuk az összes problémát egy hatalmas kísérleti tervben megoldani!
4.14. A Taguchi „szakácskönyv” L8 és L16 kísérleti terveinek átalakítása kétszintűről négyszintűvé
Megfigyelhettük, hogy a 7 alapvető kísérleti terv kétszintű és háromszintű kísérleti terveket tartalmaz, de egyikben sincsenek négyszintű faktorok. Pedig a gyakorlatban ilyen faktorok gyakran előfordulnak, pl. akkor, ha 4 különböző beszállító termékét alkalmazzuk a kísérletek során. A továbbiakban bemutatjuk, hogyan lehet egy L8 vagy egy L16 kétszintű kísérleti tervet úgy átalakítani, hogy alkalmas legyen egy vagy több négyszintű faktor vizsgálatára.
Az átalakítás alapgondolata az, hogy a kiinduló ortogonális táblázatból kiválasztunk három olyan oszlopot, amelyek egymással összefüggenek, és ezekből hozunk létre egy új négyszintű oszlopot.
Alakítsunk át például egy L8 ortogonális mátrixot úgy, hogy legyen egy négyszintű oszlopa!
A kiindulást képező L8 ortogonális táblázat (XXVI. táblázat):
XXVI. táblázat
L8 ortogonális táblázat
|
Col. No. |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
2 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
|
3 |
1 |
2 |
2 |
1 |
1 |
2 |
2 |
|
4 |
1 |
2 |
2 |
2 |
2 |
1 |
1 |
|
5 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
|
6 |
2 |
1 |
2 |
2 |
1 |
2 |
1 |
|
7 |
2 |
2 |
1 |
1 |
2 |
2 |
1 |
|
8 |
2 |
2 |
1 |
2 |
1 |
1 |
2 |
|
Group 1 |
Group 2 |
Group 3 |
|||||
Válasszuk ki a táblázat 1. 4. és 5. oszlopát! Képezzük ebből az A faktornak nevezett négyszintű faktor oszlopát oly módon, hogy minden azonos szint-mintázatot nevezzünk el 1, 2, 3 vagy 4-nek. Ezek lesznek az új faktorszintek az A oszlopban. (XXVII. táblázat).
XXVII. táblázat
Kétszintű L8 ortogonális táblázat négyszintűvé átalakításának első lépése
|
Run No. |
Az L8 tábla oszlopai |
Az A faktor szintjei |
||||
|
1 |
4 |
5 |
||||
|
1 |
1 |
1 |
1 |
1 |
||
|
2 |
1 |
2 |
2 |
2 |
||
|
3 |
1 |
1 |
1 |
1 |
||
|
4 |
1 |
2 |
2 |
2 |
||
|
5 |
2 |
1 |
2 |
3 |
||
|
6 |
2 |
2 |
1 |
4 |
||
|
7 |
2 |
1 |
2 |
3 |
||
|
8 |
2 |
2 |
1 |
4 |
||
Miután kialakítottuk az új oszlopot, az új ortogonális táblázatban már nem szerepelhet a régi 1., 4. és 5. oszlop, mert ezeket már felhasználtuk az A oszlop létrehozásához. Az új ortogonális táblázat a XXVIII.táblázatban látható.
XXVIII. táblázat
kétszintű L8 ortogonális táblázat ból kialakított négyszintű
ortogonális táblázat
|
Run |
A |
2 |
3 |
6 |
7 |
|
1 |
1 |
1 |
1 |
1 |
1 |
|
2 |
2 |
1 |
1 |
2 |
2 |
|
3 |
1 |
2 |
2 |
2 |
2 |
|
4 |
2 |
2 |
2 |
1 |
1 |
|
5 |
3 |
1 |
2 |
1 |
2 |
|
6 |
4 |
1 |
2 |
2 |
1 |
|
7 |
3 |
2 |
1 |
2 |
1 |
|
8 |
4 |
2 |
1 |
1 |
2 |
Egy L16 ortogonális táblázatátalakítható úgy is, hogy 4 négyszintű faktor vizsgálatát tegye lehetővé. A kiinduló L16 ortogonális táblázat a XXIX. táblázatban látható. A táblázat 1., 2. és 3. oszlopából alakítsunk ki egy A négyszintű oszlopot, a 4., 12. és 8. oszlopból egy B négyszintű oszlopot, az 5., 15. és 10. oszlopból egy C négyszintű oszlopot, és végül a 7., 14. és 9. oszlopból egy D négyszintű oszlopot (XXIX. táblázatban Group1,2, 3 és 4)!
|
C ol. N o. |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
||||||||||||||||
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
||||||||||||||||
|
2 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
||||||||||||||||
|
3 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
||||||||||||||||
|
4 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
1 |
1 |
1 |
1 |
||||||||||||||||
|
5 |
1 |
2 |
2 |
1 |
1 |
2 |
2 |
1 |
1 |
2 |
2 |
1 |
1 |
2 |
2 |
||||||||||||||||
|
6 |
1 |
2 |
2 |
1 |
1 |
2 |
2 |
2 |
2 |
1 |
1 |
2 |
2 |
1 |
1 |
||||||||||||||||
|
7 |
1 |
2 |
2 |
2 |
2 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
1 |
1 |
||||||||||||||||
|
8 |
1 |
2 |
2 |
2 |
2 |
1 |
1 |
2 |
2 |
1 |
1 |
1 |
1 |
2 |
2 |
||||||||||||||||
|
9 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
||||||||||||||||
|
10 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
1 |
||||||||||||||||
|
11 |
2 |
1 |
2 |
2 |
1 |
2 |
1 |
1 |
2 |
1 |
2 |
2 |
1 |
2 |
1 |
||||||||||||||||
|
12 |
2 |
1 |
2 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
1 |
1 |
2 |
1 |
2 |
||||||||||||||||
|
13 |
2 |
2 |
1 |
1 |
2 |
2 |
1 |
1 |
2 |
2 |
1 |
1 |
2 |
2 |
1 |
||||||||||||||||
|
14 |
2 |
2 |
1 |
1 |
2 |
2 |
1 |
2 |
1 |
1 |
2 |
2 |
1 |
1 |
2 |
||||||||||||||||
|
15 |
2 |
2 |
1 |
2 |
1 |
1 |
2 |
1 |
2 |
2 |
1 |
2 |
1 |
1 |
2 |
||||||||||||||||
|
16 |
2 |
2 |
1 |
2 |
1 |
1 |
2 |
2 |
1 |
1 |
2 |
1 |
2 |
2 |
1 |
||||||||||||||||
|
Group 1 |
Group 2 |
Group 3 |
Group 4 |
||||||||||||||||||||||||||||
XXIX. Táblázat
L16 ortogonális táblázat átalakítása 4 négyszintű faktor vizsgálatára
Az új négyszintű ortogonális táblázat a XXX. táblázatban látható.
Az ilyen négyszintű kísérleti tervvel megvizsgálhatjuk például egy gyártási folyamat eredményességét 4 gépkezelő, 4 különböző gép, 4 anyagféleség és 4 műveleti sorrend alkalmazása mellett. A b együtthatók azt fogják megmutatni, hogy a 4 tényező közül melyiknek van hatása a gyártási folyamat eredményességére. A faktorok 4-4 „szintjét” is megvizsgálhatjuk soronként, hogy melyiknél lettek az Y kísérleti eredmények a legjobbak.
XXX. táblázat
ortogonális táblázat négy négyszintű faktor vizsgálatára
|
Run |
A |
B |
C |
D |
6 |
11 |
13 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
2 |
1 |
2 |
2 |
2 |
1 |
2 |
2 |
|
3 |
1 |
3 |
3 |
3 |
2 |
1 |
2 |
|
4 |
1 |
4 |
4 |
4 |
2 |
2 |
1 |
|
5 |
2 |
1 |
2 |
3 |
2 |
2 |
1 |
|
6 |
2 |
2 |
1 |
4 |
2 |
1 |
2 |
|
7 |
2 |
3 |
4 |
1 |
1 |
2 |
2 |
|
8 |
2 |
4 |
3 |
2 |
1 |
1 |
1 |
|
9 |
3 |
1 |
3 |
4 |
1 |
2 |
2 |
|
10 |
3 |
2 |
4 |
3 |
1 |
1 |
1 |
|
11 |
3 |
3 |
1 |
2 |
2 |
2 |
1 |
|
12 |
3 |
4 |
2 |
1 |
2 |
1 |
2 |
|
13 |
4 |
1 |
4 |
2 |
2 |
1 |
2 |
|
14 |
4 |
2 |
3 |
1 |
2 |
2 |
1 |
|
15 |
4 |
3 |
2 |
4 |
1 |
1 |
1 |
|
16 |
4 |
4 |
1 |
3 |
1 |
2 |
2 |
4.14.1. Egyszerűsítések
Ha több kétszintű faktort akarunk vizsgálni, mint amennyit egy L8 kísérleti terv lehetővé tesz, de kevesebbet, mint egy L16, akkor használhatunk egy L16 kísérleti tervet, amelynek egyes oszlopait nem használjuk fel. Célszerűen ne fő-hatás oszlopot hagyjunk ki a tervezésnél. Előzetes információk alapján a legfontosabbnak ítélt faktorok kerüljenek a fő-hatás oszlopokba. és a kevésbé fontosak a kereszthatás oszlopokba. Ugyanezt tehetjük háromszintű és négyszintű kísérleti terveknél is.
Ha több fontosnak ítélt faktor hatását akarjuk vizsgálni, mint amennyi fő-hatás az ortogonális táblázatban van, akkor kereszt-hatás oszlopba is tehetünk fontos hatást, de előzetes információk alapján olyat, amelyről feltételezhető, hogy nincs kölcsönhatásban azzal a két fő-hatással, amelynek kölcsönhatás oszlopába kerül.