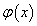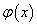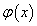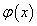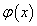5. fejezet - MATEMATIKAI STATISZTIKAI ÖSSZEFOGLALÓ
5.1. Alapfogalmak
5.1.1. A valószínűségi változó
A gyakorlatban előforduló kísérletek túlnyomó részében a kísérlet eredménye leírható egy numerikus értékkel, azaz valamilyen számmal. A kísérlet eredménye tehát egy esemény, amelyhez egy számértéket rendelünk. Ezt nevezik „elemi esemény”-nek. Mivel a kísérlet eredménye általában a kísérlet többszöri megismétlése után egy kicsit mindig más számérték lesz, a kísérlet eredményét „valószínűségi változó”-nak tekintjük.
5.1.2. Az eloszlásfüggvény és a sűrűségfüggvény
Ha a valószínűségi változókat a számegyenesen ábrázoljuk, a valószínűségeloszláshoz jutunk. A valószínűség eloszlás függvényét az alábbi módon definiálták:
F(x)=P(ξ<x)
ahol F(x)a ξ valószínűségi változó eloszlásfüggvénye
xa ξ valószínűségi változó egyik aktuális értéke a számegyenesen
P(ξ<x)annak a valószínűsége, hogy ξ kisebb mint x
A valószínűségeloszlás sűrűségfüggvénye a valószínűségeloszlás eloszlásfüggvényéből származtatható. A sűrűség értékek az eloszlásfüggvény valamilyen tetszőlegesen keskeny tartományába eső részének középértékei. Definiciója:
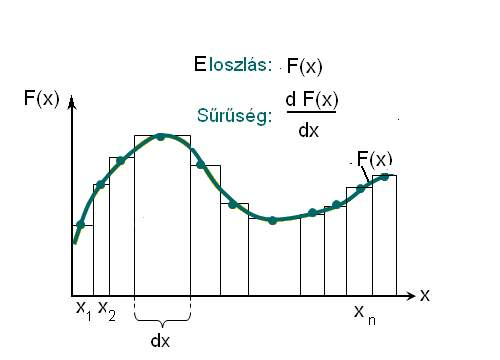
f(x)= F’(x)
A sűrűségfüggvény és az eloszlásfüggvény lehet folytonos és lehet diszkrét.
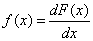
Folytonos eloszlásról beszélhetünk akkor, ha F(x) az x változó folytonos függvénye. Diszkrétnek nevezzük a ξ valószínűségi változót és annak eloszlását, ha ξ lehetséges értékei egy véges vagy végtelen x1, x2, … sorozatot alkotnak (5.1. ábra).
5.1.3. A normáleloszlás
A gyakorlati életben, a méréstechnikában és a kísérleti eredmények területén az egyik leggyakoribb és legnagyobb jelentőségű eloszlás a normális eloszlás.
Egy x valószínűségi változót normális eloszlásúnak nevezünk, ha sűrűségfüggvénye
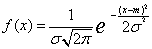
ahol m valós szám és az eloszlás várható értékét (a
sűrűségfüggvény maximumhelyét) jelenti
σpozitiv konstans és az eloszlás szórásával egyenlő
A normál eloszlás jelölése:N(m, σ)
5.1.4. A standard normál eloszlás
A sandard normál eloszlás azt a normáleloszlást jelenti, amelynek várható értéke 0, és szórása 1.
A standard normál eloszlás sűrűségfüggvénye:
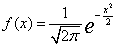
A standard normál eloszlás jelölése: N(0,1)
5.1.5. A χ2 eloszlás
n számú független, N(0,1) eloszlású valószínűségi változó négyzetösszegének eloszlását n-szabadságfokú χ2 eloszlásnak nevezzük.
Eloszlás függvénye:
χ2= ξ12 + ξ22 + ξ32 +…+ ξn2
5.1.6. A tapasztalati szórásnégyzet
A szórásnégyzet egy y változó saját középértékétől való négyzetes eltéréseinek középértéke. Jelölése s2, képlete:
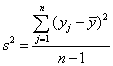
ahols2a tapasztalati szórásnégyzet
na kísérleti adatok száma
n-1a szabadságfokok száma
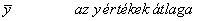
5.1.7. A szabadságfok
A szabadságfokot gyakran f betűvel szokták jelölni. Azt jelenti, hogy egy kifejezés hány független információt tartalmaz. Ha például az s2 valószínűségi változó kiszámításánál n darab adatot használtunk fel, de ezekből már kiszámítottuk az adatok átlagát és az s2 kifejezésben az átlag is szerepel, akkor az s2 csak n-1 független adatot tartalmaz, ezért f=n-1
5.1.8. A szórás
A szórás a szórásnégyzet pozitív előjelű négyzetgyöke.
5.1.9. A Steiner-formula
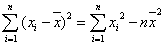
5.2. Statisztikai próbák
5.2.1. Az u-próba
Az u-próba egy statisztikai minta (statisztikai sokaság) „m” várható értékének meghatározására szolgál. Akkor használhatjuk, ha valamilyen előzetes információ alapján tudjuk, hogy a sokaság normál eloszlású, ismerjük a szórás számszerű értékét, és az m várható értékére is van már egy „m0” becslésünk. Ennek a becslésnek a megerősítésére vagy megcáfolására szolgál az u-próba
A statisztikai próba 0-hipotézise:
m=m0
A próba statisztikája („próba-statisztika”):
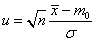
ahol x1, x2, …, xna sokaságból vett n-elemű minta,
σ a számszerűen ismert szórás,
m0az m várható érték becslése
ua próba kísérleti értéke
és az n elemű mintából számolt átlag: 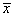
Ha helyes az m=m0 hipotézis, akkor az u valószínűségi változó standard normál eloszlású.
Ha most egy n konkrét numerikus értékből álló mintánk van, akkor ezekből u-ra egy numerikus értéket kapunk. Ezt az u-t összehasonlítjuk a standard normál eloszlás sűrűségfüggvényének táblázatából (XXXII. táblázat) vett up értékkel, és amennyiben teljesül, hogy
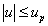
abban az esetben a 0-hipotézist elfogadjuk, azaz elfogadjuk, hogy m és m0 különbsége nem szignifikáns, nem lényeges, tehát elhanyagolható.
Az up értéket a táblázatból úgy határozzuk meg, hogy egy
0 < p <1
számhoz megkeressük azt az up-t, amelyre teljesül az alábbi reláció.
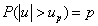
A p általában használatos értékei:
p=0,05 ; 0,01 ; 0,001
A műszaki gyakorlatban leggyakrabban a p=0,05 értéket szokták használni.
A p jelentése az, hogy ennyi a valószínűsége annak, hogy a null-hipotézis nem volt helyes. Ellenkező esetben 1-p annak a valószínűsége, hogy a null-hipotézist valóban helyes volt.
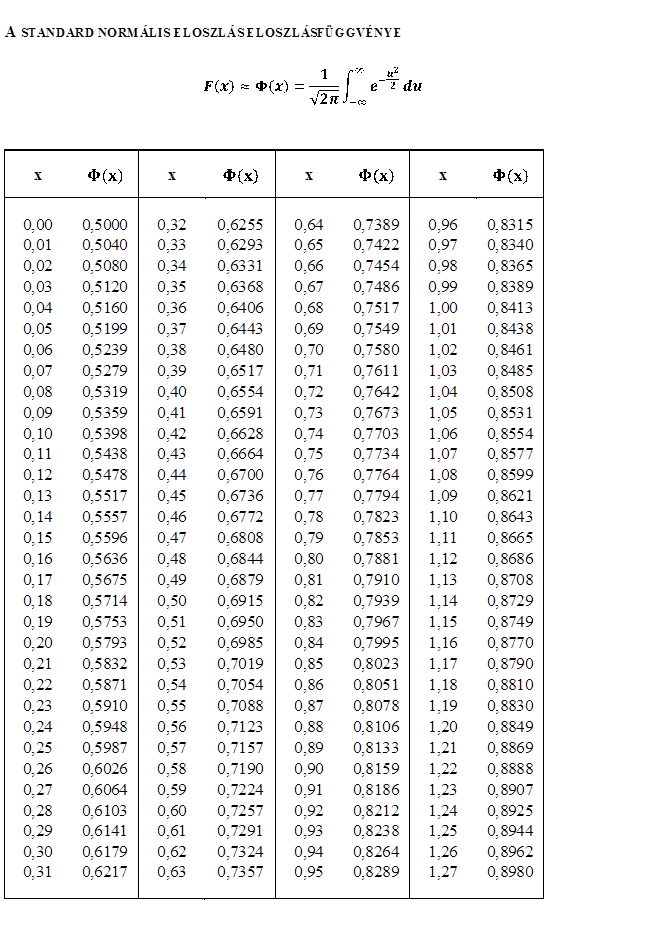
XXXI. táblázat és XXXII. táblázat
A standard normális eloszlás eloszlás- és sűrűségfüggvénye
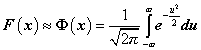
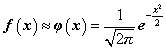
|
x |
|
x |
|
x |
|
x |
|
x |
|
|
0,00 |
0,3989 |
0,32 |
0,3790 |
0,64 |
0,3251 |
0,96 |
0,2516 |
1,28 |
0,1758 |
|
0,01 |
0,3989 |
0,33 |
0,3778 |
0,65 |
0,3230 |
0,97 |
0,2492 |
1,29 |
0,1736 |
|
0,02 |
0,3989 |
0,34 |
0,3765 |
0,66 |
0,3209 |
0,98 |
0,2468 |
1,30 |
0,1714 |
|
0,03 |
0,3988 |
0,35 |
0,3752 |
0,67 |
0,3187 |
0,99 |
0,2444 |
1,31 |
0,1691 |
|
0,04 |
0,3986 |
0,36 |
0,3739 |
0,68 |
0,3166 |
1,00 |
0,2420 |
1,32 |
0,1669 |
|
0,05 |
0,3984 |
0,37 |
0,3725 |
0,69 |
0,3144 |
1,01 |
0,2396 |
1,33 |
0,1647 |
|
0,06 |
0,3982 |
0,38 |
0,3712 |
0,70 |
0,3123 |
1,02 |
0,2371 |
1,34 |
0,1626 |
|
0,07 |
0,3980 |
0,39 |
0,3697 |
0,71 |
0,3101 |
1,03 |
0,2347 |
1,35 |
0,1604 |
|
0,08 |
0,3977 |
0,40 |
0,3683 |
0,72 |
0,3079 |
1,04 |
0,2323 |
1,36 |
0,1582 |
|
0,09 |
0,3973 |
0,41 |
0,3668 |
0,73 |
0,3056 |
1,05 |
0,2299 |
1,37 |
0,1561 |
|
0,10 |
0,3970 |
0,42 |
0,3653 |
0,74 |
0,3034 |
1,06 |
0,2275 |
1,38 |
0,1539 |
|
0,11 |
0,3965 |
0,43 |
0,3637 |
0,75 |
0,3011 |
1,07 |
0,2251 |
1,39 |
0,1518 |
|
0,12 |
0,3961 |
0,44 |
0,3621 |
0,76 |
0,2989 |
1,08 |
0,2227 |
1,40 |
0,1497 |
|
0,13 |
0,3956 |
0,45 |
0,3605 |
0,77 |
0,2966 |
1,09 |
0,2203 |
1,41 |
0,1476 |
|
0,14 |
0,3951 |
0,46 |
0,3589 |
0,78 |
0,2943 |
1,10 |
0,2179 |
1,42 |
0,1456 |
|
0,15 |
0,3945 |
0,47 |
0,3572 |
0,79 |
0,2920 |
1,11 |
0,2155 |
1,43 |
0,1435 |
|
0,16 |
0,3939 |
0,48 |
0,3555 |
0,80 |
0,2897 |
1,12 |
0,2131 |
1,44 |
0,1415 |
|
0,17 |
0,3932 |
0,49 |
0,3538 |
0,81 |
0,2874 |
1,13 |
0,2107 |
1,45 |
0,1394 |
|
0,18 |
0,3925 |
0,50 |
0,3521 |
0,82 |
0,2850 |
1,14 |
0,2083 |
1,46 |
0,1374 |
|
0,19 |
0,3918 |
0,51 |
0,3503 |
0,83 |
0,2827 |
1,15 |
0,2059 |
1,47 |
0,1354 |
|
0,20 |
0,3910 |
0,52 |
0,3485 |
0,84 |
0,2803 |
1,16 |
0,2036 |
1,48 |
0,1334 |
|
0,21 |
0,3902 |
0,53 |
0,3467 |
0,85 |
0,2780 |
1,17 |
0,2012 |
1,49 |
0,1315 |
|
0,22 |
0,3894 |
0,54 |
0,3448 |
0,86 |
0,2756 |
1,18 |
0,1989 |
1,50 |
0,1295 |
|
0,23 |
0,3885 |
0,55 |
0,3429 |
0,87 |
0,2732 |
1,19 |
0,1965 |
1,51 |
0,1276 |
|
0,24 |
0,3876 |
0,56 |
0,3410 |
0,88 |
0,2709 |
1,20 |
0,1942 |
1,52 |
0,1257 |
|
0,25 |
0,3867 |
0,57 |
0,3391 |
0,89 |
0,2685 |
1,21 |
0,1919 |
1,53 |
0,1238 |
|
0,26 |
0,3857 |
0,58 |
0,3372 |
0,90 |
0,2661 |
1,22 |
0,1895 |
1,54 |
0,1219 |
|
0,27 |
0,3847 |
0,59 |
0,3352 |
0,91 |
0,2637 |
1,23 |
0,1872 |
1,55 |
0,1200 |
|
0,28 |
0,3836 |
0,60 |
0,3332 |
0,92 |
0,2613 |
1,24 |
0,1849 |
1,56 |
0,1182 |
|
0,29 |
0,3825 |
0,61 |
0,3312 |
0,93 |
0,2589 |
1,25 |
0,1826 |
1,57 |
0,1163 |
|
0,30 |
0,3814 |
0,62 |
0,3292 |
0,94 |
0,2565 |
1,26 |
0,1804 |
1,58 |
0,1145 |
|
0,31 |
0,3802 |
0,63 |
0,3271 |
0,95 |
0,2541 |
1,27 |
0,1781 |
1,59 |
0,1127 |
5.2.2. A t-próba
A t-próba az u-próbához hasonlóan egy statisztikai minta „m” várható értékének meghatározására szolgál, ha valamilyen előzetes információ alapján tudjuk, hogy a sokaság normál eloszlású, és az m várható értékére is van már egy „m0” becslésünk, de nem ismerjük a szórás számszerű értékét. Ennek a becslésnek a megerősítésére vagy megcáfolására az u-próba alkalmazható.
A statisztikai próba 0-hipotézise:
m=m0
A próba-statisztika:
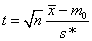
ahol x1, x2, …, xna sokaságból vett n-elemű minta,
s* az ismeretlen szórás,
m0az m várható érték becslése
ta próba kísérleti értéke
és az n elemű mintából számolt átlag:
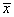
A próba lebonyolítása egyszerű. Adott p-hez (általában p=0,05) a Student-eloszlás táblázatból (XXX. táblázat) meghatározható olyan tp, amelyre teljesül az alábbi egyenlőség:
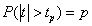
Ha most a mintából számított konkrét t érték abszolút értéke nagyobb, mint tp, az m=m0 hipotézist elvetjük. Ellenkező esetben nincs ellentmondás a minta és a hipotézis között, ezért a null-hipotézist elfogadhatjuk.
A Student-próba alkalmazható olyan esetben is, amikor egy j-szer megismételt kísérlet egyik jellemzőjének szignifikáns voltát akarjuk ellenőrizni. Ekkor alkalmazhatjuk az alábbi képletet:
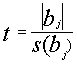
Itt 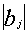 a kísérlet j-szer megismételt jellemzőjének abszolút értéke,
a kísérlet j-szer megismételt jellemzőjének abszolút értéke,
s(bj)az adatok tapasztalati szórásnégyzetének négyzetgyöke
ta t-próba számított értéke
|
Szabadsági fokok száma |
kritikus t-értékek |
Szabadsági fokok száma |
kritikus t-értékek |
Szabadsági fokok száma |
kritikust-értékek |
|
1 |
12,71 |
11 |
2,201 |
21 |
2,080 |
|
2 |
4,303 |
12 |
2,179 |
22 |
2,074 |
|
3 |
3,182 |
13 |
2,160 |
23 |
2,069 |
|
4 |
2,776 |
14 |
2,145 |
24 |
2,064 |
|
5 |
2,571 |
15 |
1,131 |
25 |
2,060 |
|
6 |
2,447 |
16 |
2,120 |
26 |
2,056 |
|
7 |
2,365 |
17 |
2,110 |
27 |
2,052 |
|
8 |
2,306 |
18 |
2,101 |
28 |
2,048 |
|
9 |
2,262 |
19 |
2,093 |
29 |
2,045 |
|
10 |
2,228 |
20 |
2,086 |
30 |
2,042 |
|
∞ |
1,960 |
XXXIII. táblázat
A Student-féle t-eloszlás táblázat
A t-próba számított értékét össze kell hasonlítani a Student táblázatból valamilyen (pl. 5%) szignifikancia szinten „f= j-1” szabadságfokkal vett tp értékkel.
Ha most a mintából számított konkrét t érték abszolút értéke nagyobb, mint tp, akkor elvetjük a null-hipotézist, vagyis azt, hogy a konkrét bj nem szignifikáns.
.
5.2.3. Az F-próba
A Fischer-féle F-próba két szórásnégyzet nagyságának összehasonlítására szolgál normál eloszlások esetén.
Az F-próba a nagyobb szórásnégyzetnek a kisebbel való osztása alapján képezett hányadosra épül. A kapott mennyiség összevethető az F-próba táblázati értékével (XXXIV. táblázat). Ha a szórásnégyzetek hányadosára kapott F érték nagyobb a megfelelő szabadsági fokokhoz és a választott szignifikanciaszinthez tarozó táblázati értéknél, ez azt jelenti, hogy a szórásnégyzetek szignifikánsan különböznek egymástól, vagyis különbségük ellentmond annak a feltevésnek (nullhipotézisnek), hogy a szórásnégyzetek megegyeznek.
A próba elvégzéséhez meg kell határozni az F számot, a két szórás hányadosát. Ezt nevezik próba-statisztikának.
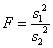
ahols12a nagyobbik tapasztalati szórásnégyzet
s22a kisebbik tapasztalati szórásnégyzet
Fa tapasztalati F érték
XXXIV. táblázat
Az F- próba táblázat
A Fisher-féle F-próba 5%-os szignifikanciaszinthez tartozó kritikus értékei
|
f2 f1 |
1 |
2 |
3 |
4 |
5 |
6 |
12 |
24 |
∞ |
|
1 |
164,4 |
199,5 |
215,7 |
224,6 |
230,2 |
234,0 |
244,9 |
249,0 |
254,3 |
|
2 |
18,5 |
19,2 |
19,2 |
19,3 |
19,3 |
19,3 |
19,4 |
19,4 |
19,5 |
|
3 |
10,1 |
9,6 |
9,3 |
9,1 |
9,0 |
8,9 |
8,7 |
8,6 |
8,5 |
|
4 |
7,7 |
6,9 |
6,6 |
6,4 |
6,3 |
6,2 |
5,9 |
5,8 |
5,6 |
|
5 |
6,6 |
5,8 |
5,4 |
5,2 |
5,1 |
5,0 |
4,7 |
4,5 |
4,4 |
|
6 |
6,0 |
5,1 |
4,8 |
4,5 |
4,4 |
4,3 |
4,0 |
3,8 |
3,7 |
|
7 |
5,5 |
4,7 |
4,4 |
4,1 |
4,0 |
3,9 |
3,6 |
3,4 |
3,2 |
|
8 |
5,3 |
4,5 |
4,1 |
3,8 |
3,7 |
3,6 |
3,3 |
3,1 |
2,9 |
|
9 |
5,1 |
4,3 |
3,9 |
3,6 |
3,5 |
3,4 |
3,1 |
2,9 |
2,7 |
|
10 |
5,0 |
4,1 |
3,7 |
3,5 |
3,3 |
3,2 |
2,9 |
2,7 |
2,5 |
|
11 |
4,8 |
4,0 |
3,6 |
3,4 |
3,2 |
3,1 |
2,8 |
2,6 |
2,4 |
|
12 |
4,8 |
3,9 |
3,5 |
3,3 |
3,1 |
3,0 |
2,7 |
2,5 |
2,3 |
|
13 |
4,7 |
3,8 |
3,4 |
3,2 |
3,0 |
2,9 |
2,6 |
2,4 |
2,2 |
|
14 |
4,6 |
3,7 |
3,3 |
3,1 |
3,0 |
2,9 |
2,5 |
2,3 |
2,1 |
|
15 |
4,5 |
3,7 |
3,3 |
3,1 |
2,9 |
2,8 |
2,5 |
2,3 |
2,1 |
|
16 |
4,5 |
3,6 |
3,2 |
3,0 |
2,9 |
2,7 |
2,4 |
2,2 |
2,0 |
|
17 |
4,5 |
3,6 |
3,2 |
3,0 |
2,8 |
2,7 |
2,4 |
2,2 |
2,0 |
|
18 |
4,4 |
3,6 |
3,2 |
2,9 |
2,8 |
2,7 |
2,3 |
2,1 |
1,9 |
|
19 |
4,4 |
3,5 |
3,1 |
2,9 |
2,7 |
2,6 |
2,3 |
2,1 |
1,9 |
|
20 |
4,4 |
3,5 |
3,1 |
2,9 |
2,7 |
2,6 |
2,3 |
2,1 |
1,8 |
|
22 |
4,3 |
3,4 |
3,1 |
2,8 |
2,7 |
2,6 |
2,2 |
2,0 |
1,8 |
|
24 |
4,3 |
3,4 |
3,0 |
2,8 |
2,6 |
2,5 |
2,2 |
2,0 |
1,7 |
|
26 |
4,2 |
3,4 |
3,0 |
2,7 |
2,6 |
2,5 |
2,2 |
2,0 |
1,7 |
|
28 |
4,2 |
3,3 |
3,0 |
2,7 |
2,6 |
2,4 |
2,1 |
1,9 |
1,7 |
|
30 |
4,2 |
3,3 |
2,9 |
2,7 |
2,5 |
2,4 |
2,1 |
1,9 |
1,6 |
|
40 |
4,1 |
3,2 |
2,9 |
2,6 |
2,5 |
2,3 |
2,0 |
1,8 |
1,5 |
|
60 |
4,0 |
3,2 |
2,8 |
2,5 |
2,4 |
2,3 |
1,9 |
1,7 |
1,4 |
|
120 |
3,9 |
3,1 |
2,7 |
2,5 |
2,3 |
2,2 |
1,8 |
1,6 |
1,3 |
|
∞ |
3,8 |
3,0 |
2,6 |
2,4 |
2,2 |
2,1 |
1,8 |
1,5 |
1,0 |
A táblázat szerkezete a következő. Az oszlopok a számlálóra, a sorok a nevezőre vonatkozóan meghatározott szabadsági fokokkal kapcsolatosak (f1 illetve f2). A megfelelő sorok és oszlopok metszésénél állnak az F-próba kritikus értékei.
A kísérlet tervezési gyakorlatban általában 5%-os szignifikanciaszinten (p=0,05) szokták a számításokat elvégezni, vagyis a becsléseket meghatározni. Ezért a megadott F-táblázat 5%-os szignifikanciaszinten adja meg a kritikus F értékeket és csak annyi szabadságfokra, amennyi a kísérletek megtervezéséhez általában szükséges. Ha ettől eltérő szignifikanciaszinten, vagy több szabadságfokkal akarjuk az F-próbát elvégezni, az [1, 2] ajánlott irodalmat lehet alkalmazni.
5.2.4. A Cochran-próba
A Cochran-próba több szórásnégyzet egyformaságának vizsgálatra szolgál. Ha az összehasonlítandó szórásnégyzetek száma nagyobb kettőnél, és az egyik szórásnégyzet lényegesen meghaladja a többit, akkor normál eloszlás esetén a Cochran-próba alkalmazható. Ez a próba azokra az esetekre vonatkozóan megfelelő, amikor az összes pontban azonos számú (mégpedig n számú) párhuzamos kísérleti beállítás van. Ekkor kiszámítandó az alábbi próba-statisztika:
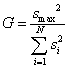
aholGa Cochran-próba kísérleti értéke
smax2 az összehasonlítandó összes szórásnégyzetek közül a legnagyobbik
si2az összes szórásnégyzet
Naz összehasonlítandó szórásnégyzetek száma
Ha a kísérletek alapján meghatározott G érték nem haladja meg a Cohran-próba táblázatban megadott kritikus értéket (XXXV. táblázat), akkor elfogadhatjuk a null-hipotézist, vagyis azt, hogy a szórásnégyzetek közt nincs szignifikáns eltérés.
A táblázat szerkezete az F táblázathoz hasonló: az oszlopok a számlálóra, a sorok a nevezőre vonatkozóan meghatározott szabadsági fokokkal kapcsolatosak (f1 illetve f2). A megfelelő sorok és oszlopok metszésénél állnak a Cochran-próba kritikus értékei.
A Cochran-próba . 5%-os szignifikanciahatárok a G=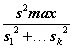 , statisztikához, ahol s1,s2,…, sk mindegyike f szabadságfokú szórásbecslés.
, statisztikához, ahol s1,s2,…, sk mindegyike f szabadságfokú szórásbecslés.
XXXV. táblázat
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
2 |
0,9985 |
0,9750 |
0,9392 |
0,9057 |
0,8772 |
0,8534 |
0,8332 |
|
3 |
9669 |
8709 |
7977 |
7457 |
7071 |
6771 |
6530 |
|
4 |
9065 |
7679 |
6841 |
6287 |
5895 |
5598 |
5365 |
|
5 |
0,8412 |
0,6838 |
0,5981 |
0,5440 |
0,5063 |
0,4783 |
0,4564 |
|
6 |
7808 |
6161 |
5321 |
4803 |
4447 |
4184 |
3980 |
|
7 |
7271 |
5612 |
4800 |
4307 |
3974 |
3726 |
3535 |
|
8 |
0,6798 |
0,5157 |
0,4377 |
0,3910 |
0,3595 |
0,3362 |
0,3185 |
|
9 |
6385 |
4775 |
4027 |
3584 |
3286 |
3067 |
2901 |
|
10 |
6020 |
4450 |
3733 |
3311 |
3029 |
2823 |
2666 |
|
12 |
0,5410 |
0,3924 |
0,3264 |
0,2880 |
0,2624 |
0,2439 |
0,2299 |
|
15 |
4709 |
3346 |
2758 |
2419 |
2195 |
2034 |
1911 |
|
20 |
3894 |
2705 |
2205 |
1921 |
1735 |
1602 |
1501 |
|
24 |
0,3434 |
0,2354 |
0,1907 |
0,1656 |
0,1493 |
0,1374 |
0,1286 |
|
30 |
2929 |
1980 |
1593 |
1377 |
1237 |
1137 |
1061 |
|
40 |
2370 |
1576 |
1259 |
1082 |
0968 |
0887 |
0827 |
|
60 |
0,1737 |
0,1131 |
0,0895 |
0,0765 |
0,0682 |
0,0623 |
0,0583 |
|
120 |
0998 |
0632 |
0495 |
0419 |
0371 |
0337 |
0312 |
|
∞ |
0000 |
0000 |
0000 |
0000 |
0000 |
0000 |
0000 |
|
8 |
9 |
10 |
16 |
36 |
144 |
∞ |
|
|
2 |
0,8159 |
0,8010 |
0,7880 |
0,7341 |
0,6602 |
0,5813 |
0,5000 |
|
3 |
6333 |
6167 |
625 |
5466 |
4748 |
4031 |
3333 |
|
4 |
5175 |
5017 |
4884 |
4366 |
3720 |
3093 |
2500 |
|
5 |
0,4387 |
0,4241 |
0,4118 |
0,3645 |
0,3066 |
0,2513 |
0,2000 |
|
6 |
3817 |
3682 |
3568 |
3135 |
2612 |
2119 |
1667 |
|
7 |
3384 |
3259 |
3154 |
2756 |
2278 |
1833 |
1429 |
|
8 |
0,3043 |
0,2926 |
0,2829 |
0,2462 |
0,2022 |
0,1616 |
0,1250 |
|
9 |
2768 |
2659 |
2568 |
2226 |
1820 |
1446 |
1111 |
|
10 |
2541 |
2439 |
2353 |
2032 |
1655 |
1308 |
1000 |
|
12 |
0,2187 |
0,2098 |
0,2020 |
0,1737 |
0,1403 |
0,1100 |
0,0833 |
|
15 |
1815 |
1736 |
1671 |
1429 |
1144 |
0889 |
0667 |
|
20 |
1422 |
1357 |
1303 |
1108 |
0879 |
0675 |
0500 |
|
24 |
0,1216 |
0,1160 |
0,1113 |
0,0942 |
0,0743 |
0,0567 |
0,0417 |
|
30 |
1002 |
0958 |
0921 |
0771 |
0604 |
0457 |
0333 |
|
40 |
0780 |
0745 |
0713 |
0595 |
0462 |
0347 |
0250 |
|
60 |
0,0552 |
0,0520 |
0,0497 |
0,0411 |
0,0316 |
0,0234 |
0,0167 |
|
120 |
0292 |
0279 |
0266 |
0218 |
0165 |
0120 |
0083 |
|
∞ |
0000 |
0000 |
0000 |
0000 |
0000 |
0000 |
0000 |
-
A normalitás vizsgálata
Ha a valószínűségi változó, amellyel dolgozunk, sok kisebb, függetlenül ható tényező befolyása alatt áll, akkor indokolt a normális eloszlás feltételezése, és nem szükséges statisztikai próbával vizsgálni a normalitást. Ha azonban nem vagyunk biztosak abban, hogy az eloszlásunk valóban normál eloszlás, χ2-próbát kell végeznünk.
5.2.5. χ2-próba, illeszkedés vizsgálat
Ha a kérdéses statisztikai függvény χ2-eloszlású, vagy legalábbis a mintanagyság minden határon túli növelésekor aszimptotikusan χ2-eloszlású, akkor a statisztikai próbát χ2-próbának nevezzük. A χ2-próbával ellenőrizhetjük egy ξ valószínűségi változó eloszlására tett hipotézisünket. Mivel most nem csupán egy általunk ismert eloszlás paramétereire tett hipotézis, hanem a ξ valószínűségi változó egész valószínűségeloszlására tett hipotézis ellenőrzéséről van szó, a megfelelő próbát illeszkedésvizsgálatnak nevezzük. Ha ezt a hipotetikus eloszlást teljesen megadjuk, akkor tiszta illeszkedésvizsgálatról, ha pedig csak az eloszlás típusát tekintjük ismertnek, és a benne levő paramétereket a mintából becsüljük, akkor becsléses illeszkedésvizsgálatról beszélünk.
A χ2-próba alkalmazásának feltétele a nagy (minimálisan 10 elemű) mintaelem-szám.
A χ2-próbával az illeszkedésvizsgálaton kívül még két további vizsgálatot végezhetünk. Tehát tulajdonképpen a χ2-próbával (kisebb módszerbeli különbségekkel) négy különböző vizsgálat végezhető:
-
Tiszta illeszkedés vizsgálat – az eloszlás típusának és paramétereinek meghatározása
-
Becsléses illeszkedésvizsgálat – ismertnek tekintett eloszlás paramétereinek meghatározása
-
Adott valószínűségi változók függetlenségének vizsgálata
-
Adott valószínűségi változók azonos eloszláshoz tartozásának vizsgálata
A továbbiakban azt a χ2-próbát ismertetjük, amikor adott valószínűségi változók azonos valószínűségeloszláshoz tartozását vizsgáljuk.
A következő próba-statisztika konstruálható:
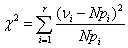
ahol N az Ai megfigyelések száma, amelyek közül A1 esemény γ1-szer,
A2 esemény γ2-ször, …, Ar esemény γr-szer következik be. (Az Ai
egymást kizáró események teljes eseményrendszere, tehát az Aí események valószínűségének összege 1.)
γiaz Ai események gyakorisága. A vizsgálat elvégzésénél törekedni kell arra, hogy minden γi értéke legalább 10 legyen. A γi értékekrenézve fennáll, hogy
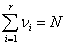
piaz Ai események valószínűsége
Ha a χ2 értéket az adatainkból kiszámoljuk, akkor a kísérleti χ2 értékhez jutunk. Ha a kísérleti χ2 érték a χ2 táblázatban (XXXVI. táblázat) található kritikus értéket nem haladja meg, akkor elfogadhatjuk a null-hipotézist, vagyis azt, hogy az A1, A2, … Ar események valószínűsége normál eloszlású, és szórásnégyzeteik megegyeznek.
A táblázatban a szabadságfokok száma
f=N-1
XXXVII. táblázat
A χ2 eloszlás táblázata
|
f |
χ2 |
f |
χ2 |
f |
χ2 |
f |
χ2 |
f |
χ2 |
|
1 |
3,841 |
21 |
32,671 |
41 |
56,942 |
61 |
80,232 |
81 |
103,010 |
|
2 |
5,991 |
22 |
33,924 |
42 |
58,124 |
62 |
81,381 |
82 |
104,139 |
|
3 |
7,815 |
23 |
35,172 |
43 |
59,304 |
63 |
82,529 |
83 |
105,267 |
|
4 |
9,488 |
24 |
36,415 |
44 |
60,481 |
64 |
83,675 |
84 |
106,395 |
|
5 |
11,070 |
25 |
37,652 |
45 |
61,656 |
65 |
84,821 |
85 |
107,522 |
|
6 |
12,592 |
26 |
38,885 |
46 |
62,830 |
66 |
85,965 |
86 |
108,648 |
|
7 |
14,067 |
27 |
40,113 |
47 |
64,001 |
67 |
87,108 |
87 |
109,773 |
|
8 |
15,507 |
28 |
41,337 |
48 |
65,171 |
68 |
88,250 |
88 |
110,898 |
|
9 |
16,919 |
29 |
42,557 |
49 |
66,339 |
69 |
89,391 |
89 |
112,022 |
|
10 |
18,307 |
30 |
43,773 |
50 |
67,505 |
70 |
90,531 |
90 |
113,145 |
|
11 |
19,675 |
31 |
44,985 |
51 |
68,669 |
71 |
91,670 |
91 |
114,268 |
|
12 |
21,026 |
32 |
46,194 |
52 |
69,832 |
72 |
92,808 |
92 |
115,390 |
|
13 |
22,362 |
33 |
47,400 |
53 |
70,993 |
73 |
93,945 |
93 |
116,511 |
|
14 |
23,685 |
34 |
48,602 |
54 |
72,153 |
74 |
95,081 |
94 |
117,632 |
|
15 |
24,996 |
35 |
49,802 |
55 |
73,311 |
75 |
96,217 |
95 |
118,752 |
|
16 |
26,296 |
36 |
50,998 |
56 |
74,468 |
76 |
97,351 |
96 |
119,871 |
|
17 |
27,587 |
37 |
52,192 |
57 |
75,624 |
77 |
98,484 |
97 |
120,990 |
|
18 |
28,869 |
38 |
53,384 |
58 |
76,778 |
78 |
99,617 |
98 |
122,108 |
|
19 |
30,144 |
39 |
54,572 |
59 |
77,931 |
79 |
100,749 |
99 |
123,225 |
|
20 |
31,410 |
40 |
55,758 |
60 |
79,082 |
80 |
101,879 |
100 |
124,342 |
5.3. Randomizálás
A kísérletek lebonyolítása több napot, esetleg több hetet vehet igénybe. Ezalatt a kísérlet körülményei fokozatosan vagy hirtelen megváltozhatnak (időjárás változás, mérőszemély cseréje, gyártó berendezés kopása, stb.), és ezáltal szisztematikus, de ismeretlen mértékű hibák adódhatnak a kísérleti eredményhez. Ezeknek a hibáknak a hatását úgy lehet kiszűrni, hogy a kísérletek sorrendjét összekeverjük, véletlenszerű sorrendbe állítjuk őket. Arra kell törekedni, hogy egyik lényeges faktor összes azonos beállítása ne történjen egymáshoz közeli időpontokban. Ezt az eljárást nevezik „randomizálás”-nak.
A randomizálást a véletlen számok táblázata alapján kell elvégezni (XXXVIII. táblázat). Ha pl. egy 16 kísérletből álló sorozatot akarunk randomizálni, akkor először a megtervezés sorrendjében sorszámmal látunk el minden kísérletet. Ezután a véletlen számok táblázatában véletlenszerűen kiválasztunk egy 16 alatti számot, mint kezdőértéket. Majd innen elindulva sorban kiírjuk a 16-nál kisebb számokat, olyan sorrendben, ahogyan rájuk találunk, figyelmen kívül hagyva a 16-nál nagyobb, és a már kiírt számokat. Az így kapott számsor lesz a kísérletek elvégzésének sorrendje. A kísérleti beállítások véletlenszerűen megválasztott sorozatát ezután már nem szabad megváltoztatni.
XXXVIII. táblázat
A véletlen számok táblázata
|
56 |
66 |
25 |
32 |
38 |
64 |
70 |
26 |
27 |
67 |
77 |
40 |
04 |
34 |
63 |
98 |
99 |
89 |
31 |
16 |
12 |
90 |
50 |
28 |
96 |
|
88 |
40 |
52 |
02 |
29 |
82 |
69 |
34 |
50 |
21 |
74 |
00 |
91 |
27 |
52 |
98 |
72 |
03 |
45 |
65 |
30 |
89 |
71 |
45 |
91 |
|
87 |
63 |
88 |
23 |
62 |
51 |
07 |
69 |
59 |
02 |
89 |
49 |
14 |
98 |
53 |
41 |
92 |
36 |
07 |
76 |
85 |
37 |
84 |
37 |
47 |
|
32 |
25 |
21 |
15 |
08 |
82 |
34 |
57 |
57 |
35 |
22 |
03 |
33 |
48 |
84 |
37 |
37 |
29 |
38 |
37 |
89 |
76 |
25 |
09 |
69 |
|
44 |
61 |
88 |
23 |
13 |
01 |
59 |
47 |
64 |
04 |
99 |
59 |
96 |
20 |
30 |
87 |
31 |
33 |
69 |
45 |
58 |
48 |
00 |
83 |
48 |
|
94 |
44 |
08 |
67 |
79 |
41 |
61 |
41 |
15 |
60 |
11 |
88 |
83 |
24 |
82 |
24 |
07 |
78 |
61 |
89 |
42 |
58 |
88 |
22 |
16 |
|
13 |
24 |
40 |
09 |
00 |
65 |
46 |
38 |
61 |
12 |
90 |
62 |
41 |
11 |
59 |
85 |
18 |
42 |
61 |
29 |
88 |
76 |
04 |
21 |
80 |
|
78 |
27 |
84 |
05 |
99 |
85 |
75 |
67 |
80 |
05 |
57 |
05 |
71 |
70 |
21 |
31 |
99 |
99 |
06 |
96 |
53 |
99 |
25 |
13 |
63 |
|
42 |
39 |
30 |
02 |
34 |
99 |
46 |
68 |
45 |
15 |
19 |
74 |
15 |
50 |
17 |
44 |
80 |
13 |
86 |
38 |
40 |
45 |
82 |
13 |
44 |
|
04 |
52 |
43 |
96 |
38 |
13 |
83 |
80 |
72 |
34 |
20 |
84 |
56 |
19 |
49 |
59 |
14 |
85 |
42 |
99 |
71 |
16 |
34 |
33 |
79 |
|
82 |
85 |
77 |
30 |
16 |
69 |
32 |
46 |
46 |
30 |
84 |
20 |
68 |
72 |
98 |
94 |
62 |
63 |
59 |
44 |
00 |
89 |
06 |
15 |
87 |
|
38 |
48 |
84 |
88 |
24 |
55 |
46 |
48 |
60 |
06 |
90 |
08 |
83 |
83 |
98 |
40 |
90 |
88 |
25 |
26 |
85 |
74 |
55 |
80 |
85 |
|
91 |
19 |
05 |
68 |
22 |
58 |
04 |
63 |
21 |
16 |
23 |
38 |
25 |
43 |
32 |
98 |
94 |
65 |
35 |
35 |
16 |
91 |
07 |
12 |
43 |
|
54 |
81 |
87 |
21 |
31 |
40 |
46 |
17 |
62 |
63 |
99 |
71 |
14 |
12 |
64 |
51 |
68 |
50 |
60 |
78 |
22 |
69 |
51 |
98 |
37 |
|
65 |
43 |
75 |
12 |
91 |
20 |
36 |
25 |
57 |
92 |
33 |
65 |
95 |
48 |
75 |
00 |
06 |
65 |
25 |
90 |
16 |
29 |
34 |
14 |
43 |
|
49 |
98 |
71 |
31 |
80 |
59 |
57 |
32 |
43 |
07 |
85 |
06 |
64 |
75 |
27 |
29 |
17 |
06 |
11 |
30 |
68 |
70 |
97 |
87 |
21 |
|
03 |
98 |
68 |
89 |
39 |
71 |
87 |
32 |
14 |
99 |
42 |
10 |
25 |
37 |
30 |
08 |
27 |
75 |
43 |
97 |
54 |
20 |
69 |
93 |
50 |
|
56 |
04 |
21 |
34 |
92 |
89 |
81 |
52 |
15 |
12 |
84 |
11 |
12 |
66 |
87 |
47 |
21 |
06 |
86 |
08 |
35 |
39 |
52 |
28 |
09 |
|
48 |
09 |
36 |
95 |
36 |
20 |
82 |
53 |
32 |
89 |
92 |
68 |
50 |
88 |
17 |
37 |
92 |
02 |
23 |
43 |
63 |
24 |
69 |
80 |
91 |
|
23 |
97 |
10 |
96 |
57 |
74 |
07 |
95 |
26 |
44 |
93 |
08 |
43 |
30 |
41 |
86 |
45 |
74 |
33 |
78 |
84 |
33 |
38 |
76 |
73 |
|
43 |
97 |
55 |
45 |
98 |
35 |
69 |
45 |
96 |
80 |
46 |
26 |
39 |
96 |
33 |
60 |
20 |
73 |
30 |
79 |
17 |
19 |
03 |
47 |
28 |
|
40 |
05 |
08 |
50 |
79 |
89 |
58 |
19 |
86 |
48 |
27 |
98 |
99 |
24 |
08 |
94 |
19 |
15 |
81 |
29 |
82 |
14 |
35 |
88 |
03 |
|
66 |
97 |
10 |
69 |
02 |
25 |
36 |
43 |
71 |
76 |
00 |
67 |
56 |
12 |
69 |
07 |
89 |
55 |
63 |
31 |
50 |
72 |
20 |
33 |
36 |
|
15 |
62 |
38 |
72 |
92 |
03 |
76 |
09 |
30 |
75 |
77 |
80 |
04 |
24 |
54 |
67 |
60 |
10 |
79 |
26 |
21 |
60 |
03 |
48 |
14 |
|
77 |
81 |
15 |
14 |
67 |
55 |
24 |
22 |
20 |
55 |
36 |
93 |
67 |
69 |
37 |
72 |
22 |
43 |
46 |
32 |
56 |
15 |
75 |
25 |
12 |
|
18 |
87 |
05 |
09 |
96 |
45 |
14 |
72 |
41 |
46 |
12 |
67 |
46 |
72 |
02 |
59 |
06 |
17 |
49 |
12 |
73 |
28 |
23 |
52 |
48 |
|
08 |
58 |
53 |
63 |
66 |
13 |
07 |
04 |
48 |
41 |
39 |
07 |
46 |
96 |
40 |
20 |
86 |
79 |
11 |
81 |
74 |
11 |
15 |
23 |
17 |
|
16 |
07 |
79 |
57 |
61 |
42 |
19 |
68 |
15 |
12 |
60 |
21 |
59 |
12 |
07 |
04 |
99 |
88 |
22 |
39 |
75 |
16 |
69 |
13 |
84 |
5.4. A durva hiba kiszűrése
Minden kísérletsorozat vagy méréssorozat során előfordulhatnak olyan események, amelyek következtében a kísérlet vagy a mérés eredménye egészen biztosan hibás lesz (pl. áramkimaradás, mérőműszer meghibásodása, stb.). Ha ezt az eseményt a kísérlet közben észrevesszük, a hibás eredményt azonnal ki kell hagyni az eredmények közül. Megeshet azonban az is, hogy a hibát nem észleljük azonnal, csak később, a mérések kiértékelése során kezdünk el gyanakodni, hogy valamely kiugró kísérleti eredményt vagy az átlagtól erősen eltérő mérési eredményt nem valami durva hiba okozhatott-e. Ilyenkor nagy valószínűséggel kiszűrhetjük a durva hibát az alábbi statisztikai becslés alapján. Ilyen számítás elvégzése nélkül azonban egyetlen kísérleti vagy mérési eredményt sem szabad kihagyni a további számításokból!
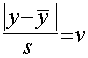
ahol ya „gyanús” kísérleti eredmény
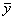
a többi eredmény átlaga, a kiugró eredményt figyelmen kívül hagyva.
sa többi eredmény szórásnégyzetének pozitív négyzetgyöke, a kiugró
eredményt figyelmen kívül hagyva
A durva hiba kiszűrésére szolgáló táblázat (XXXIX. táblázat) 5% szignifikancia szinten megadja azokat a határszámokat, amelyeknél ha nagyobb az adatokból számolt „v” érték, akkor elvetjük azt a null-hipotézist, hogy a gyanús érték nem tér el szignifikánsan a többi értéktől. Ez esetben a gyanús értéket nem szabad figyelmen kívül hagyni.
XXXIX. táblázat
A durva hiba kiszűrése
|
n |
szignifikanciahatár |
n |
szignifikanciahatár |
|
3 |
46,7 |
15 |
3,71 |
|
4 |
10,1 |
20 |
3,60 |
|
5 |
6,51 |
25 |
3,56 |
|
6 |
5,31 |
30 |
3,54 |
|
7 |
4,73 |
35 |
3,53 |
|
8 |
4,40 |
40 |
3,53 |
|
9 |
4,18 |
45 |
3,53 |
|
10 |
4,04 |
50 |
3,54 |