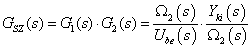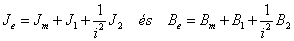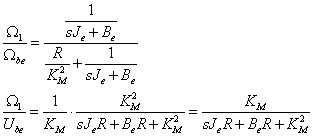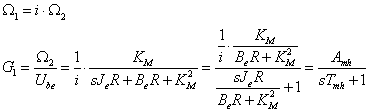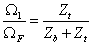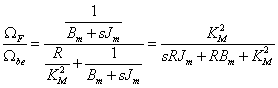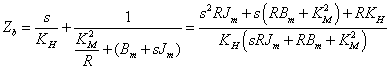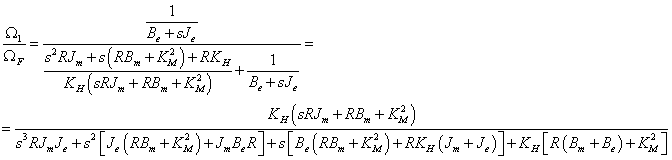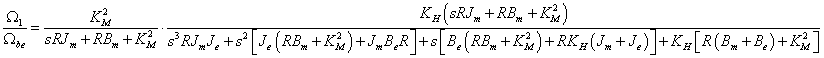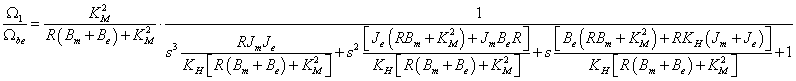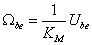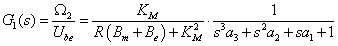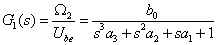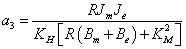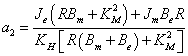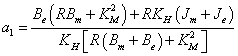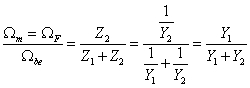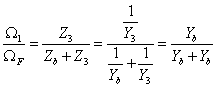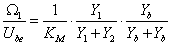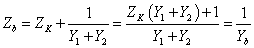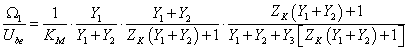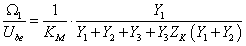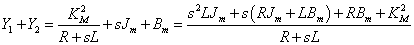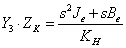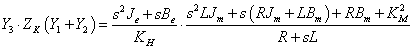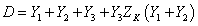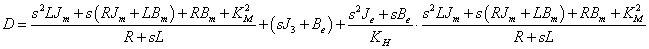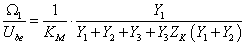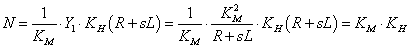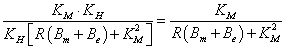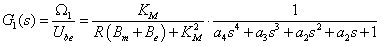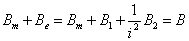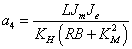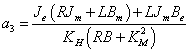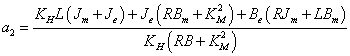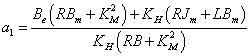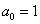8. fejezet - DC motor hajtóművel egybeépített modelljei
A gráf alapján könnyen nyomon követhető, hogy a tervezés során, az előírt paraméterek és jellemzők figyelembe vételével több esetet lehet megkülönböztetni. Ezek tárgyalásának nehézségi foka igen eltérő. Egy különleges motor-hajtómű konstrukciót láthatunk P. K. Budig munkájában [8.1.]. Röviden összefoglaljuk a jellegzetes variációkat, de nézzük kiindulásként a gráfot:
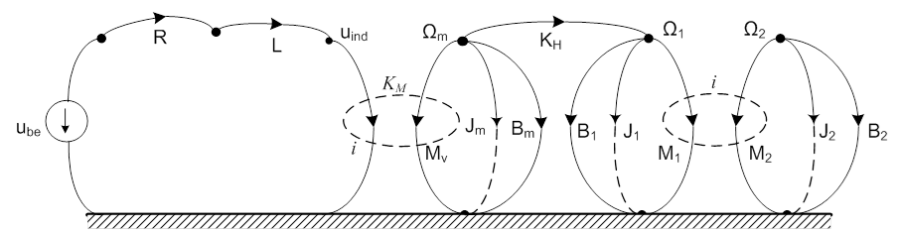
A gráfon felismerhető a DC motor gráfja, és az Ωm motortengely szögsebesség a hajtómű bemeneti szögsebessége. A két rendszer nem választható szét, ez példaképpen azt jelenti, hogy a hajtómű minden paramétere befolyásolja az armatúra áram pillanatnyi értékét is. A teljes gráf negyedrendű rendszert mutat, a független energiatárolók: L, Jm, és KH. A hajtómű kimeneti J1 és bemeneti J2 oldali tehetetlenségi nyomatékai függő tárolók, ezek egynek számítanak, de csak redukcióval vonhatóak össze.
Minden változatnál az impedancia módszert alkalmazzuk, mert egyrészt ez segíti az összehasonlítást, másrészt az átviteli függvényhez ennek a módszernek a segítségével juthatunk el a leggyorsabban.
8.1. Visszahatás nélküli hajtómű
Az alcím azt hangsúlyozza, hogy a motorral egybeépített hajtómű módosítása akkora, hogy a hajtómű kimenete felől a rendszer nem hozható mozgásba. Az ehhez szükséges módosítás több tényezőtől függ, de általánosságban i>500 értéktől felfelé ez a feltétel teljesül. Extrém példaként a csigahajtóművet szokás emlegetni, ennek esetében kizárt a visszahatás. A külföldi szakirodalomban találunk olyan formát, amelyben ezeket az eseteket úgy írják le a modellekben, hogy a transzformátor típusú átalakító után „diódát” kapcsolnak [7.1.]. Az „önzáró” (selbstsperrend) hajtómű teljesítmény-folyamának irányát a hatásfok segítségével szimulálják. A motor felől a terhelés irányában ηe=0.9…0.95, visszafelé irányban pedig ηv=0.
Ha a motor-hajtómű egység visszahatásmentesnek tekinthető, akkor ez igen leegyszerűsíti a szabályozott szakaszok méretezését. A motor-hajtómű egység, mint G1(s) átviteli tag, sorba van kapcsolva az utána következő terheléssel, vagy mozgásátalakítóval, legyen ezek átviteli függvénye G2(s).
Az eredőjük természetesen:
|
|
A G1(s) átviteli tag tehát a motor-hajtómű egység, ennek kimenete az Ω2 szögsebesség, Ube(s) bemenet hatására. A fenti egyenletet a továbbiakban úgy kell értelmezni, mintha a G2(s) átviteli tag bemenete egy ideális keresztváltozó forrás lenne, amely a visszahatás-mentes hajtómű kimenő szögsebessége. Ezt a szögsebességet a fejezetben bemutatott példákban következetesen Ω2-vel jelöltük. A hangsúly a visszahatás-mentességen van. Ha a hajtómű nem visszahatás-mentes, akkor a Gsz(s) átviteli tagot nem lehet két soros tagra bontani. Ilyen esetet modellezünk a 8.2. szakasz fejezetben.
Az ideális forrás fogalmát szó szerint kell venni ebben az esetben is. Az 1. fejezet fejezetben leírtuk, hogy az ideális forrás megtartja előírt értékét (itt szögsebesség) minden releváns (ésszerű) terhelésre, és a szükséges átmenő változót a megadott teljesítménykorlátok között (itt forgatónyomaték) szolgáltatja.
A visszahatás-mentesség tehát nem azt jelenti, hogy a motor-hajtómű egység korlátlanul terhelhető!
Ha kész G2(s) modellje (ez általában egy mozgásástalakító), akkor a paraméterek és a szabályozással szemben támasztott dinamikai követelmények (beállási idő, gyorsítási idő, stb.) ismeretében meg kell határozni a motorral szemben támasztott teljesítmény-igényt, és a hajtómű nyomaték-terhelhetőségét. Ezt részletesen bemutatjuk a 11. fejezet fejezetben.
Az adott szögsebesség tartományban a „kivehető” forgatónyomaték nem korlátlan. A visszahatás mentesség csak a stacionárius terhelés körüli tartományban teljesül.
Mit kell a visszahatás-mentes hajtómű esetében „ésszerű” terhelés alatt érteni. Az 1. fejezet fejezetben már jeleztük, hogy az ideális források többsége igen bonyolult szerkezet. Így van ez a motor-hajtómű egységgel is. A „kivehető” teljesítmény nyílván nem lehet nagyobb, mint a villamos oldalon (motor bemenetén) betáplált teljesítmény. A teljesítmény önmagában még nem elegendő, ezen túlmenően a döntő fontosságú, hogy a hajtómű elemeit meghatározott forgatónyomaték átvitelére méretezik, ezen belül különösen a fogaskerekek fogméreteire kell koncentrálni, mint „gyenge” láncszemre.
Végezzünk el egy gondolati kísérletet. Próbáljuk meg „kivenni” a hajtóműből a maximális forgatónyomatékot. Ez a kimenet mechanikai „rövidzárását” jelentené, azaz a kimenő tengelyt „lefogjuk”, rögzítjük. A szögsebesség, mint keresztváltozó, értéke minimális szintre, azaz zérusra csökken. (Analógiaként képzeljük el, mi történik, ha egy akkumulátor, mint keresztváltozó forrás sarkait rövidre zárjuk.) A motor rövid ideig még szolgáltatja a hajtómű bemenő nyomatékát, de a motor-hajtómű egység a leggyengébb láncszemnél fog tönkremenni, ott, ahol a kis forgatónyomaték miatt még relatív kis fogméretek és tengelyátmérők vannak.
A kísérletet természetesen nem maradt meg a „gondolat” szintjén. A fejezet szerzője munkatársaival mechatronikai (robot) hajtáshoz alkalmazott motor-hajtómű egységeken (un. „mikromotorok”) terheléses kísérleteket végzett. A túlterhelt hajtóművek leggyengébb láncszeme általában a második fokozat műanyag fogaskereke volt. Az specifikációban megadott stacionárius nyomatékot (állandó terhelő nyomatékot) meghaladó terhelés hatására a műanyag fogaskerék fogait a következő fokozat acél fogazata szabályosan „legyalulta”.
Mindezek meggondolása azért fontos, mert a 11. fejezet és 12. fejezet fejezetekben (golyósorsós és fogazott szíjas mozgásátalakítók, mint szakaszok méretezése) bemutatjuk, hogy a motor és hajtómű statikus és dinamikus terhelhetőségét, az előírt dinamikai követelmények figyelembevételével tervezni kell. Olyan motor-hajtómű egységet kell kiválasztani, amely a szükséges teljesítményt, dinamikát stb. szolgáltatni képes.
A mechatronikai tervezés első lépése „arról szól” tehát, hogy a modellezett szakaszban meg kell határoznunk a motor-hajtómű egység felé támasztott követelményeket, ezért szenteltük külön ennek a fázisnak a 11.1. szakasz fejezetet.
Ha a módosítás nem elegendően nagy, tehát a motor-hajtómű egység nem visszahatás mentes, akkor a teljes rendszert (szabályozott szakaszt) együtt szabad csak modellezni, mert a rendszer forrásától legtávolabb lévő elem is befolyásolja visszahatás formájában a forrás melletti elemek változóit. Ezt az esetet is bemutatjuk, a 8.2. szakasz fejezetben, ahol a motor, a hajtómű és a golyósorsós átalakító egyetlen átviteli tagot képeznek, amely legegyszerűbb formájában is hatodrendű.
-
A motor villamos időállandója (L/R) lényegesen (nagyságrendekkel) kisebb, mint a rendszer többi időállandójának értéke, ami kisebb motoroknál az induktivitás viszonylag kis értéke miatt fordul elő. Kisebb méretű pozicionáló rendszerek esetében a hajtómű rugómerevsége a tengelykapcsoló rugómerevségéhez viszonyítva nagy, a modellezésnél KH→∞ érték gond nélkül felvehető. Ennek a feltételezésnek természetesen határt szabhat a pozícionálási pontosság előírt követelménye. A módosítás kellően nagy a szétválaszthatósághoz, ezért a motor és hajtómű egység együttesen egy egytárolós arányos tagot képez, amelyhez sorosan kapcsolódik az a tag, amely lehet egy golyósorsós pozícionáló, vagy egy másfajta lineáris/rotációs rendszer.
-
A motor időállandója kicsi, de nem lehet figyelmen kívül hagyni a hajtómű KH rugómerevségét. A hajtómű módosítása nagy, tehát a szakasz ugyancsak két részre választható szét. Ebben az esetben a motor-hajtómű egység harmadrendű arányos átviteli tag, amelyhez további tag, vagy tagok csatlakozhatnak.
-
A motor időállandóját a rendszer többi időállandójához képest nem lehet figyelmen kívül hagyni, modellezni kell a KH hajtómű rugómerevséget, a módosítás viszont biztosítja a szétválaszthatóságot. Ebben az esetben az első tag (motor és hajtómű egység) már negyedrendű arányos tag lesz.
A bevezető rendszerezés után bemutatjuk a három változat modelljének levezetését.
8.1.1. Általános változat (egytárolós)
L→0; K H →∞; i»1 (visszahatás-mentes), a leggyakrabban alkalmazott modell
Az első a legegyszerűbb, és ezt a modellt szokás általában alkalmazni pozícionáló rendszerek esetében. A modell finomítása mindenképpen állapotteres tárgyalást tesz szükségessé. A súrlódások (csillapítások) nemlineáris függvényeinek figyelembe vételét, esetleg a rugómerevségek függvényeit, de mindenképpen fontos a mozgatott tömeg, valamint az előtoló erő értékének változását modellezni. Ebben az esetben csak az állapotszabályozás valamilyen válfaja jöhet szóba.
Az első modellben az 1. pontban leírtak szerint legyen L→0, KH→∞, és i»1. A következő ábra a motor és a kapcsolt hajtómű impedancia modelljét mutatja. A paraméterek nagysága miatti egyszerűsítést lépésenként mutatjuk be a könnyebb érthetőség kedvéért. Az átviteli függvényeket keressük, mert a hagyományos szabályozókör tervezéséhez ez az adekvát modell. A szakasz szétválasztása a hajtómű kimeneténél történik, ezt a gráfon is ellenőrizni lehet. A golyósorsós mozgatás forrása a hajtómű Ω2 kimeneti változója lesz.

Első lépésben egyszerűsítjük az impedancia hálózatot, a tervezési feltételek alapján.
Elhagyjuk az „sL” és az „s/KH” impedanciákat. A villamos oldal impedanciáit egyenértékű forgó mechanikai impedanciákká számoljuk át, és átszámítjuk az Ube forrást Ωbe forrássá. A két átalakító közötti impedanciák így párhuzamosakká válnak, és egyszerűen összevonhatók. A hajtómű kimeneti oldalát redukáljuk a bemenetire, és az átviteli függvény ezért először nem Ω2-re, hanem Ω1-re írjuk fel. Ez nem jelent gondot, mert a két változó között a módosítás teremt kapcsolatot. Nézzük, hogy a leírt módosításokat elvégezve, miként egyszerűsödik a kapcsolás:
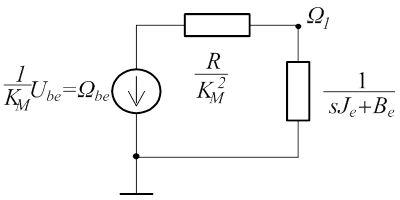
A szakasz első tagjának átviteli függvénye tehát direktben felírható, csak a keresztváltozó osztót kell alkalmazni. Úgy gondoljuk, hogy a képen látható kapcsolás egyszerűségéhez nem férhet kétség.
A villamos forrás és impedancia átszámítás eredménye az ábrán látható. A mechanikai oldalon végrehajtott redukció és a párhuzamos impedanciák összevonása eredményeként adódó terhelő impedancia kiszámítása nem fér az ábrára, ezt az alábbiakban mutatjuk meg. A számítást egyszerűsíti, hogy minden elem párhuzamos, ezért a vezetőképességek összeadhatók. Az eredő impedancia az admittanciák összegének reciproka lesz. Tudjuk, hogy a tehetetlenségi nyomaték admittanciája „sJ” és a csillapításé „B”. Az összevonás eredménye van feltüntetve a kapcsoláson.
|
|
||
|
|
Az átviteli függvényt a szokásos alakra hozzuk azzal, hogy a nevező operátortól független tagjával osztjuk a tört mindkét részét. Eredményül egy egytárolós arányos tagot kaptunk, amelynél különösen fontos, hogy levezettük, a motor és hajtómű egység mely paramétereire van szükség, és azokat milyen súlyozással kell figyelembe venni a tervezésnél. Az utolsó lépésben behelyettesítjük a hajtómű kimeneti szögsebességét.
|
|
A fenti összefüggésben az „mh” index a motor-hajtómű egységre utal, és az Amh arányos tényezőben a módosítás már benne foglaltatik.
8.1.2. Háromtárolós változat
L→0; i»1 (visszahatás mentes), a hajtómű rugómerevségével számolni kell
Ebben az esetben is az első modellnél felvázolt impedancia kapcsolásból kell kiindulnunk, amelyben a motor hajtómű egység minden impedanciája megvan. Ezt a kapcsolást nem ismételjük meg, de azt a következő ábrán már megmutatjuk, hogy miként változik a kapcsolás, ha az induktivitást elhagyjuk:

A szemléletesség kedvéért második lépésben redukáljuk a hajtómű kimenő oldalán szereplő impedanciákat a bemeneti oldalra, miközben nem feledjük, hogy számunkra nem Ω1, hanem Ω2 lesz a valódi kimenet.
A következő ábrán már azt a hálózatot látjuk, amelyen a hajtómű kimeneti oldalának impedanciáit a bemenetire számoltuk át, és elvégeztük az összevonást is.
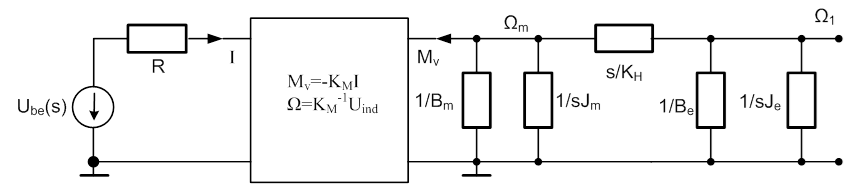
Az összevonások következő lépéseként a villamos oldal impedanciáját számítjuk át forgó mechanikaivá és kiszámítjuk az új keresztváltozó forrást is:
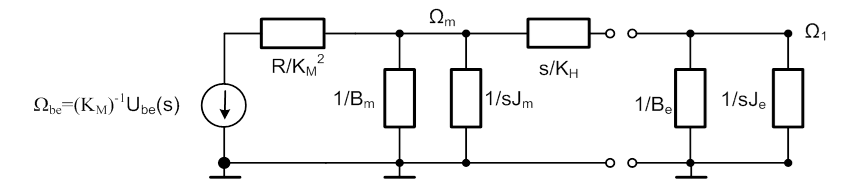
A fent látható kapcsolás még tovább egyszerűsíthető, hiszen a referenciához kötött impedanciák összevonhatók:
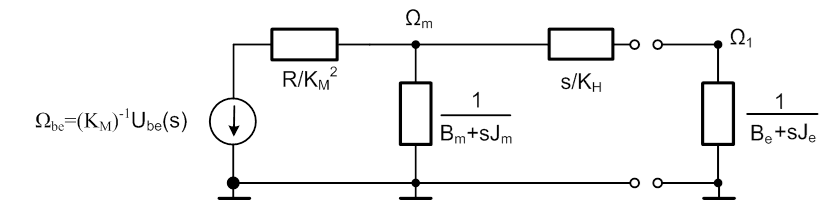
A végeredményben kapott kapcsolás tovább már nem alakítható. Látható, hogy a keresett változóhoz tartozó impedanciát (passzív rész) már leválasztottuk az aktív részről. Keresztváltozó a bemenet és a kimenet is, ezért olyan alakra alakítjuk a kapcsolást, amely egy keresztváltozó osztó, és ez egyben az átviteli függvény is, implicit formában:
|
|
Most már csupán a Zb belső impedanciát és az aktív rész új ΩF forrását kell meghatározni.
Az ΩF forrás nem azonos az Ωbe forrással, hanem az aktív rész un. üresjárati, terheletlen keresztváltozó kimenete a kapcsokon. Látható, hogy terheletlen esetben a KH torziós rugómerevségre nem hat csavaró nyomaték, deformáció nincs, az impedancia elhagyható. A keresett ΩF forrás pedig egy keresztváltozó osztó révén egyből felírható:
|
|
A Zb belső impedancia kiszámítása kicsit hosszadalmasabb feladat. Az aktív rész szabad kapcsai felől kell a rendszerbe „belenézni” és megállapítani, hogy „mit lát” a terhelő rész.
|
|
Továbblépés előtt érdemes dimenzió ellenőrzést végrehajtani, hiszen a képlet már eléggé bonyolult. Miután meggyőződtünk, hogy azonos dimenziójú tagokat adunk össze, felírhatjuk a keresett implicit átviteli függvényt:
|
|
A legtöbb hasonló kapcsolás esetében „némiképp” egyszerűsödik az explicit átviteli függvény, azaz, ha ΩF forrás helyére behelyettesítjük az eredeti forrást:
|
|
Célszerű a nevező operátortól független tagjával a számlálót és nevezőt osztani, mert a dimenzió ellenőrzés is könnyebben végrehajtható.
|
|
A könnyebb kezelhetőség érdekében érdemes az átviteli függvény szokásos jelöléseit alkalmazni. Ezen kívül az Ω1 kimenet helyére behelyettesítjük a hajtómű módosításának figyelembe vételével a valóban keresett mennyiséget, Ω2 szögsebességet, valamint Ωbe helyére az eredeti bemenő jelet, a DC motor kapocsfeszültségét osztva a KM motorállandóval.
Ez az átszámítás a harmadik impedancia kapcsoláson látható:
|
|
||
|
|
Befejezésül az átviteli függvény még tömörebb formáját adjuk meg, az együtthatók értékei a levezetésből világosan látszanak:
|
|
Az eredmény várható volt, hiszen 3 db független energia tárolót kellett figyelembe venni (Jm, KH és Je).
Az átviteli függvény nevezőjének együtthatói:
|
|
||
|
|
||
|
|
8.1.3. Négytárolós változat
Figyelembe kell venni L és K H paramétereket, i»1 (visszahatás-mentes)
Ebben a változatban a G1(s) átviteli függvény modelljének felírásához már mindenképpen ajánlatos számítógépes modellező programot alkalmazni. A G2(s) átviteli függvény természetesen változatlan, de mert G1(s) már egy negyedrendű rendszert ír le, a „kézi” számolás sok vesződséggel jár, és könnyen lehet hibázni is. A következőkben azért mutatjuk be mégis a hagyományos úton való levezetést, mert az előzőekhez képest egy olyan eljárást szemléltetünk, amely bonyolultabb kapcsolás esetén is megkönnyítheti a számításokat.
A kiindulás természetesen a motor-hajtómű rendszer, immáron minden fontos energiatároló figyelembe vételével. A következő ábrán már a célszerűen átalakított kapcsolást látjuk. A villamos rendszerrészt forgó mechanikaivá számítottuk át, és redukáltuk a hajtómű kimeneti oldalát a bemenetire. Adott esetben ennél kompaktabb formát nem lehet elérni.
Összetettebb hálózatok esetében a számítás jelentősen egyszerűsíthető, ha csupán a végeredménybe helyettesítjük be a konkrét paramétereket. Ugyanakkor láttuk egyszerűbb feladatoknál, pl. a DC motor modelljénél, hogy egyszerűbb esetben ez nem jelent különösebb segítséget. További előny, ha nem csupán impedanciákkal, hanem admittanciákkal is számolunk.
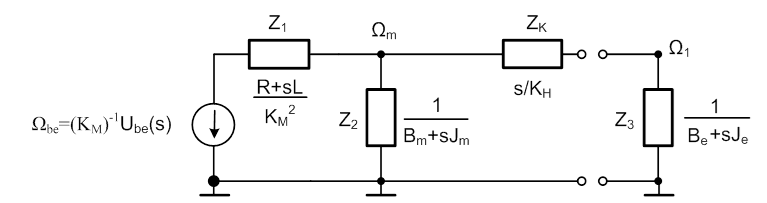
Keresett tehát az Ω1/Ube átviteli függvény, amelyhez ismét aktív és passzív részre bontunk, majd felírjuk a keresztváltozó osztót, ami közvetlenül a megoldáshoz vezet. A passzív rész változatlan, az aktív rész új forrás értéke (üresjárati keresztváltozó) az Ωm csomóponton jelenik meg, hiszen a torziós tengelyen nincsen elcsavarodás.
|
|
A kimenetre felírható osztó pedig az alábbi:
|
|
A keresett átviteli függvény a fentiekkel a következő, viszonylag egyszerű implicit alakot veszi fel:
|
|
Az átviteli függvényben azért szerepelnek az admittanciák, mert az impedanciák többsége tört, és ezért így egyszerűbb a számolás. A belső impedanciát az aktív rész szabad kapcsai felől írjuk fel:
|
|
Behelyettesítve az Yb –re kapott összefüggést, az átviteli függvényben már csak az önálló impedancia/admittancia értékek szerepelnek. Azonnal látható az ajánlott módszer előnye, az egyszerűsítések lehetősége:
|
|
Végül
|
|
A részletszámításokat érdemes külön elvégezni:
|
|
A figyelmes olvasó azonnal felismeri az összefüggés reciprokában azt a kifejezést, amely a DC motor fordulatszáma, mint kimenet és a terhelő nyomaték, mint bemenet közötti átviteli függvény.
|
|
||
|
|
A következő lépésben az átviteli függvény nevezőjével külön foglalkozunk, mert a kifejezés összetett, és törekedni kell a legegyszerűbb formára:
|
|
||
|
|
Közös nevezőre hozás után nem szabad elfelejteni (gyakori hiba), hogy a „D” (denominator) nevezője a majdani átviteli függvény számlálójának szorzó tényezője lesz, mert meg kell szüntetni az emeletes törtet.
A további számítási lépéseket nem mutatjuk be, csupán azt, hogy a végső formában törekedtünk arra, hogy a szabályozástechnikában megszokott átviteli függvény alakhoz jussunk. Az operátortól független együtthatóval osztottuk az átviteli függvény számlálóját és nevezőjét is.
A számláló Y1 az alábbi értékű, ha hozzávesszük a tört előtti állandót is, nem szabad elfeledkeznünk, hogy a nevező közös nevezőre való hozásánál volt egy szorzat, amely a számlálóba (N: nominator) kerül:
|
|
||
|
|
Ha az így kapott „N” –et osztjuk a nevező operátortól független együtthatójával, az alábbi eredményt kapjuk:
|
|
Ez a kifejezés a keresett átviteli függvény számlálójának végső formája, és mint ilyen, „ismerős” a korábbi változatokból. Az átviteli függvény az alábbi lesz:
|
|
Egyszerűbb a kifejezés, ha a csillapítási tényezőket összevonjuk:
|
|
A nevező együtthatóinak értékeit közöljük, hogy a dimenzió ellenőrzés lehetséges legyen:
|
|
||
|
|
||
|
|
||
|
|
||
|
|
8.2. DC motor és hajtómű visszahatással, pl. i<500, és golyósorsós átalakítóval
Lehetséges olyan változat is, amelyben a hajtómű módosítása nem teszi lehetővé a szétválasztást, mert a hajtómű kimeneti tengelye felől a rendszer motor felőli oldala mozgásba hozható. Ilyen esetben a teljes szakaszt egyetlen átviteli tagként lehet csak modellezni. A hajtómű a rendszer-részeket nem választja szét, a mozgás átalakító visszahat a rendszer elejére. A fejezetcímben látható módosítás-határ csak tájékoztató jellegű. Homlokkerekes hajtóművek esetében, például i~500 körüli módosításoknál még tapasztalható a visszahatás. A visszahatás hajtómű típusától, a kenési viszonyoktól és több más tényezőtől is függ.
Ebben az esetben a legnagyobb a számítási munka. Lényegileg mindegy, hogy hány átmenő változó energiatárolót (rugalmasság, induktivitás) veszünk figyelembe, az átviteli függvény egyetlen tömb lesz, a rendszám a független energiatárolóktól függ.
Legegyszerűbb esetben is hatodrendű rendszert kapunk, az átviteli függvény paraméterei igen összetettek lesznek.
A rendszer gráfja a (8.9. ábra) ábrán látható. A motor-hajtómű egységhez tengelykapcsolón keresztül golyósorsós mozgásátalakítót csatlakoztatunk. A mozgásátalakító impedancia modelljének levezetését a 11. fejezet fejezetben, és az alább alkalmazott formáját a 11.3. ábra és 11.4. ábra ábrákon találjuk.

Ebben az esetben mindenképpen célszerű olyan szimulációs programot felhasználni a matematikai modell felírásához, amely a rendszer impedancia hálózatán, vagy az elemek egymáshoz való kapcsolódásán alapul, és amelyik ebből kiindulva számítja ki az átviteli függvényt. Ilyen szimulációs programot mutat be például az M. Otter által jegyzett munka [8.2.]. Nagyméretű hálózat esetében a „papíron” történő levezetés hosszadalmas, és kétséges lehet az eredmény is. A dimenzió ellenőrzés ilyen esetben különösen fontos.
Ezt a változatot bemutatás céljából a terjedelmessége miatt nem vezetjük végig, hanem a Maxima nevű programot alkalmazzuk az átviteli függvény meghatározására.
A GNU GPL licenc által szabályozott hozzáférésű Maxima (http://maxima.sourceforge.net/) számítógépes algebra rendszerrel számoljuk a katalógusadatok alapján az átviteli függvény együtthatóit. A Maxima rendszer hivatalos dokumentációja [8.3.] mellett az interneten igen sok oktatóanyag és mintapélda található. A COMA (COntrol engineering with MAxima) szabályozástechnikai számításokat megkönnyítő kiegészítő [8.4.] angol és német leírása mellett mintapéldákat is letölthetünk.
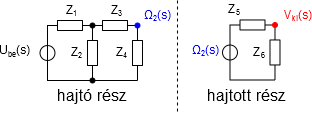
Először a 8.9. ábra alapján nagyon vázlatos impedanciahálózatot veszünk fel és számoljuk a kitüntetett pontokhoz tartozó jellemző eredő impedanciákat és keresztváltozó értékeket. A (8.10. ábra) ábrán az eredeti Ube(s) keresztváltozó forrás (feszültségforrás), a hajtómű Ω2(s) szögsebessége és a Vki(s) sebesség szerepel Laplace-operátoros tartományban. Az egyes impedanciák index szerint:
-
a villamos rész impedanciája
-
a motor tehetelenségéből és a veszteségből származó (párhuzamos) eredő impedancia
-
a hajtómű rugómerevségéből származó impedancia
-
a hajtómű fogaskerekeihez és csapágyazásaihoz kapcsolódó (párhuzamos) eredő impedancia
-
a golyósorsós mozgásátalakító rugalmasságából származó impedancia
-
a golyósorsós mozgásátalakító tömegből és veszteségből származó (párhuzamos) eredő impedanciája
A DC motor és a golyósorsós mozgásátalakító váltó, a hajtómű transzformátor típusú energiaátalakító. Mindkét típus azonos jellegű változók közötti kapcsolatot ad meg, vagyis keresztváltozót keresztváltozóval, átmenő változót átmenő változóval kapcsol össze az energiaátalakító állandója segítségével.
A részletes számításban a fejezetben korábban szereplő módszerrel a villamos oldal impedanciáit egyenértékű forgó mechanikai impedanciákká számoljuk át, és átszámítjuk az Ube feszültségforrást Ωbe szögsebesség forrássá. A későbbiekben (11.2. ábra) szereplő redukcióval vesszük figyelembe a hajtómű i módosításának hatását a tőle „balra” lévő részrendszerekre és a most már szögsebesség forrásra. Ugyanitt találjuk a golyósorsós mozgásátalakító váltóegyenleteivel felírható redukciós összefüggéseket, így a haladó mozgásra vonatkozó impedanciákat forgó mozgásra vonatkoztatva írjuk fel. Ezek az átalakítások nem változtatják az impedanciák jellegét, igen leegyszerűseítve valamennyi állandóval való szorzásként kezelhető.
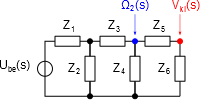
Számításainkban a load("coma")$ paranccsal betöltött COMA csomag impedance_chain(Z1, Z2, Z3, Z4, …) parancsát használjuk az impedancia lánc eredőjének számítására.
-
teljes_halozat: a Vki és Ube közötti, mind a hat összetevőt tartalmazó impedancialánc (8.10. ábra)
-
hajto_resz: az Ω2 és Ube közötti, négy összetevőt tartalmazó impedancialánc (8.11. ábra)
-
hajtott_resz: a Vki és Ω2 keresztváltozók közötti impedancialánc, tulajdonképpen keresztváltozó osztó (8.11. ábra)
-
visszahatassal: a golyósorsós mozgásátalakító visszahatását figyelembe vevő modellben a teljes rendszert viszonyítjuk a hajtott rendszerhez (impedanciáik hányadosát képezzük)
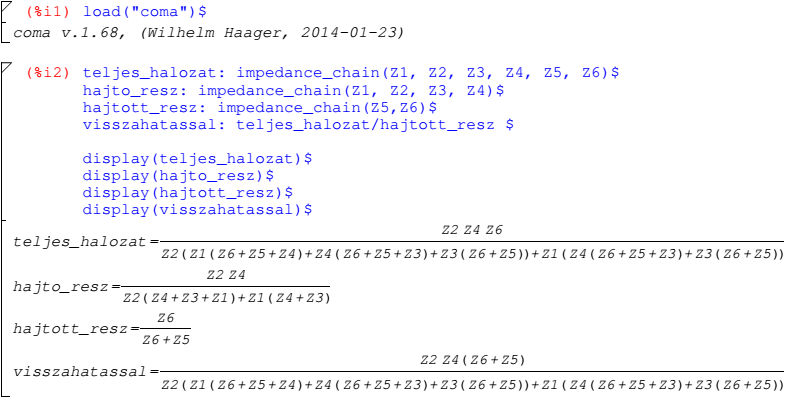
A teljes hálózat, a hajtó és hajtott rész, valamint a visszahatást figyelembe vevő eredő impedanciák paraméteres meghatározása wxMaxima programmal és a COMA csomaggal:
Az egyes impedanciák összetevőik szerint, a képletekben szereplő s-hatványoknak megfelelő együtthatókkal. Az átviteli függvények szokásos megadásához hasonlóan a számlálóbeli együtthatókat b-vel, a nevezőbelieket a-val jelöljük. Az indexek két tagúak, az első szám utal az impedancia sorszámára, a második pedig az s-hatvány kitevőjére. Az energiaátalakítókból származó konstansok az egyes impedanciák fázismódosító jellegét nem változtatják.
-
a villamos rész sorba kapcsolt ellenállás és induktivitás eredője
-
a motor tehetelenségét és a veszteséget párhuzamos eredővel számoljuk
-
a hajtómű rugómerevségéből származó impedancia
-
a hajtómű soros eredőként kezelt tehetetlenségeiből és szintén soros eredőként figyelembevett csapágyazásaiból számolt eredők párhuzamos kapcsolásából számolt impedancia
-
a golyósorsós mozgásátalakító rugalmasságából származó impedancia
-
a golyósorsós mozgásátalakító párhuzamosan kapcsolt tömegéből és veszteségéből származó eredő impedancia
Az egyes impedanciák összetevőknek megfelelő Laplace-operátoros tartománybeli megadása általános együtthatókkal a wxMaxima programban:

Az általános számláló és nevező polinommal adott impedanciákkal számolunk és az eredményeket G átviteli függvényként kezelve a COMA csomag tranftype(G) parancsával kiíratjuk a jelátvivő tagként kezelt modell típusát.
A teljes hálózat, a hajtó és hajtott rész, valamint a visszahatást figyelembe vevő eredő meghatározása a hat polinomként adott impedianciával wxMaxima programmal és a COMA csomaggal:

A teljes_halozat az eredmény alapján valóban hatodrendű, PT6, vagyis arányos hat energiatárolós. A hajto_resz PT4, a hajtott_resz PT2, soros eredőjuk nyilván PT6.
A visszahatassal modell a hajtómű kimenete és a DC motor bemenő (feszültség) jele közötti kapcsolatot írja le a golyósorsós mozgásátalakító motorra visszahatását figyelembevéve, PD2T6 tagként. A PD2T6 tag számlálója másodfokú, nevezője hatodfokú polinom.
A teljes hálózat, a hajtó és hajtott rész, valamint a visszahatást figyelembe vevő polinomiális alakú eredő impedanciák és jelátvivő tag típusok meghatározása wxMaxima programmal és a COMA csomaggal:

Már ezeken az eredményeken is látszik, hogy nem kézi számításra „termettek”. Különösen igaz ez, ha behelyettesítjük az egyes – megfelelő fizikai mennyiséggel és elemtípussal felírt – impedanciákat és az energiaátalakítók miatt szükséges redukciókat. KM a motorállandó, i a hajtómű módosítása, nv=2π/h a h menetemelkedésű golyósorsós mozgásátalakító mint váltó állandója. A felírt modell helyességét, különösen a redukciókat a mértékegységekkel ellenőrizhetjük.
Redukált impedanciákkal és forrással felírt átviteli függvények wxMaxima programmal és a COMA csomaggal:

Helyettesítés után látszik, hogy a későbbi szimulációs vizsgálatokhoz szükséges, katalógusadatokkal számított rendszermodellt sem célszerű kézzel számolni! Az egyes paraméterek numerikus adatainak megadásával a kapott matematikai modellt (pl. az átviteli függvény együtthatóit) egyszerűen átmásolhatjuk más szimulációs programba (ha nem a Maximával szeretnénk tovább vizsgálódni).
Redukált impedanciákkal és forrással, helyettesített paraméterekkel felírt átviteli függvények wxMaxima programmal és a COMA csomaggal:

Befejezésként bemutatjuk, hogy a teljesség kedvéért, a visszahatásmentes hajtóművel felépített első, harmad-és negyedrendű modelleket ellenőriztük a Maxima programmal, és azt kaptuk, hogy a programmal számított eredmények megegyeznek a „kézzel” számítottakkal.
Harmadrendű visszhatásmentes rendszer wxMaxima programmal és a COMA csomaggal:

Negyedrendű visszhatásmentes rendszer wxMaxima programmal és a COMA csomaggal:

Szakirodalom
[8.1.] Schraubgewinde-Reluktanzmotor: Ein linearer Präzisionsantrieb Maschinenmarkt. Vogel Verlag. Würzburg . 1996.
[8.2.] Objektorientirte Modellierung mechatronischer Systeme am Beispiel geregelter Roboter Fortschritt Berichte VDI Reihe 20. VDI Verlag. Düsseldorf . 1995.
[8.3.] Maxima, a Computer Algebra System: Documentation http://maxima.sourceforge.net/documentation.html.
[8.4.] COMA, Control Engineering with Maxima és Regelungstechnik mit Maxima http://www.austromath.at/daten/maxima/zusatz/Control_Engineering_with_Maxima.pdf.