5. fejezet - Mérés és modellezés
5.1. A modellezés szerepe a metrológiában
A mérés, legyen szó bármilyen fizikai, kémiai, időben állandó, vagy változó mennyiségekről, a legáltalánosabban megismerési folyamatként fogható fel. Ebben a folyamatban a modellalkotás döntő jelentőséggel bír a tevékenységünk minősége szempontjából.
A modern rendszerszemlélet kialakulásával összefüggésben, az 1960-as évektől kezdődően, alig találunk olyan mértékadó méréselméleti, vagy rendszertechnikai és irányításelméleti szakirodalmat, amelyben a megismerési tevékenység középpontjában ne a modellalkotás állana. A tudománytörténet Galileo Galileit tartja a modellezés atyjának, mivel pl. a szabadesést lejtőn való mozgatással modellezve mutatott utat a tudományos megismerés alapvető módszeréhez, a modellezéshez és az absztrakcióhoz. A mérés és modellezés elválaszthatatlanságának a Schnell László által szerkesztett Jelek és rendszerek méréstechnikája című, alapvető fontosságú magyar nyelvű, összefoglaló méréselméleti és méréstechnikai munkában két fejezetet szenteltek a szerzők [5.1.] .
A modellezés fontosságát jelzi, hogy a metrológiában (méréstudomány) már magának a mérésnek is legalább négy modellje ismert és használatos, amelyekkel magát a mérési tevékenységet kísérlik meg leírni.
Ez a négy modell a következő:
-
Hagyományos, un. „szabványos” modell
-
Folyamat modell
-
Valószínűségelméleti modell
-
Információelméleti modell
A négy modellt kifejezetten méréselméleti megközelítésként ismertetjük. Ezek az elméletek szolgálnak műszerek és mérőrendszerek tervezésének alapjául. A négy modell taglalása különböző terjedelmű , mert a valószínűségelméleti modell önmagában többféle változatot is magába foglal, aszerint, hogy milyen előzetes ismeretekkel rendelkezünk a mérendő mennyiségekről, vagy a mérőrendszer átviteli tulajdonságairól.
Mind a négy modell más-más aspektusból világítja meg a mérési tevékenység komplexitását. Egyik modell sem kizárólagos, mindegyik ismerete elengedhetetlen feltétele a mérési tevékenység helyes megtervezésének, akár tudományos kutatásról, akár ipari ellenőrzésről van szó.
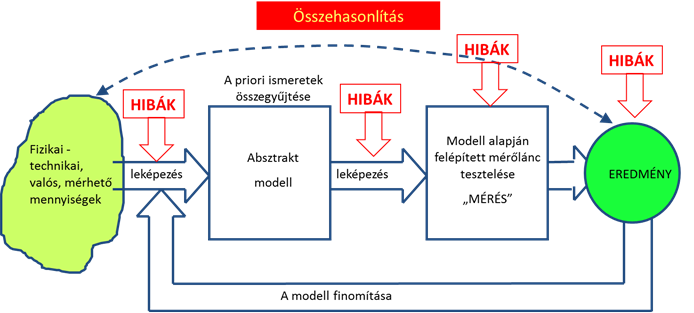
A „mi megközelítésünk” – tekintettel arra, hogy a szerzők mérnökök, valamint mérnökhallgatók számára készült a jegyzet, természetesen alapvetően mérnöki. A mérnökök vagy kutató tevékenységet végeznek, vagy az ipari termelésben vesznek részt, termékeket és gyártórendszereket terveznek, és a termelést irányítják. A mérés négy modellje közül az egyik az un. „folyamat modell”, amely a legszemléletesebben mutatja be azt, hogy a mérési tevékenység tudományos síkon a bennünket körülvevő „világ megismerésének” eszköze, ipari szinten pedig a minőségbiztosítás elengedhetetlen eszköze. Az (5.1. ábra) ábrán látjuk a mérés folyamat modelljét, de „rejtetten” megjelenik az ábrán a hagyományos, szabványos meghatározás is, amely szerint a mérés tervszerű, összehangolt tevékenységek sorozata, amely arra irányul, hogy ismeretlen mennyiséget ismert etalonokkal hasonlítsunk össze.
A gépészmérnöki szemléletet és megközelítést egyrészt a folyamat modell, másrészt az információelméleti modell tükrözi legjobban, míg a villamosmérnöki és informatikai szakmában a valószínűségelméleti modellt tekintik a legjobb általános leírásnak.
Az (5.1. ábra) ábrán a mérendő mennyiségek halmazát és az eredményt eltérő színnel és formával jelöltük. Ezzel kívánjuk kifejezésre juttatni, hogy a fizikai technikai valóság teljes körű megismerése legfeljebb elméletben lehetséges, hiszen a jellemzőkre és a mérési tevékenységre ható, és azokat befolyásoló tényezők száma végtelenül nagy, erről a 4. fejezet fejezetben már volt szó. Valamennyi befolyásoló tényező gyakorlati megismerésére nincsenek eszközeink, de nem is lenne gazdaságilag indokolható minden hatótényező figyelembe vétele. Ezért minden eredmény leegyszerűsített, és valamilyen „pontossági szintű” – helyesebben hibákkal terhelt - modellje a valóságnak.
Érdemes kiemelni azt is, hogy az ábrán a hibák eredete is nyomon követhető. A hibákat a metrológia ugyanis háromféle szempont szerint csoportosítja: Eredetük, jellegük és megjelenési formájuk szerint. Az (5.1. ábra) ábrán a hibák eredete is jól látható, a modellalkotástól a mérés kivitelezéséig és ellenőrzéséig. Eredetük szerint a hibák természetesen már a folyamat első fázisában, a modellalkotás során megjelennek és továbbiak lépnek be a mérési eljárás megválasztásából (ide tartozik a mérés fizikai elve és a mérési módszer), a mérés kivitelezéséből (eszközök jellemzői, mérési körülmények, stb.), végül a számításokból, az eredmény közléséből adódóan. A szakirodalom szerint a mérés „autonóm” (önálló) szakasza a modell alapján felépített mérőlánc tesztelése. Sajnálatos módon, a méréstechnikát sokan úgy képzelik el, hogy a méréstechnika egyszerűen csak erre az autonóm szakaszra korlátozódik, holott az a modellalkotástól és a kiértékeléstől elválaszthatatlan.
5.2. Modellalkotás
A bennünket körülvevő világ mérnöki szempontból megismerni kívánt töredék részét, a jelenségek közötti kapcsolatokat modellek segítségével kíséreljük meg leírni. A modellek nagyvonalakban három kategóriába sorolhatók: fizikai, esetleg kémiai modellek, funkcionális modellek és matematikai (absztrakt) modellek. A műszaki életben manapság használatos modellezési alapokat 1975-ben megjelent művükben Mesarovic és Takahara [5.2.] fektették le.
A fizikai modellek általános alkalmazása főként régebbi időkben volt elterjedt, ugyanakkor még ma is nélkülözhetetlenek az áramlástechnikai vizsgálatok esetében a kicsinyített, hasonlóság alapján megalkotott modellek. Ugyanakkor összetett mechanikai lengő rendszerek dinamikai vizsgálatának céljából már csak elvétve találkozhatunk analóg villamos áramkörökkel (analóg számítógéppel), hiszen a szilárdsági és dinamikai analízis területén szinte egyeduralkodóvá vált a végeselem módszer.
A funkcionális modellek mind a mai napig általánosan elterjedtek a mechanikában, valamint a mérés-és szabályozástechnikában. Ebben az esetben a vizsgálat alá vett rendszert felépítő elemeket idealizált szerepük alapján jelenítjük meg. Minden, alapozó mérnöki ismeretekkel rendelkező szakember tudja, hogy egy rugalmas szerkezeti elem sokféleképpen írható le, de a „legidealizáltabb” változat az, ha helyette egy rugót jelenítünk meg. Azonban sem a fémek, sem a műanyagok viselkedésének pontosabb leírása nem lehetséges egy ilyen módon. Fémek esetében minimálisan egy rugó és egy csillapítás párhuzamos kapcsolásával, de relaxációt és kúszást mutató, nemlineáris tulajdonságú elasztomerek esetében – bizonyos követelmények mellett - még ez a forma sem lenne elegendő.
A matematikai modellek absztrakciós lépések eredményeként jönnek létre. Ezeknek napjainkban kiemelt szerepük van, ami a számítástechnika fejlettségének köszönhető. A vizsgált rendszerekben a mérhető és nem mérhető mennyiségeket változók formájában jelenítjük meg, a rendszerre jellemző műszaki tulajdonságokat paraméterek (ezek állandóak és változóak lehetnek) formájában írjuk le. Tudjuk alapozó ismereteink alapján, hogy időben változó mennyiségek villamos jellé történő átalakítása és mérése nélkül bármely mechatronikai rendszer elképzelhetetlen, ezért a méréstechnika kiemelt fontosságú.
A mechatronikai rendszerek megtervezéséhez elengedhetetlen a négy matematikai modell-típus ismerete.
Ezek
-
a differenciálegyenlet (idő tartomány)
-
az átviteli függvény (operátor, vagy frekvencia tartomány)
-
az állapottér modell (idő és operátor tartomány) és
-
a logikai függvények.
5.3. A modellezés korlátai
A modell soha nem képes a valóságot teljes komplexitásában leírni. Mindig annak egy részét, vagy bizonyos aspektusait ragadjuk ki, esetenként leegyszerűsítjük a valóságot. A jelenségről alkotott fizikai elképzeléseink korlátozottak, sok a bizonytalansági forrás. A modell mindig célorientált. Bonyolultságát a megoldandó feladat jellege, a műszaki feltételek, az ésszerűség és gyakran az anyagi lehetőségek korlátozhatják. A mérnöki gyakorlatban a modellek a kutatást, a tervezést és az elemzést segítik, és ide sorolhatók a mérésekhez alkalmazott modellek is.
A modellezés során gyakran körül kell határolni a valós rendszernek azt a részét, amellyel az adott feladat megoldása érdekében foglalkoznunk kell. Ez a rész általában un. „zárt rendszert” képez, és ez a modellezési problémáink első forrása. A valóságban a műszaki rendszerek nem zártak , a környezettel és más rendszerekkel kölcsönhatásban állnak. Ezeket a hatásokat bizonyos mértékben természetesen figyelembe lehet, és kell is venni, de a teljesség igénye nélkül.
A méréstechnikában egy modell megalkotásához a vizsgálat kezdetén rendelkezésre álló ismeretek összességét „à priori” ismereteknek nevezik. A francia kifejezések a mérésügyben a XVIII. század végétől kezdődően igen elterjedtek, ennek kultúrtörténeti okait röviden a „Méréstechnika” c. TÁMOP által megjelentetett elektronikus jegyzetben érintettük [1.1.] . A modellezési és mérési munka végeztével ismereteink jelentősen bővülnek, és ezek következtében immár „à posteriori” információkkal is rendelkezünk. Az à priori ismeretek meghatározóak a modell minősége szempontjából, mert meghatározzák a modell típusát, bonyolultságát, a megkívánt pontosságot, és a költségeket, és ezek következtében magát a mérési eljárást és a mérés kivitelezését. A korábban ismertetett modellformákra közösen vonatkozik, hogy szükséges egy struktúra és szükségesek hozzá paraméterek. E tekintetben mindegy ugyanis, hogy fizikai, funkcionális, vagy matematikai modellről van szó
A legnagyobb probléma az, hogy az à priori ismeretek nem elegendőek a struktúra kiválasztására. Ebben még igen nagy a szerepe a mérnöki tapasztalatnak, a próbáknak és az un. mérnöki intuíciónak. A paraméterek becslésére és identifikációjára már objektívnek tekinthető módszerek állnak rendelkezésre.
A döntően, vagy kizárólagosan à priori ismeretekre támaszkodó modellalkotást „deduktív” szemléletnek, míg az à posteriori ismeretekkel, tehát kísérleti, mérési adatokkal operáló megközelítést „induktív” módszernek nevezik. Normál mérnöki gyakorlatban elvétve alkalmazzák kizárólagosan csak az egyik változatot.
5.4. A mérés hagyományos modellje és értelmezése
Az 5.1. szakasz fejezetben már röviden ismertettük a hagyományos megfogalmazást, amely szerint a mérés tervszerű, összehangolt tevékenységek sorozata, amely arra irányul, hogy ismeretlen mennyiséget ismert etalon mennyiségekkel hasonlítsunk össze. A mérés ezért fizikai vagy kémiai mennyiségek nagyságának jellemzése, a választott mértékegységben kifejezett számértékével. A mérési eredmény egy szám és egy mértékegység szorzata, amely az egységet és az egységhez való viszonyt fejezi ki. A mérési tevékenység csak akkor tekinthető befejezettnek, ha elvégeztük a kiértékelést és a hibaszámítást is.
5.5. A mérés folyamat modellje
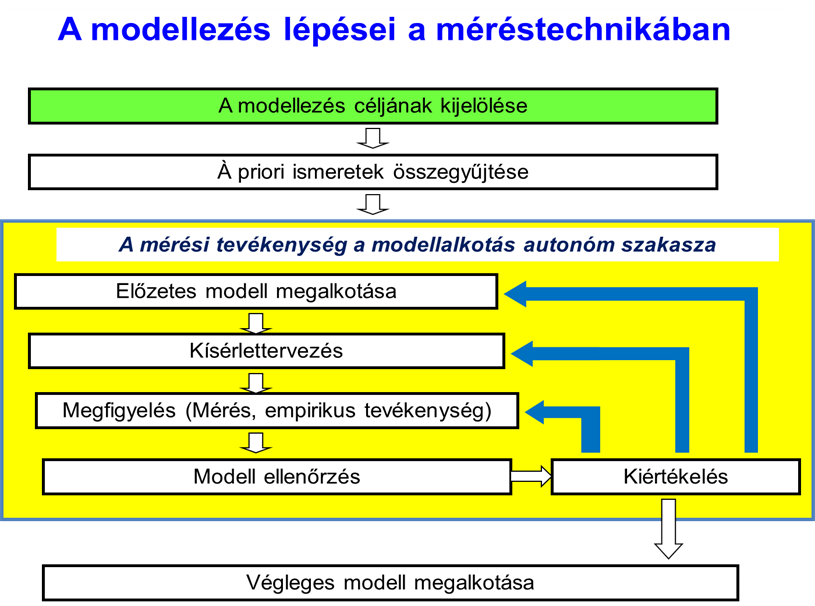
A mérés második, un. „folyamat modellje” a deduktív és az induktív személet váltakozva történő alkalmazásán alapul. Ezt igen jól szemlélteti a korábban bemutatott 5.1. ábra és az ebben az alfejezetben látható 5.1. ábra.
Mind az 5.1. ábra, mind pedig az (5.2. ábra) ábrán felismerhető, hogy a modellalkotás iterációs folyamat. A kitűzött célnak meghatározott bizonytalanság mellett eleget tenni képes modell, vagy eredmény csak több, pontosítást eredményező lépésben jöhet létre. Látható, hogy amennyiben a modell még nem a megkívánt bizonytalansági határokon belül „dolgozik”, akkor kiértékelést követően, három helyen lehet beavatkozni. A legegyszerűbb esetben „belép” az első visszacsatolás, növelni kell a mérések számát. Ha ez nem bizonyul elegendőnek, akkor hozzá kell nyúlni a mérési eljáráshoz (módszer és kivitelezés), és ha ez sem éri el a kellő hatást, akkor bizony az „à priori” modellel van baj.
Felül kell vizsgálni a modell specifikálásánál tett hipotéziseket, strukturális, vagy a paramétereket érintő módosításokat kell végrehajtani.
A mérnökhallgató évközi feladatainak megoldása során, de legkésőbb a szakdolgozat, vagy a diplomaterv elkészítésénél szembesül a folyamat modell lépéseivel. A gépészetben és a mechatronikában a műszaki munkák elsöprő többségénél ugyanis mérésekkel kell igazolni a téma kapcsán megalkotott elméleti modellek helyességét.
5.6. A valószínűségelméleti modell és sajátosságai a gépészetben
Az [5.1.] jelű, már korábban említett szakirodalmi munka arra törekszik, hogy jel- és rendszerelméleti alapon általános meghatározásokat adjon a modern méréstechnikában előforduló legtöbb feladatra. Már az első fejezetben megállapítja, hogy a mérés hagyományos értelmezése, „modellje”, miszerint a mérési eredmény egy szám és egy mértékegység szorzata, továbbá a mérési hiba az eredmény tényleges és ideális értéke közötti különbség, a napjainkban felmerülő mérési problémák jó részére nem alkalmazható. Példaként egy, a digitális rendszerek méréstechnikájában szokásos feladatot hoz fel, amikor egy digitális vezérlő belső állapotának felmérését kell elvégezni. Ebben a feladatban – és főként a villamosmérnöki gyakorlatban – nem egy mennyiség nagyságát kell megmérni, az eredmény nem is szám, és a mértékegység sem megszokott formájú.
Jegyzetünkben kísérletet teszünk arra, hogy a fent említett szakirodalomban ismertetett jel-és rendszerelméleti megközelítést kiterjesszük a gépészeti mérések világára is.
Az idézett szakirodalomi munka alapján a mérési folyamat a jel-és rendszerelméleti értelmezés szerint nem más, mint a leképezést megvalósító rendszer, azaz a mérőeszköz. A mérendő objektum a modellezés tárgya, a modell leírását az objektum bemenő és kimenő (információhordozó) jelei teszik lehetővé. A mérőeszköz feladata az információhordozó jelek begyűjtése és feldolgozása. A jelek feldolgozása egy műveletlánc, és az idézett munka a továbbiakban ezt tekinti mérési eljárásnak . A mérendő objektum jelei, mielőtt eljutnának a mérőeszköz bemenetére, különböző eredetű torzító hatásoknak, zavarásoknak vannak kitéve, olvashatjuk a munkában. Ennek a jelenségnek a matematikai leírására vezették be a jelátviteli csatorna fogalmát. Ezek szerint a jelátviteli csatorna kimenetén jelenik meg a mérőeszköz bemenetére kerülő „megfigyelt” jel. A mérőeszköz kölcsönhatásba kerül a mérendő objektummal, energia és információ átadás formájában. A mérőeszköz begyűjti a jeleket, és feldolgozza az ezek által hordozott információt. A jelfeldolgozás műveletlánc, amely a jeleket a mérés célkitűzésének megfelelő alakra hozza. Ez a jelfeldolgozás tehát az idézett munka szerint a mérési eljárás, amely műszaki teljességében egy mérőrendszerben mutatkozik meg, mert ebbe a fogalomba már a jellemzők informatikai feldolgozása is beleértendő.
Ebből a leírásból, megközelítésből kitűnik, hogy a mérőeszköz alatt villamos mennyiségeket (feszültség, áram, frekvencia, stb.) mérő műszert értenek.
Ezzel szemben a gépészeti mennyiségek mérésénél többnyire egy átalakítási láncolat segítségével jut el az információt hordozó villamos jel a jelfeldolgozó villamos egység, vagy villamos mérőrendszer bemenetére.
A valószínűségelméleti modellt a gépészet és a mechatronika esetében például úgy értelmezhetjük, hogy a jelátviteli csatorna reprezentálja azt az átalakítási láncolatot, amely a jellegzetes gépészeti mennyiségekből (elmozdulás, sebesség, gyorsulás, erő, szögelfordulás, szögsebesség, fordulatszám, szöggyorsulás, forgatónyomaték, nyomás, térfogatáram, hőmérséklet, stb.) mérhető villamos mennyiségeket állít elő. Ebben az esetben teljesen nyilvánvaló a valószínűségelméleti modellben szereplő torzítások és zavarások szükségszerű megjelenése, és hatásaikkal bizony komolyan kell számolnunk.
Elfogadva és alkalmazva az idézett jel-és rendszerelméleti, azaz valószínűségelméleti modellt a következő megállapításokat tehetjük a gépészet és a mechatronika területén jellemző mérési feladatokkal kapcsolatban.
Az a mérendő jellemző (paraméter) és az azt jelképező szimbólum – azaz c eredmény - között leképezésekkel teremtünk kapcsolatot. A mérés valószínűségelméleti modellje két fontos leképezést tartalmaz. A paraméter térben találhatóak a mérendő mennyiségek, a megfigyelési tér a paraméterek zajjal (torzítással) terhelt leképezésével jön létre, és itt találhatók a b megfigyelések. Ennek az első leképezésnek a tulajdonságait a jelkibocsátó rendszer és a megfigyelések közötti jelátviteli csatorna jellemzői határozzák meg, ennek elnevezése a csatorna karakterisztika .
A mérési eljárások a mérendő objektumon végzett b megfigyelések feldolgozásával állítják elő a mérési eredményt, c =f( b ) összefüggés szerint. Ha a mérés eredménye folytonos, tehát egy adott tartományban tetszőleges értéket vehet fel, akkor az eljárás tervezésében a becsléselmélet apparátusa alkalmazható. Ha megszámlálható (diszkrét) eredmény lehetséges, akkor a döntéselmélet módszereit kell alkalmazni. E jegyzetben a gépészetre jellemző folytonos jellemzők és az ezekhez rendelt folytonos eredmények kapcsolatára szorítkozunk.
Tehát a jelfeldolgozó egység (mérőműszer, mérőrendszer) bemenetére kerülő jelek feldolgozása révén jutunk az eredményhez. A jelfeldolgozás kifejezés igen sokféle műveletet takar, a matematikai műveletektől kezdve az erősítésen, az A/D átalakításon át a különféle szűrési feladatokig. A szűrést külön azért érdemes kihangsúlyozni, mert éppen a jel-és rendszerelméleti aspektusra alapozták a szűrők elméleti tervezését, gondolunk itt a Wiener és a Kálmán szűrőre.
A jelfeldolgozáshoz tartozik ebben a modellben a gépészeti mérések eredményeinek valószínűség számítási módszerekkel történő meghatározása. Mindez tehát a második leképezés során történik, és ennek révén jutunk a becslési térben az eredményhez. A becslő, vagy becslési eljárás olyan fizikai rendszert (műszert, mérőrendszert) modellez, amelynek bemenetén a megfigyelés, kimenetén az eredmény található.
Az (5.3. ábra) ábrán az a , b , és c vektorok eltérő színűek és helyzetűek, szimbolizálva a zajok és torzítások, valamint a leképezések hatásait.
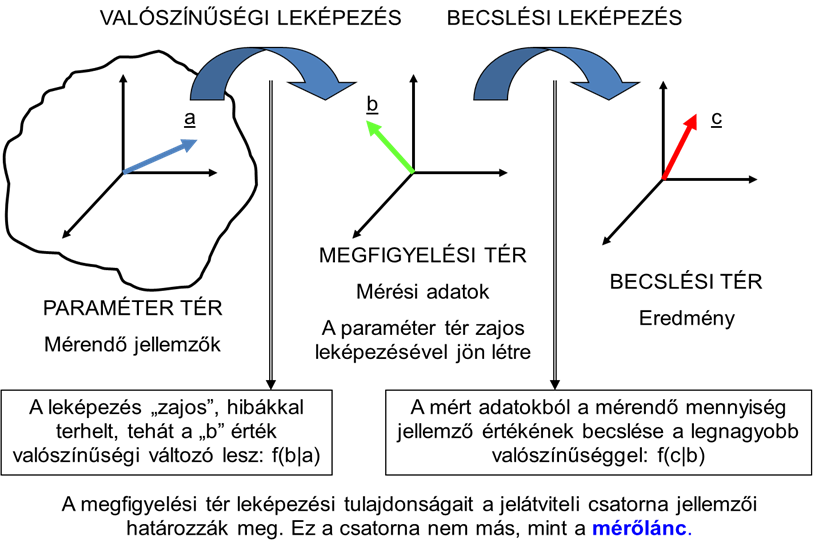
Feltételezzük, hogy a mérendő mennyiség véletlen változó, amelynek eloszlását az f( a ) függvény írja le. Értelmezésünk szerint, a gépészeti méréstechnikában legyen az első leképezés az a láncolat, amelynek révén tetszőleges fizikai mennyiségekből villamos jellemzőket hozunk létre. Ennek a láncolatnak az információ átviteli „képességét” nevezhetjük csatornakarakterisztikának . Az átvitel minőségét az f( b | a ) a feltételes sűrűség függvény írja le. A feltételes valószínűség megmutatja, hogy egy adott a paraméterhez milyen sűrűség függvénnyel rendelhető hozzá a b megfigyelt paraméter. A mérés elvégzése után természetesen már bővebb ismereteink vannak, így egy újabb feltételes valószínűséggel, amelyet f( a | b ) jelöl, már azt is le tudjuk írni a matematika nyelvén, hogy egy megfigyelt b paraméterhez a mérendő a paraméter milyen eloszlása van hozzárendelve. A valószínűség számítás nyelvén ez „à posteriori” (utólagos) ismeret, ami megfelel a valóságnak.
5.6.1. Becslési módszerek
A következőkben három olyan információelméleti módszert mutatunk be, amelyek az eredmény matematikai eszközökkel történő becslését teszik lehetővé – a becslési térben.
A becslési módszereket úgy állítjuk sorrendbe, hogy az első helyen a legtöbb „à priori” ismeretet igénylő módszer álljon, és ez után csökkenő előzetes ismeret szerint a Maximum Likelihood (ML), majd végül a „Legkisebb négyzetes hiba” (LMS) következzen.
5.6.2. Bayes-féle becslési módszer
A legtöbb előzetes ismeret a Bayes-féle becslési eljáráshoz szükséges. Ebben az esetben ismerni kell
-
a mérendő jellemző ( a paraméter) f( a ) sűrűségfüggvényét (eloszlását)
-
a mérendő jellemző és a megfigyelések közötti f( b | a ) feltételes valószínűség sűrűségfüggvényt
-
és a K( c , a ) költségfüggvényt.
A Bayes becsléshez szükséges, hogy a mérendő jellemző f( a ) eloszlásfüggvényének és a csatornakarakterisztikának ismeretében meghatározhassuk az à posteriori (utólagos) feltételes sűrűségfüggvényt. Ezen utólagos ismeret, azaz az f( a | b ) feltételes sűrűségfüggvény, rögzített (ismert) b megfigyelt érték mellett adja az a paraméter statisztikai leírását.
Az f( a | b ) feltételes valószínűség (utólagos tapasztalaton alapuló) a valószínűség számítás szabályainak alkalmazásával és a Bayes-becsléssel előre megadható, ha ismert a mérendő mennyiség sűrűségfüggvénye f(a) és a mérőrendszer csatornakarakterisztikája.
|
|
(5.1) |
Becslésnek a paraméter megfigyelése utáni legvalószínűbb ĉ értéket tekintjük. A becslésnek mindig lesz „H” hibája
|
H=ĉ – a |
(5.2) |
Tekintettel arra, hogy ez a hiba maga is változó, függ a „ c ” és „ a ” értékeitől, bevezetik az átlagos hiba fogalmát, és ez „R” jelölést kap.
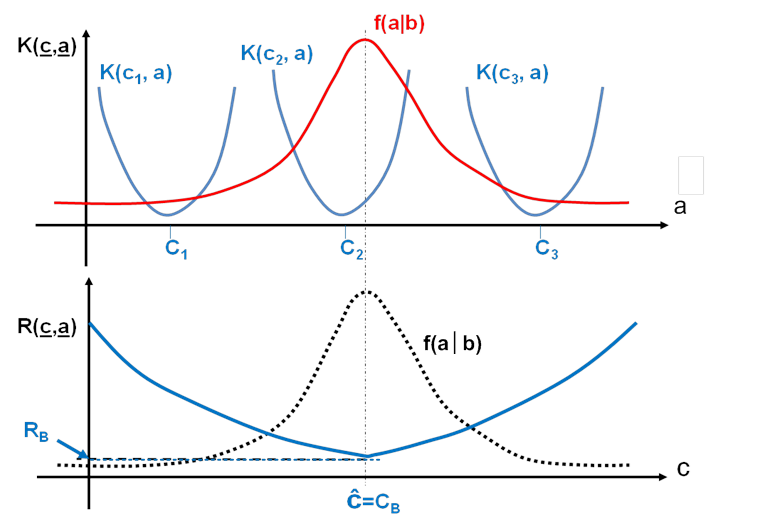
A Bayes becslés – „költségfüggvények” alkalmazásával, amelyeket K( c , a ) jelöléssel látunk a következő képletben - az „ a ” paraméter olyan „ ĉ = c B ” becsült értékét keresi, amely az „R” hibát minimalizálja.
A költségfüggvény K( c , a ) fogalom itt tehát hibakritériumot, optimum kritériumot takar. A becslés átlagos hibája a költségfüggvénnyel (optimum kritérium) súlyozott à posteriori (utólagos) feltételes sűrűségfüggvénnyel a következő módon adható meg. Az átlagos hiba minimumát kell tehát keresni:
|
|
(5.3) |
Az ilyen módon kiszámítható R B minimális átlagos hibát Bayes-hibának nevezik. A becslési hiba látható a következő ábrán:
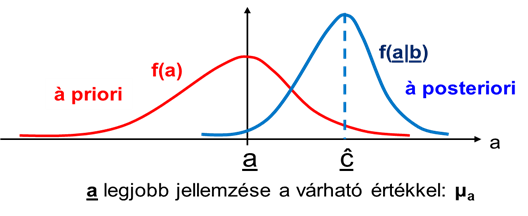
A „költségfüggvény” hatása két példán jól szemléltethető. Ha az abszolút hibát tartjuk fontosnak a becslési hiba csökkentésére, akkor abszolút érték költségfüggvényt alkalmazunk. Ha a nagyobb eltéréseket határozottabban kívánjuk súlyozni, akkor pedig a négyzetes hibafüggvényt célszerű használni.
Ezeket látjuk a következő ábrán.
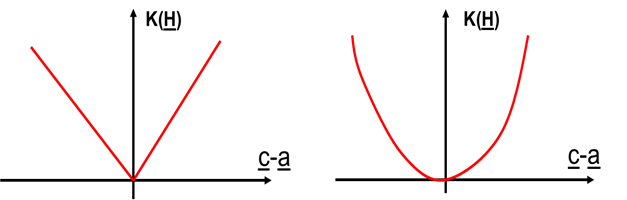
Az „à posteriori” (utólagos) feltételes sűrűségfüggvény négyzetes költségfüggvénnyel történő súlyozását és a minimális hibát mutatja az alábbi ábra.
5.6.3. Maximum Likelihood becslés (ML)
Előfordulhat a sokféle mérési feladat során, hogy nincs előzetes ismeretünk a mérendő paraméter f( a ) sűrűségfüggvényéről, és csak az f( b | a ) feltételes sűrűségfüggvény, a megfigyelés, azaz a csatornakarakterisztika adott. Ilyen esetben a Bayes becslő nem alkalmazható. Helyette a szakirodalom a Maximum Likelihood (ML) becslőt javasolja.
Az ML becslés előállításához definiálni kell az un. „likelihood” függvényt f ML ( b | c ), amelynek c szerinti maximum helyéhez tartozik az optimális becslés:
|
|
(5.4) |
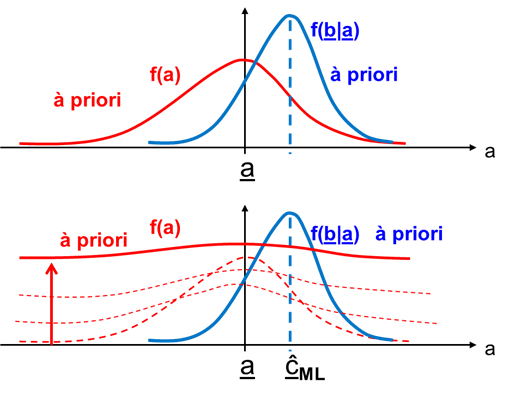
A Maximum Likelihood becslésnél tehát nem ismerjük az f( a ) sűrűségfüggvényt. Ezt a műszaki tényállást a matematika nyelvén úgy közelítik, hogy az f( a ) sűrűségfüggvény varianciáját egyre nagyobbá teszik, határátmenetben végtelen varianciát feltételeznek. Ennek következménye az (5.7. ábra) ábrán látható, azaz az f( a ) függvény egyre jobban „szétterül”. Ezért az f( a ) sűrűségfüggvénynek nincs hatása az à priori sűrűségfüggvényre, és a ML becslés majdan a f ML ( b | c ) függvény maximumához tartozó érték lesz.
Ehhez a megállapításhoz azonban még szükség van néhány lépésre. A Maximum Likelihood becslő a maximum à posteriori (utólagos) sűrűségfüggvényből vezethető le, felhasználva az ismert csatornakarakterisztikát. Felhasználva a Bayes becslőnél látott összefüggést, az alábbiakat írhatjuk fel:
|
|
(5.5) |
A továbbiak megértéséhez fontos, hogy az f( a | b ) à posteriori sűrűségfüggvényben a konstans „ a ” helyére „ c ” változó kerül, hiszen ennek a függvényében kell megkeresni a maximumhelyet. Tekintettel a változó cserére, és arra, hogy a minden határon túl megnövelt varianciájú f( a ) sűrűségfüggvény konstans lesz, f( c ) ugyancsak konstans. Ugyanakkor tudjuk, hogy f( b ) nem függ c -től, ezért az „à posteriori” sűrűségfüggvény maximum helye megegyezik a ML függvény szélső értékével, amint azt a fejezet elején láttuk.
|
|
(5.6) |
Összefoglalva megállapítható, hogy mivel nem ismerjük a mérendő paraméter eloszlását, csak a megfigyelésekre lehet a becslésnél támaszkodni. A Maximum Likelihood becslésnek azt az a = ĉ ML paraméter értéket vesszük, amely mellett a kapott f( b | a = c ) megfigyelés a legvalószínűbb, ezt szemlélteti az 5.7. ábra, ahol látható, hogy a f( b | a ) „à priori” sűrűségfüggvény maximuma az a paraméter ĉ ML értékénél van.
5.6.4. Legkisebb négyzetes hibájú becslés (LMS)
Láttuk, hogy a Bayes becslésnél a paraméter sűrűségfüggvényére és a megfigyelések (csatornakarakterisztika) sűrűségfüggvényére volt szükség, míg a ML becslésnél már csak az utóbbi áll rendelkezésre.
Ha semmilyen „à priori” ismerettel nem rendelkezünk, akkor a becslés alapja kizárólag a feltételezett modell és maga a mérendő rendszer lehet, és nyilvánvalóan az e kettő közötti eltérést kell minimalizálni.
A legkisebb négyzetes hibájú becslés (LMS) négyzetes hibakritériuma mellett sok műszaki tapasztalat szól, hiszen könnyen kezelhető, fizikailag jól megjeleníthető, és a becslő viszonylag könnyen megvalósítható.
A becslési feladat lényege tehát az, hogy a mérendő rendszer a paraméterének olyan ĉ becslését keressük, amely mellett a mérendő rendszerről nyert b megfigyelés és a modell y kimenőjelének négyzetes eltéréseként meghatározott C( a , c ) hiba minimális lesz. Tekintettel arra, hogy a paraméter, a megfigyelések, az eredmények vektor formában vannak felírva, ezt a meghatározást a következő egyenlettel lehet leírni:
|
|
(5.7) |
A C( a , c ) hibafüggvény minimumához tartozó c érték, azaz a legkisebb négyzetes hibájú becslés szélsőérték meghatározással állapítható meg:
|
|
(5.8) |
A becslési hibára vonatkozó összefüggés megjeleníthető tömbvázlat segítségével is, ezt mutatja következő ábra.
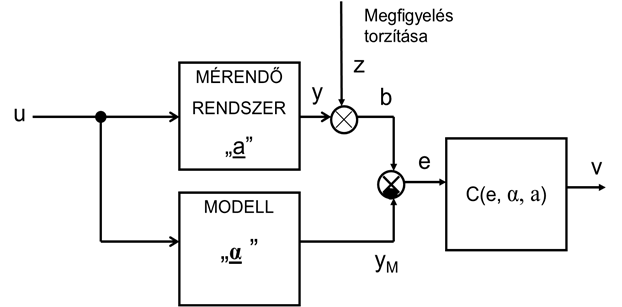
A legkisebb négyzetes hibájú becslő megvalósítására célszerű lineáris modellel való közelítést alkalmazni akkor is, ha a modell nemlineáris. Ha feltételezzük, hogy az a mérendő paraméter és a b megfigyelés közötti kapcsolat lineáris, és létezik az n torzítás, vagy zaj, akkor felírható a következő összefüggés:
|
|
(5.9) |
Az optimumkereséshez szükséges a hibafüggvény létrehozása:
|
|
(5.10) |
Az összefüggés tovább formálható:
|
|
(5.11) |
Az egyenlet c szerinti deriválásával nyerhetjük a legkisebb négyzetes hibájú becslést. Elvégezve a deriválást és figyelembe véve a számítási szabályokat, felírható, hogy
|
, |
(5.12) |
és ezzel a következő feltételt kapjuk:
|
|
(5.13) |
Átrendezés után
|
|
(5.14) |
Amennyiben az U mátrix nem szinguláris, akkor az inverzió elvégezhető, és megkapjuk az a paraméter LS becslését:
|
|
(5.15) |
Ezzel az eredménnyel kiszámítható a becslés hibája is:
|
|
(5.16) |
Tekintettel arra, hogy
|
|
(5.17) |
volt, behelyettesítéssel felírhatjuk a becslés hibáját is:
|
|
(5.18) |
Jól látható, hogy a becslési hiba nem függ a paraméter eloszlásfüggvényétől, hiszen ez amúgy is ismeretlen, viszont megjelenik benne a megfigyelés és a mérendő mennyiség lineáris kapcsolatának leírása és a zavarás hatása.
5.7. A mérés információelméleti modellje
5.7.1. A hírközlés modellje és a mérőlánc
Azon kivételektől eltekintve, ahol a mérendő mennyiség és a kijelzett villamos mennyiség között fizikai törvény formájában direkt kapcsolat létezik, általánosságban elmondható, hogy a mérendő mennyiség és a mérőeszközökre eljutó jelek között hosszabb-rövidebb átviteli láncra van szükség. Fontos kihangsúlyozni, hogy ez esetben nem villamos jelvezetékre, hanem köztes fizikai mennyiségekre gondolunk. A kijelzett érték igen sokféle zavarás torzító hatását foglalja magába. A mérés információelméleti modellje ezeket a hatásokat szemlélteti.
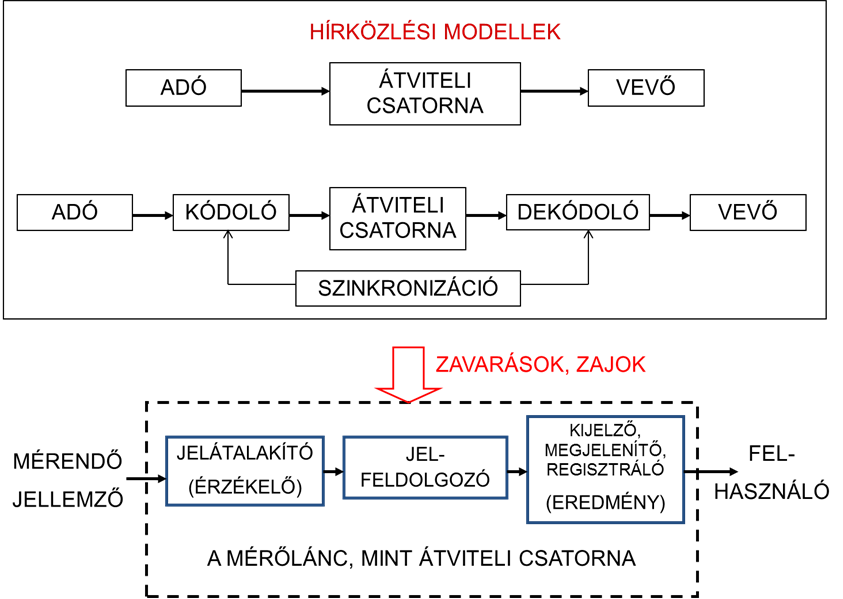
Az információelméleti modell központi része a jelátviteli csatorna, amelyet mérési feladat esetében a mérőlánc valósít meg. A mérőlánc a valóságban természetesen lényegesen több tagot tartalmazhat, esetenként átviteli tagok soros, párhuzamos és visszacsatolt formájában. A mérőlánc ebben a modellben magába foglalja a valószínűségelméleti modellben megismert mérőrendszert is, tehát az adatfeldolgozó egységet is. Az közismert, hogy a kijelzett (megjelenített) eredmény napjainkban döntően villamos jellegű mennyiség. A mérendő jellemző villamos jellé történő átalakítása már a jelfeldolgozó egység előtt megtörténik. A jelfeldolgozás alatt analóg, vagy diszkrét jelekkel való műveleteket kell érteni, amelyeket áramkörökkel, vagy számítástechnikai eszközökkel (pl. PC, adatfeldolgozó kártyák, mikrokontroller) végeznek el, de napjainkban a kijelzés és megjelenítés is gyakran már PC monitoron történik. A legfontosabb műveletek az erősítés, demoduláció, A/D és D/A átalakítás, szűrés, összegzés, integrálás, logaritmus műveletek, stb.
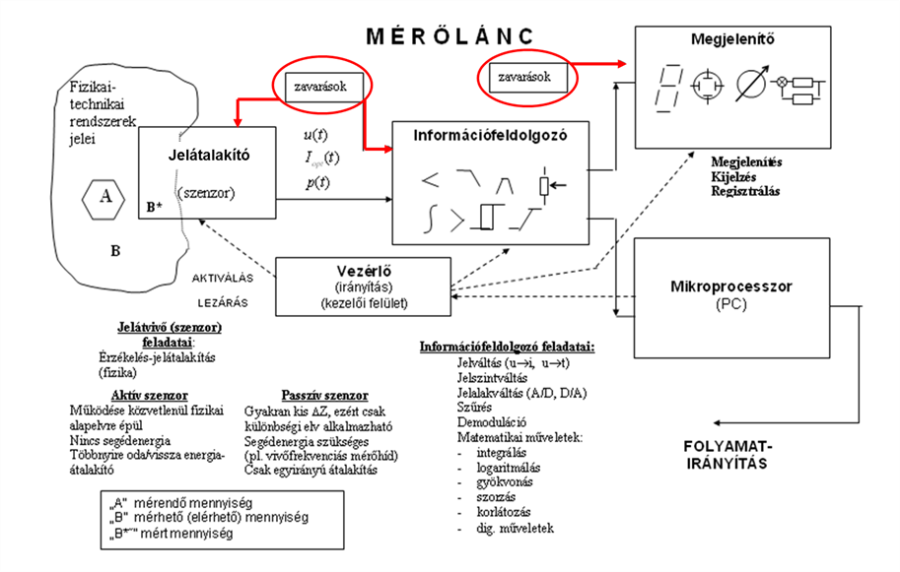
A jelátalakító a mérőlánc első tagja. Megnevezésére használatos még a jelátalakító, mérő-átalakító kifejezés is. Többnyire komplex egység, amely a mérendő fizikai mennyiséget olyan reprodukálhatóan detektálható változássá formálja, amely egy alkalmasan választott szenzor segítségével villamos (esetleg optikai, pneumatikus, stb.) jellé alakítható át.
A jelátalakító lehet persze egyben szenzor is, főként aktív (segédenergia nélkül működő) eszközök esetében, mint például a tachogenerátor esetében láthatjuk. Ez az eszköz a mozgási indukción alapulva közvetlenül, köztes mennyiségek beiktatása nélkül lehetővé teszi a fordulatszám (szögsebesség) mérését.
Igen csekély kivételtől eltekintve azonban az érzékelő (szenzor) a jelátalakítónak „csupán” egy részét képezi, és amint az előbbiekből látható, többféle mennyiség mérésére ugyanazon szenzor típus alkalmas lehet. Általában elmondható, hogy egy gépészeti mennyiség passzív szenzorokkal akkor alakítható át villamos jellé, ha olyan mérőelemet tudunk tervezni, létrehozni, amely reprodukálhatóan és kellő felbontással elmozdulássá, alakváltozássá, vagy anyagjellemző (pl. permeabilitás, optikai törésmutató, stb.) változássá képes átalakítani az eredeti mérendő mennyiséget.
Az aktív és passzív fogalmakat különböző módon lehet értelmezni . Lehet a műszer szempontjából, és lehet önmagában, a szenzor működési módja szerint vizsgálni és besorolni az eszközöket. Az [5.1.] jelű irodalomban, annak 7.1.1 fejezetében, ezt a két fogalmat a mérőeszköz „szempontjából” vizsgálják. Ezért passzív érzékelést úgy értelmezik, hogy egy fizikai rendszer energiát ad le a mérőeszköz felé. Ebben az esetben a műszer valóban passzívan viselkedik, mert kívülről „kap” energiát. Aktív az érzékelés ebben az értelmezésben akkor, ha az érzékelő működtetéséhez a mérőeszköznek energiát kell szolgáltatnia, majd információt hordozó energiát „kap vissza”, tehát az energiafolyam kétirányú.
Mi ebben a jegyzetben nem a fentiek szerint, hanem a működési módjuk szempontjából vizsgáljuk a szenzorokat . Ilyen megközelítésben teszünk különbséget „aktív” és a „passzív” érzékelők között. Működési módja szerint az aktív szenzor nem igényel segédenergiát, és a jelátalakítás többnyire fizikai törvényszerűségen alapul, amint azt a piezoelektromos, vagy elektrodinamikus eszközöknél látjuk. A passzív szenzorok ezzel ellentétben csak segédenergiával működtethetők, és gyakori a moduláció valamilyen formájának alkalmazása is. Passzív szenzorok jellegzetes példái az impedancia változáson alapuló eszközök, ilyenek az induktív, kapacitív, rezisztív elemeket tartalmazó átalakítók, mint pl. az induktív elmozdulás érzékelő, vagy a nyúlásmérő bélyeg.
A gépészeti és mechatronikai mérési feladatokra jellemző, hogy a mérendő jellemző gyakran több közvetítő mennyiségen, elérhető mennyiségen keresztül hoz létre villamosan mérhető mennyiséget, és ilyen módon villamos kimenő jelet. Ezt szemlélteti a gyorsulásérzékelés egy lehetséges formáján a következő ábra. A gyorsulást, mint mérendő jellemzőt lehet ugyanis elmozdulás, (ld.: következő ábra), vagy alakváltozás (aktív piezoelektromos szenzor, vagy passzív nyúlásmérő bélyeges szenzor), mint elérhető mennyiségek révén mérhető mennyiséggé alakítani.
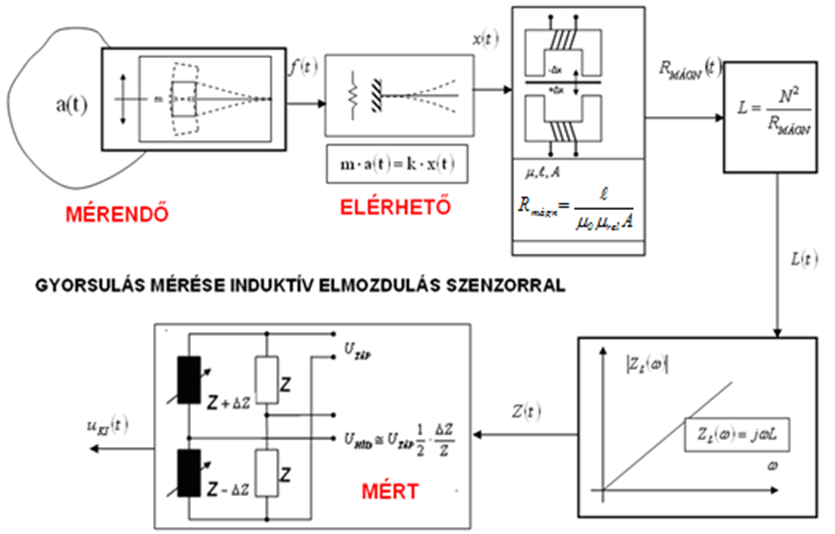
Az (5.11. ábra) ábrán bemutatott példa szemlélteti azt, hogy mérőlánc első tagja már önmagában is milyen bonyolult felépítésű lehet, és azt, hogy a többszörös átalakítás mindegyike természetesen növeli a zavarások, torzítások fellépésének eshetőségét. Az ábrán Utáp híd-tápfeszültség ω körfrekvenciájú harmonikus jel.
A bemutatott mérőlánc-részlet például önmagában már két, különböző mérési módszert is tartalmaz. Óvatosaknak kell lennünk tehát a „besorolásokkal”, mert eszközeink gyakran bonyolult felépítésűek! Meg kell jegyezni természetesen még azt is, hogy az ábrán látható Wheatstone-híd fehér színnel jelzett két impedanciája már a mérőlánc második tagjához, a vivőfrekvenciás mérőerősítőhöz tartozik, és ez a mérőerősítő szolgáltatja a híd tápfeszültségét is (UTÁP).
Mivel jelenleg nem ismeretes olyan fizikai kapcsolat, amely révén a gyorsulás közvetlenül villamos jellé átalakítható lenne, szükség van köztes mennyiségekre. A példában a szeizmikus tömegre ható gyorsító erővel tart egyensúlyt a tömeg rugalmas vezetékében ébredő rugóerő. Ez a formáció a klasszikus méréstechnika szerint „kitérítéses módszer” alapján mér. Ugyanakkor a további átalakítások végén, az előidézett impedancia változást „ különbségi módszerrel” mérjük. A műszerház és a tömeg közötti relatív elmozdulás a mérendő gyorsulással arányos. Végül a relatív távolság változását induktív elmozdulás szenzorral érzékelik, és tekintettel az így létrehozott impedancia változás rendkívül kis mértékére, az impedancia változás különbségi módszeren alapuló Wheatstone-híd szolgál.
A legdurvább, a mérési eredményt súlyos mértékben befolyásoló zavarok a híd tápfeszültségének és a vivőfrekvencia ingadozásából származhatnak, hiszen ezek a mennyiségek az eredmény részét képezik. Ha a rugalmas vezeték konstrukciója megfelelő, akkor ebből a részből jelentős zavarás nem várható, de mechanikai szempontból nagyon lényeges a jelátalakító és a csatlakozó kábel rögzítésére vonatkozó gyártói előírások betartása. Elektromágneses hatások, és földelési problémák további zavaró veszélyforrás lehetnek.
Az információelméleti modell természetesen nem csupán arra szorítkozik, hogy a mérőláncot a jelátviteli csatornának megfeleltesse, hanem elméleti megfontolásokat is tartalmaz.
Érdekesség, hogy az információelméleti modell nélkül nem lehetne például némely speciális eloszlásfüggvény esetében kiszámítani a második centrális momentumot, mert improprius integrált kapunk.
A továbbiak részletezéséhez lássuk még egyszer az információelméleti modell „méréstechnikai értelmezését”.
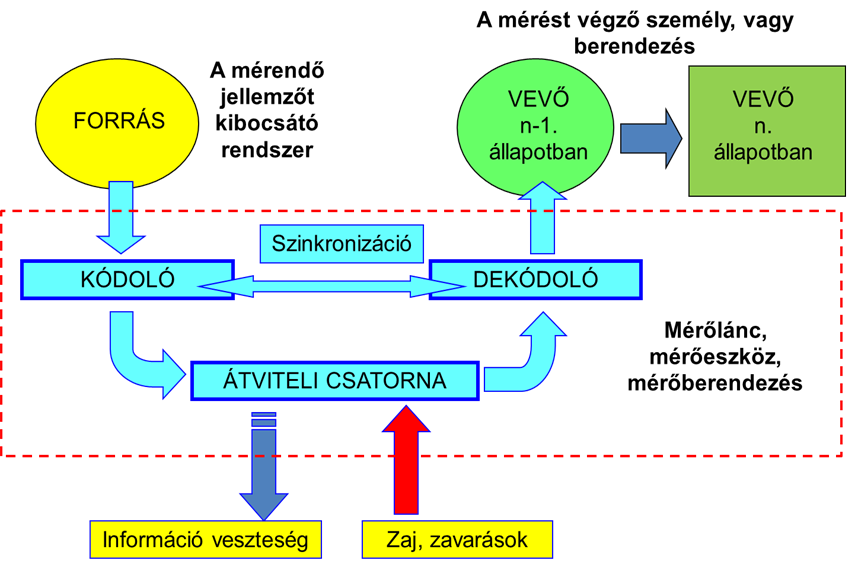
Shannon klasszikus információ átviteli modelljének „lefordítását” látjuk a fenti ábrán. Shannon szerint az információ átvitel nem öncélú, hanem a vevő (fogadó, felhasználó) oldalán a meglévő bizonytalanság, azaz információ hiány csökkentésére irányul.
5.7.2. A műszaki információ mérése
Tekintettel arra, hogy a mérést információelméleti szempontból úgy kell értelmezni, mint olyan tevékenységet, amely a mérés előtt meglévő ismerethiány (bizonytalanság) megszüntetésére irányul, természetes, hogy nézetünk szerint a műszaki információ fogalmába beletartozik a mérés útján szerzett információ is .
Ez a szemlélet a mérési tevékenység céljával tökéletes összhangban van, hiszen a mérés a hiányzó ismereteink pótlását szolgálja. Ezért nem kell meglepődni, ha a későbbiekben a méréssel szerezhető információmennyiséget a hírközlésben szokásos módon „entrópiának” nevezzük.
Az információ műszaki értelemben – látjuk a következőkben – pontosan ezt jelenti: Információ entrópia = a bizonytalanság (ismerethiány) megszűntetésének mértéke.
Méréstechnikus szemével nézve a forrás tehát a mérendő fizikai-technikai mennyiséget kibocsátó rendszer (gépi berendezés, stb.), a vevő a mérést végző személy, vagy az irányítástechnikában maga a szabályozott rendszer, pontosabban a különbségképző tag, hiszen a visszacsatolás minden szabályozott mechatronikai rendszerben mérés.
Az átviteli csatorna maga a mérőlánc, amelybe a kódoló és dekódoló is beletartozik. Ha jól meggondoljuk, nincs ebben semmi erőltetettség, hiszen például a vivőfrekvenciás mérőerősítők a legszembetűnőbben szemléltetik még a kódolás/dekódolás és ezek szinkronjának szükségességét is. A vivőfrekvenciáról csak jól szinkronozott (fázisban lévő) generátorjel segítségével lehet a hasznos, és információt hordozó moduláló jelet dekódolással leválasztani.
Az is természetes, hogy a „vevő” állapota (ismerethalmaza) a mérés eredményének függvényében megváltozik. (Másként minek fektetnénk pénzt és munkát a mérésbe, információszerzésbe?)
Mielőtt a mérés entrópiájára rátérnénk, szükséges néhány ismeret rövid összefoglalása, hiszen ahhoz, hogy a méréssel szerezhető információmennyiség „mérhető” legyen, meg kell ismernünk az információ alapegységét és mértékegységét is.
A modern információelmélet kialakulását a valószínűség számítás fejlődése alapozta meg. A valószínűség matematikai megfogalmazása régóta foglalkoztatta a gondolkodókat. Úgy tudjuk, hogy a valószínűség első tudományos igényű tárgyalása Pascal levelében olvasható, amelyet 1654. júl. 29-én Fermat-hoz írt. Bernoulli is foglalkozott a témával, és a következő megközelítést adta: „A valószínűség olyan bizonyossági fok, amely úgy viszonyul a teljes bizonyossághoz, mint rész az egészhez.” Laplace-tól származik az a formula, amelyre napjainkban is hivatkoznak: A valószínűség a „kedvező” események osztva az „összes lehetséges” eseménnyel, amennyiben minden esemény azonos valószínűséggel következhet be. Láttuk ugyanakkor a 4. fejezet fejezetben, hogy a modern valószínűségszámítás már axiómák segítségével definiál. Többek mellett Gauss, Poisson, Markov, Kotelnyikov, Hincsin, Feinstein és Fano is foglalkozott a legfontosabb véletlen folyamatok és valószínűségi eloszlások kutatásával.
Kolmogorovtól származik az a közismert egyenlőtlenség, amely az események bekövetkezésének valószínűségét a biztos (P=1) és a lehetetlen (P=0) események közé helyezte, és ezzel „számszerű” megfogalmazást tett lehetővé. Ez a gondolat „ihlette” a hírtartalom, vagy információmennyiség fogalmának megalkotóit. Már csupán olyan matematikai összefüggést kellett találni, amely jól visszatükrözi azt a felfogást, hogy a biztos eseményt sugárzó „hírforrás” (előre ismert hírtartalommal, információval) entrópiája (hírtartalma) zérus legyen, viszont, ha a hírforrás teljes bizonytalanságban hagy, azaz bármilyen hírt azonos valószínűséggel kibocsáthat, akkor az entrópiája maximális legyen. A matematikai összefüggést először Hartley javasolta 1928-ban, majd Shannon fejlesztette tovább.
H. Nyquist (1920) és R. Hartley (1928), a Bell Labs munkatársai publikáltak elsőként olyan elméleteket, amelyek később az információ „méréséhez” vezettek.
A Hartley iránti tisztelet miatt a tízes alapú logaritmus segítségével kiszámított információt „hartley (h)”-ben mérik. A „bit”-be való átszámítás a logaritmus alapok közötti áttérés segítségével lehetséges, 1 h ≈ 3,32 bit.
Az információ mérésére szolgáló mennyiség és mértékegysége nem köthető abszolút természeti állandóhoz , hanem logikai úton lett meghatározva. A Hartley, majd Shannon által javasolt „információ entrópia” (mint mennyiség) és a Tukey-féle „bit” , mint mértékegység első sorban arra való, hogy általuk a műszaki rendszerek , átviteli csatornák, tárolók, stb. műszaki kapacitásának egymás közötti objektív összehasonlítása lehetővé váljon. Az entrópia elnevezés azért került az információelmélet szótárába, mert a számításának Hartley és Shannon által javasolt módja erősen emlékeztet a termodinamikai entrópia meghatározásának módjára.
Gépészek és mechatronikusok számára ismeretes, hogy a termodinamikai entrópia gondolata R. Clausiustól származik (1822-1888), aki ezzel jellemezte a termodinamikában az anyagi rendszerek molekuláris rendezetlenségét, illetve a termodinamikai állapot valószínűségének a mértékét. Ebből következtetni lehet a maguktól végbemenő folyamatok irányára: Mindennapos tapasztalat, hogy a természetben az „egyre valószínűbb” állapotok következnek be. Például annak az állapotnak a valószínűsége, amelynél egy zárt teret úgy töltenek ki gázmolekulák, hogy azok kizárólag a tér egy meghatározott részében helyezkednek el, kisebb, mint annak a valószínűsége, hogy a molekulák a rendelkezésre álló teret egyenletesen kitöltik. Így tehát, ha P1 és P2 azokat a valószínűségeket jelzik, amelyekkel adott termodinamikus rendszer különböző állapotban való tartózkodását lehet leírni, akkor a képlet az entrópia megváltozását tükrözi („k” a Boltzmann-állandó) valamilyen folyamat során.
|
|
(5.19) |
Ilyen meggondolásból a termodinamikai entrópia a „rendezetlenség” mértéke, amely annál nagyobb, minél nagyobb az adott állapot valószínűsége.
A fentiekkel analóg módon hír (vagy hírforrás) entrópiája , azaz információmennyisége annál nagyobb, minél nagyobb a bizonytalanság, amelyet a hír közlése révén el tudunk oszlatni. Másként fogalmazva, annak a hírnek nagyobb az entrópiája, amelynek a bekövetkezési valószínűsége kisebb. Az információ tartalom mérésére szolgáló mennyiség definíciója megszületését tehát a termodinamikai rendezetlenség és az információelméleti bizonytalanság közötti hasonlóság ihlette.
Shannon, 1948-ban közölt munkájában, csak a műszaki értelemben vett információk (elsősorban digitális villamos jelek által hordozott hírtartalom) mérésére – összehasonlítás céljából - dolgozott ki módszert.
Az információmennyiségre alkalmazott „entrópia” elnevezés tehát logikai és formai okokra vezethető vissza. Az információelmélet és a valószínűségszámítás szorosan összefüggnek. A biztos esemény (itt: hír) a fogadó/vevő számára nem rendelkezik információ tartalommal (csak műszaki értelemben!), míg a lehetetlen esemény információ tartalma végtelen nagy lenne. Ezt a matematika nyelvén a valószínűség reciprokával lehetne a legjobban kifejezni.
Ugyanakkor azonban gond, hogy a biztos esemény információ tartalma ez esetben nem zérus, hanem egy lenne. Ezért a hír bekövetkezésének valószínűségét nem csak reciprokként, hanem a reciprok logaritmusaként vesszük.
Az „S” (source) hírforrás „P” valószínűséggel kibocsátott, egyetlen „h” hírének információ tartalma, más elnevezéssel hírértéke, vagy entrópiája az alábbi formula segítségével állapítható meg:
|
|
(5.20) |
Így azután az elméleti megfontolást a képlet már jobban tükrözi, és a termodinamikai entrópia képletével való formai hasonlóság szembetűnő.
Az információ alapmennyisége az „információ entrópia” (ez nem SI alapmennyiség) és alapegysége a „bit” .
Egy „S” hírforrás egyetlen „hi” hírének, valamint a hírforrás teljes jelkészletének entrópiáját a következőképpen lehet meghatározni:
|
|
(5.21) |
(ahol ld = log2 : logarithmus dualis (latin), a kettes alapú logaritmus)
Érdekesség, hogy az információ napjainkban játszott óriási szerepe ellenére, sokáig nem szerepelt az információ entrópia az SI egységek között. Ennek oka feltehetően az, hogy az információ jelenleg használt mértékegységének (bit) átszámítása anyag és/vagy energia ekvivalensbe, a kapott érték rendkívül kicsiny volta miatt, egyelőre még nehezen interpretálható. A „bit” ma már SI származtatott egység és jelenlegi energia ekvivalense 9,569940(16) × 10−24 J/K. (A Boltzmann állandó értéke 2006-ban kB = 1,380 6504(24)·10−23 J/K volt.)
Az információ mértékegységének megértéséhez és az előzőekben ismertetett összefüggések gyakorlati illusztrálásának céljából mutatunk be egy fontos számítást, mert ugyan a napi gyakorlatban ismételten használjuk információelméleti mértékegységet a „ bit ”-et, de nem biztos, hogy minden esetben világos az, hogy ez a mértékegység valójában mit takar?
Legyen egy hírforrás bináris, azaz csak két féle információt képes kibocsátani, ezek legyenek a 0, vagy 1 szintek. Ebből következően, ha rögzítjük az egyik szint valószínűségét, akkor a másik szint kiadódik: P(1)=1-P(0) és fordítva. A két jel információtartalma láthatóan nem független egymástól. Az alábbi táblázat első sorában az „1” szint valószínűségét adtuk meg 9 értékkel P(1). A második sorban ennek a jelnek az információtartalmát, míg a harmadikban a „0” jel információtartalmát tüntettük fel. Jól látszik, hogy csak a két jel valószínűsége komplementer, de az információtartalmuk már nem .
A bináris hírforrás átlagos információtartalma az előző képlet szerint összegként adódik:
|
|
(5.22) |
Megjegyezzük, hogy a táblázatban az előjelek és a log–ld átszámítás tekintetében figyelembe vettük a log azonosságokból adódó lehetőségeket.
|
P(1) |
0,00 |
0,05 |
0,1 |
0,15 |
0,2 |
0,25 |
0,3 |
0,4 |
0,5 |
|
H(1)= -[P(1) ld P(1)] |
0,00 |
0,22 |
0,33 |
0,41 |
0,46 |
0,5 |
0,52 |
0,53 |
0,5 |
|
P[1-P(1) ]=P(0) |
1,00 |
0,95 |
0,9 |
0,85 |
0,8 |
0,75 |
0,7 |
0,6 |
0,5 |
|
H(0)= -[1-P(1)]ld [1- P(1)] |
0,00 |
0,07 |
0,14 |
0,2 |
0,26 |
0,31 |
0,36 |
0,44 |
0,5 |
|
H [bit]=H(1)+H(0) |
0,00 |
0,29 |
0,47 |
0,61 |
0,72 |
0,81 |
0,88 |
0,97 |
1 |
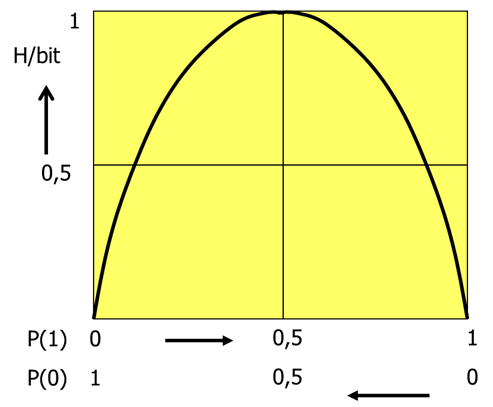
Jól látható a táblázatból, hogy ha valamelyik esemény (0 és 1) bekövetkezésének valószínűsége előre tudottan nagyobb, mint 50 %, azaz P>0.5, akkor csökken a bizonytalanság a várható eseménnyel kapcsolatban, így csökken a hír entrópiája is. Így tehát ha P(1)=0.2, akkor P(0)=0.8, azaz 80%-ban előre bizonyosak vagyunk, hogy a „0” lesz a kimenet (esemény). Ezért az erről „szóló hír” entrópiája csupán 0.72 bit. A forrás információtartalma akkor lesz maximális, ha semmilyen előzetes ismeretünk nincsen arról, hogy melyik jelszint előfordulása valószínűbb. Ugyanakkor a táblázat első oszlopában látszik, hogy amennyiben az 1 jel egyáltalán nem fordulhat elő, azaz P(1)=0, akkor a 0 jel valószínűsége 100 %-os, azaz P(0)=1. A hírtartalom mindkét jelre vonatkozóan nulla – amit az eddigi fejtegetések alapján már sejtettünk is.
Maximális lesz a hír entrópiája, azaz 1 bit, ha mindkét esemény bekövetkezési valószínűsége azonos.
Az értéktáblázat alapján készített diagram látható a következő ábrán.
A maximális hír entrópia természetesen nem csak értéktáblázattal mutatható ki. A függvényvizsgálat szabályi szerint kereshetjük az átlagos hírtartalom szélsőértékét, és első lépésben a differenciálási szabályok miatt áttérünk természetes logaritmusra:
|
|
(5.23) |
Az utolsó sor egyszerűbben is írható:
|
|
(5.24) |
A függvénynek szélső értéke van, ha
|
|
(5.25) |
Ez csak akkor lehetséges, ha a zárójelben lévő kifejezés lesz zérus, így felírható, hogy
|
|
(5.26) |
Befejezésként ellenőrizzük, hogy maximum, vagy minimum helyről van szó? A második derivált P1=0.5 értékre negatív lesz, tehát maximumot találtunk.
|
|
(5.27) |
Nagyon fontos az is, hogy a hír és az információ fogalmai ne keveredjenek! A „hír” kifejezés hétköznapi használata miatt gyakran téves képzetek keletkezhetnek.
Műszaki értelemben a hír megléte még nem feltétlenül jelenti azt, hogy annak van információtartalma is. (Némi szarkazmussal, persze ez a megállapítás tágabb értelemben is igaz lehet.)
Először tehát néhány fontos információelméleti fogalom rövidített, tömör leírása következik:
A jel időben és/vagy térben lezajló fizikai, vagy kémiai folyamat, információhordozó.
A műszaki „hír” időben és/vagy térben korlátozott jel.
A hírkészlet az összes lehetséges hír.
Az információ a bizonytalanság mértéke, amelyet a hír megszűntet.
5.7.3. Entrópia a méréstechnikában
A mérés és a mérési hiba entrópiájának objektív meghatározása lehetővé teszi, hogy a mérési tevékenység minősítésével kapcsolatban megalapozott elméleti megállapításokat tehessünk. Ezek alapja a mérés információelméleti modellje.
-
Méréssel csökkentjük az adott méréstechnikai probléma információelméleti entrópiáját (Az „ismeretlen” felderítésével csökken a bizonytalanság.)
-
Ha a mérési adatokról, amelyek valószínűségi változók, van előzetes ismeret, akkor viszont a „forrás” entrópiája csökken, és ezáltal a méréssel szerezhető információ entrópiája is csökken.
-
A hiba információelméleti entrópiája tovább csökkentheti a méréssel megszerezhető entrópiát.
-
A mérés kivitelezésére nézve fontos útmutatás, hogy az entrópia bármilyen csökkenése azt jelenti , hogy az elvégzett méréssel az adott mérési feladatról (mérendő mennyiségről) az optimálisnál kevesebb információt tudunk majd csak megszerezni.
A méréssel szerezhető információmennyiség meghatározásához támaszkodnunk kell a mérés valószínűségelméleti modelljénél megismert à posteriori ismeretek matematikai megfogalmazására, amit az f(a|b) feltételes sűrűségfüggvény ír le. Ennek a sűrűségfüggvénynek a felhasználásával meghatározható a valószínűség, és az előzőekben bemutatott összefüggésekkel az entrópia is. Az à posteriori sűrűségfüggvény segítségével tulajdonképpen a mérési hiba írható le, hiszen egy adott, megfigyelt (megismert) „b” értékhez rendeli hozzá a mérendő „a” jellemző sűrűségfüggvényét.
A mérendő jellemzőt ebben a modellben a méréstechnikában szokásos módon „a” helyett „x” és a megfigyelt mennyiséget „b” helyett xm” betűvel jelöljük. A mérési hiba entrópiáját jelöljük H(x|xm) és a mérendő jellemző sűrűségfüggvényével kiszámítható à priori (előzetes) ismerethiányunk entrópiáját H(x) függvénnyel.
A mérés eredményeként megkapható „Q” információmennyiség számítása ezekkel:
|
|
(5.28) |
A mérés információtartalmának számítását egy egyszerű példán lehet illusztrálni. Legyen a csupán egy digitális kijelzésű mérőműszerről szó, amelynek bizonytalansága a teljes mérési tartomány bármely részén egyformán 2Δ (±Δ). A mérés előtt a mérendő mennyiségről csak annyi információval rendelkezünk, hogy az [x1; x2] tartományba esik.
Az entrópiák számításához szükséges sűrűségfüggvények ezek alapján megadhatók, ezt mutatja a következő ábra.
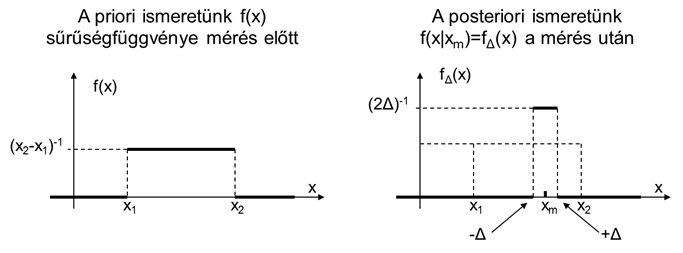
Az ábrák alapján a sűrűségfüggvények megadhatók, hiszen egyenletes eloszlásról van szó:
|
|
(5.29) |
Az entrópiák kiszámításához a valószínűségekre van szükség. Ismeretes a valószínűségszámításból, hogy:
|
|
(5.30) |
Ezzel meghatározható a mérés előtti bizonytalanság entrópiája H(x) (az ismerethiány) entrópiája:
|
|
(5.31) |
|
|
|
(5.32) |
Továbbá a hiba entrópiája H(x|xm):
|
|
(5.33) |
Ezekkel azután a méréssel szerezhető információmennyiség (entrópia) a következő lesz:
|
|
(5.34) |
Ha az így meghatározott entrópiát konkrét mérőműszer esetére alkalmazzuk, akkor a legegyszerűbb egy digitális kijelzésű finomtapintóra gondolni.
Legyen az egyszerű számítás miatt a műszer mérési (kijelzési) tartománya ±64 μm, a kijelzés bizonytalansága pedig ±1 μm. Ezekkel az értékekkel a méréssel szerzett információ mennyisége 6 bit:
|
|
(5.35) |
Már az információelméleti modell bevezető soraiban jeleztük, hogy az ilyen jellegű mérési eredmény interpretálása önmagában nem egyszerű. A modell nyújtotta lehetőség inkább abban rejlik, hogy mérőeszközöket és mérőrendszereket egymás között a matematika eszköztárával objektíven össze tudjunk hasonlítani. Akkor ugyanis, ha olyan mérőműszert választunk, amelynek mérési tartománya változatlan mérési bizonytalansággal már 200 mm lesz, ami egyébként az előzőhöz képest egy elég magas ár-kategóriájú mérőműszert jelent, a fenti információnyereség már 16,7 bit lesz.
Irodalmak
[5.1.] Jelek és rendszerek méréstechnikája. Műszaki Könyvkiadó. 1985.
[5.2.] General Systems Theory. Matematical Foundation . Academic Press. New York . 1975.