4. fejezet - Mérés és valószínűség számítás
- 4.1. Mérési adat, mint valószínűségi változó
- 4.2. Relatív gyakoriság és a valószínűség
- 4.3. Eloszlásfüggvény, sűrűségfüggvény
- 4.4. Egydimenziós eloszlások elméleti és empirikus paraméterei
- 4.5. Normál eloszlás, vagy Student eloszlás
- 4.6. Az eredményképlet konfidencia intervallumának meghatározása
- 4.7. Statisztikai próbákról röviden
- Irodalmak
A Méréstechnika című jegyzetben közölt [1.1.] olyan fontosabb valószínűség számítási ismereteket, amelyek e jegyzet megértése szempontjából nélkülözhetetlennek tartunk, ebben a fejezetben tömören összefoglaljuk. A valószínűségszámítási vonatkozásokra az eredmény alakjának ismertetésénél már utaltunk.
4.1. Mérési adat, mint valószínűségi változó
A véletlen változókat – ilyenek a mért értékek is – okok rendszere hozza létre, illetve befolyásolja. Ez az „okság törvénye”. Ha valamennyi okot, körülményt és hatótényezőt módunkban állna figyelembe venni, akkor a mérés eredményében e befolyásoló tényezők hatását korrekció formájában meg lehetne adni. Ez azonban tapasztalataink szerint lehetetlen, ezért csak az ismert hatásokat vesszük figyelembe a korrekcióban. Az előre nem ismert, véletlen hatások következményeit mérési bizonytalanságok formájában foglaljuk össze.
A mérés modellezésében beszélnek ú.n. kauzuális és sztochasztikus szkémáról. A méréselméletben a kauzalitás azt jelenti, hogy amennyiben a meghatározott feltételek összessége fennáll, akkor az esemény biztosan bekövetkezik. Ebbe a kategóriába sorolhatók a fizikai törvények által leírt jelenségek, hiszen például, ha ismerjük egy test tömegét és gyorsulását, akkor az erő statisztikai módszerekkel kiszámított bizonytalansággal mérési adatokból meghatározható. A sztochasztikus jelenségek egzakt leírása nehezebb, mert az ismereteink hiányosak. Ennek műszaki-tudományos, vagy gazdaságossági okai lehetnek. Jól példázza ezt a szkémát a rezgő gépi berendezések által kibocsátott zaj spektruma és hangnyomásszintje. Ismert a fizikai kapcsolat, de az azt leíró modellek csak közelítő jellegűek.
A mérési adatot véletlen elemi eseményként kell felfogni. A gépészetben vannak időben állandó mérési adatok, ilyenek például az alkatrészek hosszméretei, és vannak időben folytonosan változó adatok, ezek közé tartozik az előbbiekben említett rezgés amplitúdó, vagy a géprezgések által keletkező hangnyomásszint ingadozása. Valószínűség számítási szempontból mindkét típust folytonos változónak kell tekinteni, mert adott határok között elvben végtelen sok érték előfordulhat.
Ha az azonos mérési adatok, vagy egy osztály elemeinek abszolút gyakoriságát az összes mérési adatra vonatkoztatjuk, akkor kapjuk a relatív gyakoriságot.
4.2. Relatív gyakoriság és a valószínűség
A mért értékeket – kerekítés után - szokás úgy osztályokba (részintervallumokba) sorolni, hogy a legnagyobb és legkisebb mért érték közötti tartományt - ezt nevezzük terjedelemnek – felosztjuk intervallumokra. Ezek az intervallumok lehetnek azonos szélességűek, ez a méréstechnikában a gyakorlat, de lehetnek különbözőek is. Célszerűen az intervallum-határok középértékével jellemezzük az adott osztályt.
Csoportosított, osztályba sorolt adatok esetén a számításokat leegyszerűsíti, ha a részintervallumok egyforma Δx szélességűek, amint arról G.A. Korn és T.M. Korn a Matematikai kézikönyv műszakiaknak című munkájukban írnak [4.1.] .
A statisztikai jellemzők (korrigált tapasztalati szórás, átlag) értéke csupán a méréstechnikában szokásos hibahatáron belül különbözik, ha osztályba sorolással kapott, vagy az egyedi mérési adatokkal számítjuk ki ezeket.
A relatív gyakoriság alatt az adott osztályban való előfordulás összes mérési adathoz való viszonyítását értjük. A relatív gyakoriság definíciója:
|
|
(4.1) |
ahol n a mintanagyság, nA pedig az „A” esemény előfordulásának száma.
A hasonlóság miatt nagyon fontos kihangsúlyozni ezen a helyen, hogy a valószínűségre Laplace által adott értelmezést (t.i.: A kedvező események száma osztva az összes lehetséges esemény számával) a modern matematika másként fogalmazza meg. A matematika a valószínűséget nem a bekövetkezés relatív gyakoriságának segítségével értelmezi, hanem definiáló axiómákkal .
A matematikában a valószínűség fogalma ugyanis nem azonos a szó köznapi jelentésével! Ugyanakkor ezek az axiómák a relatív gyakorisággal kapcsolatban vannak, annak lényeges tulajdonságait absztraháljuk segítségükkel. A valószínűség és a relatív gyakoriság közötti kapcsolat az, hogy ha egy kísérletet egymástól függetlenül végtelen sokszor megismételnénk , akkor a bekövetkezés relatív gyakorisága minden eseményre a megfelelő valószínűséghez tartana. Ezt mutatja be a 4.1. ábra.
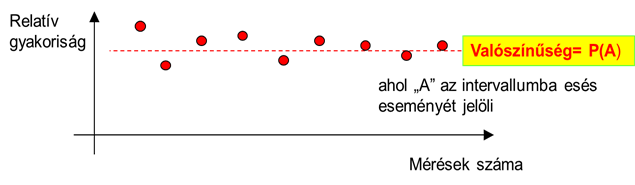
Fontos ugyanakkor hangsúlyozni, hogy a fent ábrázolt összefüggés nem azt jelenti, hogy a relatív gyakoriság limese (analízisbeli határértéke) a valószínűség lenne. E jelenség mögött egy másfajta konvergencia húzódik meg, amelyet sztochasztikus limesnek neveznek.
Az ábrán látható, hogy a relatív gyakoriság maga is valószínűségi változó , és a mérések számának növelésével, ideális esetben, csillapodik a relatív gyakoriság ingadozása. Az ábrán a valószínűséget az angol „probability” kifejezés miatt jelöltük a valószínűség számításban szokásos „P” betűvel.
Kolmogorov munkásságára alapozva a valószínűséget halmazelméleti alapon közelítik meg. Eszerint a P(A) valószínűségek az eseménytér halmazain adott halmazfüggvénynek, a valószínűségfüggvénynek értékei. Ez a függvény valószínűség eloszlást definiál az eseménytérben. A „T” halmaz a méréselméletben egy adott kísérlethez tartozó eseménytér , más kifejezéssel valószínűségi alaphalmaz . A „T” eseménytérben értelmezett, mérhető „x” függvényt valószínűségi változónak nevezzük. A valószínűségi változó értékkészletének részhalmazain ennek révén létesített valószínűség eloszlást az „x” valószínűségi változó eloszlásának nevezzük.
A méréstechnikában az „x” változó minden mintavételi értékét egy elemi eseményt definiáló mérési eredménynek feleltethetjük meg. Az adott kísérlethez tartozó valószínűségeket a valószínűségi változó egyértelműen meghatározza.
A témával mélyebben foglalkozni kívánók számára a Prékopa A.: Valószínűségelmélet című munkáját is [4.2.] ajánljuk.
4.3. Eloszlásfüggvény, sűrűségfüggvény
A relatív gyakoriság hisztogramon ábrázolható. A vízszintes tengelyen állandó, vagy változó Δx osztályszélesség, a függőlegesen a relatív gyakoriság jelenik meg. A hisztogramon látható négyszögek (oszlopok) területe a relatív gyakoriságnak felel meg:
|
|
(4.2) |
Az összefüggésben megjelenő f(x) függvény a sűrűségfüggvény . Definíciószerűen az f(x) sűrűség függvényt az F(x) eloszlásfüggvényből származtatják. Legyen „x” folytonos valószínűségi változó eloszlásfüggvénye F(x), és ha ez a függvény deriválható, akkor a sűrűségfüggvény:
|
|
(4.3) |
minden xi értékre.
Az „x” változó [-∞, xi] tartományban való előfordulásának valószínűsége az alábbi összefüggéssel számítható:
|
|
(4.4) |
A P(x≤xi) valószínűség tehát a valószínűségsűrűség-függvény értéke xi helyen.
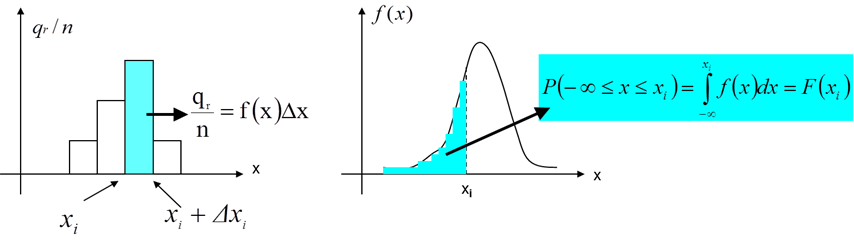
Belátható, hogy a valószínűségi változó a [-∞,+∞] tartományban bizonyosan megtalálható, és az alábbi összefüggés rendkívüli fontossággal bír a számítások során:
|
|
(4.5) |
Továbbá a fentiek alapján:
|
|
(4.6) |
A fenti valószínűségszámítási definíciók méréstechnikai alkalmazása során fontos, hogy tisztán lássuk az integrálási határokat. A méréstechnikában általában az a kérdés, hogy egy olyan adott tartományban keressük egy változó előfordulásának valószínűségét, amely tartomány alsó határa nem „-∞”. Ezért, ha azt vizsgáljuk, hogy egy változó (mérési adat) mekkora valószínűséggel fordul elő az [a, b] tartományban, akkor az alábbi összefüggést kell valamilyen formában alkalmaznunk:
|
|
(4.7) |
4.4. Egydimenziós eloszlások elméleti és empirikus paraméterei
Ha tehát az előbbiek szerint az „x” egydimenziós, folytonos valószínűségi változó, amint az a mérési adatok esetében is jellemző, akkor a változó f(x) sűrűségfüggvényének elméleti, várható értékét az alábbi képlettel lehet meghatározni:
|
|
(4.8) |
Jelölésként a szakirodalomban mind az „E”, mind pedig az „M” betű előfordul. Az utóbbi arra utal, hogy a várható érték más néven az első centrális momentum. Ugyancsak előfordul a „ξ” szimbólum mellett a „μ” jelölés is.
Ugyanezen változó varianciáját (szórásnégyzetét) pedig a következő összefüggéssel definiálják:
|
|
(4.9) |
Fontos tudni, hogy „E{x}” és „D2{x}” nem függvényei „x”-nek, hanem ezek olyan paraméterek, amelyek az „x” valószínűségi változó eloszlásának két fontos tulajdonságát jelenítik meg. A matematika nyelvén kifejezve ezek un. funkcionálok . A változó eloszlásának elhelyezkedésére az „x” tengely mentén az E{x}, és az „x” változó szóródásának mértékére a D2{x} ad jellemzést. Az egydimenziós eloszlásoknak további tulajdonságainak leírására szolgálnak még más paraméterek is, úgymint a „ kvantilisek ”, amelyek egyik formája a „medián”, vagy a „ferdeség” és a „lapultság” mérőszámai. Különböző szakterületeken (biológia, szociológia, statisztika, stb.) e további paraméterek segítségével a vizsgált jelenségek nélkülözhetetlen jellemzését biztosítják.
A méréstechnikában az empirikus (tapasztalati úton) szerzett adatok feldolgozása során nem a fenti elméleti paraméterekkel, hanem empirikus paraméterekkel dolgozunk, amelyeket más összefüggésekkel nyerhetünk. Előfordul természetesen, hogy korábbi tapasztalatok alapján ismert a valószínűségi változó f(x) sűrűségfüggvénye, vagy egy gyártási folyamatban, a műszaki rajzon rögzített (előírt) egy várható érték. Ez utóbbi esetben például az lehet a kérdés, hogy a munkadarab vizsgált mérete a gyártmányok ellenőrző mérése során milyen empirikus átlagértéket mutat, és ez milyen mértékben tér el az előírt értéktől.
Az átlag az empirikus eloszlást jellemző paraméter:
|
|
(4.10) |
Az átlag meghatározása után már sor kerülhet a tapasztalati (empirikus) szórás, vagy a korrigált tapasztalati szórás kiszámítására is. Ezek ugyancsak paraméterek:
Tapasztalati szórás:
|
|
(4.11) |
A képletben „δ” az abszolút hibát jelöli. Az összefüggés alkalmazása kellő óvatosságot igényel. Az átlagértékhez viszonyítva kis eltérések és nagyszámú mérési adat esetében mutat elfogadható egyezést a tapasztalati szórás és a korrigált tapasztalati szórás értéke. Nincs tehát általánosan érvényes szabály, de megjegyezzük, hogy statisztikai szempontból a „nagyszámú” adat 100-nál többet jelent.
A mindennapos mérési gyakorlatban használatos paraméter a korrigált tapasztalati szórás :
|
|
(4.12) |
A „szabadságfok” n-1, hiszen az átlag számításához már felhasználtunk „n” mérési adatot, és a fenti képletben szerepel az „n” adatból kiszámított átlag maga is.
Bizonyos feltételek teljesülése mellett használatos a méréstechnikában az átlag szórása is. Ha több, legalább 3 mérési sorozatot végeztünk el, és a sorozatok hossza egyenként legalább 10, továbbá az egyes sorozatok szórása kellő mértékben megegyező, akkor lehetséges a teljes minta szóródásának jellemzésére az átlag szórását is megadni. A mérési sorozatokból ugyanis külön-külön meghatározható egy-egy „xi” átlagérték. Ezek az átlagok maguk is valószínűségi változók, de nyilvánvalóan kisebb mértékben szóródnak, mint az egyes adatok.
Az átlag diszperziójának meghatározását a következő levezetésben láthatjuk, ha a leírt feltételek teljesülnek:
|
|
(4.13) |
A (minimálisan) három átlagértékből meghatározható az átlagok átlaga és az átlag szórása is. Az átlag szórása kisebb bizonytalanságot eredményez, mint a teljes minta szórása.
Az átlag szórásának becslése tehát a tapasztalati szórással és a korrigált tapasztalati szórással történhet, ha a megfelelő feltételek teljesülése adott:
|
|
(4.14) |
|
|
|
(4.15) |
4.5. Normál eloszlás, vagy Student eloszlás
A normál eloszlás sűrűségfüggvényében két paraméter (funkcionál) látható, μ „várható érték” és σ „szórás”. Ezek becslésére szolgál az átlag és a tapasztalati szórás.
Mindenekelőtt fel kell tenni a kérdést, hogy a mérési eredményeinkből számított átlagérték és a tapasztalati szórás mennyire adnak megbízható információt a valóságról?
|
|
(4.16) |
Láttuk, hogy mérési sorozatok esetében az átlagok átlagával becsüljük a várható értéket.
A szórást általában sajnos nem ismerjük, helyette a korrigált tapasztalati szórást alkalmazzuk az eredményben , a kiterjesztett bizonytalanság meghatározásához. Az eredmény szokásos alakjaival a (2.9. szakasz) fejezetben találkozhattunk. Az eredményben két fajta bizonytalanság becsléssel dolgozhatunk (A és B típus), az eredmény forma egységesítését nemzetközi szabványok írják elő.
Az eredményben látható a kiterjesztett bizonytalanság faktora, amelyet az ipari méréstechnikai előírások 95 %-os konfidencia (megbízhatósági) szintre általában k=2 értékben határoznak meg. Joggal felmerül a kérdés, miért éppen ez az előírásokban javasolt érték?
A statisztikai táblázatokból látszik, hogy n=30 darabos minta esetében, Student-eloszlást feltételezve, a bizonytalansági intervallum meghatározásához szükséges faktor 95 %-os konfidencia szinten jó közelítéssel 2. A normál eloszlás faktora nem függ a minta számától, és ismeretes, hogy 95,45 % esetén értéke éppen 2. Az összehasonlíthatóság érdekében, a következő ábrán látható a két eloszlás típushoz 95 %-os konfidencia szinten tartozó faktorok értéke. Az is látható egyúttal, hogy Student eloszlás esetében nem várható a bizonytalansági tartomány jelentősebb csökkenése, ha a minta nagyságát 30-ról 100-ra növeljük, és közben megtartjuk a 95 %-os konfidencia szintet.
Az elvégzendő munka mennyisége nincs arányban a remélhető „hozammal”.
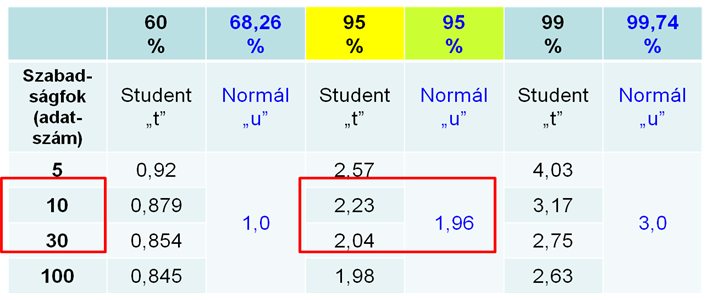
Látva a faktorok a (4.3. ábra) ábrán kiragadva bemutatott értékeinek feltűnő különbözőségét, joggal merül fel a kérdés: Milyen esetben feltételezhető normál és mikor Student eloszlás? Lehet a mintából következtetni az eloszlás típusára és paramétereire?
A gépészeti méréstechnikában alapvetően két eloszlás típussal találkozunk, a normál eloszlással és a Student eloszlással . Tapasztalható ugyanakkor, hogy a mérésekkel foglalkozó szabványok, előírások gyakran indoklás nélkül feltételezik a normál eloszlást a mintákra. Ez a feltételezés a központi határeloszlás tételen alapszik. A központi határeloszlás tétel azt mutatja meg, hogy nagyszámú, független valószínűségi változó összegének eloszlása közelítően normális eloszlást követ, ha ezen összeg minden egyes tagja külön-külön elhanyagolhatóan kicsiny az összeghez képest.
A tételre tipikus alkalmazási példaként ugyanis a véletlen mérési hibákat szokták felhozni. A mérési eredményre elméletben „végtelenül” sok, egymástól független zavaró, véletlenszerű tényező gyakorol hatást. Ezen összetett hatások eredményeként alakul ki a véletlen mérési hiba, és a gyakorlat azt igazolja, hogy az esetek túlnyomó többségénél a véletlen hibák normális eloszlást követnek.
Ha azonban a véletlen hatások nem összegződnek, hanem például szorzódnak, akkor már csak az adott mennyiség logaritmusa lesz megközelítően normális eloszlású.
Az eloszlás típusának ellenőrzésére statisztikai próbák léteznek, ezzel a témakörrel ebben a fejezetben később röviden foglalkozunk.
A gépészeti méréstechnikai gyakorlatban sokszor előfordul, hogy a rendelkezésre álló, viszonylag kisszámú adat miatt, tudományos módszerrel nem igazolható megnyugtatóan a normál eloszlás hipotézise. A Gauss-féle normál eloszlás mellett ezért kell ismerni a „t”, vagy Student eloszlás tulajdonságait is. A véletlen „x” változóra Gauss-féle eloszlást feltételezve, W. S. Gosset 1908-ban publikálta az un. „t” paraméter sűrűség és eloszlás függvényét. A „Student” elnevezés onnan ered, hogy Gosset ezen a szerzői néven jelentette meg munkáit. A „t”-eloszlás összefügg a standardizált normál eloszlással, ott, az „u” veszi át a „t” paraméter szerepét.
Ugyanakkor a gyakorlat számára érdemes tudni, hogy un. nagy elemszámok esetén, pl. 100 felett, már jogos lehet a normál eloszlás feltételezése, ha egymástól független tényezők befolyásolják a mérési hibát, és ennek alapja a központi határeloszlás tétel. Nincs éles határvonal az elemszám tekintetében, de ha – és a gépészetben ez a gyakoribb eset – nem áll rendelkezésre „nagyszámú” minta, azaz a mérési adatok száma jóval 50, pontosabban 30 alatt van, akkor járunk el helyesen, ha Student eloszlást feltételezünk. Így ugyanolyan konfidencia szint mellett nagyobb lesz a bizonytalansági tartomány, de kisebb a tévedés kockázata.
4.6. Az eredményképlet konfidencia intervallumának meghatározása
Empirikus (gyakorlati) mérési adataink alapján a várható értéket nem tudjuk meghatározni, hiszen láttuk, hogy ehhez ismerni kellene az f(x) sűrűség függvényt, és „végtelen” számú mérést kellene végrehajtani. Ezért természetesen felmerül a kérdés, hogy ebben az esetben miként lehet az átlag és a várható érték közötti eltérést megbecsülni? A várható értéket „X”-szel jelöljük. A becslés „bizonytalansági tartománya” lesz adott valószínűségi szinten a konfidencia intervallum, amint a (4.4. ábra) ábrán látható. Sőt, tovább is lépünk. Az átlag ebben az esetben az átlagok átlaga lesz, azaz a számegyesen látható x1, x2, és x3 értékek egy-egy részhalmaz átlagai. Láttuk ugyanis a (4.4. szakasz) fejezetben, hogy a várható érték legjobb becslését az átlagok átlaga adja, és az átlag szórása kisebb, mint egy részhalmaz adatainak szórása. A konfidencia intervallum szemléltető ábrája Halász G. előadási anyagának alapján készült.
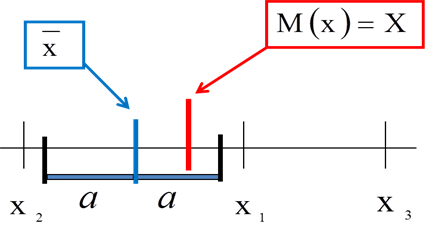
A konfidencia intervallum, akár csak az átlagérték, véletlen helyzetű, ezért csak azt tudjuk megadni, hogy „X” az adott tartományon belül mekkora valószínűséggel helyezkedik el. Az átlag körül rajzolható egy „a” sugarú intervallum, amely adott „p” valószínűséggel tartalmazza majd a várható értéket.
|
|
(4.17) |
Méréstechnikai feladtatok kiértékelése során gyakran másként fogalmazzuk meg a feladatot, de a lényeg nem változik. Meg kell keresnünk egy adott konfidencia szinthez tartozó „a” értéket.
A megoldáshoz első lépésben kissé átrendezzük az összefüggést:
|
|
(4.18) |
A továbbiakhoz szükséges két esetet megkülönböztetni:
-
Ismert a minta σ szórása (korábbi mérések, stb. alapján)
-
A szórás ismeretlen, a minta alapján kell becsülnünk: s*
Ha ismert a minta szórása, akkor a fenti összefüggésben osztunk a korábbiakban már megismert átlag szórásával (ld.: 4.4. szakasz fejezet):
|
|
(4.19) |
A következő lépésben olyan jelöléseket vezetünk be, amelyeket a későbbiekben még alkalmazni fogunk. A szakirodalomban kétféle jelöléssel találkozhatunk, „λ” helyett gyakran „u” szerepel, ha az eloszlás normális.
|
|
(4.20) |
Megfordítható az egyenlőtlenségben középen álló összefüggés számlálója
|
|
(4.21) |
mert a kifejezésből adódó érték egyik esetben az alsó, a másikban a felső határhoz esik közelebb. A táblázatokban ugyanakkor az eltérés (hiba) szabályos alakja szerepel, ez pedig a második változat.
Ha feltételezhető, hogy az „x” változó normál eloszlású, akkor a fentiekkel juthatunk el az un. standardizált normál eloszláshoz, amely egyparaméteres, a paraméter u, vagy λ. Többféle változatban és jelöléssel látható ez a szakirodalomban, és a szórás lehet az átlag szórása is:
|
|
(4.22) |
A következő ábrán a normál eloszlás sűrűségfüggvénye és az eloszlásfüggvénye van ábrázolva úgy, hogy a standardizált normál eloszlás paraméter értékeit piros színnel jelöltük.

Ha a szórás ismeretlen, és a minta alapján a korrigált tapasztalati szórással (s*) becsüljük a szórás elméleti értékét, akkor η-ról sem állíthatjuk, hogy normál eloszlású, ezért η* jelölést kap. Ezzel az egyenlőtlenségben látható kifejezés az alábbi alakú lesz:
|
|
(4.23) |
A (3. fejezet) fejezetben, a hibák bemutatásánál már említettük, hogy W. S. Gosset igazolta, hogy η * (más jelölése „t” ) eloszlása kis mintaszámok esetében jelentősen eltér a normálistól. A λ st vagy t faktor függ a szignifikancia szinttől és a mérések számától. A szabadsági fok „DF” eggyel kevesebb, mint a minta elemszáma. A különbség jelentős, mert a normál eloszlás esetében a faktor független az elemszámtól.
Összefoglalva a konfidencia intervallum „a” sugarának meghatározását a két esetre az alábbiakat állapítjuk meg:
Ha a szórás ismert, és normál eloszlást feltételezhetünk, akkor a konfidencia intervallum sugara csak a konfidencia szinttől függ. Adott „p” valószínűséghez megkeressük F(u) értékét (más jelöléssel Φ(λ)), és ezzel „a” értéke kiszámítható:
|
|
(4.24) |
Ha a kisszámú adat áll rendelkezésre, és szórás ismeretlen, becslésére a s* korrigált tapasztalati szórást alkalmazzuk, akkor adott „p” valószínűség és a szabadságfok (DF) ismeretében (DF=n-1) kiválasztjuk λSt, vagy „t” értékét, és az alábbi összefüggéssel számolunk:
|
|
(4.25) |
A „λ”faktor két tényezőtől való függését szokás a következőképpen jelölni: λ(p, n-1).
4.7. Statisztikai próbákról röviden
A következőkben G. A. Korn és T. M. Korn: Matematikai kézikönyv műszakiaknak c. [4.1.] munkájára támaszkodva összefoglaljuk azokat a próbákkal kapcsolatos legfontosabb ismereteket, amelyek a méréselmélet és méréstechnika szempontjából fontosnak tartunk.
Gyakori feladat a méréstechnikában annak eldöntése, hogy a mért adatok eloszlásával kapcsolatban egy „nullhipotézis” (kiinduló feltételezés) „kiállja-e” a próbát.
Paraméteres próba:
Ismert az eloszlás, csak az eloszlásra jellemző paramétereket kell ellenőrizni. A próba elutasítja a hipotézist, ha a minta egy előre kijelölt kis valószínűségű tartományba esik.
Nemparaméteres próba:
Az elméleti eloszlásfüggvény paraméterekkel nem kifejezhető tulajdonságaira irányul, ilyen pl.: két eloszlás azonossága, két valószínűségi változó függetlensége. Különösen előnyös a méréstechnikai gyakorlatban, mert nem követeli meg a minta sűrűségfüggvénye alakjának ismeretét.
A próba egy „ null-hipotézis ” (jele: H 0 ) felállításával indul.
A hipotézis vizsgálat során lényegében arról van szó, hogy az adott minta (mérési adatsor: X1, X2,…Xn) alapján elfogadjuk, vagy elvetjük-e a „H 0 ” feltételezést , hipotézist . Ezt nevezi a szakirodalom statisztikai próbának.
A feltételezés, idegen szóval hipotézis (jelölése „H”) lehet egyszerű és összetett. Az „egyszerű” hipotézis a vizsgált eloszlás paramétereinek μ, σ, … stb. egy-egy meghatározott értékét μ=μ0, σ=σ0, stb., azaz a paramétertér egy pontját jelöli ki. Az összetett hipotézis a μ, σ, … stb. pontok egy halmazát, illetve tartományát jelöli ki a paramétertérben.
Fejezetünkben a legegyszerűbb forma, az egyszerű hipotézis vizsgálatával foglalkozunk.
A hipotézist empirikus (kísérleti úton nyert) adatok alapján ellenőrizzük. A statisztika tudományterülete definiált egy S c kritikus tartományt, amely a statisztikai próbához tartozó azon pontok halmaza, amelyek esetében a H hipotézist elutasítjuk, ha bebizonyosodik mintáról, hogy elemei az S c –hez tartoznak. Más mintapontok esetén a hipotézist elfogadjuk.
Megjegyzés: Az elfogadás, illetve elutasítás még elvileg végtelen elemszámú minta esetén sem jelenti azt, hogy a H hipotézis teljesülése logikailag bizonyítást nyert, illetve, hogy a H nem teljesülése bizonyított.
A hipotézissel kapcsolatban következő ábrán látható esetek lehetségesek (Az ábra G. A. Korn és T. M. Korn: Matematikai kézikönyv műszakiaknak c. könyvéből származik):
-
H igaz, és a próba elfogadja. Ennek valószínűsége „1-α”
-
H hamis, és a próba elutasítja. Ennek valószínűsége „1-β”
-
H igaz, de a próba elutasítja (elsőfajú hiba). Ennek valószínűségét „α” jelöli.
-
H hamis, de a próba elfogadja (másodfajú hiba). Ennek valószínűségét „β” jelöli.
A 4.6. ábra egy feltételezett eloszlás esetére a fenti eseteket szemlélteti.
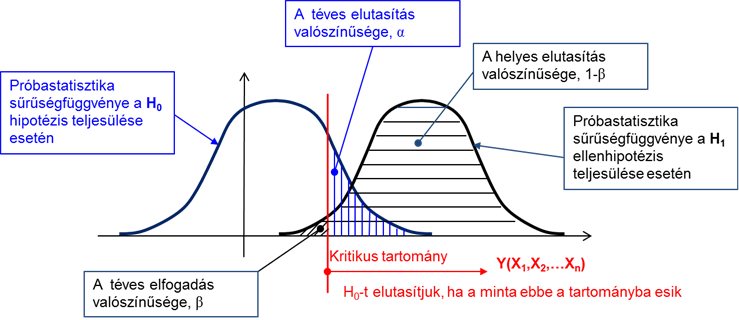
Az ábrán H0 jelöli az un. null hipotézist (kiindulási feltételezés) míg H1 az alternatív, vagy ellenhipotézist. Ugyancsak jól látható, hogy a sűrűségfüggvények alatt jól elkülöníthető módon, α, β görög betűkkel és ezek komplementerjeivel (1-α, 1-β) területeket jelöltünk meg. Ezek a területek a fejezet elején megismert definíció szerint valószínűséget jelentenek. Az α és β szimbólumokkal jelzett valószínűségek mutatják meg a hipotézisvizsgálat során, hogy mennyire jelentős, idegen kifejezéssel szignifikáns a feltételezés és a mérési adatokból nyert „valóság” közötti eltérés?
A méréstechnikában és a műszaki életben sokszor előfordul, hogy az elméleti sokaságnak paraméterekkel kifejezett tulajdonságait kell hipotézisként vizsgálni. Ilyen paraméterek lehetnek például a várható érték és a szórás, μ=μ0, σ=σ0, …stb., miközben a minta tulajdonságait empirikus adatok felhasználásával, az μ=y1(X1, X2, … Xn), σ=y2(X1, X2, … Xn) becslések írják le.
A paraméterek esetében, amint az előzőekben már láttuk, az indexben szereplő „0” jelöli a hipotetikus értéket, az index nélküli paraméter pedig a mintából nyert adatokat.
A H0 ≡ [μ=μ0, σ=σ0, …] egyszerű hipotézist adott „α” szignifikancia szinten elutasítjuk (tehát az eltérés szignifikáns), ha y értéke kívül van egy [yP1, yP2,] elfogadási intervallumon, amelyre
|
P[y P1 ≤ y ≤ y P2 ,] = P 2 – P 1 = 1-α |
(4.26) |
Az így definiált próbákat szignifikancia vizsgálatnak nevezik a statisztikában.
Illusztrálás céljából bemutatunk néhány jellegzetes, a méréstechnikában gyakran előforduló statisztikai próbát:
F-próba (paraméteres próba)
A próba alkalmazásával eldönthető, hogy két normális eloszlású statisztikai sokaság szórása azonos-e, vagy nem?
χ 2 -próba (paraméteres próba)
A méréstechnikában lényegében alább felsorolt vizsgálatokra alkalmazzák:
-
Normalitás (illeszkedés vizsgálat, azaz a várt értékek összehasonlítása a megfigyelt adatokkal)
-
Függetlenség (Két adatsor független-e egymástól?)
-
Homogenitás (Az alapsokaságból két eltérő időben vett minta között van-e kapcsolat?) Ilyen vizsgálatra például akkor lehet szükség, ha egy gyártóberendezés esetében a beállításokból, vagy a szerszámkopásokból eredő hibák után kell nyomozni.
Egymintás t-próba (paraméteres próba)
Különösen fontos a szerepe a minőség-ellenőrzés területén. Segítségével eldönthető, hogy egy mintasokaságból számított átlag szignifikánsan különbözik-e egy adott értéktől (Pl. a műszaki dokumentációban megadott mérettől)?
Legyen vizsgálat tárgya, hogy egy „n” elemszámú minta esetében teljesül-e a H0 hipotézis, miszerint az adatokból számított átlag megegyezik az előírt értékkel, vagy az eltérés szignifikáns (lényeges)? A t-eloszlás szabadságfoka ebben az esetben f=n-1. A tp érték előírt szignifikancia szinten táblázatból vehető, míg a μx az előírt érték.
|
|
(4.27) |
Ha |t| ≥ tp , akkor a H0 hipotézist el kell vetni Ha |t| < tp akkorH0 hipotézist megtartjuk.
Kétmintás t-próba (paraméteres próba)
Kalibrálás során előfordulhat a kérdés, hogy két külön mintában egy-egy változó átlagai szignifikánsan különböznek-e egymástól? (Pl.: Ugyanazt a mintát két különböző műszerrel mérték.)
Vizsgáljuk meg azt a H0 hipotézist, miszerint az „n” és az „m” elemszámú minták átlagértékei adott konfidencia szinten lényegesen (szignifikánsan) nem különböznek egymástól. A szabadságfok ebben a kétmintás próbában f=n+m-2, és táblázatból keressük meg az előírt konfidencia szinthez és az f szabadságfokhoz tartozó tp értéket.
|
|
(4.28) |
Ha a számítás alapján |t| ≥ tp akkor a H0 hipotézist elvetjük. Ha |t| < tp akkor a H0 hipotézist megtartjuk.
Egymintás u-próba (paraméteres próba)
Az átlag és a várható érték közötti különbség a mintavétel hibája miatt van, vagy szignifikáns az eltérés? A „σ” ismert, pl. korábbi mérésekből. Hasonlít a t-próbára.
Jelentőség ugyancsak a minőségellenőrzésben van, ebben az esetben a várható érték alatt a műszaki dokumentációban megadott értékeket kell érteni.
Példaképpen első lépésben felállítjuk a H0 nullhipotézist: Szignifikáns-e az átlag és az előírt érték közötti eltérés? Legyen „σ” a minta (itt sorozat) ismert szórása, és μx az ismert (itt: előírt) várható érték, esetünkben a műszaki rajzon szereplő hosszméret, az átlagértéket pedig a kész darabokon végzett mérésekkel, az „n” elemszámú minta alapján határoztuk meg.
Behelyettesítve az u-próba összefüggésébe, amely tulajdonképpen ismert a konfidencia intervallum számításából
|
|
(4.29) |
és megvizsgáljuk, hogy a kapott érték hogyan viszonyul az alábbi táblázatban szereplő feltételekhez?
Ha a kiszámított értékre teljesül valamelyik ellenhipotézis, akkor az ellenhipotézis elfogadásával elvetjük nullhipotézist, a téves elutasítást valószínűsítő „α” szinten. A szignifikancia szinteket a táblázat első oszlopában tüntettünk fel.
|
Szignifikancia szint |
Baloldali ellenhipotézis |
Kétoldali ellenhipotézis |
Jobboldali ellenhipotézis |
|---|---|---|---|
|
0.05 |
u < -uα = -1,64 |
u < - uα/2 = -1,96 vagy 1,96 = uα/2 < u |
1,64 = uα < u |
|
0.01 |
u < - uα = -2,32 |
u < - uα/2 = -2,57 vagy 2,57 = uα/2 < u |
2,32 = uα < u |
|
0.005 |
u < - uα = -2,57 |
u < - uα/2 = -2,81 vagy 2,81 = uα/2 < u |
2,57 = uα < u |
Ha a számítással kapott „u” értékre nem teljesül valamelyik H1 ellenhipotézis, akkor szakszerű kifejezéssel élve „meggyőző ellenhipotézis H1 hiányában” megtartjuk H 0 -t.
Irodalmak
[4.1.] Matematikai kézikönyv műszakiaknak. Műszaki Könyvkiadó. 1975.
[4.2.] Valószínűségelmélet műszaki alkalmazásokkal. Műszaki Könyvkiadó. 1974.