6. fejezet - Állapottér reprezentáció
Vissza		Előre

6. fejezet - Állapottér reprezentáció

Tartalom

6.1. Lineáris időinvariáns rendszerek állapottér egyenletei

A lineáris időinvariáns rendszerek általános rövidítése, az angol név alapján LTI (Linear Time Invariant).

Diszkrét időben

Azt feltételezzük, hogy minden állapotváltozó a következő k+1. időlépésben függ az összes állapotváltozó aktuális (k.) értékeinek lineáris kombinációjától valamint a bemenőjelek aktuális (k.) értékeinek lineáris kombinációjától. Az aktuális kimenőjelet az aktuális állapotváltozók és bemenőjelek lineáris kombinációjaként írjuk fel.

Megjegyzések:

Két mátrixegyenletet írhatunk fel, egyet az állapotváltozókra és egyet a kimenőjelekre.
A bemenőjelek, kezdeti értékek és állapotváltozók hatása elkülönítve számolható.
Az ARMA modellel ellentétben nincs külön memóriánk a bemenetre és a kimenetre, a kettő összevonva jelentkezik, és így kevesebb memória cellára van szükség.
Ha egy jelnek az aktuálissal együtt n értékét kell figyelembe venni, akkor azt beírjuk n db cellába. Nem vizsgáljuk, hogy egy memória cellában egy jelnek ténylegesen hány időlépéssel korábbi értéke van, csak azt vizsgáljuk, hogy az aktuális időlépésben mi az adott memória cella tartalma.

Legyen $x [k] \in ℝ^{n}$ az állapotváltozók oszlopvektora a k-adik időlépésben, $u [k] \in ℝ^{m}$ a bemenőjelek oszlopvektora a k-adik időlépésben, $y [k] \in ℝ^{p}$ a kimenőjelek oszlopvektora a k-adik időlépésben Az LTI rendszer szokásos állapotváltozós alakja diszkrét időben:

$x [k + 1] = A_{d} x [k] + B_{d} u [k]$	(6.1)
$y [k] = C x [k] + D u [k]$	(6.2)

ahol $A_{d} \in ℝ^{n \times n}$ , $B_{d} \in ℝ^{n \times m}, C \in ℝ^{p \times n}$ és $D \in ℝ^{p \times m}$ a rendszert leíró konstans elemű mátrixok. Azonos valós fizikai rendszer feltételezve $A_{d}$ és $B_{d}$ függ az időlépéstől (ezt fejezi ki a diszkrét időre utaló d index), az állapotváltozók és bemenőjelek leképezése a kimenő jelre (6.2) az időlépéstől független (csak az aktuális értékektől függ). $D$ mátrix a bemenőjel közvetlen (a dinamikai rendszert elkerülő) hatását írja le a kimenőjelre. A legtöbb esetben a $D$ mátrix minden eleme nulla.

Folytonos időben

(6.1) lényegét tekintve az állapotváltozókra felírt differenciaegyenlet, amelyet formálisan átírhatunk differenciálegyenletté. (6.2) átírása triviálisan adódik. Természetesen egy valós fizikai rendszernek először a differenciálegyenleteit szoktuk felírni és azt rendezzük át mátrixos formára. Ebben a tananyagban magával a rendszerrel foglalkozunk, így didaktikailag megengedhető, hogy a leírás szempontjából az egyszerűbb esetből haladjunk a bonyolultabb felé. (2.7) és (2.8) egyenletekből közvetlenül felírható zérus kezdeti feltétel mellett.

$\dot{x} (t) = A x (t) + B u (t)$	(6.3)
$y (t) = C x (t) + D u (t)$	(6.4)

ahol $x(t) \in ℝ^{n}$ az állapotváltozók oszlopvektora, $u(t) \in ℝ^{m}$ a bemenetek oszlopvektora, $y(t) \in ℝ^{p}$ a kimenetek oszlopvektora $A \in ℝ^{n \times n}$ , $B \in ℝ^{n \times m}, C \in ℝ^{p \times n}$ és $D \in ℝ^{p \times m}$ a rendszert leíró konstans elemű mátrixok. A (6.3) és (6.4) szokásos grafikai megjelenítése $D = 0$ esetben a 6-1. ábrán látható. $A$ és $B$ átírását $A_{d}$ és $B_{d}$ formára később tárgyaljuk

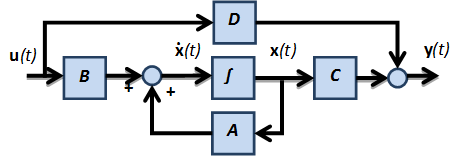
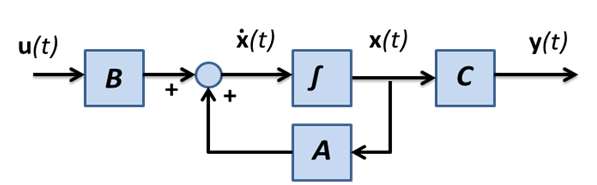
6.1. ábra - Állapottér egyenletek

6.1.1. Az átviteli függvény pólusainak és a rendszermátrix sajátértékeinek kapcsolata

A (6.3) és (6.4) állapottér egyenletek Laplace-transzformálásával a következő egyenletek írhatók fel zérus kezdeti feltétel mellett

$s X (s) = A X (s) + B U (s)$	(6.5)
$Y (s) = C X (s) + D U (s)$	(6.6)

$X (s)$ kifejezhető, így az $Y (s)$ és $U (s)$ közötti összefüggés felírható

$X (s) = {(s I - A)}^{- 1} B U (s)$	(6.7)
$Y (s) = (C {(s I - A)}^{- 1} B + D) U (s)$	(6.8)

Vektorok hányadosa csak elemenként értelmezhető

$W (s) = C {(s I - A)}^{- 1} B + D$

( 6.9 )

A $W (s)$ mátrix minden eleme átviteli függvény az adott bemenet és kimenet között. Pl. az l-edik bemenet és i-edik kimenet között az átviteli függvény:

$W_{i, l} (s) = \frac{Y_{i} (s)}{U_{l} (s)}$

( 6.10 )

Ismert, hogy egy $M$ mátrix inverze a következőképpen írható fel

$M^{- 1} = \frac{adj (M)}{det (M)}$

( 6.11 )

Ennek alapján

${(s I - A)}^{- 1} = \frac{adj (s I - A)}{det (s I - A)}$

( 6.12 )

(6.9) átírható

$W (s) = \frac{C adj (s I - A) B + det (s I - A) D}{det (s I - A)}$

( 6.13 )

A következőket olvashatjuk ki.

$det (s I - A)$ az s változóra nézve n-ed rendű polinom.
$adj (s I - A)$ és ezzel együtt $C adj (s I - A) B$ egy olyan mátrix, amelynek az elemei szintén polinomok s-re nézve, de a rendszámuk kisebb, mint n.
SISO rendszer esetén $C$ egy sorvektor, és $B$ egy oszlopvektor, így a számláló is egy polinom.
Ha $D = 0$ , akkor $W (s)$ minden mátrix eleme s-re nézve valódi racionális törtfüggvény.
Ha $D \neq 0$ , akkor a $W (s)$ mátrixnak van olyan eleme, amely s-re nézve olyan racionális törtfüggvény, ahol a számláló fokszáma megegyezik a nevező fokszámával
A $W (s)$ mátrix minden elemének a nevezője $\det (s I - A)$ , így minden átviteli függvénynél azonosak a pólusok. Ez fizikailag azt jelenti, hogy a rendszer időállandói nem függnek attól, hogy mit választunk bemenetnek és kimenetnek.
Az matematikailag elképzelhető. hogy néhány pólus megegyezik néhány zérussal, és azokkal egyszerűsíteni lehet. Ez fizikailag azt jelenti, hogy az egyszerűsítéssel megszüntetett pólushoz tartozó állapotváltozó nem megfigyelhető, vagy irányítható az adott be- és kimenet felől.
Az átviteli függvény pólusai megegyeznek az $A$ mátrix sajátértékeivel

$\det (s I - A) = 0 \Rightarrow \det (λ I - A) = 0$

( 6.14 )

6.1.2. Hasonlósági transzformáció

Az állapotváltozókat többfélekép választhatjuk meg, így (6.3) és (6.4) állapottér egyenleteket egy konkrét fizikai rendszer esetén is többfélekép írhatjuk fel. Bizonyos feladatok megoldása leegyszerűsíthető megfelelően megválasztott állapotváltozókkal. Így gyakran felmerül az igény, hogy az (6.3) és (6.4) állapottér egyenleteket átírjuk az adott feladat számára optimális formára az állapotváltozók átalakításával. Ezt a feladatot oldhatjuk meg a hasonlósági transzformációval. Ezzel sok esetben az a célunk, hogy a mátrixegyenleteket olyan formára hozzuk, amely megkönnyíti a szabályozó, illetve megfigyelő tervezését, ahogy ezt a későbbiekben látni fogjuk.

Bevezetjük az új $x_{T} = T x$ állapotváltozó vektort, ahol $T$ a hasonlósági transzformáció mátrixa. $T$ invertálhatóságát kell kikötnünk. Az állapotegyenletet $T$ mátrixszal megszorozva

$T \dot{x} (t) = T A x (t) + T B u (t)$	(6.15)
$y (t) = C x (t) + D u (t)$	(6.16)

$x = T^{- 1} x_{T}$ helyettesítéssel

${\dot{x}}_{T} (t) = T A T^{- 1} x_{T} (t) + T B u (t)$	(6.17)
$y (t) = C T^{- 1} x_{T} (t) + D u (t)$	(6.18)

A mátrixokat átnevezve

${\dot{x}}_{T} (t) = A_{T} x_{T} (t) + B_{T} u (t)$	(6.19)
$y (t) = C_{T} x_{T} (t) + D_{T} u (t)$	(6.20)

Az eredeti és a hasonlósági transzformáció után kapott mátrixok kapcsolata:

$A_{T} = T A T^{- 1}$	$B_{T} = T B$	(6.21)
$C_{T} = C T^{- 1}$	$D_{T} = D$	(6.21)

6.1.3. Az állapottér egyenletek megoldása

Bevezető példaként adott egy elsőrendű differenciálegyenlet

$\dot{x} (t) = - a_{0} x (t) + b_{0} u (t),$

( 6.22 )

ahol az $x (t)$ állapotváltozó kezdeti értéke $x (0) = X_{0}$ . Itt utalnunk kell a derivált függvény Laplace transzformálásának szabályára. Ha a (6.22) egyenletet Laplace-transzformáljuk, akkor azt feltételezzük, hogy mind $x (t)$ , mind $u (t)$ belépő-függvény, és értékük nulla a $t < 0$ tartományban. Ennek megfelelően meg kell különböztetnünk a közvetlenül a bekapcsolás előtti $x (- 0) = X_{- 0}$ és közvetlenül a bekapcsolás utáni $x (+ 0) = X_{+ 0}$ kezdeti értéket, más szavakkal $x (0)$ bal és jobb oldali határértéket. A Laplace-transzformáció $x (- 0) = 0$ értékre vonatkozik. Ha $x (- 0) = X_{- 0} \neq 0$ akkor ez a deriválási szabálynál figyelembe kell venni:

$s X (s) - X_{- 0} = - a_{0} X (s) + b_{0} U (s)$

( 6.23 )

Érdekes, és fizikailag értelmezhető eredményre jutunk, ha a (6.23) egyenletet inverz Laplace-transzformáljuk

$\dot{x} (t) = - a_{0} x (t) + b_{0} u (t) + X_{- 0} δ (t)$

( 6.24 )

Értelmezés

A (6.24) egyenletet elemezve arra a következtetésre juthatunk, hogy gondolkozhatunk úgy, hogy a Laplace-transzformáció az energiamentes kezdő állapotra vonatkozik, ezért a múlt összesített hatását egy $X_{- 0} δ (t)$ nagyságú impulzus közvetíti a rendszer felé, és beállítja a szükséges kezdeti értéket. Ez egy ugrást jelent az állapotváltozó értékében, szemléletesen azt mondhatjuk, hogy a rendszert egy $X_{- 0} δ (t)$ impulzusnyi ütéssel a kezdeti állapotba kalapáljuk, hogy onnan folytatódjon a folyamat. Ha $u (t) = δ (t)$ , akkor az egy újabb - $b_{0} δ (t)$ nagyságú - kalapácsütés, így a két Dirac-impulzus hatását össze kell vonni, ezért $x (+ 0) = b_{0} + X_{- 0}$ . Ha a bemenőjel véges értékű, akkor az állapotváltozó folytonos és $X_{- 0} = X_{+ 0}$ . Természetesen, ha később érkezik a bemenetre egy időben eltolt $δ (t - T_{h})$ Dirac-impulzus, akkor a $t = T_{h}$ időpillanatban jelent egy kalapácsütést és ugrást az állapotváltozó értékében. Ez a gondolatmenet kiterjeszthető magasabb rendű differenciálegyenletekre is.

$X (s)$ kifejezhető a (6.23) egyenletből

$X (s) = \frac{1}{s + a_{0}} X_{- 0} + \frac{b_{0}}{s + a_{0}} U (s)$

( 6.25 )

Az $X (s)$ állapotváltozó a (6.25) kifejezésében az első tag a kezdeti értéktől, a második tag a nulla kezdeti értékről indulva csak a gerjesztéstől függ. A (6.25) kifejezésből az is kiolvasható, hogy a (6.22) alakú, elsőrendű differenciálegyenletet esetén az $a_{0}$ együttható az állapotváltozó $X (s)$ Laplace-transzformáltját kifejezésében a $p$ pólus mínusz egyszerese $a_{0} = - p$ . A (6.25) kifejezés inverz Laplace-transzformációját elvégezve

$x (t) = X_{- 0} e^{- a_{0} t} + \int_{- 0}^{t} e^{- a_{0} (t - τ)} b_{0} u (τ) d τ 0 \leq t$

( 6.26 )

Több változós esetben (6.3) egyenletet Laplace-transzformálva és figyelembe véve a kezdeti értékre vonatkozó deriválási szabályt

$s X (s) = A X (s) + B U (s) + X_{- 0}$

( 6.27 )

(6.27)-t inverz Laplace-transzformálva látható, hogy a (6.3) állapottér egyenletben a kezdeti értékek a következő módon is figyelembe vehetők.

$\dot{x} (t) = A x (t) + B u (t) + X_{- 0} δ (t)$

(6.28)

Ha esetleg $u (t)$ is tartalmaz Dirac-impulzust, az úgy értelmezhető, hogy az érintett állapotváltozó(k)nak van egy bekapcsolás előtti értéke és egy bekapcsolás utáni értéke, vagyis az érintett állapotváltozó(k)nak szakadása van a $t = 0$ időpillanatban. Az érintett állapotváltozó(k)nak az ugrás előtti értékét kell az állapottér egyenlet megoldása szempontjából kezdeti értékének tekinteni. Az állapotváltozók Laplace-transzformáltjának vektora kifejezhető

$X (s) = {(s I - A)}^{- 1} B U (s) + {(s I - A)}^{- 1} X_{- 0}$

( 6.29 )

$X (s)$ (6.29) alakú kifejezésében az első tag a gerjesztéstől, a második a kezdeti értéktől függ. Egyváltozós esethez formálisan hasonló (6.26) alakú megoldást keresünk. (6.29) első tagjában felismerhetjük a bemenet és az állapotváltozók között felírható átviteli függvényt energiamentes állapotból kiindulva.

(6.29) kifejezésében mind a kezdeti értéktől függő, mind a gerjesztéstől függő megoldásban szerepel az ${(s I - A)}^{- 1}$ tényező, amely kifejezhető (6.12) segítségével. Ugyanakkor tekinthetjük egy olyan mátrixnak, amelynek minden eleme egy végtelen sor összege a következő formában:

${(s I - A)}^{- 1} = \frac{1}{s} {(I - \frac{A}{s})}^{- 1} = \frac{1}{s} • (I + \frac{A}{s} + \frac{A^{2}}{s^{2}} + \dots)$

( 6.30 )

(6.30) tagonként inverz Laplace-transzformálható, és így mátrixos formában jutunk az exponenciális függvény sorához, ezt tekinthetjük definíciónak is.

$ℒ^{- 1} {\frac{1}{s} • (I + \frac{A}{s} + \frac{A^{2}}{s^{2}} + \dots)} = I + A • t + \frac{1}{2!} A^{2} • t^{2} + \dots = e^{A • t}$

( 6.31 )

(6.31) alapján a kezdeti értéktől függő (a múlt hatását megjelenítő) tag az időtartományban.

$x_{n g} (t) = ℒ^{- 1} {{(s I - A)}^{- 1} X_{+ 0}} = e^{A t} X_{- 0}$

( 6.32 )

A gerjesztéstől függő összetevő egy konvolúciós integrál lesz

$x_{g} (t) = ℒ^{- 1} {{(s I - A)}^{- 1} • B U (s)} = \int_{- 0}^{t} e^{A (t - τ)} B u (τ) d τ$

( 6.33 )

(6.27) teljes megoldása a gerjesztéstől függő és független megoldás összege

$x (t) = x_{n g} (t) + x_{g} (t) = e^{A t} X_{- 0} + \int_{- 0}^{t} e^{A (t - τ)} B u (τ) d τ$

( 6.34 )

Az egy-energiatárolós esethez hasonlóan, ha $D = 0$ , akkor $C e^{A t} B$ tekinthető a több bemenetű rendszer súlyfüggvényének. Ha az $A$ mátrix diagonális, akkor a (6.31) összegzésben az $A^{k}$ hatványok kiszámíthatóak úgy, hogy a diagonálban található elemeket külön-külön emeljük az adott hatványra, ezért

$e^{[\begin{matrix} \begin{matrix} λ_{1} & 0 \\ 0 & λ_{2} \end{matrix} & \begin{matrix} \dots & 0 \\ 0 \end{matrix} \\ \begin{matrix} ⋮ \\ 0 & 0 \end{matrix} & \begin{matrix} ⋱ & ⋮ \\ \dots & λ_{n} \end{matrix} \end{matrix}] • t} = [\begin{matrix} \begin{matrix} e^{λ_{1} t} & 0 \\ 0 & e^{λ_{2} t} \end{matrix} & \begin{matrix} \dots & 0 \\ 0 \end{matrix} \\ \begin{matrix} ⋮ \\ 0 & 0 \end{matrix} & \begin{matrix} ⋱ & ⋮ \\ \dots & e^{λ_{n} t} \end{matrix} \end{matrix}]$

( 6.35 )

Ha az $A$ mátrix nem diagonális, akkor fontos kérdés, hogy mikor és miként diagonizálhatjuk, erre visszatérünk 6.2.9 pontban. Egy általános esetben $e^{A t}$ kiszámítása pl. (6.36) segítségével történhet

$e^{A • t} = ℒ^{- 1} {\frac{adj (s I - A)}{det (s I - A)}}$

( 6.36 )

Így (6.34) inkább tekinthető a megoldás kompakt leírásának, mint egy útmutatónak a megoldás kiszámítási módjára.

6.1.3.1. eAt néhány tulajdonsága

$e^{A • 0} = I, {(e^{A t})}^{- 1} = e^{- A t}$

( 6.37 )

Ha egy $A$ mátrixnak csak egyszeres gyökei vannak, a sajátvektorokból álló $M$ modális mátrixának segítségével diagonizálhatjuk az $A$ mátrixot.

$A = M diag [λ_{1}, λ_{2}, \dots, λ_{n}] M^{- 1}$

( 6.38 )

Bizonyítható, hogy

$A^{k} = M diag [λ_{1}^{k}, λ_{2}^{k}, \dots, λ_{n}^{k}] M^{- 1}$

( 6.39 )

ezért

$e^{A t} = M diag [e^{λ_{1} t}, e^{λ_{2} t}, \dots, e^{λ_{n} t}] M^{- 1}$

( 6.40 )

6.1.4. Kidolgozott feladatok állapottér egyenletekre és megoldásaikra

6 . 1 feladat

Határozza meg

$e^{[\begin{matrix} 0 & 1 \\ - 2 & - 3 \end{matrix}] t}$

( 6.41 )

értékét.

6.1.4.1. Megoldás

(6.36) alapján

$e^{[\begin{matrix} 0 & 1 \\ - 2 & - 3 \end{matrix}] t} = ℒ^{- 1} {\frac{adj ([\begin{matrix} s & 0 \\ 0 & s \end{matrix}] - [\begin{matrix} 0 & 1 \\ - 2 & - 3 \end{matrix}])}{\det ([\begin{matrix} s & 0 \\ 0 & s \end{matrix}] - [\begin{matrix} 0 & 1 \\ - 2 & - 3 \end{matrix}])}} = ℒ^{- 1} {\frac{[\begin{matrix} s + 3 & 1 \\ - 2 & s \end{matrix}]}{s^{2} + 3 s + 2}} =$

$= ℒ^{- 1} {[\begin{matrix} \frac{s + 3}{(s + 1) (s + 2)} & \frac{1}{(s + 1) (s + 2)} \\ \frac{- 2}{(s + 1) (s + 2)} & \frac{s}{(s + 1) (s + 2)} \end{matrix}]} = [\begin{matrix} 2 e^{- t} - e^{- 2 t} & e^{- t} - e^{- 2 t} \\ - 2 e^{- t} + 2 e^{- 2 t} & - e^{- t} + 2 e^{- 2 t} \end{matrix}]$

( 6.42 )

(6.40) alapján a MATLAB „eig” utasítás segítségével a kitevőben szereplő mátrix felbontható

$[\begin{matrix} 0 & 1 \\ - 2 & - 3 \end{matrix}] = [\begin{matrix} 0.7071 & - 0.4472 \\ - 0.7071 & 0.8944 \end{matrix}] [\begin{matrix} - 1 & 0 \\ 0 & - 2 \end{matrix}] [\begin{matrix} 2.8284 & 1.4142 \\ 2.2361 & 2.2361 \end{matrix}]$

( 6.43 )

$e^{[\begin{matrix} 0 & 1 \\ - 2 & - 3 \end{matrix}] t} = [\begin{matrix} 0.7071 & - 0.4472 \\ - 0.7071 & 0.8944 \end{matrix}] [\begin{matrix} e^{- t} & 0 \\ 0 & e^{- 2 t} \end{matrix}] [\begin{matrix} 2.8284 & 1.4142 \\ 2.2361 & 2.2361 \end{matrix}]$

( 6.44 )

6 . 2 feladat Egy RLC kör állapottér egyenletének felírása és megoldása

Tekintsük a 6-2. ábrán látható RLC áramkört

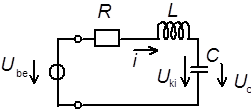
6.2. ábra - R-L-C kör

Az áramköri elemek: $L = 1 H; R = 110 Ω; C = 1000 μ F$ . A t=0 időpillanatban bekapcsoljuk az $U_{b e} = 9 V$ tápfeszültséget. (A bemenetre egységugrás jelet kapcsolunk) A kondenzátor a bekapcsolás előtt 10V-ra van feltöltve. A kondenzátor feszültsége a kimenőjel.

Írja fel a rendszer átviteli függvényét.
Válasszon állapotváltozókat és írja fel a a rendszer állapottér egyenleteit, majd oldja meg azokat.

6.1.4.2. Megoldás

Átviteli függvény

Kirchhoff huroktörvény alapján

$u_{b e} = R • i + L \frac{d i}{d t} + u_{c}$

( 6.45 )

A kondenzátor alapegyenlete

$i = C \frac{d u_{c}}{d t}$

( 6.46 )

Helyettesítéssel

$u_{b e} = R C \frac{d u_{c}}{d t} + L C \frac{d^{2} u_{c}}{d t^{2}} + u_{c}$

( 6.47 )

Ha $u_{b e}$ a bemenőjel és a kondenzátor feszültsége a kimenőjel, akkor

$u = u_{b e}$ és $y = u_{c}$

( 6.48 )

A rendszer differenciálegyenletének Laplace transzformáltja a (6.48) helyettesítéssel

$U (s) = s R C • Y (s) + s^{2} L C • Y (s) + Y (s)$

( 6.49 )

Az átviteli függvény

$\frac{Y (s)}{U (s)} = \frac{1}{L C s^{2} + R C s + 1}$

( 6.50 )

Állapottér reprezentáció

Az átviteli függvény egyedi, de az állapotteres leírás nem egyedi, például legyen

$x_{1} = i$ és $x_{2} = u_{c}$ ,

( 6.51 )

akkor

${\dot{x}}_{1} = \frac{d i}{d t} = - \frac{R}{L} i - \frac{1}{L} u_{c} + \frac{1}{L} u_{b e} = - \frac{R}{L} x_{1} - \frac{1}{L} x_{2} + \frac{1}{L} u$

( 6.52 )

${\dot{x}}_{2} = \frac{d u_{c}}{d t} = \frac{i}{C} = \frac{x_{1}}{C}$

( 6.53 )

tehát

$[\begin{matrix} {\dot{x}}_{1} \\ {\dot{x}}_{2} \end{matrix}] = [\begin{matrix} - \frac{R}{L} & - \frac{1}{L} \\ \frac{1}{C} & 0 \end{matrix}] [\begin{matrix} x_{1} \\ x_{2} \end{matrix}] + [\begin{matrix} \frac{1}{\begin{matrix} L \end{matrix}} \\ 0 \end{matrix}] u$

( 6.54 )

$y = [\begin{matrix} 0 & 1 \end{matrix}] [\begin{matrix} x_{1} \\ x_{2} \end{matrix}] + [0] • u$

( 6.55 )

Másképpen is választhatjuk az állapotváltozókat, például lehet:

$x_{1} = u_{c} é s x_{2} = \frac{d u_{c}}{d t} = {\dot{x}}_{1};$

( 6.56 )

tehát

${\dot{x}}_{2} = - \frac{1}{L C} x_{1} - \frac{R}{L} x_{2} + \frac{1}{L C} u;$

( 6.57 )

$[\begin{matrix} {\dot{x}}_{1} \\ {\dot{x}}_{2} \end{matrix}] = [\begin{matrix} 0 & 1 \\ - \frac{1}{L C} & - \frac{R}{L} \end{matrix}] [\begin{matrix} x_{1} \\ x_{2} \end{matrix}] + [\begin{matrix} 0 \\ \frac{1}{L C} \end{matrix}] u;$

( 6.58 )

$y = [\begin{matrix} 1 & 0 \end{matrix}] [\begin{matrix} x_{1} \\ x_{2} \end{matrix}] + [0] u;$

( 6.59 )

A (6.58) és (6.59) egyenletek megoldása

Behelyettesítve a valóságos értékeket:

$A = [\begin{matrix} 0 & 1 \\ - \frac{1}{L C} & - \frac{R}{L} \end{matrix}] = [\begin{matrix} 0 & 1 \\ - \frac{1}{1 • 10^{- 3}} & - \frac{110}{1} \end{matrix}] = [\begin{matrix} 0 & 1 \\ - 1000 & - 110 \end{matrix}];$

( 6.60 )

$B = [\begin{matrix} 0 \\ \frac{1}{L C} \end{matrix}] = [\begin{matrix} 0 \\ 1000 \end{matrix}];$

( 6.61 )

Tehát az adott RLC kör állapotteres leírása:

$[\begin{matrix} {\dot{x}}_{1} \\ {\dot{x}}_{2} \end{matrix}] = [\begin{matrix} 0 & 1 \\ - 1000 & - 110 \end{matrix}] [\begin{matrix} x_{1} \\ x_{2} \end{matrix}] + [\begin{matrix} 0 \\ 1000 \end{matrix}] u;$

( 6.62 )

$y = [\begin{matrix} 1 & 0 \end{matrix}] [\begin{matrix} x_{1} \\ x_{2} \end{matrix}];$

( 6.63 )

ahol a kezdeti érték

$X_{- 0} = [\begin{matrix} 10 \\ 0 \end{matrix}]$

( 6.64 )

A (6.62) és (6.63) megoldását keressük az időtartománybana (6.64) kezdeti értékkel (6.34) alakban.

Először a kezdeti értéktől függő $e^{A t} X_{- 0} = ℒ^{- 1} [{(s I - A)}^{- 1}] X_{- 0}$ tagot számítjuk ki.

$s I - A = [\begin{matrix} s & 0 \\ 0 & s \end{matrix}] - [\begin{matrix} 0 & 1 \\ - 1000 & - 110 \end{matrix}] = [\begin{matrix} s & - 1 \\ 1000 & s + 110 \end{matrix}]$ ;

( 6.65 )

${(s I - A)}^{- 1} = \frac{1}{s (s + 110) + 1000} [\begin{matrix} s + 110 & 1 \\ - 1000 & s \end{matrix}]$

$= [\begin{matrix} \frac{s + 110}{(s + 10) (s + 100)} & \frac{1}{(s + 10) (s + 100)} \\ \frac{- 1000}{(s + 100) (s + 100)} & \frac{s}{(s + 10) (s + 100)} \end{matrix}];$

( 6.66 )

Részlettörtekre bontás után

${(s I - A)}^{- 1} = [\begin{matrix} \frac{10}{9 (s + 10)} - \frac{1}{9 (s + 100)} \\ - \frac{100}{9 (s + 10)} + \frac{100}{9 (s + 100)} \end{matrix} \begin{matrix} \frac{1}{90 (s + 10)} - \\ - \frac{1}{9 (s + 10)} + \end{matrix} \begin{matrix} \frac{1}{90 (s + 100)} \\ \frac{10}{9 (s + 100)} \end{matrix}];$

( 6.67 )

$e^{A t} = ℒ^{- 1} {[\begin{matrix} \frac{10}{9 (s + 10)} - \frac{1}{9 (s + 100)} \\ - \frac{100}{9 (s + 10)} + \frac{100}{9 (s + 100)} \end{matrix} \begin{matrix} \frac{1}{90 (s + 10)} - \\ - \frac{1}{9 (s + 10)} + \end{matrix} \begin{matrix} \frac{1}{90 (s + 100)} \\ \frac{10}{9 (s + 100)} \end{matrix}]}$

$= [\begin{matrix} \frac{10}{9} e^{- 10 t} - \frac{1}{9} e^{- 100 t} \\ - \frac{100}{9} e^{- 10 t} + \frac{100}{9} e^{- 100 t} \end{matrix} \begin{matrix} \frac{1}{90} e^{- 10 t} - \\ - \frac{1}{9} e^{- 10 t} + \end{matrix} \begin{matrix} \frac{1}{90} e^{- 100 t} \\ \frac{10}{9} e^{- 100 t} \end{matrix}]$

( 6.68 )

$\begin{array}{l} e^{A t} X_{- 0} = [\begin{matrix} \frac{10}{9} e^{- 10 t} - \frac{1}{9} e^{- 100 t} \\ - \frac{100}{9} e^{- 10 t} + \frac{100}{9} e^{- 100 t} \end{matrix} \begin{matrix} \frac{1}{90} e^{- 10 t} - \\ - \frac{1}{9} e^{- 10 t} + \end{matrix} \begin{matrix} \frac{1}{90} e^{- 100 t} \\ \frac{10}{9} e^{- 100 t} \end{matrix}] [\begin{matrix} 10 \\ 0 \end{matrix}] \\ = [\begin{matrix} \frac{100}{9} e^{- 10 t} - \frac{10}{9} e^{- 100 t} \\ - \frac{1000}{9} e^{- 10 t} + \frac{1000}{9} e^{- 100 t} \end{matrix}] \end{array}$

( 6.69 )

A gerjesztéstől függő $\int_{0}^{t} e^{A (t - τ)} B u (τ) d τ$ tag kiszámításához szükség van a (6.66) összefüggésre

${(s I - A)}^{- 1} B U (s)$

$= [\begin{matrix} \frac{10}{9 (s + 10)} - \frac{1}{9 (s + 100)} \\ - \frac{100}{9 (s + 10)} + \frac{100}{9 (s + 100)} - \end{matrix} \begin{matrix} \frac{1}{90 (s + 10)} - \\ \frac{1}{9 (s + 10)} + \end{matrix} \begin{matrix} \frac{1}{90 (s + 100)} \\ \frac{10}{9 (s + 100)} \end{matrix}] [\begin{matrix} 0 \\ 100 \end{matrix}] \frac{9}{s}$

$= [\begin{matrix} \frac{9 • 1000}{90 s (s + 10)} - \frac{9 • 1000}{90 s (s + 100)} \\ - \frac{9 • 100}{9 s (s + 10)} + \frac{90 • 1000}{9 s (s + 100)} \end{matrix}] = [\begin{matrix} \frac{9}{s} - \frac{10}{s + 10} + \frac{1}{s + 100} \\ \frac{100}{s + 10} - \frac{100}{s + 100} \end{matrix}]$

(6.70)

Az inverz Laplace transzformációt elvégezve

$ℒ^{- 1} {{(s I - A)}^{- 1} B U (s)} = ℒ^{- 1} {[\begin{matrix} \frac{9}{s} - \frac{10}{s + 10} + \frac{1}{s + 100} \\ \frac{100}{s + 10} - \frac{100}{s + 100} \end{matrix}]} = [\begin{matrix} 9 - e^{- 10 t} + e^{- 100 t} \\ 100 (e^{- 10 t} - e^{- 100 t}) \end{matrix}]$

(6.71)

A megoldás (6.69) és (6.71) alapján

$[\begin{matrix} x_{1} (t) \\ x_{2} (t) \end{matrix}] = [\begin{matrix} \frac{100}{9} e^{- 10 t} - \frac{10}{9} e^{- 100 t} \\ - \frac{1000}{9} e^{- 10 t} + \frac{1000}{9} e^{- 100 t} \end{matrix}] + [\begin{matrix} 9 - e^{- 10 t} + e^{- 100 t} \\ 100 (e^{- 10 t} - e^{- 100 t}) \end{matrix}] = [\begin{matrix} 9 + \frac{91}{9} e^{- 10 t} - \frac{1}{9} e^{- 100 t} \\ - \frac{100}{9} e^{- 10 t} + \frac{100}{9} e^{- 100 t} \end{matrix}]$

(6.72)

$y = [\begin{matrix} 1 & 0 \end{matrix}] [\begin{matrix} x_{1} (t) \\ x_{2} (t) \end{matrix}] = 9 + \frac{91}{9} e^{- 10 t} - \frac{1}{9} e^{- 100 t}$

(6.73)

Az eredményül kapott állapotvektor első eleme tulajdonképpen a kondenzátor feszültsége Voltban, a második tag a kapacitással megszorozva pedig az RLC körben folyó áram erősségét adja.

6 . 3 feladat Hatásvázlat átírása állapottér egyenletté

Írja fel az ábrán látható rendszer állapottér egyenletét és eredő átviteli függvényét. Az átviteli függvényt alakítsa át és válasszon álapotváltozókat úgy, hogy az állapottér egyenlet $A$ mátrixa diagonális legyen.

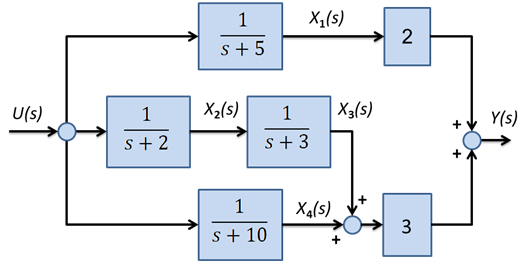
6.3. ábra - Hatásvázlat

6.1.4.3. Megoldás

Először vizsgáljuk meg az

$U (s) \frac{1}{s - p_{i}} = X_{i} (s)$

( 6.74 )

alakú elemeket, ahol $i = 1, 2 é s 4$ és $p_{i} = - 5, - 2 é s - 10$ . Az időtartományban a következőt írhatjuk

${\dot{x}}_{i} (t) = p_{i} x_{i} (t) + u (t)$

(6.75)

$i = 3$ esetén

${\dot{x}}_{3} (t) = - 3 x_{3} (t) + x_{2} (t)$

(6.76)

A fentiek és az ábra alapján

$A = [\begin{matrix} \begin{matrix} - 5 \\ 0 \\ \begin{matrix} 0 \\ 0 \end{matrix} \end{matrix} & \begin{matrix} 0 \\ - 2 \\ \begin{matrix} 1 \\ 0 \end{matrix} \end{matrix} \end{matrix} \begin{matrix} \begin{matrix} 0 \\ 0 \\ \begin{matrix} - 3 \\ 0 \end{matrix} \end{matrix} & \begin{matrix} 0 \\ 0 \\ \begin{matrix} 0 \\ - 10 \end{matrix} \end{matrix} \end{matrix}] B = [\begin{matrix} 1 \\ 1 \\ \begin{matrix} 0 \\ 1 \end{matrix} \end{matrix}] C = [\begin{matrix} 2 & 0 & \begin{matrix} 3 & 3 \end{matrix} \end{matrix}] D = [0]$

( 6.77 )

Az ábra alapján

$\frac{Y (s)}{U (s)} = \frac{2}{s + 5} + \frac{3}{s + 10} + \frac{3}{(s + 2) (s + 3)} = \frac{5 s^{3} + 63 s^{2} + 250 s + 360}{s^{4} + 20 s^{3} + 131 s^{2} + 340 s + 300}$

( 6.78 )

Az állapottér egyenlet $A$ mátrixa úgy tehető könnyen diagonálissá, ha a (6.78) kifejezést részlettörtekre bontjuk, ehhez a következő átalakítás szükséges

$\frac{3}{(s + 2) (s + 3)} = \frac{3}{s + 2} - \frac{3}{s + 3}$

( 6.79 )

Ennek alapján

$\frac{Y (s)}{U (s)} = \frac{2}{s + 5} + \frac{3}{s + 10} + \frac{3}{s + 2} + \frac{- 3}{s + 3}$

( 6.80 )

Így a rendszermátrixok

$A = [\begin{matrix} \begin{matrix} - 5 \\ 0 \\ \begin{matrix} 0 \\ 0 \end{matrix} \end{matrix} & \begin{matrix} 0 \\ - 2 \\ \begin{matrix} 0 \\ 0 \end{matrix} \end{matrix} \end{matrix} \begin{matrix} \begin{matrix} 0 \\ 0 \\ \begin{matrix} - 3 \\ 0 \end{matrix} \end{matrix} & \begin{matrix} 0 \\ 0 \\ \begin{matrix} 0 \\ - 10 \end{matrix} \end{matrix} \end{matrix}] B = [\begin{matrix} 1 \\ 1 \\ \begin{matrix} 1 \\ 1 \end{matrix} \end{matrix}] C = [\begin{matrix} 2 & 3 & - \begin{matrix} 3 & 3 \end{matrix} \end{matrix}] D = [0]$

( 6.81 )

6 . 4 feladat Egyenáramú motor és terhelő nyomaték

Adott egy külsőgerjesztésű egyenáramú motor, amelyet $M_{t}$ nyomaték terhel. Jelölések: $ω_{m}$ a motor szögsebessége és $ϕ_{m}$ az elfordulása, $J_{m}$ , $υ_{m}$ , pedig a motor másodrendű nyomatéka, illetve a viszkózus súrlódást figyelembe vevő paramétere. $u_{a}$ a motor kapocsfeszültsége, $k φ$ a motor paramétere, Ra az armatúra ellenállása, La az armatúra tekercs induktivitása. A rendszer egyenletei:

$u_{a} = i_{a} R_{a} + L_{a} {\dot{i}}_{a} + k φ ω_{m}$ $m_{v} = k φ i_{a}$ $J_{m} {\dot{ω}}_{m} = m_{v} - υ_{m} ω_{m} - m_{t}$ ${\dot{ϕ}}_{m} = ω_{m}$

( 6.82 )

Írja fel a differenciálegyenlet-rendszert (6.3), (6.4) alakban.

Legyen a két bemenőjel a motor $u_{a}$ kapocsfeszültsége és az $m_{t}$ terhelőnyomatéka az $y (t)$ kimenet a motor $ω_{m}$ fordulatszáma.

6.1.4.4. Megoldás

Legyen az állapotváltozók és a bemenőjelek oszlopvektora

$[\begin{matrix} \begin{matrix} x_{1} (t) \\ x_{2} (t) \end{matrix} \\ x_{3} (t) \end{matrix}] = [\begin{matrix} \begin{matrix} i_{a} (t) \\ ω_{m} (t) \end{matrix} \\ φ_{m} (t) \end{matrix}] és [\begin{matrix} u_{1} (t) \\ u_{2} (t) \end{matrix}] = [\begin{matrix} u_{a} (t) \\ m_{t} (t) \end{matrix}]$

(6.83)

(6.82) átrendezésével az állapováltozók deriváltjának kifejezése

$[\begin{matrix} \begin{matrix} {\dot{\dot{i}}}_{a} (t) \\ {\dot{ω}}_{m} (t) \end{matrix} \\ {\dot{φ}}_{m} (t) \end{matrix}] = [\begin{matrix} - \frac{R_{a}}{L_{a}} & - \frac{k ϕ}{L_{a}} & 0 \\ \frac{k ϕ}{J_{m}} & - \frac{ν_{m}}{J_{m}} & 0 \\ 0 & 1 & 0 \end{matrix}] [\begin{matrix} \begin{matrix} i_{a} (t) \\ ω_{m} (t) \end{matrix} \\ φ_{m} (t) \end{matrix}] + [\begin{matrix} \frac{1}{L_{a}} & 0 \\ 0 & - \frac{1}{J_{m}} \\ 0 & 0 \end{matrix}] [\begin{matrix} u_{a} (t) \\ m_{t} (t) \end{matrix}]$

(6.84)

6 . 5 feladat

Adott a következő rendszer.

$[\begin{matrix} {\dot{x}}_{1} (t) \\ {\dot{x}}_{2} (t) \\ {\dot{x}}_{3} (t) \end{matrix}] = [\begin{matrix} - 1 & - 4 & 0 \\ 2 & - 3 & 0 \\ - 5 & - 7 & - 2 \end{matrix}] [\begin{matrix} x_{1} (t) \\ x_{2} (t) \\ x_{3} (t) \end{matrix}] + [\begin{matrix} 0 \\ 0 \\ 1 \end{matrix}] u (t)$ ;

( 6.85 )

$y (t) = [\begin{matrix} 5 & 2 \end{matrix} 1] [\begin{matrix} x_{1} (t) \\ x_{2} (t) \\ x_{3} (t) \end{matrix}]$ ;

( 6.86 )

Minden állapotváltozó 0 kezdeti értékről indul. A bemenőjel egységugrás. Adja meg a kimenőjel időfüggvényét.

6.1.4.5. Megoldás

Ha 0 kezdeti értékről indul minden állapotváltozó, akkor $x_{1} (t) = x_{2} (t) = 0$ , mert sem a bemenőjel sem az $x_{3} (t)$ állapotváltozó nem hat rájuk. Ebben az esetben $y (t) = x_{3} (t)$ és a megoldandó differenciálegyenlet a következő alakra egyszerűsödik

${\dot{x}}_{3} (t) = - 2 x_{3} (t) + ε (t)$ ;

( 6.87 )

Laplace-transzformálva és átrendezve

$X_{3} (s) = \frac{1}{s (s + 2)};$

( 6.88 )

Inverz Laplace-transzformálva

$y (t) = x_{3} (t) = \frac{1}{2} - \frac{1}{2} e^{- 2 t}$

( 6.89 )

6 . 6 feladat Egy egyenáramú motor állapottér egyenletének felírása és megoldása

xxxxxxx

6 . 7 feladat 3-DOF gerjesztett rendszer

Tekintsük a 6-4. ábraán látható 3 szabadsági fokú gerjesztett lengőrendszert. A rendszer bemenete az egyes tömegre ható erők. Esetünkben legyen a bemenőjel, vagyis gerjesztés a következő

$u (t) = f (t) = [\begin{matrix} 0 \\ 0 \\ f_{3} \end{matrix}] cos (ω t)$

( 6.90 )

A rendszer kimenete legyen egyes tömegek elmozdukása.

Írja fel és oldja meg az ábrán látható rendszer egyenleteit.

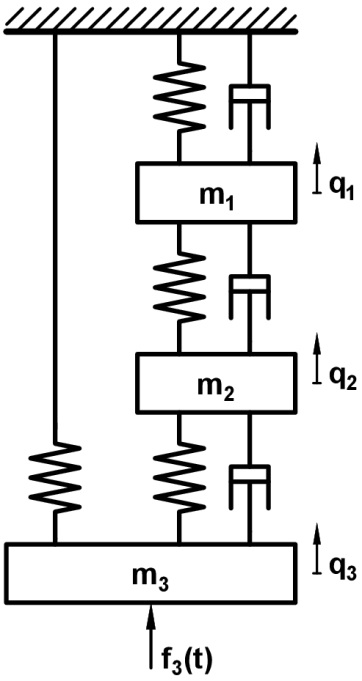
6.4. ábra - 3DOF rendszer

Egyenlet felírása Lagrange egyenlet segítségével

6.1.4.6. Tömegmátrix

$T = \frac{1}{2} m_{1} {\dot{x}}_{1}^{2} + \frac{1}{2} m_{2} {\dot{x}}_{2}^{2} + \frac{1}{2} m_{3} {\dot{x}}_{3}^{2}$

( 6.91 )

$M = [m_{i j}] = [\frac{\partial^{2} T}{\partial {\dot{q}}_{i} \partial {\dot{q}}_{j}}] = [\begin{matrix} m_{1} & 0 & 0 \\ 0 & m_{2} & 0 \\ 0 & 0 & m_{3} \end{matrix}]$

( 6.92 )

6.1.4.7. Csillapítási mátrix

$D = \frac{1}{2} k_{01} {\dot{x}}_{1} {(t)}^{2} + \frac{1}{2} k_{12} {[{\dot{x}}_{2} (t) - {\dot{x}}_{1} (t)]}^{2} + \frac{1}{2} k_{23} {[{\dot{x}}_{3} (t) - {\dot{x}}_{2} (t)]}^{2}$

( 6.93 )

$K = [k_{i j}] = [\frac{\partial^{2} D}{\partial {\dot{q}}_{i} \partial {\dot{q}}_{j}}] = [\begin{matrix} k_{01} + k_{12} & - k_{12} & 0 \\ - k_{12} & k_{12} + k_{23} & - k_{23} \\ 0 & - k_{23} & k_{23} \end{matrix}]$

( 6.94 )

6.1.4.8. Merevségi mátrix

$U = \frac{1}{2} s_{01} x_{1} {(t)}^{2} + \frac{1}{2} s_{12} {[x_{2} (t) - x_{1} (t)]}^{2} + \frac{1}{2} s_{23} {[x_{3} (t) - x_{2} (t)]}^{2} + \frac{1}{2} s_{03} x_{3} {(t)}^{2}$

( 6.95 )

$S = [s_{i j}] = [\frac{\partial^{2} U}{\partial q_{i} \partial q_{j}}] = [\begin{matrix} s_{01} + s_{12} & - s_{12} & 0 \\ - s_{12} & s_{12} + s_{23} & - s_{23} \\ 0 & - s_{23} & s_{03} + s_{23} \end{matrix}]$

( 6.96 )

6.1.4.9. A mátrix együtthatós differenciálegyenlet

$M \ddot{x} (t) + K \dot{x} (t) + S x (t) = f (t)$

( 6.97 )

6.1.4.10. Adatok

$m_{1} = 2 k g, m_{2} = 1 k g, m_{3} = 0.5 k g, s_{01} = 1000 N / m, s_{12} = 2000 N / m, s_{23} = 4000 N / m, s_{03} = 1000 N / m, k_{01} = 1000 N s / m, k_{12} = 2000 N s / m, k_{23} = 4000 N s / m, f_{3} = 10 N, ω = 12 r a d / s$

A fenti mátrixokba behelyettesítve:

$M = [\begin{matrix} 2 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0.5 \end{matrix}]$

$K = [\begin{matrix} 3000 & - 2000 & 0 \\ - 2000 & 6000 & - 4000 \\ 0 & - 4000 & 4000 \end{matrix}]$

$S = [\begin{matrix} 3000 & - 2000 & 0 \\ - 2000 & 6000 & - 4000 \\ 0 & - 4000 & 5000 \end{matrix}]$

$f (t) = [\begin{matrix} 0 \\ 0 \\ 10 \end{matrix}] cos (12 t)$

( 6.98 )

6.1.4.11. Megoldás Laplace transzformációval

A gerjesztés vektorának Laplace-transzformáltja:

$f (s) = ℒ {[\begin{matrix} 0 \\ 0 \\ f_{3} \end{matrix}] cos (ω t)} = [\begin{matrix} 0 \\ 0 \\ f_{3} \end{matrix}] \frac{s}{s^{2} + ω^{2}}$

( 6.99 )

Mátrix együtthatós differenciálegyenlet Laplace-transzformáció után:

$s^{2} M q (s) + s K q (s) + S q (s) = f (s)$

$q (s) = {(s^{2} M + s K + S)}^{- 1} f (s) = H (s) f (s)$

( 6.100 )

ahol $H (s)$ az elmozdulás-válaszra vonatkozó átviteli mátrix.

$H (s) = {(s^{2} M + s K + S)}^{- 1} =$

( 6.101 )

${[\begin{matrix} m_{1} s^{2} + (k_{01} + k_{12}) s + s_{01} + s_{12} & - k_{12} s - s_{12} & 0 \\ - k_{12} s - s_{12} & m_{2} s^{2} + (k_{12} + k_{23}) s + s_{12} + s_{23} & - k_{23} s - s_{23} \\ 0 & - k_{23} s - s_{23} & m_{3} s^{2} + k_{23} s + s_{03} + s_{23} \end{matrix}]}^{- 1}$

$= {[\begin{matrix} 3000 + 3000 s + 2 s^{2} & - 2000 - 2000 s & 0 \\ - 2000 - 2000 s & 6000 + 6000 s + s^{2} & - 4000 - 4000 s \\ 0 & - 4000 - 4000 s & 5000 + 4000 s + 0.5 s^{2} \end{matrix}]}^{- 1}$

$= \frac{A d j (s^{2} M + s K + S)}{D e t (s^{2} M + s K + S)}$

Példaként az invertálás után az $(1, 3)$ elem számítása:

$A d j {(s^{2} M + s K + S)}_{1, 3} = | \begin{matrix} - 2000 - 2000 s & 0 \\ 6000 + 6000 s + s^{2} & - 4000 - 4000 s \end{matrix} | = 8000000 + 16000000 s + 8000000 s^{2}$

$D e t (s^{2} M + s K + S) =$

$| \begin{matrix} 3000 + 3000 s + 2 s^{2} & - 2000 - 2000 s & 0 \\ - 2000 - 2000 s & 6000 + 6000 s + s^{2} & - 4000 - 4000 s \\ 0 & - 4000 - 4000 s & 5000 + 4000 s + 0.5 s^{2} \end{matrix} | = = 22000000000 + 52000000000 s + 3.805 \times 10^{10} s^{2} + 8.085 \times 10^{9} s^{3} + 3.50175 \times 10^{7} s^{4} + 15500. s^{5} + 1. s^{6}$

( 6.102 )

$h_{1, 3} = \frac{A d j {(s^{2} M + s K + S)}_{1, 3}}{D e t (s^{2} M + s K + S)} = \dots$

$= \frac{8000000 {(1 + s)}^{2}}{(1.00016 + s) (1.00092 + s) (2.775 + s) (254.9 + s) (2423 + s) (12817 + s)}$

( 6.103 )

Az inverz mátrix többi eleme hasonlóképpen számítható. Következő lépés a megoldás felírása operátortartományban:

$q (s) = [\begin{matrix} q_{1} (s) \\ q_{2} (s) \\ q_{3} (s) \end{matrix}] = H (s) f (s) = \dots$

( 6.104 )

$q (s)$ első sora:

$q_{1} (s) = h_{1, 1} • 0 + h_{1, 2} \cdot 0 + h_{1, 3} \cdot \frac{f_{3} s}{s^{2} + ω^{2}}$

( 6.105 )

$= \frac{80000000 s {(1 + s)}^{2}}{(1.00016 + s) (1.00092 + s) (2.775 + 1. s) (254.9 + 1. s) (2423 + s) (12817 + s) (s + j 12) (s - j 12)}$

Innen inverz Laplace-transzformációval lehet visszatérni az időtartományba:

$q (t) = ℒ^{- 1} {q (s)} = \dots$

Az eddigiekhez hasonlóan csak az első elem:

$q_{1} (t)$ =

$= ℒ^{- 1} {\frac{80000000 s {(1 + s)}^{2}}{(1.00016 + s) (1.00092 + s) (2.775 + 1. s) (254.9 + 1. s) (2423 + s) (12817 + s) (144 + s^{2})}}$

$\begin{array}{l} = 3.73 \times 10^{- 9} e^{- 12817 t} - 6.052 \times 10^{- 7} e^{- 2423 t} + 4.558 \times 10^{- 5} e^{- 254.9 t} - 1.8725 \times 10^{- 4} e^{- 2.775 t} \\ - 3.811 \times 10^{- 7} e^{- 1.00092 t} + 4.233 \times 10^{- 7} e^{- 1.00016 t} + (7.111 \times 10^{- 5} + j 4.0347 \\ \times 10^{- 4}) e^{- j 12 t} + (7.111 \times 10^{- 5} - j 4.0347 \times 10^{- 4}) e^{+ j 12 t} \end{array}$

A kifejezés végén lévő képzetes kitevőjű exponenciális tagok átalakíthatók. Az Euler formula szerint:

$(a + j b) e^{- j α t} + (a - j b) e^{j α t} = (a + j b) (\cos (α t) - j \sin (α t)) + (a - j b) (\cos (α t) + j \sin (α t)) = \cos (α t) (a + a) + j \sin (α t) (- j^{2} b - j^{2} b) = 2 a \cos (α t) + 2 b s i n (α t)$

$q_{1} (t) = 3.73 \times 10^{- 9} e^{- 12817 t} - 6.052 \times 10^{- 7} e^{- 2423 t} + 4.558 \times 10^{- 5} e^{- 254.9 t} - 1.8725 \times 10^{- 4} e^{- 2.775 t} - 3.811 \times 10^{- 7} e^{- 1.00092 t} + 4.233 \times 10^{- 7} e^{- 1.00016 t} + 1.422 \times 10^{- 4} \cos (12 t) + 8.069 \times 10^{- 4} \sin (12 t)$

$t \to \infty$ esetén a $q_{1} (t)$ kifejezésben a trigonometrikus tagokon kívül az összes többi tag elhal, így:

$q_{1} (t) = 1.422 \times 10^{- 4} \cos (12 t) + 8.069 \times 10^{- 4} \sin (12 t) = 8.193 \times 10^{- 4} \sin (12 t + 0.174)$

Ez megfelel az időtartománybeli megoldás partikuláris megoldásának. A $q_{2} (t)$ és $q_{3} (t)$ elmozdulásfüggvények $q_{1} (t)$ -hez hasonlóan meghatározhatók.

6.1.4.12. Állapottér modell

Állapottér egyenletek:

$\dot{x} (t) = A x (t) + B u (t)$ $y (t) = C x (t) + D u (t)$

Először állapotváltozókat kell választani. Legyenek az állapotváltozók a következő mennyiségek:

$x (t) = [\begin{matrix} x_{1} (t) \\ x_{2} (t) \\ x_{3} (t) \\ x_{4} (t) \\ x_{5} (t) \\ x_{6} (t) \end{matrix}] = [\begin{matrix} q_{1} (t) \\ {\dot{q}}_{1} (t) \\ q_{2} (t) \\ {\dot{q}}_{2} (t) \\ q_{3} (t) \\ {\dot{q}}_{3} (t) \end{matrix}] = [\begin{matrix} (1) test elmozdulása \\ (1) test sebessége \\ (2) test elmozdulása \\ (2) test sebessége \\ (3) test elmozdulása \\ (3) test sebessége \end{matrix}]$

Gerjesztés vektor

$f (t) = [\begin{matrix} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ f_{3} \cos (ω t) \end{matrix}]$

Vegyük a mátrixegyütthatós differenciálegyenlet első egyenletét:

$m_{1} {\ddot{q}}_{1} + (k_{01} + k_{12}) {\dot{q}}_{1} - k_{12} {\dot{q}}_{2} + (s_{01} + s_{12}) q_{1} - s_{12} q_{2} = 0$

Az $x_{1} = q_{1}, x_{2} = {\dot{q}}_{1}, x_{3} = q_{2}, x_{4} = {\dot{q}}_{2}, u_{1} (t) = f_{1} \cos (ω t)$ helyettesítés után:

${\dot{x}}_{2} (t) = - \frac{s_{01} + s_{12}}{m_{1}} x_{1} (t) - \frac{k_{01} + k_{12}}{m_{1}} x_{2} (t) + \frac{s_{12}}{m_{1}} x_{3} (t) + \frac{k_{12}}{m_{1}} x_{4} (t)$

Ezt és az $x_{2} (t) = {\dot{q}}_{1} (t) = {\dot{x}}_{1} (t)$ egyenleteket mátrixos formába írva:

$[\begin{matrix} {\dot{x}}_{1} (t) \\ {\dot{x}}_{2} (t) \end{matrix}] = [\begin{matrix} 0 & 1 & 0 & 0 & 0 & 0 \\ - \frac{s_{01} + s_{12}}{m_{1}} & - \frac{k_{01} + k_{12}}{m_{1}} & \frac{s_{12}}{m_{1}} & \frac{k_{12}}{m_{1}} & 0 & 0 \end{matrix}] [\begin{matrix} x_{1} (t) \\ x_{2} (t) \\ x_{3} (t) \\ x_{4} (t) \\ x_{5} (t) \\ x_{6} (t) \end{matrix}] + [\begin{matrix} 0 \\ 0 \end{matrix}] \cos (ω t)$

A mátrixegyütthatós differenciálegyenlet második és harmadik egyenletével a fentiekhez hasonló módon megkaphatjuk az ${\dot{x}}_{3}, {\dot{x}}_{4}, {\dot{x}}_{5}, {\dot{x}}_{6}$ –ra vonatkozó egyenleteket. Így előállnak az állapottér-egyenletben szereplő együttható mátrixok:

$\begin{array}{l} A = [\begin{matrix} 0 & 1 & 0 & 0 & 0 & 0 \\ - \frac{s_{01} + s_{12}}{m_{1}} & - \frac{k_{01} + k_{12}}{m_{1}} & \frac{s_{12}}{m_{1}} & \frac{k_{12}}{m_{1}} & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ \frac{s_{12}}{m_{2}} & \frac{k_{12}}{m_{2}} & - \frac{s_{12} + s_{23}}{m_{2}} & - \frac{k_{12} + k_{23}}{m_{2}} & \frac{s_{23}}{m_{2}} & \frac{k_{23}}{m_{2}} \\ 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & \frac{s_{23}}{m_{3}} & \frac{k_{23}}{m_{3}} & - \frac{s_{03} + s_{23}}{m_{3}} & - \frac{k_{23}}{m_{3}} \end{matrix}] \\ = [\begin{matrix} 0 & 1 & 0 & 0 & 0 & 0 \\ - 1500 & - 1500 & 1000 & 1000 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 2000 & 2000 & - 6000 & - 6000 & 4000 & 4000 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 8000. & 8000. & - 10000. & - 8000. \end{matrix}] \end{array}$

Mivel most egybemenetű a rendszer, ezért $B$ sorvektorrá fajul:

$B = [\begin{matrix} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ \frac{f_{3}}{m_{3}} \end{matrix}] = [\begin{matrix} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 20 \end{matrix}], B u (t) = [\begin{matrix} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 20 \end{matrix}] \cos (12 t)$

Az állapottér egyenlet Laplace transzformáltja:

$\dot{x} (s) = A x (s) + B u (s)$

Ebből az $x (s)$ operátortartománybeli megoldás kifejezhető:

$x (s) = {(s I - A)}^{- 1} B u (s)$

$s I - A = [\begin{matrix} s & - 1 & 0 & 0 & 0 & 0 \\ 1500 & 1500 + s & - 1000 & - 1000 & 0 & 0 \\ 0 & 0 & s & - 1 & 0 & 0 \\ - 2000 & - 2000 & 6000 & 6000 + s & - 4000 & - 4000 \\ 0 & 0 & 0 & 0 & s & - 1 \\ 0 & 0 & - 8000. & - 8000. & 10000. & 8000. + s \end{matrix}]$

$(s I - A)$ inverze a Laplace-os feladatban látottakhoz hasonlóan meghatározható. Példaként megmutatjuk a számítást az $(s I - A)$ mátrix $(1, 6)$ -os elemére:

$A d j {(s I - A)}_{1, 3} = (- 1) • | \begin{matrix} - 1 & 0 & 0 & 0 & 0 \\ 1500 + s & - 1000 & - 1000 & 0 & 0 \\ 0 & s & - 1 & 0 & 0 \\ - 2000 & 6000 & 6000 + s & - 4000 & - 4000 \\ 0 & 0 & 0 & s & - 1 \end{matrix} | = 4000000 + 8000000 s + 4000000 s^{2}$

$\begin{array}{l} D e t (s I - A) = | \begin{matrix} s & - 1 & 0 & 0 & 0 & 0 \\ 1500 & 1500 + s & - 1000 & - 1000 & 0 & 0 \\ 0 & 0 & s & - 1 & 0 & 0 \\ - 2000 & - 2000 & 6000 & 6000 + s & - 4000 & - 4000 \\ 0 & 0 & 0 & 0 & s & - 1 \\ 0 & 0 & - 8000. & - 8000. & 10000. & 8000. + s \end{matrix} | = \\ = 2.2 \times 10^{10} + 5.2 \times 10^{10} s + 3.805 \times 10^{10} s^{2} + 8.085 \times 10^{9} s^{3} + 3.50175 \\ \times 10^{7} s^{4} + 15500. s^{5} + s^{6} \end{array}$

Ezekből az inverz mátrix $(1, 6)$ eleme:

${[{(s I - A)}^{- 1}]}_{1, 6} = \frac{A d j {(s^{2} M + s K + S)}_{1, 3}}{D e t (s^{2} M + s K + S)} = \dots = \frac{8000000 {(1 + s)}^{2}}{(1.00016 + s) (1.00092 + s) (2.775 + s) (254.9 + s) (2423 + s) (12817 + s)}$

$\begin{array}{l} x (s) = {(s I - A)}^{- 1} B u \\ = [\begin{matrix} {[{(s I - A)}^{- 1}]}_{1, 1} & \dots & \frac{8000000 {(1 + s)}^{2}}{(1.00016 + s) (1.00092 + s) (2.775 + s) (254.9 + s) (2423 + s) (12817 + s)} \\ ⋮ & ⋱ & ⋮ \\ {[{(s I - A)}^{- 1}]}_{6, 1} & \dots & {[{(s I - A)}^{- 1}]}_{6, 6} \end{matrix}] [\begin{matrix} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 20 \end{matrix}] \frac{s}{s^{2} + 12^{2}} \\ = [\begin{matrix} \frac{80000000 s {(1 + s)}^{2}}{(1.00016 + s) (1.00092 + s) (2.775 + 1. s) (254.9 + 1. s) (2423 + s) (12817 + s) (s + j 12) (s - j 12)} \\ \dots \\ \dots \\ \dots \\ \dots \\ \dots \end{matrix}] = [\begin{matrix} x_{1} (s) \\ \dots \\ \dots \\ \dots \\ \dots \\ \dots \end{matrix}] \end{array}$

Az állapotváltozók időtartománybeli megoldását inverz Laplace-transzformációval kaphatjuk meg:

$x (t) = ℒ^{- 1} {x (s)} = ℒ^{- 1} {{(s I - A)}^{- 1} B u (s)} = \dots$

Kimenetet a másik állapottér egyenlet segítségével kaphatunk:

$y (t) = C x (t) + D u (t)$

Ezt Laplace-transzformálva:

$y (s) = C x (s) + D u (s)$

Válasszuk kimenetnek a $q_{1}$ elmozdulást! Mivel $q_{1} = x_{1}$ állapotváltozó, a megoldása megtalálható $x (s)$ vektorban. Ezért C egy olyan mátrix, amivel $x (s)$ -t megszorozva annak első sorát kapjuk, $D$ pedig nulla mátrix.

$C = [\begin{matrix} 1 & 0 & 0 & 0 & 0 & 0 \end{matrix}], D = 0$

Mivel csak egy kimenetünk van, ezért az $\underline{Y} (s)$ vektorból $Y (s)$ skalár lesz.

$y (s) = C x (s) = [\begin{matrix} 1 & 0 & 0 & 0 & 0 & 0 \end{matrix}] [\begin{matrix} x_{1} (s) \\ x_{2} (s) \\ x_{3} (s) \\ x_{4} (s) \\ x_{5} (s) \\ x_{6} (s) \end{matrix}] = x_{1} (s)$

Így a kimenet:

$\begin{array}{l} y (t) = q_{1} (t) = ℒ^{- 1} {y (s)} = ℒ^{- 1} {x_{1} (s)} = \\ = ℒ^{- 1} {\frac{80000000 s {(1 + s)}^{2}}{(1.00016 + s) (1.00092 + s) (2.775 + 1. s) (254.9 + 1. s) (2423 + s) (12817 + s) (s + j 12) (s - j 12)}} \\ = 3.73 \times 10^{- 9} e^{- 12817 t} - 6.052 \times 10^{- 7} e^{- 2423 t} + 4.558 \times 10^{- 5} e^{- 254.9 t} - 1.8725 \times 10^{- 4} e^{- 2.775 t} \\ - 3.811 \times 10^{- 7} e^{- 1.00092 t} + 4.233 \times 10^{- 7} e^{- 1.00016 t} + 1.422 \times 10^{- 4} \cos (12 t) + 8.069 \times 10^{- 4} \sin (12 t) \end{array}$

A lecsengő tagokat elhagyva (állandósult állapotban):

$y (t) \approx 1.422 \times 10^{- 4} \cos (12 t) + 8.069 \times 10^{- 4} \sin (12 t) = 8.193 \times 10^{- 4} \sin (12 t + 0.174)$

A Laplace-transzformált megoldással megegyező eredményre jutottunk.

6.2. Állapotirányítás

A 6.2 alfejezet az állapotirányítás általános eseteit ismerteti, amelyek elvi szempontból fontosak, de konkrét végig számításuk nehézkes, illetve a MATLAB használatát feltételezi. Papíron akár egyszerű zsebszámológéppel megoldható feladatok a 6.3 alfejezetben találhatók.

6.2.1. Állapotvisszacsatolás és hatása a rendszer időállandóira

Induljunk ki a (6.3) differenciálegyenletből. Tekintsük a mátrixos formában felírt (6.106) homogén differenciálegyenletrendszert.

$\dot{x} (t) = A x (t)$

( 6.106 )

(6.106) triviális megoldása $x (t) = 0$ . Tegyük fel, hogy az állapotváltozók $X_{0}$ kezdeti értéke nem nulla (pontosabban az $X_{0}$ vektornak van olyan eleme, amelynek az értéke nem nulla). Célunk az, hogy bámely $X_{0}$ kezdeti értéktől az állapotváltozók tartsanak nullához $x (\infty) = 0$ . (6.14) alapján ennek az a feltétele, hogy az $A$ mátrix összes sajátértékének valós része negatív legyen. Térjünk vissza a (6.3) differenciálegyenlethez, és változtassuk meg a rendszer viselkedését állapotvisszacsatolással. Legyen

$u (t) = K_{x} x (t), K_{x} \in ℝ^{m \times n}$

( 6.107 )

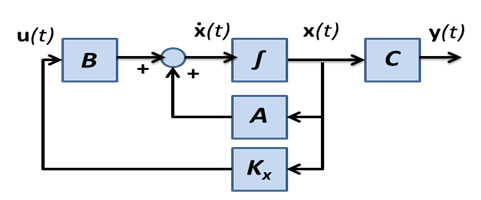
6.5. ábra - Állapotvisszacsatolás nulla referencia jellel

Behelyettesítve a (6.3) differenciálegyenletbe

$\dot{x} (t) = A x (t) + B K_{x} x (t)$

$A \in ℝ^{n \times n}, B \in ℝ^{n \times m} és K_{x} \in ℝ^{m \times n} � B K_{x} \in ℝ^{n \times n}$

( 6.108 )

$\dot{x} (t) = (A + B K_{x}) x (t)$

( 6.109 )

A (6.106) és (6.109) összevetéséből látszik, hogy a visszacsatolt rendszernél az $A$ mátrix szerepét $(A + B K_{x})$ veszi át. Az állapotvisszacsatolással megváltoztathatjuk a rendszer dinamikai tulajdonságait. Ha a $K_{x}$ mátrix megfelelő választásával az $(A + B K_{x})$ mátrix sajátértékeit tetszőlegesen beállíthatjuk, akkor a rendszer irányítható. Teljesen ellentétes eset, ha $B$ mátrix minden eleme 0, akkor állapotvisszacsatolással nem tudjuk befolyásolni a rendszer dinamikai tulajdonságait. Az irányíthatóság az $A$ és $B$ mátrixpárhoz kötődő fogalom.

6.2.2. Irányíthatósági mátrix

Definiáljuk az $M_{C}$ hipermátrixot, mint irányíthatósági mátrixot!

$M_{C} = (I A A^{2} \dots A^{n - 1}) = (B A B A^{2} B \dots A^{n - 1} B)$

( 6.110 )

megjegyzés: ha $A \in ℝ^{n \times n}$ és $B \in ℝ^{n \times m}$ akkor $M_{C} \in ℝ^{n \times (n \cdot m)}$ Az irányíthatóság feltétele, hogy $M_{C}$ mátrix rangja egyezzen meg az állapotváltozók számával. A hasonlósági transzformáció nem érinti az irányíthatóságot.

$M_{C T} = (I A_{T} A_{T}^{2} \dots A_{T}^{n - 1}) B_{T} = (B_{T} A_{T} B_{T} A_{T}^{2} B_{T} \dots A_{T}^{n - 1} B_{T})$

( 6.111 )

$M_{C T} = (T B T A T^{- 1} T B T A T^{- 1} T A T^{- 1} T B \dots) = T M_{C}$

( 6.112 )

$T = M_{C T} M_{C}^{- 1}$

( 6.113 )

6.2.3. Konstans referenciajel előírása és referenciajel kompenzáció

Eddig minden állapotváltozóra vonatkozóan a referenciajel nulla volt. Ha ettől el akarunk térni, akkor két problémával kell szembenéznünk.

Az állapotváltozók nem függetlenek egymástól, így a referenciajelet sem határozhatjuk meg egymástól függetlenül. Pl. egy robot megfogójának a pozíciója és sebessége lehet állapotváltozó. Nyilvánvaló, ezeket nem lehet egymástól függetlenül előírni, a sebesség és a pozíció egyszerre nem lehet nullától különböző konstans.
Ismert, hogy a negatív visszacsatolás esetén a visszacsatolt rendszer erősítése kisebb, mint az eredeti rendszeré, ezért a visszacsatolás értékétől függő kompenzációra van szükség.

6.2.3.1. A visszacsatolás hatásának kompenzálása MIMO esetben

Az állapotvisszacsatolással azt tudjuk elérni, hogy a rendszer tetszőleges kezdeti értékből kiindulva a $K_{x}$ visszacsatoló tag által beállított időállandóval tartson a nullához, vagyis a $K_{x}$ visszacsatoló taggal a rendszer tranziens viselkedését tudjuk beállítani. Ha azt akarjuk, hogy a kimenőjel valamilyen konstans érték legyen, pontosabban a visszacsatolt rendszer állandósult értéke azonos legyen az $U_{r}$ referencia jellel (feltételezve, hogy $D$ =0). $U_{r}$ és $y (t)$ között kell kapcsolatot teremteni. A célt úgy fogalmazhatjuk meg, hogy

$y (\infty) = U_{r}; y \in ℝ^{m}; U_{r} \in ℝ^{m}$

( 6.114 )

és a kimenőjel az $U_{r}$ referencia értéket az általunk előírt időállandóval érje el. Ekkor a szuperpozíció elvét alkalmazhatjuk (ld. 6-6. ábra).

$u (t) = K_{x} x (t) + K_{r} U_{r} ε (t), K_{x} \in ℝ^{m \times n} K_{r} \in ℝ^{m \times m}$

( 6.115 )

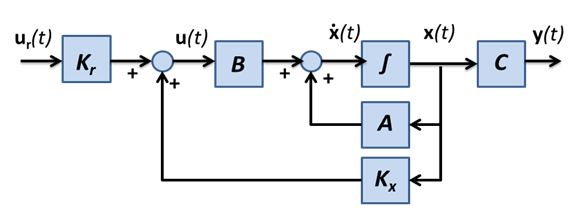
6.6. ábra - Állapotvisszacsatolás alapjel kompenzációval

A benenőjel (6.115) összefüggését behelyettesítve az állapotegyenletbe

$\dot{x} (t) = (A + B K_{x}) x (t) + B K_{r} U_{r} ε (t)$

( 6.116 )

(6.116) egyenletből kitűnik, hogy az állapotvisszacsatolással az $A$ állapotmátrix helyébe az $A + B K_{x}$ mátrix került, vagyis a tranziens viselkedést tudjuk ezzel megváltoztatni. A negatív visszacsatolás az erősítést csökkenti, ezt kompenzálhatjuk. Abból indulhatunk ki, hogy állandósult esetben az állapotváltozó értéke konstans, ezért a deriváltja nulla, továbbá $ε (\infty) = 1$ .

$x (\infty) = - {(A + B K_{x})}^{- 1} B K_{r} U_{r}$

(6.117)

Áttérve a kimenőjelre

$y (\infty) = C {(A + B K_{x})}^{- 1} B K_{r} U_{r}$

(6.118)

(6.114) és (6.118) alapján

$K_{r} = C {(A + B K_{x})}^{- 1} B)^{- 1}$

( 6.119 )

6.2.3.2. Visszacsatolástól független referenciajel kompenzáció

A (6.119) alakú korrekcióval az a gond, hogy az értéke függ a visszacsatoló $K_{x}$ mátrixtól. Létezik egy olyan megoldás, amelyben a $K_{r}$ korrekció függetleníthető $K_{x}$ értékétől. Egy ilyen megközelítés látható a 6-7. ábraán, ahol a cél: $y (\infty) = U_{r}$ . Megjegyzés: általában nem igaz, hogy minden kimenőjel egyidejűleg tetszőleges nullától különböző konstans értékű lehet. Pl. legyen a kimenőjel egy mechanikai rendszer pozoíciója és sebessége. Ha a pozíció állandó, akkor a sebesség csak nulla lehet, ha a sebesség állandó, akkor a pozíció nem lehet konstans.

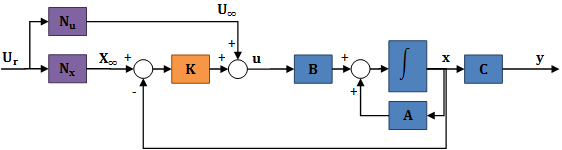
6.7. ábra - Visszacsatolástól független alapjel korrekció

$\int^{}$ $A$ $C$ $B$ $K$ $N_{x}$ $N_{u}$ $U_{r}$ $x$ $y$ $U_{\infty}$ $u$ $X_{\infty}$

$N_{x} U_{r} = x (\infty) \Rightarrow y (\infty) = C x (\infty) = C N_{x} U_{r} = U_{r}$

$ahol U_{r} \in ℝ,^{m}, u \in ℝ,^{m}, y \in ℝ,^{m} N_{x} \in ℝ^{n \times m}, N_{u} \in ℝ^{m \times m}$

( 6.120 )

$N_{u} u_{r} = u (\infty) \Rightarrow A x (\infty) + B u (\infty) = 0 \Rightarrow A N_{x} u_{r} + B N_{u} u_{r} = 0$

( 6.121 )

$[\begin{matrix} N_{x} \\ N_{u} \end{matrix}] = {[\begin{matrix} \begin{matrix} A & B \end{matrix} \\ \begin{matrix} C & 0 \end{matrix} \end{matrix}]}^{- 1} [\begin{matrix} 0 \\ I \end{matrix}] ahol N_{x} \in ℝ^{n \times m}, N_{u} \in ℝ^{m \times m}$

( 6.122 )

6.2.4. Állapotvisszacsatolás integráló taggal kiegészítve

Az alapjel kompenzáláshoz pontosan ismerni kell a rendszer paramétereit. Az így kiegészített állapotvisszacsatolás azonban a zavarójel hatását nem tudja kompenzálni. A paraméterbizonytalanság és a zavarójel hatásának kiküszöbölésére integrátort iktathatunk be a szabályozási körbe. Legyen a szabályozás célja, hogy minden kimenőjel egy konstans értéket vegyen fel

$y (\infty) = U_{r}; y (t) \in ℝ^{p}$

( 6.123 )

Azt feltételezzük, hogy ez a cél nem ütközik elvi akadályokba (pl. nem írjuk elő, hogy egy jel és deriváltja egyszerre legyen nullától különböző konstans értékű). A kiindulási egyenlet

$\dot{x} (t) = A x (t) + B u (t); A \in ℝ^{n \times n}, B \in ℝ^{n \times m}$

$y (t) = C x (t); C \in ℝ^{p \times n}$

( 6.124 )

Az integrátorok állapotát egy-egy dinamikus elemként $x_{I} \in ℝ^{p}$ állapotváltozó oszlopvektorral vehetjük figyelembe. Az integrátorokat tartalmazó alrendszer bemenőjele az előírt $u_{r} (t)$ referencia jel lesz.

$\dot{x_{I}} (t) = u_{r} (t) - y (t) = - C x (t) + I u_{r} (t) I \in ℝ^{p \times p}, x_{I} \in ℝ^{p}$

( 6.125 )

Ha az eredeti és az integrátorokhoz tartozó állapotváltozókat egyetlen oszlopvektorba összevonjuk, de különállóan meghagyjuk az $u (t)$ és $u_{r} (t)$ bemeneteket, akkor a következőt írhatjuk

$[\begin{matrix} \dot{x} (t) \\ {\dot{x}}_{I} (t) \end{matrix}] = [\begin{matrix} A & 0 \\ - C & 0 \end{matrix}] [\begin{matrix} x (t) \\ x_{I} (t) \end{matrix}] + [\begin{matrix} B \\ 0 \end{matrix}] u (t) + [\begin{matrix} 0 \\ I \end{matrix}] u_{r} (t)$

( 6.126 )

Tekintsük a 6-8. ábraát. A rendszer eredeti bemenőjelét az állapotvisszacsatolással a következő módon határozzuk meg:

$u (t) = [\begin{matrix} K_{x} & K_{I} \end{matrix}] [\begin{matrix} x (t) \\ x_{i} (t) \end{matrix}] K_{x} \in ℝ^{m \times n} K_{I} \in ℝ^{m \times p}$

( 6.127 )

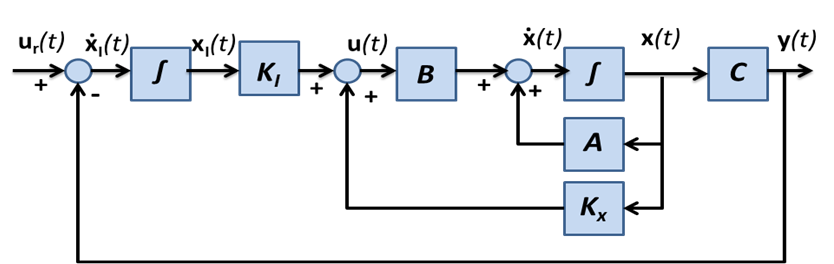
6.8. ábra - Integrátorral kiegészített állapotvisszacsatolás

6-8. ábra és (6.127) alapján az állapotvisszacsatolást a következő kiterjesztett rendszerhez kell megtervezni,

${\dot{x}}_{e x t} (t) = A_{e x t} x_{e x t} (t) + B_{e x t} u (t)$

$y_{e x t} (t) = C_{e x t} x_{e x t} (t)$

(6.128)

ahol

$A_{e x t} = [\begin{matrix} A & 0 \\ - C & 0 \end{matrix}] B_{e x t} = [\begin{matrix} B \\ 0 \end{matrix}] C_{e x t} = [\begin{matrix} C & 0 \end{matrix}]$

( 6.129 )

Látható, hogy ha $A$ irányíthatósági kanonikus alakú, akkor $A_{e x t}$ biztosan nem az. Visszacsatolás után a rendszer állapotegyenlete a következő lesz

$[\begin{matrix} \dot{x} (t) \\ {\dot{x}}_{I} (t) \end{matrix}] = [\begin{matrix} A + B K_{x} & B K_{I} \\ - C & 0 \end{matrix}] [\begin{matrix} x (t) \\ x_{I} (t) \end{matrix}] + [\begin{matrix} 0 \\ I \end{matrix}] u_{r} (t)$

( 6.130 )

6.2.5. Megfigyelő (állapotbecslő)

A legtöbb gyakorlati esetben nem tudjuk az összes állapotváltozót mérni, így az állapot visszacsatolás közvetlenül nem alkalmazható. Felmerül a kérdés, hogy a mért jelekből rekonstruálható-e az összes állapotváltozó. Korábban ezért vezettük be a megfigyelhetőség fogalmát, miszerint, ha egy rendszer teljesen megfigyelhető, akkor a mért jelekből, az összes állapotváltozó előállítható. Most arra keressük a választ, hogy hogyan.

Tegyük fel, hogy a rendszermátrixok ismertek és $D = 0$ , de nem tudjuk az állapotváltozók értékét. Feladat a bemenőjel és kimenőjel megfigyeléséből az állapotváltozók rekonstruálása. Az állapotváltozók becsült értékét jelölje $x_{e s t} (t)$ vektor.

$\dot{x} (t) = A x (t) + B u (t)$	(6.131)
$y (t) = C x (t)$	(6.132)

Fontos megjegyezni, hogy az eredeti rendszernek a bemenetei adottak, az eredeti rendszerre a definícióból adódóan csak az $u (t)$ bemenőjelen keresztül hathatunk. Ezzel szemben az állapotbecslőt mi alkotjuk meg, így az eredetitől különböző bemenetet is alkothatunk. Ismét a definíció alapján az eredeti rendszerről csak a kimenőjelen keresztül kaphatunk információt. Ezt kell felhasználnunk az állapotbecslő működésének hangolására.

${\dot{x}}_{e s t} (t) = A x_{e s t} (t) + B u (t) + L (y_{e s t} (t) - y (t)), L \in ℝ^{n \times p}$	(6.133)
$y_{e s t} (t) = C x_{e s t} (t)$	(6.134)

$A \in ℝ^{n \times n}, C \in ℝ^{n \times p} és L \in ℝ^{n \times p} � L C \in ℝ^{n \times n}$

Legyen a tényleges és a becsült vektor különbsége

$x_{e r r} (t) = x_{e s t} (t) - x (t)$

( 6.135 )

A hibára vonatkozó differenciálegyenlet a (6.133) és (6.131) különbsége

${\dot{x}}_{e r r} (t) = A x_{e r r} (t) + L (y_{e s t} (t) - y (t))$

( 6.136 )

(6.132) és (6.134) felhasználásával

${\dot{x}}_{e r r} (t) = A x_{e r r} (t) + L (C x_{e s t} (t) - C x (t))$

( 6.137 )

${\dot{x}}_{e r r} (t) = (A + L C) x_{e r r} (t)$

$A \in ℝ^{n \times n}, C \in ℝ^{n \times p} és L \in ℝ^{n \times p} � L C \in ℝ^{n \times n}$

( 6.138 )

(6.138) és (6.109) hasonlósága alapján az állapotvisszacsatolás és a megfigyelő tervezése formálisan hasonló feladat. Ha $A$ és $C$ megfigyelhető mátrixpárt alkotnak, akkor $L$ megfelelő megválasztásával beállíthatjuk az $(A + L C)$ mátrix sajátértékeit és ezzel azt tudjuk meghatározni, hogy a becslési hiba milyen időállandóval tartson a nullához.

6.2.6. Megfigyelhetőségi mátrix

$M_{O} = C {[I A A^{2} \dots A^{n - 1}]}^{T}$

( 6.139 )

6.2.7. LTI rendszerek Kálmán-féle felbontása

Egy lineáris rendszer az irányíthatóság és megfigyelhetőség szempontjából négy típusú alrendszerre bontható, az alrendszerekhez tartozó állapotváltozók

$x_{c o} (t)$ : Irányítható és megfigyelhető
$x_{c \bar{o}} (t)$ : Irányítható, de nem megfigyelhető
$x_{\bar{c} o} (t)$ : Nem irányítható, de megfigyelhető
$x_{\bar{c o}} (t)$ : Nem is irányítható és nem is megfigyelhető.

A felbontott rendszer állapottér egyenlete

$[\begin{matrix} \begin{matrix} {\dot{x}}_{c o} (t) \\ {\dot{x}}_{c \bar{o}} (t) \end{matrix} \\ \begin{matrix} {\dot{x}}_{\bar{c} o} (t) \\ {\dot{x}}_{\bar{c o}} (t) \end{matrix} \end{matrix}] = [\begin{matrix} \begin{matrix} A_{c o c o} & 0 \\ A_{c \bar{o} c o} & A_{c \bar{o} c \bar{o}} \end{matrix} & \begin{matrix} A_{c o \bar{c} o} & 0 \\ A_{c \bar{o} \bar{c} o} & A_{c \bar{o} \bar{c o}} \end{matrix} \\ \begin{matrix} 0 & 0 \\ 0 & 0 \end{matrix} & \begin{matrix} A_{\bar{c} o \bar{c} o} & 0 \\ A_{\bar{c o} \bar{c} o} & A_{\bar{c o} \bar{c o}} \end{matrix} \end{matrix}] [\begin{matrix} \begin{matrix} x_{c o} (t) \\ x_{c \bar{o}} (t) \end{matrix} \\ \begin{matrix} x_{\bar{c} o} (t) \\ x_{\bar{c o}} (t) \end{matrix} \end{matrix}] + [\begin{matrix} \begin{matrix} B_{c o} \\ B_{c \bar{o}} \end{matrix} \\ \begin{matrix} 0 \\ 0 \end{matrix} \end{matrix}] u (t)$

( 6.140 )

$y (t) = [\begin{matrix} \begin{matrix} C_{c o} & 0 \end{matrix} & \begin{matrix} C_{\bar{c} o} & 0 \end{matrix} \end{matrix}] [\begin{matrix} \begin{matrix} x_{c o} (t) \\ x_{c \bar{o}} (t) \end{matrix} \\ \begin{matrix} x_{\bar{c} o} (t) \\ x_{\bar{c o}} (t) \end{matrix} \end{matrix}] + [D] u (t)$

( 6.141 )

Írjuk fel az átviteli függvényt $D = 0$ esetén

$W (s) = \frac{C adj (s I - A) B}{\det (s I - A)} = \frac{C_{c o} adj (s I - A_{c o c o}) B_{c o}}{det (s I - A_{c o c o})}$

( 6.142 )

Látható, hogy a második egyenlőségjel után mind a nevező, mind a számláló fokszáma lecsökkent. Ez csak úgy valósulhat meg, ha néhány zésrus és pólus megegyezik, ezért a törtfüggvényből leegyszerűsíthető.

6.2.8. Megfigyelőre alapozott állapotvisszacsatolás

Amennyiben a közvetlenül nem mérhető állapotváltozókat egy megfigyelővel előállítottuk, akkor nincs akadálya az állapotvisszacsatolásnak. A tervezésnél arra kell ügyelnünk, hogy a megfigyelő sokkal gyorsabb legyen, mint maga a rendszer.

6.2.9. Kanonikus (diagonális, illetve pszeudo-diagonális) alak

Feltételezzük, hogy a rendszer állandó együtthatós közönséges differenciálegyenlettel írható le. Többféle (többféle jelzővel ellátott) kanonikus alak létezik. A kanonikus alakokhoz a természetes módon (az egyenletekből közvetlenül) felírt állapotegyenletekből hasonlósági transzformációval juthatunk el.

6.2.9.1. Szétcsatolás

A jelző nélküli kanonikus alak alapja az $A$ mátrix kanonikus diagonális alakja, ahol a diagonáljában a mátrix sajátértékei szerepelnek. Ezzel a felbontással az eredeti rendszer több, egymástól független alrendszerre esik szét. Ha ez megtehető, akkor sok előnnyel jár, hogy az alrendszerek egymástól függetlenül kezelhetők. Ezt fejezi ki a (6.35) összefüggés, és ennek alapján az állapottér egyenlet minden állapotváltozóra a többitől függetlenül oldható meg. A problémát az okozza, hogy a diagonizálásra alapozva nem lehet általános érvényű algoritmust kidolgozni, mert egyszerű hasonlósági transzformációval az $A$ mátrix nem minden esetben tehető diagonálissá. Elégséges feltétel, hogy minden sajátérték egyszeres legyen. Ha az $A$ mátrix szimmetrikus, akkor többszörös sajátértékek esetén is diagonizálható hasonlósági transzformációval. Ha az $A$ mátrix aszimmetrikus és többszörös sajátértékei vannak, akkor előfordulhat olyan speciális eset, amikor hasonlósági transzformációval az $A$ mátrix diagonálissá tehető, de általában az ún. Jordan-féle kanonikus mátrixszá alakítható. Tegyük fel, hogy ha az $A$ mátrixnak $m$ különböző sajátértéke van, akkor a Jordan-féle kanonikus pszeudo-diagonális mátrix alakja a következő:

$J = diag [J_{1}, J_{2}, \dots, J_{m}]$

( 6.143 )

ahol $J_{i}$ az i-edik sajátértékhez tartozó elemi Jordan-mátrix. Ha az i-edik sajátérték egyszeres, akkor

$J_{i} = λ_{i}$

( 6.144 )

Ha az i-edik sajátérték $L$ -szeres, akkor $J_{i} \in ℝ^{l \times l}$

$J_{i} = [\begin{matrix} \begin{matrix} λ_{i} \\ 0 \\ 0 \end{matrix} \\ ⋮ \\ 0 \end{matrix} \begin{matrix} \begin{matrix} δ_{1} \\ λ_{i} \\ 0 \end{matrix} & \begin{matrix} 0 \\ δ_{2} \\ λ_{i} \end{matrix} & \begin{matrix} 0 \\ 0 \\ δ_{3} \end{matrix} \\ ⋮ & ⋮ & ⋮ \\ 0 & 0 & 0 \end{matrix} \begin{matrix} \begin{matrix} \dots \\ \dots \\ \dots \end{matrix} \\ \dots \end{matrix} \begin{matrix} \begin{matrix} 0 \\ 0 \\ ⋮ \end{matrix} \\ δ_{L - 1} \\ λ_{i} \end{matrix}]$

( 6.145 )

ahol $λ_{i}$ az i-edik sajátérték és $δ_{l}$ értéke általában 1, speciális esetekben lehet 0 is. Jelöljük $J$ indexszel a transzformált rendszermátrixokat és állapotváltozót, ha hasonlósági transzformációval az A mátrixot Jordan-féle kanonikus pszeudo-diagonális alakra hozzuk

${\dot{x}}_{J} (t) = A_{J} x_{J} (t) + B_{J} u (t)$	(6.146)
$y (t) = C_{J} x_{J} (t) + D_{J} u (t)$	(6.147)

Ebben az esetben két különböző elemi Jordan-mátrixhoz tartozó két állapotváltozó egymástól mindig független. A $J_{i}$ mátrix legalsó sorához tartozó állapotváltozó sem függ semelyik másik állapotváltozótól. Ha $δ_{l} = 1$ , akkor az adott sorhoz tartozó állapotváltozó függ az eggyel nagyobb sorszámú állapotváltozótól, vagyis azon keresztül irányítható. Általános esetben, amikor az összes $δ_{l} = 1$ , akkor a többszörös sajátértékhez tartozó állapotváltozók nem csatolhatók szét, nem lehet azokat egymástól függetleníteni. Ez az alak alkalmas az irányíthatóság és a megfigyelhetőség egyszerű ellenőrzésére. Az egyszeres sajátértékhez tartozó állapotváltozókat és a többszörös sajátértékhez tartozó olyan állapotváltozókat, amelyekhez tartozó (mellette lévő) $δ_{l}$ értéke 0, csak közvetlenül a bemenőjellel lehet befolyásolni, ezért csak akkor irányíthatók, ha a $B_{J}$ mátrix adott sorában van legalább egy nem nulla elem.

Hasonlóan, az egyszeres sajátértékhez tartozó állapotváltozók és a többszörös sajátértékhez tartozó olyan állapotváltozók, amely felett lévő $δ_{l}$ értéke 0, csak akkor megfigyelhető, ha a $C_{J}$ mátrix megfelelő sorszámú oszlopában van legalább egy nem nulla elem.

Azok az állapotváltozók, amelyek sajátértéke mellett az $A_{J}$ mátrixban található egy 1-es, azok befolyásolhatók az eggyel nagyobb sorszámú állapotváltozón keresztül, de ezzel együtt információt is tartalmaz arról. Ha az $A_{J}$ mátrixban található egy következő alakú blokk

$J_{i} = [\begin{matrix} \begin{matrix} λ_{i} \\ 0 \\ 0 \end{matrix} \\ ⋮ \\ 0 \end{matrix} \begin{matrix} \begin{matrix} 1 \\ λ_{i} \\ 0 \end{matrix} & \begin{matrix} 0 \\ 1 \\ λ_{i} \end{matrix} & \begin{matrix} 0 \\ 0 \\ 1 \end{matrix} \\ ⋮ & ⋮ & ⋮ \\ 0 & 0 & 0 \end{matrix} \begin{matrix} \begin{matrix} \dots \\ \dots \\ \dots \end{matrix} \\ \dots \end{matrix} \begin{matrix} \begin{matrix} 0 \\ 0 \\ ⋮ \end{matrix} \\ 1 \\ λ_{i} \end{matrix}]$

( 6.148 )

akkor e blokkhoz tartozó minden állapotváltozó irányítható a legalsó sorhoz tartozó állapotváltozón keresztül, és minden állapotváltozó megfigyelhető (rekonstruálható) a legfelső sorhoz tartozó állapotváltozóból.

xxxxx

6.2.10. Kidolgozott feladatok az állapotirányításra

6 . 8 feladat

Adott a következő rendszer. Írja fel az irányíthatósági mátrixot és döntse el, hogy irányítható-e a rendszer.

$[\begin{matrix} {\dot{x}}_{1} \\ {\dot{x}}_{2} \end{matrix}] = [\begin{matrix} - 1 & 2 \\ - 3 & - 5 \end{matrix}] [\begin{matrix} x_{1} \\ x_{2} \end{matrix}] + [\begin{matrix} 1 \\ 0 \end{matrix}] u$

( 6.149 )

6.2.10.1. Megoldás

$M_{C} = [\begin{matrix} 1 & - 1 \\ 0 & - 3 \end{matrix}] \Rightarrow \det M_{C} = - 3$

( 6.150 )

A determináns nem 0, ezért a rendszer irányítható.

6 . 9 feladat

Adott a következő rendszer. Írja fel az irányíthatósági mátrixot és döntse el, hogy irányítható-e a rendszer.

$[\begin{matrix} {\dot{x}}_{1} (t) \\ {\dot{x}}_{2} (t) \\ {\dot{x}}_{3} (t) \end{matrix}] = [\begin{matrix} - 7 & 0 & 0 \\ 2 & - 4 & 3 \\ - 5 & - 2 & - 1 \end{matrix}] [\begin{matrix} x_{1} (t) \\ x_{2} (t) \\ x_{3} (t) \end{matrix}] + [\begin{matrix} 0 \\ 1 \\ 0 \end{matrix}] u (t)$

( 6.151 )

6.2.10.2. Megoldás

Látható, hogy az $x_{1} (t)$ állapotváltozóra sem egy másik állapotváltozó, sem a bemenőjel nem hat, így az irányíthatósági mátrix felírása nélkül is kimondható, hogy a rendszer nem irányítható. Ugyanerre következtetésre juthatunk az irányíthatósági mátrix alapján is.

$M_{C} = [\begin{matrix} 0 & 0 & 0 \\ 1 & - 4 & 10 \\ 0 & - 2 & 10 \end{matrix}] \Rightarrow \det M_{C} = 0$

( 6.152 )

Ha a determinánst az első sor alapján fejtjük ki, akkor minden tagban szerepel egy nulla tényező. Mivel ${(- 1)}^{(1 + 1)} = 1$ , az első tag előjele pozitív (bár ennek esetünkben nincs jelentősége).

$\det M_{C} = + 0 det [\begin{matrix} - 4 & 10 \\ - 2 & 10 \end{matrix}] - 0 det [\begin{matrix} 1 & 10 \\ 0 & 10 \end{matrix}] + 0 det [\begin{matrix} 1 & - 4 \\ 0 & - 2 \end{matrix}] = 0$

( 6.153 )

6 . 10 feladat

Adott a következő rendszer. Írja fel a megfigyelhetőségi mátrixot és döntse el, hogy megfigyelhető-e a rendszer.

( 6.154 )

$y = [\begin{matrix} 0 & 1 \end{matrix}] [\begin{matrix} x_{1} \\ x_{2} \end{matrix}] + [0] u$

( 6.155 )

6.2.10.3. Megoldás

$M_{O} = [\begin{matrix} 0 & 1 \\ - 3 & - 5 \end{matrix}] \Rightarrow \det M_{O} = 3$

( 6.156 )

A determináns nem 0, ezért a rendszer megfigyelhető.

6 . 11 feladat

Adott a következő rendszer. Írja fel a megfigyelhetőségi mátrixot és döntse el, hogy megfigyelhető-e a rendszer.

$[\begin{matrix} {\dot{x}}_{1} (t) \\ {\dot{x}}_{2} (t) \\ {\dot{x}}_{3} (t) \end{matrix}] = [\begin{matrix} - 7 & - 3 & - 2 \\ 0 & - 4 & 3 \\ 0 & - 2 & - 1 \end{matrix}] [\begin{matrix} x_{1} (t) \\ x_{2} (t) \\ x_{3} (t) \end{matrix}] + [\begin{matrix} 1 \\ 1 \\ 0 \end{matrix}] u (t)$

$[\begin{matrix} y_{1} (t) \\ y_{2} (t) \end{matrix}] = [\begin{matrix} 0 & 1 & 2 \\ 0 & 3 & 4 \end{matrix}] [\begin{matrix} x_{1} (t) \\ x_{2} (t) \\ x_{3} (t) \end{matrix}] + [\begin{matrix} 0 \\ 0 \end{matrix}] u (t)$

( 6.157 )

6.2.10.4. Megoldás

Látható, hogy az $x_{1} (t)$ állapotváltozóról sem közvetlenül (ld. C mátrix első oszlopa), sem közvetve, más állapotváltozón keresztül (ld. A mátrix első oszlopa) nem szerzünk információt. Így a rendszer nem megfigyelhető.

6 . 12 feladat

Adott egy rendszer átviteli függvénye

$W (s) = \frac{3 s + 7}{s^{3} + 7 s^{2} + 14 s + 8}$

( 6.158 )

Irjuk fel a rendszer állapottér egyenletét kanonikus alakban

6.2.10.5. Megoldás

A kimenőjel Laplace-transzformáltja

$Y (s) = \frac{3 s + 7}{(s + 1) (s + 2) (s + 4)} U (s)$

( 6.159 )

Részlettörtekre bontva

$Y (s) = (\frac{4}{3 (s + 1)} - \frac{1}{2 (s + 2)} - \frac{5}{6 (s + 4)}) U (s)$

( 6.160 )

Három állapotváltozót bevezetve

$Y (s) = \frac{4}{3} X_{1} (s) - \frac{1}{2} X_{2} (s) - \frac{5}{6} X_{3} (s)$

( 6.161 )

Az állapotváltozókra felírható egyenletek

$(s + 1) X_{1} (s) = U (s)$

$u (t) = {\dot{x}}_{1} (t) + x_{1} (t)$

$(s + 2) X_{2} (s) = U (s)$

$u (t) = {\dot{x}}_{2} (t) + 2 x_{2} (t)$

$(s + 4) X_{3} (s) = U (s)$

$u (t) = {\dot{x}}_{3} (t) + 4 x_{3} (t)$

( 6.162 )

Átrendezve mátrixos formára:

$[\begin{matrix} {\dot{x}}_{1} (t) \\ {\dot{x}}_{2} (t) \\ {\dot{x}}_{3} (t) \end{matrix}] = [\begin{matrix} - 1 & 0 & 0 \\ 0 & - 2 & 0 \\ 0 & 0 & - 4 \end{matrix}] [\begin{matrix} x_{1} (t) \\ x_{2} (t) \\ x_{3} (t) \end{matrix}] + [\begin{matrix} 1 \\ 1 \\ 1 \end{matrix}] u (t)$

( 6.163 )

$y (t) = [\begin{matrix} \frac{4}{3} & - \frac{1}{2} \end{matrix} - \frac{5}{6}] [\begin{matrix} x_{1} (t) \\ x_{2} (t) \\ x_{3} (t) \end{matrix}] + [0] u (t)$

( 6.164 )

6 . 13 feladat (pólus áthelyezés)

Egy lineáris rendszer állapottér egyenletei a következő alakban írhatóak fel.

$\dot{x} (t) = A x (t) + B u (t)$

$y (t) = C x (t) + D u (t)$

( 6.165 )

Állapotvisszacsatolással a visszacsatolt szabályozási kör pólusait kívánjuk áthelyezni az ábrán látható módon.

A rendszer „mátrixok” értékei a következők: A = -2, B = 4, C = 1, D = 0.

Számítsa ki a rendszer időállandóját. Számítsa ki a K értékét úgy, hogy a visszacsatolt szabályozási kör időállandója a felére csökkenjen. Indokolja, hogy miért van szükség az Nx és Nu kompenzációra, adja meg azok számításának módját, és numerikusan is számolja ki!

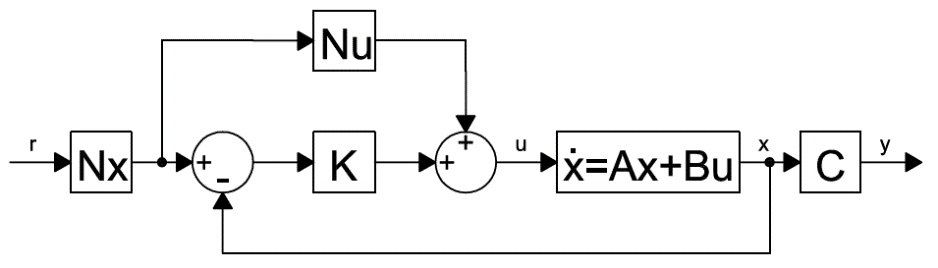
6.9. ábra - Póluspont áthelyezés visszacsatolással

Megoldás

Ez a rendszer egy állapotváltozós, SISO rendszer, mivel a rendszermátrixok skalárok. Ez a számolás során könnyebbséget jelent.

6.10. ábra - Felnyitott kör

Első lépésben az eredeti rendszerrel foglalkozunk:

Az állapottér egyenleteket átírjuk a frekvenciatartományba, és a D=0 miatt egyszerűsítjük a második egyenletet. Kifejezzük az állapotváltozót (X), majd ezt behelyettesítve, a kimenetet (Y) kifejezzük a bemenet (U) függvényeként. Végül felírjuk a rendszer átviteli függvényét, megadva a póluspontot és az időállandót.

$s X (s) = A X (s) + B U (s)$ $Y (s) = C X (s)$ $X (s) = {(s I - A)}^{- 1} B = \frac{B}{s - A} U (s)$

(Ez az átalakítás csak akkor tehető meg, ha az A ”rendszermátrix” skalár, tehát egyetlen állapotváltozó van. Az egyenletben szereplő I az egységmátrix.)

$Y (s) = \frac{C B}{s - A} U (s)$ $W (s) = \frac{Y (s)}{U (s)} = \frac{C B}{s - A} = \frac{1 * 4}{s + 2}$

A póluspontban a nevező nulla: $0 = p + 2$ ,tehát $p = - 2$

A rendszer időállandója (valós értékű pólus esetén): $T = - \frac{1}{p} = - \frac{1}{- 2} = \frac{1}{2} = 0.5$

A póluspontot az alapok ismeretében egy lépésben is megkaphatjuk. Minden

$\dot{x} (t) = A x (t) + B u (t)$ $y (t) = C x (t) + D u (t)$

alakban felírható lineáris rendszer átviteli függvénye:

$W (s) = C {(s I - A)}^{- 1} B + D = \frac{C * {a d j (s I - A)}^{T} * B}{d e t (s I - A)} + D$

Ebből az egyenletből egyértelműen látszik, hogy az ilyen rendszerek póluspontjai az A mátrix sajtértékei. Esetünkben az A mátrix skalár, tehát sajátértéke önmaga, vagyis a pólus: $p = A = - 2$

Teljes rendszer a visszacsatolt szabályozási körrel:

A kikötés: $T_{2} = \frac{T}{2} = 0.25$ legyen.

Az új póluspont így: $p_{2} = - \frac{1}{T} = - \frac{1}{0.25} = - 4$

A szabályozási kör átviteli függvényét hatásvázlat átalakítás segítségével kapjuk meg. Először az időtartománybeli hatásvázlatot a frekvenciatartománybelivel helyettesítjük, és áthelyezzük az összegzési pontot, majd felírjuk az így keletkező előre-, és visszacsatolás eredő átviteli függvényét.

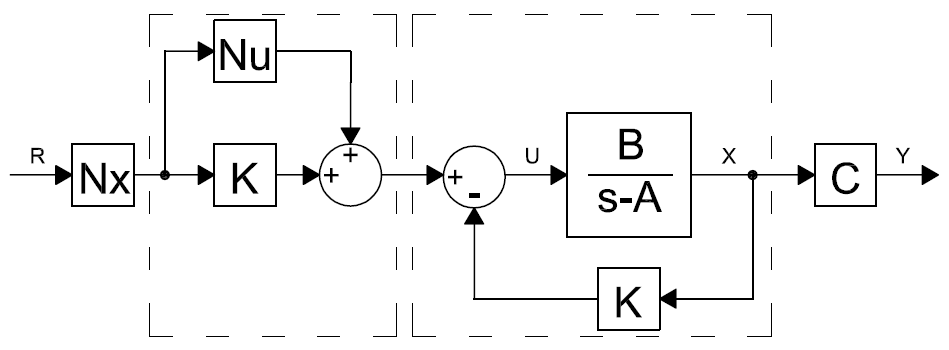
6.11. ábra - Áthelyezett összegzési pont

Az előrecsatolás eredő átviteli függvénye: $W e = N u + K$

A visszacsatolásé: $W v = \frac{\frac{B}{s - A}}{1 + \frac{B}{s - A} K} = \frac{\frac{B}{s - A}}{\frac{s - A + B K}{s - A}} = \frac{B}{s - A + B K}$

6.12. ábra - Összevont átviteli függvényekkel

A visszacsatolt szabályozási kör kimenetének függvénye:

$Y_{2} (s) = R (s) \frac{N x (N u + K) B C}{s - A + B K}$

A visszacsatolt szabályozási kör bemenete: r(t); R(s)

Így az átviteli függvény:

$W_{2} (s) = \frac{Y_{2} (s)}{R (s)} = \frac{N x (N u + K) B C}{s - A + B K}$

Az időállandóra tett kikötés miatt a pólus értéke: $p_{2} = - 4$

$0 = p_{2} - A + B K = - 4 + 2 + 4 K = - 2 + 4 K$

A kívánt eredményhez a K visszacsatoló mátrix értékét $K = \frac{2}{4} = 0.5$ -nek kell választani.

Az Nx, Nu kompenzációra azért van szükség, mert a visszacsatolással történő pólus áthelyezés a rendszer erősítését is megváltoztatja. Ezekkel a kompenzáló tagokkal lehet az eredő erősítést beállítani. Az általános elvárás, hogy a teljes rendszer erősítése egy legyen. A kompenzáló tagok számításához állandósult állapotot, azaz az elvárt értékre beállt rendszert feltételezünk.

A megadott hatásvázlattal jellemezhető feladatoknál, ha az elvárt eredő erősítés egy, akkor a bemenőjel (r(t)) valójában a kimenőjel elvárt értéke, amire be kell állnia (y(∞)). A frekvenciatartományban ekkor:

$Y (s) = R (s)$

Állandósult állapotban a régi és az új állapot azonos, tehát az állapotváltozók vektora állandó, deriváltja pedig zérus, míg a különbségképző utáni különbségi jeltől (hibajeltől) pedig elvárjuk, hogy szintén zérus legyen:

$0 = A X (s) + B U (s)$ $Y (s) = C X (s)$

A különbségi jel: $R (s) N x - X (s) = 0,$ tehát $X (s) = R (s) N x$

Az adott szabályozásnál, ha a különbségi jel zérus: $U (s) = R (s) N x N u$

Az így meghatározott X(s) és U(s) értékeket visszahelyettesítjük az állapottér egyenletekbe, majd a szabályozott jellemző minden értékét egynek választjuk. (Mivel a jelenlegi feltételezésünk szerint a rendszer állandósult állapotban van, így Y(s) értékét bármilyen konstans értéknek választhatjuk, és az állandósult állapot miatt ez a szabályozó jel értéke is.) $R (s) = Y (s) = 1$

$0 = A X (s) + B U (s) = A R (s) N x + B R (s) N x N u = A N x + B N x N u$

$Y (s) = C X (s) = C R (s) N x = C N x = 1$

Az így kapott két ismeretlenes egyenletrendszert mátrixos alakban nem tudjuk felírni, mert az ismeretlenek nem függetlenek. Azonban nincs nehéz dolgunk, mert a feladatban skalár értékekkel számolunk.

A második egyenlettel kezdve: $1 = C N x = 1 N x$

Így az első egyenlet: $0 = A N x + B N x N u = - 2 * 1 + 4 * 1 * N u = - 2 + 4 N u$

Tehát: $N x = 1$ , és $N u = \frac{2}{4} = 0.5$ a kompenzáló tagok értékei.

6.3. SISO rendszerek állapotirányítása

A 6.3 alfejezet célja a 6.2 alfejezetben szereplő ismeretek elmélyítése papíron könnyebben kiszámítható példákon keresztül.

6.3.1. Állapotvisszacsatolás kanonikus alakban

Tegyük fel, hogy az állapottér egyenletünk kanonikus alakban adott. Vizsgájuk meg, hogy az állapotvisszacsatolás hogyan hat a kanonikus alakra. Az egyszerűség kedvéért induljunk ki a 6.12 feladatban bemutatott rendszerből. Legyen

$u (t) = K_{x} x (t) = [\begin{matrix} - 1 & - 2 \end{matrix} - 4] [\begin{matrix} x_{1} (t) \\ x_{2} (t) \\ x_{3} (t) \end{matrix}]$

( 6.166 )

A (6.166) összefüggést behelyettesítve (6.163) állapotegyenletbe.

( 6.167 )

Jól látható, hogy az állapotvisszacsatolással elveszítjük a diagonális struktúrát. Célszerűnek látszik, hogy keressünk egy olyan más mátrixstruktúrát, amely az állapotvisszacsatolás után is megmarad.

6.3.2. SISO rendszerek irányíthatósági kanonikus alakja

Tegyük fel, hogy a rendszer állandó együtthatós közönséges differenciálegyenlettel írható le, amelyet Laplace-transzformálva a közvetkezőt kapjuk:

$\sum_{i = 0}^{n} a_{i} s^{i} Y (s) = \sum_{i = 0}^{r} b_{i} s^{i} U (s) \Rightarrow W (s) = \frac{\sum_{i = 0}^{r} b_{i} s^{i}}{\sum_{i = 0}^{n} a_{i} s^{i}} a_{i}, b_{i} \in ℝ, a_{n} \neq 0$

(6.168)

Vezessük be a következő jelölést:

$X (s) = \frac{1}{\sum_{i = 0}^{n} a_{i} s^{i}} U (s)$	(6.169)
$Y (s) = \sum_{i = 0}^{r} b_{i} s^{i} X (s)$	(6.170)

A (6.169) egyenletet kifejtve

$X (s) • a_{n} • s^{n} + X (s) • a_{n - 1 •} s^{n - 1} + \dots + X (s) • a_{0} = U (s)$

( 6.171 )

Inverz Laplace-transzformálva:

$a_{n} • x^{(n)} (t) + a_{n - 1} • x^{(n - 1)} (t) + \dots + a_{0} • x^{(n - n)} (t) = u (t)$

( 6.172 )

átrendezve:

$x^{(n)} (t) = - \frac{a_{n - 1}}{a_{n}} x^{(n - 1)} (t) - \frac{a_{n - 2}}{a_{n}} x^{(n - 2)} (t) - \frac{a_{0}}{a_{n}} x (t) + \frac{1}{a_{n}} u (t)$

( 6.173 )

legyen

$x (t) = [\begin{matrix} x (t) \\ x^{(1)} (t) \\ \begin{matrix} ⋮ \\ x^{(n - 2)} (t) \\ x^{(n - 1)} (t) \end{matrix} \end{matrix}]$

Az állapottér egyenlet

$\dot{x} (t) = [\begin{matrix} x^{(1)} (t) \\ x^{(2)} (t) \\ \begin{matrix} ⋮ \\ x^{(n - 1)} (t) \\ x^{(n)} (t) \end{matrix} \end{matrix}] = [\begin{matrix} \begin{matrix} 0 \\ 0 \\ 0 \end{matrix} \\ ⋮ \\ - \frac{a_{0}}{a_{n}} \end{matrix} \begin{matrix} \begin{matrix} 1 \\ 0 \\ 0 \end{matrix} & \begin{matrix} 0 \\ 1 \\ 0 \end{matrix} & \begin{matrix} 0 \\ 0 \\ 1 \end{matrix} \\ ⋮ & ⋮ & ⋮ \\ - \frac{a_{1}}{a_{n}} & - \frac{a_{2}}{a_{n}} & - \frac{a_{3}}{a_{n}} \end{matrix} \begin{matrix} \begin{matrix} \dots \\ \dots \\ \dots \end{matrix} \\ \dots \\ \dots \end{matrix} \begin{matrix} \begin{matrix} 0 \\ 0 \\ 0 \end{matrix} \\ 1 \\ - \frac{a_{n - 1}}{a_{n}} \end{matrix}] \cdot [\begin{matrix} \begin{matrix} x^{(0)} (t) \\ x^{(1)} (t) \\ x^{(2)} (t) \end{matrix} \\ ⋮ \\ x^{(n - 1)} (t) \end{matrix}] + [\begin{matrix} \begin{matrix} 0 \\ 0 \\ 0 \end{matrix} \\ ⋮ \\ \frac{1}{a_{n}} \end{matrix}] u (t)$

( 6.174 )

A kimenetre vonatkozó egyenlet

$Y (s) = b_{r} s^{r} X (s) + b_{r - 1} s^{r - 1} X (s) + \dots + b_{0} X (s)$	(6.175)
$y (t) = b_{r} x^{(r)} (t) + b_{r - 1} x^{(r - 1)} (t) + \dots + b_{0} x^{(0)} (t)$	(6.176)

Két esetet kell különválasztani.

Ha n>r, akkor (6.176) alapján $y (t)$ az állapotváltozók lineáris kombinációja

$y (t) = [\begin{matrix} b_{0} & \dots & \begin{matrix} b_{r - 1} & b_{r} & 0 \end{matrix} \end{matrix} \dots 0] • [\begin{matrix} \begin{matrix} x^{(0)} (t) \\ ⋮ \\ x^{(r)} (t) \end{matrix} \\ ⋮ \\ x^{(n - 1)} (t) \end{matrix}] + 0 u (t)$

( 6.177 )

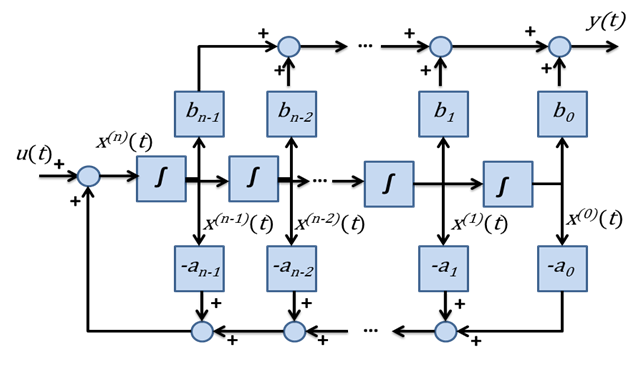
A könnyebb ábrázolhatóság kedvéért vezessük be a következő jelölést

$y (t) = [\begin{matrix} b_{0} & \dots & \begin{matrix} b_{r - 1} & b_{r} & b_{r + 1} \end{matrix} \end{matrix} \dots b_{n - 1}] • [\begin{matrix} \begin{matrix} x^{(0)} (t) \\ ⋮ \\ x^{(r)} (t) \end{matrix} \\ ⋮ \\ x^{(n - 1)} (t) \end{matrix}] + 0 u (t)$

( 6.178 )

ahol $b_{i} = 0$ , ha $i > r$ . Legyen továbbá $a_{n} = 1$ . Ezzel a jelöléssel az ún. irányíthatósági kanonikus alak blokkvázlatát a 6-13. ábra mutatja.

6.13. ábra - Irányíthatósági kanonikus alak hatásvázlata

Ha n=r, akkor (6.176) mellett (6.173), illetve (6.174) utolsó sorára is tekintettel kell lennünk.

$y (t) = [\begin{matrix} b_{0} - \frac{a_{0}}{a_{n}} b_{n} & b_{1} - \frac{a_{1}}{a_{n}} b_{n} \end{matrix} \begin{matrix} \dots & b_{n - 2} - \frac{a_{n - 2}}{a_{n}} b_{n} & b_{n - 1} \end{matrix} - \frac{a_{n - 1}}{a_{n}} b_{n}] [\begin{matrix} \begin{matrix} x^{(0)} (t) \\ x^{(1)} (t) \\ ⋮ \end{matrix} \\ x^{(n - 2)} (t) \\ x^{(n - 1)} (t) \end{matrix}] + \frac{b_{n}}{a_{n}} u (t)$

( 6.179 )

6.3.3. Pólus áthelyezés irányíthatósági kanonikus alak esetén

Tegyük fel, hogy $a_{n} = 1$ , D=0 és n>r, továbbá induljunk ki a következő átviteli függvényből

$W (s) = \frac{\sum_{i = 0}^{r} b_{i} s^{i}}{s^{n} + \sum_{i = 0}^{n - 1} a_{i} s^{i}}$

( 6.180 )

Az első lépésben az a célunk, hogy a megváltoztassük az átviteli függvény pólusait, vagyis (6.180) vevezőjének gyökeit. Jelöljük a bevezetni kívánt (desired) pólusokat $p_{i d}$ -vel és legyen $W_{d} (s)$ az állapotvisszacsatolással nyert rendszer átviteli függvénye, amely $p_{i d}$ pólusokkal rendelkezik.

$W_{d} (s) = \frac{\sum_{i = 0}^{r} b_{i} s^{i}}{\prod_{i = 1}^{n} (s - p_{i d})} = \frac{\sum_{i = 0}^{r} b_{i} s^{i}}{s^{n} + \sum_{i = 0}^{n - 1} a_{i d} s^{i}}$

( 6.181 )

ahol $a_{i d}$ az állapotvisszacsatolással elérni kívánt rendszer átviteli függvényének nevezőjében található polinom együtthatói, más szavakkal a visszacsatolt rendszer karakterisztikus egyenletének együtthatói. Vizsgáljuk meg, hogy mit eredményez az állapotvisszacsatolás egy tetszőleges $K_{x}$ sorvektoron keresztül.

$u (t) = K_{x} x (t) = [\begin{matrix} k_{0} & k_{1} & \begin{matrix} \dots & k_{n - 2} \end{matrix} \end{matrix} k_{n - 1}] [\begin{matrix} \begin{matrix} x^{(0)} (t) \\ x^{(1)} (t) \\ ⋮ \end{matrix} \\ x^{(n - 2)} (t) \\ x^{(n - 1)} (t) \end{matrix}]$

( 6.182 )

A bemeneti $B$ mátrix speciális struktúrája miatt

$[\begin{matrix} \begin{matrix} 0 \\ 0 \\ ⋮ \end{matrix} \\ 0 \\ 1 \end{matrix}] [\begin{matrix} k_{0} & k_{1} & \begin{matrix} \dots & k_{n - 2} \end{matrix} \end{matrix} k_{n - 1}] = [\begin{matrix} \begin{matrix} \begin{matrix} 0 \\ 0 \\ ⋮ \end{matrix} \\ 0 \\ k_{0} \end{matrix} & \begin{matrix} \begin{matrix} 0 \\ 0 \\ ⋮ \end{matrix} \\ 0 \\ k_{1} \end{matrix} & \begin{matrix} \begin{matrix} \begin{matrix} \dots \\ ⋱ \end{matrix} \\ \dots \end{matrix} & \begin{matrix} \begin{matrix} 0 \\ 0 \\ ⋮ \end{matrix} \\ 0 \\ k_{n - 2} \end{matrix} \end{matrix} \end{matrix} \begin{matrix} \begin{matrix} 0 \\ 0 \\ ⋮ \end{matrix} \\ 0 \\ k_{n - 1} \end{matrix}]$

( 6.183 )

Az állapotvisszacsatolás után a rendszert leíró egyenlet a következő lesz

$\dot{x} (t) = [\begin{matrix} \begin{matrix} 0 \\ 0 \\ 0 \end{matrix} \\ ⋮ \\ - a_{0} + k_{0} \end{matrix} \begin{matrix} \begin{matrix} 1 \\ 0 \\ 0 \end{matrix} & \begin{matrix} \dots \\ ⋱ \end{matrix} & \begin{matrix} 0 \\ 0 \\ 1 \end{matrix} \\ ⋮ & 0 \\ - a_{1} + k_{1} & \dots & - a_{n - 2} + k_{n - 2} \end{matrix} \begin{matrix} \begin{matrix} 0 \\ 0 \\ 0 \end{matrix} \\ 1 \\ - a_{n - 1} + k_{n - 1} \end{matrix}] \cdot [\begin{matrix} \begin{matrix} x^{(0)} (t) \\ x^{(1)} (t) \\ x^{(2)} (t) \end{matrix} \\ ⋮ \\ x^{(n - 1)} (t) \end{matrix}]$

( 6.184 )

Így egy magára hagyott rendszert kapunk (az utolsó sor egy homogén differenciálegyenlet), amelynek az együtthatóit tetszőlegesen beállíthatjuk a $K_{x}$ visszacsatoló tag helyes megválasztásával. Ha azt kívánjuk, hogy a (6.184) rendszer átviteli függvénye (6.181) legyen, akkor $K_{x}$ elemeit a következő módon kell megválasztani:

$k_{i} = a_{i} - a_{i d}$

( 6.185 )

Az állapotvisszacsatolással azt tudjuk elérni, hogy a rendszer tetszőleges kezdeti értékből kiindulva a $K_{x}$ visszacsatoló tag által beállított időállandóval tartson a nullához, vagyis a $K_{x}$ visszacsatoló taggal a rendszer tranziens viselkedését tudjuk beállítani. Ha azt akarjuk, hogy a kimenőjel valamilyen konstans érték legyen, akkor a szuperpozíció elvét alkalmazhatjuk (ld. 6-6. ábra)

$u (t) = K_{x} x (t) + K_{r} U_{r} ε (t), K_{x} \in ℝ^{1 \times n}$

( 6.186 )

A (6.116) egyenletből kitűnik, hogy az állapotvisszacsatolással az $A$ állapot mátrix helyébe $A + B K_{x}$ mátrix került, vagyis a tranziens viselkedést tudjuk ezzel megváltoztatni.

$\dot{x} (t) = (A + B K_{x}) x (t) + B K_{r} U_{r} ε (t)$

( 6.187 )

Ha az a célunk, hogy legyen $y (\infty) = U_{r}$ , akkor ehhez $K_{r}$ értékét megfelelően kell megválasztanunk. Írjuk fel a kimenőjel Laplace-transzformáltját.

$Y (s) = \frac{\sum_{i = 0}^{r} b_{i} s^{i}}{s^{n} + \sum_{i = 0}^{n - 1} (a_{i} - k_{i}) s^{i}} K_{r} U_{r} (s)$

( 6.188 )

A végérték tétel alapján

$y (\infty) = \lim_{s \to 0} s Y (s) = \lim_{s \to 0} s \frac{\sum_{i = 0}^{r} b_{i} s^{i}}{s^{n} + \sum_{i = 0}^{n - 1} (a_{i} - k_{i}) s^{i}} K_{r} U_{r} \frac{1}{s} = \frac{b_{0}}{a_{0} - k_{0}} K_{r} U_{r}$

( 6.189 )

$y (\infty) = U_{r}$ úgy érhető el, ha

$\frac{b_{0}}{a_{0} - k_{0}} K_{r} = 1$

( 6.190 )

Az állapotvisszacsatolás blokk diagramját irányíthatósági kanonikus alak esetén a 6-14. ábra mutatja.

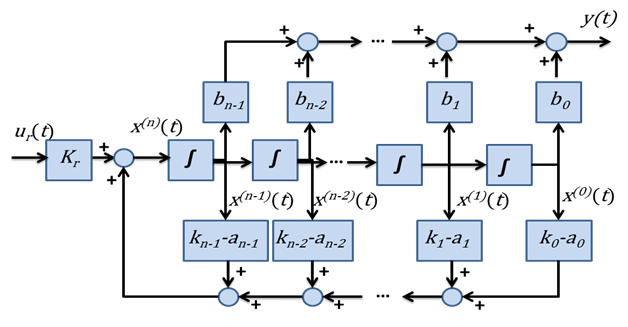
6.14. ábra - Állapotvisszacsatolás irányíthatósági kanonikus alak esetén

6.3.4. Pólus áthelyezés általános alakú LTI SISO rendszer esetén (Ackermann formula)

A 6.3.3 pontban leírt módszer elméletben nagyon hatékonynak bizonyult, de a gyakorlatban legtöbbször közvetlenül még akkor sem alkalmazható, ha minden állapotváltozót mérni tudunk, mivel a rendszer fizikai felépítése eltér az irányíthatósági kanonikus alaktól. Ezért először a mért állapotváltozókat transzformálni kell az irányíthatósági kanonikus alakara, ahol az állapotvisszacsatolás megtervezhető a 6.3.3 pontban leírt módszerrel. Az állapottranszformáció és a visszacsatoló mátrix (pontosabban esetünkben sorvektor) közvetlenül megtervezhető az Ackermann formula segítségével.

Először vizsgáljuk meg, hogy miként hat a hasonlósági transzformáció az állapotvisszacsatolásra.

Adott egy (6.3) alakú differenciálegyenlettel leírható rendszer, amelyet egy megfelelő hasonlósági transzformációval átalakítunk.

$\dot{x} (t) = A x (t) + B u (t))$	(6.191)
${\dot{x}}_{T} (t) = A_{T} x_{T} (t) + B_{T} u (t)$	(6.192)

Tegyük fel, hogy a transzformált rendszerhez valamilyen szempont szerint megterveztük a szükséges $K_{T x}$ állapotvisszacsatoló mátrixot. Ha ugyanezt a hatást (értsd ugyanezt a bemenőjelet) az eredeti rendszer állapotváltozóiból szeretnénk elérni.

$u (t) = K_{x} x (t) = K_{T x} x_{T} (t) = K_{T x} T x (t)$

( 6.193 )

A (6.193) összefüggésből kiolvasható, hogy ha ismerjük a hasonlósági transzformációs mátrixot és a transzformált rendszerhez megterveztük az állapotvisszacsatolást, akkor kiszámíthatjuk az eredeti rendszerhez szükséges állapotvisszacsatolást.

$K_{x} = K_{T x} T$

( 6.194 )

Adottakegy SISO rendszer állapottér egyenletei, ahol az $A$ , $B$ és $C$ rendszermátrix általános alakúak (azt feltételezzük, hogy $D = 0$ ). Keressük azt a $T_{c}$ hasonlósági transzformációs mátrixot, amellyel az eredeti egyenletet transzformálhatjuk az $A_{c}$ , $B_{c}$ és $C_{c}$ irányíthatósági kanonikus alakra. (6.21) alapján

$A_{c} T_{c} = T_{c} A$

( 6.195 )

Használjuk ki $A_{c}$ speciális struktúráját. Tegyük fel, hogy az $A_{c}$ mátrix alakja megegyezik a (6.174) egyenletben található rendszermátrix alakjával, azzal a kiegészítéssel, hogy legyen $a_{n} = 1$ . Jelölje a $T_{c}$ mátrix i-edik sorát a $T_{c i (1 : n)}$ . Ennek megfelelően (6.195) a következőképp írható fel

$[\begin{matrix} \begin{matrix} 0 \\ 0 \\ 0 \end{matrix} \\ ⋮ \\ - a_{0} \end{matrix} \begin{matrix} \begin{matrix} 1 \\ 0 \\ 0 \end{matrix} & \begin{matrix} \dots \\ ⋱ \end{matrix} & \begin{matrix} 0 \\ 0 \\ 1 \end{matrix} \\ ⋮ & 0 \\ - a_{1} & \dots & - a_{n - 2} \end{matrix} \begin{matrix} \begin{matrix} 0 \\ 0 \\ 0 \end{matrix} \\ 1 \\ - a_{n - 1} \end{matrix}] \cdot [\begin{matrix} \begin{matrix} T_{c 1 (1 : n)} \\ T_{c 2 (1 : n)} \\ ⋮ \end{matrix} \\ T_{c (n - 1) (1 : n)} \\ T_{c n (1 : n)} \end{matrix}] = [\begin{matrix} \begin{matrix} T_{c 1 (1 : n)} \\ T_{c 2 (1 : n)} \\ ⋮ \end{matrix} \\ T_{c (n - 1) (1 : n)} \\ T_{c n (1 : n)} \end{matrix}] A$

( 6.196 )

$[\begin{matrix} \begin{matrix} T_{c 2 (1 : n)} \\ T_{c 3 (1 : n)} \\ ⋮ \end{matrix} \\ T_{c n (1 : n)} \\ - a_{0} T_{c 1 (1 : n)} - a_{1} T_{c 2 (1 : n)} \dots - a_{n - 2} T_{c (n - 1) (1 : n)} - a_{n - 1} T_{c n (1 : n)} \end{matrix}] = [\begin{matrix} \begin{matrix} T_{c 1 (1 : n)} A \\ T_{c 2 (1 : n)} A \\ ⋮ \end{matrix} \\ T_{c (n - 1) (1 : n)} A \\ T_{c n (1 : n)} A \end{matrix}]$

( 6.197 )

Látható, hogy ha $T_{c 1 (1 : n)}$ ismert, akkor egy rekurzív formulával a $T_{c}$ mátrix többi sora is kiszámítható. A következőkben a $T_{c 1 (1 : n)}$ sort határozzuk meg, ehhez felhasználjuk $B_{c}$ ismert struktúráját. Ugyancsak(6.21) alapján

$B_{c} = T_{c} B$

( 6.198 )

A rekurziót kihasználva (6.197) összefüggésből kiolvasható, hogy

$T_{c i (1 : n)} = T_{c 1 (1 : n)} A^{i - 1} ahol i = 2, \dots, n$

( 6.199 )

(6.199) alapján (6.198)

$B_{c} = [\begin{matrix} \begin{matrix} T_{c 1 (1 : n)} B \\ T_{c 1 (1 : n)} A B \\ ⋮ \end{matrix} \\ T_{c 1 (1 : n)} A^{n - 2} B \\ T_{c 1 (1 : n)} A^{n - 1} B \end{matrix}]$

( 6.200 )

Vegyük észre, hogy (6.200) jobboldalán megjelent az irányíthatósági $M_{C}$ mátrix.

$B_{c} = {(T_{c 1 (1 : n)} M_{C})}^{T}$

( 6.201 )

$T_{c 1 (1 : n)} = B_{c}^{T} M_{C}^{- 1}$

( 6.202 )

A (6.202) és (6.199) segítségével a $T_{c}$ hasonlósági transzformációs mátrix soronként kiszámítható.

Így már van egy algoritmusunk általános alakú LTI SISO rendszer pólusáthelyezésre alapuló állapotvisszacsatolásának megtervezésére.

$T_{c}$ hasonlósági transzformációs mátrix felírása (6.202) és (6.199) segítségével
$A_{c}$ , $B_{c}$ és $C_{c}$ felírása $T_{c}$ és (6.21) segítségével (itt feltételezzük, hogy $D = 0$ és $a_{n} = 1$ )
Az állapotvisszacsatolással elérni kívánt $W_{d} (s)$ átviteli függvény felírása
$W_{d} (s)$ alapján az elérni kívánt $A_{c d}$ felírása (6.174) segítségével.
$A_{c}$ és $A_{c d}$ utolsó sorainak összehasonlításával $K_{T x}$ meghatározása
$K_{x}$ meghatározása (6.194) segítségével

$K_{x}$ közvetlenül is kiszámítható az Ackermann formula segítségével. Először kiválasztjuk a visszacsatolt rendszer pólusait, vagyis az $(A + B K_{x})$ mátrix $λ_{c l i}$ sajátértékeit. Ebből a karakterisztikus polinom $a_{c l i}$ együtthatóit meghatározhatjuk. Abból indulhatunk ki, hogy minden mátrix kielégíti a saját karakterisztikus polinomját (Cayley-Hamilton tétel).

$a_{c l n} {(A + B K_{x})}^{n} + \dots + a_{c l 1} (A + B K_{x}) + a_{c l 0} I = φ_{c l} (A + B K_{x}) = 0$

( 6.203 )

$a_{c l n} = 1$ választással és algebrai átalakításokkal

$\begin{array}{l} [B A B \dots A^{n - 1} B] [\begin{matrix} a_{c l 1} K_{x} + \dots + a_{c l n - 1} K_{x} {(A + B K_{x})}^{n - 2} + K_{x} {(A + B K_{x})}^{n - 1} \\ a_{c l 2} K_{x} + \dots + a_{c l n - 2} K_{x} {(A + B K_{x})}^{n - 3} + K_{x} {(A + B K_{x})}^{n - 2} \\ \begin{matrix} ⋮ \\ a_{c l n - 1} K_{x} + K_{x} (A + B K_{x}) \\ K_{x} \end{matrix} \end{matrix}] \\ = - φ_{c l} (A) \end{array}$

( 6.204 )

ebből már adódik

$K_{x} = - [0 0 \dots 1] M_{C}^{- 1} φ_{c l} (A)$

( 6.205 )

6.3.5. Megfigyelhetőségi kanonikus alak és a megfigyelőre alapozott állapotvisszacsatolás

Az Ackermann formula egy fontos lépés a gyakorlati alkalmazhatóság felé, de a legtöbb gyakorlati esetben egy megfigyelőre is szükség van, hogy a nem mérhető állapotváltozókat előállítsuk. Ahogy létezik egy olyan mátrix struktúra, amely esetén az állapotvisszacsatolás könnyen megtervezhető, úgy létezik egy olyan mátrix struktúra, amely a megfigyelő tervezését teszi egyszerűbbé, ezt nevezzük megfigyelhetőségi kanonikus alaknak. Az irányíthatósági kanonikus alakból úgy kapjuk a megfigyelhetőségi kanonikus alakot, ha az A mátrixot transzponáljuk, továbbá a B és C mátrix szerepét felcseréljük (D mátrix változatlan).

6.3.6. Irányíthatósági kanonikus alakban adott SISO rendszer állapotvisszacsatolása integrátorral kiegészítve

Jelöljük $c$ alsó indexszel az irányíthatósági kanonikus formában felírt változókat és mátrixokat és tegyük fel, hogy az eredeti rendszer irányíthatósági kanonikus alakban adott, továbbá figyelembe vesszük, hogy esetünkben a rendszer egy bemenetű és ezért egy integrátorra van szükségünk. (6.126) helyett a következőt írhatjuk

$[\begin{matrix} {\dot{x}}_{c} (t) \\ {\dot{x}}_{I} (t) \end{matrix}] = [\begin{matrix} A_{c} & 0 \\ - C_{c} & 0 \end{matrix}] [\begin{matrix} x_{c} (t) \\ x_{I} (t) \end{matrix}] + [\begin{matrix} B_{c} \\ 0 \end{matrix}] u (t) + [\begin{matrix} 0 \\ 1 \end{matrix}] u_{r} (t)$

( 6.206 )

Hasonlósági transzformációval a kiterjesztett egyenletet átírjuk irányíthatósági kanonikus alakra

$T [\begin{matrix} {\dot{x}}_{c} (t) \\ {\dot{x}}_{I} (t) \end{matrix}] = T [\begin{matrix} A_{c} & 0 \\ - C_{c} & 0 \end{matrix}] T^{- 1} T [\begin{matrix} x_{c} (t) \\ x_{I} (t) \end{matrix}] + T [\begin{matrix} B_{c} \\ 0 \end{matrix}] u (t) + T [\begin{matrix} 0 \\ 1 \end{matrix}] u_{r} (t)$

( 6.207 )

A transzformált mátrixokat mechanikus számítással megkaphatjuk, de logikailag is belátható, hogy a 6-14. ábraán látható visszacsatolt rendszer csak úgy terjeszthető ki egy integrátorral úgy, hogy közben az irányíthatósági kanonikus alakot megtartsuk, hogy az $x (t)$ állapotváltozót tovább integráljuk (ld. 6-15. ábra). Állandósult állapotban az összes integrátor bemenetén nullának kell lennie, így az ábráról az is leolvasható, hogy állandósult állapot csak úgy lehetséges, ha

$u_{r} (\infty) = y (\infty)$

( 6.208 )

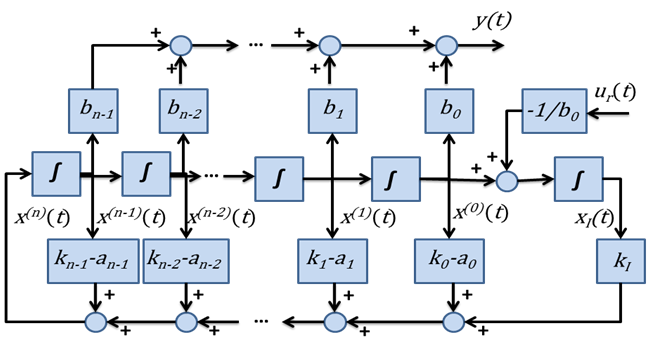
6.15. ábra - Állapotvisszacsatolás irányíthatósági kanonikus alak esetén integrátorral kiegészítve

A kiterjesztett rendszer transzformált mátrixai a következő alakúak lesznek

$A_{c_e x t} = [\begin{matrix} 0 & 1 0 \dots 0 \\ \begin{matrix} 0 \\ ⋮ \\ 0 \end{matrix} & A_{c} \end{matrix}] B_{c_e x t} = [\begin{matrix} 0 \\ B_{c} \end{matrix}] C_{e x t} = [\begin{matrix} 0 & C_{c} \end{matrix}]$

( 6.209 )

6.3.7. Kidolgozott feladatok SISO rendszerek állapotvisszacsatolására

6 . 14 feladat Irányíthatósági kanonikus alak blokk diagram alapján

Írja fel a 6.3 feladatban bemutatott rendszer állapottér egyenletét irányíthatósági kanonikus alakban.

6.3.7.1. Megoldás

A 6-3. ábra alapján

$\frac{Y (s)}{U (s)} = \frac{2}{s + 5} + \frac{3}{s + 10} + \frac{3}{(s + 2) (s + 3)} = \frac{5 s^{3} + 63 s^{2} + 250 s + 360}{s^{4} + 20 s^{3} + 131 s^{2} + 340 s + 300}$

( 6.210 )

$A = [\begin{matrix} \begin{matrix} 0 \\ 0 \\ \begin{matrix} 0 \\ - 300 \end{matrix} \end{matrix} & \begin{matrix} 1 \\ 0 \\ \begin{matrix} 0 \\ - 340 \end{matrix} \end{matrix} \end{matrix} \begin{matrix} \begin{matrix} 0 \\ 1 \\ \begin{matrix} 0 \\ - 131 \end{matrix} \end{matrix} & \begin{matrix} 0 \\ 0 \\ \begin{matrix} 1 \\ - 20 \end{matrix} \end{matrix} \end{matrix}] B = [\begin{matrix} 0 \\ 0 \\ \begin{matrix} 0 \\ 1 \end{matrix} \end{matrix}] C = [\begin{matrix} 360 & 350 & \begin{matrix} 63 & 5 \end{matrix} \end{matrix}] D = [0]$

( 6.211 )

6 . 15 feladat Állapotvisszacsatolás (két állapotváltozó)

Egy szabályozott szakasz két időállandóval rendelkezik ( $T_{1} = 1$ és $T_{2} = 0.1$ ). Az átviteli függvénye:

$W (s) = \frac{1}{(1 + s T_{1}) (1 + s T_{2})}$

( 6.212 )

Írja fel a MATLAB zp2ss paranccsal a rendszer állapottér egyenletét. Állapotvisszacsatolással és „place” parancsa segítségével változtassa meg a visszacsatolt rendszer pólusait

A legnagyobb időállandót csökkentsük ötödére

Visszacsatolással alakítsuk lengővé a rendszert. A lengések amplitúdója csökkenjen a legnagyobb időállandóval leírható burkológörbével. és a lengések frekvenciája legyen 1 Hz.

Visszacsatolással alakítsuk lengővé a rendszert. A lengések amplitúdója csökkenjen a legnagyobb időállandó ötödével leírható burkológörbével. és a lengések frekvenciája legyen akkora, hogy kb. egy túllendülés után álljon be a rendszer. Ezt azzal érjük el, hogy a lengések periódusideje legyen azonos a burkoló görbe időállandójának ötszörösével, vagyis az eredeti legnagyobb időállandóval.

A póluspárt a csillapítás ( $ξ$ ) és a Bode diagramon a $\frac{1}{T}$ töréspont helyének segítségével is megadhatjuk. Tekintsük a következő kéttárolós lengőtagot:

$W (s) = \frac{1}{1 + 2 ξ T s + T^{2} s^{2}}$

( 6.213 )

Ha $0 \leq ξ \leq 1$ , akkor az átviteli függvény pólusai:

$p_{1, 2} = - ξ ω_{0} \pm j ω_{0} \sqrt{1 - ξ^{2}} = - σ_{e} \pm j ω_{e}$

( 6.214 )

ahol:

$ω_{0} = \frac{1}{T} = \sqrt{σ_{e}^{2} + ω_{e}^{2}}$

( 6.215 )

$ξ = \frac{σ_{e}}{ω_{0}}$

( 6.216 )

Az ugrásválasz burkológörbéjéből levezethető, hogy a $k r$ százalékos szabályozási idő:

$T_{s z} = \frac{ln \frac{100}{k r}}{ξ ω_{0}}$

( 6.217 )

Ha tehát megadjuk $k r = 2$ , $ξ = 0.75$ és $T_{s z} = 1$ értékét, akkor:

$ω_{0} = \frac{ln \frac{100}{k r}}{ξ T_{s z}}$

( 6.218 )

(6.213) és (6.218) alapján a póluspár kiszámítható.

6.3.7.2. Megoldás

T1=1; T2=0.1; Tsim=T1*10;
 
%Átviteli függvény
TFzeros= [];         TFpoles= [-1/T1 -1/T2];    TFgain= 1/T1/T2;
 
%Állapot-tér modell
[A,B,C,D]=zp2ss(TFzeros,TFpoles,TFgain)
B=B*C(2); %normaizálás
C(2)=1;
%a) eset
newpoles=[-1/T1*5 -1/T2]; %A legnagyobb időállandót ötödére csökkentjük
%b) eset
newpoles =[-1/T1 +2*pi*i -1/T1-2*pi*i]; %Lengést eredményező pólusok
%c) eset
newpoles =[-1/T1*5+2*pi/T1*i -1/T1*5-2*pi/T1*i]; %aperiodikus beallás
%d) eset
Tsz=1;                              %szabályozási idő
kr=2;                               %szabályozási időhöz tartozó korlát
xi=0.75;                            %csillapítás
w0=log(100/kr)/Tsz/xi;              %sajátfrekvencia 
p1=-w0*xi+i*w0*sqrt(1-xi^2);        %pólusok
p2=-w0*xi-i*w0*sqrt(1-xi^2);
newpoles =[p1 p2];
K1=place(A,B,newpoles)
 
% Statikus hiba korrekció
s = size(A,1);
Z = [zeros([1,s]) 1];
N = inv([A,B;C,D])*Z';
Nx = N(1:s);
Nu = N(1+s);
comp=Nu + K1*Nx;

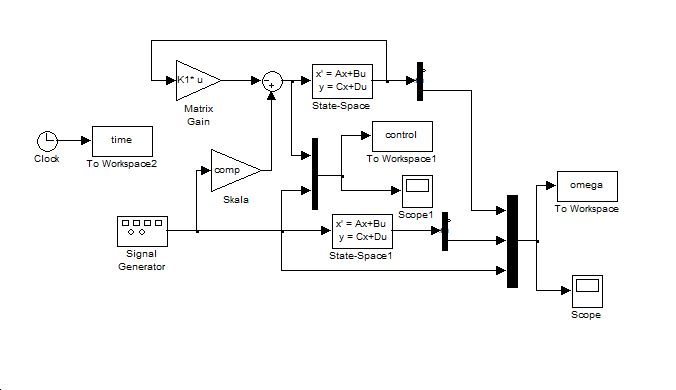
6.16. ábra - 6.15 feladat Simulink programja

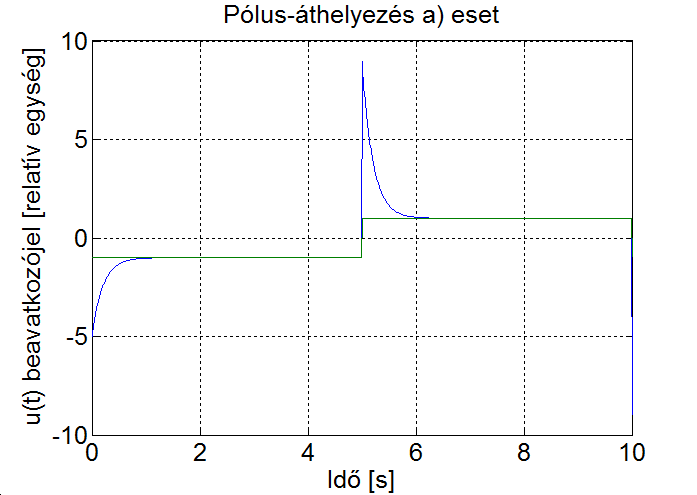
6.17. ábra - 6.15 feladat szimulációs eredménye a) eset

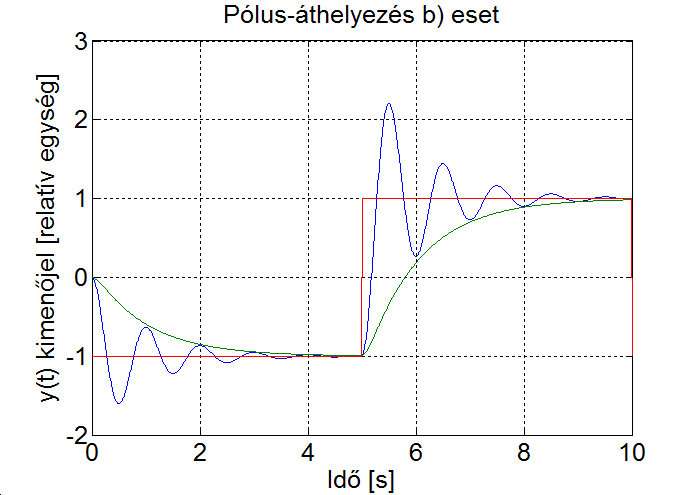
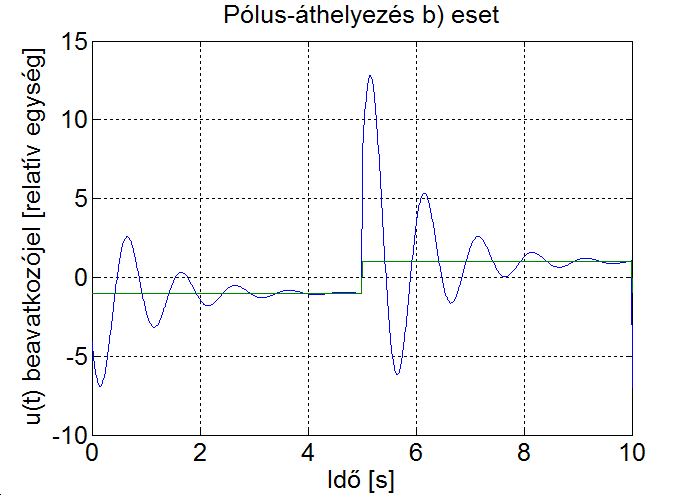
6.18. ábra - 6.15 feladat szimulációs eredménye b) eset

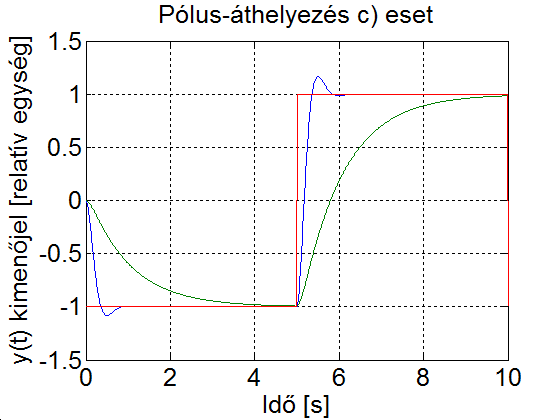
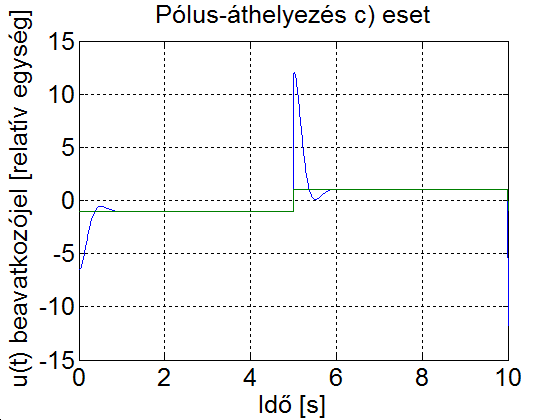
6.19. ábra - 6.15 feladat szimulációs eredménye c) eset

6.20. ábra - 6.15 feladat szimulációs eredménye d) eset

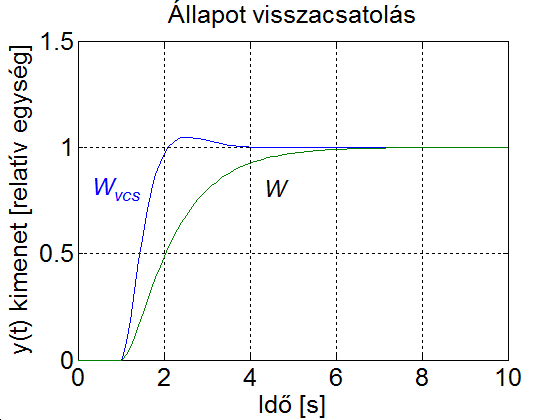
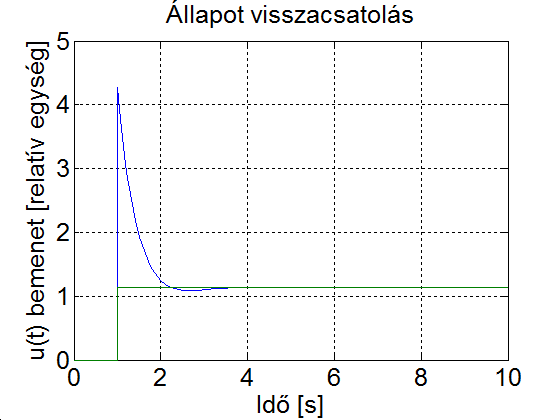
A szimulációs eredményből kitűnik, hogy az állapotvisszacsatolással a visszacsatolt rendszer tulajdonságait viszonylag szabadon tudjuk befolyásolni, a kívánt beállás jellegét a beavatkozójel segítségével tudjuk elérni.

6 . 16 feladat Állapot visszacsatolás (három állapotváltozó)

Ismét a (6.158) átviteli függvényből indulunk ki és felírjuk a kimenőjel Laplace-transzformáltját

$Y (s) = \frac{3 s + 7}{s^{3} + 7 s^{2} + 14 s + 8} U (s)$

( 6.219 )

Írjuk fel az állapotegyenleteket irányíthatósági kanonikus formában. Vezessük be az $X (s)$ állapotváltozót (ez még nem írja le teljesen a rendszer állapotát, később további állapotváltozókat vezetünk be).

$X (s) � \frac{U (s)}{s^{3} + 7 s^{2} + 14 s + 8}$

( 6.220 )

$Y (s) = (3 s + 7) X (s)$

$y (t) = 3 \dot{x} (t) + 7 x (t)$

$U (s) = (s^{3} + 7 s^{2} + 14 s + 8) X (s)$

$u (t) = \overset{⃛}{x} (t) + 7 \ddot{x} (t) + 14 \dot{x} (t) + 8 x (t)$

$[\begin{matrix} \dot{x} (t) \\ \ddot{x} (t) \\ \overset{⃛}{x} (t) \end{matrix}] = [\begin{matrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ - 8 & - 14 & - 7 \end{matrix}] [\begin{matrix} x (t) \\ \dot{x} (t) \\ \ddot{x} (t) \end{matrix}] + [\begin{matrix} 0 \\ 0 \\ 1 \end{matrix}] u (t)$

$y (t) = [\begin{matrix} 7 & 3 \end{matrix} 0] [\begin{matrix} x (t) \\ \dot{x} (t) \\ \ddot{x} (t) \end{matrix}] + [0] u (t)$

( 6.221 )

Az eredeti rendszer pólusai: -1, -2 és -4

$(s + 1) (s + 2) (s + 4) = s^{3} + 7 s^{2} + 14 s + 8$

( 6.222 )

a) eset

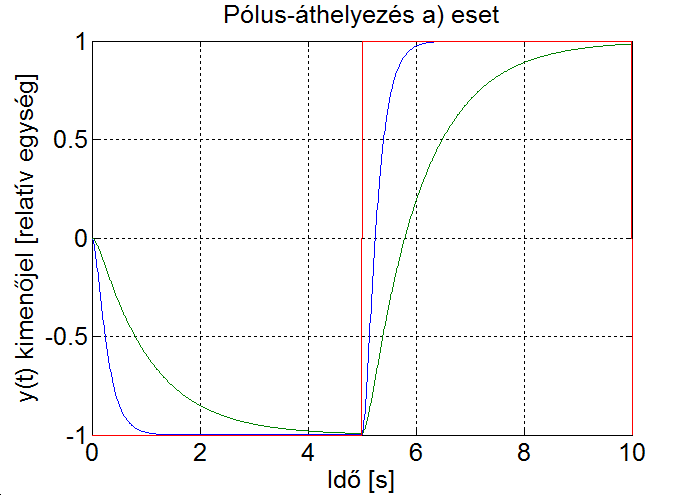
Helyezzük át a legkisebb abszolút értékű (legnagyobb időállandóhoz tartozó) pólust -1-ről -3-ra.

$(s + 3) (s + 2) (s + 4) = s^{3} + 9 s^{2} + 26 s + 24$

( 6.223 )

Látható, hogy a nevező polinom együtthatói megváltoznak: 1, 9, 26 és 24. Az állapotvisszacsatolás megtartja az eredeti struktúrát, így a visszacsatolt rendszer eredő átviteli függvénye a következő lesz

$W_{v c s} (s) = \frac{3 s + 7}{s^{3} + 9 s^{2} + 26 s + 24}$

( 6.224 )

(6.222) és (6.223) összehasonlításából kitűnik, hogy

$[\begin{matrix} {\dot{x}}_{1} (t) \\ {\dot{x}}_{2} (t) \\ {\dot{x}}_{3} (t) \end{matrix}] = [\begin{matrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ - 8 & - 14 & - 7 \end{matrix}] [\begin{matrix} x_{1} (t) \\ x_{2} (t) \\ x_{3} (t) \end{matrix}] + [\begin{matrix} 0 \\ 0 \\ 1 \end{matrix}] [\begin{matrix} - 16 & - 12 \end{matrix} - 2] [\begin{matrix} x_{1} (t) \\ x_{2} (t) \\ x_{3} (t) \end{matrix}] =$

$[\begin{matrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ - 8 & - 14 & - 7 \end{matrix}] + [\begin{matrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ - 16 & - 12 & - 2 \end{matrix}] [\begin{matrix} x_{1} (t) \\ x_{2} (t) \\ x_{3} (t) \end{matrix}] = [\begin{matrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ - 24 & - 26 & - 9 \end{matrix}] [\begin{matrix} x_{1} (t) \\ x_{2} (t) \\ x_{3} (t) \end{matrix}]$

( 6.225 )

Az eredeti (6.158) és a visszacsatolt (6.224) rendszer átmeneti függvényének állandósult értékének reciprokával kell a referenciajelet megszorozni, hogy egységnyi erősítést kapjunk.

$v (\infty) = \lim_{s \to 0} s W (s) \frac{1}{s} = \frac{7}{8}$	( 6.226 )
$v_{v c s} (\infty) = \lim_{s \to 0} s W_{c l} (s) \frac{1}{s} = \frac{7}{24}$	( 6.227 )

Látható, hogy a negatív visszacsatolás csökkenti a rendszer erősítését.

6.21. ábra - visszacsatolás

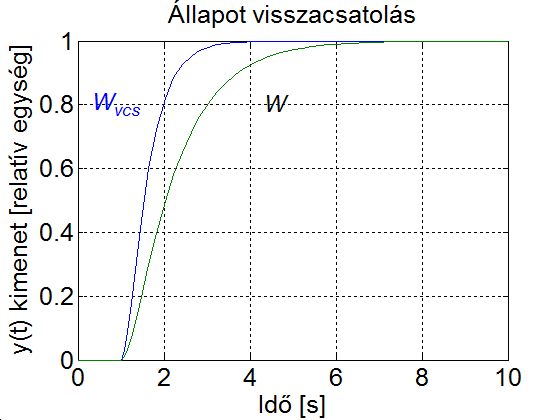
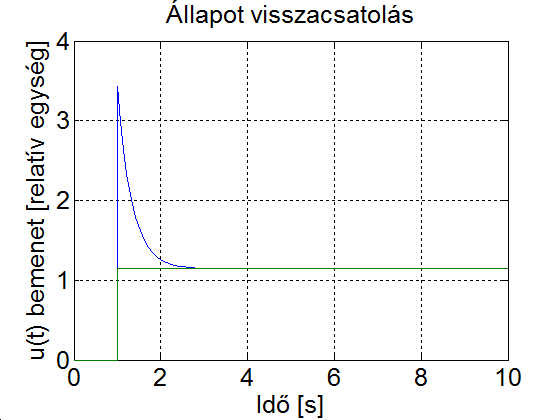
6.22. ábra - visszacsatolás szimulációja

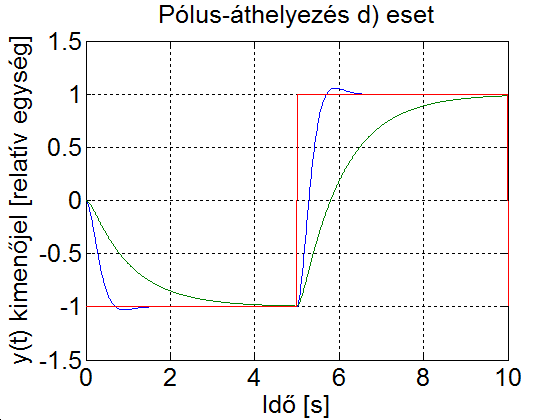
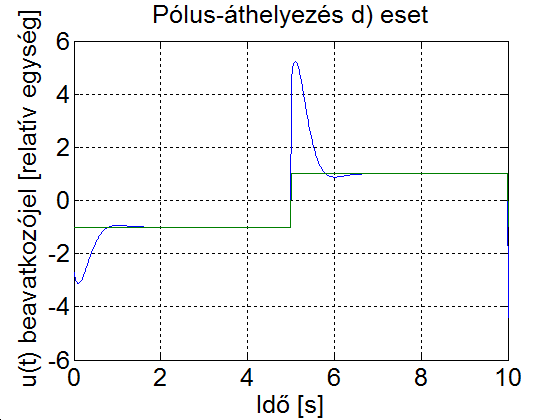
További lehetőségek

b) eset

Visszacsatolással alakítsuk lengővé a rendszert. A lengések amplitúdója csökkenjen 0.5 időállandóval leírható burkológörbével, és a lengések frekvenciája legyen akkora, hogy kb. egy túllendülés után álljon be a rendszer. Ezt azzal érjük el, hogy a lengések periódusideje legyen azonos a burkoló görbe időállandójának ötszörösével, vagyis a periódusidő legyen 2.5. A harmadik (legkisebb) időállandó legyen 0.2. Ennek megfelelően a visszacsatolt rendszer pólusai legyenek a következők

$p_{1} = - 2 + 2 π / 2.5 j p_{2} = - 2 - 2 π / 2.5 j p_{3} = - 5$

( 6.228 )

A (6.228) alapján a visszacsatolt rendszer átviteli függvényének nevezője a következő alakot ölti

$(s + 2 - 2 π / 2.5 j) (s + 2 + 2 π / 2.5 j) (s + 5) = s^{3} + 9 s^{2} + 30.3 s + 51.6$

( 6.229 )

(6.222) és (6.229) összehasonlításából a visszacsatolás sorvektora felírható

$K x = [- 43.6 - 16.3 - 2]$

( 6.230 )

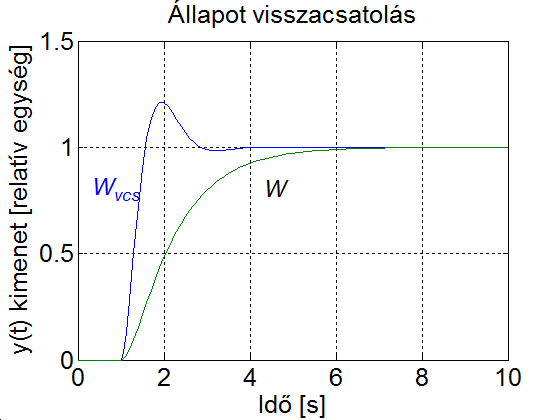
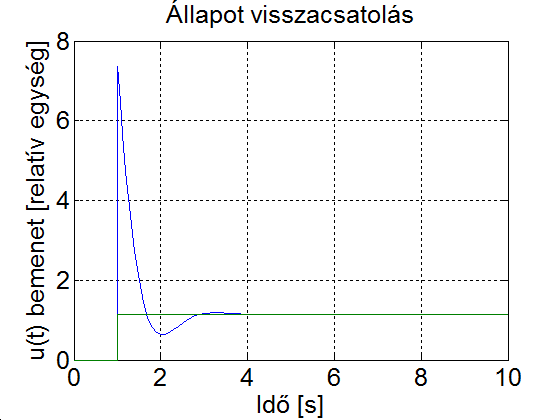
6.23. ábra - lapotvisszacsatolás szimulációja

c) eset

A póluspárt a csillapítás ( $ξ$ ) és a Bode diagramon a $\frac{1}{T}$ töréspont helyének segítségével is megadhatjuk. Tekintsük a következő kéttárolós lengőtagot:

$W (s) = \frac{3 s + 7}{(1 + 2 ξ T s + T^{2} s^{2}) (1 + T_{3} s)}$

( 6.231 )

Ha $0 \leq ξ \leq 1$ , akkor az átviteli függvény pólusai:

$p_{1, 2} = - ξ ω_{0} \pm j ω_{0} \sqrt{1 - ξ^{2}} = - σ_{e} \pm j ω_{e}$

( 6.232 )

ahol:

$ω_{0} = \frac{1}{T} = \sqrt{σ_{e}^{2} + ω_{e}^{2}}$

( 6.233 )

$ξ = \frac{σ_{e}}{ω_{0}}$

( 6.234 )

Az ugrásválasz burkológörbéjéből levezethető, hogy a $k r$ százalékos szabályozási idő:

$T_{s z} = \frac{ln \frac{100}{k r}}{ξ ω_{0}}$

( 6.235 )

Ha tehát megadjuk $k r = 2$ , $ξ = 0.8$ és $T_{s z} = 2$ értékét, akkor:

$ω_{0} = \frac{ln \frac{100}{k r}}{ξ T_{s z}}$

( 6.236 )

(6.213) és (6.218) alapján a póluspár kiszámítható.

$p_{1} = - 1.9 + 1.5 j p_{2} = - 1.9 - 1.5 j p_{3} = - 5$

( 6.237 )

6.24. ábra - lapotvisszacsatolás szimulációja

A Matlab értékadás

A=[0 1 0; 0 0 1; -8 -14 -7];
B=[0 0 1]';
C=[1 0 0; 0 1 0; 0 0 1];
D=[0; 0; 0];
Cv=[7 3 0];
 
%a) eset
newpoles=[-2 -3 -4];
 
%b) eset
newpoles=[-2+i*2*pi*2/5 -2-i*2*pi*2/5 -5];
 
%c) eset
Tsz=2;                         %szabályozási idő
kr=2;                          %szabályozási időhöz tartozó korlát
xi=0.8;                        %csillapítás
w0=log(100/kr)/Tsz/xi;         %sajátfrekvencia 
p1=-w0*xi+i*w0*sqrt(1-xi^2);   %pólusok
p2=-w0*xi-i*w0*sqrt(1-xi^2);
newpoles =[p1 p2 -5];
 
K2=-poly(newpoles)+poly([-1 -2 -4]);
Kx=[K2(4) K2(3) K2(2)]
ko_v=(-Kx(1)+8)/7
ko=8/7

6 . 17 feladat Megfigyelő tervezése

Adott egy külsőgerjesztésű egyenáramú motor a következő jelölésekkel $ω_{m}$ a motor szögsebessége. A motor paraméterei relatív egységben: a motor másodrendű nyomatéka $J_{m} = 0.12$ . nyomaték konstansa $k ϕ = 5.07$ , az armatúra ellenállása $R_{a} = 2.7$ , az armatúra tekercs induktivitása $L_{a} = 0.0011$ . Tegyük fel, hogy a terhelés lineáris (a terhelő nyomaték arányos a fordulatszámmal), az arányossági tényező $υ_{m} = 3.5$ . A motor kapocsfeszültsége ugrásszerűen változik $U_{a} = 10 ε (t)$ . A motor egyenletei:

$u_{a} = R_{a} i_{a} + L_{a} \frac{d i_{a}}{d t} + k ϕ ω_{m}$

$M_{v} = k ϕ i_{a}$

$J_{m} \frac{d ω_{m}}{d t} = M_{v} - υ_{m} ω_{m}$

( 6.238 )

Tekintsük a rendszer bemenő jelének a motor kapocsfeszültségét és tegyük fel, hogy csak a fordulatszám mérhető. Írja fel a motor állapottér egyenletét és tervezzen teljes állapotmegfigyelőt a MATLAB place parancs segítségével..

6.3.7.3. Megoldás

A motor állapottér egyenlete

$\frac{d}{d t} [\begin{matrix} ω_{m} \\ i_{a} \end{matrix}] = [\begin{matrix} - \frac{υ_{m}}{J_{m}} & \frac{k ϕ}{J_{m}} \\ - \frac{k ϕ}{L_{a}} & - \frac{R_{a}}{L_{a}} \end{matrix}] [\begin{matrix} ω_{m} \\ i_{a} \end{matrix}] + [\begin{matrix} 0 \\ \frac{1}{L_{a}} \end{matrix}] u_{a}$

$y = [\begin{matrix} 1 & 0 \end{matrix}] [\begin{matrix} ω_{m} \\ i_{a} \end{matrix}] + [0] u_{a}$

( 6.239 )

Behelyettesítve a paraméterek értékeit

$A = [\begin{matrix} - 16.6667 & 42.25 \\ - 4609.1 & - 2454.5 \end{matrix}] B = [\begin{matrix} 0 \\ 909.0909 \end{matrix}] C = [\begin{matrix} 1 & 0 \end{matrix}] D = [0]$

( 6.240 )

A rendszer pólusai

$p_{1} = - 99.3494 p_{2} = - 2371.9$

( 6.241 )

Válasszuk meg a megfigyelő két pólusát úgy, hogy a megfigyelő működése gyorsabb legyen, mint a rendszeré (vagyis a megfigyelő mindkét pólusa nagyobb abszolút értékű, mint a rendszer legkisebb pólusa).

Legyen

$p_{o 1} = - 500 p_{o 2} = - 1000$

( 6.242 )

Ez azt jelenti, hogy a valós és becsült állapotváltozók különbsége kb. 2 ms időállandóval szűnik meg. A megfigyelő visszacsatoló vektora

$L = [\begin{matrix} - 971.2121 \\ 62680 \end{matrix}]$

( 6.243 )

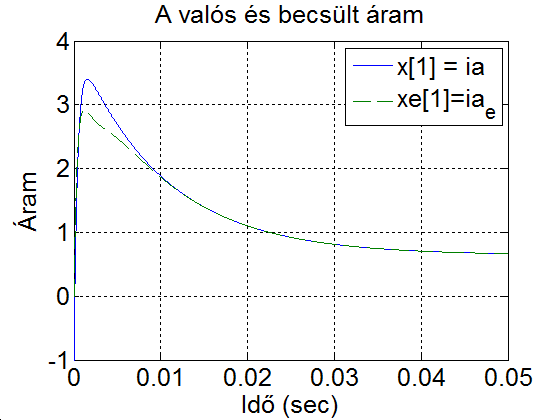
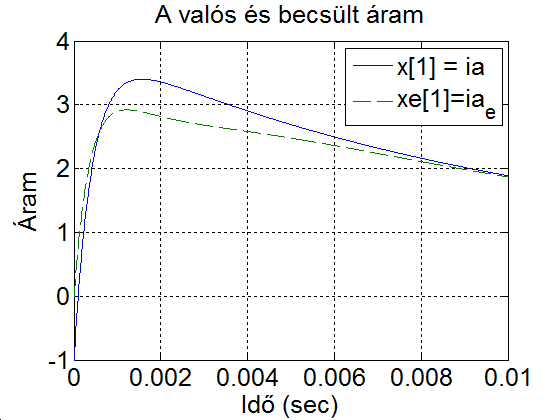
Látható, hogy a kezdeti érték gyors megszüntetése nagy abszolút értékű visszacsatolással lehetséges, ami zajos mérés esetén gondot okozhat. Legyen a valós és a becsült áram kezdeti értéke -1 és 0. A szimulációs eredmények a 6-25. ábraán láthatók.

6.25. ábra - A valós és becsült áram különböző kezdeti értékből indulva

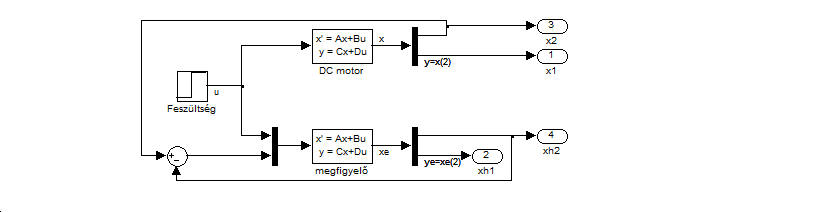
A számításnál használt MATLAB program

clear all; close all;
 
% Motor paraméterek
La = 1.1e-3; Ra = 2.7; Jm = 0.12; nu = 2; Kfi = 5.07;
 
Ua=10;
Ts=0;
Tsim=0.01;
 
% Motor állapottér mátrixai
A = [-nu/Jm Kfi/Jm; -Kfi/La -Ra/La];
B = [0; 1/La];
C = [1 0];
D = [0];
 
% Állapotváltozók: x=[omega; ia]
 
% Megfigyelhetőség ellenőrzése
O = obsv(A,C);
rank(O);
 
% Megfigyelhetőség ellenőrzése
syst_poles=eig(A);
obs_polse=[-500 -1000];
 
% A megfigyelő pólusai: 
Lt = acker(A',C',obs_polse);
Lo  = Lt';
 
% C és D mátrix átalakítása
C = [1, 0; 0, 1];
D = [0; 0];
 
% A valós rendszer áramának kezdeti értéke
x0 = [0, -1];
 
% A megfigyelő modell 
Ah = A;
Bh = [B, Lo];
Ch = eye(2);
Dh = [0, 0; 0, 0];
xh0 = [0, 0];
 
% Szimuláció simulink modell segítségével
sim('DCmotor_simu_open.mdl')
 
%Kirajzolás
 plot(tout, yout(:,1), tout, yout(:,2), '--');
 set(gca, 'fontsize', 19);
xlabel('Idő (sec)'); legend('x[1] = ia', 'xe[1]=ia_e'), ylabel('Áram'),grid,shg
title('A valós és becsült áram');
 
figure('Name', 'velocity')
plot(tout, yout(:,3), tout, yout(:,4), '--');
set(gca, 'fontsize', 19);
xlabel('Idő (sec)'); legend('om[1] = om', 'ome[1]=om_e'),
ylabel('Sebesség'),grid,shg
title('A valós és becsült sebesség');

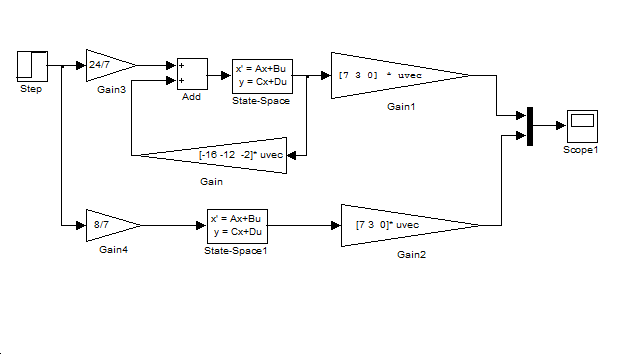
A fenti programban használt Simulink modell a 6-26. ábraán látható

6.26. ábra - A megfigyelő Simulink modellje

6 . 18 feladat Pólus áthelyezés (papíron kiszámítva )

Adott a következő rendszer:

$[\begin{matrix} {\dot{x}}_{1} (t) \\ {\dot{x}}_{2} (t) \end{matrix}] = [\begin{matrix} - 1 & 2 \\ - 3 & - 5 \end{matrix}] [\begin{matrix} x_{1} (t) \\ x_{2} (t) \end{matrix}] + [\begin{matrix} 1 \\ 0 \end{matrix}] u (t)$

$y (t) = [\begin{matrix} 1 & 1 \end{matrix}] [\begin{matrix} x_{1} (t) \\ x_{2} (t) \end{matrix}] + [0] u (t)$

( 6.244 )

Transzformálja a rendszert az irányíthatósági kanonikus lakra. Határozza meg a szükséges állapotvisszacsatolás értékét úgy, hogy a visszacsatolt rendszer pólusai a komplex számsíkon átkerüljenek a $p_{1 d} = - 10 + 0 j$ és $p_{2 d} = - 10 - 0 j$ pontokba. (Megjegyzés, a MATLAB (R2009a verzió) pólusáthelyezésre szolgáló „place” parancsával ez a feladat a kétszeres pólus miatt nem oldható meg).

6.3.7.4. Megoldás

Először írjuk fel az irányíthatósági mátrixot és invertáljuk azt

$M_{C} = [\begin{matrix} 1 & - 1 \\ 0 & - 3 \end{matrix}] \Rightarrow adj M_{C} = [\begin{matrix} - 3 & 1 \\ 0 & 1 \end{matrix}], \det M_{C} = - 3 \Rightarrow M_{C}^{- 1} = [\begin{matrix} 1 & - \frac{1}{3} \\ 0 & - \frac{1}{3} \end{matrix}]$

( 6.245 )

A $T_{c}$ transzformációs mátrix első sorát (6.202), majd a második sorát (6.199) alapján írhatjuk fel

$T_{c 1 (1 : n)} = [\begin{matrix} 0 & 1 \end{matrix}] [\begin{matrix} 1 & - \frac{1}{3} \\ 0 & - \frac{1}{3} \end{matrix}] = [\begin{matrix} 0 & - \frac{1}{3} \end{matrix}] \Rightarrow T_{c} = [\begin{matrix} 0 & - \frac{1}{3} \\ 1 & \frac{5}{3} \end{matrix}]$

( 6.246 )

Szükségünk van a $T_{c}$ transzformációs mátrix inverzére is

$adj T_{c} = [\begin{matrix} \frac{5}{3} & \frac{1}{3} \\ - 1 & 0 \end{matrix}] det T_{c} = \frac{1}{3} \Rightarrow T_{c}^{- 1} = [\begin{matrix} 5 & 1 \\ - 3 & 0 \end{matrix}]$

( 6.247 )

Végül felírhatjuk az állapotmátrixokat irányíthatósági kanonikus alakban

$A_{c} = [\begin{matrix} 0 & - \frac{1}{3} \\ 1 & \frac{5}{3} \end{matrix}] [\begin{matrix} - 1 & 2 \\ - 3 & - 5 \end{matrix}] [\begin{matrix} 5 & 1 \\ - 3 & 0 \end{matrix}] = [\begin{matrix} 0 & 1 \\ - 11 & - 6 \end{matrix}] B_{c} = [\begin{matrix} 0 \\ 1 \end{matrix}]$

$C_{c} = [\begin{matrix} 1 & 1 \end{matrix}] [\begin{matrix} 5 & 1 \\ - 3 & 0 \end{matrix}] = [\begin{matrix} 2 & 1 \end{matrix}]$

( 6.248 )

A visszacsatolatlan rendszer átviteli függvénye

$W (s) = \frac{s + 2}{s^{2} + 6 s + 11}$

( 6.249 )

A két pólus $p_{1} = - 3 + \sqrt{2} j$ $p_{2} = - 3 - \sqrt{2} j$ . A pólusokat szeretnénk áthelyezni a $p_{1 d} = - 10$ és $p_{2 d} = - 10$ értékekre.

$W_{d} (s) = \frac{s + 2}{s^{2} + 20 s + 100}$

( 6.250 )

A két átviteli függvény összehasonlításából kiderül:

$K_{T x} = [- \begin{matrix} 89 & - 14 \end{matrix}]$

( 6.251 )

Visszatérve az eredeti rendszerhez (6.194) alapján.

$K_{x} = K_{T x} T_{c} = [- \begin{matrix} 89 & - 14 \end{matrix}] [\begin{matrix} 0 & - \frac{1}{3} \\ 1 & \frac{5}{3} \end{matrix}] = [- \begin{matrix} 14 & \frac{19}{3} \end{matrix}]$

( 6.252 )

Az alapjel kompenzáló tagok értéke

$K_{r} = \frac{1}{\lim_{s \to 0} s W (s) \frac{1}{s}} = \frac{11}{2}$	( 6.253 )
$K_{r d} = \frac{1}{\lim_{s \to 0} s W_{d} (s) \frac{1}{s}} = 50$	( 6.254 )

6 . 19 feladat Ackermann formula (papíron kiszámítva)

A 6.18 feladatot oldjuk meg az Ackermann formulával.

A 6.15 feladat a) alkérdését oldjuk meg az Ackermann formulával.

6.3.7.5. Megoldás

$K_{x} = - [0 1] [\begin{matrix} 1 & - \frac{1}{3} \\ 0 & - \frac{1}{3} \end{matrix}] ({[\begin{matrix} - 1 & 2 \\ - 3 & - 5 \end{matrix}]}^{2} + 20 [\begin{matrix} - 1 & 2 \\ - 3 & - 5 \end{matrix}] + [\begin{matrix} 100 & 0 \\ 0 & 100 \end{matrix}]) = [- \begin{matrix} 14 & \frac{19}{3} \end{matrix}]$

( 6.255 )

A feladatban nem volt megkötés, hogy az állapottér egyenletet milyen formában írjuk fel, így válasszuk a kanonikus alakot

$W (s) = \frac{1}{(1 + s) (1 + 10 s)} = \frac{10}{9} \frac{1}{(1 + s)} - \frac{10}{9} \frac{1}{(1 + 10 s)}$

( 6.256 )

Ebből az állapotmátrixok kiolvashatók

$A = [\begin{matrix} - 1 & 0 \\ 0 & - 10 \end{matrix}] B = [\begin{matrix} 1 \\ 1 \end{matrix}] C = [\begin{matrix} \frac{10}{9} & - \frac{10}{9} \end{matrix}] D = [0]$

( 6.257 )

Először írjuk fel az irányíthatósági mátrixot és invertáljuk azt

$M_{C} = [\begin{matrix} 1 & - 1 \\ 1 & - 10 \end{matrix}] \Rightarrow adj M_{C} = [\begin{matrix} - 10 & 1 \\ - 1 & 1 \end{matrix}], \det M_{C} = - 9 \Rightarrow M_{C}^{- 1} = [\begin{matrix} \frac{10}{9} & - \frac{1}{9} \\ \frac{1}{9} & - \frac{1}{9} \end{matrix}]$

( 6.258 )

A feladat szerint a visszacsatolt rendszer két időállandója $T_{1} = \frac{1}{5} = 0.2$ és $T_{2} = 0.1$ , így a karakterisztikus egyenlet

$(s + 5) (s + 10) = s^{2} + 15 s + 50$

( 6.259 )

A kanonikus alak előnye, hogy könnyű a karakterisztikus egyenletbe helyettesíteni

$K_{x} = - [0 1] [\begin{matrix} \frac{10}{9} & - \frac{1}{9} \\ \frac{1}{9} & - \frac{1}{9} \end{matrix}] [\begin{matrix} {(- 1)}^{2} + 15 * (- 1) + 50 & 0 \\ 0 & {(- 10)}^{2} + 15 * (- 10) + 50 \end{matrix}] = - [0 1] [\begin{matrix} \frac{10}{9} & - \frac{1}{9} \\ \frac{1}{9} & - \frac{1}{9} \end{matrix}] [\begin{matrix} 36 & 0 \\ 0 & 0 \end{matrix}] = [- \begin{matrix} 4 & 0 \end{matrix}]$

( 6.260 )

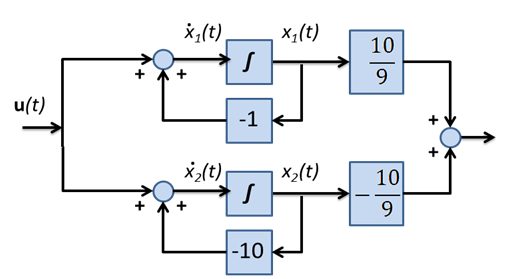
Ez az eredmény nem meglepő. Ezt az eredményt klasszikus, blokkdiagramra alapozott ismeretekkel is megkaphatjuk. Az állapottér modell belső összefüggései a (6.257) mátrix értékekkel a 6-27. ábra

segítségével szemléltethető.

6.27. ábra - Állapottér diagram

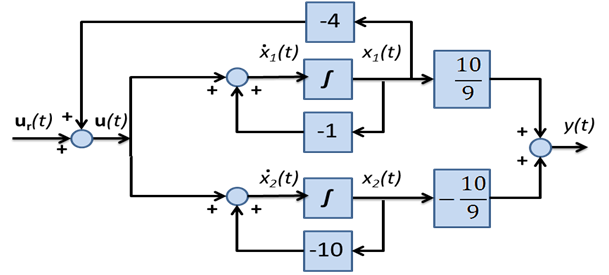
A $p_{1} = - 1$ pólushoz tartozó időállandót kívánjuk ötödére csökkenteni, vagyis az $x_{1}$ állapotváltozót nem -1, hanem -5 értékkel megszorozva kell visszacsatolni. Mivel a visszacsatolás párhuzamos lesz az eredeti visszacsatoló ággal, a visszacsatolt ágak értékei összeadódnak, vagyis -4 értékkel kell az $x_{1}$ állapotváltozót visszacsatolni (ld. 6-28. ábra).

6.28. ábra - Állapotvisszacsatolás

A 6-28. ábra hatáspont áthelyezésekkel átrajzolható.

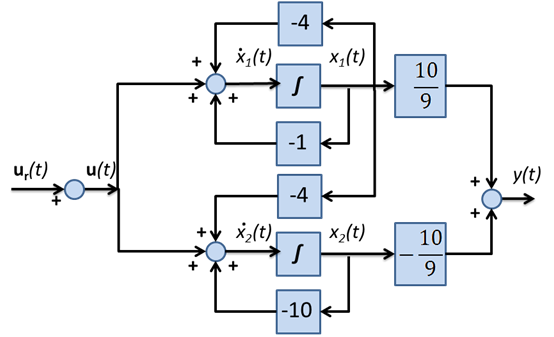
6.29. ábra - Állapotvisszacsatolás

Mind a kezdő, mind a végpontját áthelyezve az $x_{1}$ állapotváltozó visszacsatolásának az $x_{2}$ állapotváltozóhoz. Továbbá áttérve a Laplace-transzformált jelekhez kapjuk a 6-30. ábraát.

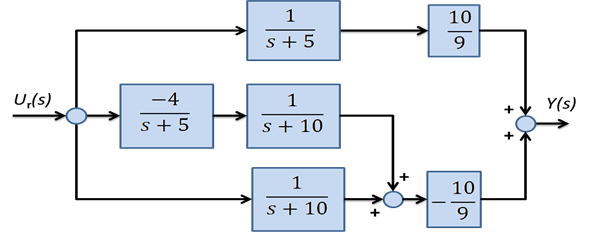
6.30. ábra - Állapotvisszacsatolás

A 6-30. ábra alapján a visszacsatolt rendszer átviteli függvénye.

$\frac{Y (s)}{U_{r} (s)} = \frac{10}{9} (\frac{1}{s + 5} - \frac{1}{s + 10} + \frac{4}{(s + 5) (s + 10)}) = \frac{10}{(s + 5) (s + 10)}$

( 6.261 )

Ismét megfigyelhető, hogy a negatív visszacsatolás csökkenti a rendszer erősítését, ez egy megfelelő erősítő taggal kompenzálható.

6 . 20 feladat Transzformálás irányíthatósági kanonikus alakra

MATLAB formában adott egy LTI SISO rendszer három rendszermátrixa (A, B és C). Az állapotváltozók száma 4. Írjon MATLAB programot, amely a rendszermátrixokat irányíthatósági kanonikus alakra transzformálja.

Alkalmazza a programot a 6.3 feladatban leírt rendszerre.

6.3.7.6. Megoldás

Mc=[B A*B A*A*B A*A*A*B]
Bc=[0 0 0 1]'
Tc1=Bc'*inv(Mc)
Tc=[Tc1; Tc1*A; Tc1*A*A; Tc1*A*A*A]
Tci=inv(Tc)
Ac=Tc*A*Tci
Cc=C*Tci

$T_{c} = [\begin{matrix} \begin{matrix} 0.0333 \\ - 0.1667 \\ \begin{matrix} 0.8333 \\ - 4.1667 \end{matrix} \end{matrix} & \begin{matrix} - 0.0298 \\ 0.1310 \\ \begin{matrix} - 0.4762 \\ 1.5952 \end{matrix} \end{matrix} \end{matrix} \begin{matrix} \begin{matrix} 0.0714 \\ - 0.2143 \\ \begin{matrix} 0.6429 \\ - 1.9286 \end{matrix} \end{matrix} & \begin{matrix} - 0.0036 \\ 0.0357 \\ \begin{matrix} - 0.3571 \\ 3.5714 \end{matrix} \end{matrix} \end{matrix}]$ $T_{c}^{- 1} = [\begin{matrix} \begin{matrix} 60 \\ 150 \\ \begin{matrix} 50 \\ 30 \end{matrix} \end{matrix} & \begin{matrix} 56 \\ 95 \\ \begin{matrix} 15 \\ 31 \end{matrix} \end{matrix} \end{matrix} \begin{matrix} \begin{matrix} 15 \\ 18 \\ \begin{matrix} 1 \\ 10 \end{matrix} \end{matrix} & \begin{matrix} 1 \\ 1 \\ \begin{matrix} 0 \\ 1 \end{matrix} \end{matrix} \end{matrix}]$

( 6.262 )

$A_{c} = [\begin{matrix} \begin{matrix} 0 \\ 0 \\ \begin{matrix} 0 \\ - 300 \end{matrix} \end{matrix} & \begin{matrix} 1 \\ 0 \\ \begin{matrix} 0 \\ - 340 \end{matrix} \end{matrix} \end{matrix} \begin{matrix} \begin{matrix} 0 \\ 1 \\ \begin{matrix} 0 \\ - 131 \end{matrix} \end{matrix} & \begin{matrix} 0 \\ 0 \\ \begin{matrix} 1 \\ - 20 \end{matrix} \end{matrix} \end{matrix}] B_{c} = [\begin{matrix} 0 \\ 0 \\ \begin{matrix} 0 \\ 1 \end{matrix} \end{matrix}] C_{c} = [\begin{matrix} 360 & 250 & \begin{matrix} 63 & 5 \end{matrix} \end{matrix}] D_{c} = [0]$

( 6.263 )

6 . 21 feladat Integrátorral kiegészített á l lapotvisszacsatolás

A 6.16 feladat b) esetében megismert rendszert egészítsük ki egy integrátorral.

$A_{e x t} = [\begin{matrix} 0 & 1 & \begin{matrix} 0 & 0 \end{matrix} \\ 0 & 0 & \begin{matrix} 1 & 0 \end{matrix} \\ \begin{matrix} - 8 \\ - 7 \end{matrix} & \begin{matrix} - 14 \\ - 3 \end{matrix} & \begin{matrix} \begin{matrix} - 7 \\ 0 \end{matrix} & \begin{matrix} 0 \\ 0 \end{matrix} \end{matrix} \end{matrix}] B_{e x t} = [\begin{matrix} 0 \\ 0 \\ \begin{matrix} 1 \\ 0 \end{matrix} \end{matrix}]$

( 6.264 )

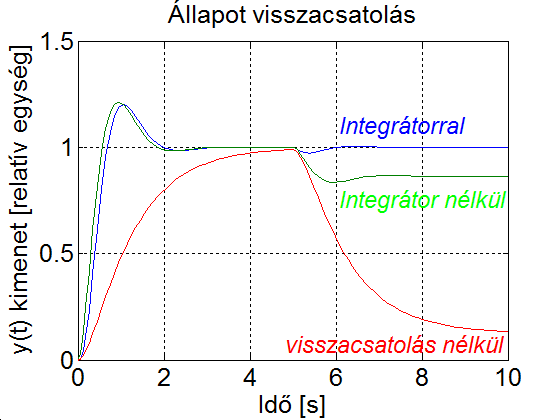
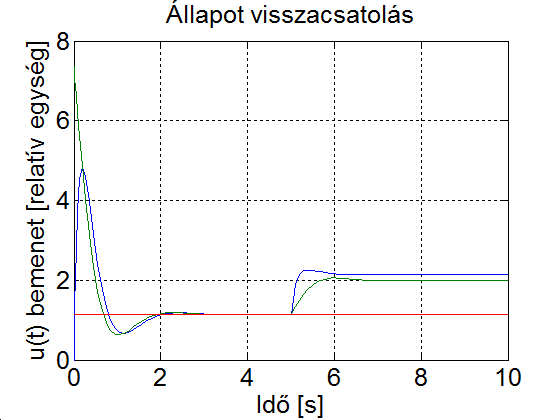
Az integrátor miatt eggyel megnöveltük az állapotváltozók számát, így a pólusok számát is meg kell növelni. Legyen a negyedik pólus értéke -10, és használjuk a MATLAB place parancsát. A bemenetre kapcsoljunk 1 egységnyi terhelésrádobást modellező zavarójelet az 5s időpontban. Hasonlítsuk össze a visszacsatolás nélkül, a visszacsatolt és az integrátorral kiegészített visszacsatolt rendszer működését a 6.16 feladat b) esetében.

$K_{e x t} = [\begin{matrix} K_{x} & k_{I} \end{matrix}] = [- 125.7 - 106.3 - 12.0000 73.7]$

( 6.265 )

A 6-31. ábraán látható, hogy a visszacsatolás nélkül a rendszer nem tudja kiküszöbölni a terhelésrádobás hatását. A visszacsatolással a rendszer válasza egyrészt gyorsítható, másrészt a terhelésrádobás hatása is csökkenthető, de teljesen nem küszöbölhető ki. Ha a visszacsatolás mellett még egy integrátort is alkalmazunk, akkor azzal a beavatkozójel hirtelen ugrásait is simíthatjuk. Ez minimális késleltetést jelent az integrátor nélkül visszacsatolt rendszerhez képest, ugyanakkor az integrátor a konstans értékű terhelés hatását teljesen ki tudja küszöbölni. A késleltetésnek az az oka, hogy az eredeti rendszer $u (t)$ bemenőjele az integrátor nélküli rendszerrel szemben az integrátor miatt nem tud ugrásszerűen megváltozni (idő kell az integrátor feltöltődéséhez), ez jól megfigyelhető 6-31. ábra jobb oldali rajzán.

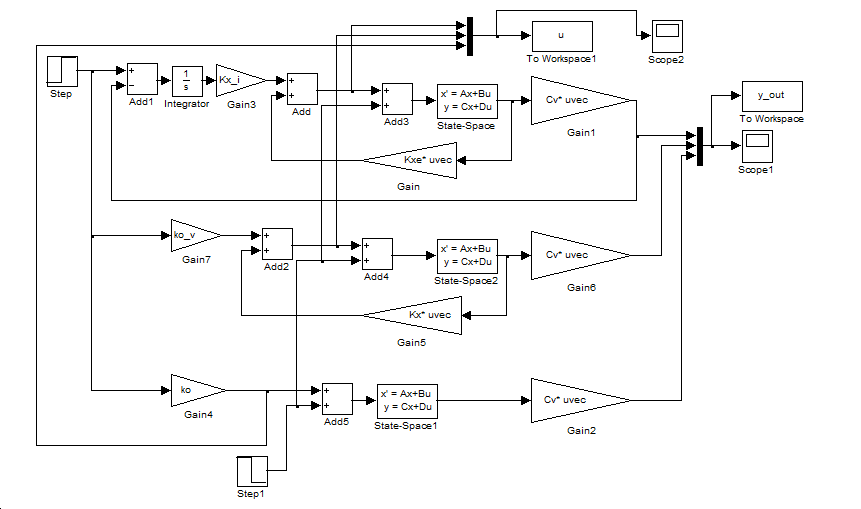
6.31. ábra - Modellek összehasonlítása, szimulációs eredmény

6.32. ábra - Modellek összehasonlítása

6.16 feladat b) esetének folytatásaként (newpolese meghatározása ott történt)

Ae=[0 1 0 0; 0 0 1 0; -8 -14 -7 0; -7 -3 0 0];
Be=[0 0 1 0]';
Ce=[1 0 0 0; 0 1 0 0; 0 0 1 0; 0 0 0 1];
De=[0; 0; 0; 0];
C1e=[7 3 0 0];
 
newpolese =[newpoles -10];
K4=place(Ae,Be,newpolese);
Kx_i=-K4(4)
Kxe=-K4(1:3)

6.20 feladatban leírtak szerint írja át (6.264) állapottér egyenletet irányíthatósági kanonikus alakra

$T_{c} = [\begin{matrix} \begin{matrix} - 0.4286 \\ 1 \\ \begin{matrix} 0 \\ 0 \end{matrix} \end{matrix} & \begin{matrix} 0 \\ 0 \\ \begin{matrix} 1 \\ 0 \end{matrix} \end{matrix} \end{matrix} \begin{matrix} \begin{matrix} 0 \\ 0 \\ \begin{matrix} 0 \\ 1 \end{matrix} \end{matrix} & \begin{matrix} - 0.1429 \\ 0 \\ \begin{matrix} 0 \\ 0 \end{matrix} \end{matrix} \end{matrix}] T_{c}^{- 1} = [\begin{matrix} \begin{matrix} 0 \\ 0 \\ \begin{matrix} 0 \\ - 7 \end{matrix} \end{matrix} & \begin{matrix} 1 \\ 0 \\ \begin{matrix} 0 \\ - 3 \end{matrix} \end{matrix} \end{matrix} \begin{matrix} \begin{matrix} 0 \\ 1 \\ \begin{matrix} 0 \\ 0 \end{matrix} \end{matrix} & \begin{matrix} 0 \\ 0 \\ \begin{matrix} 1 \\ 0 \end{matrix} \end{matrix} \end{matrix}]$

( 6.266 )

$A_{c_e x t} = [\begin{matrix} \begin{matrix} 0 \\ 0 \\ \begin{matrix} 0 \\ 0 \end{matrix} \end{matrix} & \begin{matrix} 1 \\ 0 \\ \begin{matrix} 0 \\ - 8 \end{matrix} \end{matrix} \end{matrix} \begin{matrix} \begin{matrix} 0 \\ 1 \\ \begin{matrix} 0 \\ - 14 \end{matrix} \end{matrix} & \begin{matrix} 0 \\ 0 \\ \begin{matrix} 1 \\ - 7 \end{matrix} \end{matrix} \end{matrix}] B_{c_e x t} = [\begin{matrix} 0 \\ 0 \\ \begin{matrix} 0 \\ 1 \end{matrix} \end{matrix}] C_{c_e x t} = [\begin{matrix} 0 & 7 & \begin{matrix} 3 & 0 \end{matrix} \end{matrix}] D_{c_e x t} = [0]$

( 6.267 )

Látható, hogy a kibővített rendszer könnyen átírható irányítható kanonikus alakra. Ebben az alakban visszacsatolás mértéke könnyen kiszámítható. A karakterisztikus egyenlet együtthatói

$(s + 2 + 0.8 π j) (s + 2 - 0.8 π j) (s + 5) (s + 10) =$

$s^{4} + 19 s^{3} + 120.3165 s^{2} 354.7482 s 515.8273$

( 6.268 )

$[\begin{matrix} k_{c I} & K_{c x} \end{matrix}] = [- 515.8273 - 346.7482 - 106.3165 - 12]$

( 6.269 )

Ellenőrzésképpen kiszámíthatjuk, hogy a (6.194) összefüggésnek megfelelően teljesül a következő egyenlőség

$[\begin{matrix} K_{x} & k_{I} \end{matrix}] = [\begin{matrix} k_{c I} & K_{c x} \end{matrix}] T_{c}$

( 6.270 )

6.4. Lineáris időben változó rendszerek állapottér egyenletei

A lineáris idő variáns rendszerek általános rövidítése, az angol név alapján LTV (Linear Time Varying).

Diszkrét időben

Az előző esethez képest annyi a különbség, hogy a rendszer mátrixok minden időlépésben megváltoznak (sok esetben ez a változás a mátrixoknak csak néhány elemét érintik)

$x [k + 1] = A_{d} [k] x [k] + B_{d} [k] u [k]$

$y [k] = C [k] x [k] + D [k] u [k]$

( 6.271 )

ahol $x [k] \in ℝ^{n}$ az állapotváltozók oszlopvektora a k –adik időlépésben, $u [k] \in ℝ^{m}$ a bemenetek oszlopvektora a k –adik időlépésben, $y [k] \in ℝ^{p}$ a kimenetek oszlopvektora a k –adik időlépésben $A_{d} [k] \in ℝ^{n \times n}$ , $B_{d} [k] \in ℝ^{n \times m}, C [k] \in ℝ^{p \times n}$ és $D [k] \in ℝ^{p \times m}$ a rendszert leíró mátrixok, amelyek elemei között van olyan, amelyik az egyes időlépésekben megváltozik.

Folytonos időben

$\dot{x} (t) = A (t) x (t) + B (t) u (t)$

$y (t) = C (t) x (t) + D (t) u (t)$

( 6.272 )

ahol $x(t) \in ℝ^{n}$ az állapotváltozók oszlopvektora, $u(t) \in ℝ^{m}$ a bemenetek oszlopvektora, $y(t) \in ℝ^{p}$ a kimenetek oszlopvektora $A(t) \in ℝ^{n \times n}$ , $B(t) \in ℝ^{n \times m}, C(t) \in ℝ^{p \times n}$ és $D(t) \in ℝ^{p \times m}$ a rendszert leíró mátrixok, amelyek elemei között van olyan, amelyik időben változik.

6.5. Lineáris változó paraméterű rendszerek állapottér egyenletei

A kilencvenes években került a kutatók érdeklődésének középpontjába a lineáris változó paraméterű rendszerek. A rövidítés itt is az angol névből származik LPV (Linear Parameter Varying)

Diszkrét időben

Az előző esethez képest annyi a különbség, hogy a rendszer mátrixok minden időlépésben egy paramétertől függően változnak (sok esetben ez a változás a mátrixoknak csak néhány elemét érinti)

$x [k + 1] = A_{d} [ρ] x [k] + B_{d} [ρ] u [k]$

$y [k] = C [ρ] x [k] + D [ρ] u [k]$

( 6.273 )

ahol $x [k] \in ℝ^{n}$ az állapotváltozók oszlopvektora a k –adik időlépésben, $u [k] \in ℝ^{m}$ a bemenetek oszlopvektora k –adik időlépésben, $y [k] \in ℝ^{p}$ a kimenetek oszlopvektora a k –adik időlépésben $A_{d} [ρ] \in ℝ^{n \times n}$ , $B_{d} [ρ] \in ℝ^{n \times m}, C [ρ] \in ℝ^{p \times n}$ és $D [ρ] \in ℝ^{p \times m}$ a rendszert leíró mátrixok, amelyek elemei között van olyan, amelyik az egyes időlépésekben megváltozik.

Folytonos időben

$\dot{x} (t) = A (ρ) x (t) + B (ρ) u (t)$

$y (t) = C (ρ) x (t) + D (ρ) u (t)$

( 6.274 )

ahol $x(t) \in ℝ^{n}$ az állapotváltozók oszlopvektora, $u(t) \in ℝ^{m}$ a bemenetek oszlopvektora, $y(t) \in ℝ^{p}$ a kimenetek oszlopvektora $A (ρ) \in ℝ^{n \times n}$ , $B (ρ) \in ℝ^{n \times m}, C (ρ) \in ℝ^{p \times n}$ és $D (ρ) \in ℝ^{p \times m}$ a rendszert leíró mátrixok, amelyek elemei között olyan, amelyik értéke egy $ρ$ paramétertől függ.

Vissza		Előre
5. fejezet - Adaptív szabályozás	Főoldal	7. fejezet - Dinamikus rendszerek identifikációja