7. fejezet - Dinamikus rendszerek identifikációja
Vissza		Előre

7. fejezet - Dinamikus rendszerek identifikációja

Tartalom

Szabályozási rendszerek tervezésének megvalósításához szükségünk van a szabályozott objektum dinamikai tulajdonságainak ismeretére. Valamilyen leírási mód segítségével rendelkeznünk kell az objektum matematikai modelljével, hisz a tervezőrendszerünk kérni fogja a szabályozandó objektum matematikai modelljét. Szerencsés esetben az objektum matematikai modellje – fizikai, kémiai, biológiai paraméterekkel ismert, de a legtöbb esetben nem, így valamilyen közelítő munkaponti modellekkel kell a tervezést megkezdeni.

Egy teljesen új technológiai rendszer felépítésénél a beruházási terv természetesen tartalmazza a gépészeti, technológiai, műszerezési terveket, azonban a szabályozási rendszerek tervezését nem, illetve csak a szabályozási körök elképzelt struktúráját adják meg a tervezők. A számítógépben elhelyezendő szabályozási algoritmusok struktúrája és paraméterei ezekben a kiviteli tervekben csak közelítőleg szerepelnek, hisz a tervező a visszacsatolt rendszerek pontos dinamikai tulajdonságait nem ismerik, ezeket a megépített rendszeren végzett vizsgálatokkal lehet csak pontosítani. A technológiai rendszer felépítésével, a műszerezés megvalósításával egy próbaüzemeltetés kapcsán elvégezhető a technológiai rendszer objektumainak ún. identifikációja, azaz meghatározhatjuk azt a matematikai modellt, amely az adott munkapontban visszatükrözi a rendszer időbeli viselkedését. Ezen modell bázisán a tervező képes lesz a visszacsatolások, előrecsatolások, vezérlések algoritmusainak megtervezésére.

A technológiai rendszerek irányítását, szabályozását, vezérlését folyamatirányító számítógépek végzik. A számítógép számára tervezendő szabályozási algoritmusokat a folyamatirányító számítógép differencia egyenlet formájában kéri, valamilyen tervezett T0 mintavételezési idő mellett, azaz az algoritmus egy diszkrét algoritmus, így a számítógép is egy diszkrét rendszert „szeretne látni” szabályozott objektumként, amely a valóságban természetesen időben folytonos rendszer.

Az időben folytonos rendszerek identifikációjával a szakirodalom több évtizede foglalkozik [1] és letisztultak azok az identifikációs eljárások, amelyeket a gyakorlat is közvetlenül alkalmazhat. Kialakultak azok a diszkrét rendszermodellek, melyek a gyakorlati problémák legtöbbjének leírására megfelelnek, melyek felhasználásával olyan matematikai modelleket kapunk, amelyek közvetlenül felhasználhatók digitális szabályozási algoritmusok tervezéséhez, adaptív rendszerek megalkotásához (pld. identifikációt alkalmazó adaptív rendszerek [2]).

7.1. Z - transzformáció

Ez a leképezés egy valós értékű, időben diszkrét sorozathoz rendel egy komplex függvényt. (Ugyanezt a Laplace transzformáció időben folytonos függvényre végzi.) A transzformáció szabályai alapján levezethető egy impulzus-átviteli függvény, mely a diszkrét dinamikai rendszer transzformált bemenő és kimenő jeleit algebrailag (szorzással) kapcsolja össze. Összetett rendszer (pl. egy zárt szabályozási kör) eredő átviteli függ-vényei algebrai módszerekkel fejezhetők ki (akárcsak a folytonos esetben).

7.1.1. Lépcsős függvény Laplace transzformáltja

Egyik lehetséges motiváció a szakaszonként állandó (lépcsös) függvényből (ábra) indul ki, mely egy nulladrendű tartószerv (ZOH) kimeneteként jöhet létre és a digitális szabályozás megvalósításában is fontos szerepe van. A téglalap-függvényeket két-két eltolt ugrás-függvényből építjük föl és transzformálásukhoz az eltolási tételt alkalmazzuk.

$L {f (t)} = (f (0) \cdot \frac{1}{s} - f (0) \cdot \frac{1}{s} e^{- h \cdot s}) + (f (h) \cdot \frac{1}{s} e^{- h \cdot s} - f (h) \cdot \frac{1}{s} e^{- 2 h \cdot s}) + \dots =$

$= \frac{1 - e^{- h \cdot s}}{s} (f (0) + f (h) \cdot e^{- h \cdot s} + f (2 h) \cdot e^{- 2 h \cdot s} + f (3 h) \cdot e^{- 3 h \cdot s} + \dots)$

( 7.1 )

A végtelen sor előtt álló komplex törtfüggvény a tartóra (itt ZOH) jellemző átviteli függvény. Magát a Z-transzformáltat az $f [k] = f (k \cdot h)$ és $z = \exp (h \cdot s)$ helyettesítésekkel definiáljuk az alábbi formális végtelen sorral. Ez már csak az időben diszkrét függvénysorozatot (pálcikák) tartalmazza, melyek származ-hatnak valamely folytonos jel mintavételezéséből (is).

$Z {f [k]} : = f [0] + f [1] \cdot z^{- 1} + f [2] \cdot z^{- 2} + f [3] \cdot z^{- 3} + \dots = \sum_{k = 0}^{\infty} f [k] \cdot z^{- k}$

( 7.2 )

7 . 1 feladat

Diszkrét egységugrás (ábra). Képletben: $f [k] = 0 (k < 0)$ és $f [k] = 1 (k \geq 0)$ . Végtelen mértani sort kapunk, mely csak akkor konvergens, ha hányadosára teljesül, hogy $| 1 / z | = 1 / | z | < 1.$

$Z {f [k]} : = 1 + 1 \cdot (z^{- 1}) + 1 \cdot {(z^{- 1})}^{2} + 1 \cdot {(z^{- 1})}^{3} + \dots = \frac{1}{1 - z^{- 1}} = \frac{z}{z - 1}$

( 7.3 )

7.1.2. A Z-transzformáció legfontosabb tételei

Eltolás időben. A diszkrét dinamikai modellek (ARMA, állapottér) kezelésében lesz fontos szerepük. A levezetéseket zárójelezéssel igyekeztünk követhetőbbé tenni, a $d = 2$ értékből már látszik az általános eset.

$Z {f [k - d]} = z^{- d} \cdot F (z) + \sum_{i = 0}^{d - 1} f [- d + i] \cdot z^{- i}$ késleltetett jel $(d \geq 1)$

( 7.4 )

$Z {f [k + d]} = z^{d} \cdot F (z) + \sum_{i = 0}^{d - 1} f [i] \cdot z^{d - i}$ siettetett jel $(d \geq 1)$

( 7.5 )

Késleltetéskor a függvény jobbra csúszik és a nulla időponttól balra eső értékek “beúsznak” a transzfor-mációba és ott additív tagokat generálnak. “Belépő” függvényekre ezek zérusok.

$Z {f [k - 2]} = f [- 2] + f [- 1] \cdot z^{- 1} + (f [0] \cdot z^{- 2} + f [1] \cdot z^{- 3} + \dots) =$

$= z^{- 2} \cdot (f [0] + f [1] \cdot z^{- 1} + \dots) + f [- 2] + f [- 1] \cdot z^{- 1} =$

$= z^{- 2} \cdot F (z) + f [- 2] + f [- 1] \cdot z^{- 1}$

( 7.6 )

Siettetéskor a függvény balra csúszik és a nulla időponttól jobbra eső értékek “kiúsznak” a transzfor-mációból emiatt szubtraktív (kivonandó) tagokat generálnak az általános szorzási szabály után.

$Z {f [k + 2]} = f [2] + f [3] \cdot z^{- 1} + f [4] \cdot z^{- 2} + \dots =$

$= z^{2} \cdot (f [0] + f [1] \cdot z^{- 1} + f [2] \cdot z^{- 2} + \dots) - f [0] \cdot z^{2} - f [1] \cdot z$

$= z^{2} \cdot F (z) - f [0] \cdot z^{2} - f [1] \cdot z$

( 7.7 )

$Z {k^{m} \cdot f [k]} = {(- z)}^{m} \cdot \frac{d^{m} F (z)}{d z^{m}}$

( 7.8 )

$Z {k \cdot f [k]} = \sum_{k = 0}^{\infty} (k \cdot f [k]) \cdot z^{- k} = \sum_{k = 0}^{\infty} f [k] \cdot (- k) z^{- k - 1} (- z) = (- z) \sum_{k = 0}^{\infty} f [k] \cdot \frac{d}{d z} (z^{- k}) =$

$= (- z) \cdot \frac{d}{d z} \sum_{k = 0}^{\infty} f [k] \cdot z^{- k} = (- z) \cdot \frac{d F (z)}{d z}$

( 7.9 )

7.2. Tipikus diszkrét idejű rendszermodellek

A tipikus diszkrét idejű modelleket tárgyalva a jelölésrendszerünkkel figyelembe vesszük a MATLAB/System IdentificationToolbox jelölésrendszerét, amelyet a következő fejezetekben másként fogunk használni. A két jelölésrendszer megfelelése a következő:

Polinomok

$\begin{array}{l} A (z^{- 1}) = 1 + a_{1} z^{- 1} + .... + a_{m} z^{- m} - h e l y e t t \\ A (z^{- 1}) = 1 + a_{1} z^{- 1} + .... + a_{n a} z^{- n a} \\ B (z^{- 1}) = b_{1} z^{- 1} + ... + b_{m} z^{- m} - h e l y e t t \\ B (z^{- 1}) = b_{1} + b_{2} z^{- 1} + ... + b_{n b} z^{- n b + 1} \\ C (z^{- 1}) = 1 + c_{1} z^{- 1} + ... + c_{m} z^{- m} - h e l y e t t \\ C (z^{- 1}) = 1 + c_{1} z^{- 1} + ... + c_{n c} z^{- n c} \\ D (z^{- 1}) = 1 + d_{1} z^{- 1} + ... + d_{m} z^{- m} - h e l y e t t \\ D (z^{- 1}) = 1 + d_{1} z^{- 1} + ... + d_{n d} z^{- z - d} \end{array}$

( 7.10 )

Diszkrét holtidő d helyett nk-t fogunk használni a MATLAB reprezentációkban. Még egy fontos kitétel az, hogy a zajcsatorna tárgyalásánál a MATLAB System IndentificationToolbox szerzője [ www.mathworks.com ] a

$G_{o v} (z) = \frac{n (z)}{v (z)} = \frac{C (z^{- 1})}{D (z^{- 1})}$

( 7.11 )

diszkrét idejű átviteli függvényt használja, az algoritmus tervezési fejezetükben azonban Gov(z) csatorna diszkrét idejű átviteli függvényét a

$G_{o v} (z) = \frac{n (z)}{v (z)} = \frac{D (z^{- 1})}{C (z^{- 1})}$

( 7.12 )

diszkrét idejű átviteli függvény formában fogjuk használni.

7.2.1. OE modell

Az OE (Output Error) modelle(k) mérési zajt tartalmazó modell a következő hatásvázlattal rendelkezik:

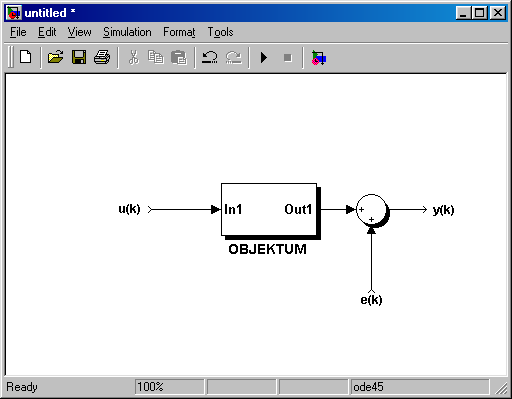
7.1. ábra - Az OE modell struktúrája

melynek impulzus-átviteli függvénye

$y (z) = \frac{B (z^{- 1})}{A (z^{- 1})} z^{- d} u (z) + e (z),$

( 7.13 )

ahol e(z) a mérési zaj z-transzformáltja.

Az impulzus-átviteli függvényt sok esetben a következő formális felírási móddal is írják:

$y (k) = \frac{B (z)}{A (z)} u (k - d) + e (k),$

( 7.14 )

vagy a MATLAB szerzői pedig a következő formát használják:

$y (k) = \frac{B (z)}{A (z)} u (k - n k) + e (k),$

( 7.15 )

azaz a d diszkrét holtidő jelölése nk.

Ezen modell olyan stacionárius folyamatok leírására szolgál, melyek külső zavaró jelcsatornákat nem tartalmaznak, azonban az e(t) mérési zaj jelen van. A modell differencia egyenlete MATLAB jelölés szerint a következő:

$\begin{array}{l} y (k) + a_{1} y (k - 1) + ... + a_{n a} y (k - n a) = \\ b_{1} u (k - n k) + b_{2} u (k - n k - 1) + ... + b_{n b} u (k - n k - n b + 1) + e (k) \end{array}$

( 7.16 )

7.2.2. ARX modell

Az ARX modell (AutoRegressive with eXternal input) a kimeneten színes zajt feltételez, aminek a következő modell felel meg.

$A (z) y (z) = B (z) \cdot z^{- d} + e (z)$

( 7.17 )

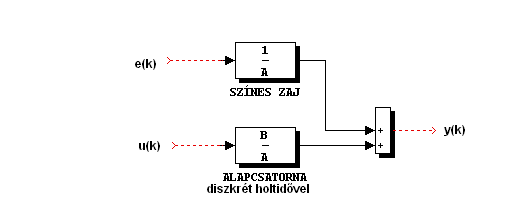
7.2. ábra - Az ARX modell struktúrája

7.2.3. ARMAX modell

Az ARMAX modell (AutoRegressive Moving Average modell with eXogenous signal) struktúrája a következő:

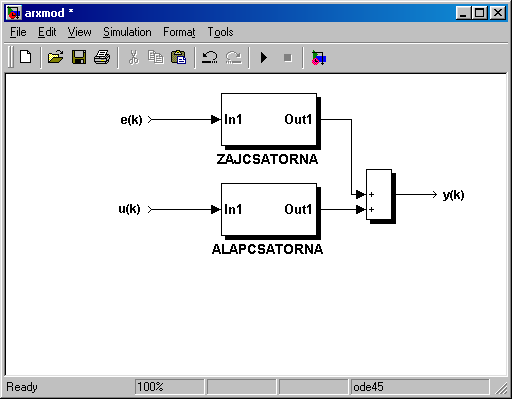
7.3. ábra - Az ARMAX modell struktúrája

ahol a zajcsatorna és az alapcsatorna impulzus-átviteli függvénye

$\begin{array}{l} G_{o v} (z) = \frac{C (z^{- 1})}{D (z^{- 1})}, \\ G_{0} (z) = \frac{B (z^{- 1})}{A (z^{- 1})} z^{- d} \end{array}$

( 7.18 )

a megfelelő polinomok pedig:

$\begin{array}{l} C (z^{- 1}) = 1 + c_{1} z^{- 1} + ... + c_{u c} z^{- n c} \\ D (z^{- 1}) = A (z^{- 1}) = 1 + a_{1} z^{- 1} + ... + a_{n a} z^{- n a} \\ B (z^{- 1}) = b_{1} + b_{2} z^{- 1} + ... + b_{n b} z^{- n b + 1} \end{array}$

( 7.19 )

Az ARMAX modell olyan esetben alkalmazható, ha a zajmodell – Gov – és az alapcsatorna karakterisztikus egyenlete megegyezik.

Ezt az egyezést a rendszer részletes analízisével tudjuk meghatározni.

Nézzük a következő példát. Legyen az identifikáló rendszer egy hőcserélő berendezés (7-4. ábra).

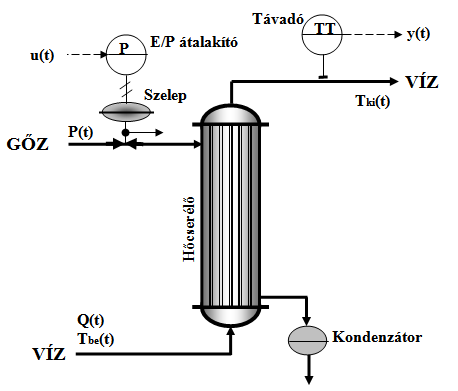
7.4. ábra - A hőcserélő – az identifikáció objektuma

A gőzzel fűtött hőcserélő feladata az, hogy a kilépő folyadék Tki hőmérsékletét adott értékre állítsa egy számítógépes digitális szabályozási algoritmus segítségével. A TT hőmérséklet távadó mA-es kimenete y(t). A gőzágat több fogyasztó is terhelheti, ezért a P(t) gőznyomást stabilizáljuk. A gőzágba építik be a szabályozó szelepet, amely a mi esetünkben pneumatikus segédenergiával működik. A számítógép folyamatperifériájánál kapott mA-es u(t) végrehajtó jel egy elektro-pneumatikus jelátalakítón keresztül működteti a végrehajtó szervet. Tételezzük fel, hogy a belépő folyadék mennyisége és hőmérséklete állandó és az y(t)-re csak a mérési zaj szuperponálódik.

Ebben az esetben az objektum jó közelítéssel modellezhető egy OE struktúrával (7-1. ábra).

Ha gőz gerincvezetékének nyomását nem tudjuk stabilizálni és az egyéb fogyasztók véletlenszerűen terhelik a gőzrendszert, akkor a P(t) gőznyomás ingadozik, amely a kilépő y(t) hőmérséklet véletlenszerű változását vonja maga után. A hőmérséklet aktuális értékét a szelepre eső nyomásesés (bevitt hőenergia) határozza meg, mely nyomásesést vagy a gőznyomásváltozás, vagy a szabályozó szelep pozíciója befolyásolják. Így feltételezhető, hogy a zajcsatorna (gőznyomás-hőmérséklet) és az alapcsatorna (szeleppozíció-hőmérséklet) karakterisztikus egyenletei megegyeznek, azaz A(z-1)=D(z-1). Ilyen esetben az objektum munkapontban egy ARMAX modellel közelíthető.

A harmadik esetként tételezzük fel, hogy a P(t) gőznyomás stabilizált, de a hőcserélőn átmenő Q(t) mennyiség sztochasztikusan változik, amely a kilépő y(t) hőmérsékletet befolyásolja. Ebben az esetben az alapcsatorna és a zavarójel csatorna (belépő folyadékáram - hőmérséklet) karakterisztikus egyenletei nem fognak megegyezni, így a fent említett modellek helyett Box-Jenkins modellt ajánlott használni.

7.2.4. Box-Jenkins (BJ) modell

A BJ modell a következő hatásvázlattal rendelkezik

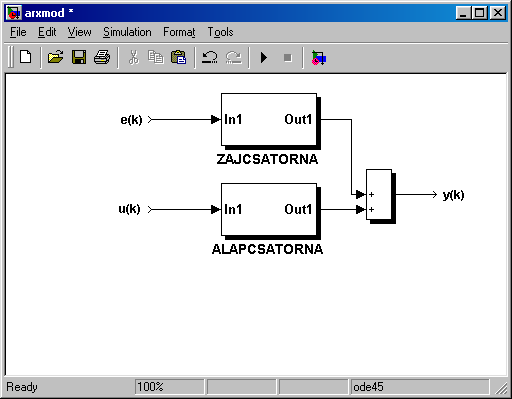
7.5. ábra - A BJ modell struktúrája

A BJ struktúra impulzus-átviteli függvénye:

$y (z) = \frac{B (z^{- 1})}{A (z^{- 1})} z^{- d} u (z) + \frac{C (z^{- 1})}{D (z^{- 1})} e (z),$

( 7.20 )

vagy MATLAB reprezentációja

$y (k) = \frac{B (z^{- 1})}{A (z^{- 1})} u (k - n k) + \frac{C (z^{- 1})}{D (z^{- 1})} e (k),$

( 7.21 )

ahol

$D (z^{- 1}) = 1 + d_{1} z^{- 1} + ... + d_{n d} q^{- n d}$

( 7.22 )

A bemutatott OE, ARX, ARMAX, BJ modellek azok, amelyeket a gyakorlatban legtöbbször alkalmazni kell, azonban a MATLAB kezelni tudja az AR, PEM modelleket (ld.MATLAB kézikönyv) is.

Ismeretlen rendszer identifikációja esetén mérjük az u(t) bemenet és a zajos y(t) kimenet értékeit, ezeket összegyűjtjük az u és y oszlopvektorokban, felépítjük a megfigyelésekből álló és két oszloppal jelentkező z=[y u] mátrixot, megválasztjuk a rendszermodellt és az abban szereplő polinomok fokszámait, megválasztjuk a holtidő értékét és elvégezzük az identifikációt az IDENT szolgáltatásaival. Az identifikációs módszerek feladata, hogy meghatározza a polinomok valamilyen értelemben optimális paramétereit, miközben az e(t) zaj értékei ismeretlenek. Erre a célra a legkisebb négyzetek módszere (LS, leastsquaresmethod) vagy ennél általánosabb paraméterbecslési technikák, a zaj fehérítését megcélzó segédváltozós (I.V., instrumentalvariables) módszer, numerikus optimum-keresés, vagy esetleg ezek kombinációja alkalmazható. Az IDENT a rendszermodell típusától függően választja meg az identifikációhoz használt numerikus módszert. A segédváltozós módszer (IV) csak ARX modell esetén alkalmazható [3]

Megjegyezzük, hogy több itt szereplő függvénynek létezik általánosabb paraméterezése is IDENT-ben, továbbá többváltozós (MIMO) rendszerek identifikációja is lehetséges.

Az IDENT toolbox a továbbiakban algoritmus szinten is részletesen tárgyalt diszkrétidejű paraméter identifikációs módszereken kívül lehetővé teszi még folytonos idejű lineáris állapotegyenletek paramétereinek becslését is speciális zajstruktúrák esetén. Szolgáltatásai között szerepelnek a paraméterbecslés rekurzív realizációi is , amelyek adaptív irányításoknál jelentősek. Ezeken túlmenően lehetőség van nemparaméteres identifikációra, valamint a korrelációs függvények és a spektrumok számítására is. Ez utóbbi számítások algoritmusai gyors Fourier-transzformáción (FFT, Fast-Fourier-Transformation) és az FFT periodicitása miatt alkalmasan választott ablakozási technikán alapulnak [4]

7.3. Az identifikáció gyakorlati alkalmazásai

Az identifikáció előkészítése nagyon körültekintő munkát igényel. A következőkben megnézzük a legfontosabb – identifikáció előtti – feladatokat, melyeket el kell végezni.

7.3.1. Általános feladatok

7.3.1.1. Az állandósult állapot vizsgálata (a)

Nagyon gyakran a technológiai rendszerek különböző munkapontokon dolgoznak. Ezek a technológiai rendszerek nemlineárisak, pld. az erősítési tényezőjük jelentősen változhat a különböző működési tartományokban. Az erősítési tényező mellett változhatnak az időállandók, változhatnak egyéb modell paraméterek is, vagy a modell struktúra is más lesz. A vizsgált identifikációs eljárások eredménye egy impulzus átviteli függvény állandó paraméterekkel és struktúrával. Ezért fontos, hogy elérjünk egy állandósult állapotot – 7-6. ábra – és a bemenet-kimenet pont párokat innen gyűjtsük össze.

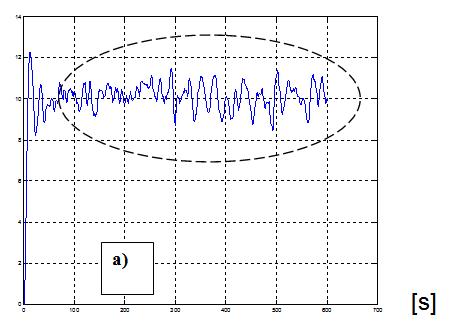
7.6. ábra - Az állandósult állapot vizsgálata

7.3.1.2. Trend figyelés (b)

A gyakorlatban előfordulhat az átlagérték lassú kúszása pld. a távadók lassú driftje miatt,

az objektum elemeinek kopása, vagy pld. az aktuális hőcserélő vízkövesedése folytán, esetleg műszakváltás, időközi leállások miatt. Ebben az esetben a kúszást – 7-7. ábra- trendfigyeléssel meg kell szüntetni, hisz a nemlineáris objektum tulajdonságok az identifikáció eredményét meghamisíthatják.

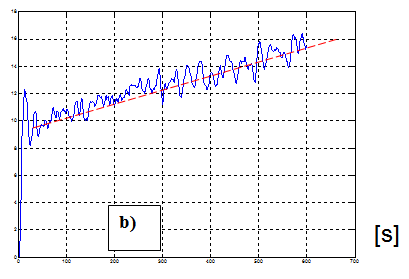
7.7. ábra - Trend figyelés

7.3.1.3. Kiugró értékek figyelése (c)

Az állandósult állapot megfigyelésekor találkozhatunk szokatlan kiugró értékek megjelenésével a mért jeleken. Ennek több oka lehet: a távadó vagy a kábelezés érzékeny az elektromágneses tér változásaira, amikor be/kikapcsolnak villamos berendezéseket, villámlás történt., stb. Az ilyen adatok nem alkalmasak az identifikációhoz.

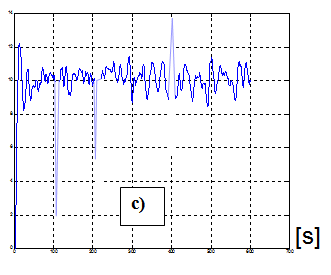
7.8. ábra - Kiugró értékek figyelése

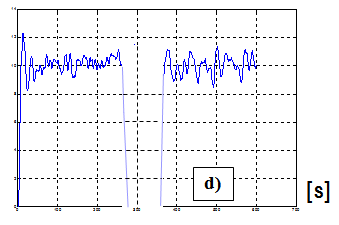
7.3.1.4. Az érzékelő kikapcsol (d)

Abban az esetben, ha az érzékelő, távadó, vagy a mérőlánc valamelyik tagja jelkimaradást okoz, akkor a mért jel identifikációra nem alkalmas (7-9. ábra)

7.9. ábra - Az érzékelő kikapcsol

7.3.1.5. A mintavételezési idő meghatározása (e)

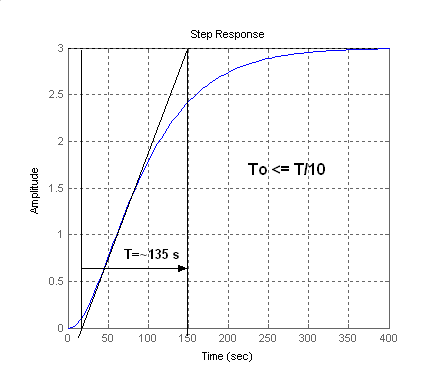
A T0 mintavételezési idő meghatározása abban az esetben, ha ismerjük a vizsgált objektum átmeneti függvényét az 7-10. ábra alapján történik. Az inflexiós pontban húzott érintő segítségével meghatározható a T időállandó, s ennek 1/10 része, vagy annál kisebb legyen a mintavételezési idő.

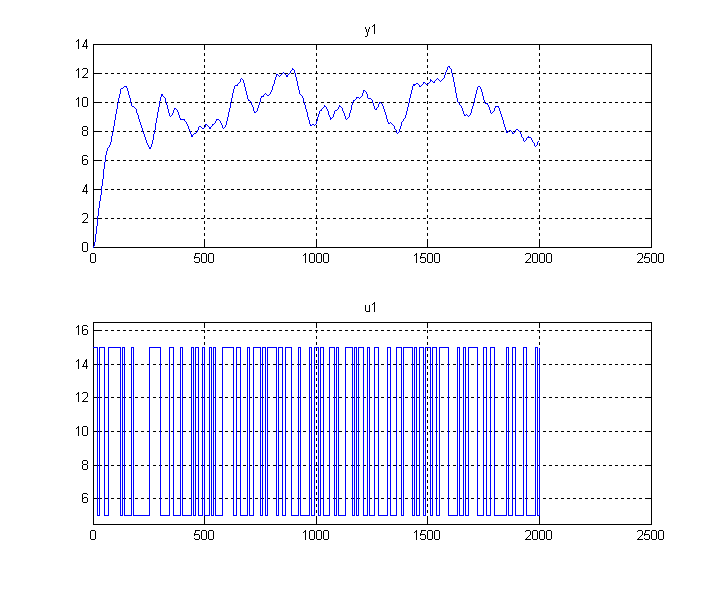
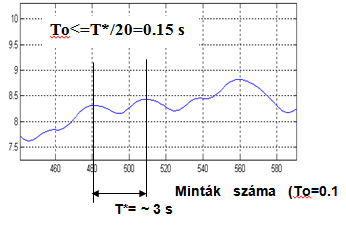
Abban az esetben, ha egy működő technológia – 7-11. ábra - jeleit akarjuk mintázni, érdemes a mért jeleket kinagyítani – 7-12. ábra – és kiválasztani azt a legnagyobb frekvenciát, mely még befolyásolja a modellalkotást.

A T0 mintavételezési idő a legnagyobb frekvenciájú összetevő periódusidejének 1/20 része legyen.

7.10. ábra - A mintavételezési idő meghatározása önbeálló rendszer esetén

7.11. ábra - A legnagyobb frekvenciájú rész kiválasztása

7.12. ábra - A mintavételezési idő meghatározása zajjal terhelt rendszer esetén

7.3.2. MATLAB System IdentificationToolbox és SIMULINK alkalmazása

Az identifikációs technikák alkalmazásának tanulmányozására a MATLAB/SIMULINK modellező rendszert fogjuk használni és az identifikálandó objektumot is szimulációval állítjuk elő, természetesen folytonos rendszerként modellezzük azt. A 7-13. ábra segítségével egy másodrendű rendszer átmeneti függvénye alapján meghatározhatjuk a diszkrét modell mintavételezési idejét. A T0 mintavételezési időt lengésmentes önbeálló rendszer esetén kiválaszthatjuk úgy, hogy megkeressük az egy időállandós, holtidős közelítő modelljét és ezen modell T időállandójának tizedét fogadjuk el mintavételezési időnek. Példaként legyen a folytonos rendszer modellje:

$G_{0} (s) = \frac{2, 7}{140 s^{2} + 45 s + 1},$

( 7.23 )

a közelítő egyidőállandós, holtidős modellje pedig

$G_{o k} (s) = \frac{2, 7 \cdot e^{- 2 s}}{51 s + 1}$ ,

( 7.24 )

ahol az időállandó T=50s, így a mintavételezési időt választhatjuk T0=T/10=50/10=5 s-ra.

7.13. ábra - A folytonos rendszer átmeneti függvénye és közelítése egyidőállandós, holtidős rendszerrel

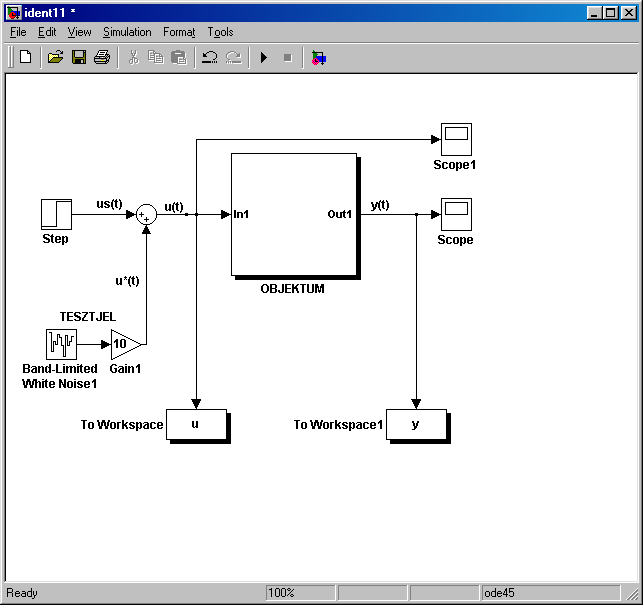
A 7-14. ábra azt a SIMULINK felületet mutatja be, ahol az identifikálandó objektum u(t) bemenetét állítjuk elő, ahol u(t)=us(t)+u*(t). A munkaponti identifikáció első fontos feladata a vizsgálat munkapontjának meghatározása, majd beállítása. Gyakori eset, hogy a folytonos technológiai rendszer különböző terheléssel működik és a rendszer nemlineáris volta miatt több munkaponti identifikáció szükséges. Ezen munkapontok meghatározásánál a technológusok segítségét, szakértelmét kell felhasználni.

Az identifikáció tesztjelének megválasztása is fontos kérdés. A vizsgáló tesztjel frekvencia spektrumát és amplitúdóját úgy kell megváltoztatni, hogy az u(t) tesztjel hatása az y(t) kimeneten mérhető és értékelhető legyen.

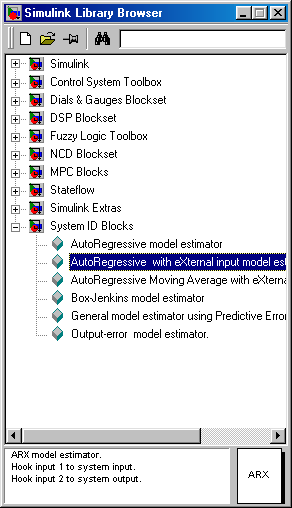
Off-line identifikáció esetén a leggyakoribb tesztjel forma a sávkorlátozott fehér zaj (Band-Limited White Noise a SIMULINK könyvtárból), vagy az álvéletlen kétállapotú jelsorozat (Psendo Random Binare Signal, PRBS). Ezek a jelalakok tartalmazzák a legtöbb frekvenciát, a frekvencia spektrumuk a legszélesebb a mesterségesen előállított jelsorozatok között. A PRBS egyik előállítási módját látjuk (7-15. ábra), ahol a mérési zaj modellezésére használjuk.

Az us(t) folytonos jel segítségével állítjuk be a rendszert a kívánt munkapontba, az u*(t) jel pedig az identifikáció bemeneti tesztjele.

7.14. ábra - Az identifikáció előkészítése SIMULINK felületen

Az objektum folytonos SIMULINK modellje a kimenetre szuperponálódó mérési zajjal alább (7-15. ábra) látható:

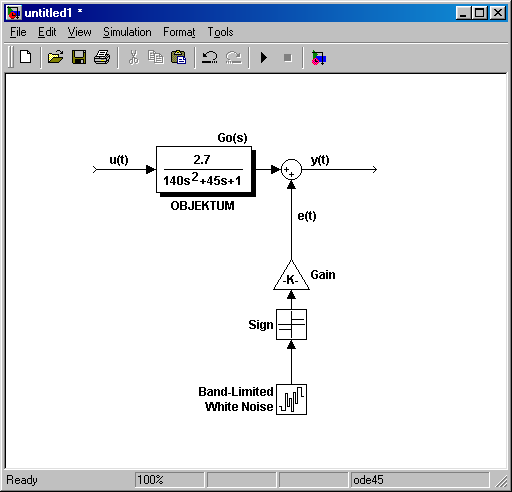
7.15. ábra - Az objektum folytonos modellje

Az u(t) bemenőjel és az y(t) kimenőjel (7-14. ábra) adatgyűjtését T0=5s-os mintavételezési idővel a ToWorkspace blokkal végzik, mely paraméterezését mutatja a 7-16. ábra, s ennek segítségével mátrix formában mentjük el a gyűjtött adatot.

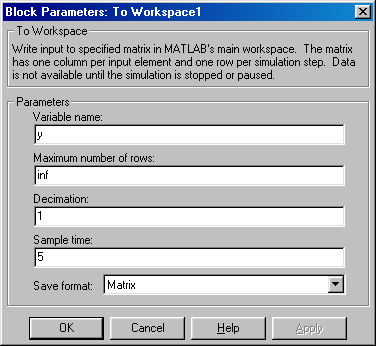
7.16. ábra - Az adatgyűjtő Workspace blokk

Állítsuk elő a bemenet-kimenet párok vektorát, és vizsgáljuk meg mérési eredményeinket a következő parancsok segítségével:

z= [ y u ]

idplot( z )

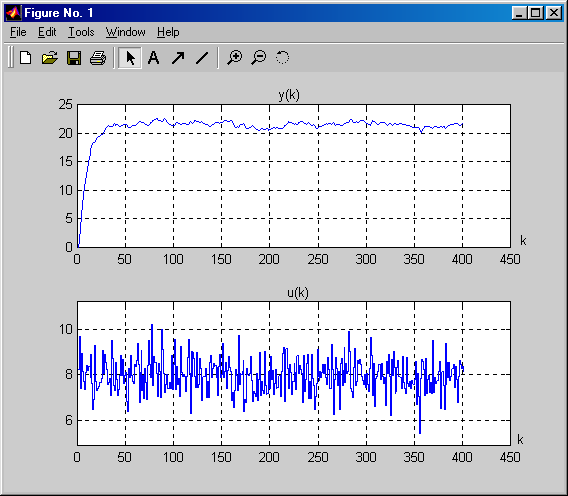
7.17. ábra - A mintavételezett adatpárok

Az identifikációs algoritmusok nemlineáris rendszerek esetében csak akkor hoznak helyes eredményeket, ha a bemenőjel és a kimenőjel átlagértéke állandó, ezért a mi esetünkben az első 50 mintavételezett adatpárt eltávolítjuk a következő paranccsal (7-18. ábra):

z1=[ y(50:400) u(50:400)]

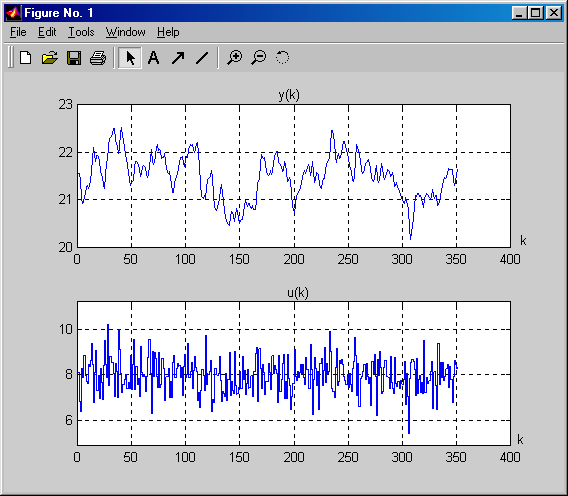
7.18. ábra - A stacionárius be- kimeneti adatpárok

Az identifikációs algoritmusok másik megkötése lehet az, hogy a bemeneti-kimeneti adatpárok nulla átlagértékűek legyenek, ezt pedig a

z2 = dtrend(z1)

paranccsal végezhetjük el. (7-19. ábra).

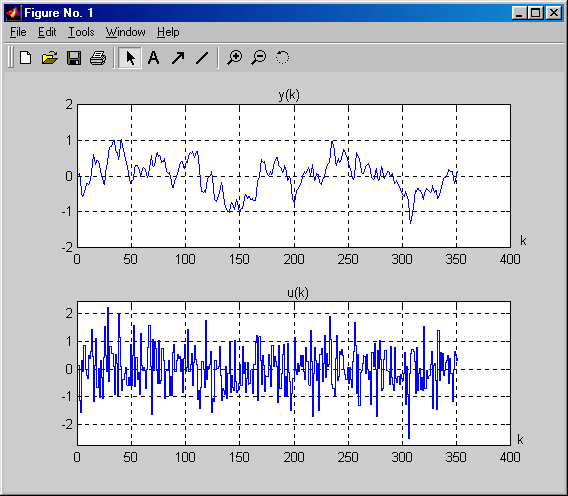
7.19. ábra - Az identifikációs algoritmus bemenetének nulla átlagértékű adatpárjai

A véglegesnek tekinthető adatpárok meghatározása után az identifikáció számára meg kell határozni az illesztendő modell (impulzus-átviteli függvény) számlálójának (nb) és nevezőjének (na) fokszámait, valamint a d diszkrét holtidőt, melyet nk-val jelöl a használt modellező rendszer. Ha az adatpárokból ezeket a paramétereket nem vagyunk képesek meghatározni, ezért egy egyszerű paranccsal

ir = cra(z2) ,

azaz korrelációs analízis segítségével meghatározhatjuk a rendszer közelítő súlyfüggvényét, melyet alább (7-20. ábra) mutatunk be.

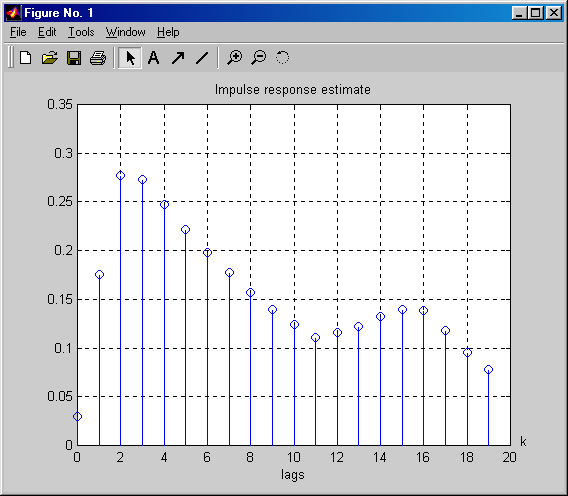
7.20. ábra - A vizsgált rendszer közelítő súlyfüggvénye

A közelítő súlyfüggvény szerint a vizsgált rendszer minimum másodrendű modellel jellemezhető, diszkrét holtideje d=0, mely a MATLAB realizációban nk=1-et jelent. A következő parancsokkal megvizsgálhatjuk a vizsgált rendszerközelítő átmeneti függvényét is (7-21. ábra):

stepr = cumsum (ir)

plot (stepr)

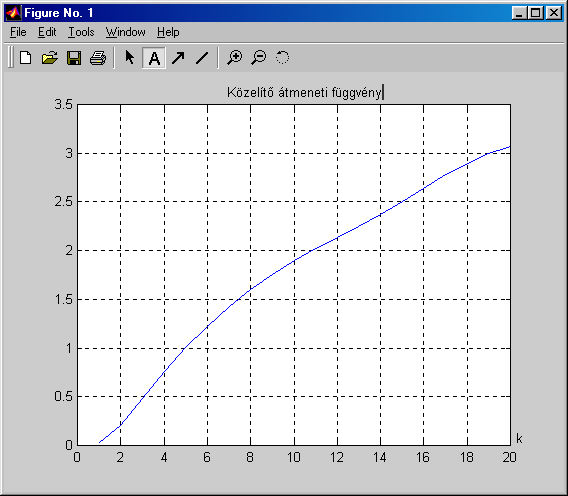
7.21. ábra - A vizsgált rendszer közelítő átmeneti függvénye (korrelációs analízissel)

A korrelációs analízis eredménye alapján másodrendű (d=0) rendszert javasolhatunk, amely számára előállítjuk a th vektort. Ez tartalmazni fogja az identifikálandó OE modell

B(z-1),A(z-1) polinomjainak együtthatóit: =[ a0 a1a2 …ana b1 b2 … bnb] a th = oe (z2, [2 2 1]) parancs segítségével.

A present(th) parancs hatására megkapjuk a B(z-1) és A(z-1) polinomok együtthatóit:

B = 0 0.1488 0.0877

A = 1.0000 -1.1129 0.2005

majd elvégezhetjük a modellünk és a tényleges mérési adatsorunk által szolgáltatott eredményeket ugyanarra a bemeneti jelre:

compare (z2, th).

A vizsgált rendszer esetén a mérési zaj e(k)=0 amplitúdóval rendelkezett és a modell kimenete ugyanazon vizsgáló jel esetén megegyezik a fizikai objektum kimenetével (7-22. ábra).

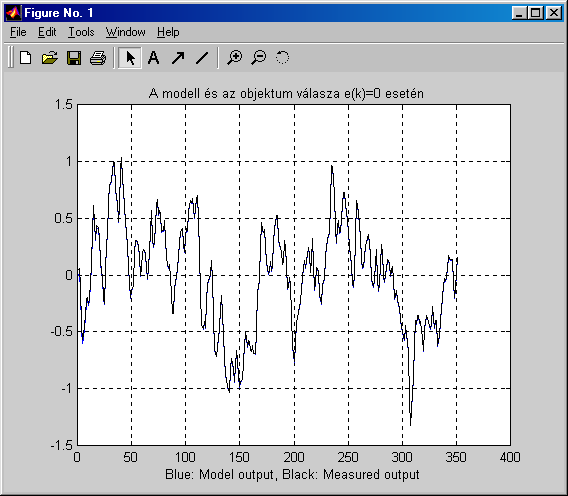
7.22. ábra - A modell és a tényleges rendszer kimenetének összehasonlítása (e(k)=0)

Az OE modell impulzus-átviteli függvénye tehát

$G_{0} (z) = \frac{0.1488 z^{- 1} + 0, 0877 z^{- 2}}{1 - 1, 1129 z^{- 1} + 0, 2005 z^{- 2}} = \frac{y (z)}{u (z)}$ ,

( 7.25 )

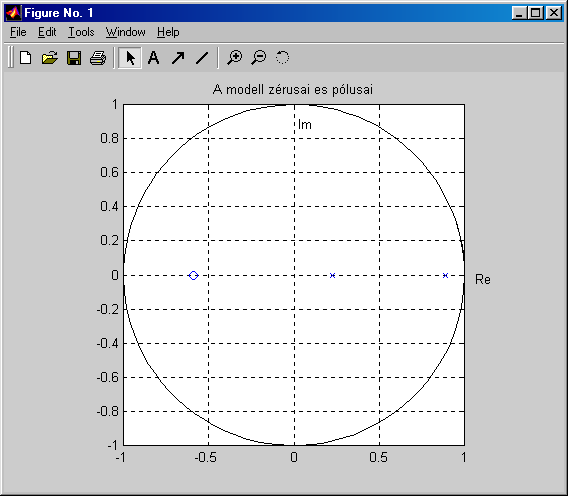
melynek pólusait és zérusait mutatja a 7-23. ábra. Ezek az e(k)=0 esetre megegyeznek a tényleges értékekkel. A tényleges rendszer és a modell frekvencia függvényének összehasonlítását mutatja be az 7-24. ábra.

7.23. ábra - A modell pólusai és zérusai

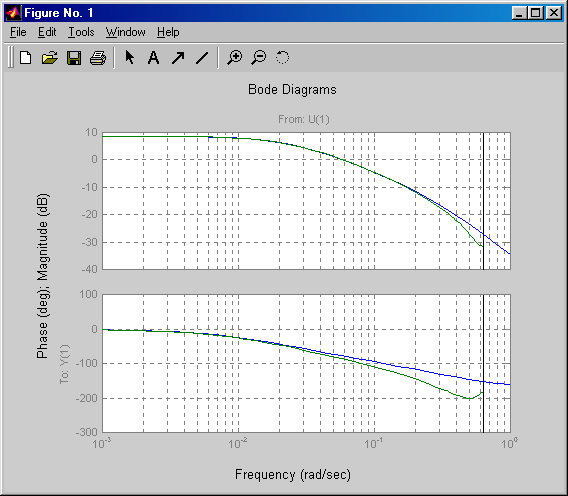
7.24. ábra - A folytonos rendszer és az identifikált modell frekvencia függvénye

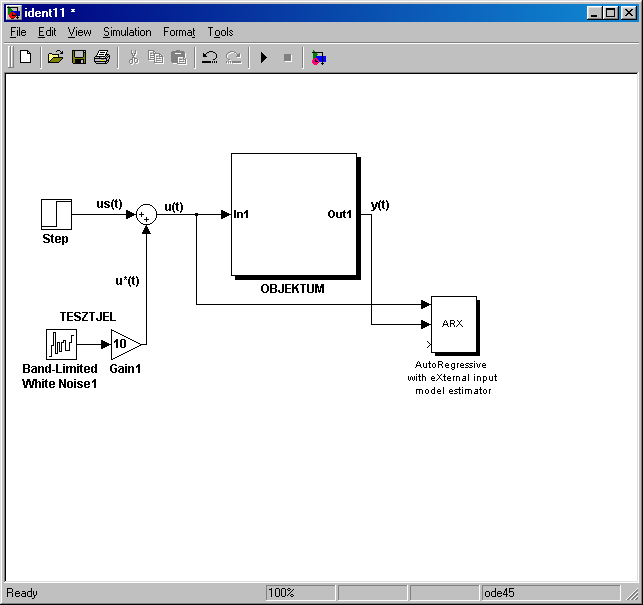
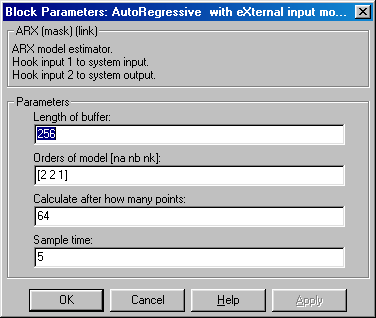
A modellező rendszer SIMULINK felülete is rendelkezik identifikációs számítási blokkokkal (7-25. ábra), melyet a 7-26. ábra szerint helyezhetünk be az identifikációs rendszerbe, és a lentebb (7-27. ábra) bemutatott paraméter beviteli felülettel rendelkezik.

Az így beillesztett ARX vagy más blokk az identifikációs eredményeket a MATLAB ablakban jeleníti meg a következő alakban:

Transferfunction:

$num / d e n = \frac{0, 1488 z + 0, 0877}{z^{2} - 1, 11289 z + 0, 20046}$ ,

( 7.26 )

7.25. ábra - A SIMULINK identifikációs blokkjai

7.26. ábra - Az ARX blokk behelyezése

7.27. ábra - Az ARX blokk paraméterezése

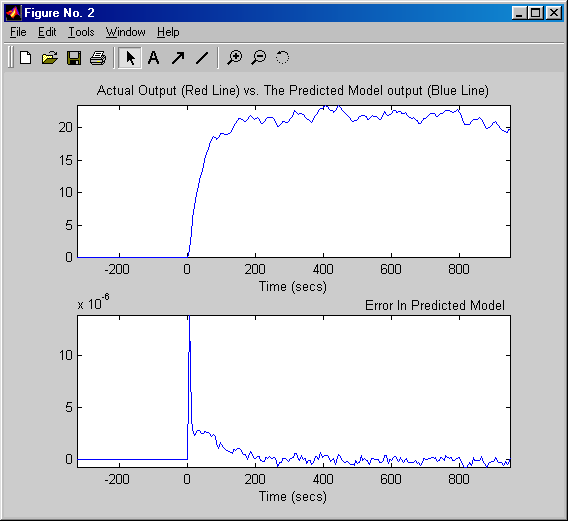
A 7-28. ábra és 7-29. ábra mutatja be az identifikáció összehasonlító eredményeit e(k)=0 és 0,2 amplitúdójú álvéletlen (PRBS) mérési zaj esetén. Az ábrák alapján levonhatjuk azt a következtetést, hogy az e(k) mérési zaj amplitúdója az identifikáció pontosságát nagyban befolyásolja, tehát törekednie kell a mérési zajok amplitúdójának csökkentésére pl. úgy, hogy az y(t) kimenetet, vagy a már mintázott y(k) kimenetet megszűrjük. Természetesen a szűrő dinamikája is az identifikált modellünkbe integrálódik.

7.28. ábra - Az identifikáció minősége e(k)=0 esetén

7.29. ábra - Az identifikáció minősége mérési zaj esetén

A 7-30. ábra egy ARMAX modell identifikációját illusztrálja. Az alapcsatorna folytonos átviteli függvénye:

$G_{0} (s) = \frac{4 (8 s + 5) e^{- 6 s}}{(20 s + 1) (32 s + 1) (11 s + 1)}$ ,

( 7.27 )

a zajcsatorna folytonos átviteli függvénye pedig

$G_{o v} (s) = \frac{8}{(20 s + 1) (32 s + 1) (11 s + 1)}$ ,

( 7.28 )

A mintavételezési időt, T0=6 s-ra választottuk.

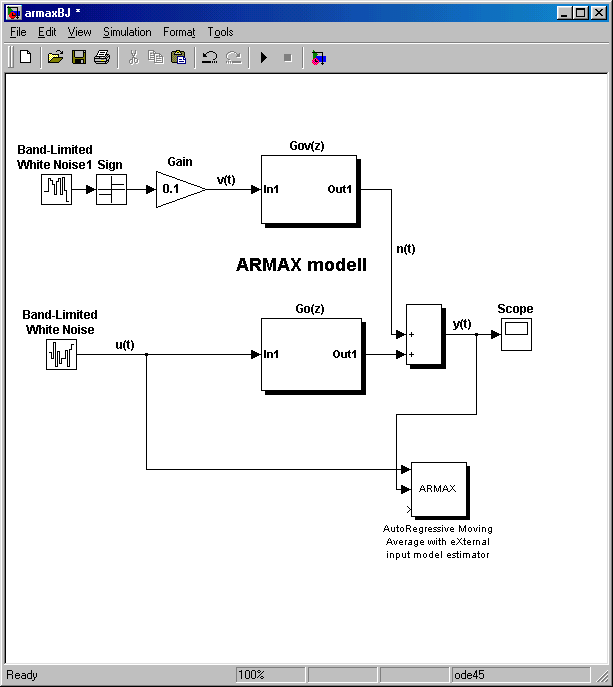
7.30. ábra - Az ARMAX modell SIMULINK felületen

A SIMULINK ARMAX blokkjának paraméterezését láthatjuk alább (7-31. ábra).

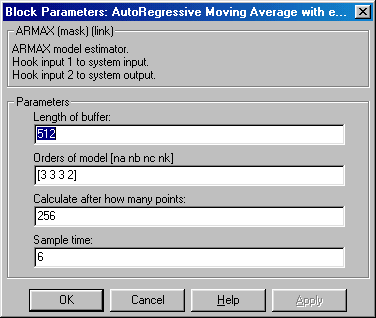
7.31. ábra - Az identifikátor paraméterezése

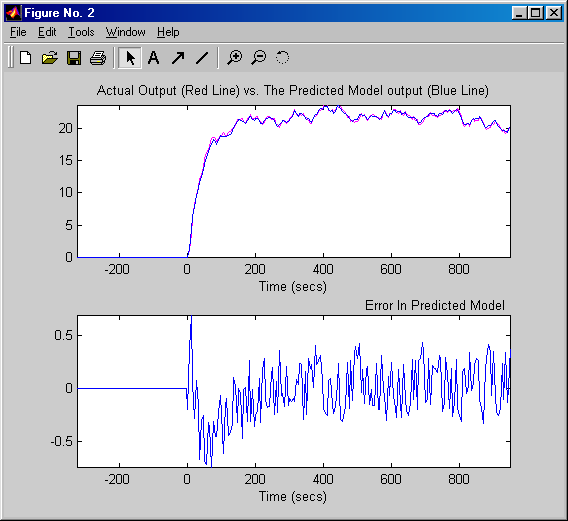
Az identifikáció minőségét mutatjuk be alább (7-32. ábra).

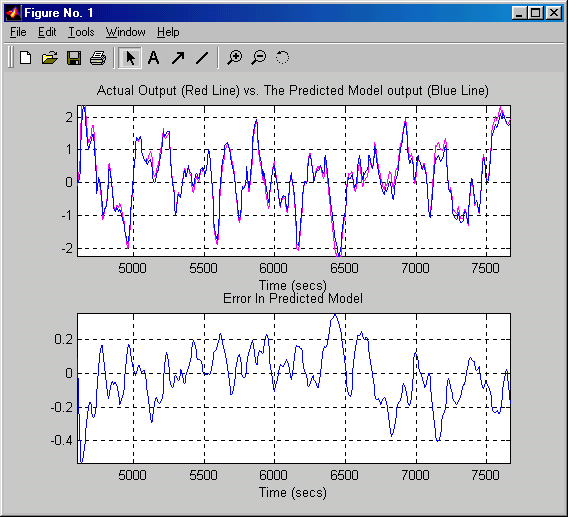
7.32. ábra - Az identifikáció minősége

A MATLAB felületen hozzáférhetünk az identifikált alapcsatorna és a zajcsatorna impulzus-átviteli függvényeihez, melyek a következők lettek:

$G_{0} (z) = \frac{0, 86633 z^{2} + 0, 37593 z - 0, 23062}{z^{4} - 1, 844 z^{3} + 1, 0601 z^{2} - 0, 18238 z}$ ,

( 7.29 )

$G_{o v} (z) = \frac{z^{3} + 0, 83757 z^{2} + 0, 34081 z + 0, 085343}{z^{3} - 1, 844 z^{2} + 1, 0601 z - 0, 18238}$ ,

( 7.30 )

A Box-Jenkins modell bemutatására a következő folytonos zajcsatorna modellt használtuk:

$G_{o v} (s) = \frac{8}{(10 s + 1) (24 s + 1) (8 s + 1)}$ ,

( 7.31 )

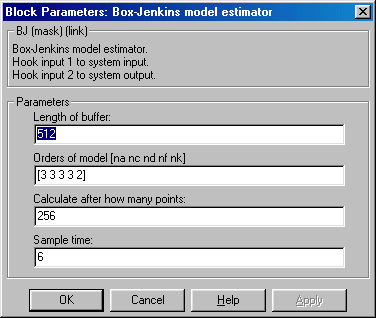
az alapcsatorna G0(s) modellje megegyezik az ARMAX modellével. A SIMULINK felületet láthatjuk alább (7-33. ábra), valamint alatta a BJ-modell paraméterezését (7-34. ábra).

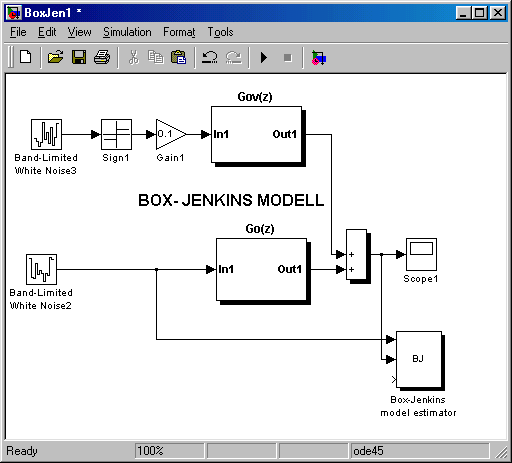
7.33. ábra - Box-Jenkins modell SIMULINK felületen

7.34. ábra - Az identifikátor paraméterezése

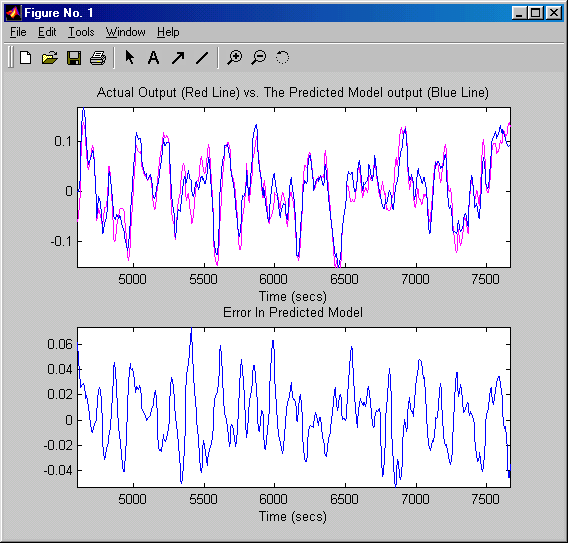
A Box-Jenkins modell alapján történt identifikáció minőségét mutatja a 7-35. ábra.

7.35. ábra - Az identifikáció minősége

7.3.3. Nemlineáris rendszerek identifikációja

A technológiai rendszerünk egy gőzös hőcserélő (7-36. ábra), gőzágba épített nemlineáris karakterisztikájú szabályozó szeleppel. Feladatunk megtervezni a visszacsatolásba építendő szabályozási algoritmust.

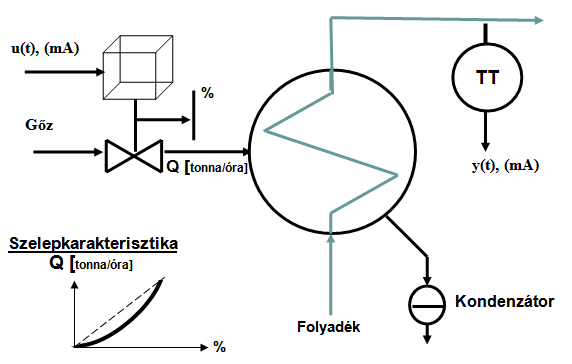
7.36. ábra - Gőzös hőcserélő

A technológiai rendszer nemlineáris viselkedését láthatjuk alább (7-37. ábra). A szelep bemenetét változtatva különböző munkapontokon vizsgáltuk a hőcserélőből kilépő folyadék hőmérséklet változásait. A mintavételezési időt T0=2 s-ra választottuk és az u(k) végrehajtó jelre +/- 1 mA PRBS jelet szuperponáltunk.

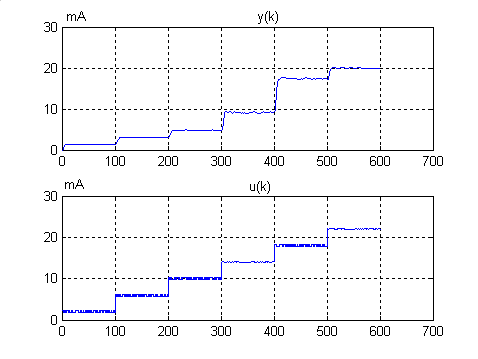
7.37. ábra - Gőzös hőcserélő nemlineáris viselkedése

Vizsgáljunk meg egy tartományt, melynél az u(k) bemenet 10 mA-ről 14 mA-re változik. Ez a k=300-400 minta közötti részminta párjai. OE modellt használva a következő diszkrét idejű átviteli függvény polinomokat kapjuk:

B(z) = 0.06827 z-1 + 0.1446 z-2 - 0.2139 z-3

A(q) = 1 - 2.306 z-1 + 1.775 z-2 - 0.4706 z-3

(7.32)

Az identifikációt elvégezve a k=200-300 intervallumban a diszkrét idejű átviteli függvény polinomjai:

B(z) = 0.02024 z-1 + 0.06032 z-2 - 0.06966 z-3

A(z) = 1 - 2.179 z-1 + 1.623 z-2 - 0.4214 z-3

(7.33)

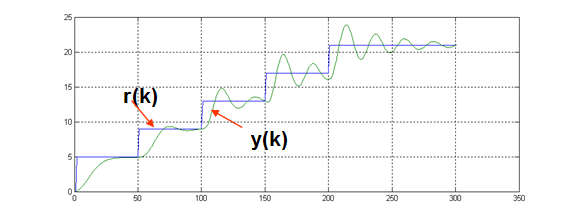
Ez azt jelenti, hogy több munkapont környékén el kell végezni az identifikációt és a más-más munkapont környékén a szabályozó algoritmus paramétereit újra kell hangolni. Az alábbi 7-38. ábra a nemlineáris rendszer szabályozását szemlélteti állandó paraméterű és struktúrájú szabályozó esetén különböző munkapontokban (ahol: r(k) – parancsolt érték)

7.38. ábra - Nemlineáris rendszer szabályozásának minősége állandó struktúrájú és paraméterű szabályozóval

(A MATLAB >>ident parancsára nem térünk ki, lásd a System Identification Toolbox-ot)

7.4. Esettanulmány az identifikáció + szabályozó tervezés alkalmazására

Bevezetés

A Pannon Egyetemen üzembe helyeztünk egy DCMCT (DC Motor ControlTrainer) rendszert.

A rendszer folyamatirányítási felülete PC bázisú, mely USB felületen kapcsolódik egy PIC18F4550 mikrokontroller alapú egységhez, az pedig egy MAXON DC motorhoz (GraphiteBrushless, 18 Watt, 26 mm).

A DCMCT dinamikus viselkedését egy rúgó-tömeg mechanikus egység segítségével megváltoztattuk és a beépített PID algoritmus helyett diszkrét Dahlin algoritmust használunk. Az analitikusan megtervezett Dahlin algoritmus tartalmaz egy notch szűrőt/szabályozót, ill. egy PI algoritmust.

7.4.1. A kísérleti rendszer felépítése

Az QUANSER rendszer [5] rendszertechnikai felépítése az alábbi ábrán (7-39. ábra) látható.

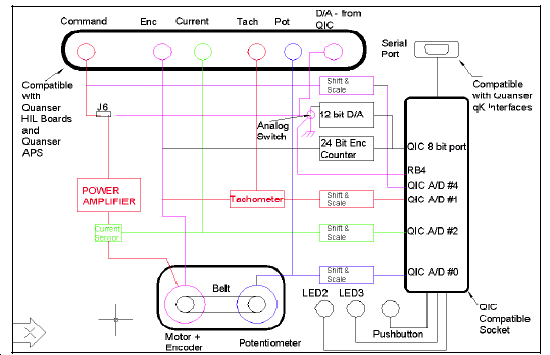
7.39. ábra - A QANSER DC motor Kit felépítése

A rendszer USB vonalon keresztül kapcsolódik a számítógéphez, melyen fut egy real-time folyamatkezelő szoftver. A mintavételezési idő T0=0.01 s. A gyakorló eszköz a rugó-tömeg kiegészítéssel alább látható (7-40. ábra, 7-41. ábra).

7.40. ábra - A QUANSER DC motor rugó-tömeg kiegészítő mechanikával

7.41. ábra - A rugó-tömeg ráépítés

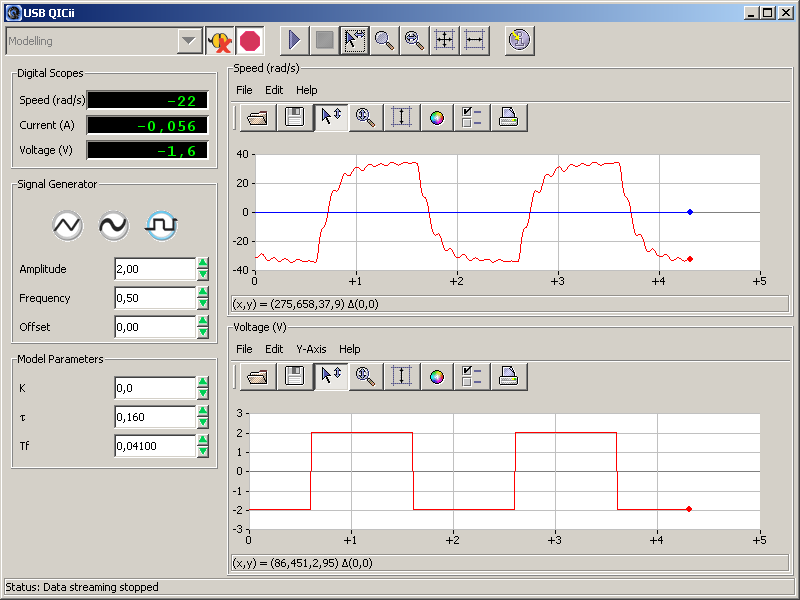
A QUANSER USB QICii szoftver kezelői felülete (7-42. ábra) pozíció és fordulatszám szabályozást enged meg, valamint rendelkezik egy egyszerű modellezési lehetőséggel is. Ez utóbbit használtuk fel a mechanikailag átalakított rendszer identifikációjánál az adatgyűjtéshez. Alább (7-42. ábra) látható, hogy a rendszer keskenysávú lengéseket végez az átmeneti állapotokban. E viselkedés notch-szűrő alkalmazását indokolhatja, melyet az algoritmus tervezés figyelembe fog venni.

7.42. ábra - Az adatgyűjtő QICii szoftver kezelői felülete

7.4.2. Az identifikáció

7.4.2.1. Modell kiválasztás

A technológiai rendszerek irányítását, szabályozását, vezérlését számítógépek végzik. A számítógép számára tervezendő szabályozási algoritmusokat a folyamatirányító számítógép differencia egyenlet formájában kéri, valamilyen tervezett T0 mintavételezési idő mellett, azaz az algoritmus egy diszkrét algoritmus, így a számítógép is egy diszkrét rendszert „szeretne látni” szabályozott objektumként, amely a valóságban természetesen időben folytonos rendszer.

Az időben folytonos rendszerek identifikációjával a szakirodalom több évtizede foglalkozik [4] és letisztultak azok az identifikációs eljárások, amelyeket a gyakorlat is közvetlenül alkalmazhat. Kialakultak azok a diszkrét rendszermodellek, melyek a gyakorlati problémák legtöbbjének leírására megfelelnek, melyek felhasználásával olyan matematikai modelleket kapunk, amelyek közvetlenül felhasználhatók digitális szabályozási algoritmusok tervezéséhez, adaptív rendszerek megalkotásához [2].

Az QICii rendszerből származtatott mérési adatok formátuma olyan, hogy a MATLAB System Identification Toolbox-a ezeket értelmezni tudja. Az 7-43. ábra mutatja a feldolgozandó be-kimeneti jelsorozatot.

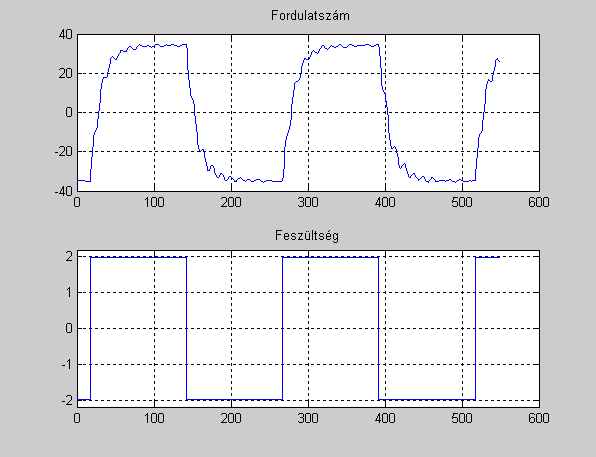
7.43. ábra - Az identifikáció adatsora 0.01s mintavételezési idő mellett

A rendszerhez illesztett OE (Output Error) modell, mely mérési zajt tartalmazó modell - a következő hatásvázlattal jellemezhető:

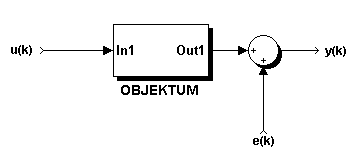
7.44. ábra - Az OE modell struktúrája

7-44. ábra Az OE modell struktúrája

A modell impulzus-átviteli függvénye:

$y(z)= \frac{{B(z}^{-1})}{{A(z}^{-1})} z^{-d} u(z)+e(z),$

( 7.34 )

ahol e(z) a mérési zaj z-transzformáltja.

7.4.2.2. A szabályozási kör mintavételezési idejének megválasztása

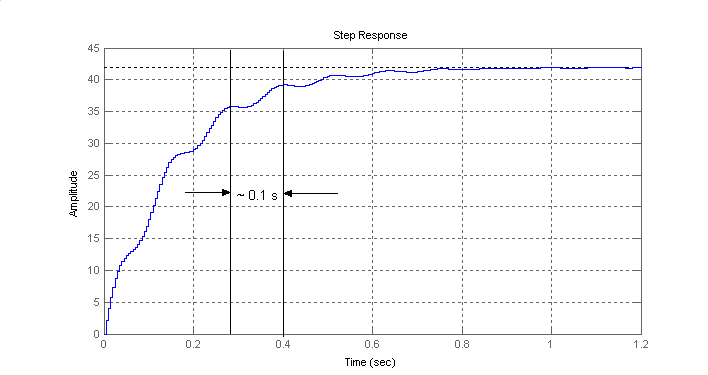
A szabályozandó objektum átmeneti függvényének viselkedése (7-45. ábra) alapján a szabályozó kör mintavételezési idejét a lengési periódusidő tized részére állítjuk be, azaz

legyen T0 = 0.01 s. Ezzel a mintavételezési idővel fogjuk üzemeltetni a megtervezendő szabályozási kört.

7.45. ábra - Az objektum átmeneti függvénye

7.4.2.3. Identifikáció MATLAB/System IdentificationToolbox segítségével

A kísérleti rendszer adatsorozatát (7-43. ábra) egy z=[y u] vektorban tároltuk el, majd felhasználva a Toolbox parancsát megkapjuk az identifikált rendszer OE modelljének B(z), A(z) polinomjait. Minkét polinom fokszáma három, a diszkrét holtidő pedig egy (d=1).

th=oe(z,[3 3 2])

Discrete-time IDPOLY model: y(t) = [B(q)/A(q)]u(t) + e(t)

B(q) = 2.009 q-2 - 3.575 q-3 + 1.897 q-4

A(q) = 1 - 2.603 q-1 + 2.489 q-2 - 0.8666 q-3

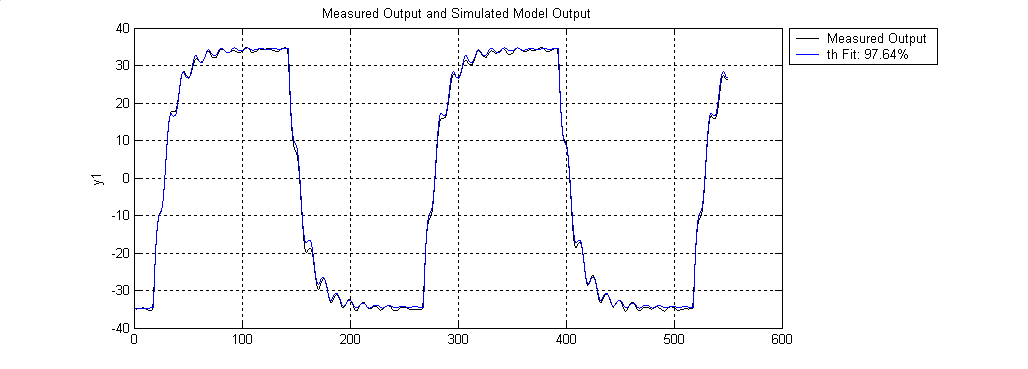
A compare(z,th) paranccsal az identifikáció minőségére kapunk választ (7-46. ábra)

7.46. ábra - A mérési adatok és az identifikált modell összehasonlítása időtartományban

7.4.3. Diszkrét algoritmus analitikus tervezése

A számítógépes folyamatirányítás területén, az ipari rendszerekben olyan folyamatokkal találkozunk, melynek tranziens viselkedését a zárt szabályozási körökben egyszerű átmenetekre kell megterveznünk. Az ilyen egyszerű viselkedésű zárt köröknek a folytonos átviteli függvénye - holtidőt feltételezve - legyen:

$G_{r} (s) = \frac{y (s)}{w (s)} = \frac{e^{- s T_{h}}}{T_{E} s + 1}$

( 7.35 )

ahol:TE – a zárt szabályozási kör időállandója, s

TH – holtidő, s

Szeretnénk megvalósítani egy olyan szabályozási kört, amelynek a viselkedése egy elsőrendű holtidős (vagy holtidő nélküli) rendszert képvisel.

Az analitikusan tervezett [6][7] algoritmus levezetéséhez induljunk ki a zárt digitális szabályozási kör összefüggéseiből. A zárt szabályozási kör diszkrét idejű átviteli függvénye:

$G_{r} (z) = \frac{G_{C} (z) G_{0} (z)}{1 + G_{C} (z) G_{0} (z)}$

( 7.36 )

ahol:G0(z)- a szabályozott objektum diszkrét modellje a tartószervvel együtt

Gc(z) - a tervezendő algoritmus diszkrét átviteli függvénye

Gr(z) - a zárt szabályozási kör viselkedése

A zárt rendszer szabályozási kör hatásvázlata látható a 7-47. ábra.

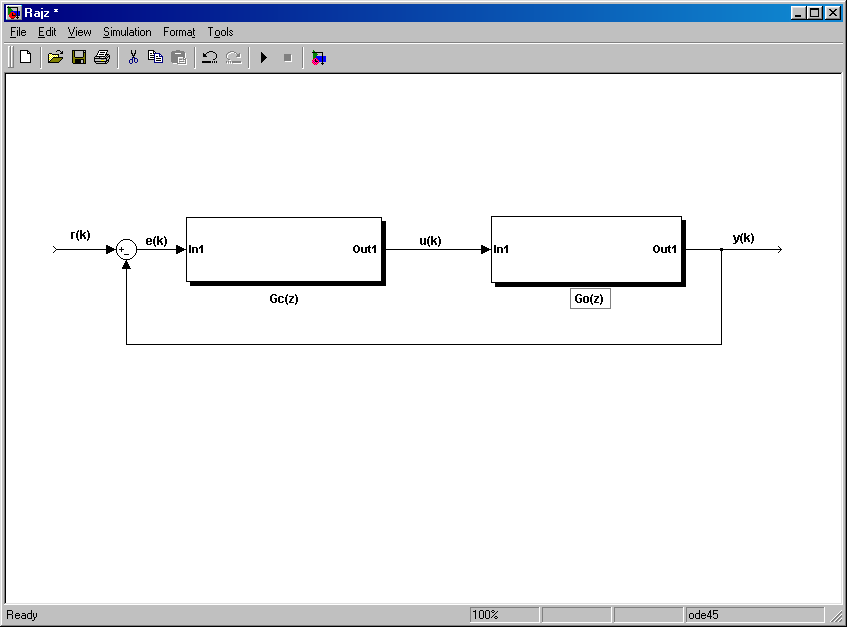
7.47. ábra - A zárt szabályozási kör hatásvázlata

Fejezzük ki a GC(z) impulzus-átviteli függvényt, és megkapjuk a digitális szabályozó algoritmus impulzus-átviteli függvényét [8]:

$G_{C} (z) = \frac{1}{G_{0} (z)} \frac{G_{r} (z)}{1 - G_{r} (z)}$

( 7.37 )

7.4.3.1. A zártköri viselkedés tervezése

A zártköri viselkedés megadásakor figyelembe kell venni a diszkrét holtidőt, mely esetünkben egy mintavételezési idő, így a zártköri folytonos modell 0,3 s-os időállandóval

$Grf (s) = \exp (- 0.01 * s) * \frac{1}{0.3 s + 1}$

( 7.38 )

A c2d(Grf,0.01) parancs segítségével T0 = 0.01s mintavételezési idő mellett megkapjuk a Grd(z) zártköri viselkedés impulzus-átviteli függvényét. Az ehhez tartozó átmeneti függvényt ábrázolja a 7-48. ábra.

$Grd (z) = z^{- 1} * \frac{0.03278}{z - 0.9672}$

( 7.39 )

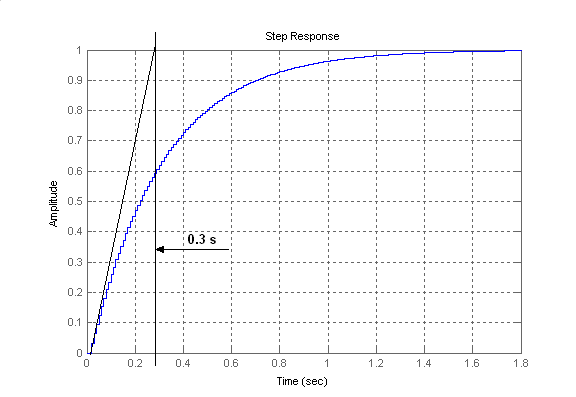
7.48. ábra - A zárt kör tervezett viselkedése

7.4.3.2. A szabályozási algoritmus

Az ismert összefüggést felhasználva a Gc=1/Go * (Grd/(1-Grd) MATLAB paranccsal megkapjuk a diszkrét algoritmus impulzus-átviteli függvényét

$G_{c} (z) = \frac{0.03278 z^{4} - 0.117 z^{3} + 0.1641 z^{2} - 0.1073 z + 0.02748}{2.009 z^{4} - 7.528 z^{3} + 10.87 z^{2} - 7.19 z + 1.835}$

és a 7-49. ábra mutatja a diszkrét algoritmus átmeneti függvényét.

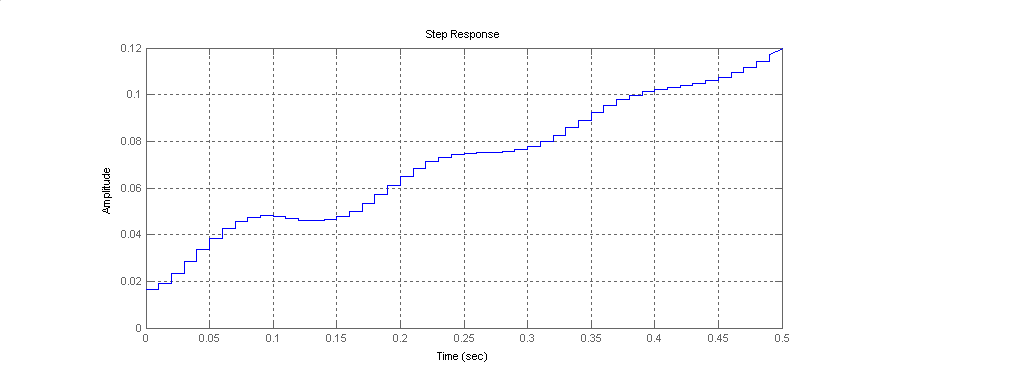
7.49. ábra - A diszkrét DAHLIN szabályozó algoritmus átmeneti függvénye

Abban az esetben, ha a zpk(Gc) paranccsal megvizsgáljuk a megtervezett algoritmus zérus és pólus helyeit:

$Gc (z) = \frac{0.016316 (z - 0.9672) (z - 0.9266) (z^{2} - 1.677 z + 0.9353)}{(z - 0.9672) (z - 1) (z^{2} - 1.779 z + 0.9443)}$

( 7.40 )

azt tapasztaljuk, hogy a megtervezett algoritmus tartalmaz egy diszkrét PI algoritmust és egy sorba kötött Notch-szűrőt, mely a keskenysávú lengéseket fogja kikompenzálni [7]

$\frac{z^{2} - 1.677 z + 0.9353}{z^{2} - 1.779 z + 0.9443}$

( 7.41 )

A nyitott köri Bode- (7-50. ábra) és a zérus-pólus (7-51. ábra) diagram is ezt reprezentálja.

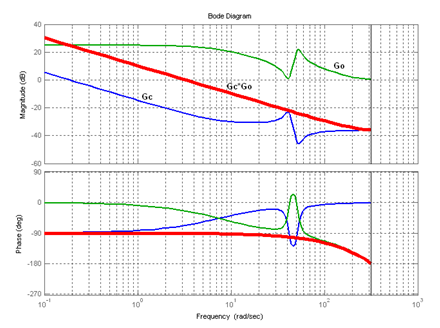
7.50. ábra - Az objektum (Go), a Dahlin algoritmus (Gc) és a nyitott kör (Gc*Go) Bode diagrammjai

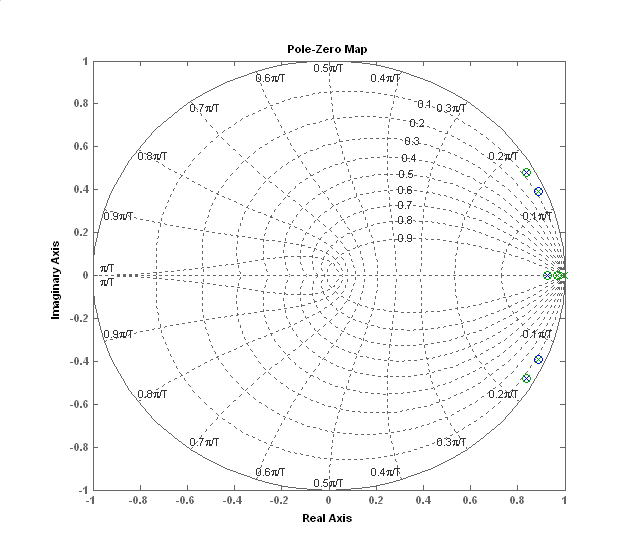
7.51. ábra - Az objektum és a diszkrét Dahlin algoritmus pólus-zérus helyei

7.4.4. A zártköri viselkedés vizsgálata

A zárt szabályozási kör SIMULINK diagramjában a szabályozási algoritmust felbontottuk egy diszkrét PI és egy diszkrét notch-szűrő/szabályozó részre.

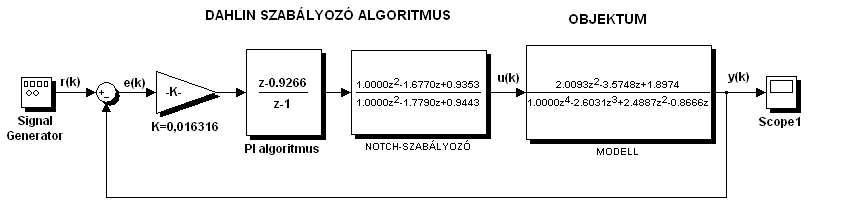
7.52. ábra - A zárt kör SIMULINK diagramja

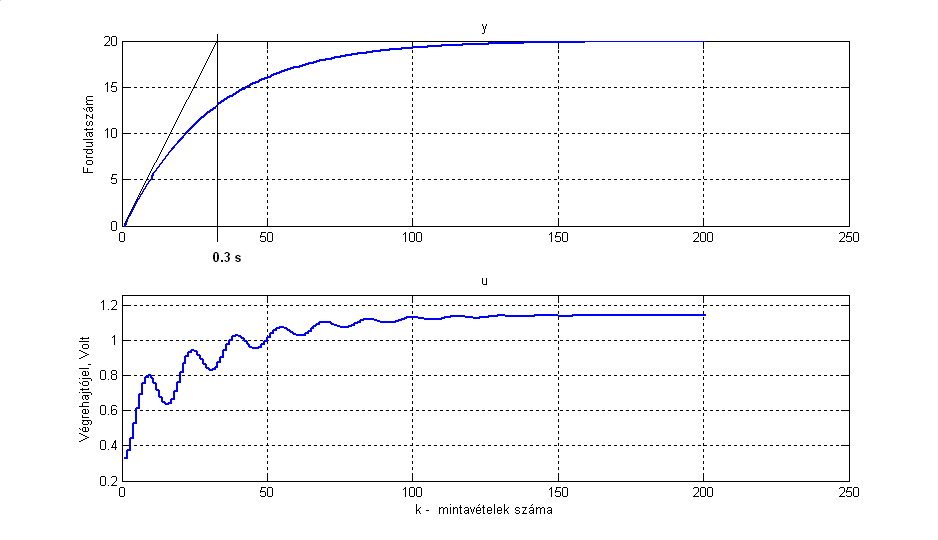
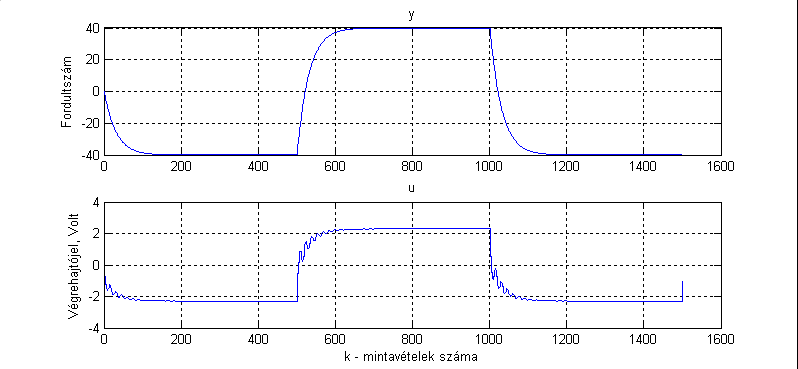
Alább (7-53. ábra) az y(k) ellenőrző jel és az u(k) végrehajtó jel viselkedését láthatjuk. A zárt kör lengésmentes, a zárt kör időállandója 0,3 s. A sztochasztikus zavarásnak kitett rendszer viselkedését a 7-54. ábra, változó alapjel esetében pedig a 7-55. ábra mutatja be a rendszer viselkedéseit.

7.53. ábra - Zártköri viselkedés ugrásfüggvény alapjel váltás esetén

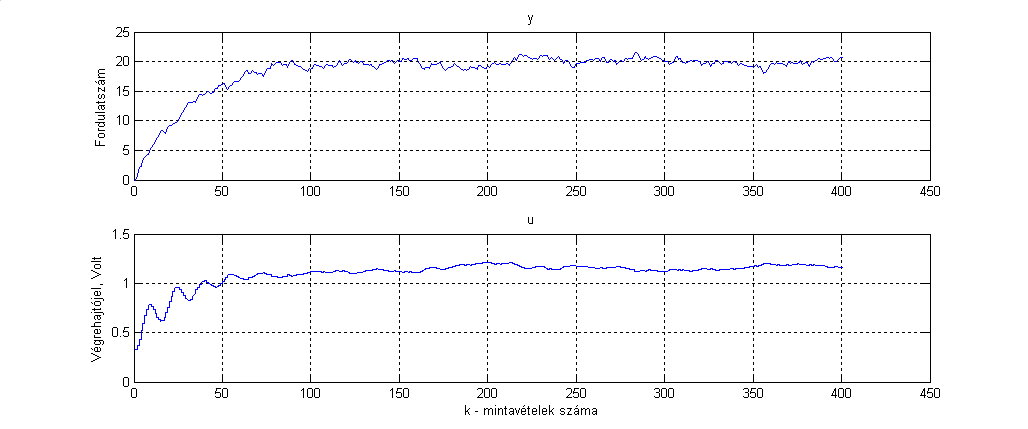
7.54. ábra - Zártköri viselkedés sztochasztikus zavarójel esetében

7.55. ábra - A zárt rendszer viselkedése változó alapjel esetén

Az esettanulmány bemutatja az identifikáció és szabályozó tervezés minden lépését, így felhasználható az irányításelmélet gyakorlati oktatásában, tervezési segédeszköze lehet a gyakorló mérnöki munkának.

Vissza		Előre
6. fejezet - Állapottér reprezentáció	Főoldal	8. fejezet - A robotirányítás mint pályakövetési feladat