8. fejezet - A robotirányítás mint pályakövetési feladat
- 8.1. A csuklónként önálló PID szabályozás
- 8.2. A számított nyomaték módszere
- 8.3. Robosztus irányító tervezése
- 8.4. A compliance-re alapozott robotirányítás
- 8.5. A mechanikai impedanciaszabályozás (impedance control)
- 8.6. A korrigált csuklóerő-szabályozás módszere
- 8.7. Az additív hibrid szabályozás módszere
- 8.8. Kidolgozott feladat a Hibrid (pozíció-erő) irányítással kapcsolatban
A mechanikai lapok összefoglalása után ebben a fejezetben már irányítástechnikai szemszögből fogjuk az ipari robotokat vizsgálni; mindazonáltal egyelőre még nem foglalkozunk legáltalánosabban az egyes robotirányítási feladatokkal, csupán azokkal, amelyeknél elegendő a robotkéz előírt pálya (trajektória) mentén történő mozgatása, és nem szükséges figyelembe venni a robotkéz és a környezet között fellépő erőket illetve forgatónyomatékokat. Az utóbbi típusú feladatok a 3. fejezet tárgyát képezik.
Amint azt az 1. fejezetben már láttuk, a robotmozgások dinamikája – talán a legtömörebb, még ésszerűnek mondható módon – az alábbi alakban írható fel:
|
, |
(8.1) |
ahol a csuklókoordináták vektora, az egész robot tehetetlenségi tenzora, az ekvivalens csuklónyomatékok vektora, a vektor pedig a korábban már részletezett nemlineáris tagokat foglalja magában, így a (8.1) egyenlet lényegében az egyenlet tömörített és általánosított alakja.
Maga az irányítástechnikai feladat lényege az, hogy a fenti egyenlet vektorának egyes elemei szabályozott módon, a , , vektorelemek mért (aktuális) és előírt értéki közötti eltérések függvényében változzanak.
A robotirányítási feladatok megvalósítására különböző módszerek terjedtek el, ezek közül az irodalomban a következő hárommal találkozhatunk a leggyakrabban:
-
csuklónként önálló PID szabályozás
-
a számított nyomatékok módszere
-
robusztus irányítóegység tervezése
8.1. A csuklónként önálló PID szabályozás
Az a) esetet az egyik irodalom szellemesen „struccpolitika”- módszernek nevezi, ez a módszer ugyanis a (8.1) egyenlettel megadott dinamikai összefüggést egyszerűen figyelmen kívül hagyja, vagyis nem számol azzal, hogy a valóságban az egyes kartagok dinamikai szempontból is kölcsönösen befolyásolják egymás mozgását. Ehelyett ez a módszer a lehető legegyszerűbb módon minden egyes csukló mozgását egy-egy önálló, közönséges analóg PID szabályozóval befolyásolja, amelyek ezáltal teljesen független rendszert alkotnak. Ez az egyszerű és kevéssé költséges módszer szinte minden olyan esetben eredményesen alkalmazható, amikor elegendő pozícióvezérlés, vagyis nem merül fel a pontos pályakövetés igénye. Ebben az esetben a szabályozó az egyes ekvivalens csuklónyomatékokat mint beavatkozó jeleket a következő alakú képlet szerint számítja:
|
|
(8.2) |
ahol a j-edik csuklókoordináta aktuális és előírt értékének (az előbbit egyszerűen -vel, az utóbbit -vel fogjuk jelölni) különbsége; a mennyiségek a PID szabályozóra jellemző (beállítható) pozitív konstansok, pedig az idő mint integrálási változó.
A továbbiakban egy viszonylag elvont és az olvasótól az eddigieknél nagyobb elmélyülést igénylő levezetéssel belátjuk, hogy az (8.2) szerinti csuklónként önálló szabályozás stabilis, azaz a rendszer (a robot) véges idő alatt eléri a munkaterén belül előírt tetszőleges pozíciót/orientációt (mint egyensúlyi helyzetet), és abból kimozdítva ugyancsak véges idő alatt ugyanoda visszaáll. A bizonyítás a Robotmechanizmusok című jegyzetben tárgyalt Lagrange-formalizmuson alapul.
A PID szabályozások elméletéből ismeretes, hogy az integrális szabályozás alkalmazásának elsődleges célja a különböző nemlineáris hatásokból (mechanikai rendszereknél pl. a Coulomb-súrlódásból) eredő véges beállási hiba kiküszöbölése. Első közelítésként tegyük fel, hogy a vizsgálandó robotnál a gravitációs és súrlódási effektusok az egyéb hatások mellett elhanyagolhatók; a fentiek értelmében ekkor elegendő csupán PD szabályozókat alkalmazni. Az (8.2) összefüggés integrális tagját elhagyva és az egyenlőségét a robot valamennyi szabadságfokára kiterjesztve a következő vektor-mátrix-}
|
|
(8.3) |
ahol és szimmetrikus, pozitív definit mátrixok, továbbá
|
|
(8.4) |
ahol a vektorok egyes elemei a (8.2) egyenletben szereplő illetve annak felírását követően definiált , és mennyiségek. (Mivel konstans elemekből álló vektor, fennáll még a összefüggés is. )
Bizonyításunk során abból indulunk ki, hogy súrlódás és gravitáció hiányában a egyenlet – könnyen belátható módon – az alábbi alakúra írható át:
|
, |
(8.5) |
ahol egy olyan -es mátrix, amellyel kapcsolatban teljesül, hogy a
|
|
(8.6) |
mátrix antiszimmetrikus. A bizonyításhoz Lyapunov ún. közvetlen stabilitásvizsgálati módszerét fogjuk felhasználni, amelynek lényegét az alábbiakban összefoglaljuk.
Lyapunov közvetlen módszere mind lineáris, mind nemlineáris módszerekre alkalmazható, és elégséges feltételt ad a rendszer stabilitására vonatkozóan. Tegyük fel, hogy az adott nemlineáris rendszer időbeni viselkedését -edrendű nemlineáris differenciálegyenlet írja le. Minden -edrendű differenciálegyenlet átírható az ún. Cauchy-féle alakba, ami azt jelenti, hogy az eredetileg -edrendű differenciálegyenletből álló differenciálegyenlet rendszert. Ez utóbbit vektoros alakban a következőképpen írhatjuk fel:
|
|
(8.7) |
ahol a rendszer jellemző állapotváltozójából és annak idő szerinti deriváltjaiból képzett dimenziós vektor. (Ld. még a matematikában tanultakat!)
Lyapunov szerint a rendszer stabilitásának elégséges feltétele az, hogy létezzék egy olyan skalár vektor, függvény, (az ún. Lyapunov-függvény), mely az alábbi tulajdonságokkal rendelkezik:
|
|
-
a függvény változója a rendszer (8.7) egyenlete szerint, Caunchy-féle alakban felírt differenciálegyenletének állapotvektora
-
pozitív vagy negatív definit a teljes állapottérben
-
idő szerint folytonosan deriválható a teljes állapottérben, és -re teljesül, hogy -szel ellentétes értelemben legalábbis szemidefinit
Ha mindezeken túlmenően valamilyen értelemben határozottan difinit (tehát az egész állapottérre nézve , akkor a rendszer aszimptotikusan stabilis.
A módszer alkalmazásának nehézsége éppen a megfelelő Lyapunov-függvény megtalálásában rejlik, ami általában intuíciót igényel. A Lyapunov-függvény többnyire a rendszer valamiféle általánosított energiafüggvényével azonosítható.
Visszatérve konkrét példánkhoz, a csuklóként önálló PD szabályozáshoz, éljünk a következő választással:
|
|
(8.8) |
Az (8.8) egyenlet második tagja a korábbiak értelmében a robot mint mechanikai rendszer teljes kinetikus energiája, az első tag pedig, mint egy egyensúlyi helyzetéből kimozdított lineáris rugó által tárolt rugalmas energia. (Gondoljunk arra, hogy egy lineáris rugó felfogható úgy is, mint arányos típusú mechanikai szabályozó!)
Az (8.8) egyenlettel definiált Lyapunov-függvény tehát tulajdonképpen nem más, mint a rendszer összenergiája.
Mivel és szimmetrikus, pozitív definit mátrixok, a
|
|
(8.9) |
egyensúlyi helyzet kivételével mindig teljesül a reláció, tehát a választott függvény pozitív definit.
Képezzük ezek után idő szerinti deriváltját! A tömörség kedvéért mellőzük a levezetés minden mozzanatának részletes magyarázatát, amiket az olvasó némi gondolkodás után maga is megtalálhat. Felírhatjuk tehát, hogy
|
|
(8.10) |
Ha a szabályozási törvényt (jobb kifejezés híján ezt fogjuk használni mint a <control law> angol kifejezés tükörfordítását) a (8.3) szerint fogalmazzuk meg, akkor a (8.10) levezetés folytatásaként a következőt írhatjuk:
|
|
(8.11) |
mivel a mátrixot úgy választottuk meg, hogy aszimmetrikus legyen.
Az (8.11) szerinti reláció teljesülése annyit jelent, hogy az (8.8) összefüggéssel definiált függvény a rendszer Lyapunov-függvénye, így a rendszer valóban stabilis a egyensúlyi helyzetben. Már csak azt kell belátnunk, hogy a rendszer nem „ragadhat be” egy helyzetbe annak ellenére, hogy integrális szabályozást nem alkalmaztunk. Ehhez azt szükséges bizonyítanunk, hogy a (azaz a ) eset csak a állapotban állhat fenn.
Képezzük a vektor második deriváltját!
|
|
(8.12) |
ami valóban minden állapotban zérustól különböző, tehát a rendszer mindig a állapot felé konvergál, vagyis asszimptotikusan stabilis.
Itt jegyezzük meg, hogy a fenti eredmény különlegesen „robosztus”, vagyis érzéketlen a robot tömegviszonyainak bizonytalanságaival szemben, minthogy a tömegre vonatkozóan semmiféle becslést nem tartalmaz.
Az (8.3) egyenlet (szabályozási törvény) speciális esete a lokális (csuklónként önálló) szabályozás:
|
, |
(8.13) |
amely összefüggés tulajdonképpen csak imitálja egy rugókból álló rendszer viselkedésének leírását.
Ha a valóságos viszonyokat jobban megközelítő modellt választunk, akkor az eddig elhanyagolt nemlineáris – gravitációs és súrlódási – effektusokat is figyelembe kell vennünk. Ekkor a rendszer dinamikai viselkedését (8.5) helyett az alábbi alakú egyenlet írja le:
|
|
(8.14) |
ahol vektor egyelőre még csak a gravitációs effektust veszi figyelembe. Ez esetben a következő alakú szabályozási törvényt kell választanunk:
|
, |
(8.15) |
Sajnálatos módon azonban ez a szabályozási törvény sem tekinthető igazán jónak, mivel a vektor egzaktul általában nem adható meg a tömegviszonyok nem kellően pontos (bizonytalan) ismerete következtében. További problémát okoz a Coulomb-súrlódás, aminek hatása valóban csak úgy küszöbölhető ki, ha eddigi rendszerünket integrális típusú szabályozó taggal is kiegészítjük (a viszkózus súrlódás hatását a puszta PD szabályozás is kiküszöböli).
Végül is tehát a lokális szabályozás minden lényeges határt figyelembe vevő, általános a lakja a következő lesz.
|
, |
(8.16) |
ahol a gravitációs hatásokat figyelembe vevő tag becsült értéke, a többi jelölés pedig a korábbiakkal megegyezik.
8.2. A számított nyomaték módszere
Ennek a módszernek az alapötlete az, hogy egy, az (8.1) egyenlethez hasonló struktúrájú szabályozási törvényt definiálunk:
|
, |
(8.17) |
úgyhogy a probléma (8.17) –ot (8.1) -be helyettesítve – ideális esetben a
|
, |
(8.18) |
differenciálegyenlet megoldására redukálódna ( pozitív definit mátrix, ennél fogva invertálható).
Ha ismét lokális szabályozásra törekszünk, akkor az egyes beavatkozó jelek a következőképpen számíthatók:
|
, |
(8.19) |
ahol a -edik csukló előírt gyorsulása.
E módszer alkalmazásának legfőbb korlátja, hogy a (8.17) egyenletben szereplő és mennyiségek általában nem egzaktul ismert, hanem csupán becsülhető mennyiségek, a valóságban mindig fennálló paraméterbizonytalanságok miatt. Ha az említett mennyiségek becsült értékeit -csal illetve -csal jelöljük, akkor (8.17) helyett csupán a következő összefüggést írhatjuk fel:
|
, |
(8.20) |
amit megint csak az eredeti (8.1) dinamikai egyenletbe helyettesítve a következő differenciálegyenletet nyerjük:
|
, |
(8.21) |
Az (8.21) összefüggésből láthatjuk, hogy a probléma valójában távolról sem olyan egyszerű, mint amilyennek azt az ideális esetre vonatkozó (8.18) kifejezés sejttette, ennél fogva nem is kezelhető megfelelően a megszokott lineáris szabályozástechnikai módszerekkel. Lényeges szempont a rendszer egészének robosztusságára való törekvés, ami annyit jelent, hogy minden lehetséges módon igyekszünk a rendszer modellezetlen effektusokkal szembeni érzékenységét a minimálisra csökkenti (annak érdekében, hogy a bizonytalanságok minél kisebbek legyenek, más szóval a becsült értékek minél kevésbé térjenek el a ténylegesektől).
Ezekre a kérdésekre a robusztus szabályozók tervezése kapcsán a későbbiekben még visszatérünk, előbb azonban megismerkedünk egy korszerű elmélet (az ún. „csúszásfelületek elmélete”, <theory of sliding surfaces>) alapjaival, amely robotirányítási célokra is eredményesen alkalmazható.
8.3. Robosztus irányító tervezése
Szerte a világon sok erőfeszítés történt és történik manapság is annak érdekében, hogy hatékony real-time eljárásokat fejlesszenek ki robotirányítási célokra. Amint azt a Robotmechanizmusok című jegyzetben említettük, az eljárások hatékonysága jelentősen növelhető, ha azonban rekurzív algoritmusokat alkalmazunk, pl. egy előírt mozgás megvalósításához szükséges ekvivalens csuklónyomatékok kiszámítására. Azonban az inverz dinamikai feladat eképpen történő megoldása még a nemlineáris hatások számításba vételekor is abból a feltételezésből indul ki, hogy a vizsgálat alapjául szolgáló modell minden részletében egzaktul ismert.
Ezzel szemben jól tudjuk, hogy vannak bizonyos jelenségek, amelyek hatása „a priori” nem jósolható meg pontosan, mégpedig előfordulnak különféle zavarok (mint pl. a Coulomb- és a viszkózus súrlódás), továbbá modellezési hibák, így pl. a geometriai és tömegviszonyokban fellépő bizonytalanságok (mondjuk, a terhelés tömege és a robot kézben való pontos elhelyezkedése stb.), figyelembe nem vett nagyfrekvenciás rezonanciajelenségek; elhanyagolt, de a valóságban mérhető hatású késleltetéssel, és így tovább. Ezért célszerű a robotból és az irányítóegységből álló teljes rendszert minél robosztusabban tervezni, ti. hogy az minél kevésbé legyen érzékeny a fentiekben csak kiragadott példaként felsorolt és azokhoz hasonló, előre ki nem számítható hatású, de a valóságban több-kevesebb valószínűséggel fellépő jelenségekre.
A Robotmechanizmusok című jegyzetben az inverz kinematikai feladat megoldhatóságának vizsgálatakor már utaltunk rá, hogy sokszor célszerű egy hatszabadságfokú robot első három szabadságfokát „kar”-nak, második három szabadságfokát pedig „kéz”-nek tekinteni, melyek közül az előbbi a pozícionálást, az utóbbi a kívánt orientáció beállítását végzi el. Dinamikai téren is lehetséges, sőt szokásos az ilyesfajta szétcsatolás, „kar-kéz-szemlélet” alkalmazása, ami általában az egész rendszert robosztusabbá teszi. Ilyen esetekben a kar és a kéz dinamikai szempontból is egymástól viszonylag független „életet él”, a ténylegesen fennálló egymásra hatásukat pedig egyszerűen egymás kölcsönös „zavarásaként” fogják fel. Ez a szemlélet tehát jelentősen leegyszerűsíti az irányítási feladatot mint dinamikai problémát is.
8.4. A compliance-re alapozott robotirányítás
A mai ipari robotok jelentős részét „pick and place”-típusú feladatokra, ponthegesztésre, festékszórásra stb. használják. Ezek a feladatok minden további nélkül megvalósíthatók az eddigiekben tárgyalt pont- illetve pályavezérléssel (az utóbbiakra jó példa a plazmahegesztés vagy lézersugaras vágás illetve megmunkálás). Ezzel szemben viszonylag kevés ipari robot képes olyan, látszólag egyszerű feladatok elvégzésére, mint pl. egy csavar behajtása vagy egy forgattyús mechanizmus hajtása.
Többször találkozunk tehát olyan feladattal, amikor a robot helyes, célirányos mozgásának kritériumát a robotkéz által valamilyen adott irányban kifejtett erővel illetve nyomatékkal egyszerűen (esetleg csak ilyen módon) fejezhetjük ki. A fent említetteken túlmenően ilyen feladat lehet például két munkadarab illesztése, valamilyen felület vagy él követése, sík felület csiszolása, öntvények sorjátlanítása stb. Ha a pozíció- vagy pályavezérelt robot a környezetében lévő tárgyakkal érintkezésbe kerül, akkor általában mindig számolhatunk reakcióidők keletkezésével a szabályozási kör hibája, a robot szerkezetének deformációja, a pozícióadatok pontatlan megadása és egyéb geometriai pontatlanságok miatt. Ezeket a hatásokat azonban a robotkonstrukció rugalmassága általában mindig képes kompenzálni. A robotnak ezt a tulajdonságát strukturális compliance-nek (engedékenységnek) nevezzük. A fent felsorolt feladatok eredményes megvalósítása érdekében azonban meg kell teremtenünk annak a lehetőségét, hogy a compliance-t programozás útján befolyásolni tudjuk.
Ezért a továbbiakban compliance alatt mindig a robot és környezete között létrejövő kölcsönhatásra a robot pozíció- illetve pályavezérlésében bekövetkező programozható (vagy legalábbis hardver eszközökkel előre megtervezhetően lejátszódó) változást fogjuk érteni.
A compliance-t a robotprogram nyelvi eszközeivel írjuk elő a robot részére (robotok programozásával a jelen tárgyon belül nem foglalkozunk). Ez utóbbiakkal adjuk meg az ún. compliance feltételeket. A compliance fogalmi meghatározásakor láttuk, hogy viszonylag általános módszerről van szó. A compliance gyakorlati megvalósítására több különböző is elterjedt, ezek közül a legfontosabbak alapvonásait a következőkben ismertetni fogjuk. Valamennyi módszer közös vonása, hogy a feladatot egy alkalmasan választott ún. compliance középpont (<compliance center>). A compliance középpont definíciója: az ebben a pontban ható erő csak vele megegyező irányú lineáris elmozdulást (transzlációt), míg az e pontban ható forgatónyomaték csak vele megegyező értelmű szögelfordulást (rotációt) okoz. Az esetek többségében a compliance középpont egybeesik a compliance koordinátarendszer origójával.
A compliance tervezésének fő lépései:
-
a compliance koordinátarendszer kiválasztása
-
a szabadságfokok felosztása pozíció- (pálya) illetőleg erőszabályozás szerint
-
a pozíció- (pálya) és erőszabályozások céljának és mozgás közbeni stratégiájának meghatározása.
A compliance koordinátarendszer elhelyezkedése és a compliance feltételek természetszerűleg feladatról feladatra változnak. A compliance feltételek között megkülönböztetünk ún. természetes és mesterséges kényszereket: az előbbiek a geometriai és kinematikai viszonyok által meghatározottak, míg az utóbbiakat maga a robotalkalmazó írja elő a feladat célirányos megvalósítása érdekében.
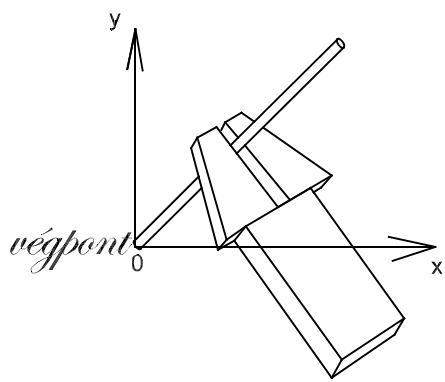
Az eddigiek könnyebb megértésére nézzük meg egy tipikusnak ugyan nem, ám annál szemléletesebbnek tekinthető konkrét példát. Legyen a robot feladata az, hogy a táblára krétával fölírja a „compliance” szót (lásd az 8-1. ábra). Ha a feladat kezdetén a kréta még nincs a robotmegfogóban, akkor a kréta megfogása kapcsán máris erőszabályozási problémával találjuk szemben magunkat: a robotkéz által a krétára kifejtett erő ugyanis sem túl kicsi nem lehet (ekkor a robot elejtheti a krétát), sem pedig túl nagy (ti. akkor összetörhet a kréta). Tegyük fel ezek után, hogy a megfogóerő megfelelő, és a továbbiakban csak a kréta és a tábla közötti kapcsolatot vizsgáljuk.
Mindaddig, amíg a kréta el nem éri a táblát, tehát a tábla megközelítésének során a kréta és a tábla között még nem lép fel kölcsönhatás, így a mozgásnak ez a szakasza tiszta háromszabadságfokú pályavezérléssel (helyesebben szabályozással) megoldható. (A kréta orientációját állandónak tekintjük). Mihelyt azonban a kréta eléri a tábla síkját, megváltozik a helyzet. Célszerű mindenekelőtt felvenni egy compliance koordinátarendszert úgy, ahogy az az 8-1. ábrán látható. A tábla megérintésének pillanatában elveszítünk egy pozíciószabályozási szabadságfokot (nevezetesen a tábla síkjában az arra merőleges természetes kényszer), ezzel szemben lehetővé, sőt szükségessé válik a tengely menti erőszabályozás.
Ha a táblát első közelítésben súrlódásmentesnek tekintjük, akkor az és irányú erők – ugyancsak természetes kényszerként – zérusnak adódnak: és . Az orientáció kötöttsége miatt természetes kényszerként adódik az is, hogy valamennyi szabadságfok mentén zérus forgatónyomaték lép fel.
A legfontosabb mesterséges kényszer az írás megkezdésének pillanatától az és irányú pozíció lesz, hiszen ezekkel adható meg a táblára felírandó szöveg, jelen esetben a „végpont” szó. Ugyancsak mesterséges kényszerként, további három szabadságfokot igénybe véve megadhatjuk a krétának a táblához viszonyított orientációját is, bár ennek az adott esetben nincs túl nagy jelentősége. Az eddigieket összefoglalva megállapíthatjuk, hogy mind a természetes, mind a mesterséges kényszerekből – külön-külön – annyi van, amennyi a szabadságfokok száma (általában hat).
|
Mesterséges kényszerek |
Természetes kényszerek ideális esetben |
Természetes kényszerek valóságos esetben |
|
|
|
|
|
|
|
|
|
|
|
|
Megjegyezzük, hogy a természetes és mesterséges kényszerek időnként összefüggenek egymással (ha pl. a tábla és a kréta között a valóságban jelenlévő Coulomb-súrlódást figyelembe vesszük, akkor a irányú erő mint mesterséges kényszer meghatározza az és irányú erőket) A tábla egyenetlensége irányú mozgást is eredményezhet.
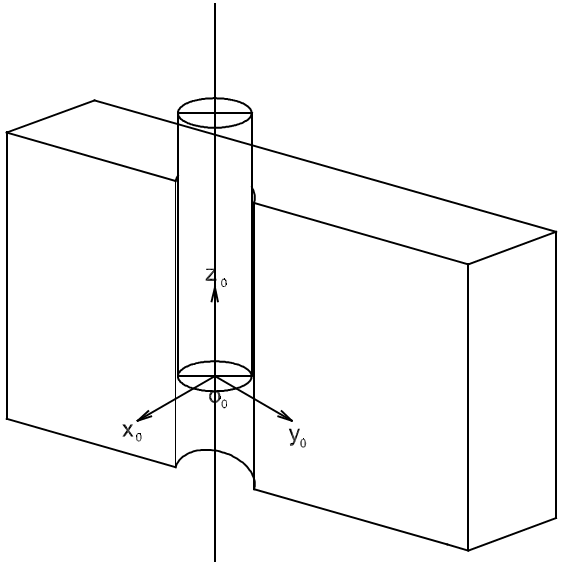
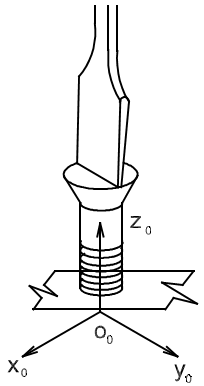
További – két egyszerűnek mondható, mégis compliance-re alapozott irányítást igénylő – feladat a csapillesztés és a csavarbehajtás. Az előbbi az egyszerűbb, ekkor joggal hnyagolhatjuk el a súrlódást. Az utóbbi esetén ideális (súrlódásmentes) esetben csak a csavarhúzó elfordulását írhatjuk elő. De ha nincs súrlódás, akkor nincs csavarkötés. Ha egy csavar behajtásakor a csavarhúzót állandó erővel nyomjuk és állandó nyomatékot fejtünk ki. A két feladathoz legcélszerűbb módon hozzárendelhető compliance koordinátarendszerek a 8-2. ábraról és a 8-3. ábraról leolvashatók, míg a compliance-feltételeket (a természetes és a mesterséges kényszereket) a 8.2. táblázat és a 8.3 táblázat tartalmazza.
|
Természetes kényszerek surlódásmentes eset |
Mesterséges kényszerek surlódásmentes eset |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Természetes kényszerek surlódásmentes eset |
Mesterséges kényszerek surlódásmentes eset |
Természetes kényszerek surlódás jelenlétével |
Mesterséges kényszerek surlódás jelenlétével |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ahol: p - a csavar menet emelkedése
8.5. A mechanikai impedanciaszabályozás (impedance control)
Ez a módszer a compliance-re alapozott irányítások egyik válfaja. Az „impedancia” kifejezés alatt itt most természetesen nem az elektrotechnikából ismert fogalmat kell érteni, hanem egyfajta rugóállandó jellegű merevségi tényezőt, amely lineáris kapcsolatot teremt erő és elmozdulás, illetőleg forgatónyomaték és szögelfordulás között.
Az impedancia szabályozás lényege – viszonylagos egyszerűsége is éppen ebben rejlik -, hogy egy-egy szabadságfok mentén nem közvetlen pozíció-/orientáció vagy erő-/nyomatékszabályozást valósítunk meg, hanem csupán ennek kapcsolatát írjuk elő.
A passzív impedancia szabályozás egyik lehetséges módja az ún. RCC eszköz alkalmazása (a <remote center compliance> kifejezésnek nincs jó magyar megfelelője, ezért használjuk – jobb híján – az „RCC eszköz” megnevezést). Ez az eszköz nem más, mint egy, rugókból és csillapítókból felépített és a robotkézben elhelyezett mechanikai elem, mely bizonyos szabadságfokok irányában viszkózusan csillapított rugóként viselkedik. A compliance megtervezése ez esetben az egyes rugóállandók és csillapítási tényezők megfelelő értékűre történő megválasztására korlátozódik, ennél fogva egy-egy ilyen RCC eszköz általában csak egy adott célfeladat megoldására használható.
Az egyes izületekre vonatkozóan felírhatunk egy merevségi egyenletet
|
(i=1…n) |
(8.22) |
A bevezetjük a robot merevségi mátrixát, amely diagonális és elemeket tartalmazza.
|
|
( 8.23 ) |
Első közelítésben megállapítothatjuk, hogy csak diagonális elemeket tartalmaz. Egy adott RCC eszköz megtervezése – kissé elvontan – úgyis megfogalmazható, hogy ha az -edik szabadságfok mentén pozíció- (pálya) szabályozást kell megvalósítani, akkor a megfelelő mátrixelemet igen nagy (elméletileg végtelen nagy) értékűnek kell választani, míg pl. az erőszabályozást igénylő -edik szabadságfokhoz rendelhető mátrixelemet a kívánt értékűre kell beállítani.
A most ismertetett módszer általánosítása illetőleg kiterjesztése az ún. aktív impedancia szabályozás, amely már programozás útján, tehát szoftver eszközökkel teszi lehetővé a compliance-viszonyok beállítását. Tekintsük ugyanis a következő szabályozási törvényt:
|
, |
(8.24) |
ahol az ekvivalens csuklónyomatékok vektora, a gravitációs hatásokat kifejező vektor becsült értéke, a robot Jakobi-mátrixa,
|
, |
(8.25) |
végpontok az előírt pozíciótól/orientációtól való eltérésének vektora, a és (arányos illetve differenciális hatást reprezentáló) mátrixok elemei pedig a megfelelő szoftver eszközökkel a kívánt értékűre beállíthatók, így „aktív”, programozható compliance-t valósíthatunk meg.
8.6. A korrigált csuklóerő-szabályozás módszere
A comlpiance-feladatokban – mint ahogy azt az előzőekben láttuk – a cél a robotkar célirányos mozgatása úgy, hogy néhány kitüntetett irányban a robotra ható reakcióerők és –nyomatékok a programozott érték szerint változzanak. Ez a feladat megköveteli, hogy a robotkéz állandó kontaktusban legyen a környezettel, a robot mozgása és erőkifejtési programja (azaz a compliance-feltételek) között ne legyen ellentmondás, a kitűzött programok a robotkonstrukcióval végrehajthatók legyenek (pl. ne legyen az aktuális robotkonfiguráció szinguláris állapotban vagy mozgási tartományának határán stb.). A módszer lényege abban áll, hogy a kívánt szintre szabályozzuk azokat a csuklókat, amelyek a legnagyobb mértékben járulnak hozzá a compliance-feltételek által megadott irányokba eső reakcióerők illetve nyomatékok keletkezéséhez. Ezalatt a robotkézhez rendelt referencia-koordinátarendszer megváltoztatja helyzetét, ezért a compliance-feltételek által ki nem jelölt irányokban is változás következik be, amit a következő szabályozási ciklusban pozíciószabályozással korrigálunk úgy, hogy az első szabályozási ciklus alatt beállított compliance-erő-(nyomaték-) értékek változatlanok maradjanak. A fenti szabályozási elv blokkdiagramja a 8-4. ábra látható.
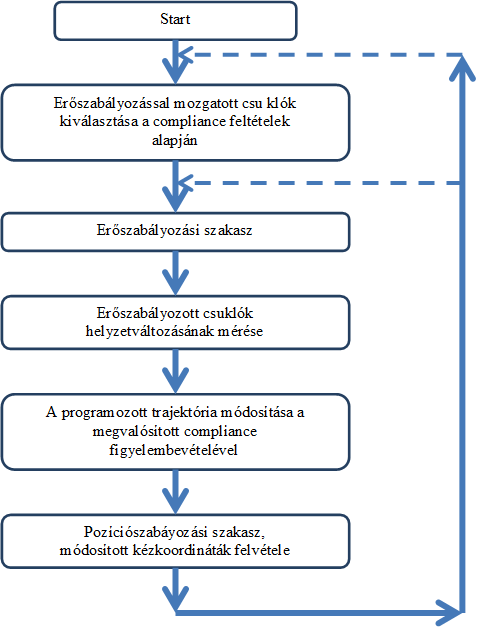
A módszer lényegéből következik, hogy nem általánosítható, így alkalmazási területe korlátozott. A feladat kitűzésekor az alábbi két megkötést szokás tenni:
-
Az erő- és nyomaték-compliance irányát a referencia-koordinátarendszer egyik fő tengelyével megegyezőnek választjuk. Ez megkönnyíti a programozó munkáját, de a szükséges számítások is jelentősen leegyszerűsödnek.
-
A comliance-feltételek számát kettőben vagy háromban maximáljuk. (A választott referncia-koordinátarendszer tetszőleges orientációjú lehet, és rögzíthető akár a robot törzséhez, akár a manipulált tárgyhoz is).
8.7. Az additív hibrid szabályozás módszere
A címben említett szabályozási módszer algoritmusának lényege, hogy a pozíció- és erőszabályozásban mindegyik csukló részt vesz. Az algoritmus működésének alapelve az, hogy a compliance-koordinátarendszer egyes koordinátatengelyei mentén mért hibajeleket egy ún. szelekciós mátrix alapján vagy a pozíciószabályozási, vagy erőszabályozási körben használjuk fel. A hibajelek csuklókoordinátákra transzformált és a megfelelő erősítési tényezővel szorzott komponenseinek összege adja meg az egyes csuklókban elhelyezett aktuátorok beavatkozó jelét. Általában a robotnak a compliance-koordinátarendszerben értelmezett valamely állapotát megkaphatjuk úgy is, mint
|
, |
(8.26) |
ahol az -edik csuklókoordináta, az inverz kinematika valamilyen függvénye, pedig a compliance-koordinátarendszerben értelmezett -edik koordináta.
Az (8.26) összefüggésből látható, hogy egy-egy csukló helyzetének meghatározásához általában mindegyik Descartes-koordinátára szükség van. Az additív hibrid szabályozásban is – hasonlóan a (8.26) szerinti inverz kinematikai problémához – mindegyik koordinátát felhasználjuk, de a compliance-koordinátarendszer kijelölése szerint annak egyes koordinátái mentén vagy az erő-, vagy a pozíciókoordináták hibáit használjuk fel az egyes ekvivalens csuklónyomatékok kiszámításához, éspedig a következő összefüggés szerint:
|
, |
(8.27) |
ahol az -edik ekvivalens csuklónyomaték, a C koordinátarendszer -edik koordinátája mentén mért erőhiba, a C koordinátarendszer -edik koordinátája mentén mért pozícióhiba; illetve az erő- illetve a pozíció-visszacsatolási mátrix (-edik eleme; pedig az ún. compliance szelekciós vektor -edik eleme. Ez utóbbi értéke 0 illetve 1 lehet, attól függően, hogy a koordinátarendszer -edik koordinátája mentén pozíció- vagy erőszabályozást alkalmazunk.
|
, |
(8.28) |
akkor
|
, |
(8.29) |
Az szelekciós vektor elemeiből képezhetünk egy – csak diagonális elemeket tartalmazó - szelekciós mátrixot:
|
, |
(8.30) |
A 8-5. ábrán látható a hibrid szabályozó blokk diagramja. Itt láthatók a szükséges visszacsatolások: a felső részen látható a pozíció-visszacsatolás, az ábra alsó fele pedig az erő-visszacsatolást mutatja.
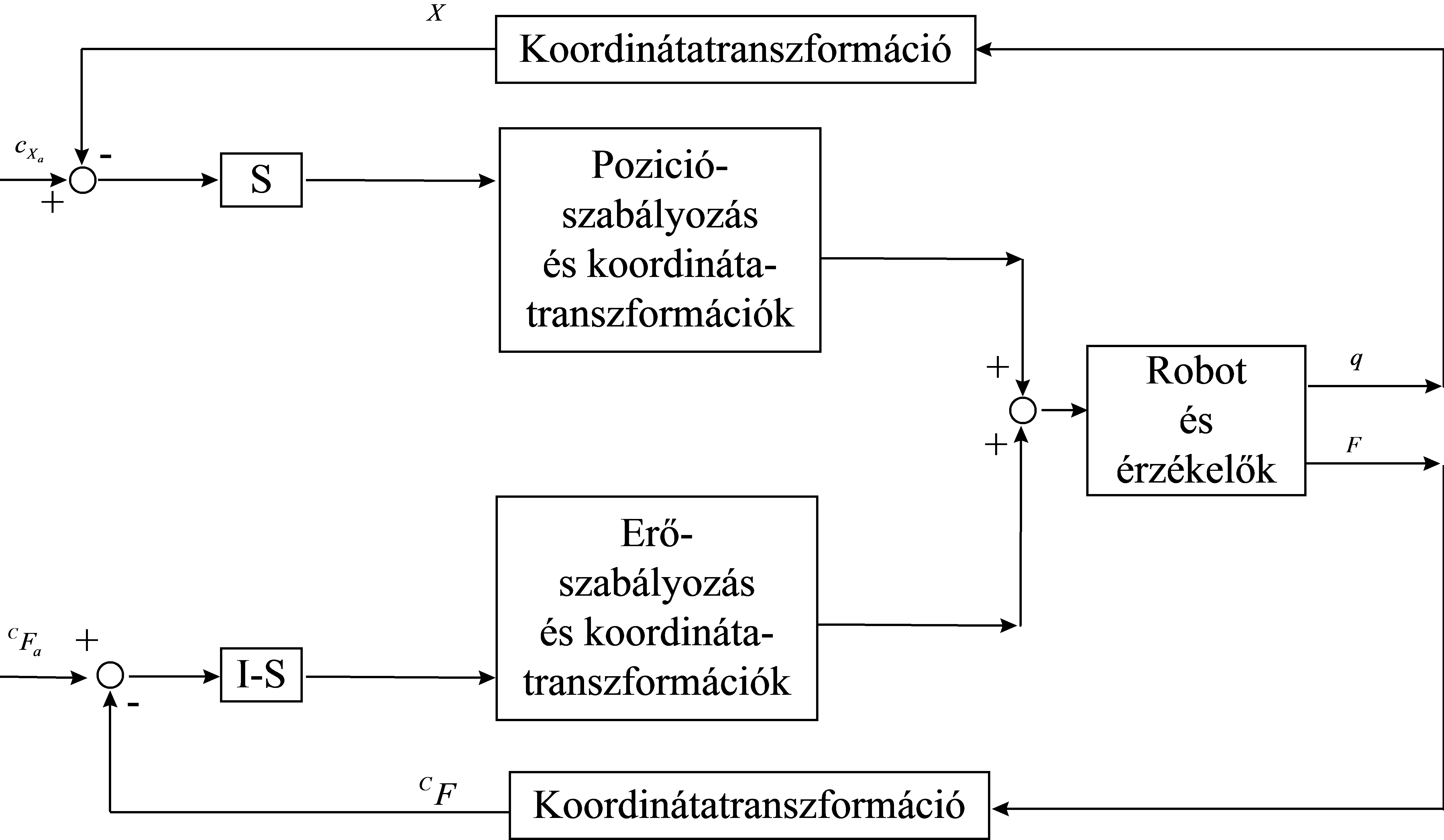
A 8-6. ábra bővebben tünteti fel a hibrid szabályozó működési elvét, ahol már fel vannak tüntetve a PID szabályozók is, valamint a transzformációkhoz használt mátrixok.
|
|
(8.31) |
(10)
|
|
(8.32) |
A robotkarba bevezetett jel a következő összetevőkből adódik:
|
|
(8.33) |
-
A pozíció- szabályozásból adódó rész:
-
A erő-szabályozásból adódó rész:
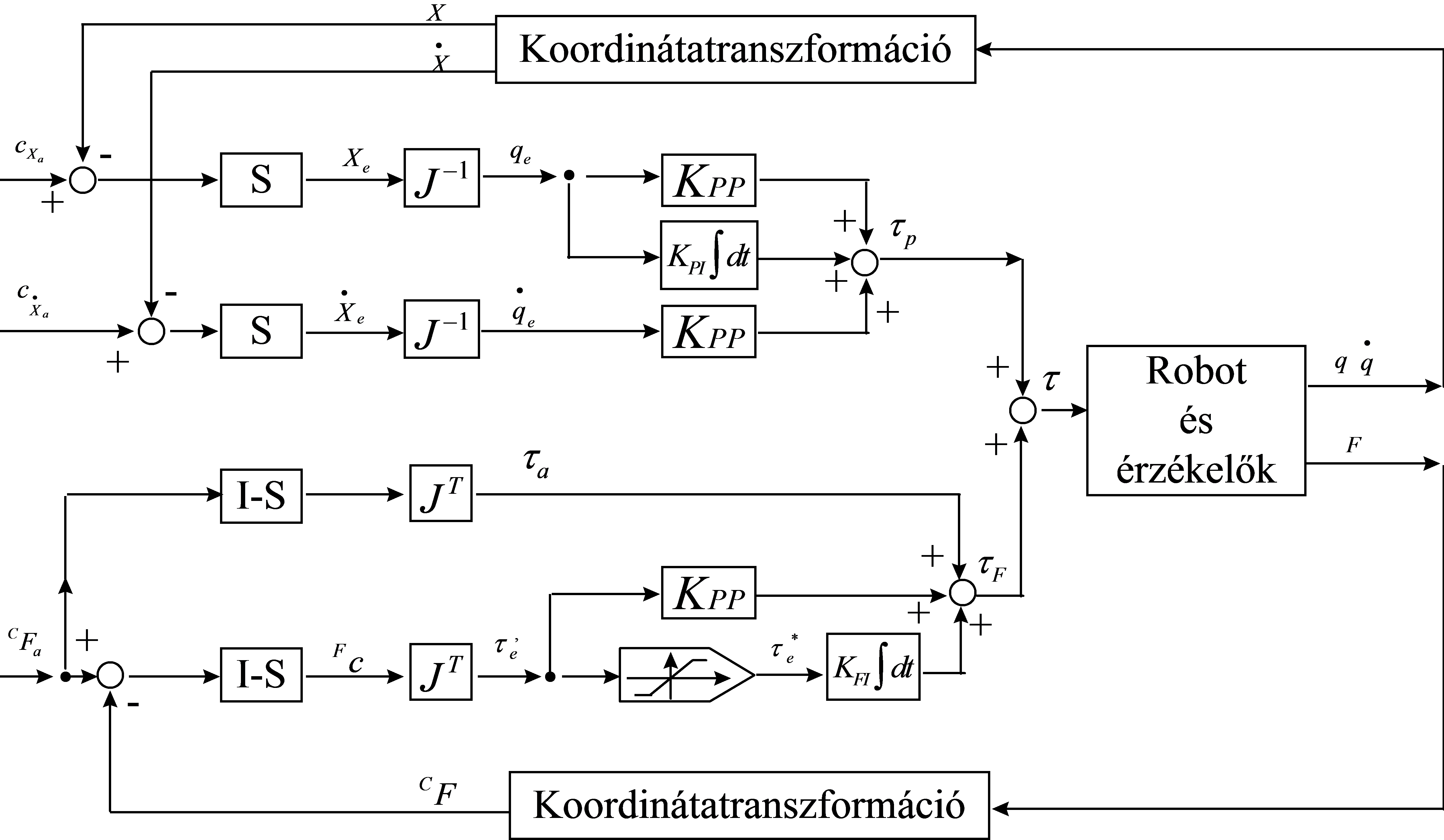
8.8. Kidolgozott feladat a Hibrid (pozíció-erő) irányítással kapcsolatban
8 . 4 feladat egy robotkar modellezése
Legyen a 8-7. ábrán feltüntetett robotkar, amely q2 hosszú és q1 szöggel fordulhat el az engedékenységi keretben. Ez a robotkar egy bizonyos tömegű test fenntartását biztosítja függőleges (Cx) irányban. A robotkarra ható erő fx, amely w1 illetve w2 , a rugók által kifejtett erőkből tevődik össze.
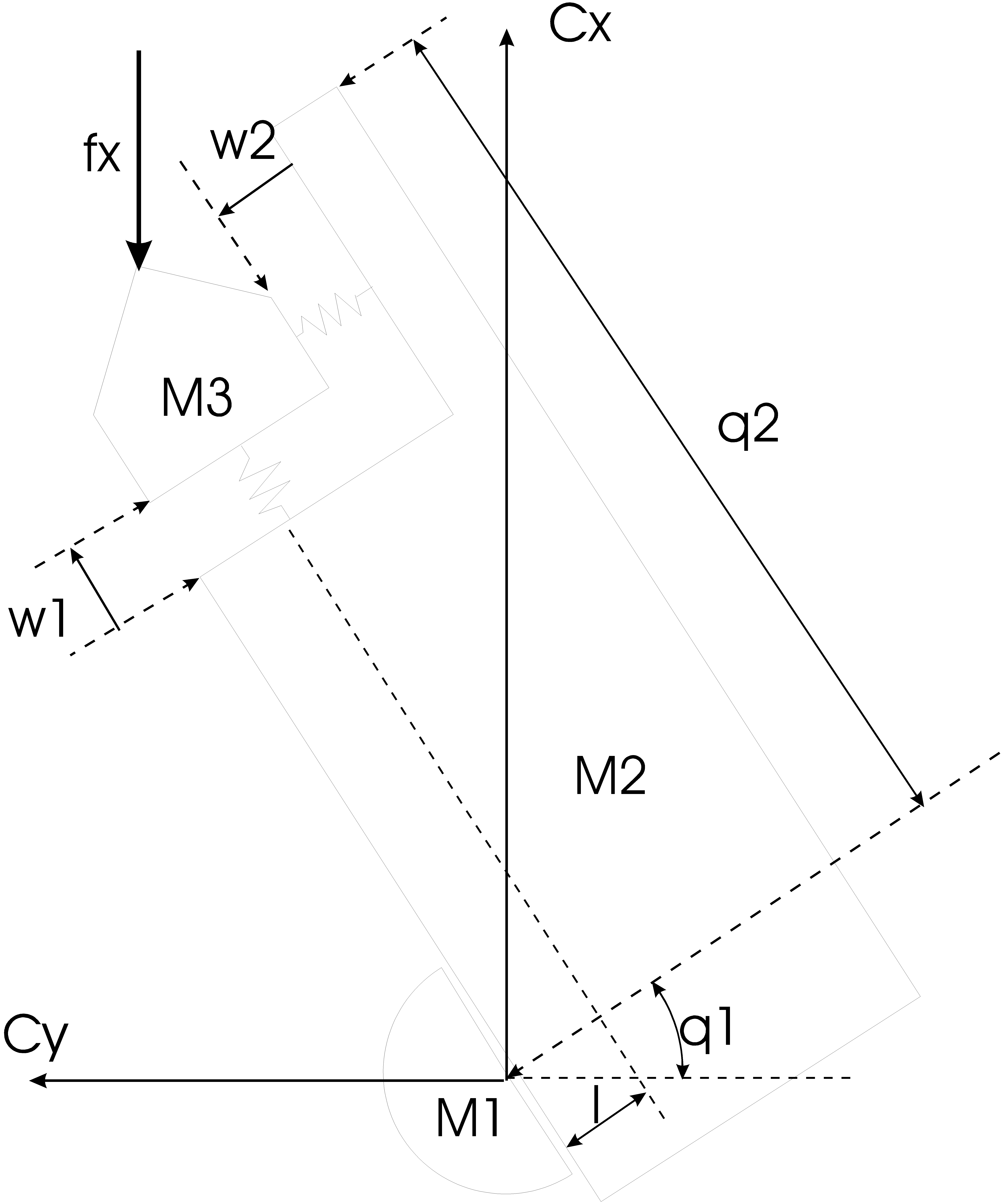
A robotkart a következő egyenletek jellemzik:
A hibrid szabályozót egy MATLAB programmal szimuláltam. A MATLAB “simulink”-ja lehetővé tette a szabályozó folyamatábra jellegű feltüntetését, a 8-6. ábrához hasonló formában:
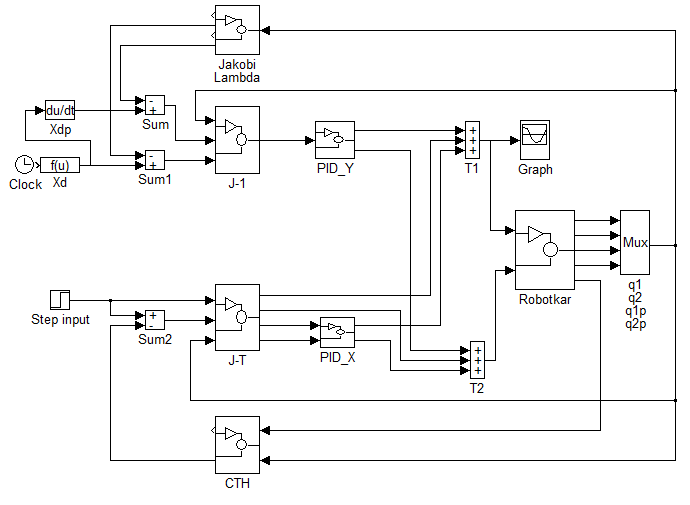
A robotkar egyenletei MATLAB-ba átírva a következőképpen néznek ki:
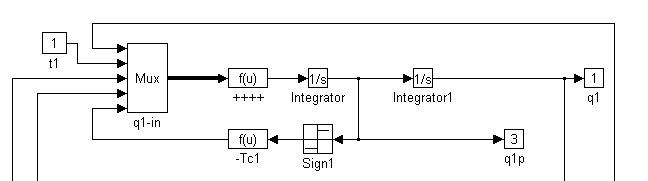
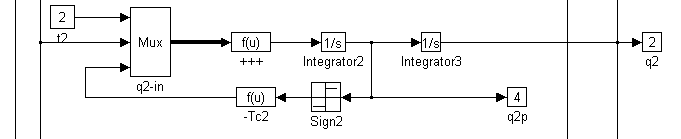


Amint a fenti ábrákból kivehető, a t1 és t2 bemenő értékekből kiszámolható q1, q2, w1, w2 és fx . Ezek lesznek a robotkar “kimenő értékei”.
A transzformációk a következőképpen írhatók át MATLAB-ba:
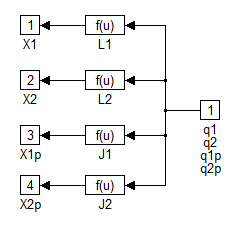
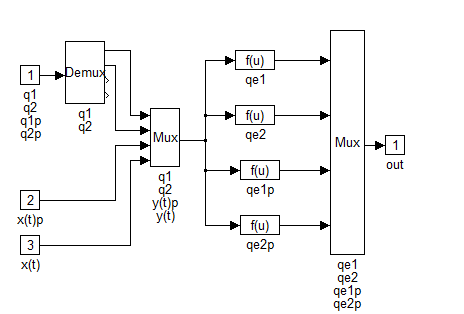
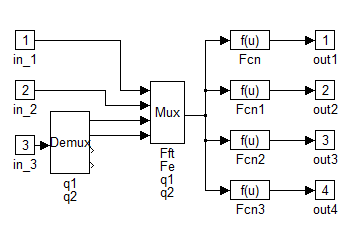
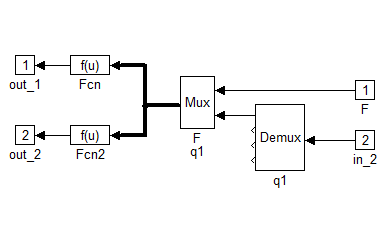
A következőkben a PID szabályozók feltüntetésére kerül sor:
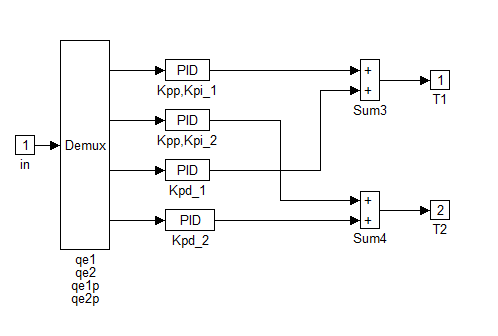
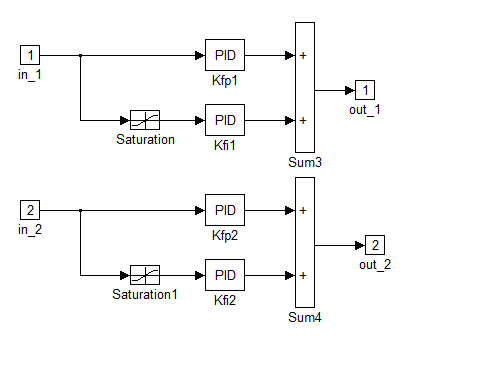
Az eredmények tárgyalása
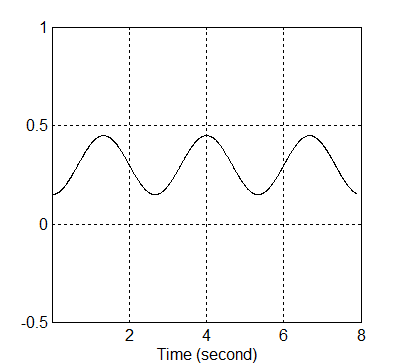
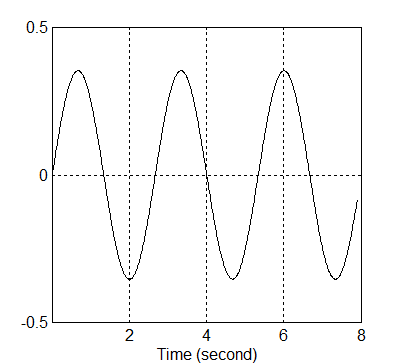
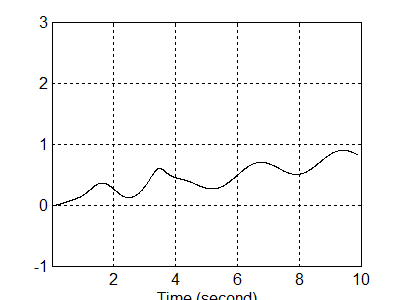
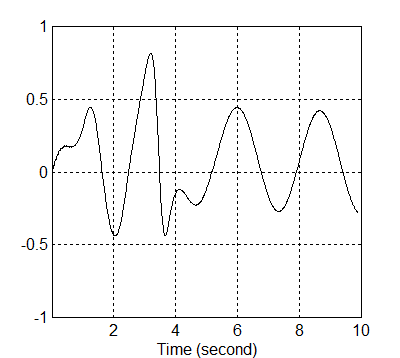
A megadott Xd illetve ennek deriváltjának időbeli változását a 8-19. illetve a 8-20. ábra mutatja.
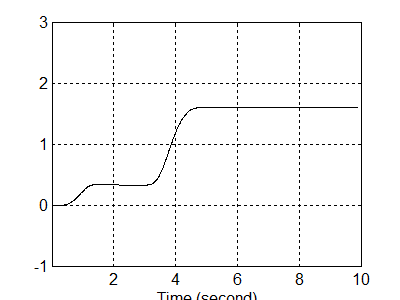
A 8-21. ábra a q1 elfordulást mutatja, amint ez a robotkar egyenleteiből adódik. Látható, hogy q1 kétszer áll rá a megfelelő értékre. Először a kezdeti egyensúly beálltát biztosítja, amikor meg nincs erő, utána pedig az erőviszonyok változásából adódó új egyensúlyi helyzet áll be.
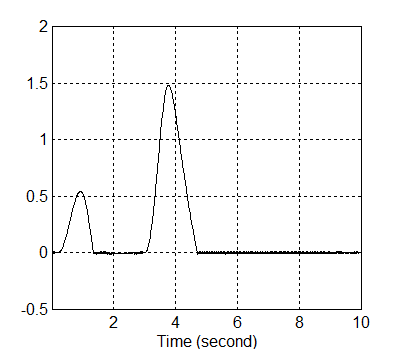
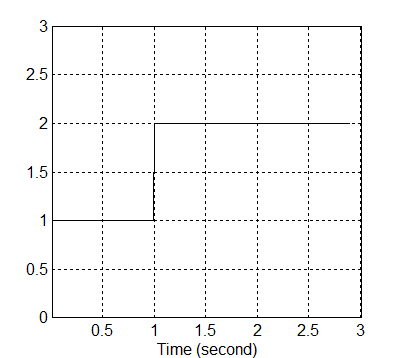
Az erő-bemenet (Fd) az egységlépés segítségével van megadva (8-25. ábra). Az erő kezdetleges értéke 1N, és 1s múlva 2N értékre ugrik fel. A hibrid szabályozó feladata az, hogy mindvégig ráálljon az erő és pozíció egyensúlyi helyzetnek megfelelő értékekre.
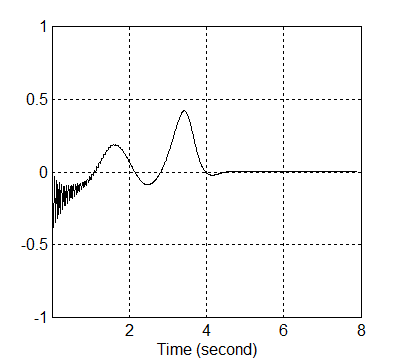
A 8-26. ábra az fx visszajelzést jeleníti meg. Észrevehető, hogy a folyamat elején az erő nagysága tág intervallumban változik. Ez a kezdeti feltételeknek megfelelő ingadozás (káosz). Ez függ az integrálási módszer megválasztásától, a mintavételi időtől, az integrátorok kezdeti értékeinek megválasztásától és más olyan paraméterektől, amiket többszöri próbálgatás során optimizálni lehet.
A T transzformáció után, ami az fx jelet a H keretből a C-be alakítja át, az erő a következőképpen változik az időben:
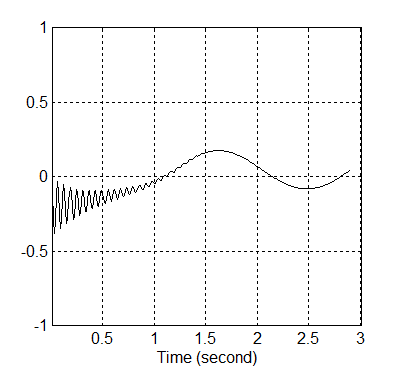
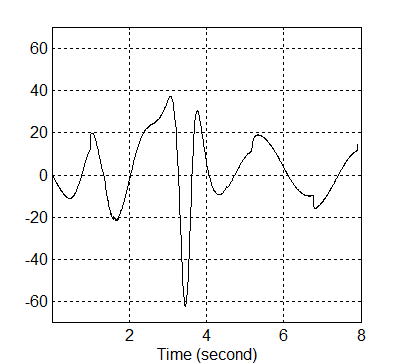
A robotkarba bevezető kompenzált t1 illetve t2 változása a 8-28. illetve 8-29. ábrán követhető.
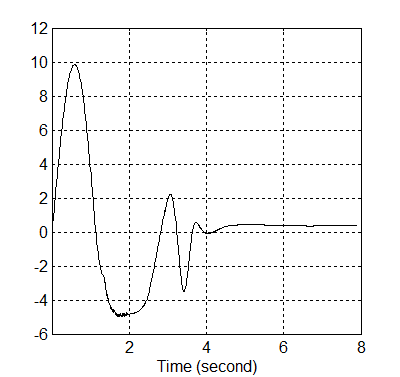
8-28. ábra t1 időbeli változása
IRODALOMJEGYZÉK
[1] Brady, Hollerbach: Robot motion planning and control, MIT, 1982, pp 419-438
[2] Lantos: Robotok irányítása, AK, 1991, pp 226-230