C. függelék - Dinamikus rendszerek szimulációs eszközei (LabVIEW MathScript RT Module)
- C.1. Bevezetés a LabVIEW programnyelvbe
- C.2. LabVIEW MathScript RT Module alkalmazása
- C.3. LabVIEW MathScript
- C.4. Lineáris algebrai mintapéldák (Linear Algebra)
- C.5. Irányítás-tervezés és szimuláció
- C.6. A MathScript blokk a LabVIEW programban (MathScript Node)
A LabVIEW program számos modult tartalmaz, amelyekkel egyszerűbbé válik a folytonos és mintavételes rendszerek irányításának tervezése. A programcsomagban a következő elemek találhatók:
-
Rendszertervezés (LabVIEW Control Design Module)
-
Szimulációs modul (LabVIEW Simulation Module)
-
MathScript Rt modul (LabVIEW MathScript RT Module)
-
Identifikációs eszköz (LabVIEW System Identification Toolkit)
-
PID szabályozó és Fuzzy szabályozó tervezése (LabVIEW PID and Fuzzy Logic Toolkit)
-
Matlab-LabVIEW szimulácós modell kapcsolati eszköz (LabVIEW Simulation Interface Toolkit)
Ebben a részben a LabVIEW MathScript RT modullal ismerkedünk meg.
Mi a LabVIEW program?
A LabVIEW (betűszavakat, betűket kiemelve az angol elnevezésből Laboratory Virtual Instrumentation Engineering Workbench) egy programozási és fejlesztői környezet, egy vizuális programozási nyelv a National Instruments-től A grafikus nyelvet „G” nyelvnek nevezik.
Mi a MATLAB program?
A MATLAB egy programozási eszköz a műszaki számítások elvégzéséhez - számítások és megjelenítés egy integrált környezetben. A MATLAB egy rövidítés, amely a MATrix LABoratory-ból jött létre, így a program nagyon alkalmas mátrix elrendezésű adatokkal törénő műveletek elvégzére, valamint lineáris algebrai problémák megoldására. A MATLAB számos eszköz dobozt (toolbox) ajánl különböző területekre, így irányítás tervezésre (Control Design), képfeldolgozásra (Image Processing), digitális jelfeldolgozásra (Digital Signal Processing) valamint még számos egyéb területre.
Mi a MathScript program?
A MathScript egy magas szintű, szöveg-alapú programozási nyelv. A MathScript mintegy 800 beépített függvényt tartalmaz, és szintaxisa teljesen megegyezik a MATLAB-ban alkalmazottal. A MATLAB-hoz hasonlóan ebben a környezetben is lehet felhasználó által készített .m fájlokat létrehozni.
A MathScript a LabVIEW egy hozzáadott modulja, de nem szükséges a LabVIEW programozását ismerni, azért hogy használhassuk a MathScriptet. Ha szeretnénk alkalmazni a (beépített vagy a felhasználó által készített) MathScript függvényeket, mint a LabVIEW program egy részét, és kombinálni a grafikus és szöveg típusú programozást, akkor alkalmazhatjuk a MathScript struktúrát.
A Mathlab beépített függvényeihez különböző kiegészítő modulok és eszközök (toolkit) adhatók hozzá. A LabVIEW Irányítás Tervezés és Szimuláció modul (Control Design and Simulation Module) és a Digitális Szűrő tervezés Eszköz (Digital Filter Design Toolkit) számos ilyen .m fájlt hoz létre telepítésekor.
További információkat a következő Internet címen találunk a MathScript-ről: http://www.ni.com/labview/mathscript.htm
C.1. Bevezetés a LabVIEW programnyelvbe
A LabVIEW (a hosszú angol elnevezésből Laboratory Virtual Instrumentation Engineering Workbench rövidítve) egy programozási és fejlesztői környezet, egy vizuális programozási nyelv a National Instruments-től. A grafikus nyelvet „G” nyelvnek nevezik. Legelső verziója egy Apple Macintosh számítógépre készült 1986-ban. A LabVIEW-t általánosan használják adatgyűjtésre, berendezések irányítására valamint ipari automatizálásra különböző operációs rendszerekben, amelyek a következők: Microsoft Windows, különböző UNIX verziók, LINUX és Mac OS X. A legutolsó LabVIEW verzió a LabVIEW 2013 amelyet 2013 augusztusában bocsájtottak ki. További információk a National Instruments honlapján, a www.ni.com oldalon találhatók.
A LabVIEW nagyszámú kiegészítő programot (add.on) és eszközkészletet (toolkit) ajánl a különböző feladatú programok fejlesztéséhez.
C.1.1. Adatfolyam programozás
A LabVIEW által alkalmazott programozási nyelv, amelyet G nyelvnek is nevezünk – egy adatfolyam programozási nyelv. A végrehajtás sorrendjét a program grafikus blokk diagramjának struktúrája határozza meg (ez a LabVIEW „forráskód”), amelyben a programozó a különböző funkciójú blokkokat vezetékekkel kapcsolja össze. Ezek a vezetékek továbbítják a kiszámított értéket, és bármelyik blokk azonnal végrehajtódik, amint minden bemeneti adata megérkezik.
A G nyelv alkalmas a blokkok (struktúrák) párhuzamos működtetésére. A többprocesszoros lehetőséget és többszálon működő programszervezést automatikusan kihasználja a beépített program ütemező, amely az operációs rendszer szálai között kapcsolgat, amikor a blokkot a végrehajtáshoz előkészíti.
C.1.2. Grafikus programozás
A LabVIEW a felhasználói kiszolgáló felület - az elnevezése front (előlap) panel – szervesen hozzákapcsolódik a programfejlesztéshez. A LabVIEW programokat/alprogramokat virtuális berendezésnek VI-nak nevezzük az angol elnevezés – virtual instrument- kezdőbetűiből.
Minden VI-nak három fő része van: a front panel, a diagram panel és az ikon konnektor. Az ikon konnektor feladata, hogy megjelenítse a VI-t egy blokk diagramban, ahol ez a VI meghívódik egy feladat végrehajtására.
A vezérlők (controls) és a megjelenítők (indicators) a front panelen biztosítják a program kezelőjének, hogy megadjon egy bemeneti adatot, vagy megjelenítsen egy kiszámított értéket a futó VI-ból.
A front panel ezen kívül programozási felületként is szolgál. Egy virtuális berendezés (.VI) vagy programként fut, ebben az esetben a front panel a programozó felé felhasználói felületként szolgál, vagy egy másik VI blokk diagramjában szerepel végrehajtandó blokként, ahol az ikon konnektor segítségével viszi be a kiszámítandó blokkba a bemeneti adatokat, majd ugyanezen ikon konnektoron keresztül olvassa ki az eredményeket. Ez azt is magában foglalja, hogy a VI-ok egyszerűen tesztelhetők, mielőtt elhelyeznénk őket egy nagyobb program blokk diagramjába alprogramként.
A grafikus programozás szintén előnyös lehetőséget biztosít olyan „nem-programozó” típusú alkalmazóknak is, akik bizonyos, előre megírt VI-okat egyszerűen csak le akarnak emelni az eszközök palettájáról és be akarnak építeni a saját programjukba. A LabVIEW programozói környezet, amely számos példát és dokumentumot tartalmaz, egyszerűvé teszi, hogy kis alkalmazásokat (VI-okat) gyorsan elkészítsünk.
Ez valóban előny az egyik oldalról, de ugyanakkor egy bizonyos veszély is, hogy alábecsüljük a szakértelmünket, amely egy jó minőségű „G” program előállításához szükséges. A komplex algoritmusok esetén, illetve a nagyméretű adatkezelésnél nagyon fontos, hogy a programozónak részletes, biztos tudása legyen a speciális LabVIEW szintaxisról és a memória felhasználás rejtelmeiről. A legbonyolultabb LabVIEW fejlesztői rendszer is kínál lehetőséget, hogy egyéni alkalmazásokat készítsünk.
Továbbá, lehetséges olyan elosztott alkalmazást készíteni, amely az ügyfél/kiszolgáló sémán keresztül kommunikál, és amelyet mindkét oldalon könnyű létrehozni a „G” kód párhuzamos működése miatt.
C.1.3. Kapcsolat a külvilággal
A LabVIEW előnye más fejlesztői rendszerek mellett, hogy egyre nagyobb mennyiségű támogatás ad az egyre nagyobb mennyiségű hardvereszköz alkalmazásához. Eszközmeghajtó programokat biztosít a világon létező, szinte összes mérőberendezéshez és információs vonalhoz, amelyek kiszolgáló felülete szabványos programokkal működve kommunikál a hardver berendezésekkel.
A javasolt eszközmeghajtók nagyon sok programozási időt takarítanak meg.
További információkért érdemes felkeresni a http://ni.com Internet oldalt.
C.1.4. A LabVIEW MathScript RT Module
A LabVIEW MathScript RT Module egy hozzáadott modul a LabVIEW programhoz.
A LabVIEW rendszer a MathScript RT Module segítségével a következő feladatok megoldására lesz képes:
-
Alkalmazhatunk felhasználói ”.m” file-okat az NI valós idejű hardverekhez.
-
Újra felhasználhatunk sok-sok programot, amelyet „The MathWorks, Inc. MATLAB®” programmal korábban létrehoztunk.
-
Fejleszthetünk saját ”.m” fájlokat egy interaktív, utasítássor végrehajtó programmal.
-
Elhelyezhetjük a kifejlesztett ”.m” kódokat a LabVIEW programban a MathScipt végrehajtó blokk alkalmazásával.
C.2. LabVIEW MathScript RT Module alkalmazása
A LabVIEW MathScript program két felületen keresztül hajthat végre utasításokat:
-
A LabVIEW MathScript interaktív ablakban (LabVIEW MathScript Interactive Window) vagy a
-
MathScript blokkban (MathScript Node) elhelyezett utasításokkal a LabVIEW programban.
A LabVIEW MathScript RT Module kiegészíti a LabVIEW tradicionális grafikus programozási rendszerét a legfrisebb fejlesztésű jelfeldolgozási és jelanalízis programokkal. A LabVIEW MathScript RT Module felgyorsítja ezek és más egyéb feladatok végrahajtási sebességét azzal, hogy lehetővé teszi a felhasználó számára ugyanabban a fejlesztői környezetben a szöveges vagy grafikus, vagy ezek kombinációjával megvalósított programfejlesztést. Mindehhez még felhasználhatók a legjobb LabVIEW programok és a több ezer publikált ”.m” fájlok a webről, a különböző könyvekből vagy saját fejlesztésből.
A LabVIEW MathScript RT Module képes olyan programok futtatására, amely a jelenlegi MathScript szintaxist alkalmazza, de alkalmas arra is, hogy a korábbi verziók örökölt MathScript műveleteit is végrehajtsa.
A LabVIEW MathScript RT Module szintén képes végrehajtani bizonyos utasításokat, amelyeket más szöveg típusú nyelven írtak, mint például MATLAB programnyelven. A LabVIEW MathScript RT Module támogatja a MATLAB-ban megvalósított programozási struktúrák többségét, és a szintaxis is teljesen hasonló.
A MathScript RT végrehajtó programot (engine) alkalmazzuk, hogy végrehajtsunk olyan programrészeket, amelyeket a MathScript ablakban (MathScript Windows) vagy a MathScript blokkban (MathScript Node) helyeztünk el.
További részleteket találhatunk a http://zone.ni.com/devzone/cda/tut/p/id/3257 Internet címen.
C.3. LabVIEW MathScript
C.3.1. Bevezetés
Követelmény: MathScript RT Module
Hogyan indítsuk el a MathScript programot LabVIEW környezetben? Először telepítenünk kell a LabVIEW rendszert, majd ezután a LabVIEW MathScript RT Module-t. Amikor a szükséges programokat telepítettünk a számítógépre, a LabVIEW megnyitása után elindíthatjuk a MathScript programot.
C.3.1.1. Hogyan indítsuk el a MathScript programot LabVIEW környezetben?
Amikor a szükséges programokat telepítettük, a MatScript elindítását a LabVIEW indításával kell elkezdenünk.
A MathScript-et a LabVIEW indító ablakának (Getting Started) Tools menüjéből a MathScript Window...: menüponttal indíthatjuk el.
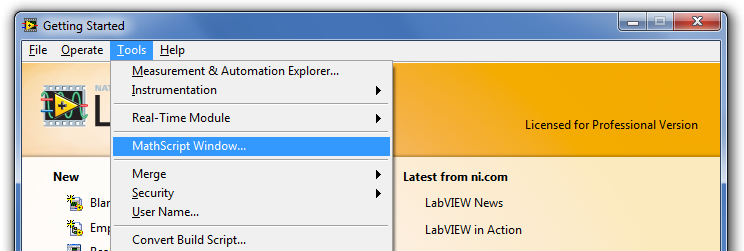
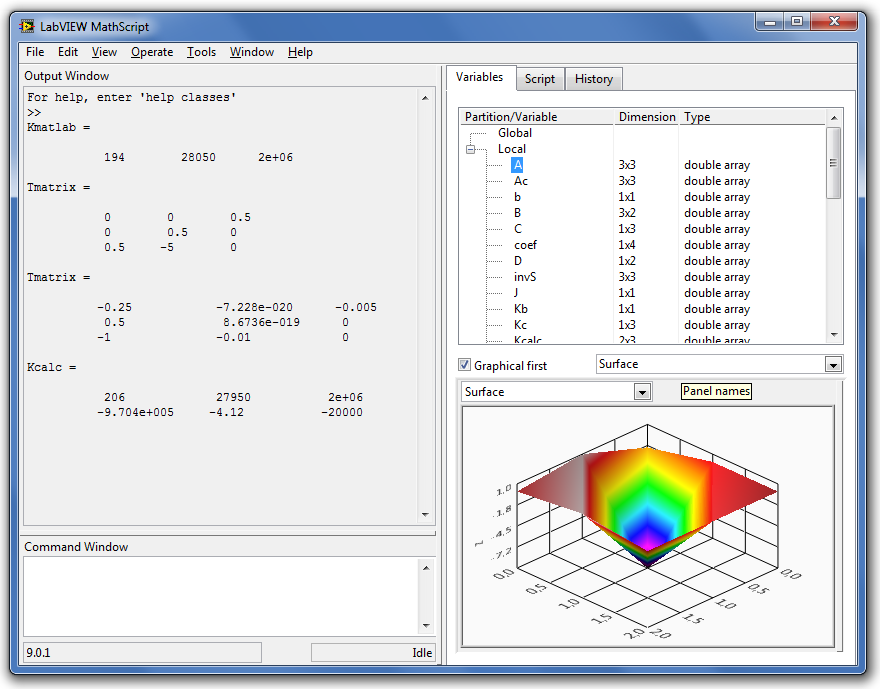
A LabVIEW MathScript Window egy interaktív adatbeviteli/megjelenítő ablak, amelyekben megadhatunk ”.m” utasításfájlokat, és azonnal megtekinthetjük az eredményeket, a programban szereplő változók értékeit és a korábban végrehajtott utasításokat.
Az ablak tartalmaz egy utasításablakot is, amely lehetővé teszi, hogy sorról sorra utasításokat adjunk meg gyors számítások elvégzéséhez, az utasítások szintaktikájának ellenőrzéséhez vagy tanuláshoz. Alternatívaként az utasítások egy csoportját (egy sornál hosszabb utasítást) végrehajthatunk a program szerkesztő ablakában (script editor window).
Ahogy fut a program, a változói folyamatosan frissülnek ebben az ablakban, hogy szövegesen vagy grafikus formában megtekinthessük az eredményeket valamint a korábbi utasítások ablakában visszanézhetjük, hogy milyen utasításokat hajtott végre korábban.
A korábbi utasításokat bemutató ablakban megtekinthetők az algoritmus fejlesztésének lépései, továbbá a vágólapon keresztül lehetőség van ismételten felhasználni a korábban végrehajtott utasításokat.
A LabVIEW MathScript Window-t arra is használhatjuk, hogy begépeljünk egy utasítássort vagy megadjunk egy utasításcsoportot, amelyet az egyszerű szövegszerkesztő ablakban állítottunk elő, vagy betöltöttük egy szöveg típusú állományból, illetve egy másik szövegszerkesztőből.
A LabVIEW MathScript Window azonnal megjeleníti az eredményeket különböző alakban, szövegesen vagy grafikusan.
Mintapéldák a különböző ablaktípusokra a (C.4. ábra, C.5. ábra és C.6. ábra) ábrákon láthatók.
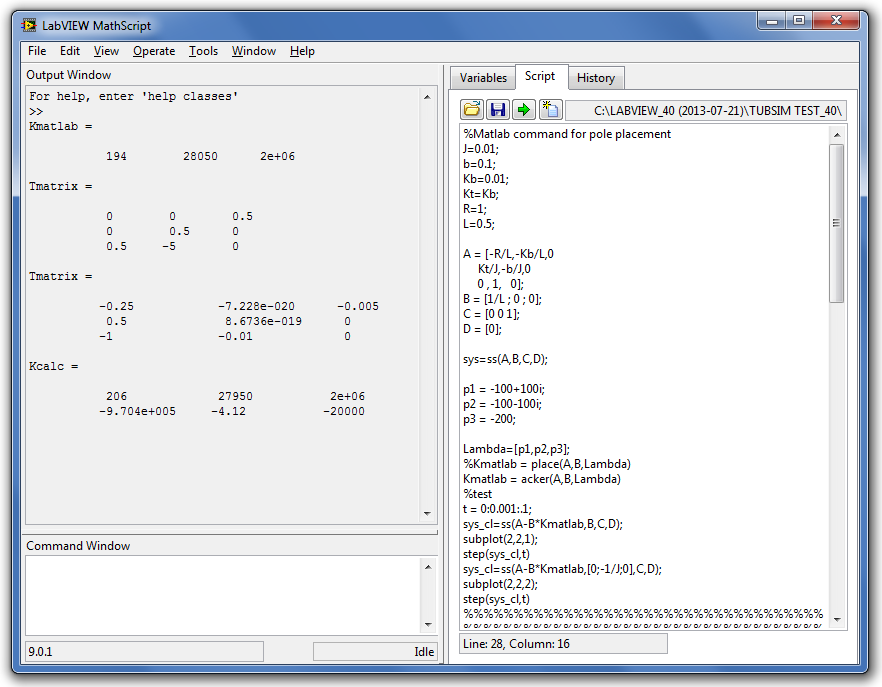
C.3.2. Programozási segítség
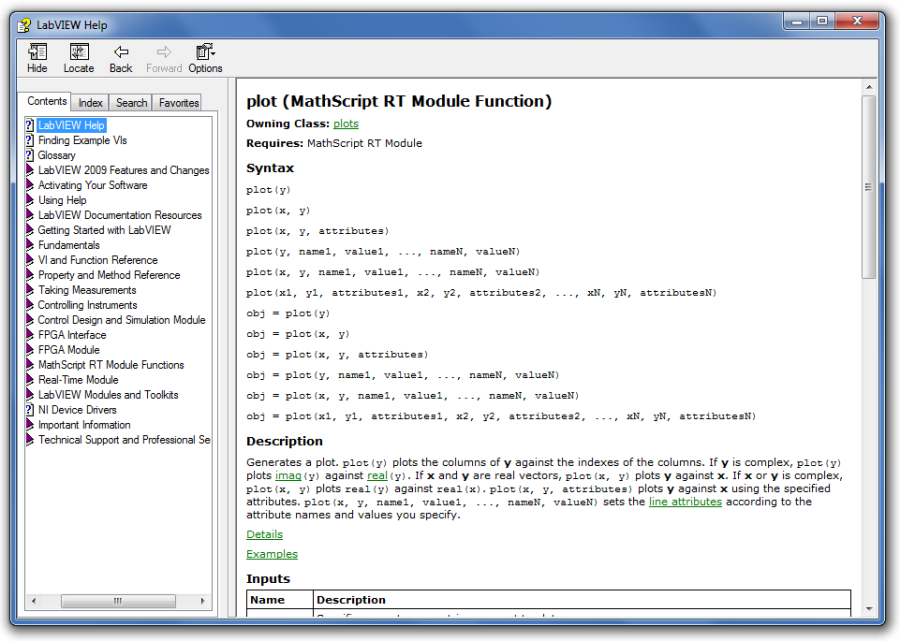
Begépelhetjük a segítségkérést az utasítás ablakba
>>help
Vagy ettől pontosabb kérésmegadással:
>>help plot
Az utasításablakban megjelenő segítségkérésre a LabVIEW Segítség ablakának a keresett témához kapcsolódó része jelenik meg. (C.7. ábra)
C.3.3. Mintapéldák
Azt tanácsolom az Olvasónak, hogy dolgozza fel az összes LabVIEW MathScript mintapéldát ebből a leírásból, hogy gyakorlatot szerezzen a program használatában és szintaxisának megismerésében. Minden mintapélda ebben a leírásban ugyanilyen keretben jelenik meg
>> …
Az utasításokat az utasításablakba (Command Window) kell beírni.
A ”>>” szimbólum fogja jelezni, hogy az ezt következő szöveg egy utasítás, amelyet az utasítás ablakba kell beírni.
Mintapélda: Mátrixok
Definiáljuk MathScript-ben a következő mátrixot:
|
|
(C.1) |
A megadás formája:
>> A = [1 2;0 3]
vagy
>> A = [1,2;0,3]
Ha például meg akarjuk határozni a következő számítás eredményét
|
a+b ahol a=4; és b=3; |
(C.2) |
akkor a következő utasításokat kell begépelni:
>>a=4 >>b=3 >>a+b
A MathScript a következő választ adja a kimeneti ablakban (Output Window):
ans =
7
A MathScript egyszerű módon definiálja a kezdőértékkel feltöltött vektorokat: “init:increment:terminator”, ahol (init=kezdőérték; increment=növekmény; terminator= végérték). Például:
>> array = 1:2:9 array = 1 3 5 7 9
Az utasítás definiálja a változó nevét, amely most array (vagy hozzárendel egy új értéket a már létező array változóhoz). A vektor típusú array változó, a következő értékeket fogja tartalmazni: 1, 3, 5, 7 és 9.
Az array elnevezésű változó első elemének értéke az (init=kezdőérték), minden további vektorelemnél az elem értéke növekedni fog 2-vel (increment=növekmény) amíg el nem éri (vagy túl nem lépi) a 9-et, a végértéket (terminator= végérték).
A növekmény értékét elhagyhatjuk, a nyelv szintaxisa ebben az esetben 1-el helyettesíti a növekmény értékét.
>> ari = 1:5
ari =
1 2 3 4 5
Az utasítás hozzárendelte az 1-től 5-ig értékeket az ari vektor megfelelő indexű elemihez, úgy hogy növekményként automatikusan 1-et alkalmazott.
Megjegyezzük, hogy az indexelés a MathScript-ben eggyel (1) kezdődik, ami a matematikában általános megállapodás. Ez azonban nem általános a programozási nyelvekben, ahol a mátrixok indexelése gyakran nullával (0) kezdődik.
A mátrixok definiálása úgy történik, hogy az egyes indexek maximális értékét vesszővel vagy szóköz karakterrel választjuk el egymástól, és pontosvesszőt használunk az egyes sorok elválasztására. A mátrixelemek listáját szögletes zárójelek közé írjuk.
A zárojeleket () használjuk, hogy elérjük a mátrix egyes elemeit vagy almátrixát (amelyeket szintén alkalmazhatunk, amikor függvényeket adunk meg az argumentumlistában)
>> A = [16 3 2 13; 5 10 11 8; 9 6 7 12; 4 15 14 1]
A =
16 3 2 13
5 10 11 8
9 6 7 12
4 15 14 1
>> A(2,3)
ans =
11
Az indexek egy halmaza adható meg például a "2:4" kifejezéssel, amely a következő értéklistát jelenti:[2, 3, 4]. Például ha szeretnénk egy almátrixot kijelölni a 2. sortól a 4. ig és a 3. oszloptól a 4. ig, akkor a következő utasítást kell írnunk:
>> A(2:4,3:4)
ans =
11 8
7 12
14 1
Egy négyzetes egységmátrix könnyen megadható az eye függvény segítségével, valamint a zeros és ones függvényekkel tetszőleges méretű nullával vagy eggyel feltöltött mátrixot létrehozhatunk:
>> eye(3)
ans =
1 0 0
0 1 0
0 0 1
>> zeros(2,3)
ans =
0 0 0
0 0 0
>> ones(2,3)
ans =
1 1 1
1 1 1
C.3.4. Hasznos utasítások
Néhány gyakran alkalmazott utasítást a (Táblázat C.1) táblázatban gyűjtöttünk csokorba.:
|
Utasítás |
Leírás |
|---|---|
|
eye(x) |
x sorú és oszlopú egységmátrix, |
|
ones(x), ones(x,y) |
x sorú és y oszlopú, egységnyi elemeket tartalmazó mátrix, |
|
zeros(x), zeros(x,y) |
x sorú és y oszlopú, zérus elemeket tartalmazó mátrix, |
|
size(A) |
az A mátrix dimenzióinak értéke, |
|
A’ |
az A mátrix inverz mátrixa. |
C.3.4.1. Függvények hívása a MathScript-ben
A MathScript több mint 800 beépített függvényt tartalmaz.
Mintapélda : Beépített függvények
Adott egy vektor:
>>x=[1 2 5 6 8 9 3]
› Keressük meg az x vektor átlagértékét!
› Keressük meg az x vektor minimum értékét!
› Keressük meg az x vektor maximum értékét!
A feladatok megoldását szolgáltató MathScript kód a következő:
x=[1 2 5 6 8 9 3] mean(x) min(x) max(x)
[ Mintapélda vége]
C.3.4.2. Felhasználó által definiált függvények a MathScript-ben (User-Defined Functions)
A MathScript beépített függvényei mellett számos esetben szükséges, hogy saját magunk hozzunk létre függvényeket.
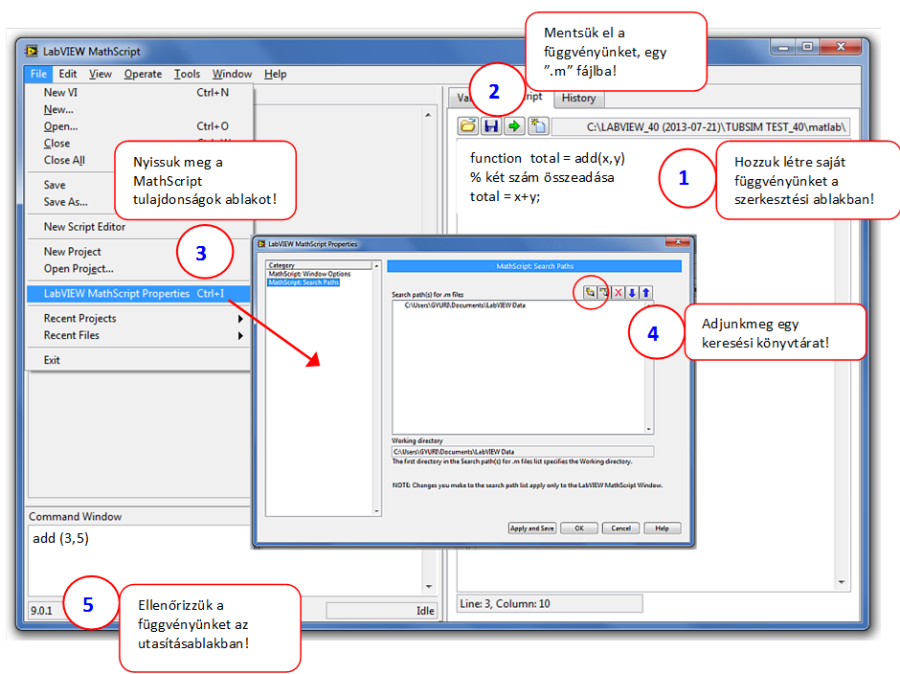
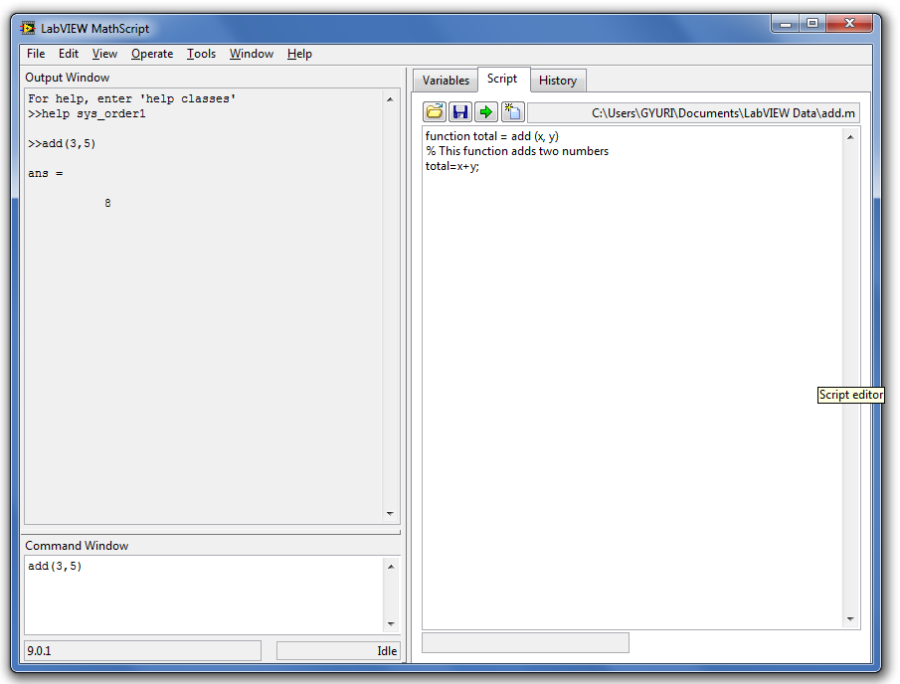
Ahhoz, hogy saját függvényt hozzunk létre a MathScript-ben, alkalmazzuk a következő szintaxist:
function output = function_name (inputs) % documentation …
A (C.8. ábra) ábrán láthatók a függvénydefiniálás egyes lépései a MathScript-ben.
C.3.4.3. Scripts
Az alprogram (script) a MatScript utasítások sorozata, amelyet egy feladat megoldásánál akarunk végrehajtani. Amikor létrehoztuk az alprogramot, (scriptet), eltárolhatjuk azt egy ”.m” fájlban későbbi felhasználásra.
Egyszerre több script ablakot is nyitva tarthatunk a program szerkesztéséhez, amelyeket a New Script Editor (Új scriptszerkesztő) paranccsal hozhatunk létre a File menüből:
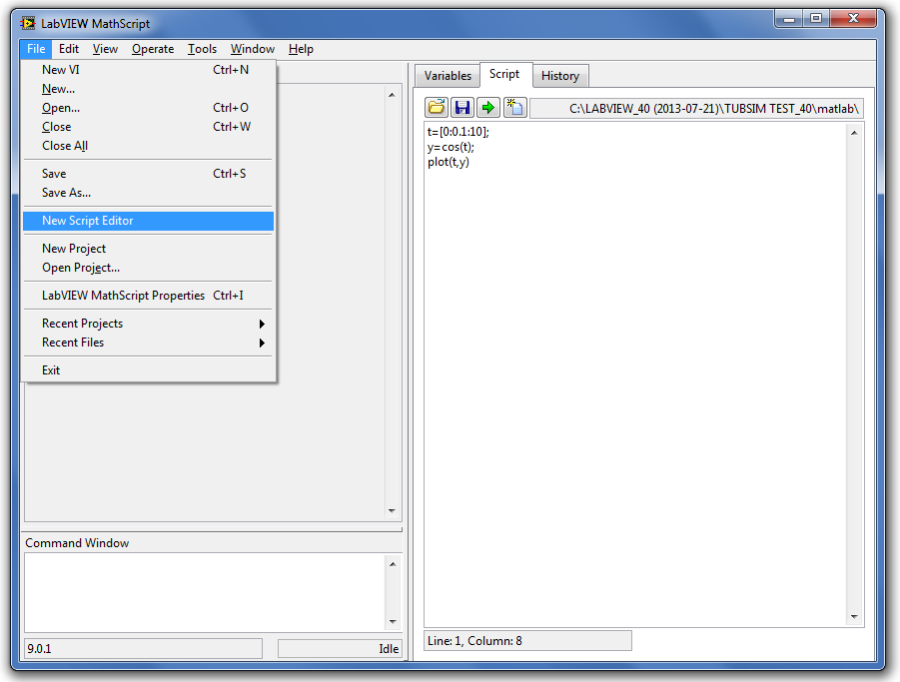
A menüválasztás a (C.12. ábra) ábrán látható ablakot eredményezi.
C.3.5. Programozási struktúrák
Ez a fejezet bemutatja a MathScript-ben alkalmazható alapvető programstruktúrákat.
A programozási struktúrák a következők:
-
If-else utasítás
-
Switch és case utasítás
-
For ciklus
-
While ciklus
C.3.5.1. If-else utasítás
Az if (ha) utasítás kiszámít egy logikai kifejezést és végrehajtja az utasítások egy csoportját, ha a logikai kifejezés igaz. Az utasítás tartalmazhat egy else (egyébként) ágat is, amelyet a kifejezés hamis értéke esetén hajt végre a program. Az end (vége) utasítás a feltételes utasítás befejezését jelenti, mint a feltételes utasítás utolsó eleme. Az utasítások egyes csoportjait a négy if alapelem határolja – nincsenek zárójelek vagy kapcsos zárójelek.
Mintapélda : If-Else utasítás
Próbáljuk ki a következő MathScript kódsorozatot:
n=5
if n > 2
M = eye(n)
elseif n < 2
M = zeros(n)
else
M = ones(n)
end
[ Mintapélda vége]
C.3.5.2. Switch és case utasítás
A switch (kapcsoló) az utasítások egy csoportját hajtja végre, amelyet egy érték vagy egy kifejezéssel meghatározott változó értékével jelölünk ki.
A case (eset) kulcsszó határolja az egyes csoportokat. A switch struktúra csak a kiválasztott eset (case) utasításait hajtja végre.
Az utasítást egy end (vége) utasítás zárja be, mint a struktúra utolsó utasítása.
Mintapélda : Switch és case utasítás
Próbáljuk ki a következő MathScript kódsorozatot:
n=2
switch(n)
case 1
M = eye(n)
case 2
M = zeros(n)
case 3
M = ones(n)
end
[ Mintapélda vége]
C.3.5.3. For ciklus (véges számú végrehajtás)
A for cikus meghatározott számszor ismétli az utasítások egy csoportjának végrehajtását. A legutolsó utasításként szereplő end (vége) utasítás az utasításcsoport határolója.
Mintapélda : For ciklus
Próbáljuk ki a következő MathScript kódsorozatot:
m=5 for n = 1:m r(n) = rank(magic(n)); end r
[ Mintapélda vége]
C.3.5.4. While cilus (feltételtől függő számú végrehajtás)
A while ciklus egy logikai változó értékétől függően ismétli az utasítások egy csoportjának végrehajtását (akár végtelenszer is!). A legutolsó utasításként szereplő end (vége) utasítás az utasításcsoport határolója.
Mintapélda : While ciklus
Próbáljuk ki a következő MathScript kódsorozatot:
m=5;
while m > 1
m = m - 1;
zeros(m)
end
[ Mintapélda vége]
C.3.6. Rajzolás (Plotting )
Ez a fejezet bemutatja, hogy hogyan hozhatunk létre rajzokat a MathScript-ben. A mintapéldák feldolgozásával megismerkedünk az alapvető rajzoló utastásokkal.
Mintapélda : Rajzolás 2D (Plotting )
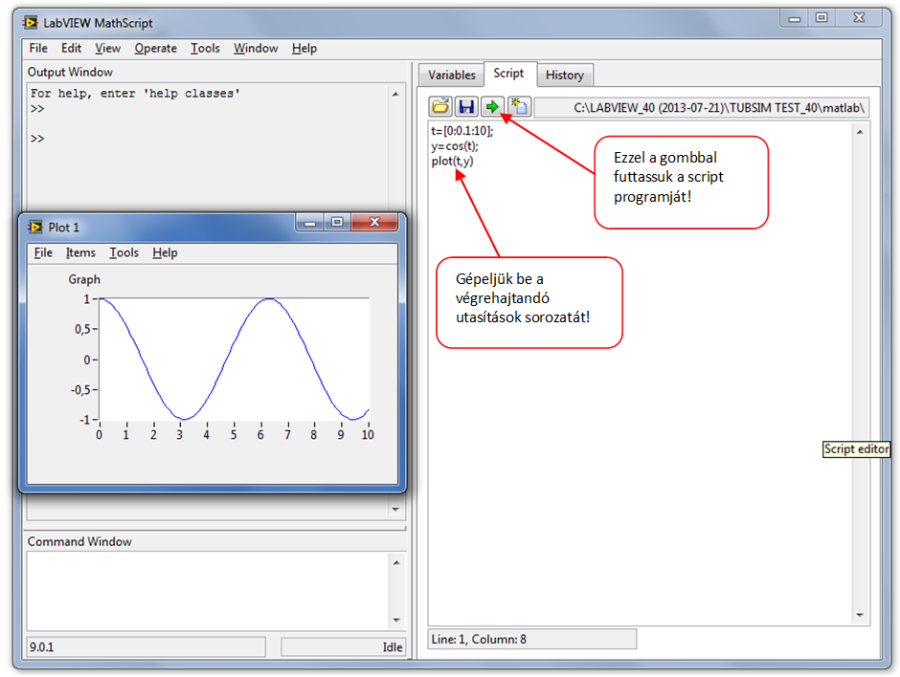
A plot (rajzolás) függvényt arra használjuk, hogy két vektorból x-ből és y-ból egy grafikont hozzunk létre. A MathScript kód a (C.13. ábra) ábrán látható szinusz függvényt hozza létre.
x = 0:pi/100:2*pi; y = sin(x); plot(x,y)
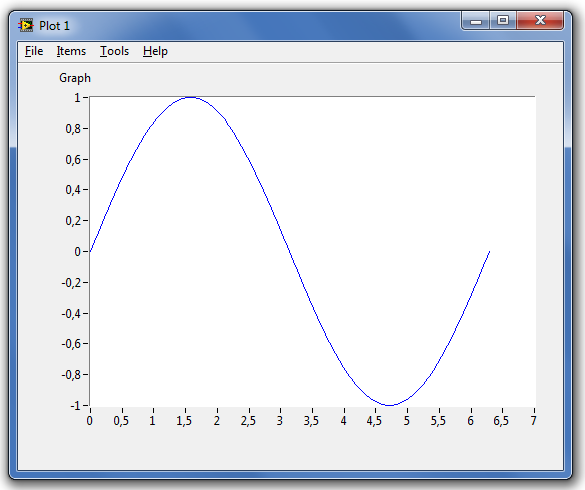
[ Mintapélda vége]
Mintapélda : Rajzolás 3D (Plotting )
Háromdimenziós grafikus felület ábrája készíthető a surf, plot3 vagy a mesh rajzoló utasításokkal.
[X,Y] = meshgrid(-10:0.25:10,-10:0.25:10);
f = sinc(sqrt((X/pi).^2+(Y/pi).^2));
mesh(X,Y,f);
axis([-10 10 -10 10 -0.3 1])
xlabel('{\bfx}')
ylabel('{\bfy}')
zlabel('{\bfsinc} ({\bfR})')
hidden off
A fenti MathScript kód a (C.14. ábra) ábrán látható 3D-s rajzot hozza létre.
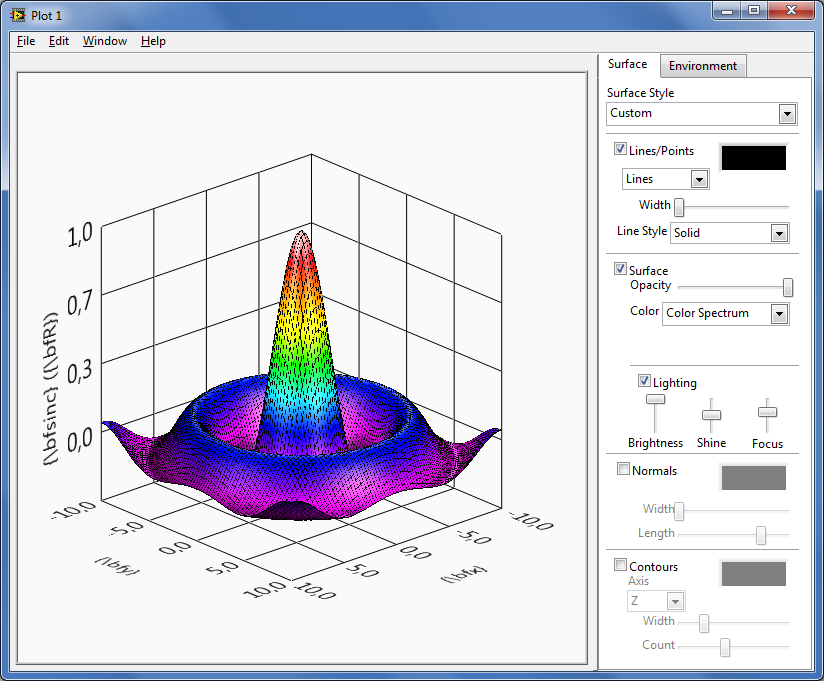
[ Mintapélda vége]
C.4. Lineáris algebrai mintapéldák (Linear Algebra)
A Linear Algebra (lineáris algebra) a matematikai utasítások csoportja, amely lehetővé teszi a mátrixok és vektorok, valamint vektorterek (más elvezéssel lineáris terek), lineáris térképek (más néven lineáris transzformációk) és lineáris egyenletrendszerek tanulmányozását.
C.4.1. Vektorok (Vectors)
Adott egy x vektor:
|
|
(C.3) |
Mintapélda : vektorok
Adott a következő vektor
|
|
(C.4) |
>> x=[1; 2; 3]
x =
1
2
3
Az x vektor transzponáltja (transpose):
>> x'
ans =
1 2 3
[ Mintapélda vége]
C.4.2. Mátrixok (Matrix)
Adott egy A mátrix:
|
|
(C.5) |
Mintapélda : mátrixok
Adott a következő mátrix:
|
|
(C.6) |
>> A=[0 1;-2 -3]
A =
0 1
-2 -3
[ Mintapélda vége]
C.4.2.1. Transzponálás (Transpose)
Az A mátrix transzponáltja:
|
|
(C.7) |
Mintapélda : transzponálás
Adott a következő mátrix:
|
|
(C.8) |
>> A'
ans =
0 -2
1 -3
[ Mintapélda vége]
C.4.2.2. Főátlóelemek (Diagonal)
Az A mátrix diagonális (főátlóbeli elemei) egy vektort alkotnak
|
|
(C.9) |
Mintapélda : diagonál
Keressük meg az A mátrix diagonális elemeit:
>> diag(A)
ans =
0
-3
[ Mintapélda vége]
C.4.2.3. Mátrixszorzás (Matrix Multiplication)
Adottak az és a matrixok és
|
|
(C.10) |
ahol
|
|
(C.11) |
Mintapélda : mátrixszorzás
>> A=[0 1;-2 -3]
A =
0 1
-2 -3
>> B=[1 0;3 -2]
B =
1 0
3 -2
>> A*B
ans =
3 -2
-11 6
[ Mintapélda vége]
Megjegyzés!
|
|
(C.12) |
C.4.2.4. Mátrixösszeadás és -kivonás (Matrix Addition)
Adottak az és a matrixok és
|
|
(C.13) |
ahol
|
|
(C.14) |
Mintapélda : mátrixok összadása és kivonása
>> A=[0 1;-2 -3]
A =
0 1
-2 -3
>> B=[1 0;3 -2]
B =
1 0
3 -2
>> A+B
ans =
1 1
-5
>> A-B
ans =
-1 1
-5 1
[ Mintapélda vége]
C.4.2.5. Mátrix determinánsa (Matrix Determinant)
Egy négyzetes mátrix determinánsát a következő módon jelöljük:
|
|
(C.15) |
Ha van egy 2x2 mátrixunk:
|
|
(C.16) |
Akkor a mátrix determinánsát a következő módon kapjuk
|
|
(C.17) |
Mintapélda : determináns
Határozzuk meg a determináns értékét:
A =
0 1
-2 -3
>> det(A)
ans =
2
Megjegyezzük, hogy
|
|
(C.18) |
|
|
|
(C.19) |
Határozzuk meg a determináns értékét:
>> det(A*B)
ans =
-4
>> det(A)*det(B)
ans =
-4
>> det(A')
ans =
2
>> det(A)
ans =
2
[ Mintapélda vége]
C.4.2.6. Inverz mátrix (Inverse Matrix)
Egy négyzetes mátrix inverz mátrixát a következő módon jelöljük:
|
|
(C.20) |
ha
|
|
(C.21) |
Ha van egy 2x2 mátrixunk:
|
|
(C.22) |
Az inverz mátrixot a következő módon kapjuk
|
|
(C.23) |
Mintapélda : inverz mátrix
A =
0 1
-2 -3
>> inv(A)
ans =
-1.5000 -0.5000
1.0000 0.0000
[ Mintapélda vége]
C.4.3. Sajátértékek (Eigenvalues)
Adott egy négyzetes mátrix, melynek sajátérték vektorát a következő módon számítjuk:
|
|
(C.24) |
ahol
|
a sajátértékek vektora |
Mintapélda : sajátértékek
Keressük meg a sajátértékeket:
A =
0 1
-2 -3
>> eig(A)
ans =
-1
-2
[ Mintapélda vége]
C.4.4. Lineáris egyenletrendszer megoldása (Solving Linear Equations)
Adott a következő lineáris egyenletrendszer:
|
|
(C.25) |
melynek megoldása:
|
|
(C.26) |
(Feltételezzük, hogy A inverze létezik.)
Mintapélda : Lineáris egyenletrendszer megoldása
Oldjuk meg a következő egyenletet,
|
|
(C.27) |
amit felírhatunk a következő formában is
|
|
(C.28) |
A lineáris egyenlet megoldása a következő:
A =
1 2
3 4
>> b=[5;6]
b =
5
6
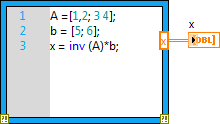
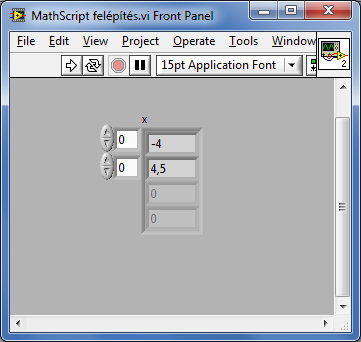
>> x=inv(A)*b
x =
-4.0000
4.5000
A MathScript-ben alkalmazható a ”x=A\b” forma, amely ugyanazt az eredményt adja. Ez a szinataxis akkor is alkalmazható, amikor A mátrix inverze nem létezik.
Illegális művelet nem négyzetes mátrix esetén:
>> A=[1 2;3 4;7 8]
>> x=inv(A)*b
??? Error using ==> inv
Matrix must be square.
>> x=A\b
x =
-3.5000
4.1786
[ Mintapélda vége]
C.5. Irányítás-tervezés és szimuláció
Amennyiben a LabVIEW MathScript lehetőségeit irányítás-tervezési feladatok megoldására szeretnénk használni, teleptenünk kell a LabVIEW program egy további eszközkészletét az Irányítás tervezés és szimulációs modult (Control Design and Simulation Module) a korábban telepített MathScript RT Module-hoz.
Az Irányítás-tervezés és szimuláció MathScript RT Module függvényeit alkalmazhatjuk lineáris szabályozási körök tervezéséhez, analíziséhez és szimulációjához úgy, hogy közben egy szöveg típusú nyelvet használunk. A következő rész bemutatja az Irányítás-tervezés és szimuláció MathScript RT Module azon függvényosztályait és utasításait, amelyeket a LabVIEW MathScript támogat.
Az Irányítás-tervezés eszközkészlet MathScript függvényeinek alkalmazásához segítséget kapunk, ha a MathScript utasítás ablakába begépeljük a ”help cdt” utasítást.
A (Táblázat C.2) táblázatban összefoglaltuk a létező függvényosztályokat.
|
Függvény osztály |
Leírás |
|---|---|
|
cdops |
Aritmetikai operátorfüggvények |
|
cdplots |
Diagram XY síkon |
|
cdsolvers |
Egyenletmegoldó függvények |
|
connect |
Modell-összekapcsolási függvények |
|
construct |
Modell-konstrukciós függvények |
|
convert |
Modell-átalakító függvények |
|
dynchar |
Dinamikus karakterisztika függvények |
|
frqrsp |
Frekvencia válasz függvények |
|
info |
Modell-információs függvények |
|
reduce |
Modellméretet(bonyolultságot) csökkentő függvények |
|
ssanals |
Állapottér-analízis függvények |
|
ssdesign |
Állapot-visszacsatolás tervezési függvények |
|
timeresp |
Időtartománybeli analízis függvények |
A továbbiakban néhány függvényosztályt és függvényt részletesebben is bemutatunk.
C.5.1. Állapottérmodellek és átviteli függvények
A MathScript számos függvényt ajánl arra, hogy definiáljuk, illetve kezeljük az állapottérmodelleket és az átviteli függvényeket.
Függvényosztály neve : contruct (Modell-konstrukciós függvények)
Függvényosztály leírása :
A függvényosztályban szereplő függvényeket arra használjuk, hogy lineáris, állandó eggyütthatós rendszermodelleket hozzunk létre, és átalakítsuk azokat a különböző modellmegjenési formákra.
A következő függvényeket lehet alkalmazni a contruct (Modell konstrukciós függvények) osztályban:
|
Függvény |
Leírás |
|---|---|
|
drandss |
Mintavételes állapottér rendszer létrehozása véletlenszerűen felvett paraméterekkel |
|
drandtf |
Mintavételes rendszer létrehozása véletlenszerűen felvett paraméterekkel impulzusátviteli függvény alakban |
|
drandzpk |
Mintavételes rendszer létrehozása véletlenszerűen felvett paraméterekkel zérus-pólus függvény alakban |
|
pid |
Folytonos PID szabályozó modell létrehozása |
|
randss |
Folytonos állapottér rendszer létrehozása véletlenszerűen felvett paraméterekkel |
|
randtf |
Folytonos rendszer létrehozása véletlenszerűen felvett paraméterekkel impulzusátviteli függvény alakban |
|
ss |
Folytonos állapottér rendszer létrehozása vagy állapottér alakra történő átalakítása |
|
sys_filter |
Létrehoz egy mintavételes szűrőt impulzusátviteli függvény alakban |
|
sys_order1 |
Folytonos, egytárolós rendszer létrehozása átviteli függvény alakban |
|
sys_order2 |
Folytonos, kéttárolós rendszer létrehozása átviteli függvény alakban |
|
tf |
Folytonos átviteli függvény létrehozása vagy átviteli függvény alakra történő átalakítása |
|
zpk |
Folytonos zérus-pólus függvény létrehozása vagy zérus-pólus függvény alakra történő átalakítása |
A továbbiakban néhány példát mutatunk be, hogy miként alkalmazzuk az osztály leggyakrabban használt függvényeit.
C.5.1.1. PID (Arányos-integráló-differenciáló szabályozó)
Jelenleg az arányos-integráló-differenciáló (PID) szabályozó algoritmus a leggyakrabban használt szabályozó algoritmus az iparban.
A PID szabályozóban meg kell adni egy szabályozott jellemzőt és egy alapjelértéket. A szabályozott jellemző az a rendszerparaméter, amelyet szabályozni szeretnénk, nyomás vagy folyadékáram nagysága, az alapjel pedig az az előírt érték, amelyre a szabályozás történik.
A PID szabályozó meghatározza a szabályozó kimeneti értékét olyanokat, mint fűtési teljesítmény vagy szeleppozíció. A szabályozó kimeneti jelét a szabályozott szakaszra bocsájtva, azonnal elkezdődik a szabályozott jellemző értékének közeledése az alapjel értékéhez.
A PID szabálozó a következő módon számítja a bevatkozást, u(t)-t:
|
|
(C.29) |
ahol
|
K c |
A szabályozó erősítése, |
|
|
T i |
Integrálási idő, |
|
|
T d |
Deriválási idő. |
és az e(t) a szabályozási eltérés:
|
|
(C.30) |
|
SP |
alapértéke (Setpoint) |
|
|
PV |
szabályozott jellemző (Process Variable) |
Függvény : pid
Leírás :
Ez a függvény létrehoz egy arányos-integráló-differenciáló (PID) szabályozó modellt, párhuzamos, soros vagy elméleti (academic) alakban.
MIntapélda :
Kc = 0.5; Ti = 0.25; SysOutTF = pid(Kc, Ti, 'academic');
[ Mintapélda vége]
C.5.1.2. Állapottérmodell (State-space model)
Az állapottérmodell a redszert leíró differenciálegyenlet-rendszer egy struktúrált megjelenési formája.
Egy lineáris állapottérmodell:
|
|
(C.31) |
ahol az x(t) az állapotok vektora, u(t) pedig a bemenetek vektora. Az A mátrix elnevezése rendszermátrix, amely minden esetben négyzetes mátrix.
Mintapélda :
A differenciálegyenlet-rendszer:
|
|
(C.32) |
átírva állapottér alakba:
|
|
(C.33) |
Függvény : ss
Leírás :
Ez a függvény létrehoz egy folytonos vagy mintavételes, lineáris rendszermodellt állapottér formában. Ez a függvény szintén alkalmazható arra, hogy átalakítsuk az átviteli függvény vagy zérus-pólus-erősítés modellt állapottér alakra.
Mintapélda :
% Létrehozunk egy állapottérmodellt A = eye(2) B = [0; 1] C = B' SysOutSS = ss(A, B, C) % Átalakítjuk a zérus-pólus-erősítés modellt állapottér alakra z = 1 p = [1, -1] k = 1 SysIn = zpk(z, p, k) SysOutSS = ss(SysIn)
[ Mintapélda vége]
C.5.1.2.1. Átviteli függvény (Transfer function)
A lineáris rendszer átviteli függvényét a kimeneti jel és a bemeneti jel Laplace transzformáltjainak hányadosával definiáljuk.
Függvény : tf
Leírás :
Ez a függvény létrehoz egy folytonos vagy mintavételes, lineáris rendszermodellt átviteli függvény alakban. Ez a függvény szintén alkalmazható arra, hogy átalakítsuk az állapottér- vagy zérus-pólus-erősítés modellt átviteli függvény alakra.
Mintapélda :
>>s = tf('s')
Ez az utasítás megadja, hogy egy folytonos átviteli függvényt kívánunk definiálni ( s / 1). Ha begépeltük ezt az utasítást, használhatjuk a LabVIEW MathScript függvényeket ezen az átviteli függvényen, hogy megkapjunk egy zérus-pólus-erősítés vagy egy átviteli függvény modellt.
SysOutZPK = 4*(s + 2) / (s + 1)
Ez a mintapélda egy zérus-pólus-erősítés modellt hoz létre 4-szeres erősítéssel és két nevezőbeli gyökkel a -2 és a -1 helyen.
SysOutTF = (3*(s*s*s) + 2) / (4*(s*s*s*s) + 8)
Ez a mintapélda egy átviteli függvény modellt hoz létre, amely a következő alakú:
|
|
(C.34) |
[ Mintapélda vége]
C.5.1.3. Elsőrendű arányos rendszer PT1 (First Order Systems)
A következő függvény egy elsőrendű arányos rendszert definiál:
|
|
(C.35) |
ahol
|
K |
erősítés, |
|
|
T |
időállandó [s], |
|
|
τ |
késleltetési idő [s]. |
Függvény : sys_order1
Leírás :
Ez a függvény létrehoz egy elsőrendű arányos rendszermodellt, amely egy erősítés, egy időállandó és egy késleltetési idő paramétert tartalmaz. A függvényt arra is alkalmazhatjuk, hogy állapottérmodellt vagy átviteli függvény modellt hozzunk létre a kimeneti paraméterektől függően, amelyeket mi adunk meg.
Bemeneti paraméterek :
|
K |
Megadja az erősítés mátrixot. K egy valós értékeket tartalmazó mátrix. |
|
|
tau |
Megadja az időállandó értékét másodpercben, amely a modellkimenet számára szükséges, hogy az állandósult érték 63%-át elérje. Alapértéke 0. |
|
|
delay |
Megadja a modell kimeneti válaszának késleltetési idejét másodpercben. Alapértéke 0. |
Mintapélda :
K = 0.5; tau = 1.5; SysOutTF = sys_order1(K, tau, delay);
[ Mintapélda vége]
C.5.1.4. Másodrendű arányos rendszer PT2 (Second Order Systems)
A következő függvény egy másodrendű arányos rendszert definiál:
|
|
(C.36) |
ahol
|
K |
erősítés, |
|
|
ζ |
(zeta) a relatív csillapítási tényező [], |
|
|
a csillapítatlan rezonancia frekvencia [rad/s]. |
Függvény : sys_order2
Leírás :
Ez a függvény létrehoz egy másodrendű arányos rendszermodellt, amely egy erősítés, egy relatív csillapítási tényező és egy csillapítatlan rezonancia frekvencia paramétert tartalmaz. A függvényt arra is alkalmazhatjuk, hogy állapottérmodellt vagy átviteli függvény modellt hozzunk létre a kimeneti paraméterektől függően, amelyet mi adunk meg.
Mintapélda :
Amely megmutatja, hogy miként használjuk a sys_order2 függvényt:
dr = 0.5 wn = 20 [num, den] = sys_order2(wn, dr) SysTF = tf(num, den) [A, B, C, D] = sys_order2(wn, dr) SysSS = ss(A, B, C, D)
[ Mintapélda vége]
C.5.2. A Kapcsolat (connect) függvényosztály
Leírás :
A függvényosztály elemeit arra használjuk, hogy különböző topológiájú hálózatba kapcsoljunk össze rendszermodelleket.
A (Táblázat C.4) táblázatban megtekinthetők a connect függvényosztályban rendelkezésre álló különböző függvények.
|
Függvény |
Leírás |
|---|---|
|
append |
Összefűzi a rendszermodelleket |
|
diag |
Olyan rendszermodellt hoz létre, amelynek diagonális elemei másolatai egy másik modellnek |
|
feedback |
Két rendszermodellt összekapcsol visszacsatolt hurok struktúrában |
|
hconcat |
Horizontálisan öszekapcsol két vagy több rendszermodellt |
|
parallel |
Két rendszermodellt párhuzamosan kapcsol |
|
series |
Két rendszermodellt sorosan kapcsol |
|
vconcat |
Vertikálisan öszekapcsol két vagy több rendszermodellt |
C.5.2.1. Soros kapcsolat (series)
Leírás :
Ez a függvény összekapcsol két rendszermodellt soros kapcsolásban, hogy létrehozza a SysSer eredő rendszermodellt azzal a bementi és kimeneti összekapcsolásokkal, amelyet definiált. A bemeneti modellek lehetnek folytonos vagy mintavételes modellek megadott mintavételi idővel.
Mintapélda :
SysIn_1 = tf([1, 1], [1 -1, 3]) SysIn_2 = zpk([1], [1, -1], 1) SysSer = series(SysIn_1, SysIn_2)
[ Mintapélda vége]
C.5.3. Az Átalakítás (convert) függvényosztály
Leírás :
A függvényosztály elemeit arra használjuk, hogy átalakítsuk a folytonos rendszermodelleket mintavételes modellé vagy fordítva a mintavételes modellekből folytonos modelleket hozzunk létre, és újra mintavételezzük a mintavételes modellt. A függvényosztály elemeivel létrehozhatunk késleltetéseket egy rendszermodellben.
A (Táblázat C.5) táblázatban tanulmányozhatók a convert függvényosztályban rendelkezésre álló különböző függvények.
|
Függvény |
Leírás |
|---|---|
|
c_to_d |
Folytonos rendszermodellt mintavételes rendszermodellé transzformál megadott mintavételi idővel. |
|
d_to_c |
Mintavételes rendszermodellt (megadott mintavételi idővel), folytonos rendszermodellé transzformál. |
|
d_to_d |
Új mintavételezési időhöz kiszámítja a korábbi mintavételezési idővel felírt rendszermodellt. |
|
delay_to_z |
Késleltetést hoz létre a mintavételes rendszerben. |
|
distributedelay |
Minimalizálja a szállítási késleltetést a rendszermodellben. |
|
pade |
Létrehoz egy folytonos késleltetést a Pade approximáció alkalmazásával. |
|
polycoef |
Megadja, hogy az átviteli függvény együtthatói növekvő vagy csökkenő sorrendben legyenek felírva. |
|
ss_to_ss |
Állapottranszformációt alkalmaz a rendszermodellre. |
C.5.3.1. Padé approximáció (Padé-approximation)
A késleltetés átviteli függvénye:
|
|
(C.37) |
Néhány helyzetben ezt az exponenciális kifejezést helyettesíteni kell egy közelítéssel, például a Padé közelítéssel:
|
|
(C.38) |
Függvény : pade
Leírás :
Ez a függvény egy időkésleltetést hoz létre a rendszermodellben a Pade approximáció segítségével.
Az időkésleltetést a bemeneten és a kimeneten a set függvény segítségével állíthatjuk be.
Arra szintén alkalmazhatjuk a függvényt, hogy meghatározzuk a számlálóban és a nevezőben szereplő polinom együtthatóit, amelyek létrehozzák a késleltetést.
Mintapélda :
SysCon = zpk(1, 3.2, 6) SysCon = set(SysCon, 'inputdelay', 6, 'outputdelay', 1.1) SysDel = pade(SysCon, 2) delay = 1.2 order = 3 [num, den] = pade(delay, order)
[ Mintapélda vége]
C.5.4. Frekvenciaválasz analízis (Frequency Response Analysis)
A dinamikus rendszer frekvenciaválasza egy frekvenciafüggő függvény, amely kifejezi, hogy adott frekvenciájú és adott amplitúdójú szinuszos jel hogyan jut keresztül a vizsgált rendszeren.
A frekvenciaválasz nagyon fontos eszköz, amellyel a szűrő kapcsolásokat, illetve szabályozási köröket vizsgálhatunk.
A frekvenciaválaszt meghatározhatjuk kisérletileg (méréssel), illetve az átviteli függvény modell alapján.
Egy rendszer frekvenciaválaszát a rendszer bementére adott szinuszos jel kimeneten megjelenő állandosult állapotbeli értékével adjuk meg. Amikor egy lineáris, állandó együtthatós rendszer állandósult állapotban van, akkor a kimenő jelben csak az amplitúdó (A) és fázistolás () tér el a bemeneti jel azonos paramétereitől.
Ha van egy bemeneti jelünk:
|
|
(C.39) |
A kimeneti jel állandósult állapotban a következő lesz:
|
|
(C.40) |
Az A és a frekvencia függvényei: A = A(ω) és =(ω)
Így az átviteli függvényből:
|
|
(C.41) |
kaphatjuk:
|
|
(C.42) |
Ahol H(jω) a rendszer frekvenciaválasza, amelyet az átviteli függvényből kapunk s=jω helyettesítéssel.
C.5.4.1. Bode diagram (Bode Diagram )
A Bode diagramok nagyon hasznosak a frekvenciaválasz analízisében. A Bode diagram 2 diagramot tartalmaz, a Bode amplitúdó diagramot A(ω) és a Bode fázistolás diagramot (ω).
Az A(ω)-tengely dB-ben (deciBell) van skálázva, ahol x érték deciBell értékét a következő függvénnyel határozzuk meg:
|
|
(C.43) |
A (ω)-tengelyen fokokban (nem radiánokban) adjuk meg a fázistolás értékét.
Függvény : bode
Leírás :
Ez a függvény létrehozza (megrajzolja) a vizsgált rendszer Bode amplitúdó és Bode fázis diagramját. Ezt a függvényt arra is alkalmazhatjuk, hogy egy modell frekvenciafüggvényének amplitúdó- és fázisértékét meghatározza egy megadott frekvencián. Ha nem adjuk meg a kimenet értékét, a függvény kirajzolja a Bode függvényeket.
Mintapélda :
Átviteli függvényünk a következő:
|
|
(C.44) |
Ennek az átviteli függvénynek szeretnénk megrajzolni a Bode diagramjait:
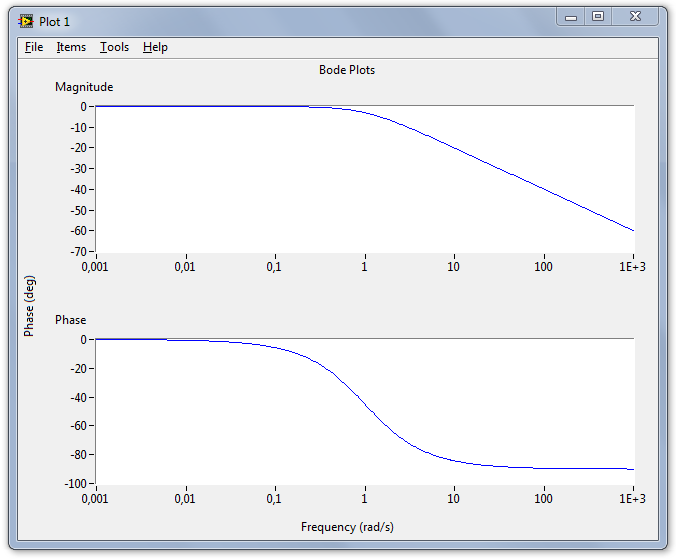
A MathScript-ben ezt kell beírnunk:
num=[1]; den=[1,1]; H1=tf(num,den) bode(H1)
[ Mintapélda vége]
Függvény : margin
Leírás :
Ez a fügvény meghatározza és/vagy megrajzolja egy egybementű és egykimenetű (SISO) rendszermodell legkisebb amplitúdó- és fázistartalék értékét.
A rendszer fázistartalékát azon a frekvenciaértéken határozzuk meg, amelynél az amplitúdó függvény metszi a 0 dB-es tengelyt. (amplitudóvágási frekvencia = ω c )
|
|
(C.45) |
ahol ω c -t a rendszer sávszélességének is nevezzük.
Az amplitudótartalék értékét azon a frekvenciaértéken határozzuk meg, amelynél a fázisfüggvény metszi a -180o-os tengelyt. (fázisvágási frekvencia = ω 180 )
|
|
(C.46) |
Mintapélda :
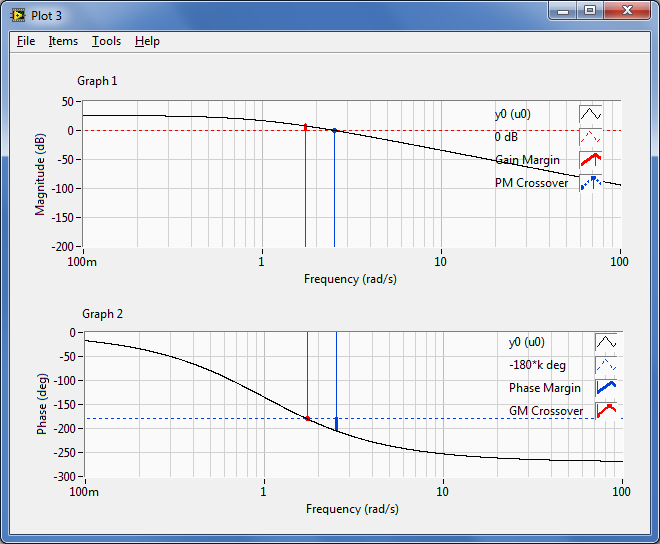
Adott a következő rendszer:
|
|
(C.47) |
Meg akarjuk rajzoltatni a Bode diagramot, és megkeresni a metszési frekvenciákat a MathScript segítségével.
A következő függvényeket fogjuk használni: tf, bode, margins és margin. A következő mennyiségeket határozzuk meg a MatScript-el.
-
gmf erősítés határfrekvencia (gain margin frequency) [rad/s]. Az erősítés határfrekvencia azt frekvenciát jelenti, ahol a modell fázisdiagramja metszi a -180o-os tengelyt.
-
gm a rendszer erősítéstartaléka (gain margins).
-
pmf fázishatárfrekvencia (phase margin frequenciy), [rad/s]. A fázis határfrekvencia azt frekvenciát jelenti, ahol a modell amplitúdó-diagramja metszi a 0 dB-es tengelyt.
-
pm a rendszer fázistartaléka (phase margin).
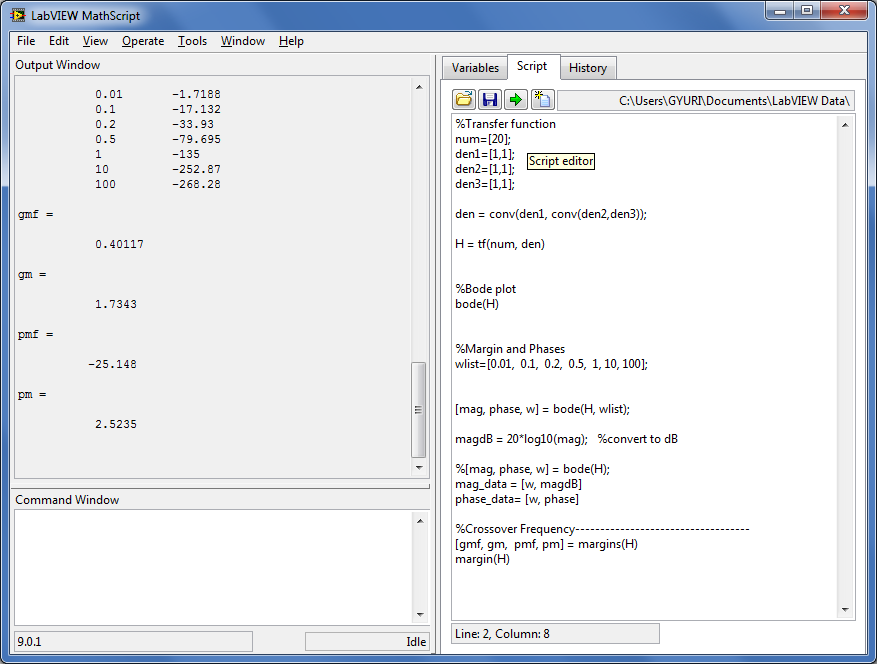
A (C.17. ábra) ábrán láthatjuk a Bode diagramot a metszési frekvenciákkal valamint az erősítés- és fázistartalékokkal, amelyet a program rajzolt meg:
[ Mintapélda vége]
C.5.5. Időtartománybeli válaszfüggvények (Time Response)
Függvényosztály : timeresp (Válaszfüggvény időtartományban)
Leírás :
A válaszfüggvények időtartománybeli meghatásozását arra használjuk, hogy lineáris rendszerek szimulációját valósítsuk meg tetszőleges bemenő jelre, valamint, hogy időtartománybeli diagramokat készítsünk egységugrás, impulzus valamint kezdeti feltétellel rendelkező rendszerhez.
A (Táblázat C.6) táblázatban megtekinthetők a timeresp függvényosztályban rendelkezésre álló függvények.
|
Függvény |
Leírás |
|---|---|
|
impulse |
Meghatározza a rendszermodell impulzusválaszra adott időfügvényét. |
|
initial |
Meghatározza a rendszermodell kimeneteinek időfügvényét, ha rendszermodell állapotai rendelkeznek kezdeti feltételekkel. |
|
lsim |
Meghatározza a rendszermodell tetszőleges bementi jelre adott kimeneti időfügvényét. |
|
randvector |
Létrehoz egy vagy két véletlen vektort. |
|
step |
Meghatározza a rendszermodell egységugrásra adott időfügvényét. |
C.5.5.1. Egységugrásra adott válaszfüggvény (step )
Leírás :
Ez a függvény megrajzolja a rendszermodell egységugrásra adott válaszfüggvényét. Arra is használhatjuk, hogy meghatározzuk az egységugrásra adott válaszfüggvény pontjainak koordinátáit. Ha a modell állapottér alakban van, akkor arra is használhatjuk, hogy meghatározzuk az egyes állapotok egységugrás bemenetre adott válaszfüggvényét. Ez a függvény feltételezi, hogy a számításoknál a rendszer kezdeti állapotai zero (0) értékűek. Ha nem adja meg a kimeneti változó elnevezését, akkor egy diagramot hoz létre.
Mintapélda :
Adott a következő rendszer:
|
(C.48) |
A step függvény alkalmazásával kirajzoljuk a rendszer egységugrás bemenetre adott válaszfüggvényét. Az eredmény a (C.18. ábra) ábrán látható.
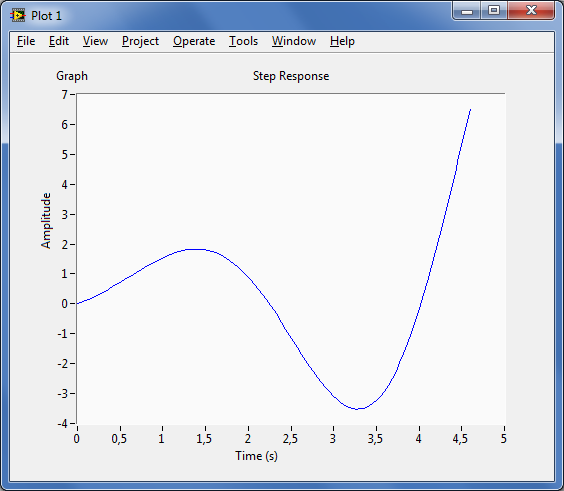
A MathScript kód:
H = tf([1, 1], [1, -1, 3]) step(H)
[ Mintapélda vége]
C.6. A MathScript blokk a LabVIEW programban (MathScript Node)
A MathScript blokk (MathScript Node) egy kombinált szöveg típusú és grafikus programozási lehetőséget biztosít LabVIEW-ban. A C.19. ábra ábra bemutatja a MathScript blokkot, amelyet a kék négyszög keret reprezentál. A MathScript blokkot úgy használjuk, hogy belegépeljük a végrehajtandó utasításokat, vagy beolvassuk a végrehajtandó kódot egy ”.m” fájlból.
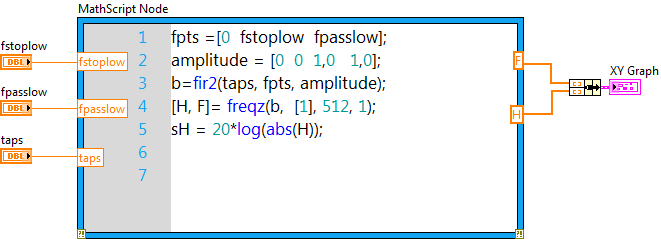
Megadhatunk névvel rendelkező bemeneteket és kimeneteket a MathScript blokk keretén, ezzel biztosítva az adatforgalmat a grafikus LabVIEW környezet és a szöveges MathScript kód között.
Hozzárendelhetjük az ”.m” fájlban tárolt program script változóit a LabVIEW változóihoz azzal, hogy egyszerűen összehuzalozzuk a MathScript változóit a LabVIEW változókkal. Ezután a változók átadják aktuális értéküket a másik program-interpretáció változóinak. Így a szöveg típusú ”.m” fájlokok elérhetik a LabVIEW szolgáltatásait és megfordítva.
A MathScript blokkot a LabVIEW Function palettájáról a Programming > Structures (1) ikonoknál találjuk(C.20. ábra).
A MathScript blok a LabVIEW Function palettájáról a Mathamatics > Scripts & Formulas (2) ikonoknál is megtalálható (C.21. ábra).
Ha lenyomjuk a Ctrl+H billentyűket, megtekinthetjük a MathScript segítségnyújtó (help) ablakát (C.22. ábra).
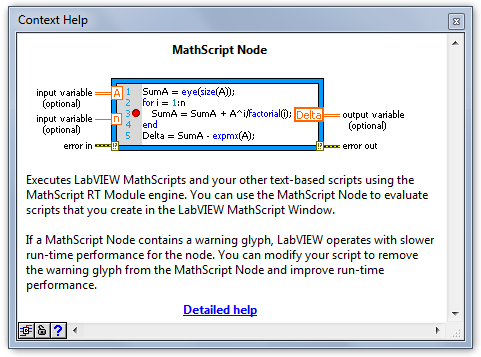
A Részletezett segítség (Detailed help) hivatkozásra kattintva (C.22. ábra) még több információt kapunk a MathScript blokk működéséről.
Használhatjuk az NI Example Finder (Példa keresőt) is, hogy további példákat találjunk a MathScript alkalmazására (C.23. ábra).
C.6.1. MathScript blokkok átvitele számítógépek között (Transferring MathScript Nodes between Computers)
Ha egy MathScript blokkban egy felhasználó által definiált függvény hívunk, a LabVIEW az alapéretlemezett keresési könyvtárat használja, hogy meghívja a megadott ”.m” fájlt. Miután beállítottuk az alapértelmezett keresési könyvtárlistát, és mentjük a VI-t, amely tartalmazza a MathScript blokkot, nem kell újra konfigurálnunk a MathScript keresési listát, amikor megnyitjuk a VI-t egy másik számítógépen. Ekkor a LabVIEW megkeresi az ”.m” állomány könyvtárát, amely a legutolsó programmentéskor tartalmazta a fájlt. Összesítve csak néhány relatív könyvtárat kell módosítanunk a VI és az ”.m” fájl kapcsolatában.
C.6.2. Mintapéldák
Mintapélda : A MathScript blokk használatára:
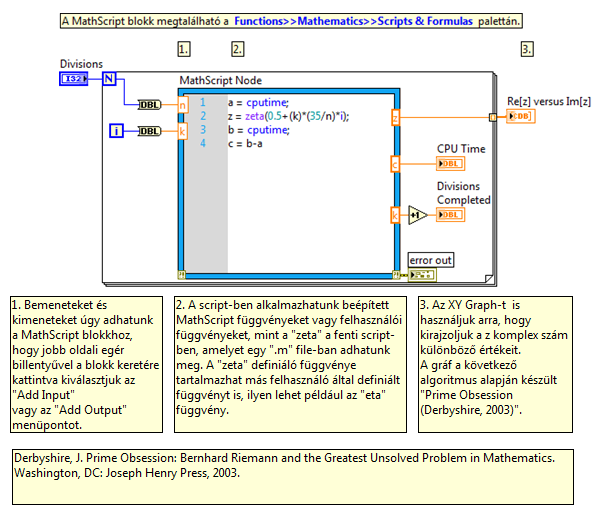
Itt van egy mintapélda hogyan használhatjuk a MathScript blokkot. A blokk bal oldalán köthetjük be a bemeneti változókat és jobb oldalán a kimeneti változókat. A blokk keretén jobb egérbillentyűvel kattintva hozhatjuk létre a változókat, ha a felbukkanó menüből kiválasztjuk az “Add Input” vagy “Add Output” menüpontokat.
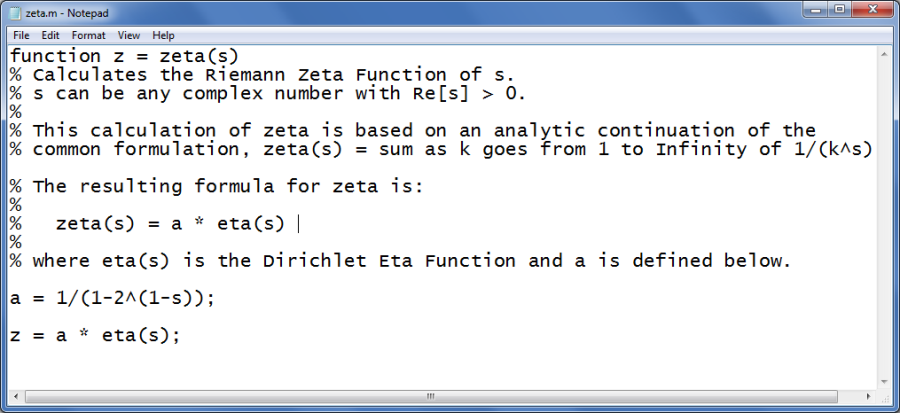
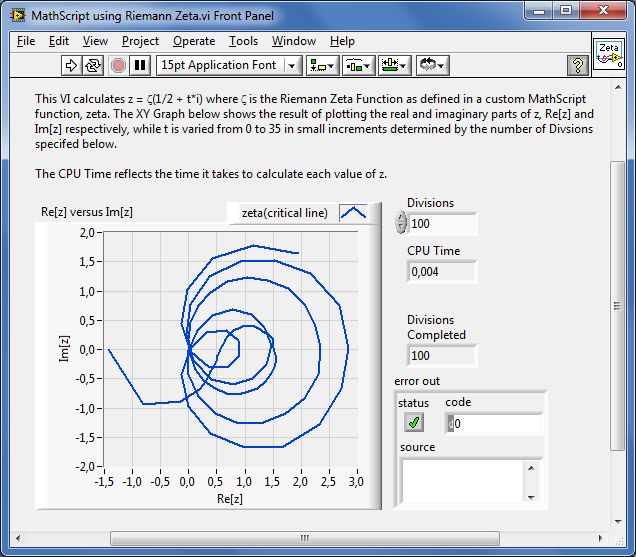
[ Mintapélda vége]
Mintapélda : Windows DLL függvényeinek hívása MathScript-ben:
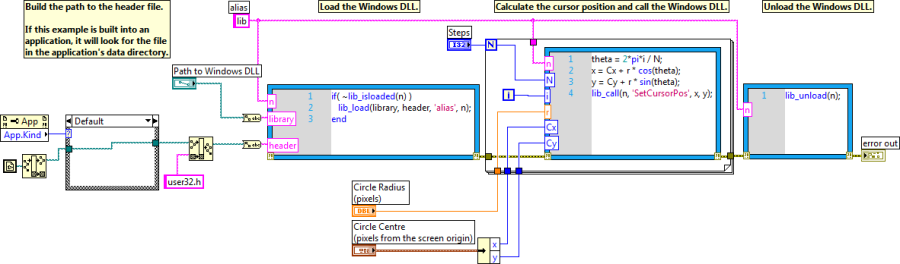
[ Mintapélda vége]
Mintapélda : ”.m” fájlok használata MathScript blokkban:
A LabVIEW MathScript-et arra használjuk, hogy létrehozzunk vele egy ”.m” fájlt (de létrehozhatjuk ugyanezt a programscriptet a MATLAB-al is) (C.28. ábra).
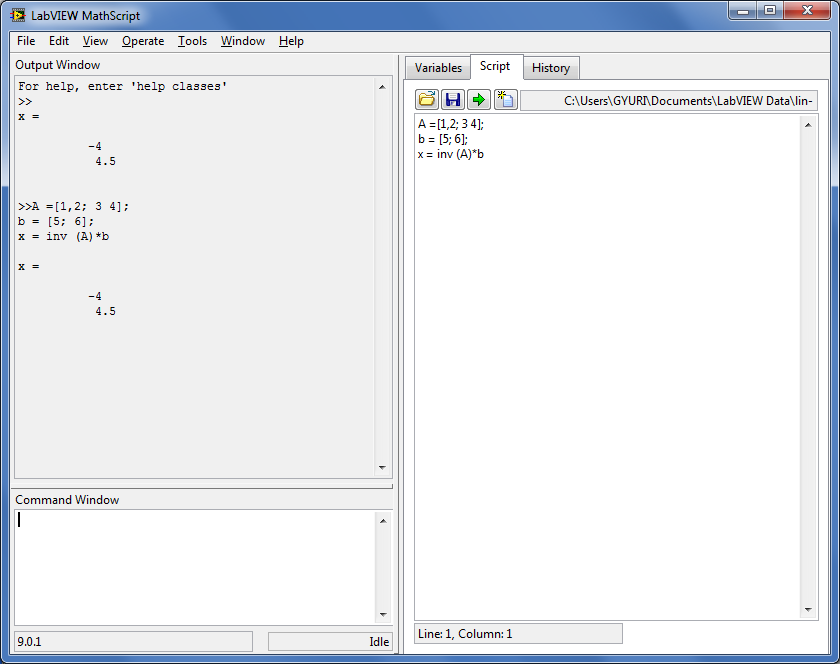
Egy korábban megírt scriptet úgy olvashatunk be, hogy a MathScript blokk keretén a jobb oldali egérbillentyűvel kattintva kiválaszthatjuk az Import (Behozás) menüpontot, és kijelöljük azt az ”.m” fájlt, amit be akarunk másolni a blokkba.
Ha a MathScript blokk keretén a jobb oldali egérbillentyűvel kattintunk, kiválaszhatjuk az Add Output (Hozz létre egy új kimeneti változót) menüpontot. Ezután a változó területén kattintva a jobb oldali egérbillentyűvel válasszuk ki a Create Indicator (Hozz létre kimeneti változót a Front panelen) menüpontot!
Blokk diagram :
A program eredménye a futtatás után (Kattintsunk a Run gombra!):
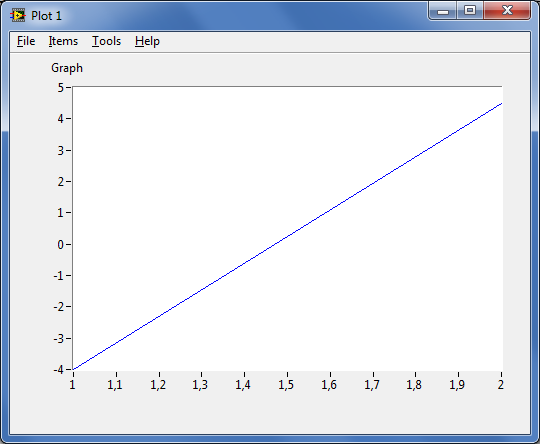
Ha például hozzáadjuk a plot(x) utasítást a MathScript blokkhoz, a (C.32. ábra) ábrán látható ablak jelenik meg.
[ Mintapélda vége]