B. függelék - Dinamikus rendszerek szimulációs eszközei – a LabVIEW Simulation Module
- B.1. Modell létrehozása
-
- B.1.1. Jelgenerátorok (Signal Generation)
- B.1.2. Jelaritmetika (Signal Arithmetics)
- B.1.3. Jelmegjelenítési elemek (Graph Utilities)
- B.1.4. Folytonos lineáris rendszerek (Continuous Linear Systems)
- B.1.5. Folytonos nemlineáris rendszerek (Nonlinear Systems)
- B.1.6. Mintavételes lineáris rendszerek (Discrete Linear Systems)
-
- B.1.6.1. Discrete Unit Delay (Mintavételes egységnyi késleltetés függvény)
- B.1.6.2. Discrete Zero-Order Hold (Mintavételes nulladrendű tartó függvény)
- B.1.6.3. Discrete First-Order Hold (Mintavételes elsőrendű tartó függvény)
- B.1.6.4. Discrete State-Space (Mintavételes állapottér modell)
- B.1.6.5. Discrete Transfer Function (Mintavételes impulzus-átviteli függvény modell)
- B.1.7. Táblázattal megadott szimulációs paraméterek (Lookup Tables)
- B.2. Modellelemek összekapcsolása
- B.3. Almodell (Subsytem) létrehozása
- B.4. A szimulációs modell vizsgálata időtartományban
A LabVIEW program számos modult tartalmaz, amelyekkel egyszerűbbé válik a folytonos és a mintavételes rendszerek irányítási tervezése. A programcsomagban a következő elemek találhatók:
-
Rendszertervezés (LabVIEW Control Design Module)
-
Szimulációs modul (LabVIEW Simulation Module)
-
MathScript Rt modul (LabVIEW MathScript RT Module)
-
Identifikációs eszköz (LabVIEW System Identification Toolkit)
-
PID szabályozó és Fuzzy szabályozó tervezése (LabVIEW PID and Fuzzy Logic Toolkit)
-
Matlab-LabVIEW szimulácós modell kapcsolati eszköz (LabVIEW Simulation Interface Toolkit)
Ebben a programismertetőben a Szimulációs modullal (LabVIEW Simulation Module) ismerkedünk meg.
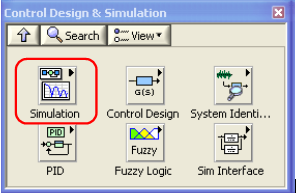
A B.1. ábra bemutatja a Rendszertervezés és Szimuláció (Control Design & Simulation) palettát a LabVIEW-ban
Ebben az ismertetőben elsősorban a folytonos és mintavételes rendszerek átviteli függvényének és állapottér leírásának elemeit kívánjuk bemutatni.
Ha a felsorolt programcsomagok utasításait szeretné részletesen megismerni az Olvasó, akkor tanulmányozza a programcsomagokat ismertető kézikönyveket, amelyek megtalálhatók az ni.com/manuals Internet címen.
A B.2. ábra a Szimuláció (Simulation) palettát mutatja be.
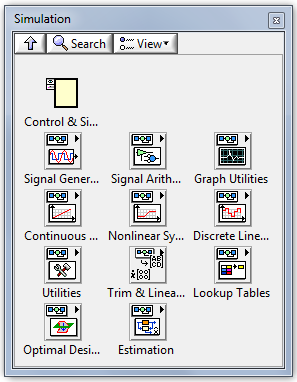
Az elkövetkező fejezetekben bemutatjuk a szimulációs eszközök, alpalettáiban elhelyezett műveleteket, amelyek segítségével modelldefiniálást, illetve a modell adott időtartományban történő szimulációját valósíthatjuk meg.
A Szimuláció (Simulation) paletta elemeinek alkalmazásával tudunk valós időben mérési adatok alapján történő beavatkozást meghatározni.
A Szimuláció (Simulation) paletta elemeiből felépített szimulációs programot két üzemmódban futtathatjuk:
-
Amikor a szimulációs időlépés végrehajtási ideje nincs szinkronizálva a számítógép valós belső óragenerátorához , a szimuláció olyan sebességgel zajlik, mint amit az adott számítógép működési sebessége lehetővé tesz (processzor-órajel, felhasználható memória, számítógép-architektúra)
-
Amikor a szimulációt pontosan annyi időként futtatjuk le, mint a szimulációs időlépés. Ezt nevezzük valós idejű (real time) futásnak, ami azt jelenti, hogy minden művelet pontosan ugyanannyi ideig történik, mint ahogy az a valós rendszerben történne.
A Szimuláció (Simulation) paletta elemeinek alkalmazásával elsősorban ilyen, valós futási idejű (real time) alkalmazásokat tudunk megvalósítani, de természetesen a szimulációs modellek futhatnak úgynevezett időtartam-független (off-line) futási állapotban is, amikor a számítógép által megvalósított szimulációs sebesség eltér a valós rendszer sebességétől.
Az időtartam-független futási állapotban történő futtatásnak is van jelentősége, amikor egy valós időben gyorsan lezajló folyamatot részletesebben szeretnénk tanulmányozni, ezért kis lépésköz alkalmazásával „lelassítjuk a folyamatot”. Más esetben a rendkívül hosszú ideig zajló valós folyamatot a szimulációval „felgyorsítjuk”, és a hosszú, valós (napokig, évekig tartó) időtartamnak megfelelő vizsgálatot néhány másodperc alatt elvégezhetünk.
B.1. Modell létrehozása
A Szimuláció (Simulation) paletta bal felső sarkában látható (B.3. ábra) a While ciklushoz hasonló, a Control & Simulation Loop (Irányítás és szimulációs hurok) elnevezésű struktúra. Ez a struktúra lesz a későbbi szimulációs modell határvonala - ebben a struktúrában elhelyezett szimulációs elemek (LabVIEW VI-ok) a szimulációs keret paramétereivel fognak futni.
Nézzük meg, hogyan is néz ki egy Control & Simulation Loop struktúra, és melyek a tulajdonságai (attribute)

Az Irányítás és szimulációs hurok ( Control & Simulation Loop ) struktúra bal oldalán találhatók azok a szimulációs paraméterek (attribútumok), amelyek meghatározzák, hogy a szimuláció
-
milyen kezdeti időponttól induljon,
-
milyen időtartamig tartson, azaz mi legyen a szimuláció befejezési időpontja,
-
mekkora legyen a szimulációs időlépés,
-
milyen integrálási metódust alkalmazzon a szimulációs modellben található integráló elemek számításához (ebben a választásban az is megjelenik, hogy azonos lépésközű vagy változó lépésközű integrálási metódust alkalmazzon),
-
milyen nagyságú lehet az összes integrátorra a relatív és az abszolút hiba nagysága a szimuláció alatt,
-
mi történjen, ha a szimuláció egy időlépésének kiszámításához szükséges időtartam hosszabb (lett), mint az előírt szimulációs időlépés hossza.
Ehhez hasonló és még számos egyéb paraméter beállítására van lehetőség az Irányítás és szimulációs hurok ( Control & Simulation Loop ) struktúrába történő belépés előtt.
Természetesen a sok-sok bemeneti paramétert nem kell minden egyes szimulációs hurok futtatásakor egyenként megadni, hanem lehetőség van a struktúra keretére történő jobb egérgomb kattintással, majd a „ Configurate Simulation Parameters” (A szimuláció paramétereinek beállítása) menüpont kiválasztásával megnyitni a struktúra paramétereinek beállítását biztosító ablakot.
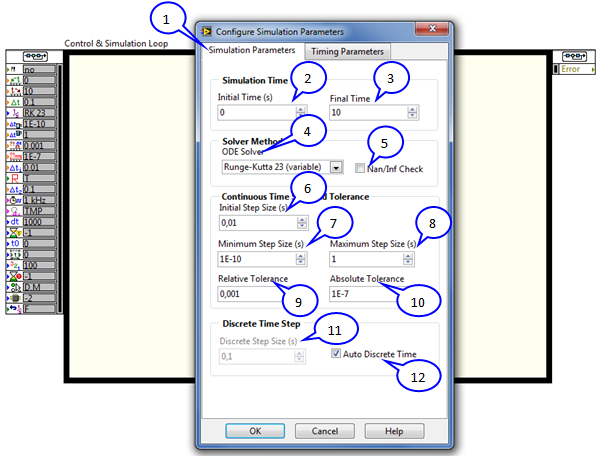
Az ablakban megjelenő fülek közül a szimulációs paraméterek (Simulation Parameters) fület kiválasztva elvégezhetjük a Control & Simulation Loop szimulációja alatt érvényes paraméterek beállítását. Ezek a beállított paraméterek - a szimulációs modell tárolásakor - a modellel és annak paramétereivel együtt tárolódnak.
Lássuk, hogy milyen paramétereket lehet beállítani a szimulációs paraméterek ablakban!
|
# |
Elnevezés |
Feladat |
|---|---|---|
|
1. |
Szimulációs paraméterek (Simulation Parameters) |
A szimulációs alapparaméterek beállítását tudjuk ebben az ablakban beállítani. |
|
2. |
Kezdeti időpont (s) ( Initial Time (s) ) |
A szimuláció kezdő időpontja, másodperc (secundum) dimenzióval. |
|
3. |
A szimuláció befejezésének időpontja (s) ( Final Time (s) ) |
A szimuláció befejeződésének időpontja, másodperc (secundum) dimenzióval. |
|
4. |
Differenciálegyenlet megoldási metódus ( ODE Solver =O rdinary D ifferential E quation Solver ) |
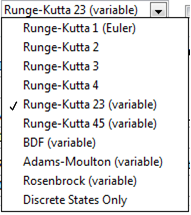
A differenciálegyenlet megoldásnál a következő integrálási metódusokat alkalmazhatjuk. Zárójelben (variable) megjelöléssel szerepelnek a változó lépésközű eljárások. Az eredmények kiírása ezeknél is a megadott szimulációs lépésköznek megfelelő időpontonként történik.
|
|
5. |
Nem megfelelő alakú számérték ( NaN = N ot A N umber) vagy végtelen érték ( Inf = Inf inite) ellenőrzésése a szimuláció során. ( Nan/Inf Check ) |
Ezzel a kapcsolóval (jelölőnégyzettel) lehetőségünk van, hogy előírjuk a szimulációs program megállítását, ha valamelyik szimulált érték nem megfelelő alakú számérték (pl. komplex szám valós szám helyett) vagy ha szimulált érték végtelen nagyságú. |
|
6. |
Kezdeti időlépés méret [s] ( Initial Step Size (s) ) |
A szimuláció időlépésének kijelölt értéke másodperc [s] dimenzióban. Nem változó lépésközű integrálásnál az integrálás ezzel a lépésközzel történik. Változó lépésközű integrálásnál az eredmények kiírása ezzel a lépésköz mérettel történik. Két lépésköz között pedig a kisebb lépésközzel – tehát pontosabban érték meghatározásával történik a szimuláció. |
|
7. |
Minimális lépésköz érték [s] (Minimum Step Size (s)) |
Változó lépésközű integrálási eljárás esetén a lépésköz csökkentése, amely pontosabb számítást eredményez - eddig az értékig csökkenthető. |
|
8. |
Maximális lépésköz érték [s] (Maximum Step Size (s)) |
Változó lépésközű integrálási eljárás esetén a lépésköz növelése, amely gyorsabb számítást eredményez, eddig az értékig növelhető. |
|
9. |
Relatív hiba [] (Relativ Tolerance) |
Elméletben az abszolút hiba osztva a valódi értékkel . Miután azonban ezt nem ismerjük, helyére osztóként a helyes érték kerül. |
|
10. |
Abszolút hiba [] (Absolute Tolerance) |
Elméletben a mért és a valódi érték közötti különbség . A gyakorlatban a valódi érték helyére a helyes érték kerül. |
|
11. |
Mintavételes (idő) lépésköz értéke [s] (Discrete Step Size (s)) |
Az Irányítás és szimulációs hurok (Control & Simulation Loop) struktúra biztosítja a folytonos rendszerek szimulációja mellett a mintavételes rendszerek adott mintavételi időtartammal történő futtatását is. A mintavételes rendszereket az Irányítás és szimulációs hurok az itt megadott mintavételezési (idő) lépésköz értékkel határozza meg. A mintavételezési időtartam értékét tetszőlegesen választott értékre állíthatjuk be, ha nincs bekapcsolva a Mintavételes érték automatikus kiválasztása (Auto Discrete Time) kapcsoló. A „tetszőlegesen választott érték” meghatározásánál, figyelembe kell venni, hogy a mintavételezési időnek minimálisan 10-szer nagyobbnak kell lennie, mint a szimuláció lépésközeként megjelenő legnagyobb érték. Ha a Mintavételes érték automatikus kiválasztása (Auto Discrete Time) kapcsoló bekapcsolt állapotban van, akkor a mintavételi időtartam megegyezik a kezdeti időlépés mérettel (Initial Step Size (s)). |
|
12. |
Mintavételes érték automatikus kiválasztása (Auto Discrete Time) |
A mintavételi idő automatikus kiválasztása esetén a mintavételi idő kiválasztása a szimulációs rendszer paraméterei alapján történik. Általános ökölszabályként megállapítható, hogy a mintavételezési időtartam általában a kezdeti időlépés méret [s] minimum 10-szerese. |
A szimuláció paramétereinek beállítása ( Configurate Simulation Parameters ) ablak második fülén az időzítési paraméterek ( Timing Parameters ) helyezkednek el, ahol be lehet állítani a paramétereket a szimuláció valós idejű futtatásához.
Ha NEM valós idejű futtatást szeretnénk megvalósítani, akkor nem kell semmilyen paramétert beállítani ebben az ablakban!
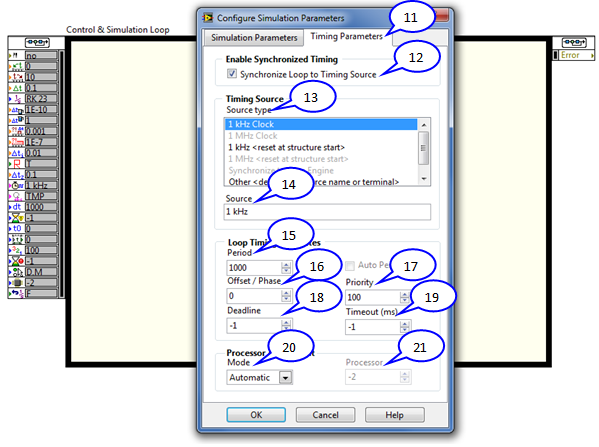
|
# |
Elnevezés |
Feladat |
|---|---|---|
|
11. |
Időzítési paraméterek ( Timing Parameters ) |
Az időzítési paraméterek kiválasztását biztosító ablak. |
|
12. |
A szimulációs hurok szinkronizálása egy időalap-generátorhoz ( Syncronize Loop to Timing Source ) |
Ezzel a kiválasztó elemmel (jelölőnégyzettel) lehetőségünk van a szimuláció időparamétereinek értékét összekapcsolni a valós idejű futást biztosító időalap-generátorok egyikével. Ha a kiválasztó elem kikapcsolt állapotban van , akkor a szimuláció a számítógép tulajdonságaival meghatározott maximális sebességgel fut (off-line futás). Ha a kiválasztó elem bekapcsolt állapotban van , akkor a számítógép összerendeli a szimulációs lépésközt az időalap-generátorok egyikével, és a szimulációs lépésközt az időgenerátorral meghatározott értékre állítja. |
|
13. |
Az időalap-generátor típusa ( Source Type ) |
Az időalap-generátor egyszerű PC környezetben futó LabVIEW esetén 1 kHz értékű, ami azt jelenti, hogy a legkisebb megvalósítható időlépés 1 ms nagyságú. Külső egység hozzákapcsolásával (külső RT (Real Time) rendszer) az időalap-generátorának frekvenciaértéke megnövelhető, mivel egy külső egységnek nem kell az operációs rendszert is futtatnia, csakis az elvégzendő mérési/beavatkozási feladattal foglakozhat. Az NI külső a PC-hez hozzákapcsolható rendszerekben ez a frekvencia 1MHz. Ez az időgenerátor már 1 mikroszekundumos mintavételi időtartamot is lehetővé tesz. |
|
14. |
Az időalap-generátor elnevezése ( Source ) |
A kiválasztott időalap-generátor elnevezése. |
|
15. |
A mintavételezés periódusideje ( Periode ) |
A szimuláció lépésközeként kiválasztott érték és a kiválasztott időalap-generátor periódusidejének szorzata. Például, ha Periode=1000 és az időalap-generátor 1 kHz frekvenciájú (1 ms periódusidejű), akkor az így kialakított mintavételezési periódusidő 1 s nagyságú lesz. |
|
16. |
A mintavételezés periódusidejének eltolása ( Offset / Phase ) |
Több, ugyanazon VI-ban elhelyezett Irányítás és szimulációs hurok (Control & Simulation Loop) struktúra számítási időpontjai közötti eltérést lehet ezzel a paraméterrel megadni. Időben a két struktúra számítási időpontjai közötti eltérés a mintavételezés periódusidejének eltolása és a kiválasztott időalap-generátor periódusidejének szorzata. |
|
17. |
Prioritás ( Priority ) |
Több, ugyanazon VI-ban elhelyezett Irányítás és szimulációs hurok (Control & Simulation Loop) struktúra számítási sorrendjét lehet ezzel a paraméterrel megadni. Nagyobb pozitív számérték nagyobb prioritást jelent! |
|
18. |
Határidő ( Deadline ) |
Megadja azt az időtartamot, amely alatt az Irányítás és szimulációs hurok (Control & Simulation Loop) struktúrának be kell fejeznie egy iterációt. A Határidő értéke megegyezik a mintavételezés periódus idejével, ha nem változtatjuk meg az alapállapotként beállított -1 értéket. A Határidő paraméter értékét a szimuláció kezdő (eltolással megnövelt) időpontjától számítjuk. A Határidő értékét a beírt számérték és az időalap-generátor periódusidejének szorzatával kapjuk meg. |
|
19. |
Időtúllépés [ms] ( Timeout (ms) ) |
Azt az időtartamot adja meg ms-ban, amelynek letelte után a program megszakítja a szimulációt, mert működési rendellenességet észlelt. Az Időtúllépés paraméter beállításával tudjuk megvizsgálni, hogy az összekapcsolt berendezések az Időtúllépésnél kisebb idő alatt reagálnak az őket ért hatásra. Ha az Időtúllépés-értéknél hosszabb idő alatt sem reagálnak, akkor a szimulációs program futása megszakad. Mi okozhatja ezt a problémát? A szimulációs rendszer blokkjai között az irányítási feladat megoldása esetén mérési adatokat szolgáltató A/D, illetve számított adatokat analóg mennyiségekké alakító D/A átalakítók szerepelnek. Ezek működési meghibásodása „késleltetheti” a számítások adott ütemben történő elvégzését. |
|
20. |
Processzor kiválasztási mód ( Processor Mode ) |
A Processzor kiválasztási mód lehetséges értékei:
Automatikus processzor kiválasztás esetén a LABVIEW kiválasztja a számítógépben erőforrásként rendelkezésre álló processzorok egyikét, hogy hajtsa végre a szimulációs időzítési feladatokat. A feladat erőforrásigénye alapján több, lassú folyamat ugyanazt a processzort használhatja. Alapértéke = -2. Kézi processzor kiválasztás esetén egy 0-tól 255-ig terjedő szám segítségével megadhatjuk, hogy a szimulációs hurok melyik processzoron fusson. |
|
21. |
A kiválasztott processzor sorszáma ( Processor ) |
Automatikus processzor kiválasztás esetén, alapértéke = -2. Kézi processzor kiválasztás esetén 0-tól 255-ig beállított érték. |
Miután létrehoztuk a szimuláció keretét, felépíthetjük a dinamikus rendszermodell szimulációs programját.
Ezt a szimulációs rendszert úgy tervezték, hogy a dinamikus rendszermodell alapvető (építő) elemeiből felépített számítási blokkdiagramot létrehozzuk a szimulációs keretben , és így valósítjuk meg a számítási algoritmust.
A modellépítő elemek között találunk egyszerű és bonyolult blokkokat, de biztosak lehetünk benne, hogy minden olyan szimulációs programot felépíthetünk a segítségükkel, amely meghatározott bemenő jelre egy dinamikus modell alapján válaszfüggvényt határoz meg az időtartományban.
A felhasználható modellelemeket a Szimuláció (Simulation) palettán (B.7. ábra) találjuk meg funkció szerinti csoportokban.
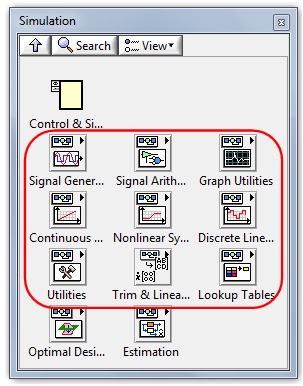
A modell létrehozásához leggyakrabban használt alpaletták:
|
|
Signal Generation (Jelgenerátorok) |
|
|
|
Signal Arithmetics (Jelaritmetika) |
|
|
|
Graph Utilities (Jelmegjelenítési elemek) |
|
|
|
Continuous Linear Systems (Folytonos lineáris rendszerek) |
|
|
|
Nonlinear Systems (Folytonos nemlineáris rendszerek) |
|
|
|
Discrete Linear Systems (Mintavételes lineáris rendszerek) |
|
|
|
Lookup Tables (Táblázattal megadott szimulációs paraméterek) |
B.1.1. Jelgenerátorok (Signal Generation)
A Jelgenerátorok palettán olyan szimulációs elemeket találunk, amelyeknek csak kimeneti jele van !
Ez azt jelenti, hogy ezeknek a blokkoknak nincs bemenő jele, hanem a bementi paraméterek alapján egy adott mintázatú kimenő jelet bocsájtanak ki.
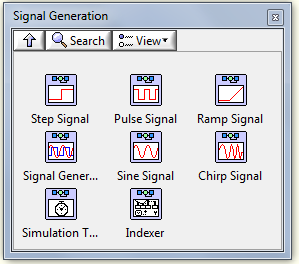
A modell létrehozásához leggyakrabban használt alpaletták:
|
|
Step Signal Generation (Ugrás függvény) |
|
|
|
Pulse Signal (Négyszögjel függvény) |
|
|
|
Ramp Signal (Sebességugrás függvény) |
|
|
|
Signal Generator (Jelgenerátor) |
|
|
|
Chirp Signal (Végigsöprő szinusz jelgenerátor) |
|
|
|
Simulation Time (A szimuláció aktuális időpontja) |
B.1.1.1. Step Signal Generation (Ugrás függvény)
A Step Signal Generation (Ugrás függvény) definíciója a következő:
|
y(t) = kezdeti érték( initial value ) (ha t < ugrási időpont( step time )) |
(B.1) |
|
|
y(t) = végérték ( final value ) (ha t >= ugrási időpont( step time )) |
|
ahol t az aktuális szimulációs időpont, y a generátorblokk kimenete. A jel aktuális értéke az aktuális szimulációs időponttól függ.
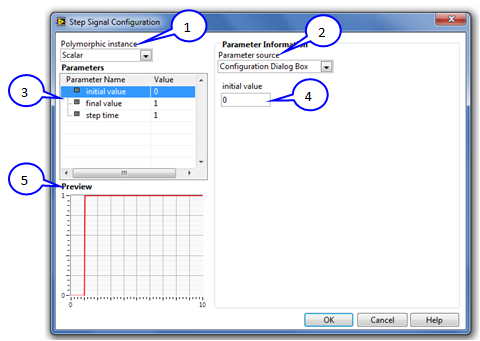
Az B.9. ábra 1. pontjánál szereplő Polimorphic Instance (Jeltípus választó) legördülő menüben beállíthatjuk, hogy csak egyetlen vagy hasonló típusú blokkokból egy vektorfüggvényt szeretnénk megvalósítani. A vektor típusú adat esetén a vektorban szereplő Ugrásfüggvény- generátorok mindegyike egyéni paraméterekkel rendelkezhet (kezdeti érték, végérték, ugrási időpont).
Az B.9. ábra 2. pontjánál szereplő Parameter Source (Paraméter forrás) legördülő menüben beállíthatjuk, hogy az aktuális paraméter értékét a dialógus ablakban megadott értékből (Configuration Dialog Box (Konfigurációs Dialógus ablakból)), vagy a blokk bemeneti paramétereként (Terminal (Ikon paraméterként)) szeretnénk ellátni adattal.
A Terminal (Ikon paraméterként) megjelenő bemeneti érték teljesen hasonló, mint a szokásos VI-ok bemeneti paramétere, azaz a program futása alatt tetszőleges értéket vehet fel. Ennek a bemeneti paramétertípusnak az a jelentősége, hogy a szimuláció időtartama alatt is változtathatjuk az értékét, így időben változó paraméterértékeket valósíthatunk meg.
Az B.9. ábra 3. pontjánál szereplő Parameters (Paraméterek) táblázatban a megfelelő paraméterre kattintva az egérrel, a B.9. ábra 4. pontjánál szereplő, a változó típusához aktualizálódó, a paraméter elnevezésével azonos mezőben állíthatjuk be a paraméter értékét.
Az B.9. ábra 5. pontjánál szereplő grafikonban tekinthetjük meg a kialakított jelalak időbeni lefutását.
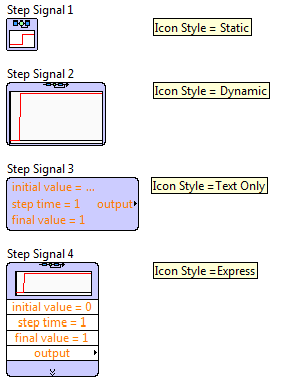
A Step Signal Generation (Ugrás függvény) (és az összes további szimulációs blokk ehhez hasonlóan) a következő alakban jelenhet meg a programban. A megjelenítés formáját a blokk területére jobb egérgombbal kattintva, a megjelenő menüből az „Icon Style” menüpontnál állíthatjuk be, ahogy azt az előző ábrán (B.10. ábra) láthatjuk.
-
A Static ikon stílus a LabVIEW-ban szokásosan megjelenő normál ikonalak.
-
A Dynamic ikon stílusnál lehetőség van az ikon méretét megváltoztatni (növelni), és a jel alakját bemutató kép automatikusan kitölti az aktuális ikonméretet.
-
A Text Only ikon stílusnál a blokk bemenő paraméterei szöveges formában jelennek meg az ikon képében. Az ikon megmutatja azokat az értékeket, amelyek a szimulációs blokkban beállított értékkel rendelkeznek.
-
Az Express ikon stílusnál a bemeneti és kimeneti paraméterek táblázatszerűen jelennek meg. Itt is láthatók az ikonban azok az értékek, amelyek már beállított értékkel rendelkeznek.
B.1.1.2. Pulse Signal (Négyszögjel függvény)
A Pulse Signal (Négyszögjel függvény) definíciója a következő:
|
y(t) = A * negyszog |
ahol
|
|
(B.2) |
|
A |
az amplitúdó ( amplitude ), |
|
|
f |
a frekvencia (1/ periode ) [Hz], |
|
|
p |
a jel eltolásának értéke ( offset ), |
|
|
D |
a kitöltés mértéke [0..100%] ( duty cycle ), |
|
|
mod |
modulo – maradékos osztás maradék értéke. |
t az aktuális szimulációs időpont, y a generátorblokk kimenete. A jel aktuális értéke az aktuális szimulációs időponttól függ.
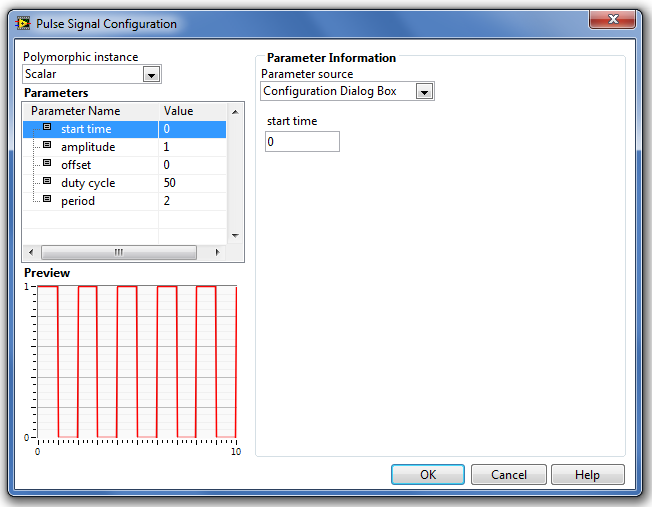
A paraméterek típusát és beállításuk módját a Step Signal Generation (Ugrás függvény) fejezetben részletesen ismertettük.
B.1.1.3. Ramp Signal (Sebességugrás függvény)
A Ramp Signal (Sebességugrás függvény) definíciója a következő:
|
y(t) = y(0) (ha t <= kezdeti időpont( start time )) |
(B.3) |
|
|
y(t) = y(0)+m*t (ha kezdeti időpont( start time ) < t) |
|
ahol
|
y(0) |
a kimenet kezdeti értéke t=0 időpillanatban ( initial value ), |
|
|
m |
meredekség ( slope), |
|
|
kezdési időpon t |
a sebességugrás függvény kezdő időpontja ( start time ), |
ahol t az aktuális szimulációs időpont, y a generátorblokk kimenete.
Ramp Signal (Sebességugrás függvény) kimenete a kezdeti értékkel indul, és azzal a meredekség értékkel változik, amely az adott időpontban érvényes (konstans vagy a bemeneten változtatott érték).
A jel aktuális értéke az aktuális szimulációs időponttól függ.
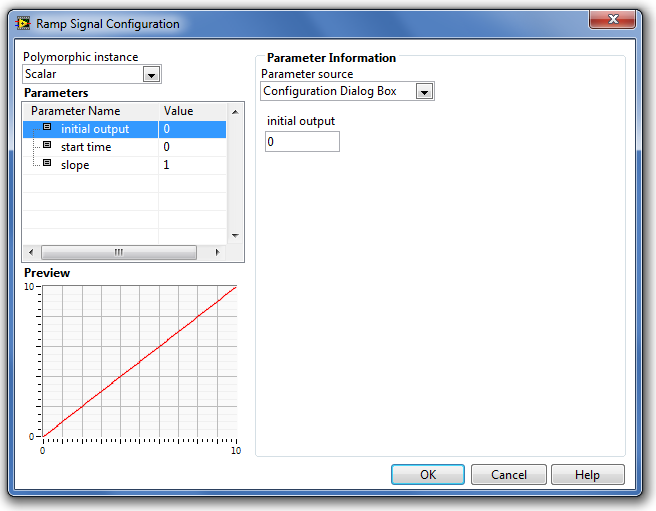
A paraméterek típusát és beállításuk módját a Step Signal Generation (Ugrás függvény) fejezetben részletesen ismertettük.
B.1.1.4. Signal Generator (Jelgenerátor)
A Signal Generator (Jelgenerátor) különböző függvényeinek definíciója a következő:
Szinusz függvény ( Sinus ):
|
|
(B.4) |
Négyszögjel függvény ( Pulse ):
|
y(t) = A * negyszog |
(B.5) |
|
|
|
(B.6) |
ahol
|
mod |
modulo – maradékos osztás maradék értéke. |
Fűrészfog függvény ( Sawtooth ):
|
y(t) = A * fűrészfog(q) |
(B.7) |
|
|
fűrészfog(q)= |
(B.8) |
ahol
|
A |
az amplitúdó ( amplitude ), |
|
|
f |
frekvencia ( frequency ) [Hz], |
|
|
p |
a jel eltolásának értéke ( offset ), |
ahol
|
mod |
modulo – maradékos osztás maradék értéke. |
t az aktuális szimulációs időpont, y a generátor blokk kimenete.
A Signal Generator (Jelgenerátor) függvényei ( signal type ):
-
Sine (Szinusz függvény).
-
Square (Négyszögjel függvény).
-
Sawtooth (Fűrészfog függvény).
-
Random (Véletlen szám függvény).
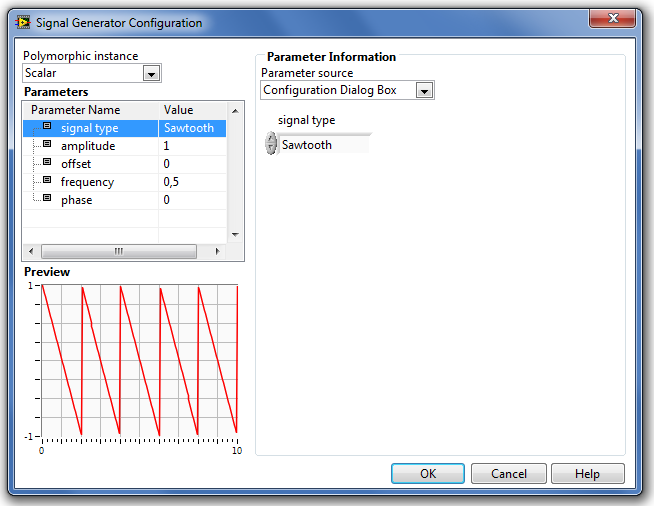
A paraméterek típusát és beállításuk módját a Step Signal Generation (Ugrás függvény) fejezetben részletesen ismertettük.
B.1.1.5. Chirp Signal (Végigsöprő szinusz jelgenerátor)
A Chirp Signal (Végigsöprő szinusz jelgenerátor) egy olyan szinuszos jelgenerátor, amely a kijelölt időtartományban megadott alsó frekvenciától egy ugyancsak megadott felső frekvenciáig változtatva a jelgenerátor frekvenciáját, szinuszos jelet bocsájt ki.
Végisöprő szinusz függvény ( Chirp Signal ):
|
|
(B.9) |
ahol
|
f(t) |
frekvencia [Hz], |
|
|
f 0 |
kezdeti (alsó) frekvencia ( initial frequency ), |
|
|
f 1 |
befejezési (felső) frekvencia ( target frequency ), |
|
|
t cél |
a végigsöprés befejezési időpontja ( target time ), |
|
|
T |
a szimulációs lépések száma a szimuláció kezdési időpontja és a t cél időpont között. |
t az aktuális szimulációs időpont, y a generátor blokk kimenete.
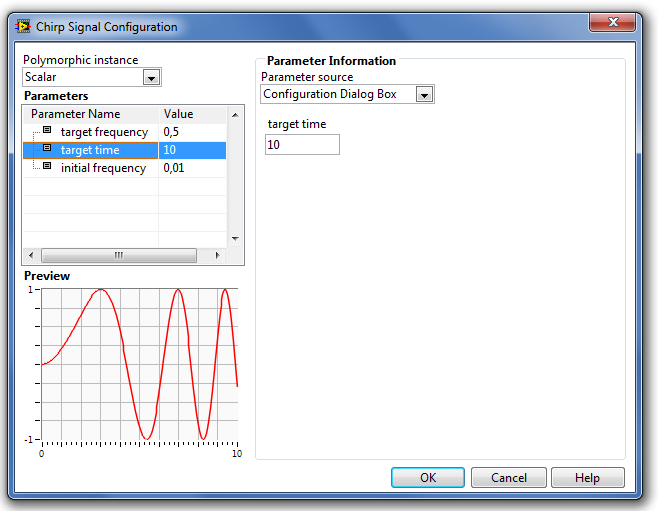
A paraméterek típusát és beállításuk módját a Step Signal Generation (Ugrás függvény) fejezetben részletesen ismertettük.
B.1.1.6. Simulation Time (A szimuláció aktuális időpontja)
A blokkot a szimulációs programban elhelyezve, kimeneti értékként megkapjuk az aktuális szimulációs időpontot.
A szimulációs blokknak nincs kiszolgáló ablaka, nem lehet semmilyen paramétert beállítani hozzá!
B.1.2. Jelaritmetika (Signal Arithmetics)
A Jelaritmetika (Signal Arihmetic) palettán olyan szimulációs elemek találhatók, amelyek a jelek összeadását/kivonását és konstans értékekkel történő szorzását valósítják meg.
Gyakorlati szempontból ezeket a műveleteket a LabVIEW hasonló műveleteket megvalósító blokkjaival (+ összeadás; - kivonás; * szorzás) is elvégezhetnénk, azonban ezek a blokkok az ikonjaik kinézetével jobban illeszkednek a blokkdiagramok elemeihez.
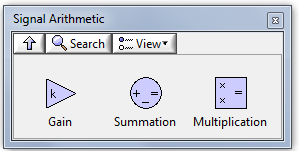
A modell létrehozásához leggyakrabban használt alpaletták:
|
|
Gain (Erősítés függvény) |
|
|
|
Summation (Összegzés függvény) |
|
|
|
Multiplication (Szorzás függvény) |
B.1.2.1. A Gain (Erősítés függvény)
A Gain (Erősítés függvény) segítségével konstans értékű számot, illetve ha a Paraméter forrás (Parameter Source) legördülő menüben a „Terminal”-t állítjuk, akkor pedig az aktuális szimulációs időpillanathoz rendelhető változó erősítés értéket állíthatunk be.
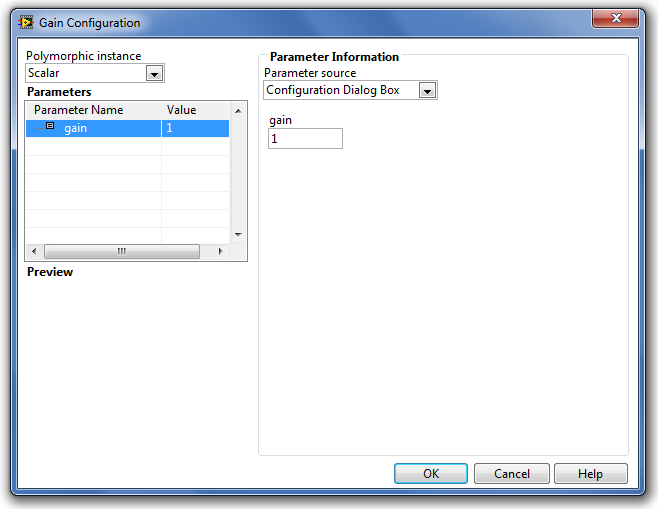
A paraméterek típusát és beállításuk módját a Step Signal Generation (Ugrás függvény) fejezetben részletesen ismertettük.
B.1.2.2. A Summation (Összegzés függvény)
A Summation (Összegzés függvény) segítségével definiálható számú bemenetet hozhatunk létre. A bemenetek mindegyike esetén megadható, hogy pozitív (+) vagy negatív előjellel adja hozzá a bemenetet az összegzett kimeneti értékhez. A bementeknek a modellezéskor nagyon hasznos tulajdonságuk is van, az aktivitásuk megszüntethető , azaz hozzá vannak kötve az összegző bemenethez, de a rajtuk megjelenő jel nem adódik hozzá az összegzési kimenethez.
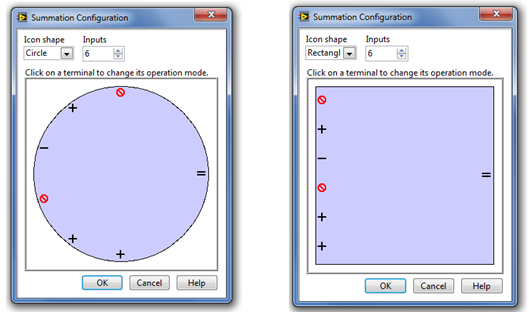
A paraméterablakban látható jelek a pozitív(+) előjelet, a negatív(-) előjelet, illetve a bemenet átmeneti megszüntetését ( ) jelölik.
) jelölik.
A bementek tulajdonságait megváltoztathatjuk, ha az egérmutatóval a bemeneti szimbólum területére kattintunk, ekkor ciklikusan változnak az előjel és a bemenet átmeneti megszüntetése ikonok.
A bementek számára vonatkozóan a program LabVIEW 2009 verziójában nincs felső korlát, de a blokkdiagram olvashatósága miatt már tízes nagyságrendű bemenet is nehezen olvasható a diagram panelen!
B.1.2.3. A Multiplication (Szorzás függvény)
A Multiplication (Szorzás függvény) segítségével definiálható számú bemenetet hozhatunk létre. A bemenetek mindegyike esetén megadható, hogy szorzás (*) vagy osztás műveletet valósítson meg a kimeneti érték meghatározásánál. A bementeknek a modellezéskor nagyon hasznos tulajdonsága is van, az aktivitásuk megszüntethető , azaz hozzá vannak kötve a műveletet végző bemenethez, de a rajtuk megjelenő jellel nem történik műveletvégzés.
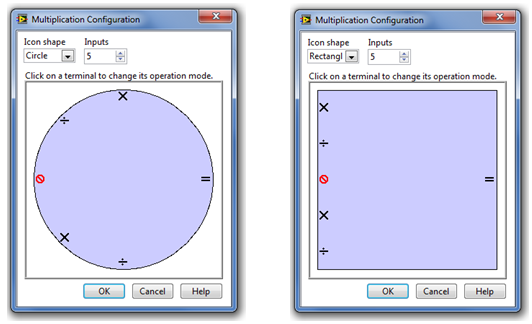
A paraméterablakban látható jelek a szorzást (x), az osztást (÷), illetve a bemenet átmeneti megszüntetését ( ) jelölik.
) jelölik.
A bementek tulajdonságait megváltoztathatjuk, ha az egérmutatóval a bemeneti szimbólum területére kattintunk, ekkor ciklikusan változnak a szorzás, az osztás és a bemenet átmeneti megszüntetése ikonok.
A bementek számára vonatkozóan a program LabVIEW 2009 verziójában nincs felső korlát, de a blokkdiagram olvashatósága miatt már tízes nagyságrendű bemenet is nehezen olvasható a diagram panelen!
B.1.3. Jelmegjelenítési elemek (Graph Utilities)
A Jelmegjelenítési elemek (Graph Utilities) palettán olyan elemek találhatók, amelyekkel lehetőségünk van a szimuláció futása közben kirajzolni a szimulációs blokkok bemenő és kimenő jeleket.
A modell létrehozásához leggyakrabban használt alpaletták:
|
|
Sim Time Waveform (Szimulációs időfüggvény kirajzolása) |
|
|
|
Buffer XY Graph (az XY grafikon adatainak tárolása függvény) |
B.1.3.1. Sim Time Waveform (Szimulációs jel időfüggvényének kirajzolása)
A Sim Time Waveform (Szimulációs jel időfüggvényének kirajzolása) blokk segítségével a szimulációban meghatározott jelek időbeli kirajzolását végezhetjük el.
A Sim Time Waveform (Szimulációs jel időfüggvényének kirajzolása) blokk definiálásakor automatikusan megjelenik a blokkdiagramban egy Waveform Chart (Hullámforma diagram), amely a blokkhoz kapcsolt jelek megjelenítését végzi.
Ha Táblázat B.2 Időzítési paraméterek (Timing Parameters) 12. sorszámú paramétere, A szimulációs hurok szinkronizálása egy időalap-generátorhoz (Syncronize Loop to Timing Source) nincs bekapcsolt állapotban – nincs időszinkronizálás – akkor a blokk átmenetileg tárolja (összegyűjti) a szimuláció alatt keletkezett összes adatot, és a szimuláció befejezési időpontjának elérése után egyszerre rajzolja ki a bemenetére kapcsolt adatokat.
Ha a szimuláció időlépése szinkronizálva van egy időalap-generátorhoz , akkor a szimulációs adatok kiírása az adott valós időpontban történik, és így a szimulált rendszer jeleinek valós idejű értékeit láthatjuk a diagramon.
A blokk a megadott szimulációs időlépés egész számú többszöröseinek időpontjában rajzolja ki az adatokat!
A Sim Time Waveform (Szimulációs jel időfüggvényének kirajzolása) blokk paraméter-beállító ablaka nem tartalmaz olyan információt, amelyet érdemben be lehetne állítani. A bemeneti érték, amely skalár (egy bemenet) vagy vektor típusú lehet, automatikusan beállítódik, és meghatározott értékű a bemeneti adatstruktúra alapján.
B.1.3.2. Buffer XY Graph (az XY grafikon adatainak tárolása függvény)
A Buffer XY Graph (az XY grafikon adatainak tárolása függvény) blokk segítségével a szimulációban meghatározott jelek kirajzolását végezhetjük el úgy, hogy az egyes ábrázolási tengelyeken (2D) a bemeneti jeleket alkalmazzuk. Így az idő ezeken a diagramokon csak paraméter, és az első jel változásának függvényében ábrázoljuk a második jelet (trajektória rajzolása).
A bemeneti jel egy olyan vektorcsoport (cluster vector), amelynek egy elemét a következő ábra mutatja be:
A Buffer XY Graph (az XY grafikon adatainak tárolása függvény) blokk definiálásakor automatikusan megjelenik a blokkdiagramban egy XY Graph (XY grafikon), amely a blokkhoz kapcsolt adatstruktúra (B.20. ábra) megjelenítését végzi.
Ha table_AII_2 Időzítési paraméterek (Timing Parameters) 12. sorszámú paramétere, A szimulációs hurok szinkronizálása egy időalap-generátorhoz (Syncronize Loop to Timing Source) nincs bekapcsolt állapotban – nincs időszinkronizálás –, akkor a blokk átmenetileg tárolja (összegyűjti) a szimuláció alatt keletkezett összes adatot, és a szimuláció befejezési időpontjának elérése után egyszerre rajzolja ki a bemenetére kapcsolt adatokat.
Ha a szimuláció időlépése szinkronizálva van egy időalap-generátorhoz , akkor a szimulációs adatok kiírása az adott valós időpontban történik, és így a szimulált rendszer jeleinek valós idejű értékeit láthatjuk a diagramon.
A Buffer XY Graph (az XY grafikon adatainak tárolása függvény) blokk paraméter-beállító ablakában (B.21. ábra) a következő paramétereket állíthatjuk be:
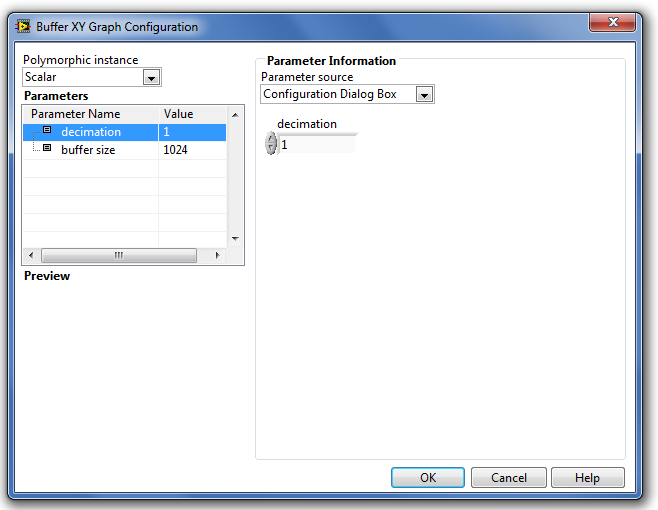
A paraméterek típusát és beállításuk módját a Step Signal Generation (Ugrás függvény) fejezetben részletesen ismertettük.
A Parameters (Paraméterek) listában található paraméterek a következő tulajdonságúak:
-
a decimation (tizedelés) paraméter lehetővé teszi, hogy ne rajzoljuk ki az összes szimulációs adatot, hanem csak a decimation paraméterrel megadott sorszámú értékeket. Így a szimuláció pontos (kis lépésközű) kiszámítása mellett jelentős memóriát takaríthatunk meg a kirajzolásnál.
-
a buffer size ((adat)puffer mérete) paraméterrel adhatjuk meg az adatok tárolását végző puffer méretét. Ennyi adatot tárolunk a szimulációról. A paraméter értékét nem változtathatjuk meg a szimuláció időtartama alatt . Az alapértelmezésben beállított puffer méret 1024 adat. Ha ettől több adat keletkezik a szimulációs modell futása során, akkor csak az utolsó, a puffer mérettel megegyező adat marad meg a szimulációs adatok kirajzolásakor.
B.1.4. Folytonos lineáris rendszerek (Continuous Linear Systems)
A Folytonos lineáris rendszerek (Continuous Linear Systems) palettán találjuk meg azokat a dinamikus rendszer szimulációs elemeket, melyek segítségével blokkdiagramszerűen adhatjuk meg a differenciálegyenletek alapján felírt átviteli függvényeket valamint az állapottér modelleket.
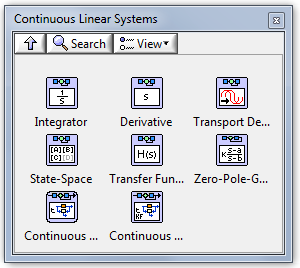
A modell létrehozásához leggyakrabban használt alpaletták:
|
|
Integrator (Idő szerinti integrálás függvény) |
|
|
|
Derivative (Idő szerinti differenciálási függvény) |
|
|
|
Transport Delay (Jelkésleltetési függvény) |
|
|
|
State Space (Állapottér modell) |
|
|
|
Transfer Function (Átviteli függvény modell) |
B.1.4.1. Integrator (Idő szerinti integrálás függvény)
Az Integrator (Idő szerinti integrálás függvény) egy olyan hisztórikus típusú blokk, amely a bemenő jel idő szerinti integrál értékét határozza meg az adott szimulációs időpontig.
Hisztórikus blokkoknak nevezzük azokat a szimulációs blokkokat, amelyek kimeneti jele nem csak a bemeneti jel értékétől, hanem a kimenő jel korábbi értékétől is függ.
Javaslat, hogy mindenképpen integráló blokkot alkalmazzunk, ha a folytonos differenciálegyenlet megoldásához blokkdiagramot építünk fel!
Az integrálási metódust az Irányítás és szimulációs hurok egyik paramétereként már be kellett előzőleg állítanunk. Az Irányítás és szimulációs hurok (Control & Simulation Loop) az összes integrátor számítását ugyanazzal az integrálási eljárással határozza meg.
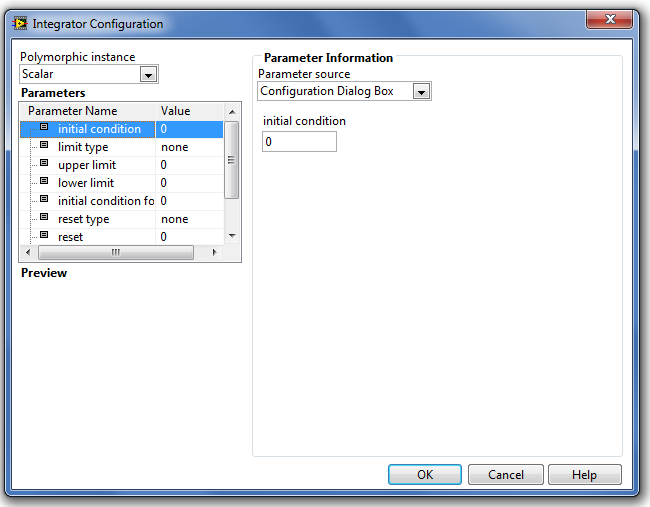
A paraméterek típusát és beállításuk módját a Step Signal Generation (Ugrás függvény) fejezetben részletesen ismertettük.
A Parameters (Paraméterek) listában található paraméterek a következő tulajdonságúak:
-
az initial condition (kezdeti feltétel) paraméter megadja az integrátor kimeneti jelének értékét a szimuláció kezdő időpontjában. Alapértéke nulla (0).
-
a limit type (korlátozás típusa) paraméterrel adhatjuk meg az integráló blokk kimenő jelének korlátozását. Ez azt jelenti, hogy a korlátozások értékénél nagyobb/kisebb kimenő jel értéke helyett a korlátozás értékét adjuk ki kimenő jelként. A korlátozást a felső határra, az alsó határra külön-külön vagy együttesen elő lehet írni. Hasonlóan be lehet állítani, hogy az integrátor ne vegye figyelembe a korlátozásokat.
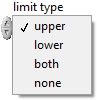 B.24. ábra - Az Integrator (Idő szerinti integrálás függvény) limit type (korlátozás típusa) paraméterének értékei
B.24. ábra - Az Integrator (Idő szerinti integrálás függvény) limit type (korlátozás típusa) paraméterének értékei
-
upper (korlátozás a felső határnál),
-
lower (korlátozás az alsó határnál),
-
both (korlátozás mindkét határnál),
-
none (nincs korlátozás).
-
-
az upper limit (felső határ) paraméter az integráló tag kimenő jelének korlátozásakor a felső határ értékét adja. Ezen határértéknél nagyobb értéket az integráló tag nem bocsájt ki, ehelyett a felső határ értékét adja ki kimenő jelként. Alapértéke nulla (0).
-
a lower limit (alsó határ) paraméter az integráló tag kimenő jelének korlátozásakor az alsó határ értéke. Ezen határértéknél kisebb értéket az integráló tag nem bocsájt ki, ehelyett a alsó határ értékét adja ki kimenő jelként. Alapértéke nulla (0).
-
az initial condition for reset (kezdeti feltétel a kimenet visszaállításához az újraindítás után) paraméter az integráló tag kimenő jelének értéke, amikor a reset (újraindítás) bemenetre visszaállítási feltétel érkezik. A szimulációs program nem használja ezt a paramétert, ha a reset type (újraindítás típusa) paraméter értéke none (nincs újraindítás). Alapértéke nulla (0).
-
a reset type (újraindítás típusa) paraméterrel adhatjuk meg az integrátor blokk újraindítását előíró feltételt
 B.25. ábra - Az Integrator (Idő szerinti integrálás függvény) reset type (újraindítás típusa) paraméterének értékei
B.25. ábra - Az Integrator (Idő szerinti integrálás függvény) reset type (újraindítás típusa) paraméterének értékei
-
rising (újraindítás emelkedésnél) Az integrátor újraindítása, amikor az újraindítás ( reset ) jel pozitív meredekséggel metszi az x-tengelyt .
-
falling (újraindítás csökkenésnél) Az integrátor újraindítása, amikor az újraindítás ( reset ) jel negatív meredekséggel metszi az x-tengelyt .
-
either (újraindítás emelkedésnél vagy csökkenésnél) Az integrátor újraindítása, amikor az újraindítás ( reset ) jel pozitív vagy negatív meredekséggel metszi az x-tengelyt .
-
none (nincs újraindítás) Alapbeállítás. Az integrátor nem indítható újra.
-
-
a reset (kimenet visszaállítása az újraindítás kezdeti feltételére) paraméter érték megszabja, hogy az integrátor újrainduljon vagy sem.
-
a reset offset (a kezdeti feltétel határoló értéke a kimenet visszaállításához) paraméterrel adhatjuk meg, hogy milyen érték esetén minősítsük újraindításnak az x-tengely keresztezését a reset type (újraindítás típusa) feltételnél. Ha a következő függvény igaz értékű, akkor az x-tengely metszése is valós.
sgn( reset (t–1)– reset offset (t)) ≠ sgn( reset (t)– reset offset (t))
(B.10)
B.1.4.2. Derivative (Idő szerinti differenciálási függvény)
A Derivative (Idő szerinti differenciálási függvény) egy olyan, nem hisztórikus típusú blokk , amely a bemenő jel idő szerinti differencia értékét határozza meg az adott szimulációs időpontban.
Nem hisztórikus blokkoknak nevezzük azokat a szimulációs blokkokat, amelyek kimeneti jele csak a bemeneti jel értékétől függ.
Javaslat, hogy mindenképpen kerüljük a Derivative (Idő szerinti differenciálási függvény) alkalmazását, ha a folytonos differenciálegyenlet megoldásához blokkdiagramot építünk fel!
A Derivative (Idő szerinti differenciálási függvény) a következő időfüggvényt valósítja meg:
|
|
(B.11) |
ahol
|
t |
a szimuláció aktuális időpontja, |
|
|
u(t) |
a bemenetjel időfüggvénye, |
|
|
y(t) |
a kimenetjel időfüggvénye, |
|
|
h |
a szimuláció időlépése. |
A Derivative (Idő szerinti differenciálási függvény) tipikus alkalmazása, amikor egy jel időbeni változási sebességét akarjuk meghatározni.
A differenciálegyenletek megoldásánál ez a visszalépéses differenciaszámítási mód insatbil működést okoz!
B.1.4.3. Transport Delay (Jelkésleltetési függvény)
A Transport Delay (Jelkésleltetési függvény) egy olyan, nem hisztórikus típusú blokk , amely a bemenő jel késleltetését valósítja meg egy megadott késleltetési időtartammal.
A Transport Delay (Jelkésleltetési függvény) a következő időfüggvényt valósítja meg:
|
|
(B.12) |
ahol
|
t |
a szimuláció aktuális időpontja, |
|
|
u(t) |
a bemenetjel időfüggvénye, |
|
|
y(t) |
a kimenetjel időfüggvénye, |
|
|
Th |
a blokk késleltetési időtartama. |
A Transport Delay (Jelkésleltetési függvény) paramétereinek kiszolgáló ablaka a következő ábrán (B.26. ábra) látható.
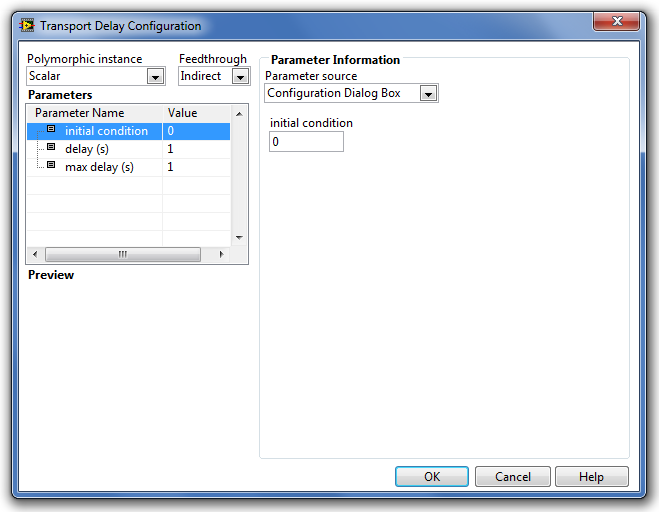
A paraméterek típusát és beállításuk módját a Step Signal Generation (Ugrás függvény) fejezetben részletesen ismertettük.
A Parameters (Paraméterek) listában található paraméterek a következő tulajdonságúak:
-
az initial condition (kezdeti feltétel) paraméter megadja a Jelkésleltetési függvény kimeneti jelének értékét a szimuláció kezdő időpontjában. Alapértéke nulla (0).
-
a delay (s) (korlátozás típusa) paraméterrel adhatjuk meg a Jelkésleltetési függvény kimenő jelének késleltetését. Alapértéke egy (1) másodperc [s]. Ha a késleltetési idő alapján két mintavételezési időpont között kell a függvényértéket meghatározni, akkor a blokk extrapolálja a megfelelő értéket a két mintavételezési pont között. A késleltetés értéke csak pozitív valós szám lehet!
-
a max delay (s) (kezdeti feltétel) paraméter megadja a Jelkésleltetési függvény kimenő jelének maximális késleltetését. Alapértéke egy (1) másodperc [s]. A maximális késleltetés értéke csak pozitív valós szám lehet!
B.1.4.4. State Space (Állapottér modell)
A State Space (Állapottér modell) egy olyan hisztórikus típusú blokk , amely az adott szimulációs időpontban az állapottér modell új állapotait, és az azokhoz tartozó új kimenő jel értékeket határozza meg.
|
|
(B.13) |
Hisztórikus blokkoknak nevezzük azokat a szimulációs blokkokat, amelyek kimeneti jele nem csak a bemeneti jel értékétől, hanem a kimenő jel korábbi értékétől is függ.
A State Space (Állapottér modell) paramétereinek kiszolgáló ablaka a következő ábrán (B.27. ábra) látható.
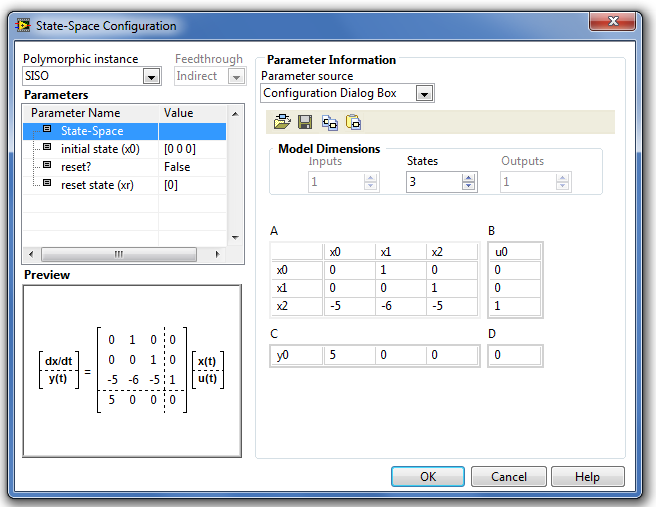
A paraméterek alaptípusát és azok beállítási módját a Step Signal Generation (Ugrás függvény) fejezetben részletesen ismertettük.
A Parameters (Paraméterek) listában található paraméterek a következő tulajdonságúak:
-
a State-Space (Állapottér) paraméter megadja az állapottér leírás A, B, C és D mátrixainak méretét és értékeit. Alapesetben a modell egy bemenetű és egy kimenetű állapottér modell paramétereinek megadását teszi lehetővé. Ha a bemenetre egy vektor típusú adatot kapcsolunk, akkor azonnal lehetőség van a bemenetekhez tartozó B mátrix paramétereinek megadására, és ekkor állíthatjuk be a többi kimenet értékét meghatározó C és D mátrixot is. Lehetőségünk van az állapottér modellt fájlban való tárolására, illetve a korábban tárolt állapottér modellek háttértárról való betöltésére.
A B.28. ábra bemutatja a több-bemenetű és több-kimenetű (MIMO) rendszer állapottér modelljének paraméterablakát.
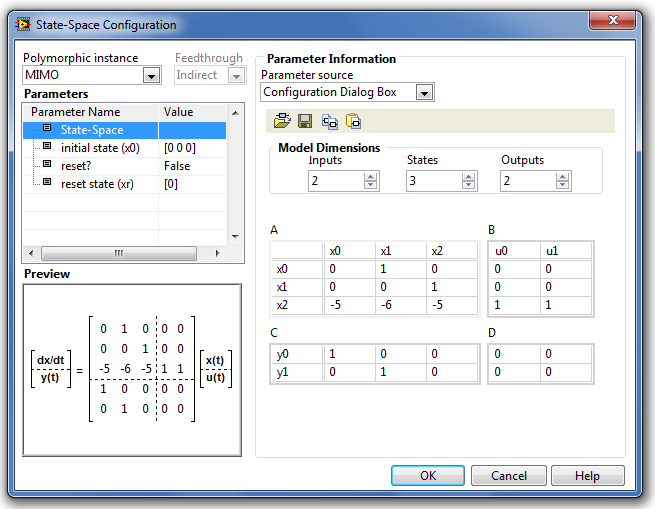 B.28. ábra - A MIMO State Space (Állapottér modell) paraméter-beállító ablaka
B.28. ábra - A MIMO State Space (Állapottér modell) paraméter-beállító ablaka
-
az initial state (x0) (kezdeti állapotok) paramétervektor megadja az állapotváltozók értékét a szimuláció kezdő időpontjában. Alapérték nulla (0) elemű vektor.
A B.29. ábra a kezdeti állapotok beállítási lehetőségét mutatja be az állapottér modell paraméterablakában:
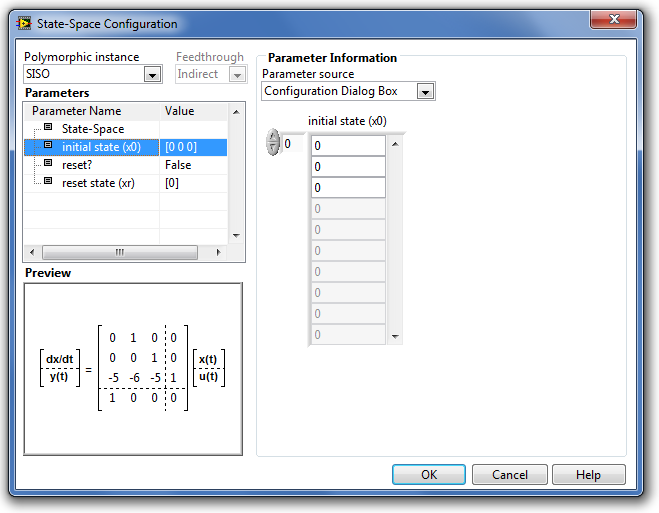 B.29. ábra - A State Space (Állapottér modell) kezdeti állapotainak beállítása
B.29. ábra - A State Space (Állapottér modell) kezdeti állapotainak beállítása
-
a reset? (újraindítás?) paraméter megadja, hogy az állapottér modell a szimuláció egy megadott pillanatában újraindítódik vagy sem.
Az újraindítás azt jelenti, hogy a szimuláció adott időpillanatában az állapottér modell korábbi működését megszakítjuk, és új kezdeti állapotokkal, de az aktuális bemenő jellel folytatjuk tovább a szimulációt. Alapértéke nem (False).
-
a reset initial state (xr) (kezdeti állapotok újraindításkor) vektorparaméterrel adhatjuk meg az állapottér modell újraindítás utáni új állapotait.
B.1.4.5. Transfer Function (Átviteli függvény modell)
A Transfer Function (Átviteli függvény modell) egy olyan hisztórikus típusú blokk , amely az adott szimulációs időpontban egy folytonos átviteli függvénnyel leírt modell kimenő jelének értékeit határozza meg a bemenő jel alapján.
Hisztórikus blokkoknak nevezzük azokat a szimulációs blokkokat, amelyek kimeneti jele nem csak a bemeneti jel értékétől, hanem a kimenő jel korábbi értékétől is függ.
Az átviteli függvényt egy bemenet és egy kimenet esetén a következő egyenlettel írjuk le:
|
|
(B.14) |
A Transfer Function (Átviteli függvény modell) paramétereit a következő ábrán (B.30. ábra) látható paraméter-beállító ablakban adhatjuk meg.
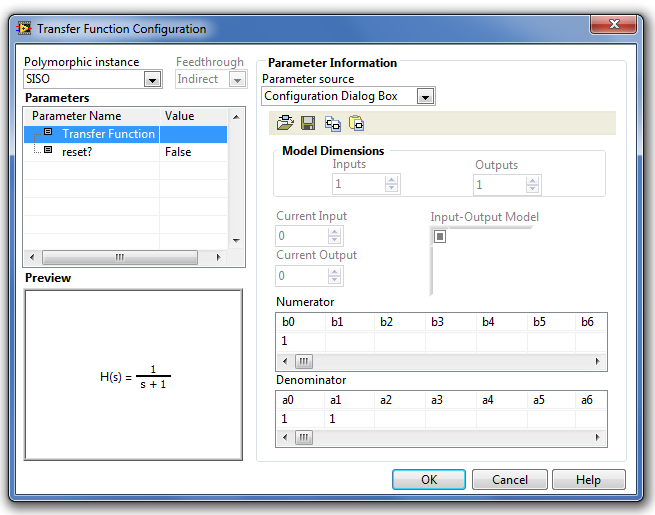
A paraméterek alaptípusát és beállításuk módját a Step Signal Generation (Ugrás függvény) fejezetben részletesen ismertettük.
A Parameters (Paraméterek) listában található paraméterek a következő tulajdonságúak:
-
a Transfer Function (Átviteli függvény modell) paraméter megadja az átviteli függvény számlálójában (numerator) és nevezőjében (denominator) s egész hatványainak együtthatóit. A 0. indexű elem s0 hatványának együtthatóját jelenti az 1. indexű elem s szorzója a 2. indexű elem s2-é és így tovább.Az átviteli függvényben nincs lehetőség kezdeti állapot megadására, vagyis minden állapotváltozó értéke nulla a szimuláció elindulásakor (t=0). Lehetőségünk van az átviteli függvény modellt fájlként tárolni, illetve korábban tárolt átviteli függvény modelleket a háttér tárolóról betölteni.
A következő ábra a több-bemenetű és több-kimenetű (MIMO) rendszer átviteli függvény (mátrix) paraméterablakát mutatja be. Ilyen esetben minden bemenet és minden kimenet között meg kell adnunk az kimenet-bemenet pároshoz tartozó átviteli függvény együtthatóit.
A következő ábrán (B.31. ábra) látható Input-Output Modell (Bemeneti-Kimeneti modell) mátrixában a megfelelő elemre kattintva megadhatjuk, hogy melyik kimenet és bemenet közötti átviteli függvény paramétereit láthatjuk a számláló és a nevező vektor elemeiben.
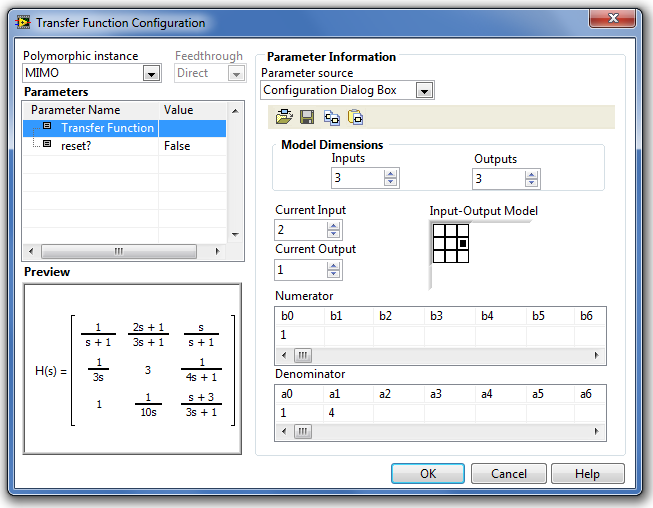 B.31. ábra - A MIMO Transfer Function Matrix (Átviteli függvény modell mátrix) paraméter-beállító ablaka
B.31. ábra - A MIMO Transfer Function Matrix (Átviteli függvény modell mátrix) paraméter-beállító ablaka
-
a reset? (újraindítás?) paraméter megadja, hogy az átviteli függvény modell a szimuláció egy megadott pillanatában újraindítódik vagy sem.
Az újraindítás azt jelenti, hogy a szimuláció adott időpillanatában az átviteli függvény-modell korábbi működését megszakítjuk, és nulla (0) kezdeti állapotokkal, valamint az aktuális bemenő jellel folytatjuk tovább a szimulációt. Alapértéke nem (False).
B.1.5. Folytonos nemlineáris rendszerek (Nonlinear Systems)
A Folytonos nemlineáris rendszerek (Nonlinear Systems) palettán olyan elemek találhatók, amelyek tipikus nemlineáris tulajdonságok modelljeit írják le. Ilyenek például a kotyogás, súrlódás, telítődés függvények.
A modell létrehozásához leggyakrabban használt alpaletták:
|
|
Dead Zone (Kotyogás függvény) |
|
|
|
Friction (Súrlódás függvény) |
|
|
|
Quantizer (Érték-diszkretizáló függvény) |
|
|
|
Rate Limiter (Sebességkorlát függvény) |
|
|
|
Relay (Relé függvény) |
|
|
|
Saturation (Telítődés függvény) |
|
|
|
Switch (Kapcsoló függvény) |
B.1.5.1. Dead Zone (Kotyogás függvény)
A Dead Zone (Kotyogás függvény) egy olyan nem hisztórikus típusú blokk , amely a bemenő jel megadott értékhatárai között nem reagál (nem ad ki kimenő jelet) majd ezután a bemenő jellel meghatározott kimenő jelértéket bocsájt ki.
A Dead Zone (Kotyogás függvény) a következő időfüggvényt valósítja meg:
|
y(t) = 0, ha sodz <= u(t) <= eodz |
(B.15) |
|
|
y(t) = u(t)- sodz , ha u(t) < sodz |
(B.16) |
|
|
y(t) = u(t)- eodz , ha u(t) > eodz |
(B.17) |
ahol
|
|
t |
a szimuláció aktuális időpontja, |
|
u(t) |
a bemeneti jel időfüggvénye, |
|
|
y(t) |
a kimeneti jel időfüggvénye, |
|
|
sodz |
start of dead zone - a holtsáv kezdete, |
|
|
eodz |
end of dead zone - a holtsáv vége. |
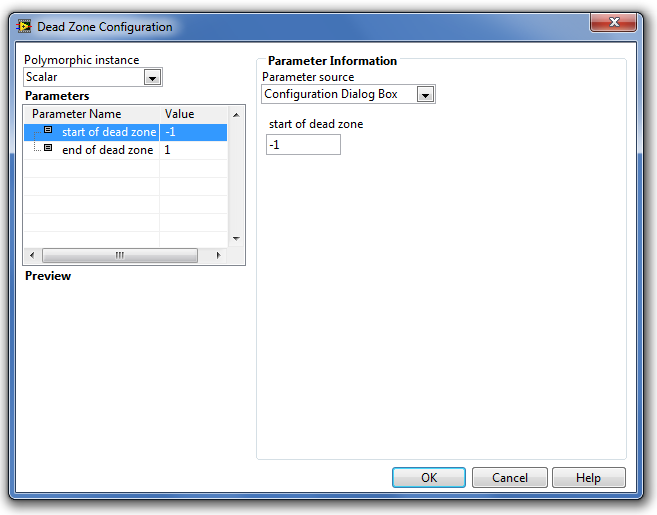
A Dead Zone (Kotyogás függvény) paramétereinek kiszolgáló ablaka a következő ábrán (B.33. ábra) látható.
A paraméterek típusát és beállításuk módját a Step Signal Generation (Ugrás függvény) fejezetben részletesen ismertettük.
A Parameters (Paraméterek) listában található paraméterek a következő tulajdonságúak:
-
a start of dead zone (a holtsáv kezdete) paraméter megadja a bemenő jel holtsávjának kezdeti értékét.
Alapértéke -1.
-
az end of dead zone (a holtsáv vége) paraméter megadja a bemenő jel holtsávjának kezdeti értékét.
Alapértéke +1.
B.1.5.2. Friction (Súrlódás függvény)
A Friction (Súrlódás függvény) egy olyan nem hisztórikus típusú blokk , amely a bemenő jel előjelétől függő, adott értékkel eltolt, a bemenetre lineáris függvényt valósít meg.
A Friction (Súrlódás függvény) a következő időfüggvényt valósítja meg:
|
y(t) = 0, ha u(t)=0 |
(B.18) |
|
|
y(t) = u(t) * gain + offset , ha u(t) > 0 |
(B.19) |
|
|
y(t) = u(t) * gain + offset , ha u(t) < 0 |
(B.20) |
ahol
|
|
t |
a szimuláció aktuális időpontja, |
|
u(t) |
a bemeneti jel időfüggvénye, |
|
|
y(t) |
a kimeneti jel időfüggvénye, |
|
|
offset |
az eltolás értéke, |
|
|
gain |
az erősítés értéke. |
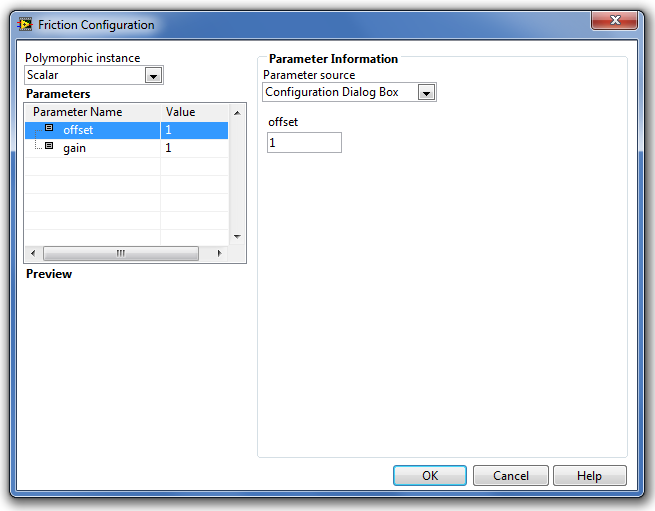
A Friction (Súrlódás függvény) paramétereinek kiszolgáló ablaka a következő ábrán (B.34. ábra) látható.
A paraméterek típusát és beállításuk módját a Step Signal Generation (Ugrás függvény) fejezetben részletesen ismertettük.
A Parameters (Paraméterek) listában található paraméterek a következő tulajdonságúak:
-
az offset (eltolásérték) paraméter megadja a kimenő jel eltolásának értékét ha u(t)=0. Alapértéke +1.
-
a gain (erősítés) paraméter megadja a nullától eltérő bemenő jel erősítésének értékét. Alapértéke +1.
B.1.5.3. Quantizer (Érték-diszkretizáló függvény)
A Quantizer (Érték-diszkretizáló függvény) egy olyan nem hisztórikus típusú blokk , amely a bemenő jel értékét megadott lépcsőértékekhez (quantization interval) rendeli. Így a kimenő jel csak meghatározott kvantált értékeket vehet fel.
A Quantizer (Érték-diszkretizáló függvény) a következő időfüggvényt valósítja meg:
|
y(t) = int [ u(t) * qi ] * qi |
(B.21) |
ahol
|
|
t |
a szimuláció aktuális időpontja, |
|
u(t) |
a bemeneti jel időfüggvénye, |
|
|
y(t) |
a kimeneti jel időfüggvénye, |
|
|
qi |
quantization interval - a lépcsőérték, |
|
|
int |
függvény a legközelebbi egész értéket adja meg. |
A Quantizer (Érték-diszkretizáló függvény) paramétereinek kiszolgáló ablaka a következő ábrán (B.35. ábra) látható.
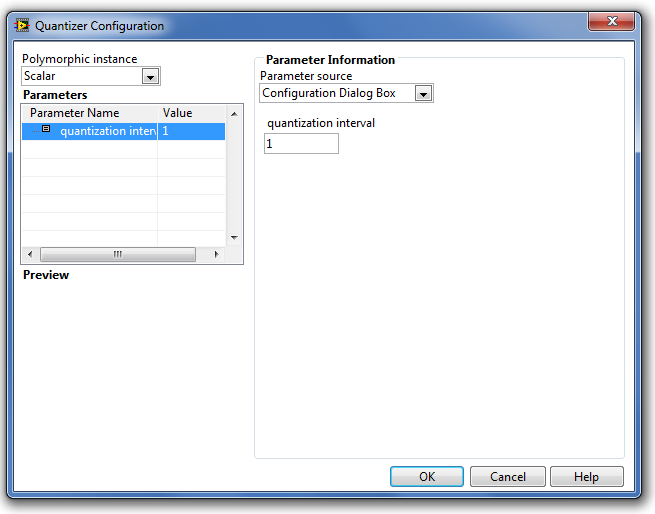
A paraméterek típusát és beállításuk módját a Step Signal Generation (Ugrás függvény) fejezetben részletesen ismertettük.
A Parameters (Paraméterek) listában található paraméter a következő tulajdonságú:
-
a quantization interval (lépcsőértéke) paraméter adja meg a kimenő jel lépcsőzésének értékét. Alapértéke +1.
B.1.5.4. Rate Limiter (Sebességkorlát függvény)
A Rate Limiter (Sebességkorlát függvény) egy olyan nem hisztórikus típusú blokk , amely a bemenő jel értékét megadott lépcsőértékekhez (quantization interval) rendeli. Így a kimenő jel csak meghatározott kvantált értékeket vehet fel.
A Rate Limiter (Sebességkorlát függvény) a következő időfüggvényt valósítja meg:
|
|
(B.22) |
|
|
y(t) = nsr * h +y(t-h), ha D < nsr |
(B.23) |
|
|
y(t) = psr * h +y(t-h), ha D > psr |
(B.24) |
|
|
y(t) = u(t) egyébként |
(B.25) |
ahol
|
|
t |
a szimuláció aktuális időpontja, |
|
h |
a szimuláció lépésköze, |
|
|
u(t) |
a bemeneti jel időfüggvénye, |
|
|
y(t) |
a kimeneti jel időfüggvénye, |
|
|
D |
a jelváltozás sebessége, |
|
|
nsr |
negative slew rate - negatív meredekség határ, |
|
|
psr |
positive slew rate - pozitív meredekség határ. |
A Rate Limiter (Sebességkorlát függvény) paramétereinek kiszolgáló ablaka a következő ábrán (B.35. ábra) látható.
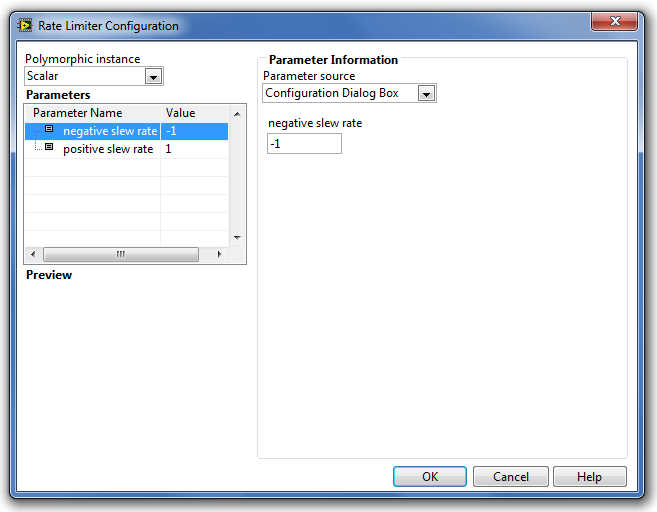
A paraméterek típusát és beállításuk módját a Step Signal Generation (Ugrás függvény) fejezetben részletesen ismertettük.
A Parameters (Paraméterek) listában található paraméterek a következő tulajdonságúak:
-
a negative slew rate (negatív meredekség határ) paraméter adja meg a kimenő jel negatív meredekségének határát. Alapértéke -1.
-
a positive slew rate (pozitív meredekség határ) paraméter adja meg a kimenő jel pozitív meredekségének határát. Alapértéke +1.
B.1.5.5. Relay (Relé függvény)
A Relay (Relé függvény) egy olyan hisztórikus típusú blokk , amely a bemenő jel és a kimenő jel aktuális értékétől függően bekapcsolt vagy kikapcsolt állapotba kerül. A Relé függvény úgynevezett kétértékű függvény, amelynek értékét a kimenő jel egy szimulációs lépéssel korábbi állapota határozza meg. A Relé függvény kezdeti értéke kikapcsolt (off) állapot.
A Relay (Relé függvény) a következő időfüggvényt valósítja meg:
|
y(t) = output when off , ha relé on állapotban van |
(B.26) |
|
|
y(t) = output when on , ha relé off állapotban van |
(B.27) |
ahol
|
|
t |
a szimuláció aktuális időpontja, |
|
u(t) |
a bemeneti jel időfüggvénye, |
|
|
y(t) |
a kimeneti jel időfüggvénye, |
|
|
output when off |
a kimenet kikapcsolt állapotban, |
|
|
output when on |
a kimenet bekapcsolt állapotban. |
A Relay (Relé függvény) paramétereinek kiszolgáló ablaka a következő ábrán (B.37. ábra) látható.
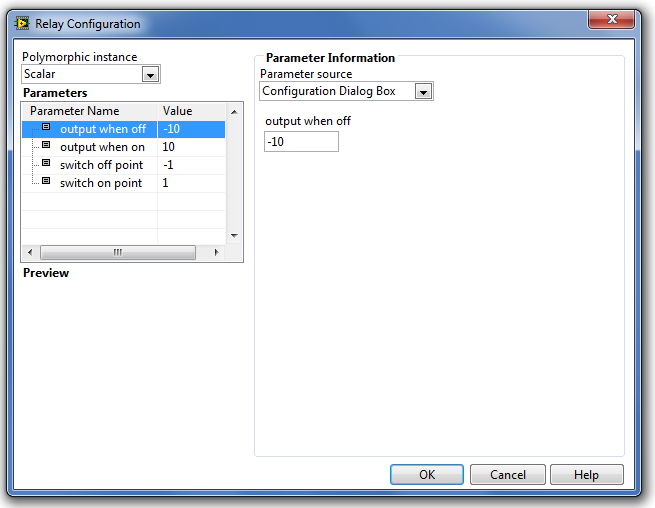
A paraméterek típusát és beállításuk módját a Step Signal Generation (Ugrás függvény) fejezetben részletesen ismertettük.
A Parameters (Paraméterek) listában található paraméterek a következő tulajdonságúak:
-
az output when off (a kimenet kikapcsolt állapotban) paraméter adja meg a kimenő jel értékét a relé kikapcsolt állapotában. Alapértéke -10.
-
az output when on (a kimenet bekapcsolt állapotban) paraméter adja meg a kimenő jel értékét a relé bekapcsolt állapotában. Alapértéke +10.
-
a switch off point (a bemeneti jel kikapcsolási értéke) paraméter megadja a bemenő jel kikapcsolási értékét. Alapértéke -1.
-
a switch on point (a bemeneti jel bekapcsolási értéke) paraméter megadja a bemenő jel bekapcsolási értékét. Alapértéke +1.
B.1.5.6. Saturation (Telítődés függvény)
A Saturation (Telítődés függvény) egy olyan nem hisztórikus típusú blokk , amely a bemenő jel értékét megadott határértékekkel összehasonlítva nem ad ki a határértékeknél nagyobb/kisebb kimenő jelet.
A Saturation (Telítődés függvény) a következő időfüggvényt valósítja meg:
|
y(t) = upper limit , ha (u(t) > upper limit) |
(B.28) |
|
|
y(t) = lower limit , ha (u(t) < lower limit) |
(B.29) |
|
|
y(t) = u(t) egyébként |
(B.30) |
ahol
|
|
t |
a szimuláció aktuális időpontja, |
|
u(t) |
a bemeneti jel időfüggvénye, |
|
|
y(t) |
a kimeneti jel időfüggvénye, |
|
|
upper limit |
felső határ, |
|
|
lower limit |
alsó határ. |
A Saturation (Telítődés függvény) paramétereinek kiszolgáló ablaka a következő ábrán (B.38. ábra) látható.
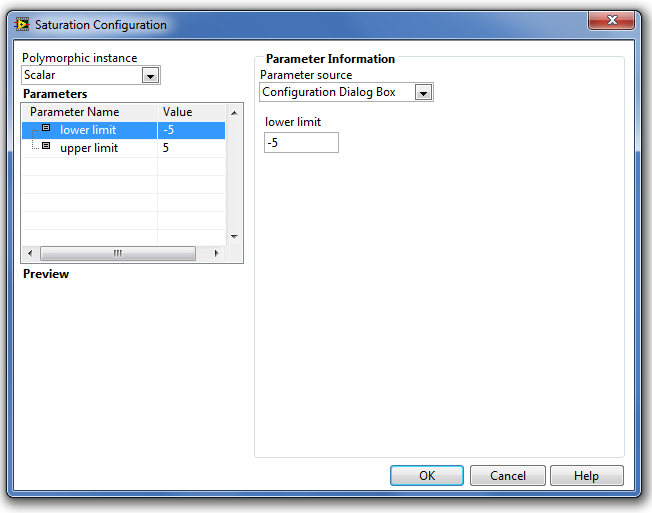
A paraméterek típusát és beállításuk módját a Step Signal Generation (Ugrás függvény) fejezetben részletesen ismertettük.
A Parameters (Paraméterek) listában található paraméterek a következő tulajdonságúak:
-
lower limit (alsó határ) – ha a bemenő jel kisebb, mint az alsó határ értéke, akkor a blokk az alsó határ értékét adja ki kimenő jelként. Alapértéke -5.
-
upper limit (felső meredekség határ) - ha a bemenő jel nagyobb, mint a felső határ értéke, akkor a blokk a felső határ értékét adja ki kimenő jelként. Alapértéke +5.
B.1.5.7. Switch (Kapcsoló függvény)
A Switch (Kapcsoló függvény) egy olyan nem hisztórikus típusú blokk , amely a bemenő jel értékét megadott küszöbértékekkel összehasonlítva két kimeneti értéket bocsájt ki attól függően, hogy a bementi jel kisebb vagy nagyobb, mint a küszöbjel.
A Switch (Kapcsoló függvény) a következő időfüggvényt valósítja meg:
|
y(t) = value above threshold , ha (u(t) > threshold) |
(B.31) |
|
|
y(t) = value below threshold , ha (u(t) <= threshold) |
(B.32) |
ahol
|
|
t |
a szimuláció aktuális időpontja, |
|
u(t) |
a bemeneti jel időfüggvénye, |
|
|
y(t) |
a kimeneti jel időfüggvénye, |
|
|
threshold |
küszöb, |
|
|
value above threshold |
érték a küszöb feletti jel értéknél, |
|
|
value below threshold |
érték a küszöb alatti jel értéknél. |
A Switch (Kapcsoló függvény) paramétereinek kiszolgáló ablaka a következő ábrán (B.39. ábra) látható.
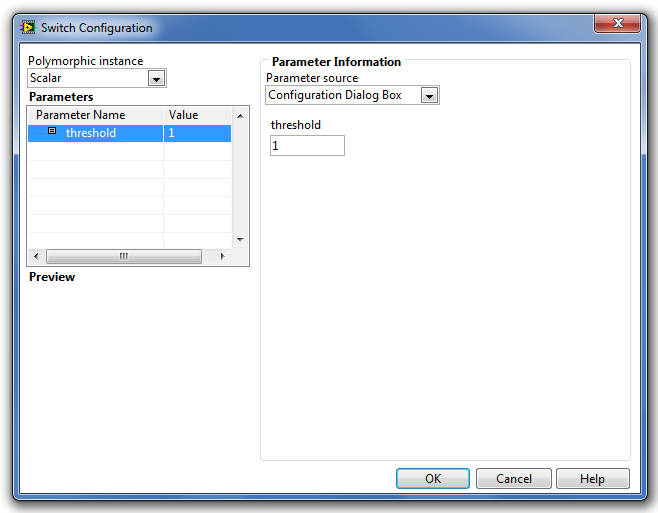
A paraméterek típusát és beállításuk módját a Step Signal Generation (Ugrás függvény) fejezetben részletesen ismertettük.
A Parameters (Paraméterek) listában található paraméter a következő tulajdonságú:
-
threshold (küszöb) - ha a bemenő jel kisebb, mint a küszöb értéke, akkor a blokk kimenete a küszöb alatti értékhez rendelt kimenő jelet adja ki. Ha a bemenő jel nagyobb, mint a küszöb értéke, akkor a blokk kimenete a küszöb feletti értékhez rendelt kimenő jelet adja ki. Alapértéke +1.
B.1.6. Mintavételes lineáris rendszerek (Discrete Linear Systems)
A Mintavételes lineáris rendszerek (Discrete Linear Systems) palettán olyan elemek találhatók, amelyekkel lehetőségünk van a mintavételes rendszerek állapottér és impulzusátviteli függvény modelljeinek definiálására.
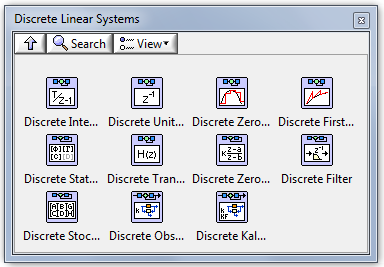
A modell létrehozásához leggyakrabban használt alpaletták:
|
|
Discrete Unit Delay (Mintavételes egységnyi késleltetés függvény) |
|
|
|
Discrete Zero-Order Hold (Mintavételes nulladrendű tartó függvény) |
|
|
|
Discrete First-Order Hold (Mintavételes elsőrendű tartó függvény) |
|
|
|
Discrete State-Space (Mintavételes állapottérmodell) |
|
|
|
Discrete Transfer Function (Mintavételes impulzusátviteli függvénymodell) |
B.1.6.1. Discrete Unit Delay (Mintavételes egységnyi késleltetés függvény)
A Discrete Unit Delay (Mintavételes egységnyi késleltetés függvény) egy olyan hisztórikus típusú blokk , amely a bemenő jel mintavételezett értékét egy mintavételi idővel később bocsájtja ki kimenő jelként.
A Discrete Unit Delay (Mintavételes egységnyi késleltetés függvény) a következő időfüggvényt valósítja meg:
|
y(0) = initial condition |
(B.33) |
|
|
y(t k ) = u(t k - sample period (s) ) |
(B.34) |
|
|
t k = t i + sample skew (s) + k * sample period (s) , k =0,1,2,…. |
(B.35) |
ahol
|
|
k |
a mintavételek száma, |
|
ti |
a szimuláció kezdési időpontja, |
|
|
tk |
a mintavételezés időpontja, |
|
|
tk-1 |
az előző mintavételezés időpontja, |
|
|
u(tk) |
a mintavételezett bemenő jel a k. mintavételi időpontban, |
|
|
y(tk) |
a mintavételezett kimenő jel a k. mintavételi időpontban, |
|
|
initial condition |
a kimenő jel értéke a k=0 mintavételi időpillanatban, |
|
|
sample skew (s) |
mintavételi meredekség [s], |
|
|
sample period (s) |
mintavételi periódus időtartam [s]. |
A Discrete Unit Delay (Mintavételes egységnyi késleltetés függvény) paramétereinek kiszolgáló ablaka a következő ábrán (B.41. ábra) látható.
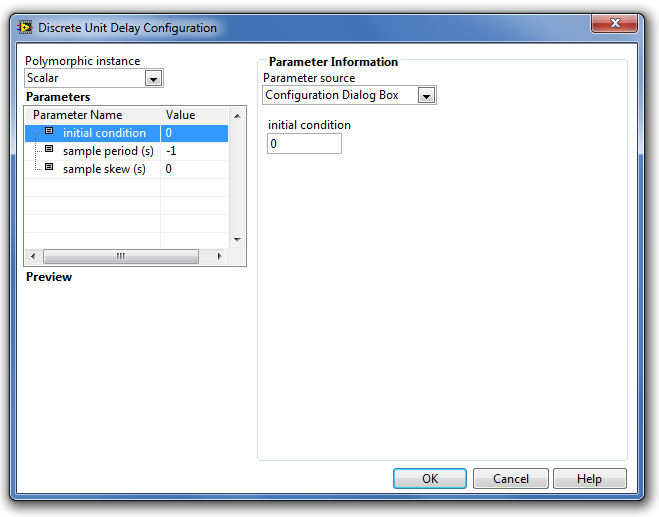
A paraméterek típusát és beállításuk módját a Step Signal Generation (Ugrás függvény) fejezetben részletesen ismertettük.
A Parameters (Paraméterek) listában található paraméterek a következő tulajdonságúak:
-
az initial condition (kezdeti feltétel) a kimenő jel értéke a k= 0 mintavételi időpontban. Alapértéke 0.
-
sample period (s) (a mintavételi idő) a mintavételi idő értéke másodpercben [s]. Alapértéke -1.
-
a sample skew (s) (mintavételi meredekség) paraméter értékét a mintavételi időpont meghatározásánál alkalmazzuk. Alapértéke 0.
B.1.6.2. Discrete Zero-Order Hold (Mintavételes nulladrendű tartó függvény)
A Discrete Zero-Order Hold (Mintavételes nulladrendű tartó függvény) egy olyan hisztórikus típusú blokk , amely a bemenő jel mintavételezett értékét a következő mintavételi időpontig változatlan értékkel bocsájtja ki kimenő jelként.
A Discrete Zero-Order Hold (Mintavételes nulladrendű tartó függvény) a következő időfüggvényt valósítja meg:
|
y(t i ) = u(t i ), ha t i <= t < t i + sample skew (s) |
(B.36) |
|
|
y(t k ) = u(t k ), ha t k <= t < t k+1 |
(B.37) |
|
|
t k = t i + sample skew (s) + k * sample period (s) , k =0,1,2,…. |
(B.38) |
ahol
|
|
k |
a mintavételek száma, |
|
ti |
a szimuláció kezdési időpontja, |
|
|
tk |
a mintavételezés időpontja, |
|
|
u(tk) |
a mintavételezett bemenő jel a k. mintavételi időpontban, |
|
|
y(tk) |
a mintavételezett kimenő jel a k. mintavételi időpontban, |
|
|
sample skew (s) |
mintavételi meredekség [s], |
|
|
sample period (s) |
mintavételi periódus-időtartam [s]. |
A Discrete Zero-Order Hold (Mintavételes nulladrendű tartó függvény) paramétereinek kiszolgáló ablaka a következő ábrán (B.42. ábra) látható.
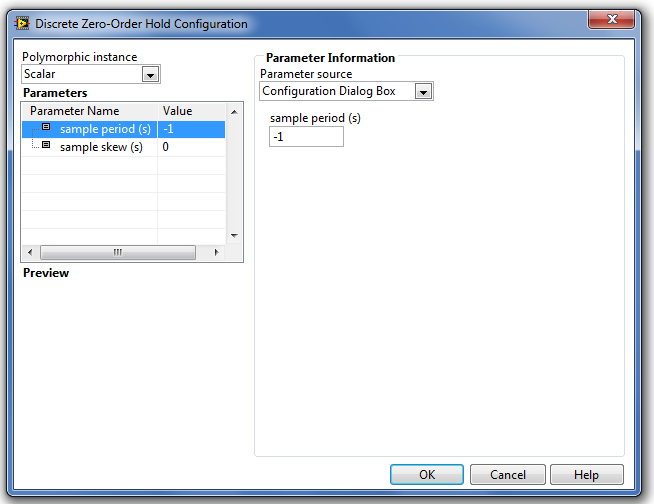
A paraméterek típusát és beállításuk módját a Step Signal Generation (Ugrás függvény) fejezetben részletesen ismertettük.
A Parameters (Paraméterek) listában található paraméterek a következő tulajdonságúak:
-
sample period (s) (a mintavételi idő) a mintavételi idő értéke másodpercben [s]. Alapértéke -1.
-
a sample skew (s) (mintavételi meredekség) paraméter értékét a mintavételi időpont meghatározásánál alkalmazzuk. Alapértéke 0.
B.1.6.3. Discrete First-Order Hold (Mintavételes elsőrendű tartó függvény)
A Discrete First-Order Hold (Mintavételes elsőrendű tartó függvény) egy olyan hisztórikus típusú blokk , amely a bemenő jel mintavételezett értékét a következő mintavételi időpontig változatlan értékkel bocsájtja ki kimenő jelként.
A Discrete First-Order Hold (Mintavételes elsőrendű tartó függvény) a következő időfüggvényt valósítja meg:
|
y(t i ) = u(t i ), ha ( sample skew (s) < 0) és (t i <= t < t i + sample skew (s) ) |
(B.39) |
|
|
vagy ha ( sample skew (s) = 0) és (t i <= t < t i + sample peroid (s) |
||
|
y(t k ) = u(t k ) + m·(t- t k ), ha t k <= t < t k+1 |
(B.40) |
|
|
t k = t i + sample skew (s) + k * sample period (s) , k =0,1,2,…. |
(B.41) |
|
|
|
(B.42) |
ahol
|
|
k |
a mintavételek száma, |
|
ti |
a szimuláció kezdési időpontja, |
|
|
tk |
a mintavételezés időpontja, |
|
|
u(tk) |
a mintavételezett bemenő jel a k. mintavételi időpontban, |
|
|
y(tk) |
a mintavételezett kimenő jel a k. mintavételi időpontban, |
|
|
sample skew (s) |
mintavételi meredekség [s], |
|
|
sample period (s) |
mintavételi periódus-időtartam [s]. |
A Discrete First-Order Hold (Mintavételes elsőrendű tartó függvény) paramétereinek kiszolgáló ablaka a következő ábrán (B.43. ábra) látható.
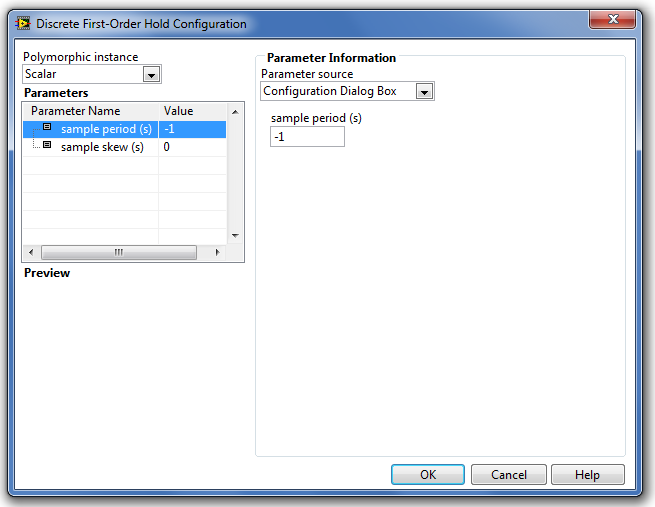
A paraméterek típusát és beállításuk módját a Step Signal Generation (Ugrás függvény) fejezetben részletesen ismertettük.
A Parameters (Paraméterek) listában található paraméterek a következő tulajdonságúak:
-
sample period (s) (a mintavételi idő) a mintavételi idő értéke másodpercben [s]. Alapértéke -1. Dimenziója másodperc [s].
-
a sample skew (s) (mintavételi meredekség) paraméter értékét a mintavételi időpont meghatározásánál alkalmazzuk. Alapértéke 0, dimenziója másodperc [s].
B.1.6.4. Discrete State-Space (Mintavételes állapottér modell)
A Discrete State-Space (Mintavételes állapottér modell) egy olyan hisztórikus típusú blokk , amely az adott szimulációs időpontban egy mintavételes állapottér modell új állapotait és az azokhoz tartozó új kimenő jelértékeket határozza meg a mintavételi időpontban.
|
|
(B.43) |
A mintavételes állapottér modellben a jelölések a következők:
|
|
k |
a mintavételezés k.· időpillanata, |
|
h |
a mintavételezési idő, |
|
|
x[k] |
az állapotváltozó a k·h időpillanatban, |
|
|
x[k+1] |
az állapotváltozó a (k+1)·h időpillanatban, |
|
|
u[k] |
a mintavételezett bemenő jel a k. mintavételi időpontban, |
|
|
y[k] |
a mintavételezett kimenő jel a k. mintavételi időpontban, |
|
|
Ad, Bd, Cd, Dd |
a mintavételes állapottér modell együtthatóinak mátrixai. |
A Discrete State-Space (Mintavételes állapottér modell) paramétereinek kiszolgáló ablaka a következő ábrán (B.44. ábra) látható.
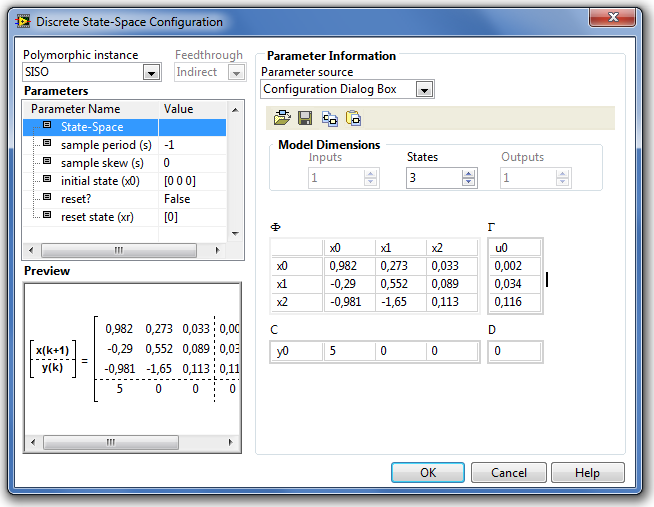
A paraméterek alaptípusát és azok beállításuk módját a Step Signal Generation (Ugrás függvény) fejezetben részletesen ismertettük.
A Parameters (Paraméterek) listában található paraméterek a következő tulajdonságúak:
-
a State-Space (Állapottér) paraméter megadja az állapottér leírás Ad, Bd, Cd és Dd mátrixainak méretét és értékeit. Alapesetben a modell egy bemenetű és egy kimenetű mintavételes állapottér modell paramétereinek megadását teszi lehetővé. Ha a bemenetre egy vektor típusú adatot kapcsolunk, akkor azonnal lehetőség van a bemenetekhez tartozó Bd mátrix paramétereinek megadására, és ekkor állíthatjuk be a többi kimenet értékét meghatározó Cd és Dd mátrixot is. Lehetőségünk van a mintavételes állapottér modellt fájlként tárolni, illetve korábban tárolt mintavételes állapottér modelleket a háttértárolóról betölteni.
A B.45. ábra a több bemenetű és több kimenetű (MIMO) mintavételes rendszer állapottér modelljének paraméterablakát mutatja be.
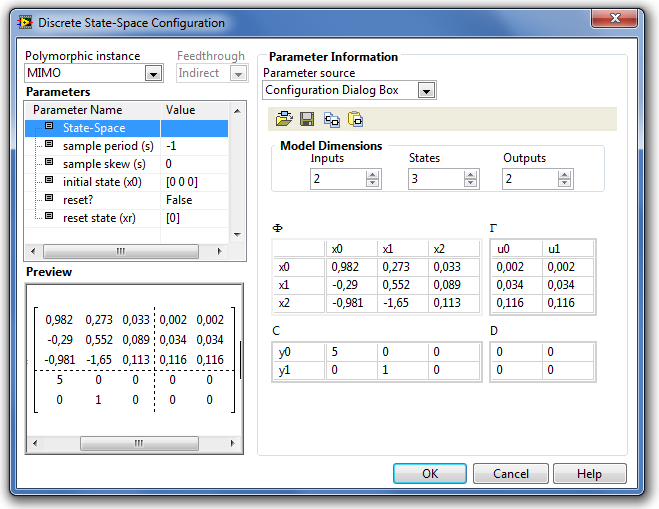 B.45. ábra - MIMO Discrete State-Space (Mintavételes állapottér modell) paraméter-beállító ablaka
B.45. ábra - MIMO Discrete State-Space (Mintavételes állapottér modell) paraméter-beállító ablaka
-
a sample period (s) (mintavételi idő = h) paraméter megadja a mintavételes szimulációs rendszer mintavételezési idejét. Alapértéke -1 (nincs megadva mintavételezési idő), dimenziója másodperc [s].
-
a sample skew (s) (mintavételi meredekség) paraméter értékét a mintavételi időpont meghatározásánál alkalmazzuk. Alapértéke 0, dimenziója másodperc [s].
-
az initial state (x0) (kezdeti állapotok) paramétervektor megadja az állapotváltozók értékét a szimuláció kezdő időpontjában. Alapértékük nulla (0) elemű vektor.
A B.46. ábra a kezdeti állapotok beállítási lehetőségét mutatja be az állapottér modell paraméterablakában:
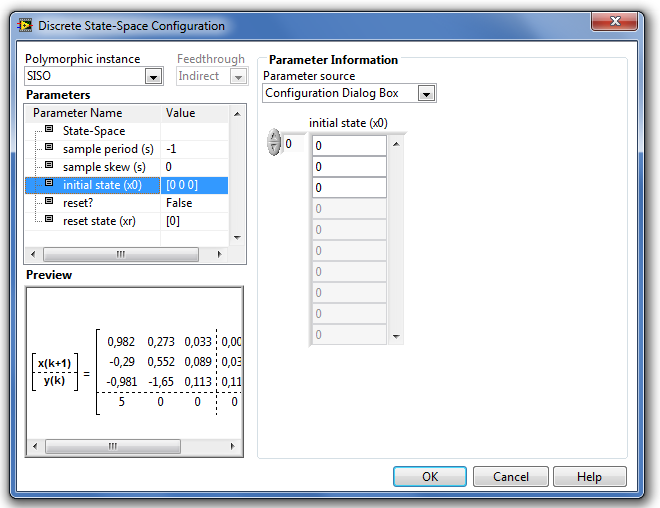 B.46. ábra - Discrete State-Space (Mintavételes állapottér modell) kezdeti állapotainak beállítása
B.46. ábra - Discrete State-Space (Mintavételes állapottér modell) kezdeti állapotainak beállítása
-
a reset? (újraindítás?) paraméter megadja, hogy az állapottér modell a szimuláció egy megadott pillanatában újraindítódik vagy sem.
Az újraindítás azt jelenti, hogy a szimuláció adott időpillanatában a mintavételes állapottér modell korábbi működését megszakítjuk, és új kezdeti állapotokkal az aktuális bemenő jellel folytatjuk tovább a szimulációt. Alapértéke nem (False).
-
a reset initial state (xr) (kezdeti állapotok újraindításkor) vektorparaméterrel adhatjuk meg az állapottér modell újraindítás utáni új állapotait.
B.1.6.5. Discrete Transfer Function (Mintavételes impulzus-átviteli függvény modell)
A Discrete Transfer Function (Mintavételes impulzus-átviteli függvény modell) egy olyan hisztórikus típusú blokk , amely az adott szimulációs időpontban egy folytonos átviteli függvénnyel leírt modell kimenő jelének értékeit határozza meg a bemenő jel alapján.
A Mintavételes impulzus-átviteli függvényt egy bemenet és egy kimenet esetén a következő egyenlettel írjuk le:
|
|
(B.44) |
A Discrete Transfer Function (Mintavételes impulzus-átviteli függvény modell) paramétereit a B.47. paraméterbeállító ablakban adhatjuk meg.
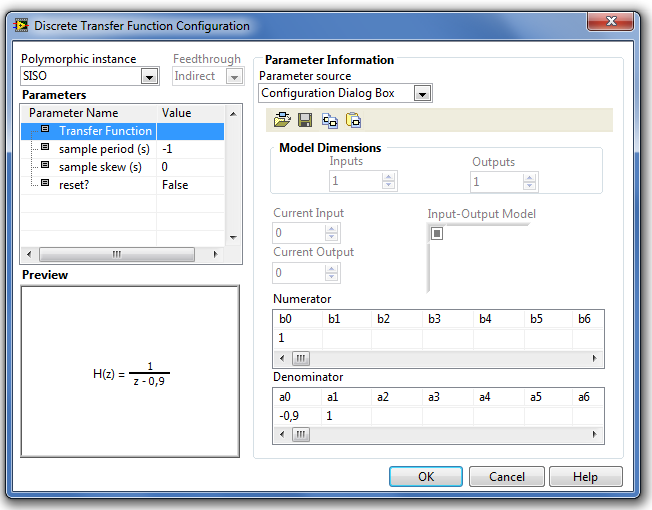
A paraméterek alaptípusát és azok beállításuk módját a Step Signal Generation (Ugrás függvény) fejezetben részletesen ismertettük.
A Parameters (Paraméterek) listában található paraméterek a következő tulajdonságúak:
-
a Transfer Function (Átviteli függvény modell) paraméter megadja az átviteli függvény számlálójában (numerator) és nevezőjében (denominator) s egész hatványainak együtthatóit. A 0. indexű elem s0 hatványának együtthatóját jelenti, az 1. indexű elem s szorzója, a 2. indexű elem s2-é és így tovább.Az átviteli függvényben nincs lehetőség kezdeti állapot megadására, vagyis minden állapotváltozó értéke nulla a szimuláció elindulásakor (t=0). Lehetőségünk van az átviteli függvény modellt fájlként tárolni, illetve korábban tárolt átviteli függvény modelleket a háttértárolóról betölteni.
A B.48. ábra a több bemenetű és több kimenetű (MIMO) rendszer átviteli függvény (mátrix) paraméterablakát mutatja be. Ilyen esetben minden bemenet és minden kimenet között meg kell adnunk az kimenet-bemenet pároshoz tartozó átviteli függvény együtthatóit.
Az ábrán látható Input-Output Modell (Bemeneti-Kimeneti modell) mátrixában a megfelelő elemre kattintva megadhatjuk, hogy melyik kimenet és bemenet közötti átviteli függvény paramétereit láthatjuk a számláló és a nevező vektor elemeiben.
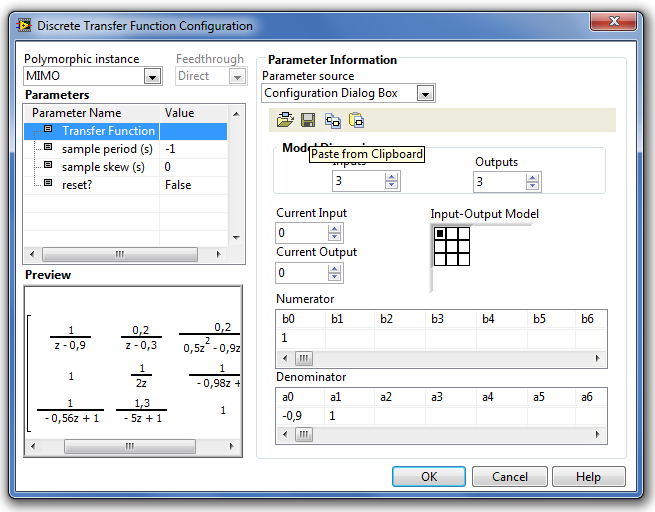 B.48. ábra - MIMO Transfer Function Matrix (Átviteli függvény modell mátrix) paraméter-beállító ablaka
B.48. ábra - MIMO Transfer Function Matrix (Átviteli függvény modell mátrix) paraméter-beállító ablaka
-
a sample period (s) (mintavételi idő = h) paraméter megadja a mintavételes szimulációs rendszer mintavételezési idejét. Alapértéke -1 (nincs megadva mintavételezési idő), dimenziója másodperc [s].
-
a sample skew (s) (mintavételi meredekség) paraméter értékét a mintavételi időpont meghatározásánál alkalmazzuk. Alapértéke 0, dimenziója másodperc [s].
-
a reset? (újraindítás?) paraméter megadja, hogy az állapottér modell a szimuláció egy megadott pillanatában újraindítódik vagy sem.
Az újraindítás azt jelenti, hogy a szimuláció adott időpillanatában a mintavételes állapottér modell korábbi működését megszakítjuk, és új kezdeti állapotokkal az aktuális bemenő jellel folytatjuk tovább a szimulációt. Alapértéke nem (False).
B.1.7. Táblázattal megadott szimulációs paraméterek (Lookup Tables)
A Táblázattal megadott szimulációs paraméterek (Lookup Tables) palettán olyan elemek találhatók, amelyekkel lehetőségünk van a szimulációban táblázatosan megadott adatokat feldolgozni. Ezek a blokkok a táblázatban megadott függvényértékek esetén meghatározható interpolációs értékeket adják meg.
A modell létrehozásához leggyakrabban használt alpaletták:
|
|
Lookup Table 1D (Egydimenziós táblázati függvény) |
|
|
|
Lookup Table 2D (Kétdimenziós táblázati függvény) |
B.1.7.1. Lookup Table 1D (Egydimenziós táblázati függvény)
A Lookup Table 1D (Egydimenziós táblázati függvény) nem hisztórikus típusú blokk , amely diszkrét pontokban megadott bemenő jel és a hozzájuk rendelt kimenő jel alapján interpolációt valósít meg, hogy azokban a pontokban is meghatározhassa a kimenő jel értékét, amelyekben az nincs megadva.
A Lookup Table 1D (Egydimenziós táblázati függvény) a következő ábrán (B.50. ábra) látható időfüggvényt valósítja meg.
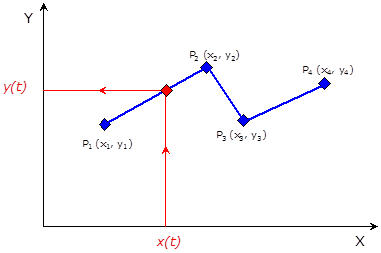
Az ábrán az
|
x(t) |
a bemenő jel a szimulációs időpontban, |
|
|
y(t) |
a kimenő jel a szimulációs időpontban. |
A Lookup Table 1D (Egydimenziós táblázati függvény) paramétereinek beállító ablaka a következő ábrán (B.51. ábra) látható.
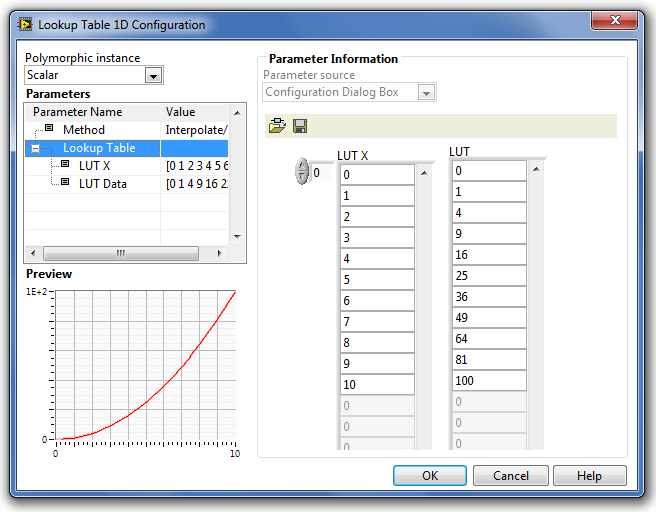
A paraméterek típusát és beállításuk módját a Step Signal Generation (Ugrás függvény) fejezetben részletesen ismertettük.
A Parameters (Paraméterek) listában található paraméterek a következő tulajdonságúak:
-
Method (Függvényközelítési eljárás) a megadott pontok alapján a közelítés módja.
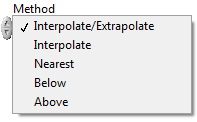 B.52. ábra - A Lookup Table 1D (Egydimenziós táblázati függvény) Method (Függvényközelítési eljárás) paraméter-beállító legördülő menüje
B.52. ábra - A Lookup Table 1D (Egydimenziós táblázati függvény) Method (Függvényközelítési eljárás) paraméter-beállító legördülő menüje
Néhány jellemző közelítési eljárás kimenő jeleinek ábráját mutatjuk be a következő ábrákon.
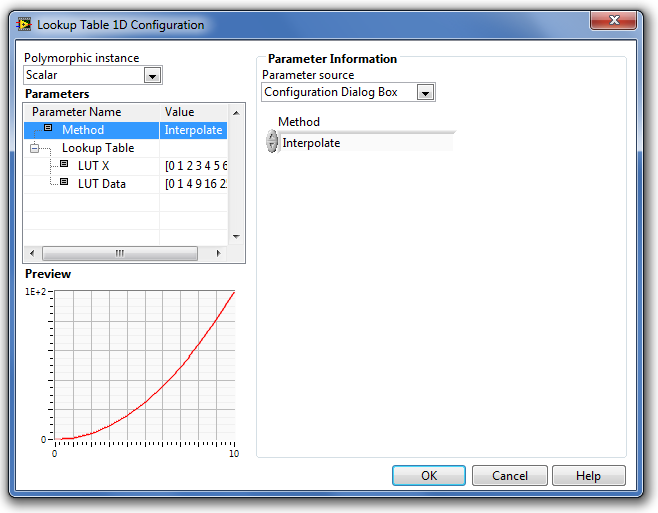 B.53. ábra - A Lookup Table 1D (Egydimenziós táblázati függvény) Method paraméter = Interpolate (közelítés)
B.53. ábra - A Lookup Table 1D (Egydimenziós táblázati függvény) Method paraméter = Interpolate (közelítés)
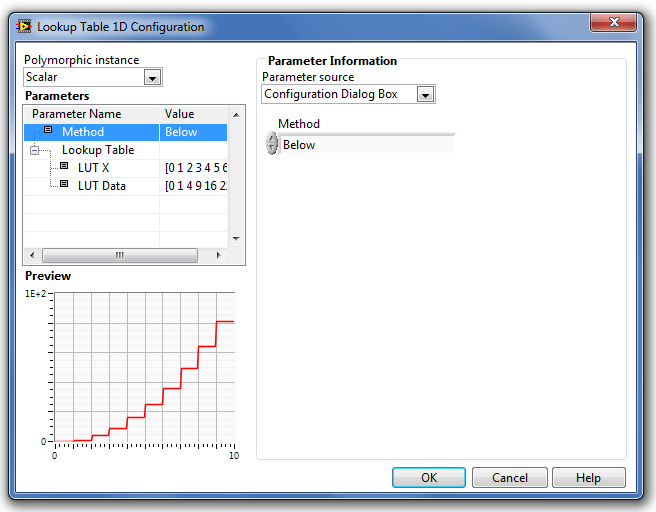 B.54. ábra - A Lookup Table 1D (Egydimenziós táblázati függvény) Method paraméter = Below (alulról közelítés)
B.54. ábra - A Lookup Table 1D (Egydimenziós táblázati függvény) Method paraméter = Below (alulról közelítés)
-
Lookup Table (a függvénydefiniáló pontok táblázata) - ezek a pontkoordináták adják meg a függvény „ismert pontjait”. Az itt nem szereplő bementi értékekhez a Method (Metódus) menüben megadott közelítési eljárással történik a közelítő függvény alapján a kimenő jel közelítő értékének meghatározása.
B.1.7.2. Lookup Table 2D (Kétdimenziós táblázati függvény)
A Lookup Table 2D (Kétdimenziós táblázati függvény) nem hisztórikus típusú blokk , amely diszkrét pontokban megadott bemenő jelek és a hozzájuk rendelt kimenő jelek alapján interpolációt valósít meg, hogy azokban a pontokban is meghatározhassa a kimenő jel értékét, amelyekben az nincs megadva.
A Lookup Table 2D (Kétdimenziós táblázati függvény) a következő ábrán (B.55. ábra) tanulmányozható időfüggvényt valósítja meg.
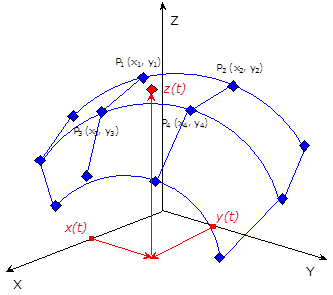
Az ábrán
|
x(t) |
az első bemenő jel a szimulációs időpontban, |
|
|
y(t) |
a második bemenő jel a szimulációs időpontban, |
|
|
z(t) |
az interpolált kimenő jel a szimulációs időpontban, |
A Lookup Table 2D (Kétdimenziós táblázati függvény) paramétereinek beállító ablaka a következő ábrán (B.56. ábra) látható.
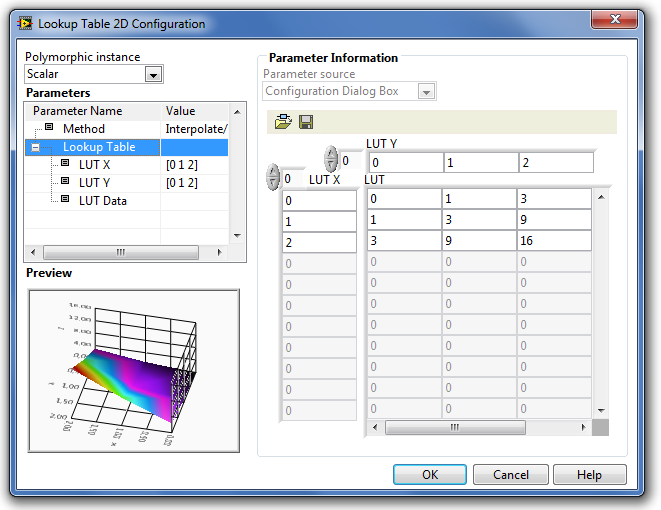
A paraméterek típusát és beállításuk módját a Step Signal Generation (Ugrás függvény) fejezetben részletesen ismertettük.
A Parameters (Paraméterek) listában található paraméterek a következő tulajdonságúak:
-
Method (Függvényközelítési eljárás) a megadott pontok alapján a közelítés módja.
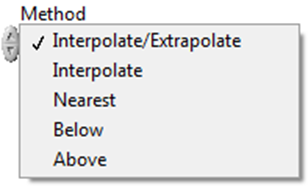 B.57. ábra - A Lookup Table 2D (Kétdimenziós táblázati függvény) Method (Függvényközelítési eljárás) paraméter-beállító legördülő menüje
B.57. ábra - A Lookup Table 2D (Kétdimenziós táblázati függvény) Method (Függvényközelítési eljárás) paraméter-beállító legördülő menüje
Néhány jellemző közelítési eljárás kimenő jeleinek ábráját mutatjuk be a következő ábrákon.
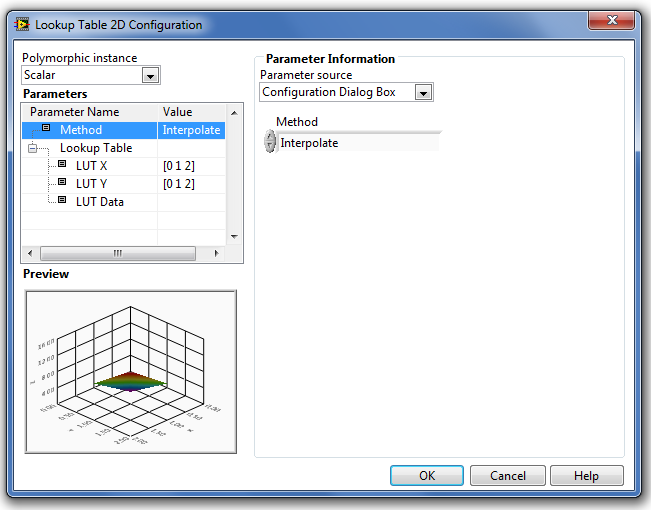 B.58. ábra - A Lookup Table 2D (Kétdimenziós táblázati függvény) Method paraméter = Interpolate (közelítés)
B.58. ábra - A Lookup Table 2D (Kétdimenziós táblázati függvény) Method paraméter = Interpolate (közelítés)
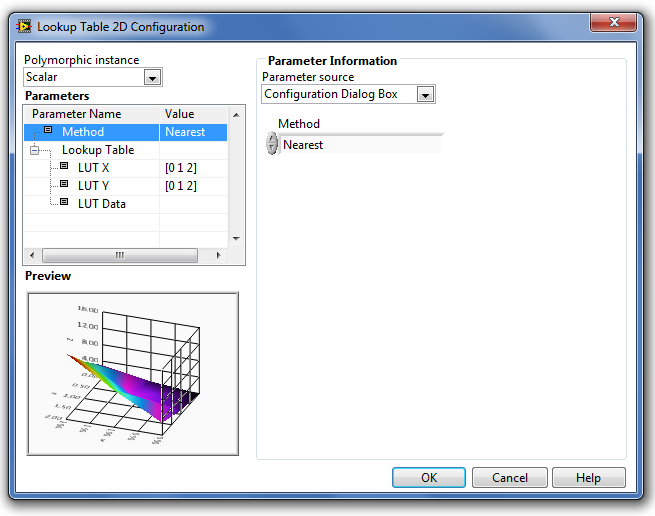 B.59. ábra - A Lookup Table 2D (Kétdimenziós táblázati függvény) Method paraméter = Nearest (legközelebbi)
B.59. ábra - A Lookup Table 2D (Kétdimenziós táblázati függvény) Method paraméter = Nearest (legközelebbi)
-
Lookup Table (a függvénydefiniáló pontok táblázata) - ezek a pontkoordináták adják meg a függvény „ismert pontjait”. Az itt nem szereplő bementi értékekhez a Method (Metódus) menüben megadott közelítési eljárással történik a közelítő függvény alapján a kimenő jel közelítő értékének meghatározása.
B.2. Modellelemek összekapcsolása
A LabVIEW-ban minden programozási elem egy objektum , amely rendelkezik attribútumokkal (saját változókkal), metódusokkal (eljárásokkal, amelyeket csak az objektum adataival hajthatunk végre), valamint eventekkel (eseményekkel). Az Irányítás és szimulációs hurok (Control & Simulation Loop) is egy ilyen objektum.
A korábban definiált szimulációs alaptagok csak az Irányítási és szimulációs hurok által rendelkezésükre bocsájtott paraméterekkel valamint a blokkban elhelyezve képesek számolni! Önállóan nem használhatók, mint LabVIEW VI-ok.
Ez azt is jelenti, hogy a szimulációs blokkoknak mindig egy Irányítás és szimulációs hurok (Control & Simulation Loop) belsejében kell elhelyeznünk. Ennek az a következménye, hogy egy Irányítás és szimulációs hurok összes időzítési paraméterének beállítása után tetszőleges bonyolultságú modellt építhetünk fel a szimulációs keretben.
Ez a szimulációs hurok párhuzamosan működtethető más hasonló tulajdonságú szimulációs hurkokkal, ezért egyszerre, egy időben, több szimulációs hurok is futtatható, amelyek globális változókon keresztül értékeket is átadhatnak egymásnak.
Az Irányítás és szimulációs hurok (Control & Simulation Loop) egyik különleges grafikai tulajdonsága a többi LabVIEW programelemmel szemben, hogy az összekötő vezetékeknek van adatfolyam iránya, amelyet minden vezetéken egy nyíl jelöl. Az elemek összekötése, illetve az összekötés törlése teljesen hasonló módon történik, mint minden más LabVIEW programban. A B.60. ábra a szimulációs blokkban elhelyezett elemek összekötését mutatja be.
Az (B.60. ábra) ábrán a szimulációs blokkok soros kapcsolását láthatjuk. A blokkok polimorf tulajdonsága alapján minden szimulációs blokk képes skalár (egyváltozós) vagy vektor típusú adatokkal számítást végezni. Így a Signal Generator kimenő jeléből és a Transfer Function kimenő jeléből egy vektort hoztunk létre és ezt juttatjuk el a Simulation Time Waveform blokkba, amely az adatokat az idő függvényében egy ábrába rajzolja.
Szimulációs blokkok párhuzamos kapcsolására látunk példát a következő ábrán (B.61. ábra).
A harmadik példa (B.62. ábra) szimulációs blokkok visszacsatolással történő összekapcsolására mutat mintapéldát. Ebben az esetben is a megvalósítandó modell blokkdiagramját kell bemásolnunk a szimulációs keretbe:
Az eddig bemutatott példákban a szimulációs blokkok paramétereit kézi adatbevitellel adtuk meg. Lehetőség van azonban arra is, hogy a szimulációs paramétereket egy a szimulációs blokkon kívül elhelyezett számítással adjuk meg, és a kiszámított paramétert juttassuk el a szimulációs programunkba. Hogy láthassuk, melyik bementhez kapcsoljuk a kiszámított paramétert, a külső paraméterrel ellátott blokk megjelenítését váltsuk át a jobb oldali egér gombbal az „Icon Style” menüpontnál „Text Only” menüponttal a szimulációs blokk paramétereinek szöveges megjelenítésére.
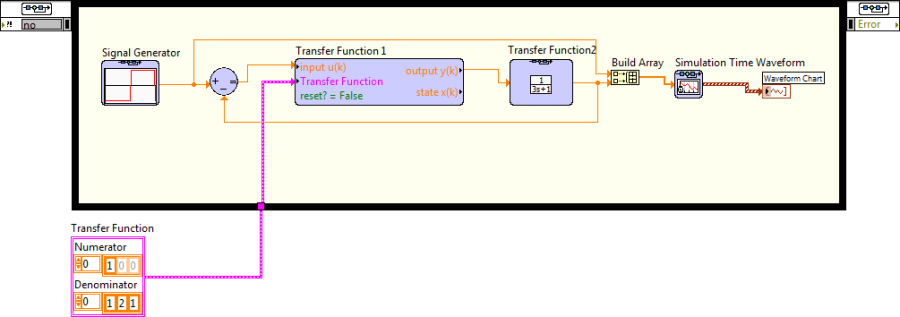
Külső paraméterátadást a Szabályozó tervezés (Control Design) rendszerből is megvalósíthatunk. Ilyenkor szükséges a Szabályozó tervezés (Control Design) programban tárolt átviteli függvény, állapottér alakot az Irányítás és szimulációs hurokban (Control & Simulation Loop) alkalmazott átviteli függvény és állapottér alakra áttranszformálni.
Hasonlóan szükséges lehet, hogy a Irányítás és szimulációs hurokban (Control & Simulation Loop) létrehozott modellezési elemek paramétereit juttassuk el a Szabályozó tervezés (Control Design) programba. Ezeket a feladatokat a következő ábrán (B.64. ábra) látható VI-ok oldják meg, amelyek a Szabályozó tervezés (Control Design) programban a Model Conversion (Modell konverzió) alpaletta elemei között találhatók.

B.3. Almodell (Subsytem) létrehozása
A szimulációs modellekben gyakran vannak olyan részek (blokkdiagram részletek), amelyek megismétlődnek a modellben csak más paraméter értékkel. Jó lenne, ha ezeket a kis blokkdiagram részleteket tárolhatnánk, mint egy alprogramot és a különböző helyeken a megfelelő bemeneti paraméterekkel beillesztenénk a modellbe.
Másik gyakorlati igény a modellépítésnél, hogy a nagyon sok blokkból álló részletes modellt funkcionális blokkokból építhessük fel, illetve mi határozzuk meg, hogy mely elemek (blokkok) tartoznak az adott funkcionális blokkba. Ez az igény is azt jelenti, hogy a szimulációs modell blokkdiagramjának bizonyos részét egy alprogramba szeretnénk tárolni.
Vegyünk egy egyszerű példát, amelyben egy szabályozott szakaszhoz PID szabályozót építünk (B.65. ábra).
Kék kerettel jelöltük meg a PID szabályozóhoz tartozó programrészt, ebből szeretnénk egy szimulációs alprogramot készíteni. A szimulációs alprogram létrehozása eltér a „normál” VI alprogram létrehozásától!
Az egérmutatóval jelöljük ki azokat a blokkokat és összekötéseket, amelyeket szeretnénk elhelyezni a szimulációs alprogramba.
Ezután az Edit menüben válasszuk ki a Create Simulation Subsystem (Szimulációs alprogram létrehozása) menüpontot
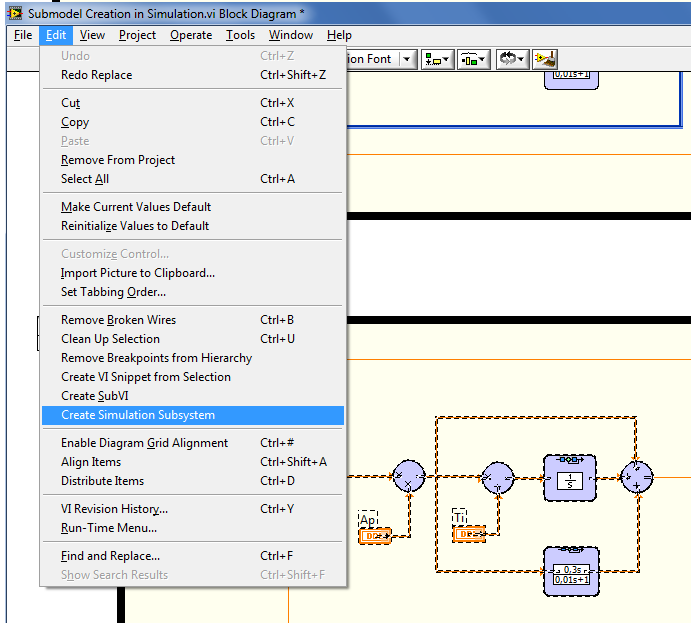
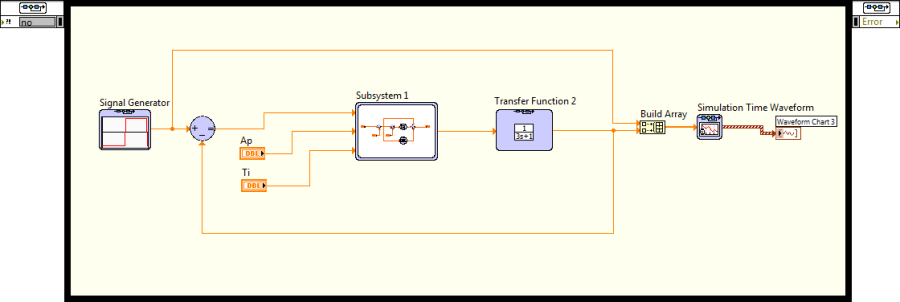
Ha a létrehozott alprogram területére kattintunk az egérgombbal, megjelenik az újonnan készített alprogram kiszolgáló ablaka. Az új szimulációs blokk teljesen ugyanolyan kezelési felülettel rendelkezik, mint a többi szimulációs blokk.
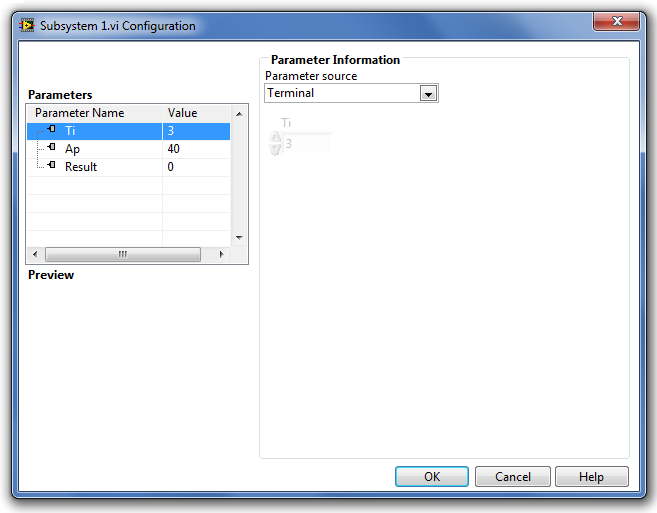
Ha az újonnan létrehozott alprogram területére kattintunk a jobb egérgombbal a megjelenő felugró menüből kiválaszthatjuk az Open Subsystem (Nyisd meg a alprogramot) menüpontot. Ekkor megjelenik az elkészített alprogram front panelja, amely a következő ábrán (B.70. ábra) látható alakú.
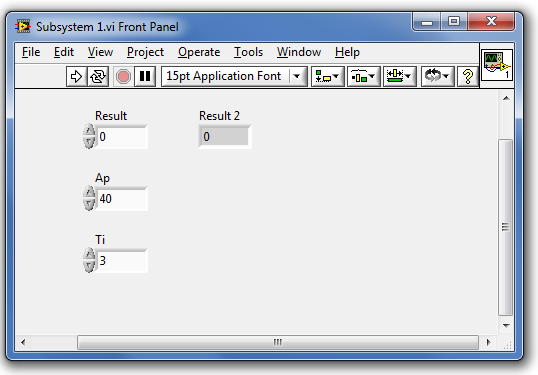
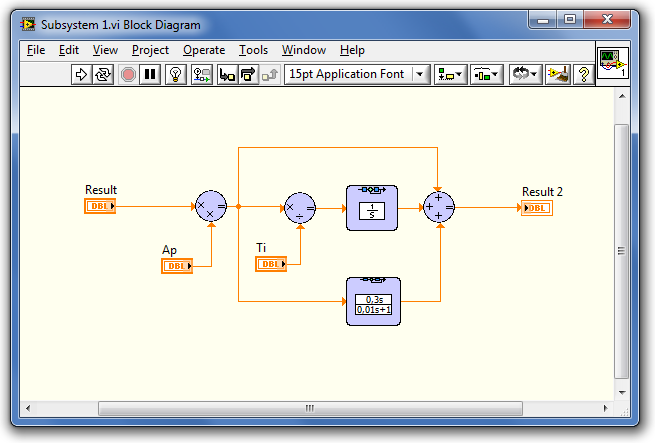
A szimulációs program tetszőlegesen kijelölt blokkcsoportjából létrehozhatunk újabb alprogramokat. Az alprogramok tartalmazhatnak korábban készített alprogramokat is. Így lehetőségünk van adott feladatot elvégző, egymáshoz tartozó szimulációs programrészek egy blokkban történő egyesítésére, és jól áttekinthető modell készítésére.
B.4. A szimulációs modell vizsgálata időtartományban
A szimuláció működésének bemutatására a következő ábrán (B.72. ábra) látható szabályozási kör szimulációs programját vizsgáljuk meg.
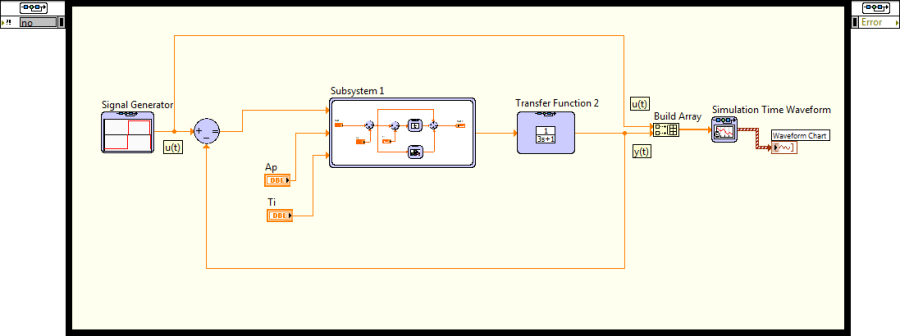
A szimulációs mintapélda szimulációs kereténél beállított paraméterek a következő ábrán (B.73. ábra) tanulmányozhatók.
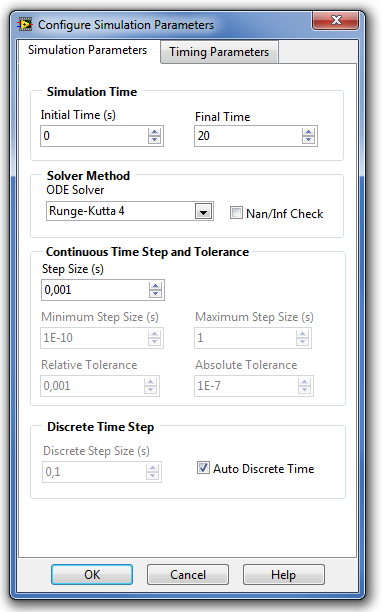
A szimulációs paraméterek ablakban beállított érték a következők:
-
A szimulációs program nulla (0) szimulációs kezdeti időponttól 20 s időtartamig számítja ki a keretben felépített modellt bementi és kimeneti jeleit.
-
A folytonos rendszerek szimulációjában alkalmazott integrálási formula állandó lépésközű Runge-Kutta4 (negyedrendű) eljárás.
-
A szimulációs adatokat 0,001 s mintavételi időpontokban fogjuk kirajzolni.
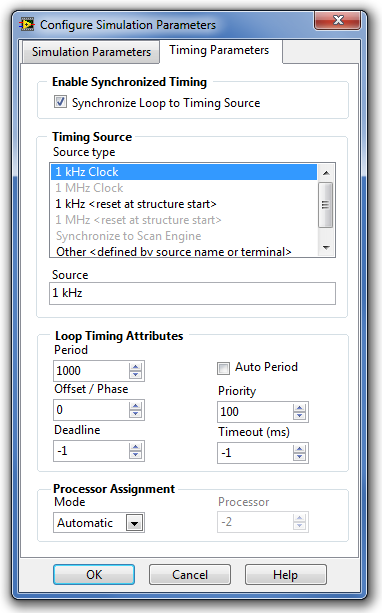
Az időzítési ablakban beállított paraméterek közül a legfontosabb az Syncronize Loop to Timing Source (A szimulációs hurok szinkronizálása egy időalap-generátorhoz) jelölőnégyzet állapota. Ha ez a jelölőnégyzet kijelölt állapotban van, akkor a szimuláció időlépése a SourceType (Időalap forrásnál) kijelölt frekvencia periódusideje és a Period (Periódus) paraméternél kijelölt számérték szorzata.
Az ábrán (B.74. ábra) szereplő adatokkal ez az időtartam 1 kHz-es időalapnál megfelel 1 ms-os időalap-generátor periódusidőnek, amely a szimulációs keret periódus paraméterével (1000) megszorozva 1000 ms = 1 s időtartamot jelent.
Ez az időtartam telik el két szimulációs lépésköz között, függetlenül attól, hogy a szimulációs lépésköz milyen értékű.
Ha valóságos időszinkronizációt szeretnénk megvalósítani, akkor a szimulációs időlépés időtartamát (Step Size (s)) és a szinkronizációs időalap és a szimulációs keret „Periódus” paraméterével meghatározott értékeknek meg kell egyeznie.
Ez azt jelenti, hogy időszinkronizált futás esetén a következő ábrán (B.75. ábra) látható időzítési paramétereket kell beállítanunk.
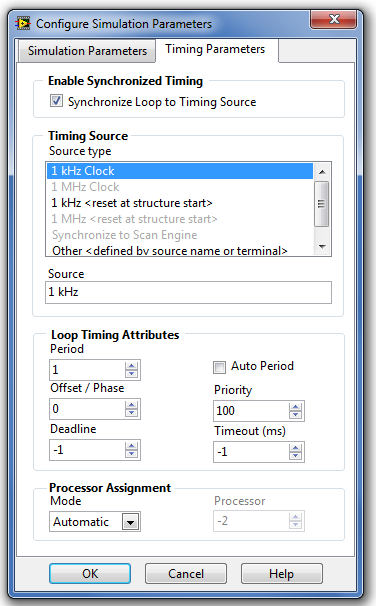
B.4.1. A modell vizsgálata időtől független (off-line) futtatási módban
Az elkészített szimulációs program időtől független futtatása azt jelenti, hogy a szimuláció időlépése (StepSize (s)) nincs semmiféle kapcsolatban a valós idővel, és a szimulációs program futási sebessége csak a számítógép sebességétől (órajelének frekvenciájától és operatív memória nagyságától) függ.
A szimulációs keret ebben az esetben a következő ábrán (B.76. ábra) tanulmányozható paramétereket tartalmazza.
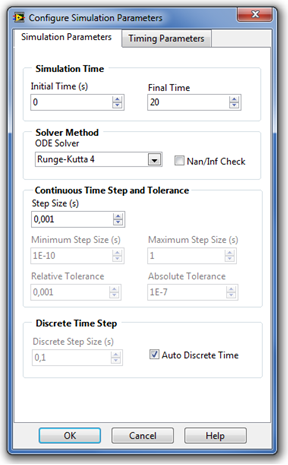
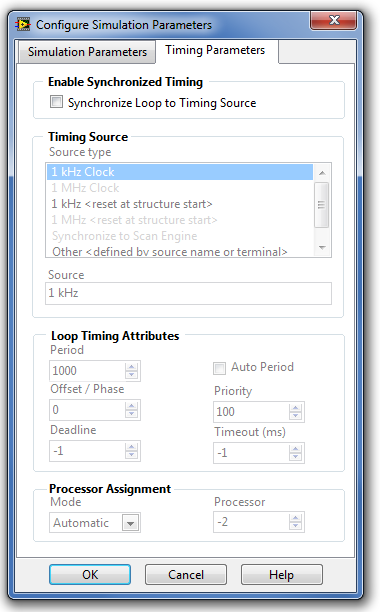
Időfüggetlen szimulációs programfuttatás esetén a program elindítása után addig nem látjuk az eredményeket, amíg a teljes szimuláció le nem fut. Ez a szimuláció kezdő időpontjától a szimuláció befejezési időpontjáig elvégzett összes szimulációs adatra vonatkozik. Ezután a grafikus megjelenítőkön és az indikátorelemeken lesznek láthatók a szimuláció eredményei.
A szimulációs program futtatása után a front panel a következő ábrán (B.78. ábra) látható formában jelenik meg.
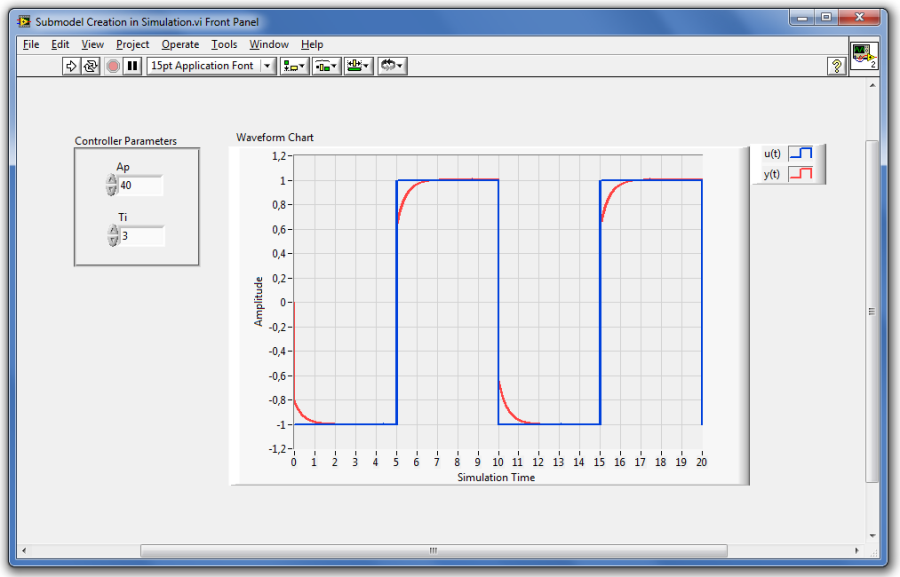
B.4.2. A modell vizsgálata időtől függő (on-line) futtatási módban
A szimulációs mintapélda szimulációs kereténél beállított paraméterek ( időtől függő) időszinkronizált működés esetén a következő ábrán (B.79. ábra) követhetők nyomon.
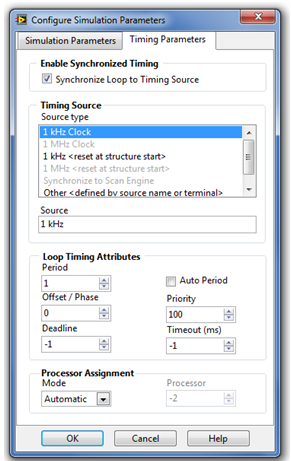
A szimuláció óragenerátorának frekvenciája 1 kHz. A Periode = 1, ami 1/1kHz = 1 ms időtartammal, 1 ms-os mintavételi időt jelent, ugyanazt az értéket, mint a Step Size (s) a (B.79. ábra) ábrán.
Ez azt jelenti, hogy a mintavételi időlépés és a beállított időlépés azonos érték, tehát a szimuláció időszinkronban fog futni, azaz 1 ms a szimulációs modell számításban 1 ms alatt fog lezajlani.
A szimulációs program futtatása után a front panel a következő ábrán (B.81. ábra) látható formában jelenik meg.
A front panelen megjelelő ábra a valós idővel szinkronizálva jelenik meg, azaz az ábrán csak annyi időadatot látunk, mint az addig eltelt szimulációs idő. Az ábrán éppen a 11. és 12. másodperc között jártunk a szimulációval, amikor megállítottuk a számításokat.