A. függelék - Dinamikus rendszerek szimulációs eszközei - LabVIEW Control Design Module
Vissza		Előre

A. függelék - Dinamikus rendszerek szimulációs eszközei - LabVIEW Control Design Module

Tartalom

A LabVIEW program számos modult tartalmaz, amelyekkel egyszerűbbé válik a folytonos és mintavételes rendszerek irányítási tervezése. A programcsomagban a következő elemek találhatók:

Rendszertervezés (LabVIEW Control Design Module)
Szimulációs modul (LabVIEW Simulation Module)
MathScript Rt modul (LabVIEW MathScript RT Module)
Identifikációs eszköz (LabVIEW System Identification Toolkit)
PID szabályozó és Fuzzy szabályozó tervezése (LabVIEW PID and Fuzzy Logic Toolkit)
Matlab-LabVIEW szimulácós modell kapcsolati eszköz (LabVIEW Simulation Interface Toolkit)

Ebben a programismertetőben a Rendszertervezés (LabVIEW Control Design Module) modullal ismerkedünk meg.

Az A.1. ábra bemutatja a Rendszertervezés és Szimuláció (Control Design & Simulation) palettát a LabVIEW-ban

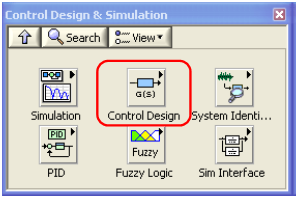
A.1. ábra - A Rendszertervezés és Szimuláció (Control Design & Simulation) paletta

Ebben az ismertetőben elsősorban a folytonos és mintavételes rendszerek átviteli függvényének és állapottér leírásának elemeit szeretnénk bemutatni.

Ha a felsorolt programcsomagok utasításait szeretné részletesen megismerni, akkor tanulmányozza a programcsomagok ismertető kézikönyvét, amelyet az ni.com/manuals Internet címen talál meg.

Az A.2. ábra a Szabályozó tervezés (Control Design) paletta elemeit mutatja be:

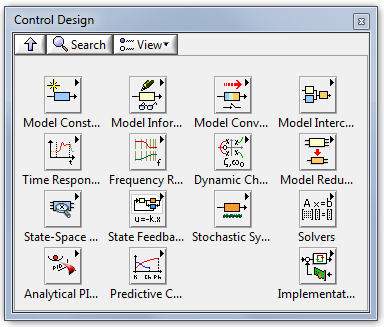
A.2. ábra - A Szabályozó tervezés (Control Design) paletta

A következő fejezetekben bemutatjuk a Szabályozó tervezés (Control Design) alpalettáiban elhelyezett műveleteket, amelyek segítségével megvalósíthatjuk a modell-definiálást, illetve a modell idő- és frekvencia-tartományban történő szimulációját.

A Szabályozó tervezés (Control Design) alpaletta elemei elsősorban adott időtartamra vonatkozó rendszervizsgálatot tesznek lehetővé. Ez azt jelenti, hogy a paletta elemeivel nem tudunk dinamikus tulajdonságú rendszerelemeket valós időben szimulálni, hanem úgynevezett futási időtartamtól független analízis feladatokat oldhatunk meg. Más szóval úgy is mondhatnánk, hogy az alpaletta elemeivel meg tudjuk tervezni a különböző dinamikus irányítási rendszerek optimális működését, de ezzel a programcsomaggal nem működtethetjük közvetlenül az irányított elemeket.

A.1. Modell létrehozása

Amikor megalkotjuk a megfelelő matematikai modellt a szimulált rendszer viselkedésének leírásához, az első lépés, hogy létrehozzuk a dinamikus rendszermodell leírását LabVIEW-ban.

A Rendszertervezés és Szimuláció (Control Design & Simulation) modulban létrehozhatunk különböző modelleket, amelyek átviteli függvény vagy állapottér leírású formában adják meg a vizsgált modell paramétereit.

A Rendszertervezés (Control Design) paletta számos alpalettát tartalmaz, amelyek a modell definiálását segítik - ezek a következők:

Modell létrehozása (Model Construction)
Információ a modellről (Model Information)
Modell konverzió (Model Conversion)
Modell összekapcsolás (Model Interconnection)

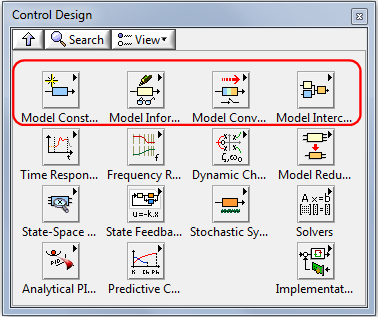
A.3. ábra - A Szabályozó tervezés (Control Design) paletta

Az (A.3. ábra) ábrán a modell definiálásánál leggyakrabban használt alpalettákat mutatjuk be, amelyek a következők:

A.1.1. Modell létrehozása (Model Construction) alpaletta:

Ebben az alpalettában hozhatunk létre átviteli függvényeket és állapottér modelleket.

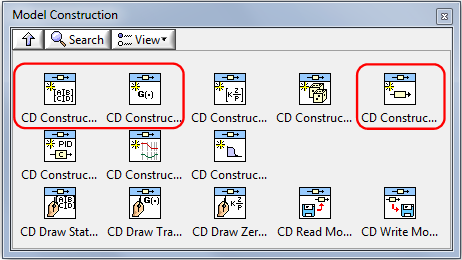
A.4. ábra - Modell létrehozása (Model Construction) alpaletta

A VI-ok alkalmazásával lineáris rendszermodelleket készíthetünk, és/vagy módosíthatjuk modellek paramétereit. A Modell létrehozása (Model Construction) VI-okat arra is alkalmazhatjuk, hogy elmentsük egy file-ba a modell paramétereit, és/vagy visszaolvassuk őket a file-ból, illetve hogy vizuálisan is megjelenítsük a vizsgált átviteli függvényt valamint az állapottér-paramétereket.

A modell létrehozásához leggyakrabban használt VI-ok

		CD Construct State-Space Model.vi
		CD Construct Transfer Function Model.vi
		CD Construct Special TF Model.vi

A.1.1.1. Állapottér modell létrehozása

Adott a következő állapottér modell:

$\begin{array}{l} \dot{x} = A \cdot x + B \cdot u \\ y = C \cdot x + D \cdot u \end{array}$

(A.1)

Az Állapottér modell létrehozása CD Construct State-Space Model.vi program segítségével állapottér modellt hozhatunk létre a LabVIEW-ban:

A.5. ábra - Állapottér modell létrehozása (CD Construct State-Space Model.VI) program ikonja

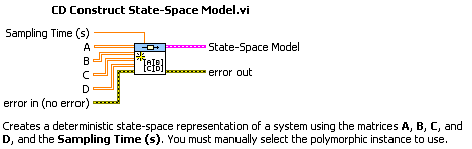
A.6. ábra - Állapottér modell létrehozása (CD Construct State-Space Model.VI) program segítség (Help) információs ablaka

Az A, B, C és D mátrixok elemeit megadhatjuk numerikus értékekkel vagy szimbolikus formában ha az (A.5. ábra) ábrán látható ikon alsó kiválasztó menüje segítségével kiválasztjuk a “Numeric” vagy “Symbolic” menüpontot:

A.7. ábra - Az Állapottér modell numerikus vagy szimbolikus adatokkal történő feltöltése

Mintapélda: Állapottér modell (State-Space model) létrehozása.

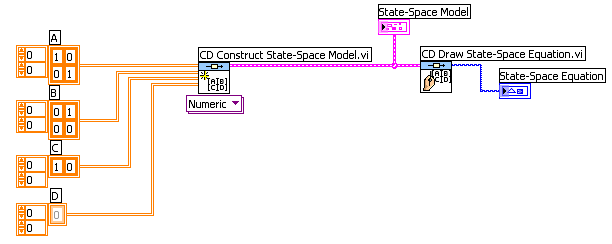
A.8. ábra - Állapottér modell numerikus adatokkal történő feltöltése és az adatok kiírása blokk diagram

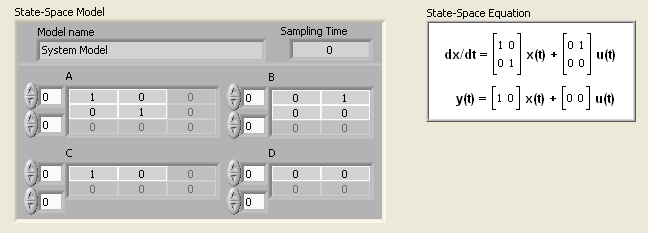
A.9. ábra - Az Állapottér modell numerikus adatokkal történő feltöltése, és az adatok megjelenítése a front panelen

Az Állapottér egyenlet kiírása (CD Draw State-Space Equation.vi) programot arra használjuk, hogy a képernyőn grafikus állapottér alakban láthassuk az egyenleteket.

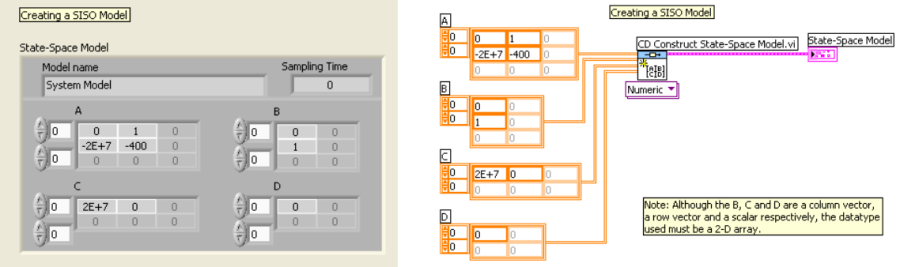
Mintapélda: SISO/MIMO állapottér modellek létrehozása.

SISO modell (Single Input, Single Output):

A.10. ábra - A SISO (Single Input, Single Output) állapottér modell numerikus adatokkal történő feltöltése

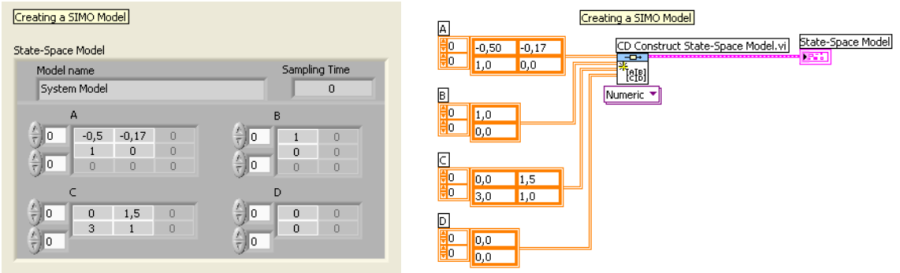
SIMO modell (Single Input, Multiple Output):

A.11. ábra - A SIMO (Single Input, Multiple Output) állapottér modell numerikus adatokkal történő feltöltése

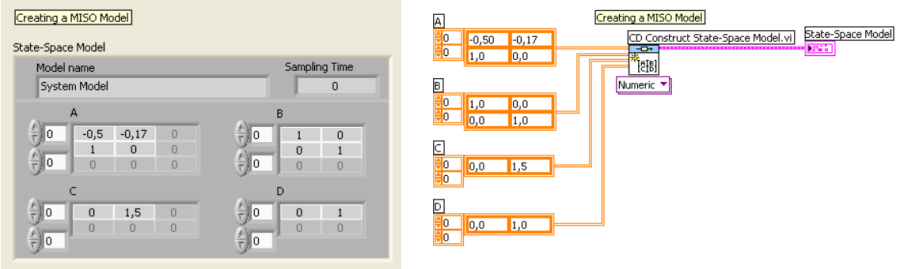
MISO modell (Multiple Input, Single Output):

A.12. ábra - A MISO (Multiple Input, Single Output) állapottér modell numerikus adatokkal történő feltöltése

MIMO modell (Multiple Input, Multiple Output):

A.13. ábra - A MIMO (Multiple Input, Multiple Output) állapottér modell numerikus adatokkal történő feltöltése

A.1.1.2. Átviteli függvény (Transfer Function) létrehozása

Adott a következő átviteli függvény:

$G (s) = \frac{n u m e r a t o r}{d e n o \min a t o r} = \frac{b_{0} + b_{1} \cdot s + b_{2} \cdot s^{2} + ... + b_{m} \cdot s^{m}}{a_{0} + a_{1} \cdot s + a_{2} \cdot s^{2} + ... + a_{n} \cdot s^{n}}$

(A.2)

Az Átviteli függvény létrehozása (CD Construct Transfer Function Model.vi) program segítségével átviteli függvény modellt hozhatunk létre a LabVIEW-ban:

A.14. ábra - Átviteli függvény modell létrehozása (CD Construct Transfer Function Model.VI) program ikonja

A.15. ábra - Átviteli függvény modell létrehozása (CD Construct Transfer Function Model.VI) program segítség (Help) információs ablaka

Mintapélda: Átviteli függvény (Transfer Function) létrehozása numerikus adatokkal

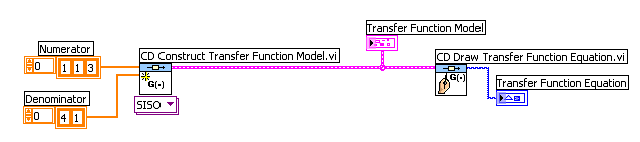
A.16. ábra - Az Átviteli függvény modell numerikus adatokkal történő feltöltése és az adatok kiírása blokkdiagram

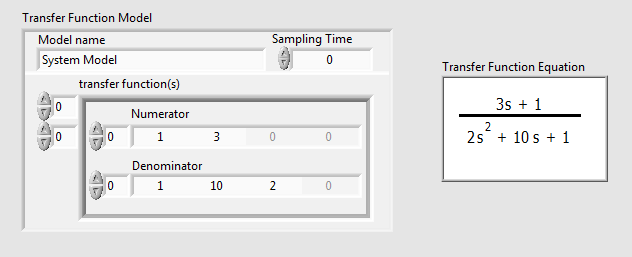
A.17. ábra - Az Átviteli függvény modell numerikus adatokkal történő feltöltése és az adatok kiírása front panel

Az átviteli függvény megadása numerikus adatokkal olyan függvényalakot jelent, amelyben az (A.17. ábra) ábrán szereplő számláló és nevező együtthatók értékei az s indexszel kijelölt hatványkitevőjű értékeivel vannak megszorozva.

Azaz a 0 indexű együttható az s⁰ értékkel van megszorozva, az 1 indexű értékek s¹ hatványával és így tovább, míg az m indexű tag az s^m-ik hatványú tagjának együtthatója.

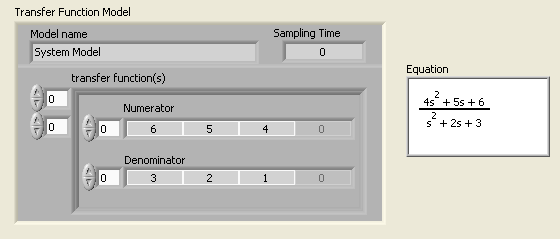
Mintapélda: Átviteli függvény (Transfer Function) létrehozása szimbolikus (képlet) adatokkal.

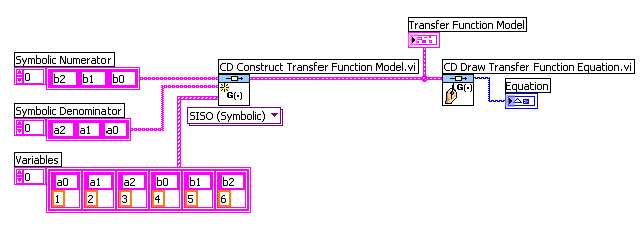
A.18. ábra - Az Átviteli függvény modell szimbolikus adatokkal történő feltöltése és az adatok kiírása blokkdiagram

Az átviteli függvény szimbolikus elemekkel történő leírása esetén az együtthatókra a Matlab rendszerben megszokott leírási módot alkalmazzák, amely különbözik a numerikus adatok bevitelénél alkalmazott indexelési eljárástól.

Ennél az átviteli függvény leírási módnál az s legmagasabb (pozitív) hatványának együtthatóját kell a 0 indexű elembe írnunk, a következő, eggyel kisebb s hatványkitevőjű tag együtthatóját az 1 indexű elembe és így tovább egészen (m-1) indexig, ahová az átviteli függvény legkisebb s együtthatójú értéket kell beírnunk. Ez az átviteli függvény leírási mód a Matlab program átviteli függvény megadási metódusának felel meg.

A két átviteli függvény leírási mód:

Az együtthatók indexei megegyeznek a tároló vektor indexével (Ascending (LabVIEW))
Az együtthatók indexei fordított sorrendben jelennek meg a tároló vektor indexeinél (Descending (Mathscript))

A két átviteli függvény leírási mód közötti átváltás egyszerűen megvalósítható a Vektor elemek sorrendjének megfordítása (Reverse 1D Array.VI) program segítségével - a számláló és a nevező együtthatóinál egyaránt.

A.19. ábra - Az Átviteli függvény modell szimbolikus adatokkal történő feltöltése és az adatok kiírása front panel

A gyakran használt átviteli függvények létrehozására alkalmazhatjuk a Speciális átviteli függvény létrehozása (CD Construct Special TF Model.VI) programot.

A.1.1.3. Elsőrendű rendszer (PT1) átviteli függvényének létrehozása

Az elsőrendű rendszer átviteli függvénye a következő:

$G (s) = \frac{K}{1 + s \cdot T} \cdot e^{- s \cdot T_{h}}$

(A.3)

ahol

	K	az erősítési tényező [a kimeneti és a bemeneti jel dimenzióinak hányadosa]
	T	az egytárolós rendszer időállandója [idő dimenzió]
	T _h	az egytárolós rendszer késleltetése [idő dimenzió]

Válasszuk ki a Speciális átviteli függvény létrehozása (CD Construct Special TF Model.VI) program polimorf választó menüjéből a menüpontot, hogy kijelöljük az elsőrendű rendszert!

A.20. ábra - Az egytárolós tag modelljének létrehozása (CD Construct Special TF Model.VI) program ikonja

A.21. ábra - Az egytárolós tag modelljének létrehozása (CD Construct Special TF Model.VI) program segítség (Help) információs ablaka

A.1.1.4. Másodrendű rendszer (PT2) átviteli függvényének létrehozása

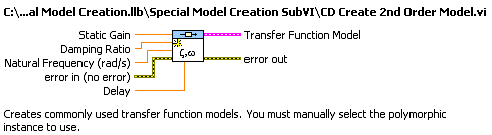
A másodrendű rendszer átviteli függvénye a következő:

$G (s) = \frac{K \cdot ω_{0}^{2}}{s^{2} + 2 \cdot ξ \cdot s \cdot ω_{0} + ω_{0}^{2}} = \frac{K}{(\frac{s^{2}}{ω_{0}^{2}}) + 2 \cdot ξ \cdot \frac{s}{ω_{0}} + 1}$

(A.4)

ahol

	K	az erősítési tényező [a kimeneti és a bemeneti jel dimenzióinak hányadosa]
	ζ	a másodrendű rendszer relatív csillapítási tényezője [ ]
	ω ₀	a másodrendű rendszer csillapítatlan rezonancia körfrekvenciája [rad/idő dimenzió]

Válasszuk ki a Speciális átviteli függvény létrehozása (CD Construct Special TF Model.VI) program polimorf választó menüjéből a menüpontot, hogy kijelöljük a másodrendű rendszert!

A.22. ábra - A másodrendű tag modelljének létrehozása (CD Construct Special TF Model.VI) program ikonja

A.23. ábra - A másodrendű tag modelljének létrehozása (CD Construct Special TF Model.VI) program segítség (Help) információs ablaka

A.1.1.5. A jelet időben Pade közelítéssel késleltető rendszer (PTh) átviteli függvényének létrehozása

Az időbeni késleltető rendszer átviteli függvénye a következő alakú:

$G (s) = e^{- s \cdot T_{h}}$

(A.5)

ahol

T _h

az egytárolós rendszer késleltetése [idő dimenzió]

Az időbeni késleltető rendszer átviteli függvényének egy közelítő formulája az ún. Pade approximációs formula, amely a következő alakú:

$e^{- s \cdot T_{h}} \approx \frac{1 - k_{1} \cdot s + k_{2} \cdot s^{2} + ... \pm k_{n} \cdot s^{n}}{1 + k_{1} \cdot s + k_{2} \cdot s^{2} + ... + k_{n} \cdot s^{n}}$

(A.6)

Ezt az algoritmust alkalmazza az időbeni késleltetést megvalósító rendszer átviteli függvénye megadott n érték esetén.

Válasszuk ki a Speciális átviteli függvény létrehozása (CD Construct Special TF Model.VI) program polimorf választó menüjéből a menüpontot, hogy kijelöljük az időbeni késleltetést megvalósító rendszert!

A.24. ábra - Az időbeni késleltetést megvalósító tag modelljének létrehozása (CD Construct Special TF Model.VI) program ikonja

Az időbeni késleltetést megvalósító tag modelljének létrehozása (CD Construct Special TF Model.VI) program segítség (Help) információs ablaka

A.25. ábra - Az időbeni késleltetést megvalósító tag modelljének létrehozása (CD Construct Special TF Model.VI) program segítség (Help) információs ablaka

A.1.2. Modell-információk (Model Information) alpaletta

Ebben az alpalettában információt kapunk az alkalmazott átviteli függvény és/illetve állapottér modell paramétereiről.

A.26. ábra - A Modell-információ (Model Information) alpaletta

A VI-ok alkalmazásával beállíthatjuk és/vagy lekérdezhetjük a lineáris rendszermodellek paramétereit és a rendszermodelljének elnevezését. A modell-információk között szerepelnek a rendszermodell paraméterei - a rendszer-késleltetési időtartamok, a rendszerdimenziók (számláló, nevező fokszámok, rendszermátrix dimenziók), a mintavételezési időtartam valamint a bemenetek, kimenetek és az állapotok elnevezései.

A.1.3. Modell-átalakítás (Model Conversion) alpaletta

Ebben a alpalettában lehetőségünk van arra, hogy a rendszermodell-leírás egyik formájáról másik leírási alakra transzformáljuk át a rendszermodellt.

A.27. ábra - A Modell-átalakítás (Model Conversion) alpaletta

A VI-ok alkalmazásával lehetőségünk van arra, hogy átalakítsuk a rendszermodellt az egyik leírási alakról egy másik alakra, időben folytonos leírású modellből mintavételes modellt hozzunk létre.

Ebben a alpalettában található VI-ok segítségével lehetőségünk van a Rendszertervezés modulban létrehozott modelleket átalakítani a Szimulációs modulban alkalmazható modellekké, ezen kívül a visszaalakítást is megvalósíthatjuk.

A modell átalakításhoz leggyakrabban használt VI-ok

		CD Convert to State-Space Model.vi
		CD Convert to Transfer Function Model.vi
		CD Convert Continuous to Discrete.vi

Ezeket és még néhány VI-t a következőkben ismertetjük.

A.1.3.1. Modell átalakítása állapottér modell alakra (Convert to State-Space Models.vi)

A.28. ábra - A Modell átalakítása állapottér modell alakra (CD Convert to State-Space Model.vi) program ikonja

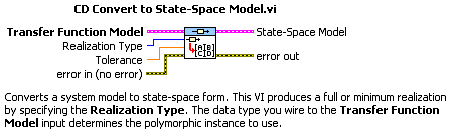
A.29. ábra - A Modell átalakítása állapottér modell alakra (CD Convert to State-Space Model.vi) program segítség (Help) információs ablaka

Mintapélda: Átviteli függvény (Transfer Function) alakból állapottér modell (State Space Model) létrehozása numerikus adatokkal

A.30. ábra - Átviteli függvény alakból állapottér modell létrehozása blokkdiagram

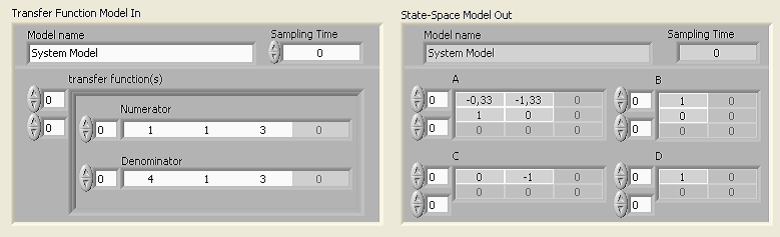
A.31. ábra - Átviteli függvény alakból állapottér modell létrehozása front panel

A.1.3.2. Modell átalakítása átviteli függvény alakra (Convert to Transfer Function Model.vi)

A.32. ábra - Modell átalakítás átviteli függvény alakra (CD Convert to Transfer Function Model.vi) program ikonja

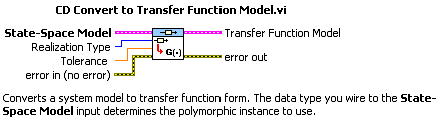
A.33. ábra - Modell átalakítás átviteli függvény alakra (CD Convert to Transfer Function Model.vi) program segítség (Help) információs ablaka

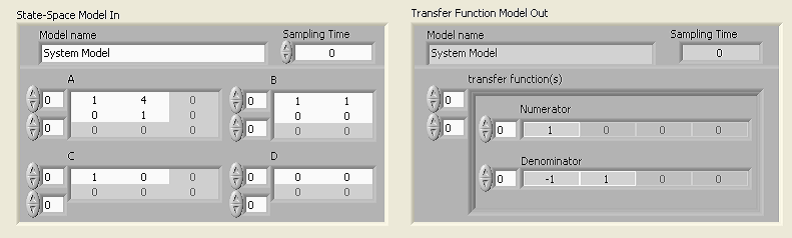
Mintapélda: Állapottér modell (State Space Model) alakból átviteli függvény (Transfer Function) létrehozása numerikus adatokkal.

A.34. ábra - Állapottér modell alakból átviteli függvény létrehozása blokkdiagram

A.35. ábra - Állapottér modell alakból átviteli függvény létrehozása front panel

A.1.3.3. Időben folytonos modell átalakítása mintavételes modellé (Convert Continuous to Discrete.vi)

Időben folytonos modell átalakítása mintavételes állapottér függvény alakra adott mintavételi időtartammal (CD Convert Continuous to Discrete.vi) program ikonja

A.36. ábra - Időben folytonos modell átalakítása mintavételes állapottér függvény alakra adott mintavételi időtartammal (CD Convert Continuous to Discrete.vi) program ikonja

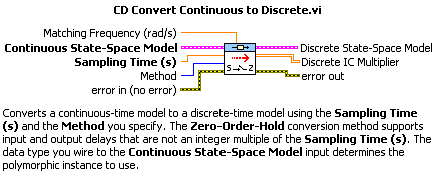
A.37. ábra - Időben folytonos modell átalakítása mintavételes állapottér függvény alakra adott mintavételi időtartammal (CD Convert Continuous to Discrete.vi) program segítség (Help) információs ablaka

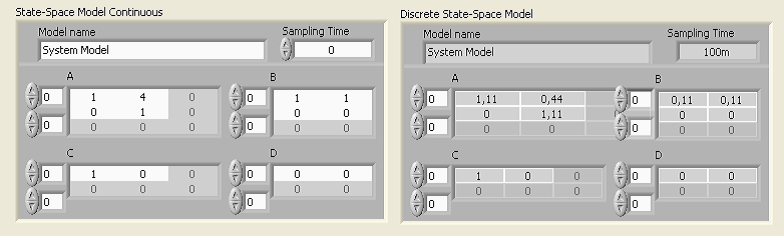
Mintapélda: Időben folytonos modell átalakítása mintavételes állapottér függvény alakra adott mintavételi időtartammal

A.38. ábra - Időben folytonos modell átalakítása mintavételes állapottér függvény alakra adott mintavételi időtartammal blokkdiagram

A.39. ábra - Időben folytonos modell átalakítása mintavételes állapottér függvény alakra adott mintavételi időtartammal front panel

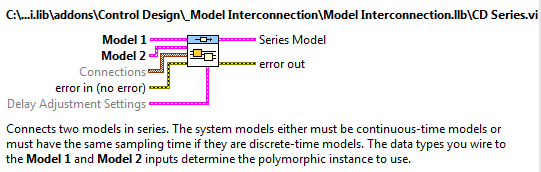
A.1.4. Modell-összekapcsolás (Model Interconnection) alpaletta

Ebben az alpalettában elhelyezett alprogramokkal lehetőségünk arra van, hogy a létrehozott rendszermodelleket tetszőleges topológiával összekapcsoljuk, és így tetszőleges rendszerstruktúrát hozzunk létre.

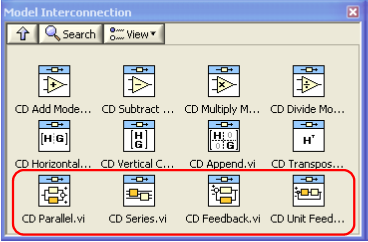
A.40. ábra - Modell összekapcsolás (Model Interconnection) alpaletta

A modell összekapcsolás (Model Interconnection) alpaletta VI-jait arra használjuk, hogy a különböző típusú lineáris rendszereket összekapcsoljuk egymással.

A kisméretű alapmodellek összekapcsolásával egy nagy rendszermodellt hozhatunk létre.

A modell összekapcsoláshoz leggyakrabban használt VI-ok

		CD Parallel.vi
		CD Series.vi
		CD Unit Feedback.vi

Ezeket VI-okat a következőkben ismertetjük.

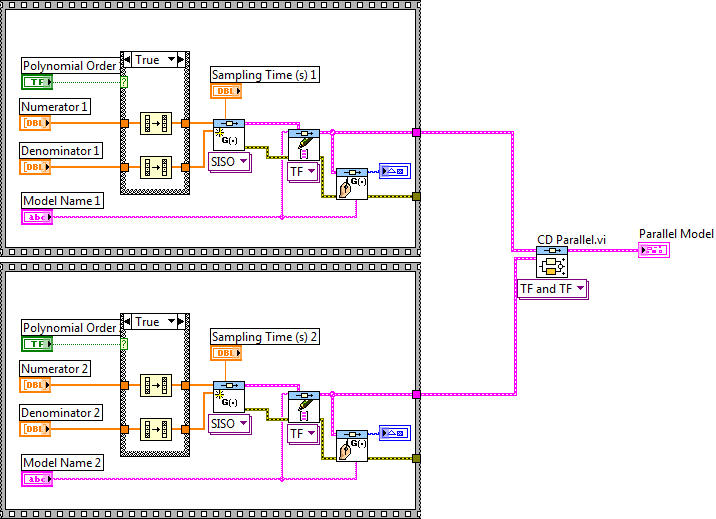
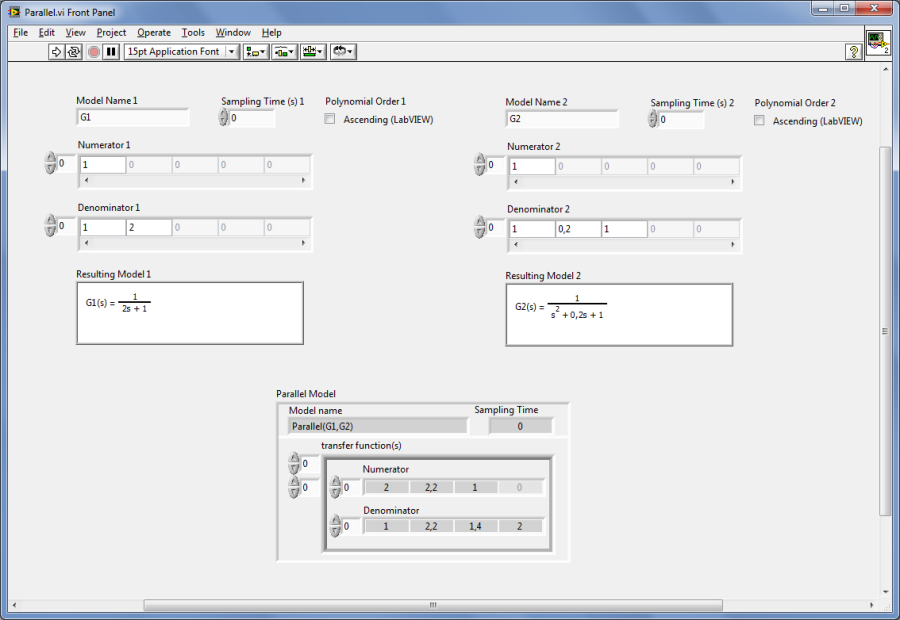
A.1.4.1. Modellek párhuzamos kapcsolása (CD Parallel.vi)

A.41. ábra - Modellek párhuzamos kapcsolása (CD Parallel.vi) program ikonja

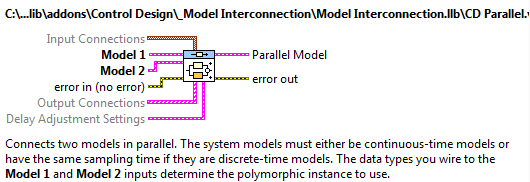
A.42. ábra - Modellek párhuzamos kapcsolása (CD Parallel.vi) program segítség (Help) információs ablaka

Mintapélda: Modellek párhuzamos kapcsolása.

A.43. ábra - Modellek párhuzamos kapcsolása blokkdiagram

A.44. ábra - Modellek párhuzamos kapcsolása front panel

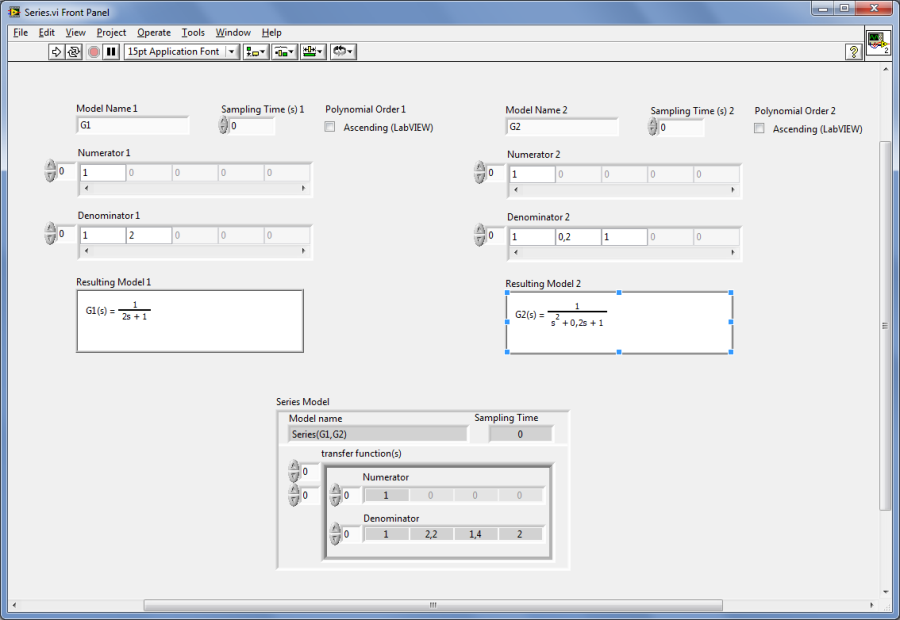
A.1.4.2. Modellek soros kapcsolása (CD Series.vi)

A.45. ábra - Modellek soros kapcsolása (CD Series.vi) program ikonja

A.46. ábra - Modellek soros kapcsolása (CD Series.vi) program segítség (Help) információs ablaka

Mintapélda: Modellek soros kapcsolása

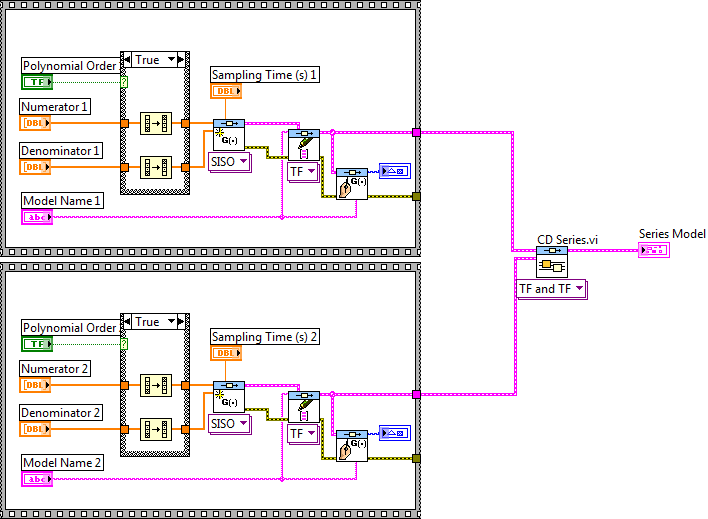
A.47. ábra - Modellek soros kapcsolása blokkdiagram

A.48. ábra - Modellek soros kapcsolása front panel

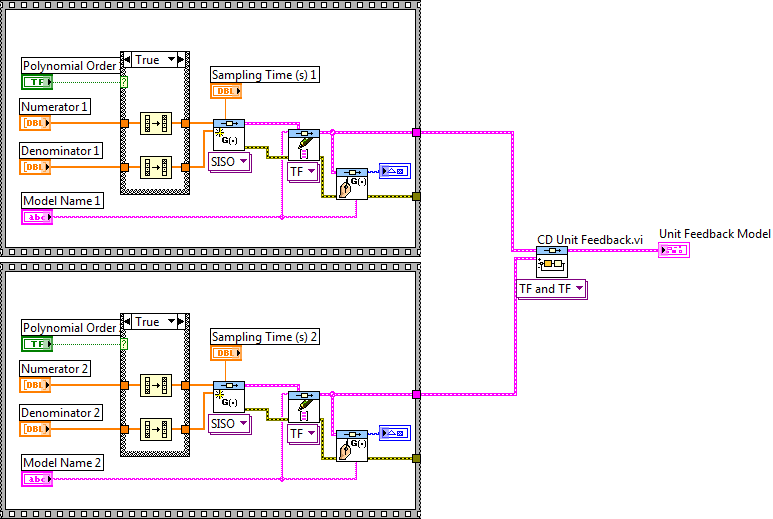
A.1.4.3. Modellek visszacsatolt összekapcsolása egységnyi visszacsatolási tényezővel (CD Unit Feedback.vi)

A.49. ábra - Modellek visszacsatolt összekapcsolása (CD Feedback.vi) program ikonja

A.50. ábra - Modellek visszacsatolt összekapcsolása (CD Feedback.vi) program segítség (Help) információs ablaka

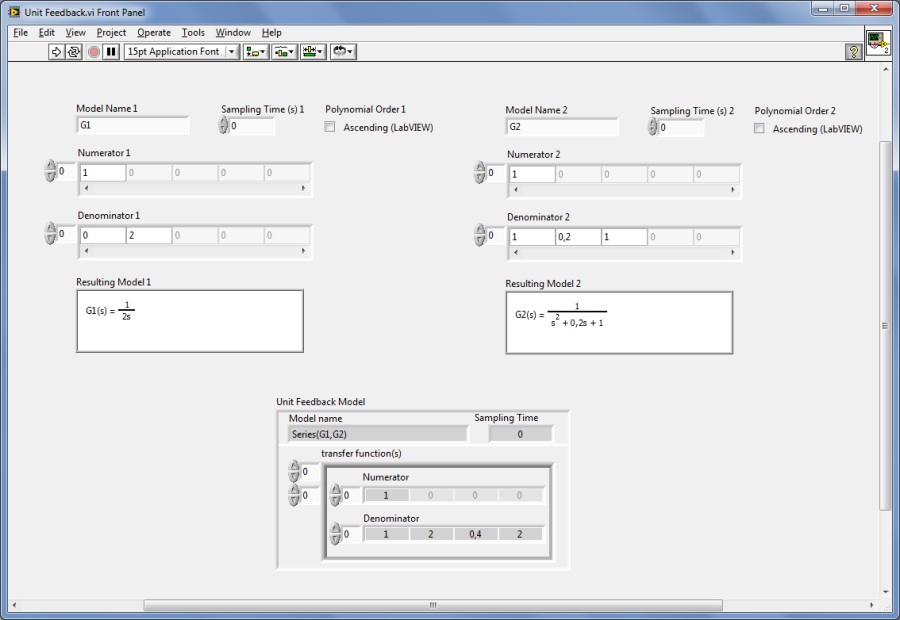
Mintapélda: Modellek visszacsatolt összekapcsolása.

A.51. ábra - Modellek visszacsatolt összekapcsolása blokkdiagram

A.52. ábra - Modellek visszacsatolt összekapcsolása front panel

A.2. A modell vizsgálata időtartományban és frekvenciatartományban

A dinamikus rendszermodell elkészítése után időtartományban illetve frekvenciatartományban készíthetünk szimulációs futtatásokat.

A Rendszertervezés (Control Design) paletta olyan alpalettákat tartalmaz, amelyek az előkészített modell analízisét segítik, ezek a következők:

Modell időtartománybeli vizsgálata (Time Response)
Modell frekvenciatartománybeli vizsgálata (Frekvency Response)
Modell dinamikus tulajdonságai (Dynamic Characteristic)

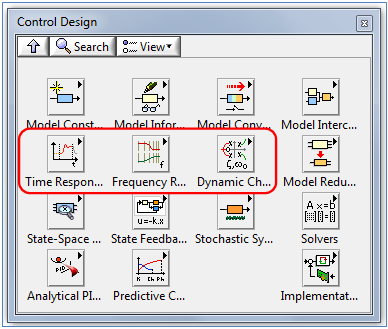
A.53. ábra - A Rendszertervezés (Control Design) paletta

Az (A.53. ábra) ábrán a modell időtartománybeli és frekvenciatartománybeli vizsgálatánál leggyakrabban használt alpalettákat láthatjuk, melyek ismertetését a következő alfejeztetek tartalmazzák.

A.2.1. Modell időtartománybeli vizsgálata (Time Response) alpaletta

Ebben a alpalettában elhelyezett programokkal tudjuk a korábban definiált dinamikus modellek időtartománybeli válaszfüggvényét meghatározni.

A.54. ábra - Időtartománybeli válaszfüggvény (Time Response) alpaletta

A dinamikus modell időtartománybeli analíziséhez leggyakrabban használt VI-ok:

		CD Step Response.vi
		CD Impulse Resonse.vi
		CD Initial Response.vi
		CD Linear Simulation.vi

A.2.1.1. Egységugrás bemenetre adott válaszfüggvény (CD Step Response.vi)

Az elkészített rendszermodell egységugrás bemenetre adott válaszfüggvényét a CD Step Response.vi program segítségével tudjuk meghatározni.

A.55. ábra - Az egységugrás bemenetre adott válaszfüggvény (CD Step Response.vi) program ikonja

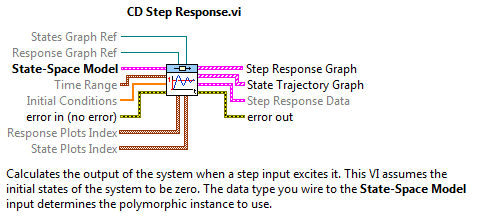
A.56. ábra - Az egységugrás bemenetre adott válaszfüggvény (CD Step Response.vi) program segítség (Help) információs ablaka

Bár az egységugrásra adott válaszfüggvénynél az ikon rajza alapján úgy látszik, hogy csak állapottér leírású rendszereket képes fogadni, de ez így nem igaz. Ez az ikon, hasonlóan a továbbiakban bemutatandó programokhoz, úgynevezett polimorf tulajdonságú, azaz a bemenet „felismeri”, hogy milyen alakban leírt modellformát kapcsolunk hozzá, és ennek struktúráját és paramétereit alkalmazza futáskor.

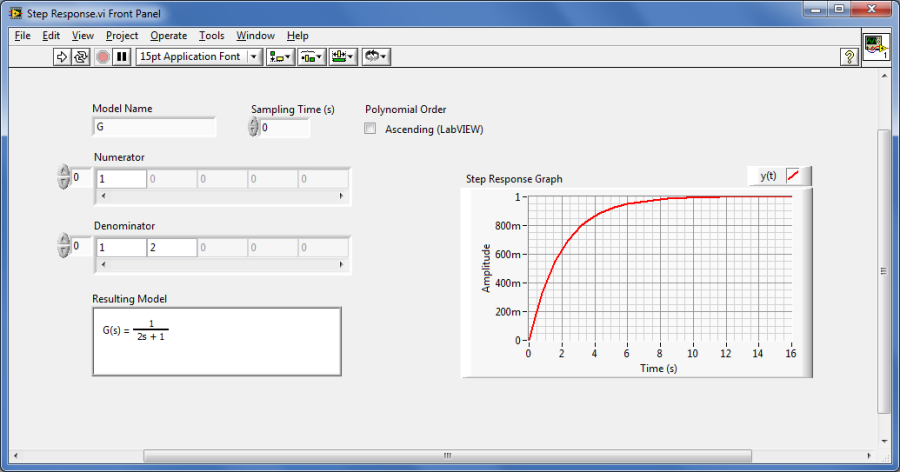
Mintapélda: Egységugrás bemenetre adott válaszfüggvény (időfüggvény) meghatározása:

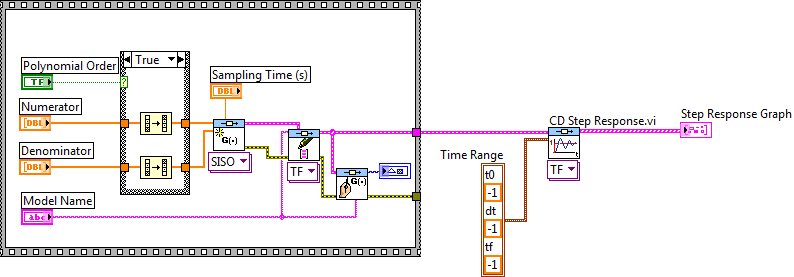
A.57. ábra - Az egységugrás bemenetre adott válaszfüggvény (időfüggvény) meghatározása blokkdiagram

A blokkdiagramon láthatók az időparaméterek (Time Range), amelyek bemeneti adatként meghatározzák a szimuláció kezdő időpontját (t0), a szimuláció lépésközét (dt), illetve a szimuláció befejezésének időpontját (tf). A clusterben megjelenő negatív (-1) időadatok azt jelentik, hogy ebben az esetben a modell paraméterei alapján a program határozza meg, hogy milyen hosszúságú szimulációs időtartamot igényel az egységugrás bementre adott válaszfüggvény. Ez az érték kb. (5 - 8)*T_max, ahol T_max a modell nevezőjében szereplő legnagyobb időállandó. Ebben az esetben a szimulációhoz alkalmazott lépésközt is automatikusan határozza meg a program.

Ha megadott lépésközzel, kezdő és befejezési időponttal szeretnénk meghatározni a kimeneti jelet, akkor ezeket az értékeket beírva a „Time Range” cluster megfelelő elemébe, a program ezekkel a bemeneti értékekkel fut.

A.58. ábra - Egységugrás bemenetre adott válaszfüggvény (időfüggvény) meghatározása front panel

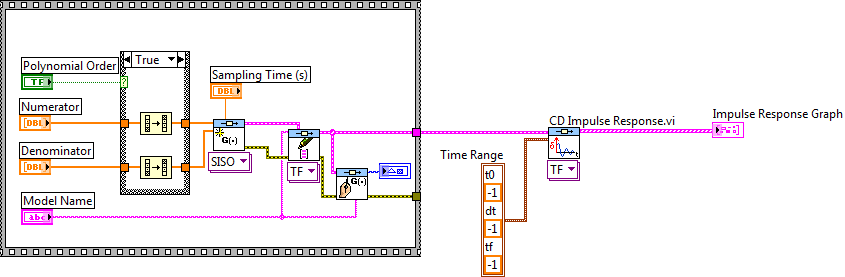
A.2.1.2. Egységimpulzus bemenetre adott válaszfüggvény (CD Impulse Response.vi)

Az elkészített rendszermodell egységimpulzus bemenetre adott válaszfüggvényét a CD Impulse Response.vi program segítségével tudjuk meghatározni. (Az egységimpulzus alatt az egységnyi területű impulzus időfüggvényt értjük.)

A.59. ábra - Az egységimpulzus bemenetre adott válaszfüggvény (CD Impulse Response.vi) program ikonja

A.60. ábra - Az egységimpulzus bemenetre adott válaszfüggvény (CD Impulse Response.vi) program segítség (Help) információs ablaka

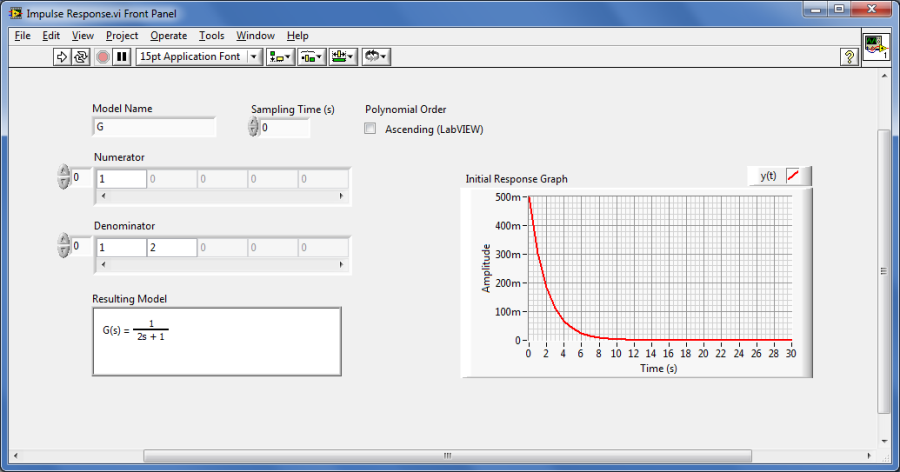
Mintapélda: Egységimpulzus bemenetre adott válaszfüggvény (időfüggvény) meghatározása.

A.61. ábra - Egységimpulzus bemenetre adott válaszfüggvény (időfüggvény) meghatározása blokkdiagram

A.62. ábra - Egységimpulzus bemenetre adott válaszfüggvény (időfüggvény) meghatározása front panel

A.2.1.3. Kezdeti értékkel rendelkező rendszer válaszfüggvénye (CD Initial Response.vi)

Az elkészített rendszermodell kezdeti értékkel rendelkező válaszfüggvényét tudjuk a CD Initial Response.vi program segítségével meghatározni.

A bementi jel ennél az időfüggvény számításnál nulla (0) értékű. A futtatással kapott időfüggvény azt határozza meg, hogy adott kezdeti értékek (állapottér modell állapotainak kezdeti értékei) mellett milyen végértékre áll be modell kimeneti jele „végtelen idő” eltelte után. Ezzel a vizsgálattal tudjuk a modell stabilitását meghatározni, megadott kezdeti feltételek esetén.

A.63. ábra - A kezdeti értékkel rendelkező rendszer válaszfüggvényének (CD Initial Response.vi) program ikonja

A.64. ábra - A kezdeti értékkel rendelkező rendszer válaszfüggvényének (CD Initial Response.vi) program segítség (Help) információs ablaka

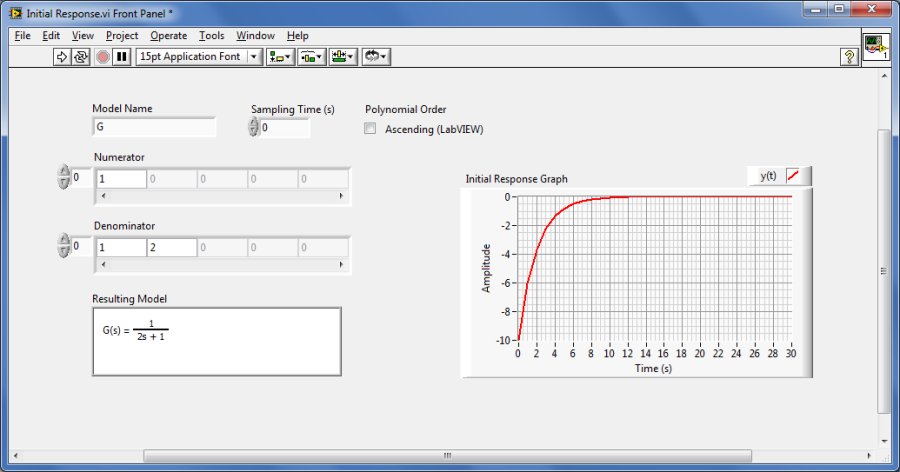
Mintapélda: A kezdeti értékkel rendelkező rendszer válaszfüggvényének (időfüggvény) meghatározása.

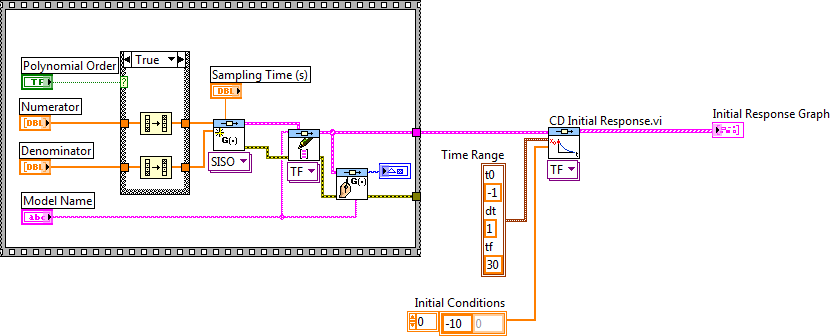
A.65. ábra - A kezdeti értékkel rendelkező rendszer válaszfüggvényének (időfüggvény) meghatározása blokkdiagram

A mintapéldában szereplő rendszer egy nevezőbeli gyökkel rendelkezik, így az állapottér leírásban egy állapota van, amelynek beállíthatjuk a kezdeti értékét.

A.66. ábra - A kezdeti értékkel rendelkező rendszer válaszfüggvényének (időfüggvény) meghatározása front panel

A.2.1.4. Tetszőleges bemeneti időfüggvény jellel rendelkező rendszer válaszfüggvénye (CD Linear Simulation.vi)

Az elkészített rendszermodell válaszfüggvényét tudjuk meghatározni tetszőleges bemeneti időfüggvény jellel a CD Linear Simulation.vi program segítségével.

Tetszőleges bemeneti időfüggvény jellel rendelkező rendszer válaszfüggvényének meghatározása (CD Linear Simulation.vi) program ikonja

A.67. ábra - Tetszőleges bemeneti időfüggvény jellel rendelkező rendszer válaszfüggvényének meghatározása (CD Linear Simulation.vi) program ikonja

Tetszőleges bemeneti időfüggvény jellel rendelkező rendszer válaszfüggvényének meghatározása (CD Linear Simulation.vi) program segítség (Help) információs ablaka

A.68. ábra - Tetszőleges bemeneti időfüggvény jellel rendelkező rendszer válaszfüggvényének meghatározása (CD Linear Simulation.vi) program segítség (Help) információs ablaka

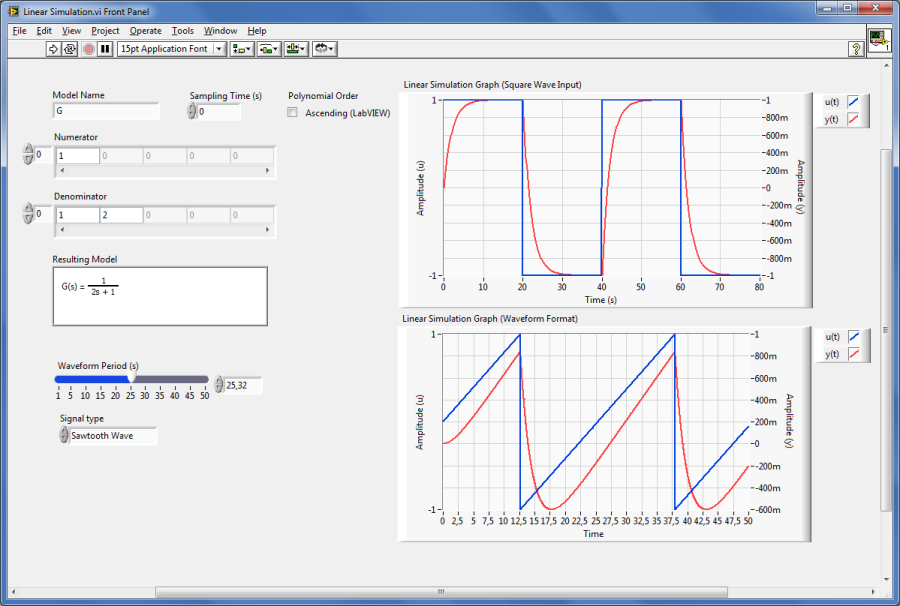
Mintapélda: Tetszőleges bemeneti időfüggvény jellel rendelkező rendszer válaszfüggvényének (időfüggvény) meghatározása.

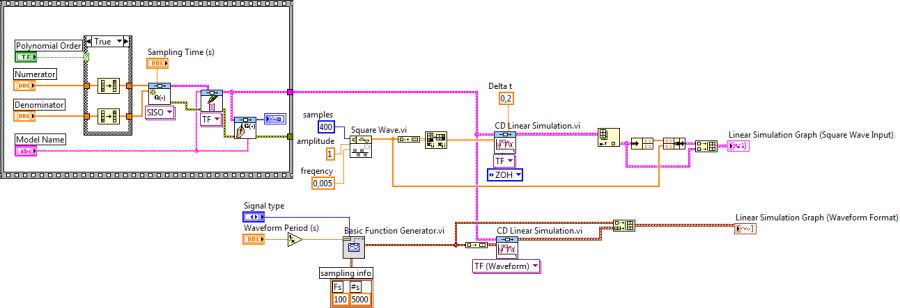
A.69. ábra - Tetszőleges bemeneti időfüggvény jellel rendelkező rendszer válaszfüggvényének (időfüggvény) meghatározása blokkdiagram

A tetszőleges bemeneti időfüggvény jellel rendelkező rendszer válaszfüggvényének meghatározása (CD Linear Simulation.vi) program bemeneti adatként egy olyan vektort kér, amely minden egyes számítási időpillanatban megadja a (bemeneti) jel értékét. Ilyen jelet előállíthatunk program segítségével, mint ahogy az a mintapéldában is látható, vagy minden egyes számítási időpillanatbeli értéket manuálisan is meghatározhatunk.

A Négyszögjel (Square Wave) bemenettel rendelkező szimulációs rész 400 bemeneti értéket határoz meg (samples) 0,005Hz frekvenciával. A szimulációs adatokat az időlépés (Delta t) paraméterrel megadott helyeken írjuk ki.

A második modellben szereplő Alapfüggvény Generátor (Basic Function Generator) a jeltípus (Signal type) megadása mellett a jel periódusidejét (Waveform Period (s)) kéri bemeneti adatként, és külön bemenet (sampling info) adja meg, hogy a számítást milyen mintavételezési frekvenciával (Fs) és hány mintavételi pontban (#s) határozzuk meg.

A.70. ábra - Tetszőleges bemeneti időfüggvény jellel rendelkező rendszer válaszfüggvényének (időfüggvény) meghatározása front panel

A.2.2. Dinamikus rendszermodell frekvenciatartománybeli vizsgálata (Frequency Response) alpaletta

Ebben az alpalettában elhelyezett programokkal tudjuk a korábban definiált dinamikus modellek frekvenciatartománybeli tulajdonságait meghatározni.

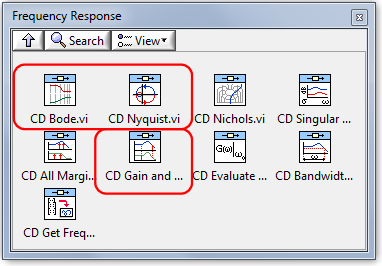
A.71. ábra - Modell létrehozása (Model Construction) alpaletta

A dinamikus rendszermodell frekvenciatartománybeli analíziséhez leggyakrabban használt VI-ok:

		CD Bode.vi
		CD Nyquist.vi
		CD Gain and Phase Margin.vi

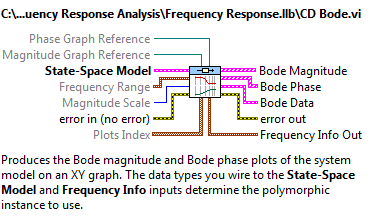
A.2.2.1. Dinamikus rendszermodell Bode frekvenciafüggvénye (CD Bode.vi)

Az elkészített rendszermodell Bode frekvenciafüggvényét a CD Bode.vi program segítségével tudjuk meghatározni.

A.72. ábra - A Bode frekvenciafüggvény (CD Bode.vi) program ikonja

A.73. ábra - A Bode frekvenciafüggvény (CD Bode.vi) program segítség (Help) információs ablaka

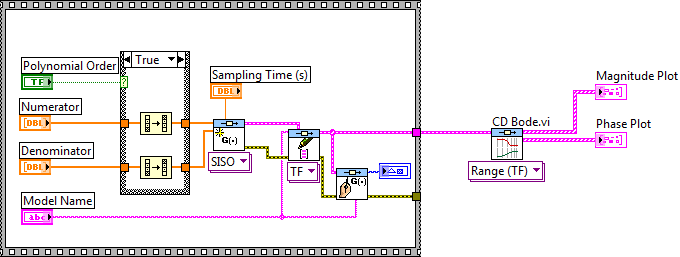
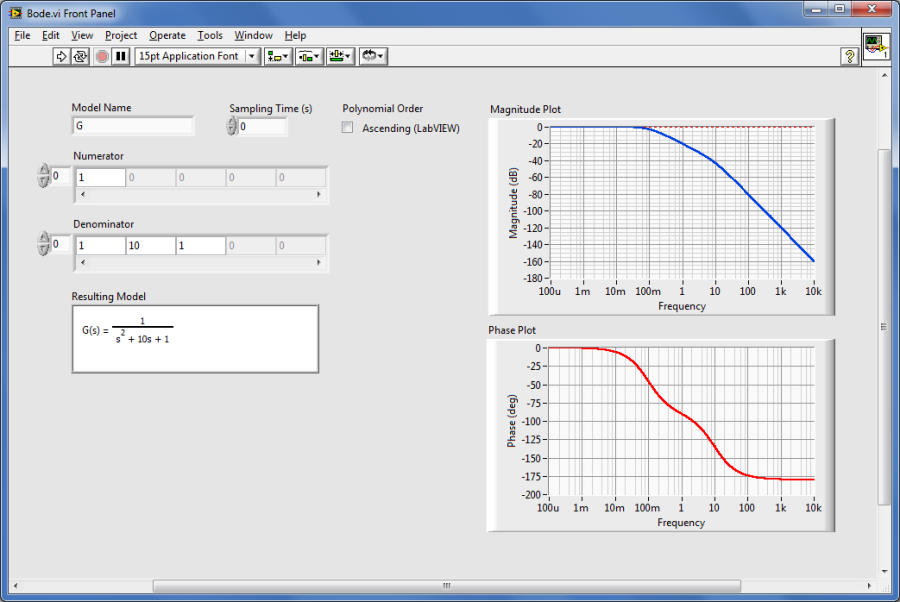
Mintapélda: Dinamikus rendszer Bode frekvenciafüggvényének meghatározása.

A.74. ábra - A Bode frekvenciafüggvény meghatározása blokkdiagram

A.75. ábra - A Bode frekvenciafüggvény meghatározása front panel

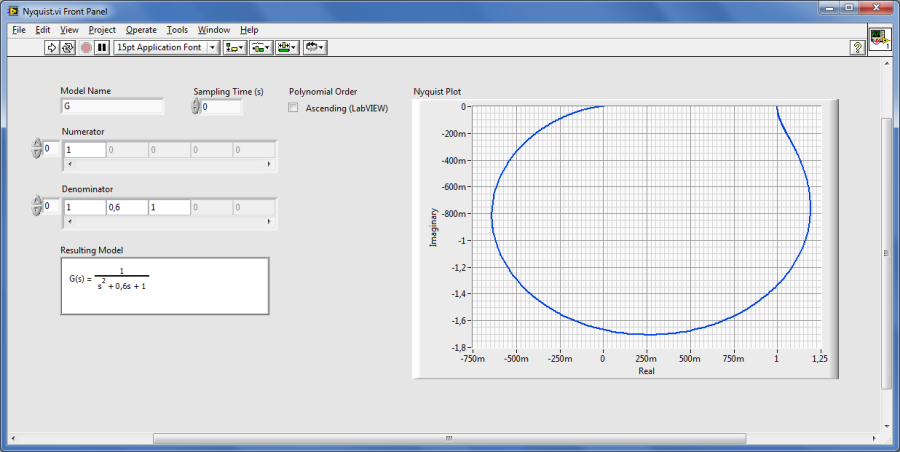
A.2.2.2. Dinamikus rendszermodell Nyquist frekvenciafüggvénye (CD Nyquist.vi)

Az elkészített rendszermodell Nyquist frekvenciafüggvényét a CD Nyquist.vi program segítségével tudjuk meghatározni.

A.76. ábra - A Nyquist frekvenciafüggvény (CD Nyquist.vi) program ikonja

A.77. ábra - A Nyquist frekvenciafüggvény (CD Nyquist.vi) program segítség (Help) információs ablaka

Mintapélda: Dinamikus rendszer Nyquist frekvenciafüggvényének meghatározása.

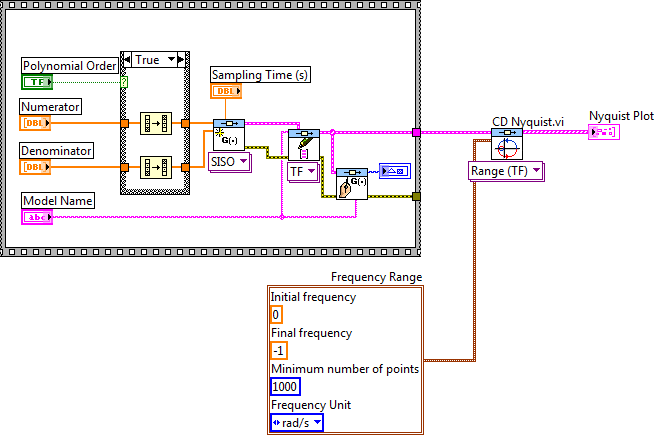
A.78. ábra - A Nyquist frekvenciafüggvény meghatározása blokkdiagram

A Nyquist frekvenciafüggvény program bemeneti adataként megadhatjuk a számítás frekvenciahatárait. Alapértelmezésben a kezdeti frekvencia (Initial freqency) és a befejezési frekvencia (Final freqency) értéke negatív érték (-1). Ezek a számértékek nem valós értékek, így ebben az esetben a program automatikusan választ a rendszermodell paraméterei (nevezőbeli gyökei) alapján frekvenciahatárokat. Ebben az esetben a program meghatározza a Nyquist diagram paramétereit –végtelen (-Inf) frekvenciától +végtelen (+Inf) frekvenciáig. Ahogy az ábrán is látható, a kezdeti frekvencia értékét nullára állítva csak a pozitív frekvenciához tartozó frekvenciafüggvényt határozzuk meg.

A.79. ábra - A Nyquist frekvenciafüggvény meghatározása front panel

A.2.2.3. Dinamikus rendszermodell Bode frekvenciafüggvényének erősítési és fázistartaléka (CD Gain and Phase Margin.vi)

Az elkészített rendszermodell Bode frekvenciafüggvényének erősítési és fázistartalékát a CD Gain and Phase Margin.vi program segítségével tudjuk meghatározni.

A.80. ábra - A Bode frekvenciafüggvényének erősítés és fázis tartaléka (CD Gain and Phase Margin.vi) program ikonja

A.81. ábra - Bode frekvenciafüggvényének erősítés és fázis tartaléka (CD Gain and Phase Margin.vi) program segítség (Help) információs ablaka

Mintapélda: Dinamikus rendszer Bode frekvenciafüggvényének erősítés és fázistartalék meghatározása.

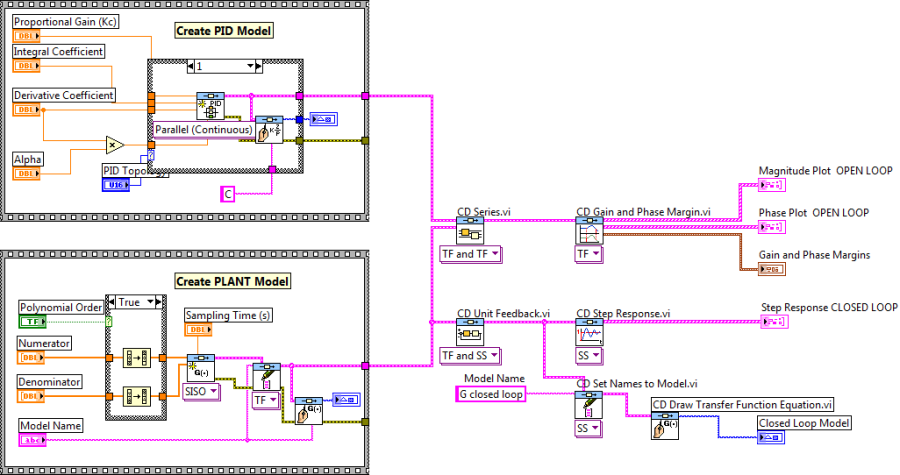
A.82. ábra - A Bode frekvenciafüggvényének erősítés és fázistartalékának meghatározása blokkdiagram

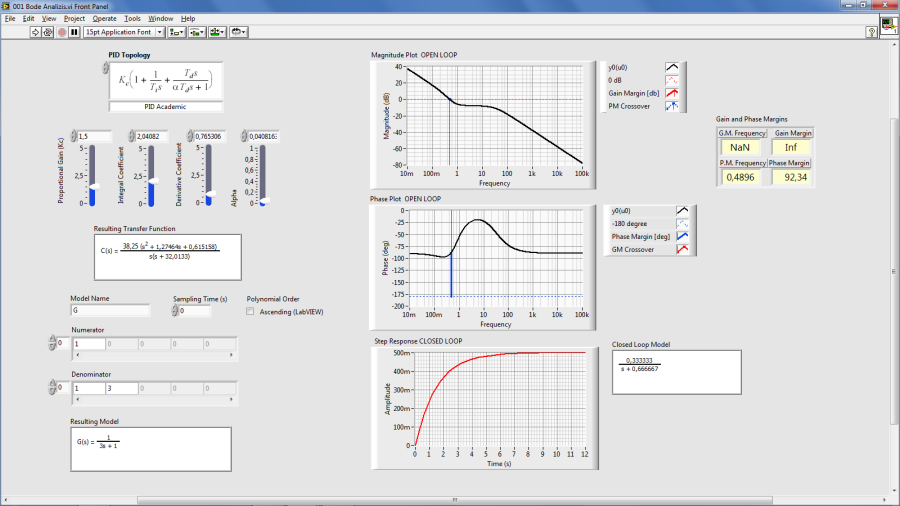
A.83. ábra - A Bode frekvenciafüggvényének erősítés és fázistartalékának meghatározása front panel

A mintapéldában egy PID szabályozó és egy egytárolós (PT1) rendszer felnyitott körének Bode diagramját valamint az amplitúdó és fázistartalékát láthatjuk. A amplitúdó és fázistartalék dimenziója fok (°).

A legalsó diagramon a zárt szabályozási kör átviteli és átmeneti függvényét láthatjuk.

A.2.3. Modell dinamikus tulajdonságai (Dynamic Characteristic) alpaletta

Ebben a alpalettában elhelyezett programokkal tudjuk a korábban definiált dinamikus modellek számláló- és nevezőbeli gyökeit meghatározni.

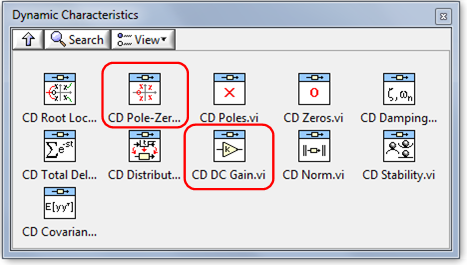
A.84. ábra - A Modell dinamikus tulajdonságai (Dynamic Characteristic) alpaletta

A dinamikus rendszermodell tulajdonságainak meghatározásához leggyakrabban alkalmazott VI-ok

		CD Pole-Zero Map.vi
		CD DC Gain.vi

A.2.3.1. Rendszermodell pólusainak és zérusainak elhelyezkedése (CD Pole-Zero Map.vi)

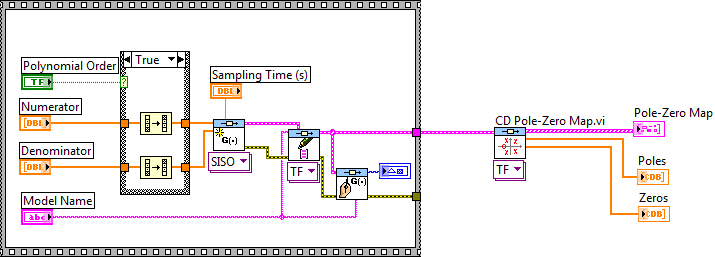
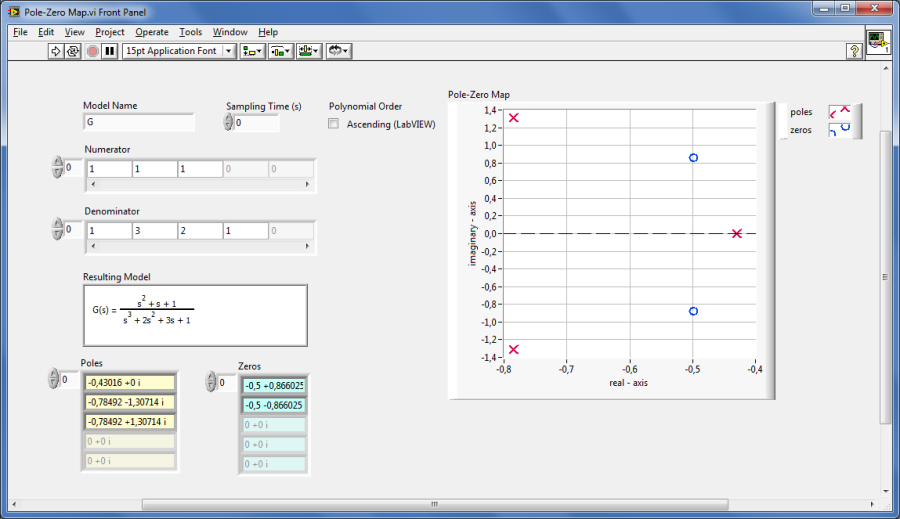
Az elkészített rendszermodell számlálóban és nevezőben elhelyezkedő gyökhelyeinek meghatározását végzi a CD Pole-Zero Map.vi program:

A.85. ábra - A rendszermodell számlálóban és nevezőben elhelyezkedő gyökhelyeinek meghatározását végző (CD Pole-Zero Map.vi) program ikonja

A rendszermodell számlálóban és nevezőben elhelyezkedő gyökhelyeinek meghatározását végző (CD Pole-Zero Map.vi) program segítség (Help) információs ablaka

A.86. ábra - A rendszermodell számlálóban és nevezőben elhelyezkedő gyökhelyeinek meghatározását végző (CD Pole-Zero Map.vi) program segítség (Help) információs ablaka

Mintapélda: A dinamikus rendszermodell számlálóban és nevezőben elhelyezkedő gyökhelyeinek meghatározása.

A.87. ábra - A rendszermodell számlálóban és nevezőben elhelyezkedő gyökhelyeinek meghatározása blokkdiagram

A.88. ábra - A rendszermodell számlálóban és nevezőben elhelyezkedő gyökhelyeinek meghatározása front panel

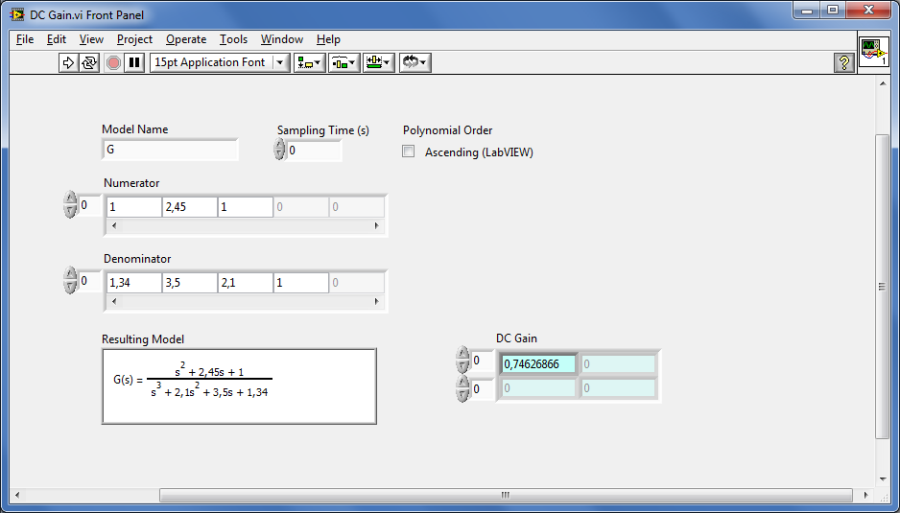
A.2.3.2. Rendszermodell állandósult állapotbeli erősítése (CD DC Gain.vi)

Az elkészített rendszermodell állandósult állapotban megvalósuló erősítésének értékét határozza meg a CD DC Gain.vi program.

A.89. ábra - A rendszermodell állandósult állapotban megvalósuló erősítésének értékét meghatározó (CD Pole-Zero Map.vi) program ikonja

A rendszermodell állandósult állapotban megvalósuló erősítésének értékét meghatározó (CD Pole-Zero Map.vi) program segítség (Help) információs ablaka

A.90. ábra - A rendszermodell állandósult állapotban megvalósuló erősítésének értékét meghatározó (CD Pole-Zero Map.vi) program segítség (Help) információs ablaka

Mintapélda: A dinamikus rendszermodell állandósult állapotban megvalósuló erősítésének értékét meghatározó program.

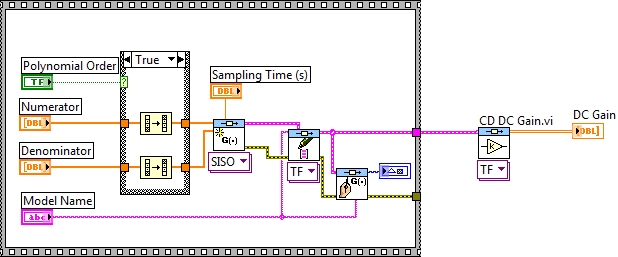
A.91. ábra - A rendszermodell állandósult állapotban megvalósuló erősítés értékének meghatározása blokkdiagram

A mintapéldában egy bemenetű és egy kimenetű folytonos átviteli függvény állandósult állapotbeli erősítésének meghatározását végeztük el. A program az eredményt egy mátrixban adja meg, aminek az oka, hogy több bemenetű és több kimenetű rendszerek esetén is alkalmazható, és ilyenkor minden bemenet és minden kimenet között meghatározza az állandósult erősítés értékeket.

A.92. ábra - A rendszermodell állandósult állapotban megvalósuló erősítés értékének meghatározása front panel

Vissza		Előre
7. fejezet - Numerikus módszerek	Főoldal	B. függelék - Dinamikus rendszerek szimulációs eszközei – a LabVIEW Simulation Module