7. fejezet - Numerikus módszerek
- 7.1. Hibajelenségek közelítő módszerek esetén
- 7.2. Egyváltozós függvények gyökkeresése
-
- 7.2.1. Intervallum keresés
- 7.2.2. Általános gyökkereső algoritmusok
- 7.2.3. Gyökkereső algoritmusok polinomok esetében
-
- 7.2.3.1. Horner-séma
- 7.2.3.2. Polinomok osztása polinommal
- 7.2.3.3. Primitív gyökök kezelése
- 7.2.3.4. Harmadfokú egyenlet megoldása: Cardano-formula
- 7.2.3.5. A többszörös gyökök eltüntetése
- 7.2.3.6. A gyököket tartalmazó intervallum meghatározása
- 7.2.3.7. Valós gyökök száma egy adott intervallumban
- 7.2.3.8. Gyökök keresése közelítő módszerrel
- 7.3. Többváltozós függvények gyökkeresése
7.1. Hibajelenségek közelítő módszerek esetén
Azt, hogy a számítógép nem úgy számol, mint az ember papíron mindenki tudja tapasztalatból. Az ebből következő jelenségekkel (legalábbis egy részükkel) fogunk foglalkozni ebben a fejezetben.
Nézzünk néhány fogalmat:
Képlethiba : a közelítő összefüggés hibája, amit általában csak becsülni tudunk. Ilyen például a trapéz integrál hibatagja.
Kerekítési hiba : a számítógép számábrázolásából adódik. Leginkább úgy szokás magyarázni, hogy -al, hiszen a számítógép véges hosszú számábrázolással dolgozik (például a PC-ken double típus esetén 15 értékes jegyet használhatunk).
Öröklött hiba : a közelítő algoritmusok számítások sorozatából állnak. A számítások csak (kerekítési, esetleg képlet) hibával végezhetők el, így az eredmény nem pontos. Az így kapott pontatlan érték hibáját örökségként, mint a kiinduló adat részét kapja a következő számítás.
Az előzőekben már szó volt a különböző hibákról, de mi is az pontosan, és milyen fajtái lehetnek? Ha a közelítő értéke x, akkor a hiba x-a. Beszélhetünk abszolút hibáról és relatív hibáról .
Az előző definíciókban többször volt szó a számítógép számábrázolásáról. PC esetén egy double típusú számot nyolc bájton tárol a számítógép. A nyolc bájt összesen féle értéket vehet fel, azaz ennyiféle valós számot ismer ebben az esetben a rendszer. Tehát mivel csak véges számú számot tud megkülönböztetni, a számítógépen ábrázolható számok halmaza véges, így az algebra legelemibb szabályai sem teljesülnek!
Nézzünk ezekre néhány – talán mellbevágó – példát, ahol a számábrázolás az egyszerűség kedvéért 10 jegyű (PC esetén a lebegőpontos számoknál 7, 15 és 19 jegy lehet)
-
A matematikai tanulmányaink szerint , de ez számítógép használata esetén nem mindig igaz. Abban az esetben például, ha , akkor a baloldal értéke 1010 mivel – a 10 értékes jegy miatt – 1010+4=1010, a jobboldalé pedig 1010+10, mivel 4+4 kerekítve 10 és már éppen befér az utolsó értékes jegy helyére.
-
Nézzük meg, hogy hány gyöke van például a 2x+2=2 egyenletnek! A klasszikus matematika azt mondja az algebra alaptétele szerint, hogy csak egy gyök van és az az x=0. Helyettesítsünk be azonban számítógéppel bármely 10-10-nél kisebb értéket, és azt kapjuk, hogy teljesül az egyenlőség. Ebből azonban az következik, hogy ennek az elsőfokú egyenletnek a számítógépen rengeteg (de nem végtelen számú, lásd ábrázolható számok halmaza) megoldása van!
-
Végül – bár még lehetne más példákat is mutatni – hány valós gyöke van a következő egyenletnek: ? Minden matematikán pallérozódott elme rávágja, hogy egy, mégpedig . Igen ám, de mivel a köbgyök nem számítható ki pontosan a számítógéppel, a visszahelyettesítés után azt látjuk, hogy nem elégíti ki az egyenletet, azaz nincs valós gyök!
A numerikus közelítő módszerek alkalmazásánál állandó küzdelmet folytatunk az ilyen és ehhez hasonló anomáliák elhárítására. Mivel nagyon sok jó szimulációs program létezik, elmondhatjuk, hogy a „harc” általában emberi „győzelemmel” végződik. Nézzünk meg a következőkben néhány főbb jelenséget, amelyekre programok írásakor (néha alkalmazásakor is) ügyelnünk kell:
7.1.1. Kiegyszerűsödés
Ez a jelenség akkor fordul elő, ha két, közel azonos számot vonunk ki egymásból. Ilyenkor az eredmény sokkal kevesebb értékes jegyből fog állni, ami információvesztést jelent. A deriváltak numerikus közelítésénél is ez e jelenség okozza a legtöbb gondot.
Oldjuk meg a következő másodfokú egyenletet:
|
|
(7.1) |
Visszahelyettesítés után x1-nél nullát, x2-nél -3,4⋅10-7-ot kapunk. A kiegyszerűsödés jelensége a kivonásnál, azaz x2meghatározásánál jelentkezik. Próbáljuk meg másképpen előállítani ezt a gyököt, kihasználva, hogy van egy viszonylag pontos, másik megoldásunk! Ismert a másodfokú egyenlet gyökei és együtthatói közötti következő összefüggés:
|
|
(7.2) |
Ennek felhasználásával az új x2 érték 0,00000666666666696296, ami visszahelyettesítés esetén már szintén nullát eredményez. Ez a hiba ugyan nem jelentős, de könnyűszerrel el tudtuk tüntetni, és egy esetleges „öröklődési folyamatban” jobb, ha minél pontosabb értékkel kezdünk.
Nézzünk egy másik példát, ahol a jelenség ugyanaz, csak a javítás más (bár végül ugyanaz jön ki)! Legyen most a másodfokú egyenlet , és (hogy ne kelljen olyan hosszú számokkal bajlódni) az értékes jegyek száma csak négy! A számítás a következő:
|
|
(7.3) |
A pontos értékek 139,9928 és 0,007143, amiből a relatív hibák rendre 6,6⋅10-4 és 2,85⋅10-1, ami közel 30%-os eltérés! Ha azonban az
|
|
(7.4) |
összefüggésben a helyére 70-et, b helyére pedig 4899-et írunk és elvégezzük a számítást, akkor sokkal pontosabb értéket kapunk:
|
|
(7.5) |
Látható, hogy ez csak az utolsó értékes jegyben tér el a „pontos” megoldástól.
Az előző két példa is mutatta, hogy sokszor viszonylag egyszerű eszközökkel lehet tenni a kiegyszerűsödés ellen.
7.1.2. Kiejtés
A kiejtés általában sorok összegzésekor fordul elő, akkor ha a részösszegek számításkor a kiegyszerűsödés jelenségével találkozunk. Tulajdonképpen úgy is felfoghatjuk, mint az előző fejezetben tárgyalt fogalom általánosítását.
Leggyakrabban alternáló (változó előjelű) sorok összegzésekor találkozunk vele. Szemléltetésként nézzük a következő példát! Az ex függvény nulla körüli Taylor sora (MacLaurin sor) a következő:
|
|
(7.6) |
Amikor az x kitevő negatív, alternáló sort kell összegeznünk. Kis x-ek esetén nem is szokott gond lenni, de a nagyobbaknál nem a függvényértékhez konvergál a sorozat. Táblázatkezelővel végeztünk számításokat e-22 esetén. A táblázat első oszlopában az összeg i indexe, a másodikban a hozzá tartozó tört értéke szerepel. Az utolsó két oszlopban az részösszegek láthatók, de a harmadikban – a képletnek megfelelően – fentről lefelé, a negyedikben pedig lentről felfelé számítva. Mivel a számításokat n=100-ig végeztük el, ezért a táblázatnak csak az elejét és a végét közöljük (Táblázat 7.1).
|
i |
TAYLOR tagok |
LE |
FEL |
|---|---|---|---|
|
0 |
1 |
1 |
-7,04756E-08 |
|
1 |
-22 |
-21 |
-1,00000007 |
|
2 |
242 |
221 |
20,99999993 |
|
3 |
-1774,66667 |
-1553,666667 |
-221,0000001 |
|
4 |
9760,666667 |
8207 |
1553,666667 |
|
5 |
-42946,9333 |
-34739,93333 |
-8207 |
|
6 |
157472,0889 |
122732,1556 |
34739,93333 |
|
80 |
3,46008E-12 |
-8,47404E-08 |
2,71951E-12 |
|
81 |
-9,3978E-13 |
-8,47413E-08 |
-7,40574E-13 |
|
82 |
2,52135E-13 |
-8,4741E-08 |
1,99202E-13 |
|
83 |
-6,6831E-14 |
-8,47411E-08 |
-5,29333E-14 |
|
98 |
3,82873E-23 |
-8,47411E-08 |
3,16508E-23 |
|
99 |
-8,5083E-24 |
-8,47411E-08 |
-6,63646E-24 |
|
100 |
1,87182E-24 |
-8,47411E-08 |
1,87182E-24 |
A táblázatban szürke háttérrel jelöltük az összegek számított végeredményét. Látható, hogy a két érték kissé ugyan, de eltér egymástól - ami azonban a legnagyobb gond, hogy mindkettő negatív, ami lehetetlen! A pontos érték: 2,789468E-10. A példa helyes megoldása egyébként nem okoz gondot, mert számoljuk ki e22 értékét, majd vegyük a reciprokát! Mivel ez nem alternáló sor, az összegzéssel sem lesz bajunk, megkapjuk a pontos értéket. Ez a lehetőség azonban nem minden alternáló sor esetén adott. Mindig meg kell próbálnunk olyan – az adott feladatnak megfelelő – változatot előállítani, ahol a kiejtés jelensége nem áll fenn.
Az előző feladatban nemcsak az okozta az eltérést, hogy az előjel változott, hanem az is, hogy az összeadandók nagyságrendje nagyon különböző volt. Ilyen esetekben – ha csak módunk van rá – először a kisebb adatokat adjuk össze, úgy haladjunk a nagyobbak felé. Ennek a gondolatmenetnek az indoklását a 7.1. szakasz részben, az A. pont alatt találhatjuk meg. Ezért is végeztük el az összegzést az előző feladat esetében két irányban, bár itt nem segíthetett, mert a nagy értékek valahol a sorozat közben voltak. Ha az összeadás előtt nagyság szerint rendezzük a sort, majd úgy adjuk össze, akkor sem lesz jobb a helyzet, mert az eredmény zérus (bár legalább nem negatív).
A következő példa ugyan nem kiejtés, de abban is az ex sorozat összegzésével foglalkozunk. A program LabVIEW-ban készült. A képernyőképeket mutatja a 7.1. ábra.
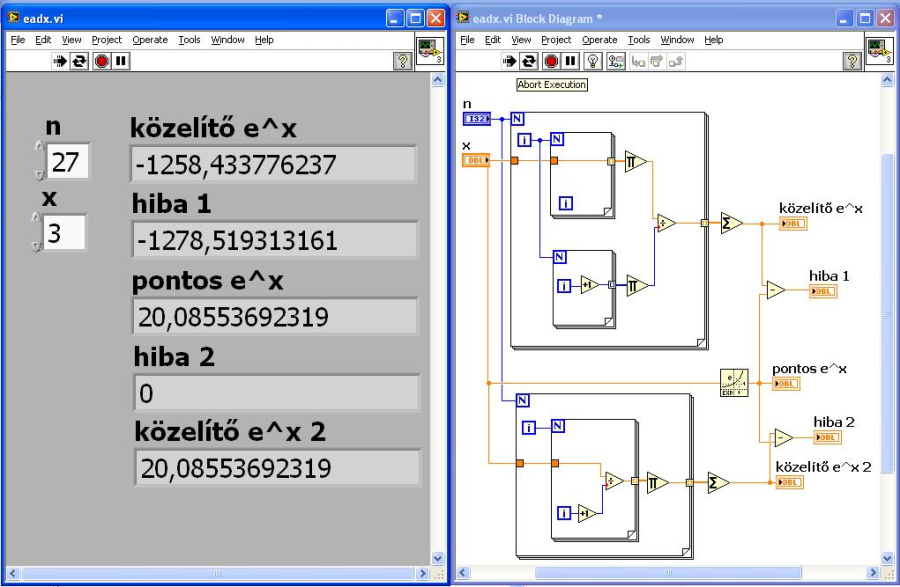
A kétféle számítás közötti különbség csak meghatározásának módjában van. A felső esetben egy-egy külön ciklussal határozzuk meg a számlálót és a nevezőt, majd az eredményeket osztjuk el. Ekkor azonban a faktoriális számítással előbb-utóbb gondok lesznek, mert túl gyorsan nő az értéke, és nem fog „beleférni” a változója értéktartományába. A másik esetben – ugyan sokkal többet kell osztani – pontos eredményt kapunk, mert kihasználjuk, hogy a számláló és nevező ugyanannyi szorzást tartalmaz, így a feladatot visszavezetjük törtek szorzására:
|
|
(7.7) |
Ennek az algoritmusnak az eredményeként garantáltan nem lesz túlcsordulás, a szorzásnál pedig a nagyságrendi különbség nem okoz adatvesztést, mint a kivonás esetében. Az eredményeket a Táblázat 7.2 foglalja össze (a fejlécek a programban használt jelöléseket tartalmazzák).
|
x |
n |
hiba 1 |
hiba 2 |
|---|---|---|---|
|
1 |
18 |
-1,3⋅10-9 |
0 |
|
2 |
18 |
-3,9⋅10-4 |
-1,3⋅10-9 |
|
2 |
24 |
3,5⋅10-3 ? |
0 |
|
3 |
18 |
-0,41 |
-7,17⋅10-8 |
|
3 |
24 |
48,47 ? |
-5,2⋅10-13 |
|
3 |
27 |
-1278,52 ? |
0 |
A kérdőjelek a nyilvánvaló anomáliákat jelzik, ahol a hibának csökkeni kellene, és ehelyett nő. x=3 esetben elfogadhatatlan értékeket kapunk!
7.1.3. Numerikus instabilitás
A számítások során – mint arra már utaltunk az öröklött hibánál – a kerekítési hiba tovább terjed. Instabilitásról akkor beszélünk, ha a közbenső hibák nagymértékben befolyásolják az eredményt.
Nézzük például a következő sort, melynek tagjai:
|
|
(7.8) |
A kezdeti érték a következő integrálból határozható meg:
|
|
(7.9) |
A sorozat tagjait rekurzív képlettel állíthatjuk elő – parciális integrálást alkalmazva – a következőképpen:
|
|
(7.10) |
Bizonyítható, hogy a sorozat határértéke zérus, azaz .
Számoljuk ki az első húsz értéket táblázatkezelő programmal! Az eredmény egy olyan sorozat, amely eleinte az elvártnak megfelelő értékeket veszi fel, majd „elszáll” (instabilitás). Érdekes azonban, hogyha visszafelé dolgozunk, akkor jó eredményt kapunk. Ez a következőt jelenti: feltesszük, hogy például a huszadik tag már olyan közel esik a határértékhez, hogy közelítőleg megegyezik vele, így értéke legyen nulla.
A rekurziós formulából rendezéssel a következő alak is előállítható:
|
|
(7.11) |
Ennek segítségével visszafelé is számolhatunk egészen a nulladik tagig. Ezeket az adatokat tartalmazza a harmadik oszlop a (Táblázat 7.3) táblázatban.
|
n |
y n |
vissza |
|---|---|---|
|
0 |
1,718282 |
1,718282 |
|
1 |
1 |
1 |
|
2 |
0,718282 |
0,718282 |
|
3 |
0,563436 |
0,563436 |
|
4 |
0,464536 |
0,464536 |
|
5 |
0,3956 |
0,3956 |
|
6 |
0,344685 |
0,344685 |
|
7 |
0,30549 |
0,30549 |
|
8 |
0,274362 |
0,274362 |
|
9 |
0,249028 |
0,249028 |
|
10 |
0,228002 |
0,228002 |
|
11 |
0,210265 |
0,210265 |
|
12 |
0,1951 |
0,1951 |
|
13 |
0,181983 |
0,181983 |
|
14 |
0,170519 |
0,170524 |
|
15 |
0,160496 |
0,160426 |
|
16 |
0,150348 |
0,15146 |
|
17 |
0,162363 |
0,143465 |
|
18 |
-0,20425 |
0,135914 |
|
19 |
6,599099 |
0,135914 |
|
20 |
-129,264 |
0 |
7.1.4. Rosszul kondicionáltság
Egy feladatot akkor hívunk rosszul kondicionáltnak, ha a paramétereinek csekély megváltoztatása az eredmény nagymértékű módosulását eredményezi. Ilyen kismértékű változás a számítástechnikában szinte mindig előfordul, elég csak a kerekítési hibákra gondolnunk.
Tekintsük a következő egyenletet:
|
|
(7.12) |
Ennek nyilvánvaló valós megoldása az x=1. Mi a helyzet akkor, ha a polinom nulladfokú tagja kismértékben (10-6) megváltozik? Ekkor az egyenlet a következő lesz:
|
|
(7.13) |
Ennek valós megoldása x=1,1. Az eredményváltozás tehát 10%-nyi, pedig a paraméter csak 0,0001%-al változott. Ugyanezt tapasztalhatjuk a komplex gyökök vizsgálatakor is.
A feladatok kondicionáltságával foglalkozunk még a lineáris egyenletrendszerek tárgyalásánál is.
7.2. Egyváltozós függvények gyökkeresése
A következőkben az egyváltozós egyenletek gyökkeresési módszereivel foglalkozunk. A polinomokat külön kezeljük.
7.2.1. Intervallum keresés
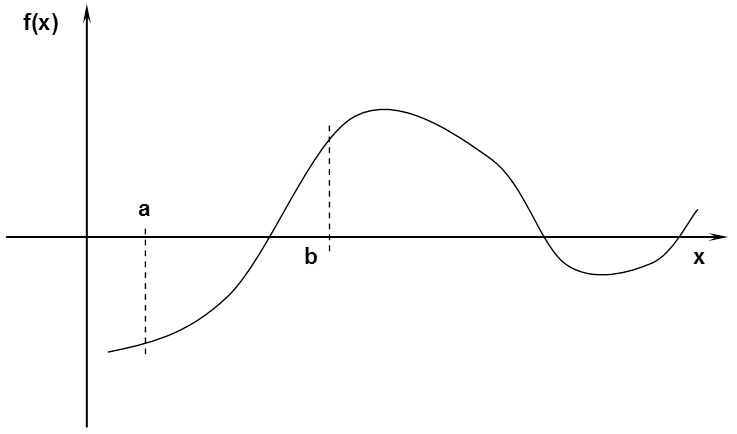
A későbbiekben majd látni fogjuk, hogy a legnagyobb probléma olyan intervallum meghatározása, amelyben biztosan van gyök. Annak eldöntése, hogy egy adott intervallumban van-e gyök már egyszerűbb, mert alkalmazható Bolzano tétele. Egyszerűen megfogalmazva:
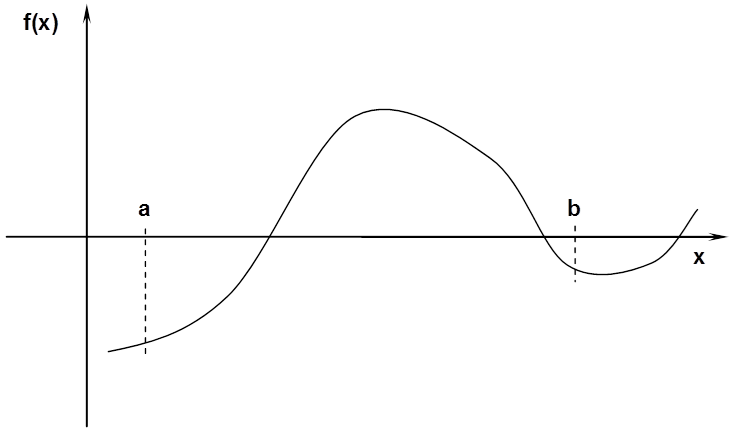
ha egy folytonos függvénynek két pontban eltérő az előjele, akkor a két pont között biztosan van gyök (7.2. ábra). A tétel megfordítása nem igaz (7.3. ábra).
7.2.1.1. Grafikus módszer
Ábrázoljuk a függvényt, és a grafikon alapján elkülöníthetjük a gyököket tartalmazó intervallumokat. Mindez valós gyökök esetén – főleg a mai számítástechnikai eszközökkel – roppant egyszerű. Ha komplex gyököket keresünk, akkor az f(z)=0 egyenletre alkalmazzuk a következő módszert:
-
az egyenletben minden számot, változót írjunk fel a komplex szám algebrai alakjával (z=x+iy),
-
a függvényt válaszuk szét valós és képzetes részre (f(z)=u(x,y)+iv(x,y)), így az eredeti egyenletet helyettesíthetjük az u(x,y)=0 és v(x,y)=0 egyenletekkel,
-
ábrázoljuk mindkét egyenletet az x,y síkon, a görbék metszéspontjai a gyökhelyek!
7.2.1.2. Analitikus módszer
Olyan módszerről, amely egy tetszőleges függvény esetén megadja a gyököket tartalmazó intervallumot, nem tudunk. Általában a következőket tesszük:
-
a számegyenes egy akkora intervallumát jelöljük ki, ahol a számunkra érdekes gyököket sejtjük (ne törekedjünk pontosságra, legyünk „bőkezűek”),
-
bontsuk kisebb intervallumokra, és ezeket ellenőrizzük a Bolzano-tétel alapján, reménykedve, hogy a (7.3. ábra) ábrán láthatóhoz hasonlóan nem kerülünk el fontos gyököt.
7.2.2. Általános gyökkereső algoritmusok
A következő módszereket azonos példával fogjuk szemléltetni. A megoldandó egyenlet a következő:
|
|
(7.14) |
7.2.2.1. Intervallum-felezés
Talán ez a legegyszerűbb módszer. Előnye, hogy mindig használható, a gyök tetszőleges pontosságú megközelítésére biztosít lehetőséget. Hátránya a közelítés sebessége.
Legyen adott az f(x)=0 egyenlet, ahol f(x) folytonos függvény, és a 1 valamint b 1 , ahol f(a 1 )‑nek és f(b 1 )-nek ellentétes az előjele, azaz f(a 1 )⋅f(b 1 )<0. Vegyük fel c 1 -et az a 1 , b 1 intervallum felező pontjaként, azaz:
|
. |
(7.15) |
A két félintervallum közül válasszuk azt, ahol teljesül a Bolzano-tétel, azaz
|
|
(7.16) |
Az algoritmus tetszőlegesen sokáig folytatható, így egyre jobb közelítést nyerhetünk. Ha például 10 lépésben közelítünk, akkor az eredeti intervallum hosszának már csak 210-en, azaz 1024-ed része lesz az új intervallum hossza. Másképpen, mivel 1024≈103, ezért kb. hárommal több pontos tizedesünk lesz, tehát minden újabb pontos tizedes jegy meghatározásához kb. három iterációs lépésre van szükség. Természetesen ennél gyorsabb módszerek is léteznek, de akkor az f(x) függvénynek bizonyos követelményeknek meg kell felelnie.
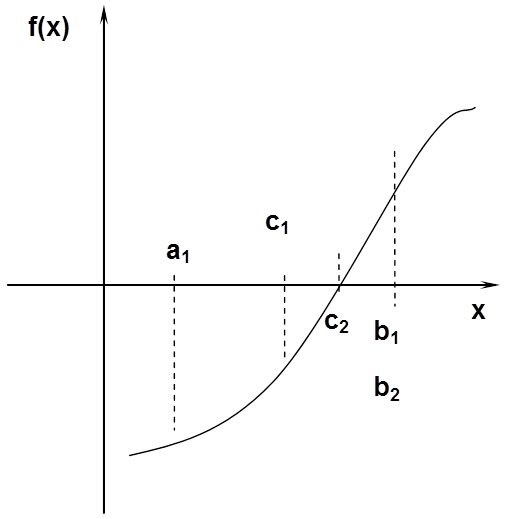
A példa megoldását táblázatkezelővel Táblázat 7.4 tartalmazza, míg az eredményeket a (Táblázat 7.5) táblázatban tanulmányozhatjuk.
|
A |
B |
C |
D |
E |
F |
G |
|
|
1 |
i |
a |
b |
c |
f(a) |
f(b) |
f(c) |
|
2 |
1 |
-1 |
1 |
=(A2+B2)/2 |
=cos(A1)+A2 |
=cos(B2)+B2 |
=cos(C2)+C2 |
|
3 |
2 |
=ha(E2*G2<0;B2;D2) |
=ha(E2*G2<0;D2;C2) |
=(A2+B2)/2 |
=cos(A1)+A2 |
=cos(B2)+B2 |
=cos(C2)+C2 |
|
i |
a |
b |
c |
f(a) |
f(b) |
f(c) |
|---|---|---|---|---|---|---|
|
1 |
-1 |
1 |
0 |
-0,46 |
1,54 |
1 |
|
2 |
-1 |
0 |
-0,5 |
-0,46 |
1 |
0,378 |
|
3 |
-1 |
-0,5 |
-0,75 |
-0,46 |
0,378 |
-0,018 |
|
4 |
-0,75 |
-0,5 |
-0,625 |
-0,018 |
0,378 |
0,186 |
|
5 |
-0,75 |
-0,625 |
-0,6875 |
-0,018 |
0,186 |
0,085 |
|
6 |
-0,75 |
-0,6875 |
-0,7188 |
-0,018 |
0,085 |
0,034 |
|
7 |
-0,75 |
-0,7188 |
-0,7344 |
-0,018 |
0,034 |
0,008 |
|
8 |
-0,75 |
-0,7344 |
-0,7422 |
-0,018 |
0,008 |
-0,005 |
|
9 |
-0,7422 |
-0,7344 |
-0,7383 |
-0,005 |
0,008 |
0,001 |
|
35 |
-0,7391 |
-0,7391 |
-0,7391 |
-1E-10 |
5E-11 |
-5E-11 |
|
36 |
-0,7391 |
-0,7391 |
-0,7391 |
-5E-11 |
5E-11 |
-2E-12 |
7.2.2.2. Húrmódszer (regula falsi)
Az algoritmus lépései sokban hasonlítanak az előzőekben leírt intervallum-felezéshez, csak a c k pontok meghatározása történik másként. Most az a 1 ,f(a 1 ) valamint a b 1 ,f(b 1 ) pontokon át fektessünk egy egyenest (ami a függvénynek egy „húrja”), és ennek az x tengellyel való metszéspontja legyen c 1 . Ezt az értéket úgy is tekinthetjük, mint a gyök egy közelítő értékét, bár tudjuk, hogy az érték „hamis”, azaz „false” (innen a módszer elnevezése is). Ha az eredményt nem tarjuk elég pontosnak, akkor a két intervallum közül az előzőekben leírtak szerint választunk, majd egy újabb húr segítségével pontosítunk. A módszer tetszőlegesen sokáig folytatható, tehát a közelítés pontossága határtalanul fokozható, csak kellően türelmesnek kell lennünk. Egy idő után általában már csak az intervallum egyik oldalán lesz változás, ettől a húrok alig változnak, tehát a közelítés „lelassul”. Számos módszer van, amely ezen a problémán próbál segíteni (például minden n-edik lépésnek egy intervallum-felezést iktatunk be).
Nézzük most az előzőekben szövegesen leírt módszert egyenletekkel, a 7.4. ábra jelöléseit használva! Írjuk fel a két ponton átmenő egyenes egyenletét
|
, |
(7.17) |
majd határozzuk meg a metszéspontot, azaz y=0 helyen x=c 1 értékét:
|
|
(7.18) |
|
|
|
(7.19) |
A következő lépés az új intervallum meghatározása. Eljárhatunk az intervallum-felezésnél ismertetett módon is, de néha alkalmazhatunk feltételek nélküli rekurziót is. Abban az esetben, ha az -ben – tehát nincs inflexiós pont, azaz a görbe homorú, vagy domború – az új intervallum meghatározása egyértelmű. Nézzük például az ábrán látható esetet! Ekkor az egyenes mindig a görbe fölött fog haladni, tehát a tengelyt mindig „előbb” metszi, mint a görbe, azaz az intervallumnak mindig az „ a ” vége fog mozogni. Jelöljük ekkor b 1 -et c -1 -gyel, a 1 -et c 0 -val:
|
. |
(7.20) |
Mivel az új intervallumok esetén c 0 =c 1 , majd c 1 =c 2 helyettesítéseket alkalmazunk, ezért a rekurziós összefüggés a következőképpen írható fel:
|
. |
(7.21) |
Kérdés most, hogy mi a teendő akkor, ha a görbe nem ilyen helyzetű. A rekurziós módszer mindig alkalmazható, ha . Ekkor a -1-es indexűnek azt a pontot kell választani, amelynek előjele megegyezik a második derivált előjelével.
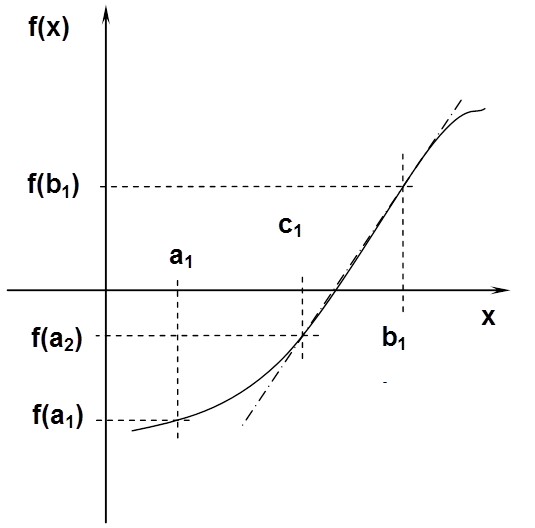
A példa megoldása táblázatkezelővel a (Táblázat 7.6) táblázatban látható.
|
A |
B |
C |
D |
E |
F |
G |
|
|
1 |
i |
a |
b |
c |
f(a) |
f(b) |
f(c) |
|
2 |
1 |
-1 |
1 |
=C2-F2*(B2-A2)/(F2-E2) |
=cos(A1)+A2 |
=cos(B2)+B2 |
=cos(C2)+C2 |
|
3 |
2 |
** |
** |
=(A2+B2)/2 |
=cos(A1)+A2 |
=cos(B2)+B2 |
=cos(C2)+C2 |
A B3 és a C3 cellák tartalma megegyezik az intervallum-felezésnél leírtakkal. Az eredményeket a Táblázat 7.7 tartalmazza.
|
i |
a |
b |
c |
f(a) |
f(b) |
f(c) |
|---|---|---|---|---|---|---|
|
1 |
-1 |
1 |
-0,5403 |
-0,4597 |
1,5403 |
0,3173 |
|
2 |
-1 |
-0,5403 |
-0,728 |
-0,4597 |
0,31725 |
0,0185 |
|
3 |
-1 |
-0,728 |
-0,7385 |
-0,4597 |
0,01849 |
0,0009 |
|
4 |
-1 |
-0,7385 |
-0,7391 |
-0,4597 |
0,00093 |
5E-05 |
|
5 |
-1 |
-0,7391 |
-0,7391 |
-0,4597 |
4,7E-05 |
2E-06 |
|
6 |
-1 |
-0,7391 |
-0,7391 |
-0,4597 |
2,3E-06 |
1E-07 |
|
7 |
-1 |
-0,7391 |
-0,7391 |
-0,4597 |
1,2E-07 |
6E-09 |
|
8 |
-1 |
-0,7391 |
-0,7391 |
-0,4597 |
5,9E-09 |
3E-10 |
|
9 |
-1 |
-0,7391 |
-0,7391 |
-0,4597 |
2,9E-10 |
1E-11 |
Mint látható, sokkal gyorsabban közelítette a gyököt, mint az intervallum-felezés, bár ezt általánosan nem lehet garantálni!
7.2.2.3. Iteráció
Az eddigi módszerek minden esetben a gyököt közelítették, de néha kissé lassan. A következőkben két olyan módszert nézünk meg, amelyek nem mindig konvergensek, de vagy nagyon könnyen használhatók, vagy nagyon gyorsan adnak eredményt.
Az első módszer az iteráció. Az egyenlet sokszor f(x)=0 alakban adott, és a gyököt az [a,b] intervallumban keressük. Ilyen esetben a következőképpen kell átalakítanunk az egyenletet:
|
|
(7.22) |
Most képezzük a következő sorozatot:
|
|
(7.23) |
Az így kapott x0, x1, …, x n számsorozat (ha konvergál) az f(x) egyenlet gyökéhez tart, hiszen ha x∞ a sorozat határértéke, akkor:
|
|
(7.24) |
A következőkben nézzük meg grafikusan, milyen esetek fordulhatnak elő!
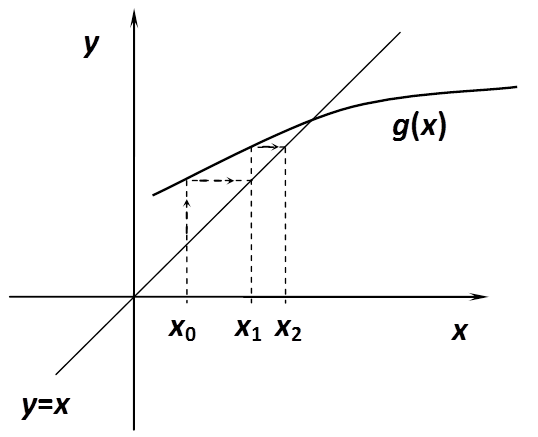
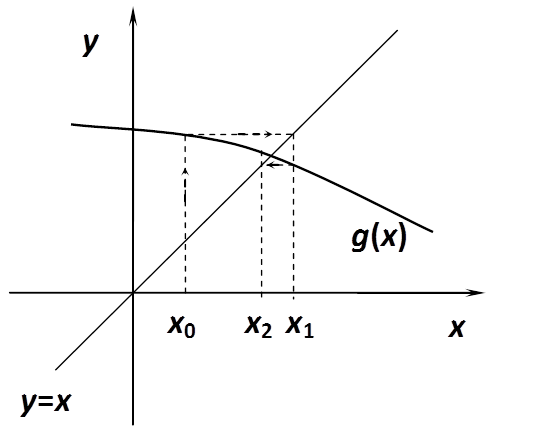
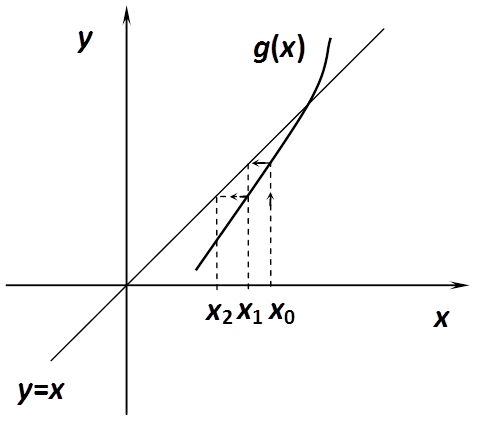
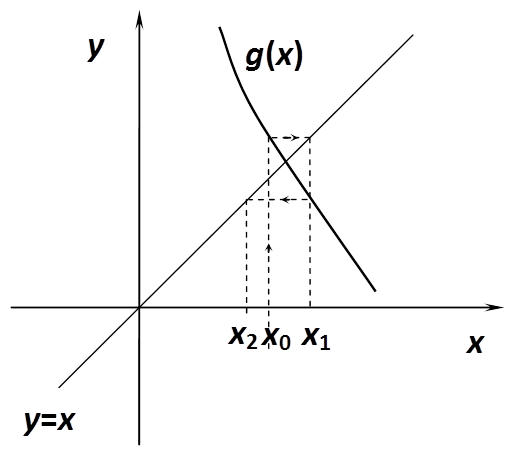
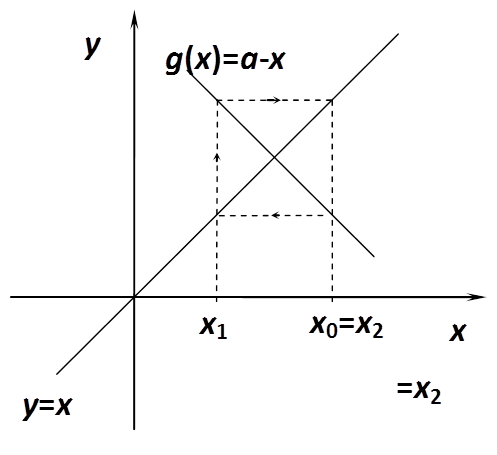
Az előző ábrákból is leolvasható, hogy konvergenciára csak akkor számíthatunk, ha g(x) meredeksége kisebb, mint 45°, azaz abban az intervallumban, ahol a gyököt keressük. Az egyszerű iterációt előszeretettel használják, mert rendkívül könnyen alkalmazható akár egy táblázatkezelővel is.
A mintapéldánk (7.14. egyenlet) esetén az iteráció nem működne, mert a derivált értéke:
|
|
(7.25) |
A gondot az okozza, hogy a függvényünk túl „meredek”. Ha egy alkalmas konstanssal megszorozzuk, akkor a zérus helye nem változik, de a meredeksége igen, hiszen:
|
|
(7.26) |
Nézzük, milyen feltétel van f-re:
|
|
(7.27) |
Legyen , ahol igaz, hogy , azaz M az első derivált maximális, vagy – negatív esetben – minimális értékével egyezik meg az adott intervallumon. Most, ha , akkor a konvergencia feltétele:
|
|
(7.28) |
ami mindig teljesül, hiszen M nagyobb, vagy egyenlő, mint a derivált, ezért a tört értéke egynél kisebb! Írjuk fel még az így kapott iterációs alakot:
|
|
(7.29) |
Nézzük először az eredeti példa megoldását képletekkel (Táblázat 7.8), majd pedig értékekkel (Táblázat 7.9)!
|
A |
B |
C |
D |
|
|
1 |
i |
x |
f(x) |
g(x) |
|
2 |
1 |
-0,73 |
=cos(B2)+B2 |
=C2+B2 |
|
3 |
2 |
=D2 |
=cos(B3)+B3 |
=C3+B3 |
|
i |
x |
f(x) |
g(x) |
|---|---|---|---|
|
0 |
-0,73 |
0,01517 |
-0,7148 |
|
1 |
-0,71483 |
0,04038 |
-0,6744 |
|
2 |
-0,67444 |
0,10661 |
-0,5678 |
|
3 |
-0,56783 |
0,27524 |
-0,2926 |
|
4 |
-0,2926 |
0,6649 |
0,3723 |
|
5 |
0,372304 |
1,3038 |
1,6761 |
|
6 |
1,6761 |
1,57099 |
3,24709 |
|
7 |
3,247091 |
2,25265 |
5,49974 |
Ahogy azt vártuk, az x i sorozat divergens. Mivel az függvény maximuma akkor lesz, ha a szinusz értéke -1, így az M=2. Ebből α-ra -0,5 adódik. Az átalakított egyenletet tartalmazza a Táblázat 7.10, valamint a megoldást értékekkel szemlélteti a Táblázat 7.11.
|
A |
B |
C |
D |
|
|
1 |
i |
x |
α*f(x) |
g(x) |
|
2 |
1 |
-0,73 |
=-(cos(B2)+B2)/2 |
=C2+B2 |
|
3 |
2 |
=D2 |
=-(cos(B3)+B3)/2 |
=C3+B3 |
|
i |
x |
α *f(x) |
g(x) |
|---|---|---|---|
|
0 |
-1 |
0,22985 |
-0,77015 |
|
1 |
-0,77015 |
0,02617 |
-0,74398 |
|
2 |
-0,74398 |
0,0041 |
-0,73988 |
|
3 |
-0,73988 |
0,00066 |
-0,73921 |
|
4 |
-0,73921 |
0,00011 |
-0,73911 |
|
5 |
-0,73911 |
1,8E-05 |
-0,73909 |
|
6 |
-0,73909 |
2,9E-06 |
-0,73909 |
Mint látható, a konvergencia viszonylag gyors.
7.2.2.4. Érintőmódszer (Newton-Raphson módszer)
Legyen most adott az f(x)=0 egyenlet, és tudjuk, hogy az [a,b] intervallumban van gyöke! Legyen , és helyettesítsük a függvényt az x 0 -nál húzott érintőjével. Az érintő és az x tengely metszéspontját (x 1 ) tekintsük a gyök egy közelítésének! Az eljárás folytatásaként tegyünk mindent ugyan így, csak most az x 1 értékkel! Írjuk fel az egyenleteket és az összefüggéseket a 7.11. ábra alapján! Az egyenes egyenlete:
|
, |
(7.30) |
vagy másképpen:
|
|
(7.31) |
Az x tengellyel való metszéspontban y=0, így x kifejezhető:
|
|
(7.32) |
Az eljárás folytatásaként írhatjuk, hogy:
|
(7.33) |
Vegyük észre, hogy ez az összefüggés és a 7.29 egyenlet nagyon hasonlít egymásra, az ott szereplő M tulajdonképpen az itteni nevezőben lévő derivált maximális értéke! Gyanítható ezek után, hogy az érintő módszer konvergenciájával nem lesz gond. Ez általában így is van. Ha elég közel vesszük fel a kezdeti x0 pontot a gyökhöz, akkor majdnem mindig konvergens a közelítés. A gond az, hogy általában fogalmunk sincs, hogy hol a gyök, örülünk, ha egy intervallumra sikerül leszűkíteni a keresést! Alkalmazása során általában meg szoktak adni egy maximális iteráció számot is.
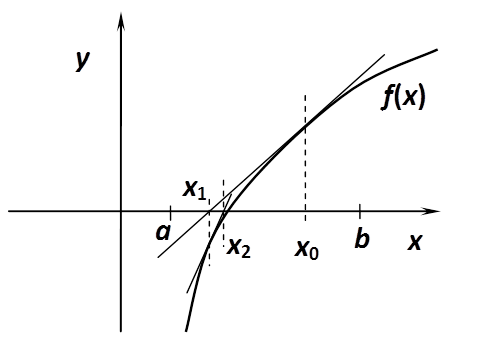
Miért használják mégis? Például azért, mert komplex gyökök meghatározására is alkalmas, vagy azért, mert ha konvergens, akkor majdnem mindig „másodrendűen” gyors, azaz:
|
, |
(7.34) |
ahol x a gyök, C pedig egy állandó érték. Ez azt jelenti, hogy lépésenként általában megduplázódik a helyes jegyek száma a gyökközelítő értékében. Nézzük meg most a megszokott példánkat a (Táblázat 7.12 és Táblázat 7.13) táblázatokban!
|
A |
B |
C |
D |
|
|
1 |
i |
x |
f(x) |
f’(x) |
|
2 |
1 |
-1 |
=cos(B2)+B2 |
=-sin(B2)+1 |
|
3 |
2 |
=B2-C2/D2 |
=cos(B3)+B3 |
=-sin(B3)+1 |
|
i |
x |
f(x) |
f'(x) |
|---|---|---|---|
|
0 |
-1 |
-0,46 |
1,84147 |
|
1 |
-0,7504 |
-0,019 |
1,6819 |
|
2 |
-0,7391 |
-5E-05 |
1,67363 |
|
3 |
-0,7391 |
-3E-10 |
1,67361 |
|
4 |
-0,7391 |
0 |
1,67361 |
A (Táblázat 7.13) táblázatban szereplő számsor mindennél jobban illusztrálja a konvergencia sebességét! Milyen problémák léphetnek fel mégis, mikor lehet gond? Például, ha az érintő mentén kilépünk az [a,b] intervallumból (7.12. ábra), vagy szerencsétlenül választjuk meg a kezdőértéket: , és . Ekkor , és így . A számítást tovább folytatva: . Látható, hogy körbe-körbe járunk (7.13. ábra)!
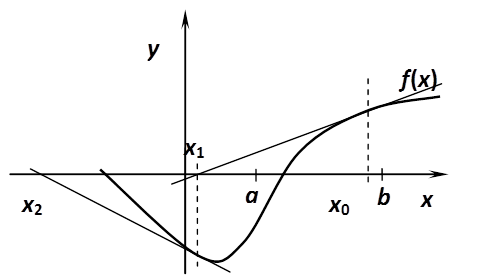
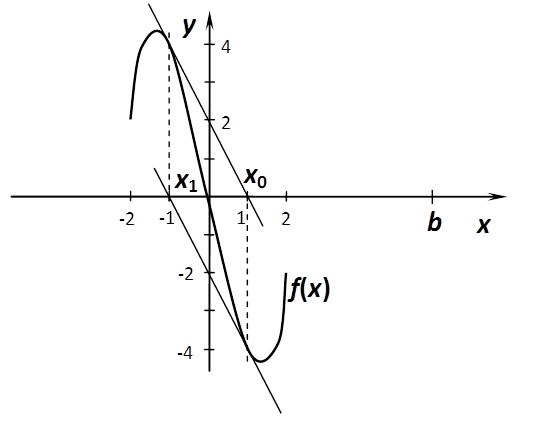
A konvergenciával kapcsolatban azonban nemcsak rosszat mondhatunk. Azt várnánk, hogy nem működik az eljárás, ha a gyök például egy minimumhely is egyben, hiszen ott a derivált értéke zérus. A deriválttal pedig osztunk! Nem szabad elfelejtenünk, hogy a gyököt csak közelítjük, de sosem érjük el, így a derivált sem lesz nulla a közelítés közben. Az [a,b] intervallumban lehet szélsőértékhely, de akkor könnyen úgy járhatunk, hogy kilépünk az intervallumból, hasonlóan, mint az a (7.13. ábra) ábrán is látható. Arra mindenképpen ügyeljünk, hogy a közelítést ne indítsuk minimum-, vagy maximumhelyről! Az előzőek illusztrálására nézzük meg, hogy az függvény gyökét hogyan közelíti a módszer (Táblázat 7.14)!
|
x |
f(x) |
f'(x) |
|---|---|---|
|
1 |
1 |
2 |
|
0,5 |
0,25 |
1 |
|
0,25 |
0,0625 |
0,5 |
|
0,125 |
0,015625 |
0,25 |
|
0,0625 |
0,003906 |
0,125 |
|
0,03125 |
0,000977 |
0,0625 |
|
0,015625 |
0,000244 |
0,03125 |
|
0,007813 |
6,1E-05 |
0,015625 |
|
0,003906 |
1,53E-05 |
0,007813 |
Mint látható, a konvergencia itt is megvan, csak sokkal lassabb. Bizonyítható, hogy többszörös gyökök esetén a gyököt közelítése csak lineáris.
A módszer egy utolsó érdekessége, hogy segítségével könnyedén készíthetünk gyökvonó algoritmust. Legyen az egyenletünk az . Ennek zérus helye nyilvánvalóan: . Ekkor a közelítő formula:
|
. |
(7.35) |
Speciálisan, ha k=2, akkor négyzetgyökvonásra a következő összefüggést kapjuk:
|
. |
(7.36) |
7.2.3. Gyökkereső algoritmusok polinomok esetében
Mivel egy polinomot is kezelhetünk függvényként, az előző fejezetben közölt gyökkereső eljárások itt is alkalmazhatók. Miért tárgyaljuk mégis külön a polinomok esetét? Mert a polinomok esetén általában nem csak egy adott környezetbe eső gyökre van szükségünk (például szimuláció interpolációs formulákkal), hanem az összesre, beleértve a komplex gyököket is (gondoljunk csak a rendszerek stabilitásának vizsgálatára)!
Célunk tehát olyan algoritmus bemutatása, amellyel egy polinom összes gyökét meghatározhatjuk. Több lehetséges módszer is létezik, azonban ebben a fejezetben egy általunk megvalósított, többszörösen tesztelt eljárás lépéseit ismertetjük. A programot Microsoft Excelben azaz Visual Basic for Applications nyelven készítettük el - a későbbiekben ennek néhány alapelemét be is mutatjuk.
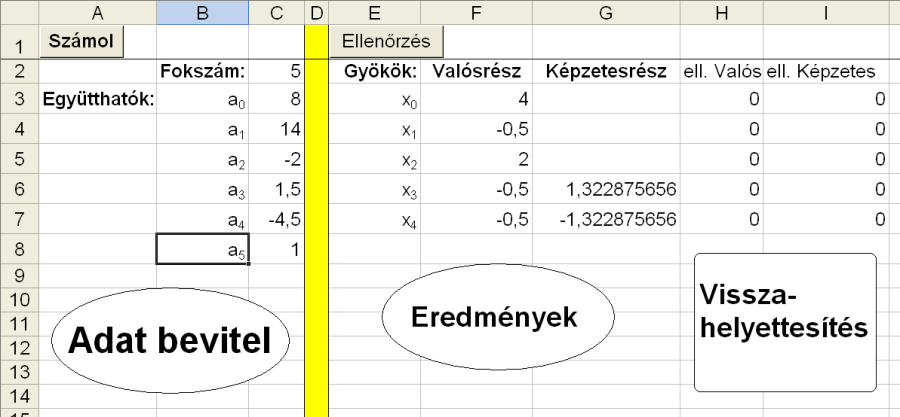
A program ablaka a (7.14. ábra) ábrán látható.
|
Index |
Teendő |
Alkalmazott eljárások |
|---|---|---|
|
1. |
Triviális gyökök (0, ±1) kigyűjtése, osztás gyöktényezővel |
Horner-séma Polinomosztás |
|
2. |
A maradék polinom fokszáma<4 Igen: megoldás analitikusan, és vége Nem: tovább a következő pontra |
Elsőfokú megoldó képlet, Másodfokú megoldó képlet, |
|
3. |
A főegyüttható legyen egy, és csak egyszeres gyökök legyenek (gyökök multiplicitásának eltüntetése) |
Vektor osztása skalárral, Polinomosztás |
|
4. |
Valós gyökök kigyűjtése |
|
|
4. a |
Gyököket tartalmazó intervallum meghatározása |
|
|
4. b |
Valós gyökök száma |
Polinomosztás |
|
4. c |
A gyök közelítése |
Horner-séma, Érintőmódszer |
|
4. d |
Az eredeti polinom osztása a gyöktényezővel ahányszor csak lehet (többszörös gyökök) |
Polinomosztás |
|
4. e |
Lásd 2. |
|
|
4. f |
Vissza 4. c-re, amíg el nem fogynak a valós gyökök |
|
|
5. |
Komplex gyökök meghatározása |
|
|
5. a |
Intervallum keresés |
|
|
5. b |
Gyökkeresés |
Komplex érintőmódszer |
|
5. c |
Az eredeti polinom osztása másodfokú gyöktényezővel ahányszor csak lehet (többszörös gyökök) |
Polinomosztás |
|
5. d |
Lásd 2. |
|
|
5. e |
Vissza 5. a-ra |
7.2.3.1. Horner-séma
Az egyik leggyakoribb tevékenység, amit egy polinommal el kell végeznünk, hogy meghatározzuk egy adott helyen a helyettesítési értékét. A Horner-séma ennek a számításnak a műveletek számára optimalizált eljárása, azaz itt kell a legkevesebbet számolnunk. Gyakorlatilag csak egy átrendezésről van szó.
Legyen az egyenletünk
|
|
(7.37) |
alakú.
Ekkor átrendezhetjük a következő alakra:
|
|
(7.38) |
Példaként nézzük azt az egyenletet, amely a (7.14. ábra) ábrán is szerepel:
|
|
(7.39) |
Valós x esetén a következő függvény valósítja meg az eljárást:
Function BehelyValos(x AsDouble, n AsInteger, a() AsDouble) AsDouble
' a() az együttható vektor
' n a polinom fokszáma
Dim i AsInteger, y AsDouble
y = a(n) ' a legmagasabb fokú tag együtthatója
For i = n - 1 To 0 Step -1
If a(i) <> 0 Then ' ellentetes elojellel megegyeznek
If Abs(1 + y * x / a(i)) < 0.0000000000001 Then
y = 0 ' a numerikus hibák csökkentésére
Else
y = y * x + a(i)
End If
Else
y = y * x ' mert a(i)=0
End If
Next i
BehelyValos = y
End Function
Komplex esetben eljárást kellett írni, mert két visszaadott érték van. A program listája a következő:
Sub BehelyKomplex0(xr AsDouble, xi AsDouble, n AsInteger, a() AsDouble,_
ByRef yr AsDouble, ByRef yi AsDouble)
' a() az együttható vektor
' n a polinom fokszáma
' xr x reális része; xi x imaginárius része
' y az eredmény
' yr y reális része; yi y imaginárius része
Dim i AsInteger, y AsDouble
yr = a(n)
yi = 0
For i = n - 1 To 0 Step -1
If a(i) <> 0 Then
If Abs(1 + (yr * xr - yi * xi) / a(i)) < 0.0000000000001 Then
y = 0
Else
y = yr * xr - yi * xi + a(i)
End If
Else
y = yr * xr - yi * xi
End If
If yi * xr <> 0 Then
If Abs(1 + yr * xi / yi / xr) < 0.0000000000001 Then
yi = 0
Else
yi = yr * xi + yi * xr
End If
Else
yi = yr * xi + yi * xr
End If
yr = y
Next i
End Sub
7.2.3.2. Polinomok osztása polinommal
Az eljárás teljes mértékben a megszokott kézi módszert követi, ami tulajdonképpen az általános iskolákban tanított osztás általánosítása. Ismétlésként álljon itt egy példa:
|
|
(7.40) |
Az osztás eredménye, és a maradék (18) is kiadódott. Az ezt megvalósító programkód pedig a következő:
Sub PolDiv(n As Integer, m As Integer, _ ByRef a() As Double, ByRef b() As Double, ByRef c() As Double) ' a/b=c, ahol a, b és c a polinomok együtthatóit tartalmazó vektorok ' a 0. fokú tag a vektor 0 elemében van ' ha van maradék, akkor a-ban lesz Dim i As Integer, j As Integer ReDim c(n - m) For i = n - m To 0 Step -1 c(i) = a(i + m) / b(m) For j = 0 To m If j = 0 Then a(i + m - j) = 0 Else If a(i + m - j) <> 0 Then If Abs(1 - c(i) * b(m - j) / a(i + m - j)) < 0.0000000001 Then a(i + m - j) = 0 ' a különbség közel nulla Else a(i + m - j) = a(i + m - j) - c(i) * b(m - j) End If Else a(i + m - j) = -c(i) * b(m - j) ' mert a(i+m-j)=0 End If End If Next j Next i End Sub
7.2.3.3. Primitív gyökök kezelése
Az egyszerűen, szinte ránézésre meghatározható gyökökről van szó ebben a fejezetben. Ilyen például, ha a 7.37. egyenletben a0 értéke zérus. Ekkor biztosan van olyan gyök, amely nulla, és a polinom fokszáma csökkenthető. A későbbi eljárásoknál fontos lesz, hogy az egyenlet nulladfokú tagja nem lehet zérus, mert osztunk vele!
Általában ritkán fordul elő, hogy egy polinomnak az 1 gyöke, de könnyen ellenőrizhető, és lehet, hogy a későbbiekben a közelítések során nem tudnánk pontosan előállítani. Az 1 akkor gyök, ha a polinom együtthatóinak összege zérus, hiszen behelyettesítéskor minden x hatvány helyére 1 kerül! Ha az 1 gyök, akkor az egyenletet osszuk el gyöktényezővel!
Hasonló a helyzet a -1-el is, de ekkor a páros kitevőjű tagok együtthatóinak összege fog megegyezni a páratlan kitevőjű tagok együtthatóinak összegével, hiszen a párosaknál a behelyettesítés eredményeként az x hatvány 1 lesz, a páratlanoknál pedig -1. Ha a -1 gyök, akkor az egyenletet osszuk el gyöktényezővel!
Természetesen ne feledkezzünk meg arról, hogy mindegyik primitív gyök többszörös gyök is lehet, tehát az eljárást addig kell folytatni, amíg mindet meg nem kapjuk. Ha szerencsénk van, a fokszám csökkenés miatt nem is kell közelítő módszert alkalmaznunk.
7.2.3.4. Harmadfokú egyenlet megoldása: Cardano-formula
A pontosság miatt (mivel a közelítő eljárások csak „közelítenek”) hacsak lehet, szeretjük az egyenlet megoldását valamilyen képletből megkapni. Az első- és a másodfokú esetet mindenki ismeri, de a harmadfokút már nem. Ennek megoldását – ugyan nem ő találta ki, csak ő publikálta – Gerolamo Cardanoról nevezték el. Van azonban valami, ami nem alaptalanul viseli az ő nevét: a kardántengely.
Ennyi technika történet után térjünk vissza a matematikához! Az általános harmadfokú egyenlethez nem létezik megoldó képlet, csak olyan változatához, amelyben nem szerepel másodfokú tag:
|
. |
(7.41) |
Az általános egyenletből azonban ez az alak mindig előállítható a teljes négyzethez hasonló eljárással, csak itt természetesen köbről van szó. Ekkor az átszámítás a következő módon végezhető el:
|
|
(7.42) |
Az (7.41) egyenlet megoldása:
|
|
(7.43) |
ahol
|
|
(7.44) |
|
|
|
(7.45) |
Mint látható, ezt a számítást elvégezni nem olyan egyszerű, mint a másodfokú egyenlet gyökeit meghatározni. Érdekeség talán, hogy abban az esetben, ha a megoldás három valós gyökből áll, már u és v meghatározása során is komplex számokat kapunk! Sokszor nem is bajlódnak vele, inkább közelítő módszert alkalmaznak. Mi nem így tettünk, itt a programkód:
Sub harmadfoku(s As Integer, ByRef a() As Double)
' s annak a sornak a száma, ahová a gyököt ki kell írni
' a az együttható vektor
Dim p As Double, q As Double, u As Double, v As Double, diszkr As Double
Dim uabsz As Double, fi As Double
Ifa(3) = 0 Then
Call masodfoku(s, a)
Else ' az egyenlet átalakítása z^3+p*z+q=0 -ra
kesz = True
p = (3 * a(1) - a(2) * a(2)) / 3
q = a(0) - a(2) * a(2) * a(2) / 27 - a(2) / 3 * p
If p = 0 Then ' z^3+q=0
p = Sgn(-q) * (Abs(q)) ^ (1 / 3)
' gyökök kiírása az eredménylapra
Range("F" + Szam(s)).Value = p - a(2) / 3
s = s + 1
Range("F" + Szam(s)).Value = -p / 2 - a(2) / 3
Range("G" + Szam(s)).Value = 3 ^ 0.5 * p / 2
s = s + 1
Range("F" + Szam(s)).Value = -p / 2 - a(2) / 3
Range("G" + Szam(s)).Value = -3 ^ 0.5 * p / 2
Exit Sub
End If
If q = 0 Then ' z^3+p*z=0 => z=0 => x=-B/3/A, de A=1
Range("F" + Szam(s)).Value = -a(2) / 3
a(0) = a(1) - 2 * a(2) * a(2) / 9
a(1) = 2 / 3 * a(2)
a(2) = 1
Call masodfoku(s + 1, a)
Exit Sub
End If
diszkr = q * q / 4 + p * p * p / 27
If diszkr < 0Then ' a valós gyök meghatározása
fi = Sqr(Abs(q * q / 4 + p * p * p / 27))
uabsz = (q * q / 4 + fi * fi) ^ (1 / 6)
fi = (1 - Sgn(-q)) / 2 * 3.1415926536 + Atn(fi / (-q / 2))
u = 2 * uabsz * Cos(fi / 3) - a(2) / 3 / a(3)
Else ' diszkr > 0, az egyetlen valós gyök meghatározása
fi = -q / 2 + Sqr(diszkr)
u = Sgn(fi) * Abs(fi) ^ (1 / 3)
v = -p / 3 / u
u = u + v - a(2) / 3
End If
v = Round(u) ' egész megoldások pontosítása
If Abs(((u + a(2)) * u + a(1)) * u + a(0)) > _
Abs(((v + a(2)) * v + a(1)) * v + a(0)) Then u = v
Range("F" + Szam(s)).Value = u
a(0) = a(1) + u * (u + a(2))
a(1) = u + a(2)
a(2) = 1
Call masodfoku(s + 1, a)
End If 'harmadfokú-e
End Sub
7.2.3.5. A többszörös gyökök eltüntetése
Több oka is van annak, hogy szeretnénk előállítani egy olyan polinomot, amelynek az eredeti polinom minden gyöke a megoldása, egyszeres multiplicitással. Az egyik ok, hogy ez nyilvánvalóan fokszámcsökkenéssel jár, és lehet, hogy nem is lesz szükségünk közelítő (azaz pontatlanabb) módszer alkalmazására. A másik ok, hogy – a későbbiekben ismertetésre kerülő – a valós gyökök számát meghatározó módszer csak ilyen esetben működik.
Legyen adott az f(x) polinom, melynek főegyütthatója (a n ) egy[3], és amelynek s darab különböző gyöke (x i ) van, rendre α i multiplicitással. Ekkor a polinom gyöktényezős alakja a következő:
|
. |
(7.46) |
A polinom deriváltja előállítható a következő alakban:
|
, |
(7.47) |
ahol egyszeres gyökök esetén α i -1=0, így az adott gyök nem szerepel a szorzatban. Legyen g(x) (7.46) és (7.47) legnagyobb közös osztója, azaz:
|
|
(7.48) |
Látható, hogy lesz a keresett csak egyszeres gyököket tartalmazó polinom. A g(x) polinomot az ún. Euklidesz-féle algoritmussal lehet előállítani. Állítsuk elő az f(x) és deriváltja hányadosát (q0(x)) és az osztás maradékát (r1(x))! Ekkor felírható a következő egyenlőség:
|
|
(7.49) |
Folytassuk, és készítsünk egy sorozatot mindaddig, amíg a maradék nullává nem válik:
|
|
(7.50) |
Bizonyítható, hogy r k (x) lesz a legnagyobb közös osztó, azaz g(x). Most már csak p(x) meghatározása van hátra:
|
|
(7.51) |
Az algoritmust megvalósító programrészlet a következő:
…………… 'a az eredeti polinom együtthatói Call Derivalt1(n, a, bb)'bb a derivált együtthatót tartalmazza Call AegyenloB(n, aa, a) ' az eredeti tömb aa-ba i = n ' a polinom fokszáma j = n - 1 ' a derivált fokszáma Do Call PolDiv(i, j, aa, bb, cc) Call PolFokszam(i, aa) ' a maradék fokszáma ' aa-t es bb-t fel kell cserélni, valamint a fokszámaikat is Call AegyenloB(i, cc, aa) Call AegyenloB(j, aa, bb) Call AegyenloB(i, bb, cc) k = i i = j j = k LoopUntil (k = 0) And (cc(0) = 0) ' osztás, amíg a maradék 0nem lesz Call AegyenloB(n, bb, a) ' az eredeti polinom bb-be Call PolDiv(n, i, bb, aa, cc) ' osztva a legnagyobb közös osztóval k = n - i Call PolFokszam(k, cc) ' cc-ben csak egyszeres gyökök vannak, fokszáma=k ……………
7.2.3.6. A gyököket tartalmazó intervallum meghatározása
A következőkben igazolás nélkül közlünk egy olyan eljárást, amellyel intervallum határozható meg a gyökök abszolút értékére. Legyen adott a 7.37. alakú egyenlet. Tegyük fel, hogy a n és a0 nem zérus. Határozzuk meg a következő értékeket:
|
|
(7.52) |
Bizonyítható, hogy az egyenlet minden gyökére igaz a következő egyenlőtlenség:
|
|
(7.53) |
Az algoritmust megvalósító eljárás a következő:
Sub GyokInterv(n As Integer, ByRef a() As Double, _ ByRef al As Double, ByRef fel As Double) Dim ak1 As Double, ak2 As Double Dim i As Integer ak1 = Abs(a(0)) ak2 = Abs(a(1)) For i = 1 To n - 1 If Abs(a(i)) > ak1 Then ak1 = Abs(a(i)) If Abs(a(i + 1)) > ak2 Then ak2 = Abs(a(i + 1)) Next i fel = 1 + ak1 / Abs(a(n)) al = 1 / (1 + ak2 / Abs(a(0))) End Sub
7.2.3.7. Valós gyökök száma egy adott intervallumban
Az algoritmusnak a n =1 főegyütthatójú, csak egyszeres gyököket tartalmazó polinomra van szüksége. Ilyet mi már elő tudunk állítani.
Az eljárás két részből áll. Az első részben egy polinomokból álló sorozatot (Sturm-lánc) kell meghatározni. Az algoritmus emlékeztet az Euklideszi algoritmusra, mert itt is polinomosztással kell dolgoznunk, csak a kiinduló két polinom lesz más, és az osztási maradék mínusz egyszeresére lesz szükségünk. Nézzük ezek után a számítás leírását, ahol p(x) a (7.51) szerint előállított k-ad fokú polinom:
|
|
(7.54) |
Az így előállított p0(x),…, p k (x) polinomsorra lesz szükségünk. Ha egy [a,b] intervallumban szeretnénk megtudni a valós gyökök számát, akkor állítsuk elő a p0(a),…,p k (a) sorozatot, hagyjuk ki belőle az esetleges nullákat, majd számoljuk meg, hogy p0(a)-tól p k (a)-ig hány előjelváltás volt. Az így kapott értéket jelöljük v a -val. Hasonlóan járjunk el b-vel is, az eredmény legyen v b . Bizonyítható, hogy az [a,b]-ben lévő valós gyökök száma megegyezik a v a -v b különbséggel.
A következő két eljárás az algoritmus egy lehetséges megvalósítására mutat példát. Vegyük észre, hogy az előző pontban bemutatott intervallumkereső eljárás két intervallumot – egyet a pozitív számokra, egyet a negatívokra – adott. Ez a magyarázata, hogy az eljárások két darabszámot állítanak elő:
Function ElojelValtas(n As Integer, a() As Double) As Integer Dim s As String, i As Integer ' Megszámolja, hogy az a-ban levő sorozatban hány előjelváltás van. ' A nulla nem számít. s = "" ' a számokat az előjelükkel helyettesíti, a nullát kihagyja For i = 0 To n Select Case Sgn(a(i)) Case 1: s = s + "+" Case -1: s = s + "-" End Select Next i Do While InStr(s, "++") > 0 'az ismétlődések kiszűrése i = InStr(s, "++") s = DeleteStr(s, i, 1) Loop Do While InStr(s, "--")> 0 ' az ismétlődések kiszűrése i = InStr(s, "--") s = DeleteStr(s, i, 1) Loop ' csak +-+- szerű elemek maradnak a sorozatban ElojelValtas = Len(s) - 1 EndFunction SubValosDb(n As Integer, ByRef a() As Double, _ ByRef negdb As Integer, ByRef pozdb As Integer) Dim aa() As Double, bb() As Double, cc() As Double Dim al As Double, fel As Double Dim v1() As Double, v2() As Double, v3() As Double, v4() As Double Dim i As Integer, j As Integer, k As Integer, L As Integer Dim vege As Boolean ' Sturm-féle gyökszámlálás ' A két intervallum szélein vizsgál. ' A tömbökben a Sturm-sorozat helyettesítési értékei vannak. ReDim v1(n) ReDim v2(n) ReDim v3(n) ReDim v4(n) Call GyokInterv(n, a, al, fel) v1(0) = BehelyValos(fel, n, a) v2(0) = BehelyValos(al, n, a) v3(0) = BehelyValos(-fel, n, a) v4(0) = BehelyValos(-al, n, a) Call AegyenloB(n, aa, a) i = n L = 2 Call Derivalt1(n, a, bb) j = n - 1 Call PolFokszam(j, bb) v1(1) = BehelyValos(fel, j, bb) ' a derivált helyettesítési értékei v2(1) = BehelyValos(al, j, bb) v3(1) = BehelyValos(-fel, j, bb) v4(1) = BehelyValos(-al, j, bb) vege = False Do Call PolDiv(i, j, aa, bb, cc) Call PolFokszam(i, aa) Call NegalA(i, aa) v1(L) = BehelyValos(fel, i, aa) v2(L) = BehelyValos(al, i, aa) v3(L) = BehelyValos(-fel, i, aa) v4(L) = BehelyValos(-al, i, aa) L = L + 1 If i = 0 Then vege = True Call AegyenloB(i, cc, aa) Call AegyenloB(j, aa, bb) Call AegyenloB(i, bb, cc) k = i i = j j = k Loop Until vege L = L - 1 pozdb = ElojelValtas(L, v2) - ElojelValtas(L, v1) negdb = ElojelValtas(L, v3) - ElojelValtas(L, v4) End Sub
7.2.3.8. Gyökök keresése közelítő módszerrel
Közelítő módszernek az érintőmódszert választottuk. Mint láttuk, az eljárás általában konvergens, de ha rossz helyről indulunk, akkor körbe-körbe járhat. A másik probléma, hogy kiléphet az intervallumból kevésbé zavaró, mert akkor is talál gyököt, csak másikat. Mivel mi minden gyököt szeretnénk megkeresni, és a sorrend nem számít, ezzel a „hibával” nem foglalkozunk. A körbe-körbe járás csak speciális esetben fordul elő, ezért a kezdeti értékét véletlenszám-generátor felhasználásával úgy állítottuk elő, hogy még a feltétel is teljesüljön. Ha ezer lépés után sem elég pontos a közelítés, akkor a program átvált az intervallumfelezésre.
A valós esetet megvalósító programrészlet a következő:
Call GyokInterv(k, cc, al, fel)
al = -al
fel = -fel
' első derivált cv, nv
Call Derivalt1(k, cc, cv)
nv = k - 1
Call PolFokszam(nv, cv)
' második derivált cvv, nvv
Call Derivalt1(nv, cv, cvv)
nvv = nv - 1
Call PolFokszam(nvv, cvv)
' megfelelő kezdeti érték keresése ->sign(f)=sign(f")
j = 0
Do
If negdb > 0 Then
x = (fel - al) * Rnd + al
Else
x = (-al + fel) * Rnd - fel
End If
j = j + 1
If j = 25 Then
al = al / 1.1
fel = 1.1 * fel
j = 0
End If
Loop UntilSgn(BehelyValos(x, k, cc)) = Sgn(BehelyValos(x, nvv, cvv))
' megoldás érintővel
x0 = x
j = 0
Do
x = x0 - BehelyValos(x0, k, cc) / BehelyValos(x0, nv, cv)
If (Abs(1-x/x0)<epsz) And (Abs(BehelyValos(x, k, cc)) < epsz) ThenExit Do
x0 = x
j = j + 1
If j = 1000 Then
x = IntervFelezes(al, fel, k, cc)
Exit Do
End If
Loop
Range("F" + Szam(gysz)).Value = x
If x < 0Then
negdb = negdb - 1
Else
pozdb = pozdb - 1
End If
gysz = gysz + 1
bb(1) = 1
bb(0) = -x
Call PolDiv(k, 1, cc, bb, aa) ' osztás a gyöktényezővel
k = k - 1
Call PolFokszam(k, aa)
Call AegyenloB(k, cc, aa)
Hasonlóan jártunk el komplex esetben is, de ott az első közelítő érték valós részét választottuk véletlenszerűen, a képzetes mindig egy lett:
Call GyokInterv(k, cc, al, fel)
' elsőderivált cv, nv
Call Derivalt1(k, cc, cv)
nv = k - 1
Call PolFokszam(nv, cv)
' második derivált cvv, nvv
Call Derivalt1(nv, cv, cvv)
nvv = nv - 1
Call PolFokszam(nvv, cvv)
' megfelelő kezdeti érték keresése ->sign(f)=sign(f')
Do
xr = (fel - al) * Rnd + al
Loop Until Sgn(BehelyValos(xr, k, cc)) = Sgn(BehelyValos(xr, nvv, cvv))
' megoldás érintővel
xr0 = xr
xi = 1
xi0 = 1
Do
Call BehelyKomplex0(xr0, xi0, k, cc, yr, yi)
Call BehelyKomplex0(xr0, xi0, nv, cv, yr0, yi0)
nev = yr0 * yr0 + yi0 * yi0
xr = xr - (yr * yr0 + yi * yi0) / nev
xi = xi - (yr0 * yi - yi0 * yr) / nev
If (Abs(1 - Sqr((xi * xi + xr * xr) / (xi0 * xi0 + xr0 * xr0))) < epsz) _
And (Sqr(BehelyKomplex(xr, xi, k, cc)) < epsz) Then ExitDo
xr0 = xr
xi0 = xi
Loop
If Abs(BehelyValos(xr, k, cc)) < epsz Then
Range("F" + Szam(gysz)).Value = xr
gysz = gysz + 1
n = n - 1
bb(1) = 1
bb(0) = -xr
Call PolDiv(k, 1, cc, bb, aa)
k = k - 1
Else
Range("F" + Szam(gysz)).Value = xr
Range("G" + Szam(gysz)).Value = xi
Range("F" + Szam(gysz + 1)).Value = xr
Range("G" + Szam(gysz + 1)).Value = -xi
gysz = gysz + 2
n = n - 2
bb(2) = 1
bb(1) = -2 * xr
bb(0) = xr * xr + xi * xi
Call PolDiv(k, 2, cc, bb, aa)
k = k - 2
End If
Call PolFokszam(k, aa)
Call AegyenloB(k, cc, aa)
Mint látható, mindkét programrészben szerepel a gyöktényezővel való osztás. Valós esetben ez magától értetődő, de vajon mi a helyzet a komplex gyökök esetén? Ha megtaláltunk egy komplex gyököt, akkor igazából kettőt találtunk, mert a konjugáltja is gyök. Legyen például a gyök. Ekkor behelyettesítve egy 7.37. egyenletbe, majd a valós és képzetes részeket szétválogatva:
|
|
(7.55) |
Az egyenlőség nyilván csak akkor állhat fenn, ha mind a valós, mind pedig a képzetes rész zérus. Mivel gyököt helyettesítettünk be, ez nyilván így is van. Abban az esetben, ha a konjugáltat írjuk az egyenletbe, akkor csak annyi változik, hogy a képzetes rész előjele ellentétes lesz:
|
|
(7.56) |
Azonban az előzőekben leírtak miatt ez is kielégíti az egyenletet, tehát a konjugált is gyök. Ezek után lehetőségünk van egyszerre két gyöktényezővel osztani. Ennél is jobb azonban a helyzet, mert:
|
|
(7.57) |
Azaz egy valós együtthatójú másodfokú polinommal oszthatunk.
7.3. Többváltozós függvények gyökkeresése
7.3.1. Lineáris egyenletrendszer – Gauss elimináció
Egy n egyenletet és ismeretlent tartalmazó lineáris egyenletrendszert sokféleképpen lehet megadni. A klasszikus (7.58), a mátrixos részletes (7.59) és a mátrixos tömör (7.60) írásmód közül választhatunk.
|
|
(7.58) |
|
|
|
(7.59) |
|
|
|
(7.60) |
A lineáris egyenletrendszereket általában Gauss-eliminációval szoktuk megoldani. Ennek lényege a következő: az első egyenlet -szeresét hozzáadjuk a másodikhoz. Ennek hatására a második egyenlet első együtthatója zérus lesz. Hasonlóan folytatjuk az eljárást, az első egyenlet -szeresét adjuk hozzá az i. egyenlethez. Ha az összes egyenlettel elvégeztük ezt az összegzést, akkor az x 1 ismeretlen az első egyenlet kivételével mindenhol eltűnik. Most a második egyenlettel csináljuk ugyanezt minden nála nagyobb sorszámú sorra, azaz például a második egyenlet -szeresét adjuk az i. sorhoz. Az eljárást addig folytatjuk, amíg a következő struktúrájú egyenletrendszert nem kapjuk:
|
|
(7.61) |
A betűk „kalapozására” azért volt szükség, mert az együtthatók – az első egyenlet kivételével – megváltoznak. Az így kapott egyenletrendszerből a megoldás már könnyűszerrel előállítható, hiszen az utolsóban csak egy ismeretlen van, tehát . Az utolsó előttiegyenletben eredetileg két ismeretlen van, ebből x n értékét már ismerjük, tehát ez is meghatározható. Az eljárást így folytatva visszafelé, az összes gyököt meg tudjuk határozni.
Az elmondottak bemutatására nézzük a következő konkrét példát:
|
|
(7.62) |
vagy mátrixos alakban:
|
|
(7.63) |
Az egyszerűség kedvéért az együttható mátrixot és az egyenlet jobb oldalát egy nx(n+1)‑szeres mátrixba szoktuk összefoglalni, és így számolunk:
|
|
(7.64) |
Az első sor -szeresét adjuk hozzá a második sorhoz. A harmadik sor esetén ez a szorzótényező -7:
|
|
(7.65) |
A következő – és esetünkben egyben az utolsó – lépésként a második egyenletet vonjuk ki a harmadikból:
|
|
(7.66) |
Ezzel a rendezés végére értünk, most már csak ki kell fejezni a megoldásokat. Az x 3 az utolsó egyenletből kiolvasható:3. Ezt a másodikba behelyettesítve x 2 =2, majd az első egyenletből x 1 =1.
Most térjünk vissza az általános esethez! Mikor lehet gondunk az eljárás során? Akkor ha, például a j. sort akarjuk hozzáadni az alatta állókhoz, de az a jj érték zérus. Ekkor keresnünk kell alatta olyan sort, ahol a j. oszlopban nincs nulla, és azzal felcserélhetjük. Ha nem találtunk ilyen sort, akkor az egyenlet nem oldható meg! Matematikából már megtanították mindenkinek, hogy egy lineáris egyenletrendszer akkor nem oldható meg, ha az együttható mátrixának determinánsa nulla. Nézzünk meg most ezzel a „félbehagyott” egyenletrendszerrel mi a helyzet.
Az egyenlet együttható mátrixa a következő alakú:
|
|
(7.67) |
Kezdjünk hozzá a determináns meghatározásához! Ha az első oszlop szerint fejtjük ki, akkor ott csak egy nullától különböző érték van, ezért a determinánsszámítást visszavezetjük egy eggyel kisebb dimenziójú esetre, azaz a11-szer a hozzá tartozó aldetermináns. Ezt az eljárást addig folytathatjuk, amíg el nem érjünk a j. aldeterminánst, de ott az első oszlop minden értéke zérus. Ebből adódóan a determináns értéke is zérus!
Egy nagyméretű egyenletrendszer megoldása sok számítást igényel. Közben a kerekítési és egyéb hibák csak halmozódnak. Ennek következménye lehet az, hogy egy jól elkészített program is hibás eredményt ad. Ilyen probléma akkor szokott előfordulni, ha az együttható mátrix rosszul kondicionált. A kondíció mérőszáma: , ahol egy mátrix és inverzének normáját szorozzuk össze. Ha nagy a kondíciószám, akkor a számítási hibák jelentős eltérést fognak okozni. Ilyen hiba nemcsak a számítógépek pontatlanságának következménye, hanem – a műszaki életben igen gyakori – méréseknél elkövetett pontatlanságokból is adódhat. Nézzük például a következő egyenletrendszert:
|
|
(7.68) |
Az egyenletrendszer megoldása x=y=1. Ha két értéket kismértékben megváltoztatunk:
|
|
(7.69) |
akkor a megoldások nagymértékben eltérnek az előzőtől: x=0 és y=2. Ennél a példánál szemléletesen is látható az eltérés, hiszen a két egyenletet tekinthetjük egy-egy egyenes egyenletének, a megoldás pedig a metszéspontjuk. Mint az egyenletekből is látszik, az egyenesek meredeksége majdnem megegyezik, azaz a meredekség csekély módosítása is jelentősen elmozdítja a metszéspontot.
Mátrix normából többféle is létezik. A vektorhosszhoz leginkább az un. Euklideszi norma áll közel, melynek definíciója a következő:
|
|
(7.70) |
A kondíciószám meghatározásával, értékelésével kapcsolatban két probléma is felmerül:
Lehet adni más jellegű – bár kevésbé egzakt – definíciót, vagyis rosszul kondicionált az a mátrix, amely közel van az „invertálhatatlansághoz”, azaz a szingularitáshoz. Ha az előző példában az együtthatómátrix egyetlen, nem egész paraméterét kerekítjük (1‰), máris szinguláris (nulla determinánsú) mátrixot kaptunk.
Egyenletrendszer esetében könnyű meggyőződnünk arról, hogy a megoldás megfelelő-e, hiszen csak vissza kell helyettesíteni. Ha megoldás nem megfelelő, akkor próbálkozhatunk ún. főelem-kiválasztással. Részleges főelem-kiválasztás esetén nem az első egyenlettel fogjuk az alatta levők első paraméterét kinullázni, hanem azzal, ahol az első paraméter abszolút értéke maximális, azaz . Ilyenkor a két egyenletet felcseréljük, és folytatjuk az eljárást. Az újabb kinullázások során hasonlóan járunk el.
Teljes főelem-kiválasztás esetén annyiban módosul az eljárás, hogy a teljes maradék mátrixban keressük a legnagyobb abszolút értékű elemet, azaz ha a j. sornál tartunk, akkor . Most nemcsak a sorokat, hanem az oszlopokat is cserélni kell.
Ez annyiban nehezíti a dolgunkat, hogy az ismeretlenek sorrendje is megváltozik. Ekkor egy segédvektort kell létrehozni, amiben nyilvántarthatjuk, hogy melyik ismeretlen most melyik oszlopban található.
Ha a főelem-kiválasztás sem segít, akkor általában iterációs módszerekhez folyamodunk. A lineáris egyenletrendszerek iterációs megoldásának módszereit a 7.3.2. szakasz fejezetben tárgyaljuk.
7.3.1.1. Mátrix invertálás
A klasszikus matematikai módszer nagyon jól használható a mátrixokkal kapcsolatos tételek bizonyítására, de gyakorlatilag használhatatlan számítógépes algoritmusként. Egy 12x12-es mátrix invertálása esetén a tárigény kevéssel nagyobb, mint double (8 bájt helyigényű) számábrázolás esetén. Több különböző numerikus módszer is ismert a mátrix invertálásra, melyek közül most egy olyat tárgyalunk, amely végeredményben nagyon hasonlít a Gauss-eliminációnál megismert algoritmusra.
Az eljárás alapgondolatát nézzük meg egy konkrét példán! Legyen az invertálandó mátrixunk a következő:
|
|
(7.71) |
Szorozzuk meg -t a következő transzformációs mátrixszal:
|
|
(7.72) |
Az eredmény:
|
|
(7.73) |
Tulajdonképpen az első sor -4-szeresét hozzáadtuk a második sorhoz. A transzformációs mátrix valójában egy módosított egységmátrix, amely a Gauss-eliminációnál már ismertetett szorzót tartalmazza abban a pozícióban, ahová nullát szeretnénk kapni. Hasonlóan kaphatunk egy következő mátrixot is és így tovább, mindaddig, amíg a szorzat eredménye egységmátrix nem lesz:
|
|
(7.74) |
A szorzat legyen egyenlő -vel. Azt látjuk, hogy , azaz az egységmátrix. Ez azonban csak úgy lehet, ha . Ha kezdetben felvettünk volna egy az -val azonos dimenziójú egységmátrixot, és sorba megszoroztuk volna a transzformációs mátrixokkal, akkor megkaptuk volna az inverz mátrixot. A szorzások azonban – mint láttuk – tulajdonképpen sorműveletek voltak, éppen úgy, mint a Gauss-eliminációnál. Összefoglalva, az algoritmus főbb lépései az alábbiakban láthatók:
-
hozzunk létre az invertálandó () mátrixszal azonos méretű egységmátrixot,
-
sorozatos sorműveletekkel alakítsuk át az mátrixot felső háromszög mátrixszá, mint a Gauss eliminációnál, és minden sorműveletet végezzünk el az egységmátrixon is,
-
ismételt sorműveletekkel nullázzuk ki a főátló feletti részt is, és tegyünk ugyanígy az egységmátrixszal is,
-
az mátrixban már csak a főátlóban vannak nem nulla értékek, ezért osszuk végig a sorokat a főátló elemeivel (az eredeti egységmátrixban is), így végül megkapjuk ‑ban az egységmátrixot, az eredeti egységmátrix helyén pedig az inverz mátrixot.
Az algoritmust megvalósító Basic nyelvű függvények a következők:
Function Csere(n As Integer, i As Integer, ByRef a() As Double, _ ByRefinv() As Double) As Integer ' sorokat cserél mindkét mátrixban ' n a mátrix dimenziója ' az i. sor alatt kell keresni nem nulla értékeket ' a ebből lesz egység mátrix ' inv ez volt az egységmátrix Dim j As Integer, k As Integer, cs As Double Csere = 1 ' nem sikerült For j = i + 1 To n If a(j, i) <> 0 Then Exit For Next j If a(j, i) = 0 Then Exit Function For k = 1 To n cs = a(i, k) a(i, k) = a(j, k) a(j, k) = cs cs = inv(i, k) inv(i, k) = inv(j, k) inv(j, k) = cs Next k Csere = 0 ' sikerült End Function Function MInverz(n As Integer,a() As Double,ByRef inv() As Double) As Integer ' a mátrix dimenziója ' a az invertálandó mátrix ' inv itt lesz az inverz mátrix Dim i As Integer, j As Integer, k As Integer Dim sz As Double ReDim inv(n, n) For i = 1 To n ' kezdetben egységmátrix inv(i, i) = 1 Next i For i = 1 To n - 1 ' alsó háromszög kinullázása For j = i + 1 To n If a(i, i) = 0 Then err = Csere(n, i, a, inv) If err <> 0 Then Exit Function sz = -a(j, i) / a(i, i) For k = 1 To n a(j, k) = a(j, k) + sz * a(i, k) inv(j, k) = inv(j, k) + sz * inv(i, k) Next k Next j Next i If a(n, n) = 0 Then Exit Function For i = n To 2 Step -1 ' felső háromszög kinullázása For j = i - 1 To 1 Step -1 sz = -a(j, i) / a(i, i) For k = 1 To n a(j, k) = a(j, k) + sz * a(i, k) inv(j, k) = inv(j, k) + sz * inv(i, k) Next k Next j Next i For i = 1 To n ' ettől lenne az egységmátrix sz = a(i, i) For j = 1 To n inv(i, j) = inv(i, j) / sz Next j Next i MInverz = 0 EndFunction
Abban az esetben, ha a mátrix rosszul kondicionált, ugyanazok a lehetőségek állnak rendelkezésünkre, mint a lineáris egyenletrendszer megoldásánál. Az eljárás közben – ha szükségünk van rá – előállíthatjuk a mátrix determinánsának az értékét is. Ezt akkor tehetjük meg, amikor az eredeti mátrixunk főátlója alatt már minden nulla. Ekkor a főátló elemeit összeszorozva megkapjuk a determináns értékét.
7.3.1.2. Független egyenletek kiválogatása - bázisfaktorizáció
A gyakorlatban sokszor előfordul, hogy egy feladat megoldása során felírunk minden egyenletet, amit csak tudunk. Ekkor könnyen előfordulhat, hogy néhány egyenlet összefügg a többivel, tehát azokból előállítható. Szükségünk van tehát egy olyan módszerre, amellyel a „rengeteg” egyenletből egy olyan egyenletrendszert kapunk, amelyben már csak független egyenletek szerepelnek.
Mit is jelent az, hogy egy egyenlet független a többitől? Azt, hogy nem lehet előállítani a többiek lineáris kombinációjaként. Vegyük észre a hasonlóságot a vektorok függetlenségével! Legyenek az egyenletek együtthatói egy n elemű vektor koordinátái, és jelöljük őket v 1, v 2,… v k -val. Ha most például n=k és a v i vektorokkal minden n dimenziós vektor előállítható, akkor v i -k függetlenek és teljes bázist alkotnak. Ha azonban van olyan v j a vektorok között, amely előállítható a következőképpen:
|
, |
(7.75) |
akkor a vektorok összefüggőek, és nem alkotnak bázist. A bázisfaktorizáció célja az, hogy a v 1, v 2,… v k vektorokból olyan w 1, w 2,… w l vektorokat állítson elő, amelyek függetlenek, így bázist alkotnak (általánosan ).
Nézzünk egy konkrét példát! Legyen adva a háromdimenziós térben három vektor: . Ha ezek egy síkba esnek, akkor nem feszítik ki a háromdimenziós teret, azaz nem lehet tetszőleges 3-dimenziós vektort előállítani a segítségükkel. Annak eldöntése, hogy függetlenek-e ránézésre nem mindig egyszerű. Erre szolgál a bázisfaktorizáció.
Az eljárást az előző példán mutatjuk be. Hozzuk létre a sorvektorokként kezelt v 1, v 2, v 3 vektorokból az mátrixot! Végezzük el a felső háromszög mátrixszá alakítást a Gauss‑eliminációnál ismertetett módon:
|
|
(7.76) |
Látható, hogy a harmadik vektor zérussá vált, így a bázisvektorok:
|
|
(7.77) |
Ez a módszer általánosságban is így működik. Eredményként egy trapéz (szerencsés eseten háromszög) alakú elrendezéshez jutunk, amely már megkönnyíti az egyenletrendszer megoldását (7.78).
Természetesen előfordulhat, hogy kevesebb az egyenletünk, mint az ismeretlenek száma. Ekkor vagy fel tudunk még írni kellő számú független egyenletet, vagy marad néhány szabad paraméterünk. Az irodalomban erre a feladatra is – nevezetesen kevesebb az egyenletünk, mint az ismeretlen – sok módszer található, például az ún. projektor mátrixokra építő Purcell-módszer [8.] .
|
|
(7.78) |
7.3.2. Lineáris egyenletrendszer – iteráció
Lineáris egyenletrendszerek megoldására, hacsak lehet, az előzőekben bemutatott közvetlen módszereket használjuk, mert általában sokkal kevesebb számítást igényelnek. Előfordulhat azonban, hogy néha nem alkalmazhatók. Elsősorban akkor van gond, ha az együttható mátrix determinánsa zérus. Szerencsére a mátrixok között az ilyenek rendkívül ritkák, annak esélye, hogy egy tetszőleges (pl. véletlenszám-generátorral előállított) mátrix szinguláris legyen, gyakorlatilag nulla (pl. lottó öttalálatos). Inkább a teljesség igénye miatt írunk röviden az iterációról is.
Mikor alkalmazzuk mégis az iterációt? Ha a nagyméretű együttható mátrix „ritka”, azaz majdnem minden eleme zérus, akkor lehetséges, hogy az iteráció során kevesebbet kell számolnunk, amennyiben kihasználjuk ezt a tulajdonságot. A másik esetről már volt szó, nevezetesen amikor a numerikus pontatlanságok, a rosszul kondicionáltság miatt a megoldás pontossága nem kielégítő.
Tekintsük ismét a klasszikus lineáris egyenletrendszert (7.60)! Ezt még át kell alakítanunk. Írjuk fel az mátrixot két mátrix különbségeként, majd rendezzük a következőképpen:
|
|
(7.79) |
Az iteráció során egy kezdeti közelítő x 0-ból indulunk ki és ezzel a számítás menete a következőképpen alakul:
|
|
(7.80) |
Mikor használható ez a módszer? Természetesen, ha invertálható, és ha normája kisebb, mint egy, azaz:
|
|
(7.81) |
Ez utóbbi visszavezethető a következő feltételre:
|
|
(7.82) |
Ez azt jelenti, hogy az együttható mátrix főátlójában lévő elemek erősen dominálnak, nagyobb abszolút értékűek, mint a sor többi elemének abszolút összege! Az iterációs eljárásoknak léteznek más változatai is (pl. Gauss-Seidel), de a konvergencia feltételekkel ott is baj szokott lenni.
7.3.3. Nemlineáris egyenletrendszerek megoldási módszerei
Ebben az alfejezetben általánosságban foglalkozunk az egyenletrendszerek megoldásával.
7.3.3.1. Egyszerű iteráció
Nemlineáris egyenletrendszereket alapvetően kétféleképpen szokás megadni:
|
|
(7.83) |
|
|
|
(7.84) |
Bármelyiket is ismerjük, a másik egyszerűen előállítható a következő helyettesítéssel:
|
|
(7.85) |
Az iterációs sorozatot (7.84) alakból állíthatjuk elő a szokásos módon:
|
|
(7.86) |
feltéve, hogy az x i vektorok benne maradnak ɸ értelmezési tartományában. A konvergencia feltétele, hogy:
|
. |
(7.87) |
Ha egy kicsit figyelmesebben megnézzük ezt a feltételt, akkor észrevehetünk egy differenciahányados szerű kifejezést is benne. Abban az esetben, ha és folytonosak, az értelmezési tartományon a feltétel így írható fel:
|
|
(7.88) |
ahol
az ún. Jacobi mátrix. Ez már nagymértékben hasonlít az egyváltozós iterációnál megismert konvergencia feltételre. A feltétel eléggé szigorú, azaz sokszor nem elégíti ki az egyenletrendszerünk. Az egyváltozós esetben bemutatott módszer azonban – természetesen átalakítva – itt is alkalmazható. Induljunk ki a (7.83) alakból! Ekkor a részletek mellőzésével, ha x 0 az első közelítés:
|
, |
(7.89) |
és
|
|
(7.90) |
Bár kicsi az esélye, de ha nem állítható elő, mert a mátrix nem invertálható, akkor próbáljunk másik kezdeti értéket választani.
Példaként nézzünk egy feladatot!. Legyen adott a (7.15. ábra) ábrán látható mechanizmus. Szeretnénk megtudni, mi lesz a C csukló pozíciója, amikor B csukló vízszintesen az x=-1, y=0 pontban van. Az adatok: egység.
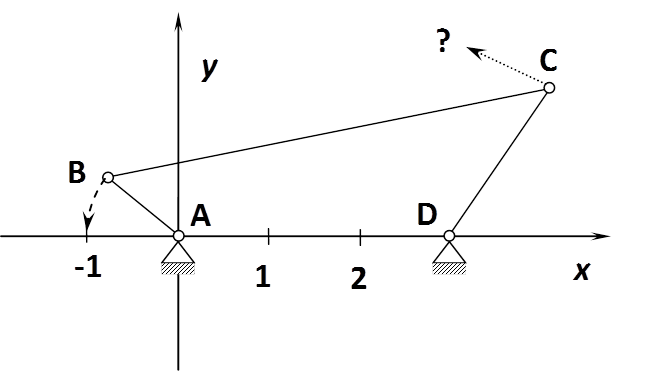
A megoldáshoz két kör metszéspontját kell meghatároznunk, mivel ekkor a C pont egy (-1,0) középpontú, 5 egység sugarú, és egy D középpontú, 2 egység sugarú kör közös pontjában lesz. Az egyenletrendszer tehát a következő:
|
|
(7.91) |
Ennek az egyenletrendszernek viszonylag könnyű előállítani a pontos megoldását, éppen ezért lesz kiváló arra, hogy a módszereket ellenőrizni tudjuk vele. A levezetés mellőzésével a megoldás:
|
|
(7.92) |
Nézzük most a klasszikus iterációt! Ekkor az egyenletrendszer alakja:
|
|
(7.93) |
Kezdeti értéknek válasszuk az x=1 és y=2 kiindulási adatokat. Táblázatkezelőbe behelyettesítve a (Táblázat 7.16) táblázatban látható adatokat kapjuk.
|
x |
fi |
|---|---|
|
1 |
-16 |
|
2 |
6 |
|
-16 |
220 |
|
6 |
399 |
|
220 |
208237 |
|
399 |
206685 |
|
208237 |
8,61E+10 |
|
206685 |
8,61E+10 |
|
8,61E+10 |
|
|
8,61E+10 |
|
|
DIVERGENS |
|
Próbálkozzunk a javított változattal is! Ebben az esetben az
|
|
(7.94) |
alakú egyenletrendszerre van szükségünk. A derivált mátrix pedig az Jacobi mátrix, mely most a következő:
|
|
(7.95) |
Behelyettesítve a kezdőértéket és invertálva a mátrixot:
|
|
(7.96) |
Most már felírhatjuk az iterációs összefüggést:
|
|
(7.97) |
Táblázatkezelő alkalmazásával a (Táblázat 7.17) táblázatban látható eredményeket kapjuk.
|
x |
kivonandó |
|---|---|
|
1 |
-2,625 |
|
2 |
-1,625 |
|
3,625 |
0 |
|
3,625 |
2,382813 |
|
3,625 |
0 |
|
1,242188 |
-0,51659 |
|
3,625 |
0 |
|
1,758774 |
-0,12902 |
|
3,625 |
1,11E-16 |
|
1,899803 |
-3,1E-05 |
|
3,625 |
-2,2E-16 |
|
1,899834 |
-1,5E-06 |
|
3,625 |
-5,6E-17 |
|
1,899835 |
-7,7E-08 |
Az iteráció viszonylag gyors, mert tíz lépés után leállíthattuk. Meg kell azonban jegyezni, hogy nem mindegy, hogy honnan indítjuk a számítást, mert lehet divergens is a sorozat.
7.3.3.2. Az érintőmódszer általánosítása
Az érintőmódszer általánosításához az előző fejezetben bemutatott, javított iterációs módszert kell csak aktualizálni. Az mátrix meghatározása során mindig az aktuális értékeket helyettesítsük be, azaz:
|
|
(7.98) |
Nézzük most meg ennek hatását az előző feladat esetében! A számításokat a Táblázat 7.18 tartalmazza.
|
x |
f' |
f'inverz |
f |
kivonandó |
||
|---|---|---|---|---|---|---|
|
1 |
4 |
4 |
0,125 |
-0,125 |
-17 |
-2,625 |
|
2 |
-4 |
4 |
0,125 |
0,125 |
4 |
-1,625 |
|
3,625 |
9,25 |
7,25 |
0,125 |
-0,125 |
9,53125 |
0 |
|
3,625 |
1,25 |
7,25 |
-0,02155 |
0,159483 |
9,53125 |
1,314655 |
|
3,625 |
9,25 |
4,62069 |
0,125 |
-0,125 |
1,728318 |
-1,1E-16 |
|
2,310345 |
1,25 |
4,62069 |
-0,03382 |
0,250233 |
1,728318 |
0,374039 |
|
3,625 |
9,25 |
3,872612 |
0,125 |
-0,125 |
0,139905 |
-2,2E-16 |
|
1,936306 |
1,25 |
3,872612 |
-0,04035 |
0,298571 |
0,139905 |
0,036127 |
|
3,625 |
9,25 |
3,800358 |
0,125 |
-0,125 |
0,001305 |
0 |
|
1,900179 |
1,25 |
3,800358 |
-0,04111 |
0,304248 |
0,001305 |
0,000343 |
|
3,625 |
9,25 |
3,799671 |
0,125 |
-0,125 |
1,18E-07 |
0 |
|
1,899836 |
1,25 |
3,799671 |
-0,04112 |
0,304303 |
1,18E-07 |
3,1E-08 |
|
3,625 |
9,25 |
3,799671 |
0,125 |
-0,125 |
0 |
0 |
|
1,899836 |
1,25 |
3,799671 |
-0,04112 |
0,304303 |
0 |
0 |
A konvergencia itt – hasonlóan az egyváltozós változathoz – gyors. Annak vizsgálata azonban, hogy az adott esetben a számítások eredményre fognak-e vezetni, azaz az adott paraméterekkel az iteráció konvergens-e, eléggé bonyolult, időigényes, éppen ezért nem is szokták elvégezni. Ehelyett azt figyelik, hogy nem tartanak-e az értékek (elég, ha csak egyikük) végtelenhez.
Mint a 7.98. összefüggésből látható, minden iterációs lépésnél el kell végeznünk egy mátrix invertálását. Ennél valamivel kevesebb számítást igényel, ha az egyenletet megszorozzuk a Jacobi mátrixszal, mert akkor csak egy lineáris egyenletrendszer kell megoldanunk minden lépés során:
|
|
(7.99) |