6. fejezet - Rendszer-identifikáció (mérési adatok alapján)
Egy rendszer matematikai modelljét eddig fizikai megfontolások és kísérletek alapján létrehozott differenciálegyenlettel írtuk le. A differenciálegyenlet a modellek többségénél koncentrált paraméterű egyenletként jelent meg, ami azt jelentette, hogy a fizikai modellnek nem voltak olyan geometriai méretekből adódó paramétermódosító hatásai, amelyek szerepet játszottak volna a differenciálegyenlet együtthatóinak értékében.
A fizikai megfontolások alapján történő rendszer feldarabolás részrendszerekre, és ezen részrendszerek matematikai modelljének létrehozása, majd a részmodellek blokkdiagram- műveletekkel történő összekapcsolása a modellezés általánosan alkalmazott módszere.
Számos esetben a vizsgálandó rendszer szerkezetileg zárt felépítése nem teszi lehetővé, hogy részrendszerekre bontsuk, csak egy egészként vizsgálhatjuk a rendszerünket. A rendszer bementi jeleként tetszőleges időfüggvényt megadhatunk, és ezek hatására megjelenő kimenő jeleket tudjuk érzékelni, de magáról a vizsgált rendszerről, annak belső szerkezetéről nem áll rendelkezésre több információ. Ilyen esetben, amikor a vizsgált rendszerről csak bemeneti és ezekhez a bemenetekhez tartozó kimeneti mérési adatok állnak rendelkezésre a matematikai modell meghatározásához, rendszer-identifikációról beszélünk.
A rendszer-identifikáció segítségével tehát olyan matematikai modellt hozhatunk létre, melynek felépítése ugyanazon bementi és az ehhez tartozó kimeneti jelhez az egyik lehetséges (legjobb) megoldás. Helyesebben ugyanahhoz a bemeneti és kimeneti jelhez több matematikai modellt is létrehozhatunk, amelyek mindegyike meghatározható nagyságú hibaértékkel, de teljesíti a feltételeket.
A rendszer-identifikáció feladata, hogy kiválassza az adott válaszfüggvény előállításához szükséges legegyszerűbb felépítésű differenciálegyenletet. A legegyszerűbb felépítés az időváltozós, állandó együtthatós differenciálegyenletnél olyan alak, amelyben a bemenetek és kimenetek deriváltjainak fokszámai (a rendszer minden feladatrészének teljesítése mellett) minimális értékek. Ez egyben azt is jelenti, hogy megtörténik a feladat megoldásához szükséges minimális számú paraméter - differenciálegyenlet együttható – meghatározása.
Ha ideális esetben sikerülne a pontos differenciálegyenlet-struktúrát meghatároznunk, és ezt túlbecsülnénk, azaz a szükséges differenciálegyenlet fokszámoknál magasabb értékeket vennénk fel, akkor azok az együtthatók, amelyek a magasabb fokszámhoz tartoznak közelítően nullaértékűek, mivel nem vesznek részt a kimenő jel létrehozásában.
Az identifikációnál tehát meghatározó a vizsgált időváltozós differenciálegyenlet-struktúra fokszámainak helyes vagy közelítően helyes becslése. A magasabb fokszámú első becslés alapvetően nem jelent problémát, ezt sokkal több számítás követi, ha szükséges fokszámokat alábecsüljük, és ezekkel keressük a megoldást - általában siker nélkül vagy nagyon rossz jel azonossággal érünk célba.
6.1. Rendszerstruktúra-becslés
A vizsgált rendszer matematikai modelljének helyes felépítéséhez a bemeneti és az erre válaszként kapott kimeneti jel grafikus megjelenítését kell megvizsgálnunk és az ebből levont következtetések alapján rendszerstruktúra javaslatot hozhatunk létre.
Általában a rendszert vizsgáló bementi jelként egységugrás bemenetet alkalmazunk, amely arányos típusú rendszereknél a kiindulási állapotból az egységugrás jel hatására létrejövő új állapotba viszi át a rendszert. Ha a rendszer stabil, akkor egy korábbi állandósult állapotból a bemenő jel hatására létrejövő újabb állandósult állapotba kerül.
A rendszerstruktúra-becslés szempontjából számunkra a kimeneti jel egyik állapotból másik állapotba történő átmenetének időtartama alatt lejátszódó jelenségek – az úgynevezett tranziens viselkedés - a meghatározó. Ebből tudunk következtetést levonni a vizsgált rendszer (alapvető) típusára, illetve pólusainak elhelyezkedésére.
Az átmeneti függvényből megállapítható, hogy a vizsgált rendszer arányos, integráló vagy differenciáló típusú. Erre mutatunk be a következőken néhány példát.
A példák elsősorban azt a célt szolgálják, hogy a segítségükkel megállapíthassuk, hogy egységugrás bemenő jel és ehhez tartozó kimeneti jel esetén milyen átviteli függvény típussal próbálkozhatunk, hogy sikeres identifikációt valósítsunk meg.
Ezek a mintapéldák a legegyszerűbb eseteket mutatják be, ezektől jelentősen eltérő kimenő jelalak vagy nem egységugrás bemenő jel esetén a modellezőnek saját belátása szerint kell felvennie az identifikált rendszer struktúráját. Ez nagyon nagy tapasztalatot igénylő feladat, amely sok intuíciót is tartalmaz.
A következő alfejezetekben az alapvető átviteli függvénytípusok esetén mutatjuk be az egységugrásra adott válaszokat, és megadjuk azt is, hogy milyen átviteli függvényt ábrázoltunk. Ezzel szeretnénk elősegíteni, hogy adott átviteli függvényhez tartozó jelalak és annak időbeni lefutása mintaként szolgáljon a jelalak azonosításához és a sikeres struktúra kiválasztáshoz. Más paraméterértékekkel pedig a vizsgálandó jelalakhoz legközelebb eső jelalakot tudjuk előállítani.
A holtidőt tartalmazó tag átmeneti függvényéből le kell választani a holtidő okozta jelkésleltetést, és csak a késleltetés nélküli jelet kell identifikálni. A kimeneti jelkésleltetésből - lineáris rendszer esetén - egyértelműen meghatározható a jelkésleltető tag időkésleltetési paramétere (TH=holtidő).
6.1.1. Arányos típusú tagok átmeneti függvényei
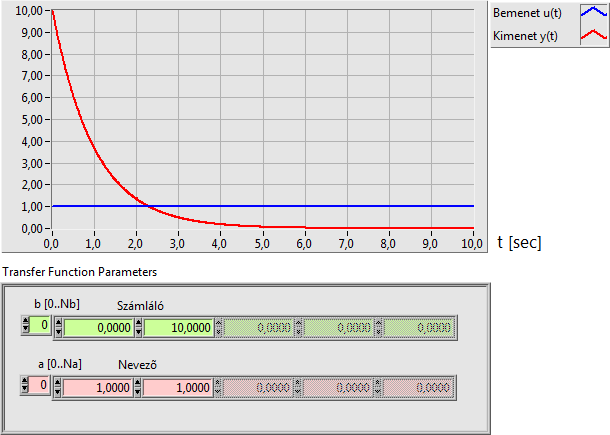
Az arányos vagy P típusú (proporcionális) rendszer tulajdonsága, hogy az egységugrás bemenő jelre arányos erősítésének megfelelő kimenő jellel válaszol. A tranziens állapotot az határozza meg, hogy hány darab nevezőbeli valós vagy konjugált komplex pólussal rendelkezik. A kimeneti jel a bementi egységugráshoz képest egy késleltetést szenvedhet, amelynek időtartamát leolvashatjuk a kimenő jel diagramjáról.
A arányos tagok jellemzője, hogy egy állandósult értékből az egységugrás bemenő jel hatására egy újabb állandósult állapotba (értékre) mennek át a tranziens állapot lezajlása után.
A PT1 egytárolós arányos tag átviteli függvénye:
|
|
(6.1) |
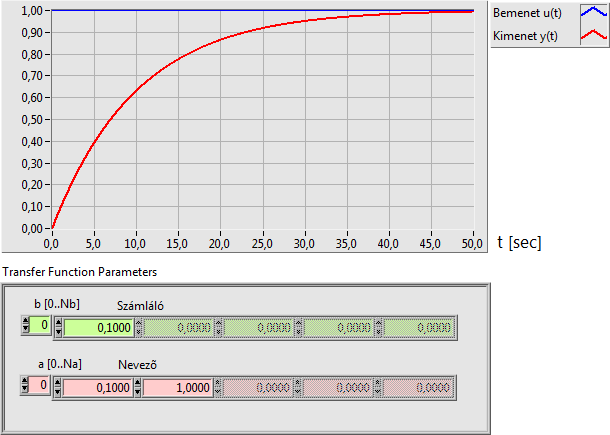
A PT2 kéttárolós arányos tag átviteli függvénye (két valós pólus esetén):
|
|
(6.2) |
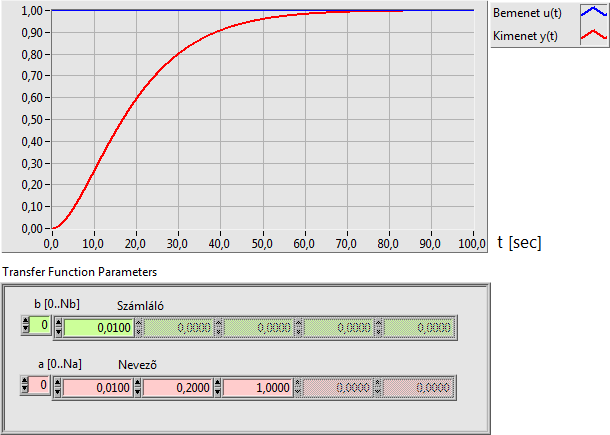
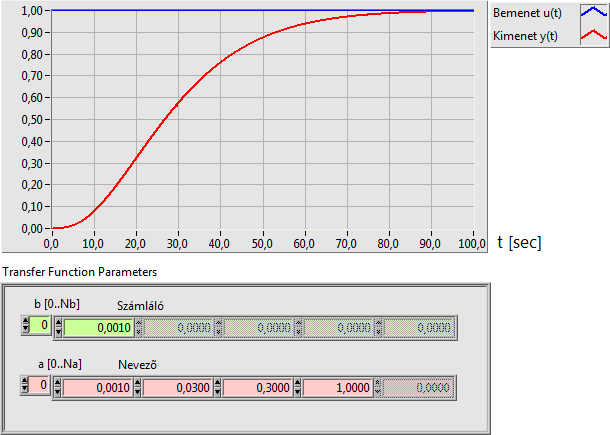
A PT3 háromtárolós arányos tag átviteli függvénye (három valós pólus esetén):
|
|
(6.3) |
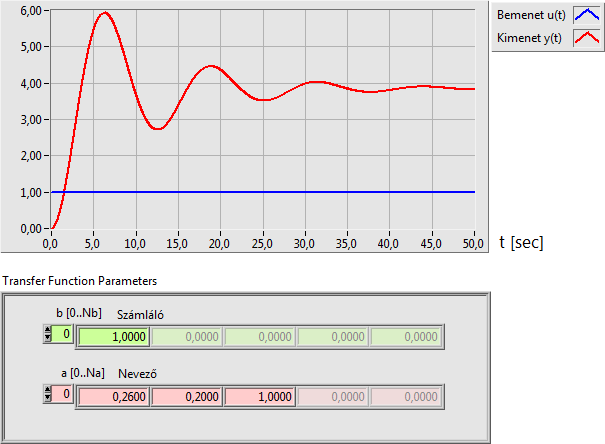
A PT2 kéttárolós arányos tag átviteli függvénye (két konjugált komplex pólus esetén):
|
|
(6.4) |
A PT1 egytárolós holtidős arányos tag átviteli függvénye:
|
|
(6.5) |
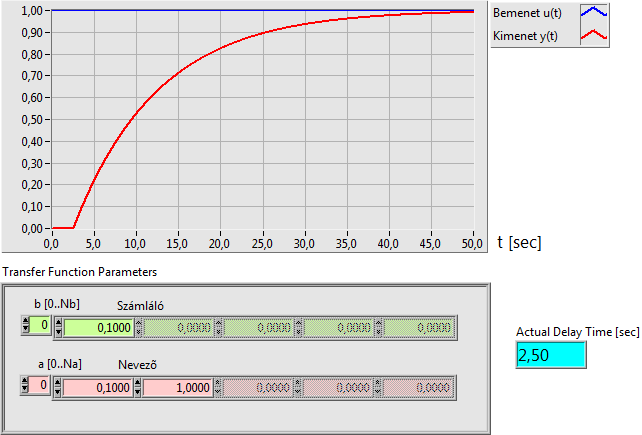
6.1.2. Integráló típusú tagok átmeneti függvényei
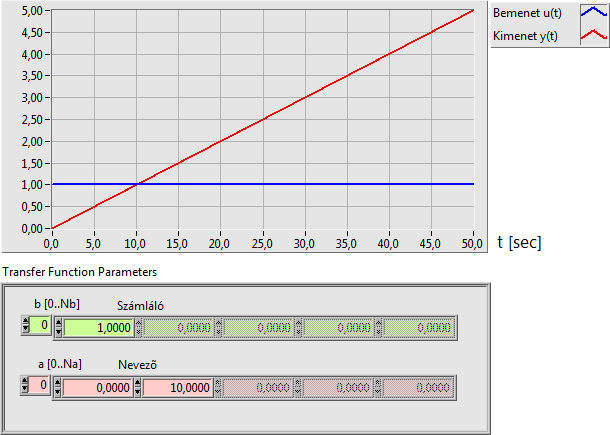
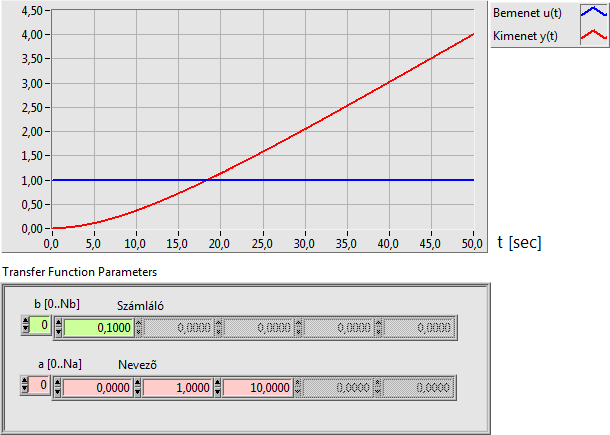
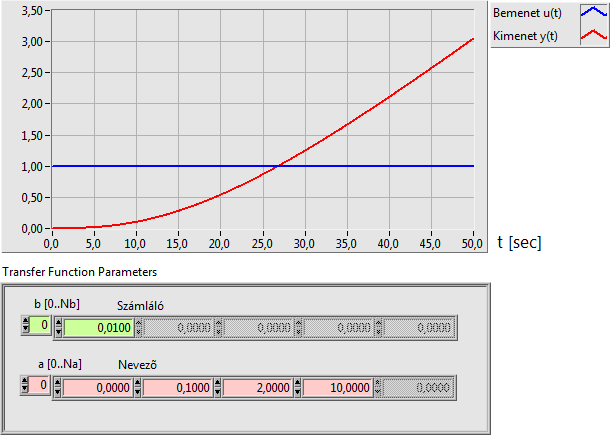
Az integráló vagy I típusú (integráló) rendszer tulajdonsága, hogy az egységugrás bemenő jelre integrálási erősítésének megfelelő meredekségű kimenő jellel válaszol. A tranziens állapotot az határozza meg, hogy hány darab nevezőbeli valós vagy konjugált komplex pólussal rendelkezik. A kimeneti jel ilyenkor egy időkésleltetést szenved a nevezőbeli pólus nélküli kimeneti jelalakhoz képest, amelynek időtartama meghatározható.
Az I integráló tag átviteli függvénye:
|
|
(6.6) |
Az IT1 integráló egytárolós tag átviteli függvénye (egy valós pólus esetén):
|
|
(6.7) |
Az IT2 integráló kéttárolós tag átviteli függvénye (két valós pólus esetén):
|
|
(6.8) |
Az IT3 integráló háromtárolós tag átviteli függvénye (három valós pólus esetén):
|
|
(6.9) |
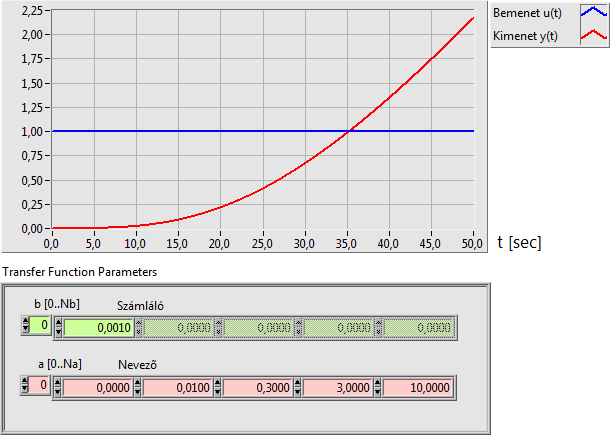
Az IT2 integráló kéttárolós tag átviteli függvénye (két konjugált komplex pólus esetén):
|
|
(6.10) |
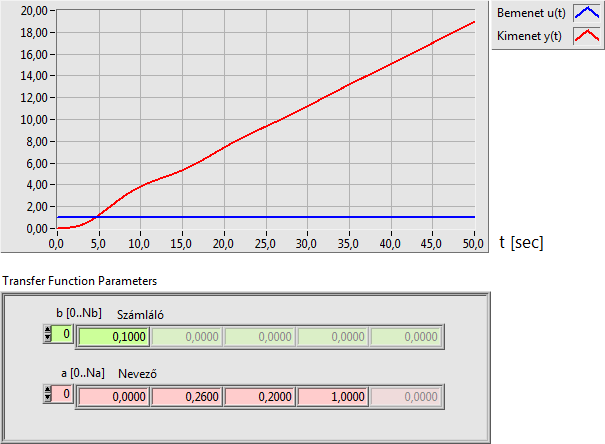
Az IT1 integráló egytárolós holtidős tag átviteli függvénye:
|
|
(6.11) |
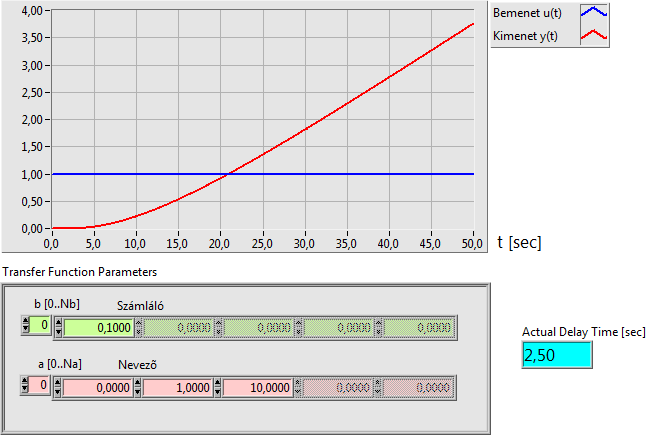
6.1.3. Differenciáló-tárolós típusú tagok átmeneti függvényei
Mivel ideális differenciáló tag (nevezőbeli pólussal nem rendelkező deriváló tag) nem valósítható meg a differenciáló tagok tárolós változataival foglalkozunk. A differenciáló-tárolós vagy DT típusú (differenciáló-tárolós) rendszer tulajdonsága, hogy az egységugrás bemenő jelre differenciálási és tároló tulajdonsága hányadosának megfelelő kezdő amplitúdójú kimenő jellel válaszol. A tranziens állapotot az határozza meg, hogy hány darab nevezőbeli valós vagy konjugált komplex pólussal rendelkezik.
DT1 differenciáló egytárolós tag átviteli függvénye (egy valós pólus esetén):
|
|
(6.12) |
A DT2 differenciáló kéttárolós tag átviteli függvénye (két valós pólus esetén):
|
|
(6.13) |
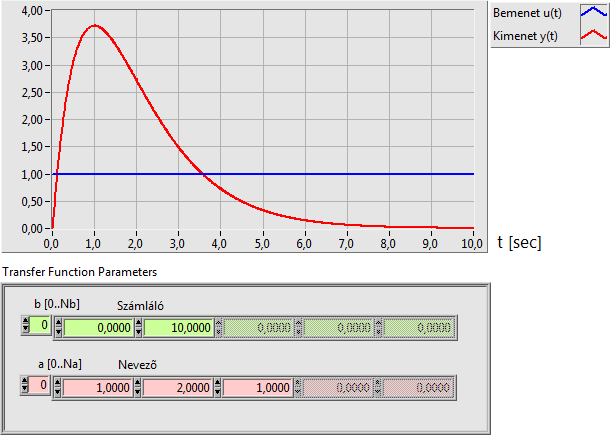
A kimeneti jel a bementi egységugráshoz képest egy késleltetést szenvedhet, amelynek időtartamát leolvashatjuk a kimenő jel diagramjáról.
A DT3 differenciáló háromtárolós tag átviteli függvénye (három valós pólus esetén):
|
|
(6.14) |
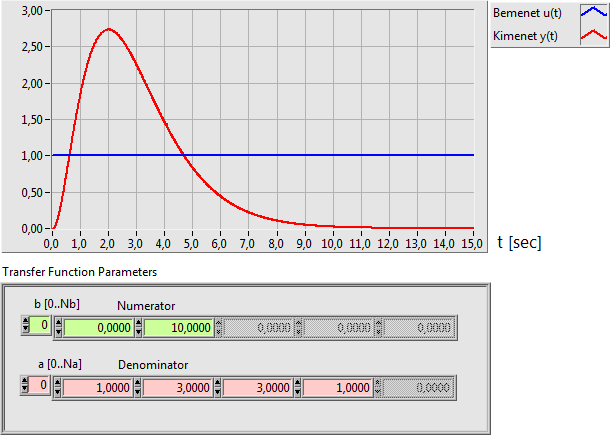
A DT2 differenciáló kéttárolós tag átviteli függvénye (két konjugált komplex pólus esetén):
|
|
(6.15) |
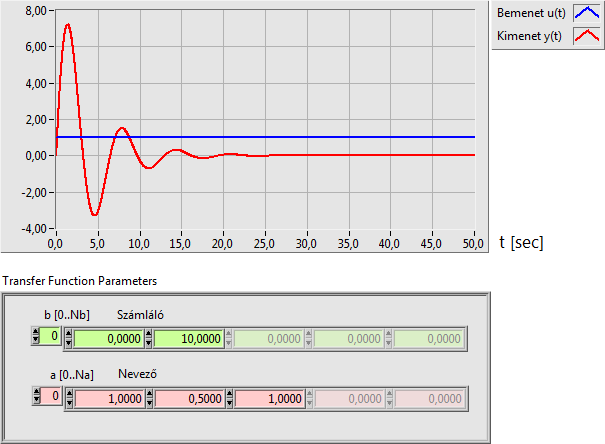
A DT1 differenciáló egytárolós holtidős tag átviteli függvénye:
|
|
(6.16) |
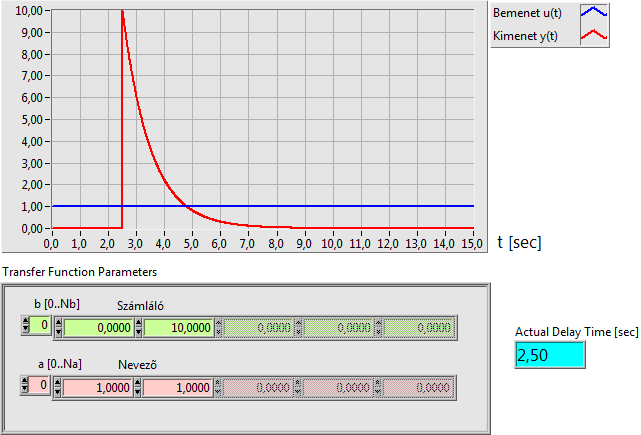
6.1.4. Identifikáció nem egységugrás bemeneti vizsgáló jel esetén
A korábbi fejezetekben bemutattuk, hogy melyek azok a jelalak típusok, amelyek a leggyakrabban várhatók az alaptagok vizsgálatánál. Gyakran előfordul azonban, hogy az identifikációt nem ilyen, matematikailag egyértelműen leírható, bemenő jel segítségével kell elvégeznünk, hanem bemenő jelként más (matematikailag) leírható függvény szerepel, vagy nem is tudjuk matematikailag leírni a bementi jel alakját, csak mérési adatokból dolgozhatunk.
Ilyen esetben csak meghatározott időpillanatokban áll rendelkezésünkre a bemenő jel értéke mérési eredményként, illetve ugyanezen időpillanatban a kimeneti jel értéke is.
Matematikai úton adott időpillanatokban rendelkezésre álló, időben diszkrét adatokból számos eljárás segítségével meghatározható az identifikálandó rendszer struktúrája és paraméterei. Ezen eljárások közül mutatja be az egyiket a következő fejezet.
6.2. A rendszerparaméter becslése (időtartománybeli) mérési adatok alapján
A következő paraméterbecslési eljárás tetszőleges bemeneti és kimeneti jelalak mellett alkalmazható.
Az eljárás sikeres működéséhez a következő adatoknak kell rendelkezésre állnia:
-
mintavételi időpontok értékei,
-
a identifikálandó rendszer bemeneti jelének értékei a mintavételi időpontokban,
-
a identifikálandó rendszer kimeneti jelének értékei a mintavételi időpontokban,
-
az identifikálandó rendszer struktúrájának pataméterei:
-
a differenciálegyenlet kimenő jeleinek legmagasabb derivált fokszáma,
-
a differenciálegyenlet bemenő jeleinek legmagasabb derivált fokszáma.
-
A differenciálegyenlet együtthatóinak paraméterbecslési eljárása a következő:
-
Tetszőleges szimulációs környezetben létre kell hoznunk az identifikálandó rendszer struktúrájának paramétereivel egy időváltozós differenciálegyenlet modelljét.
A differenciálegyenlet általános alakja:
(6.17)
ahol
F
a differenciálegyenlet együtthatóinak függvénye,
y (0) (t)
a rendszer kimenő jele,
y (k) (t)
a rendszer kimenő jelének idő szerinti k. deriváltja; k = 0..n,
u (0) (t)
a rendszer bemenő jele,
u (k) (t)
a rendszer bemenő jelének idő szerinti k. deriváltja; k = 0..m,
t
az időváltozó.
A következő alakban keressük a differenciálegyenletet:
(6.18)
ahol
a 0 (t)..a n (t)
a differenciálegyenlet kimenő jelének és deriváltjainak együtthatói,
b 0 (t)..b m (t)
a differenciálegyenlet bemenő jelének és deriváltjainak együtthatói,
y(t)
a rendszer kimenő jele,
u(t)
a rendszer bemenő jele,
t
az időváltozó.
-
Meg kell határoznunk a differenciálegyenlet kimeneti és bementi jelének valamint deriváltjaik együtthatóinak várható minimális és maximális értékét.
Ezek az értékek lesznek a genetikus algoritmusban a paraméter-keresés határai. (Ha nem tudunk pontos értéket megállapítani a minimális vagy maximális értékre, vegyünk fel nagy abszolút értékű kezdeti értékeket!)
(a i_min - a i_max ),
i = 0..n
(b j_min - b j_max ),
j = 0..m
-
Egy genetikus algoritmus populációjának minden eleméhez paraméterekként definiáljuk a differenciálegyenlet keresett együtthatóit!
-
A mintavételi időpontokban határozzuk meg a bemenő jel értékeivel és a genetikus algoritmussal kiválasztott populáció-elem paramétereivel a kimeneti jelet (yidentifikált[k.h])! Az eljárást végezzük el a genetikus algoritmus populációjának minden elemére!
-
A genetikus algoritmus populációjának elemeire jósági (fitness) függvényeként határozzuk meg a következő funkcionált (6.17. ábra, (6.17))!
(6.19)
![Az ymért[k.h] - yidentifikált[k.h] funkcionál elemei](images/image_VI_17.png) 6.17. ábra - Az ymért[k.h] - yidentifikált[k.h] funkcionál elemei
6.17. ábra - Az ymért[k.h] - yidentifikált[k.h] funkcionál elemei
Az Fi jósági (fitness) értékekből meg kell határozni a minimális jósági értékhez tartozó elemet genetikus algoritmus segítségével. Ha adott pontossággal minimalizáltuk a funkcionál értékét, a mért értékek és az identifikált értékek különbségeinek abszolút értékei minden mérési pontban minimális értékűek, és az összegük is minimális lesz.
-
Eredményként megkapjuk a populáció azon elemét, amelynél a jósági (fitness) érték minimális. Ennek az elemnek a genetikus algoritmus paraméterei – a differenciálegyenlet együtthatói – lesznek azok az értékek, amelyekkel ugyanazon bemenő jelértékek mellett a kimenő jelhez legjobban hasonlító kimenő jelet kapjuk. Ennél az elemnél valósul meg, hogy a mért kimeneti jel legjobban hasonlít az adott differenciálegyenlet paraméterekkel kiszámított kimeneti jeléhez.
6.3. Rendszerparaméter becslése mintapélda
A paraméterbecslés bemutatásához mérjük le, és adjuk meg adatfájlban egy PT3 háromtárolós arányos tag átmeneti függvényét, amelynek átviteli függvénye a következő:
|
|
(6.20) |
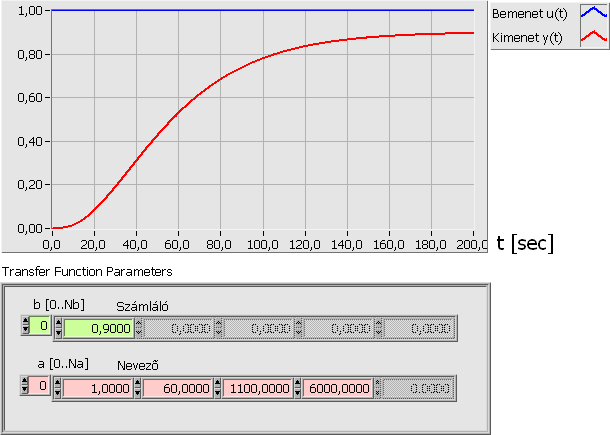
A feladat megoldásához alkalmazott genetikus algoritmus programban a génparaméterek a következő átviteli függvény paramétereket jelölik a 6.20 képletből:
|
Genes [0] = T1 időállandó |
(T1min=0,1 s |
T1max=100 s), |
|
Genes [1] = T2 időállandó |
(T2min=0,1 s |
T2max=100 s), |
|
Genes [2] = T3 időállandó |
(T3min=0,1 s |
T3max=100 s), |
|
Genes [3] = A erősítés |
(Amin=0,01 |
Amax=10 ). |
A megadott génparaméter-kiosztással a genetikus algoritmus program futtatása után az eredmény a következő ábrán (6.19. ábra) látható.
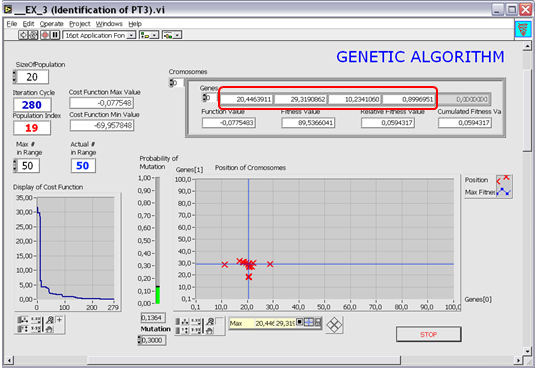
Az algoritmus a kiindulási értékként magadott populációszámot exponenciálisan csökkenti a az iterációk során a megadott minimális értékig. A továbbiakban ezzel a minimális számú, de eddig legjobb tulajdonságúnak ítélt egyeddel folytatja a paraméter-keresést.
A költségfüggvény értékét az egyes iterációknál szintén megtekinthetjük a Display of Cost Function diagramon.
A következő ábrán (6.20. ábra) a költségfüggvényt (Cost Function) meghatározó alprogram futási eredményeit láthatjuk. A hibaértékek összege (Summa of Errors) kis abszolút értékű negatív szám. Mivel a genetikus algoritmussal maximális értéket határozunk meg, ezért a 6.19 képlettel kiszámított hibaértékek összege függvényt megszoroztuk mínusz 1-el, hogy így továbbra is - a maximum érték keresésével - a negatív értékek minimumát határozza meg az algoritmus.
A paraméterbecslés költségfüggvényének eredménye a következő ábrán (6.20. ábra) látható.
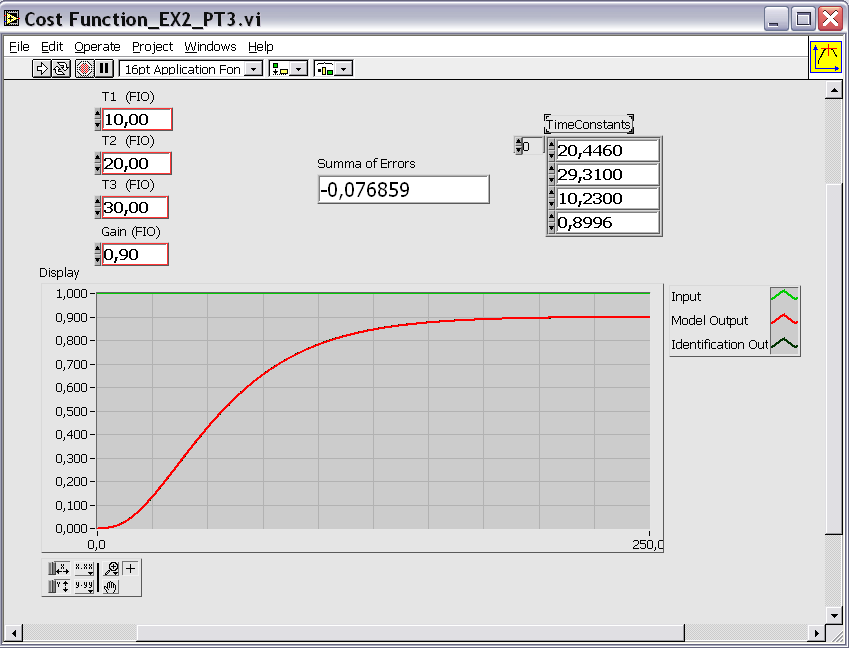
A genetikus algoritmus leállítási feltétele, hogy a futtatás során megadott számú esetben (Max # in range) az algoritmus már ne változtasson a legjobbnak ítélt paraméterértékeken.