5. fejezet - Optimum kereső módszerek
- 5.1. Az optimalizáló eljárások általános jellemzői
-
- 5.1.1. Az optimalizáló eljárások típusai
-
- 5.1.1.1. Determinisztikus vagy sztochasztikus problémát megoldó eljárások
- 5.1.1.2. Kísérletező vagy matematikai eljárások
- 5.1.1.3. Statikus vagy dinamikus eljárások
- 5.1.1.4. Direkt (numerikus) vagy indirekt (analitikus) módszerek
- 5.1.1.5. Paraméter- vagy függvény-optimalizáló eljárások
- 5.1.1.6. Korlátozott vagy korlátozás nélküli optimalizáló eljárások
- 5.1.2. Hegymászó stratégiák
- 5.1.3. Többdimenziós stratégiák
- 5.1.4. Gradiens stratégiák
- 5.1.5. Random (véletlenszerű) stratégiák
- 5.1.6. Evolúciós módszerek
-
- 5.1.6.1. Szimulált hőkezelés
- 5.1.6.2. Evolúciós algoritmusok (EA)
-
- 5.1.6.2.1. Evolúciós stratégiák (ES=Evolution Strategies)
- 5.1.6.2.2. Az egyszerű Evolúciós Stratégia
- 5.1.6.2.3. Az evolúciós stratégiák típusai
- 5.1.6.2.4. Egymásba ágyazott evolúciós stratégiák
- 5.1.6.2.5. Genetikus algoritmusok (GA)
- 5.1.6.2.6. Evolúciós programozás (EP)
- 5.1.6.2.7. Genetikus programozás (GP)
- 5.2. Genetikus algoritmusok
-
- 5.2.1. Genetikai alapok
- 5.2.2. A genetikus algoritmus
- 5.2.3. A genetikus algoritmusok működési mechanizmusa
- 5.2.4. A genetikus algoritmusok típusai
-
- 5.2.4.1. A gének ábrázolása
- 5.2.4.2. Fitness számítás
- 5.2.4.3. Szelekció
- 5.2.4.4. Kereső operátorok
-
- 5.2.4.4.1. Mutáció
- 5.2.4.4.2. Mutáció bináris ábrázolás esetén
- 5.2.4.4.3. A valós ábrázolás mutációs operátorai
- 5.2.4.4.4. Mutációs operátorok permutációs ábrázolásmód esetén
- 5.2.4.4.5. Rekombináció
- 5.2.4.4.6. Bináris keresztezés
-
- 5.2.4.4.6.1. Egypontos keresztezés:
- 5.2.4.4.6.2. K-pontos keresztezés:
- 5.2.4.4.6.3. Egyenletes keresztezés (uniform crossover):
- 5.2.4.4.6.4. A valós ábrázolásmódnál alkalmazott keresztezési módszerek
- 5.2.4.4.6.5. Heurisztikus keresztezés (WRIGHT 1994)
- 5.2.4.4.6.6. Szimplex keresztezés (RENDERS és BERSINI 1994)
- 5.2.4.4.6.7. Geometriai keresztezés (MICHALEWITZ 1996)
- 5.2.4.4.7. A permutációs ábrázolásmód keresztező eljárásai
- 5.2.4.5. Korlátkezelési technikák
- 5.2.5. A populáció szerkezete
- 5.3. A genetikus algoritmusok speciális területei
- 5.4. A genetikus algoritmusok előnyei és hátrányai
- 5.5. A genetikus algoritmus alkalmazásának területei
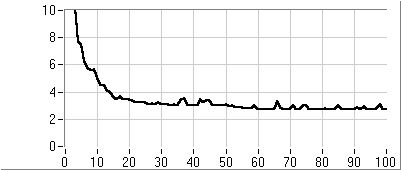
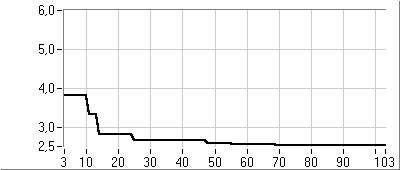
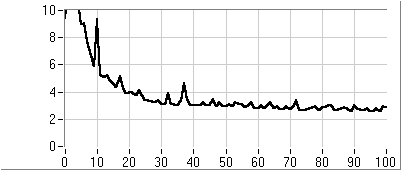
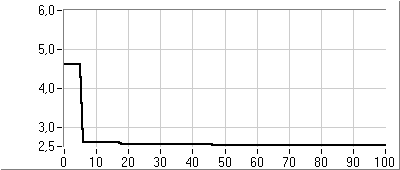
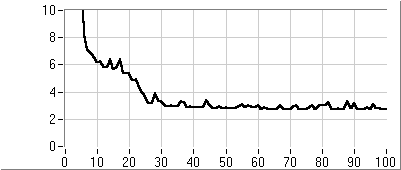
- 5.6. PI kompenzáció paraméter optimalizálása genetikus algoritmussal
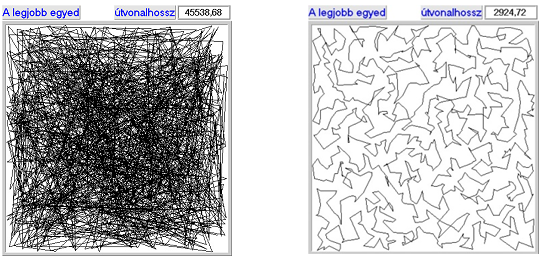
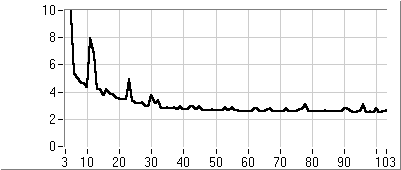
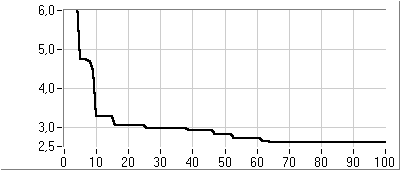
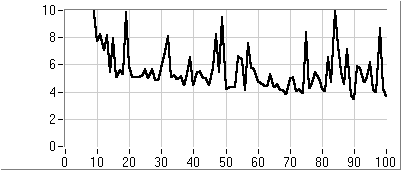
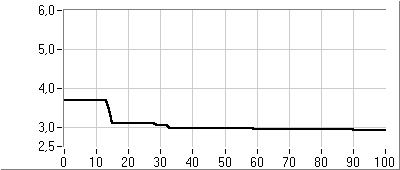
- 5.7. Az utazó ügynök probléma megoldása genetikus algoritmussal
Ha egy feladatot csak egyféleképpen tudunk végrehajtani, akkor nincs lehetőségünk az optimalizálásra. Ha nem tudjuk, hogy megoldható-e a feladat, akkor a további kutatás és a megoldás megtalálása lehet a célunk. Ha azonban két vagy több megoldás áll rendelkezésünkre, és választanunk kell közülük valamilyen előírt szempont szerint, akkor már optimalizálási feladatról beszélünk.
5.1. Az optimalizáló eljárások általános jellemzői
Az optimalizálási feladatoknál azokat a független tulajdonságokat, melyek megkülönböztetik egymástól az egyes megoldásokat, paramétereknek nevezzük. Ahhoz, hogy a megoldási lehetőségek között dönteni tudjunk, szükségünk van egy mennyiségi változóra, ezt a függő változót célfüggvénynek nevezzük.
Különböző célfüggvényekhez különböző optimális rendszerparaméter-értékek tartoznak. Más megfogalmazásban, a rendszer optimális működése mindig egy célfüggvény szerinti optimalizálás eredményeként születik meg. Ha például a rendszer leggyorsabb működését szeretnénk elérni, akkor a célfüggvénynek nem szabad foglalkoznia a feladat megoldásához szükséges energia felhasználásával. Ha viszont a rendszer gazdaságos működésére optimalizálunk, akkor kompromisszumot kell kötnünk a működési sebesség csökkentésével, hogy a felhasznált energia (a lehetőségeket figyelembe véve) a legkisebb legyen.
Az optimum vagy optimális megoldás a paraméterek azon értékeinél jelentkezik, ahol a célfüggvény minimális vagy maximális értéket vesz fel, a probléma típusától függően.
Gyakran a legnehezebb feladat egy „jó” célfüggvény meghatározása, a másik probléma pedig a keresés stratégiájának kiválasztása. Még akkor is nehéz maradhat az optimum megtalálása ha a célfüggvény matematikailag pontosan meghatározott, mert a számítások elvégzéséhez korlátozott idő áll rendelkezésünkre.
5.1.1. Az optimalizáló eljárások típusai
5.1.1.1. Determinisztikus vagy sztochasztikus problémát megoldó eljárások
-
Determinisztikus esetben az optimalizálandó rendszer nem tartalmaz ismeretlen vagy véletlenszerű elemeket.
-
Ha a rendszerben az események véletlenszerűen, de valamilyen törvényszerűséggel leírható formában következnek be (és nem lehet kiküszöbölni a véletlenszerűséget), akkor a problémát sztochasztikusnak nevezzük. Ez azt jelenti, hogy a rendszerben véletlen tényezők is vannak.
5.1.1.2. Kísérletező vagy matematikai eljárások
-
A kísérletező eljárásokat olyan esetekben használjuk, amikor nem ismert a célfüggvény, ezért a valós tárgyon vagy annak modelljén kell kísérleteznünk. A szisztematikus keresés több változó esetén nagyon költséges, a véletlenszerű pedig megbízhatatlan, ezért az algoritmusnak a két módszert ötvözve, szisztematikusan kell hasznosítania az előző kísérletekből származó információkat.
-
A matematikai eljárások a rendszer matematikai modelljén végzik az optimalizálást úgy, hogy a következő lépést az előző lépések eredményeinek segítségével határozzák meg.
5.1.1.3. Statikus vagy dinamikus eljárások
-
A statikus módszerek esetében az optimum az időtől független.
-
A dinamikus optimalizálás feladata egy adott célfüggvény szerinti optimális állapot fenntartása a változó körülmények között. Így az optimalizáló algoritmusnak folyamatosan működnie kell.
5.1.1.4. Direkt (numerikus) vagy indirekt (analitikus) módszerek
-
Direkt eljárásoknak nevezzük azokat a módszereket, melyek az optimumot lépések sorozatán át úgy érik el, hogy a célfüggvény értékét lépésről-lépésre javítják.
-
Az indirekt esetben az eljárás a célfüggvény szerinti optimális megoldást, tesztek és próbálkozások nélkül, egy lépésben határozza meg, például a célfüggvény adott paraméter szerinti változásának (deriváltjának) segítségével.
5.1.1.5. Paraméter- vagy függvény-optimalizáló eljárások
-
Paraméter-optimalizálónak nevezzük az eljárást akkor, ha a célfüggvény és a független paraméterek is skaláris mennyiségek.
-
A függvény-optimalizáló eljárásnál a meghatározandó változók maguk is paraméterek függvényei, ezért a célfüggvény értéke is függvény.
5.1.1.6. Korlátozott vagy korlátozás nélküli optimalizáló eljárások
-
Korlátokat akkor használunk, ha azt akarjuk, hogy az eljárás az optimumot csak egy meghatározott intervallumban keresse, ennek oka lehet például az, hogy a célfüggvény értéke egyes helyeken nem határozható meg, és ezeket a pontokat el akarjuk kerülni. A korlátok egyik fajtája a büntetőfüggvény, ez a módszer a büntetett esemény bekövetkezésekor a célfüggvény értékét úgy módosítja, hogy az kedvezőtlenebb esetet jelentsen.
5.1.2. Hegymászó stratégiák
A hegymászó stratégiák olyan matematikai módszerek, amelyek nem diszkrét, nem sztochasztikus, és többnyire korlátozó feltételek nélküli függvények optimumkeresésére alkalmasak. Nevüket onnan kapták, hogy egy bekötött szemű hegymászóhoz hasonlóan, tapogatva keresik az utat a völgyből a csúcs felé. A hegymászó stratégiák az alkalmazott algoritmus következtében nem mindig képesek megtalálni a globális szélsőértéket, a legközelebbi lokális szélsőértékhez konvergálnak.
A hegymászó stratégiákat a mérnöki gyakorlatban azokban az esetekben alkalmazzák, ahol az analitikus módszerek nem használhatók:
-
A célfüggvény és deriváltjai nem folytonosak.
-
Nehézségek adódnak a differenciálok meghatározásakor.
-
Az egyenletek megoldása nem vezet mindig a globális szélsőértékhez.
-
A rendszert általánosan leíró, nemlineáris egyenletek, nem oldhatók meg közvetlenül.
Az optimalizálási feladatot, minimumkeresésként megfogalmazva, a következő egyenlet segítségével írhatjuk le:
|
|
(5.1) |
ahol
|
|
|
a célfüggvény, |
|
a paramétervektor, |
||
|
a szélsőérték, |
||
|
a paramétervektor az optimális esetben. |
5.1.2.1. Egydimenziós stratégiák
Egydimenziós esetben a célfüggvény csak egy paramétertől függ, ami az optimumkeresés legegyszerűbb esete. A többdimenziós stratégiák gyakran ezeket az egyszerű eljárásokat alkalmazzák a különböző paraméterirányokban.
5.1.2.1.1. Szimultán módszerek
A szimultán eljárásoknál egyszerre több ponton vizsgáljuk a célfüggvény értékét, melyekben a számítások párhuzamosan végezhetők. Azt, hogy a célfüggvény szélsőértéke milyen távol esik a vizsgált pontoktól, a pontok száma és helyzete határozza meg.
5.1.2.1.2. Egyenlő távolságú keresés
Az [a,b] intervallumban, egymástól egyenlő távolságra, N darab pontot veszünk fel. Az N megválasztásánál vigyázni kell arra, hogy elegendően nagyszámú pontot vegyünk fel ahhoz, hogy a minták használható pontossággal adják vissza a célfüggvény alakját.
A felvett pontoknál kiszámoljuk a célfüggvény értékeket, és a minimális (maximális) célfüggvény értékű pontot tekintjük optimumnak.
Ebben az esetben a bizonytalansági tartomány mérete (a paraméter pontossága):
|
|
(5.2) |
5.1.2.1.3. Sorrendi módszerek
Ha a próbákat egymás után végezzük, akkor lehetőségünk van a közbenső eredményeket felhasználni a következő próba helyének meghatározása során. A legtöbb sorrendi módszer csak akkor képes a célfüggvény globális szélsőértékét megtalálni, ha a vizsgálatot annak közelében kezdjük, egyébként a keresés lokális szélsőértéket is eredményezhet. Ha a célfüggvény egyetlen minimummal, (maximummal) rendelkezik, akkor ezzel a problémával nem kell számolnunk.
5.1.2.2. A minimum bekerítése (Boxing in the Minimum)
Az eljárás az pontból kiindulva, s lépésközzel haladva (), sorra meghatározza a célfüggvény értékeket. A megfelelő irány kiválasztásához az első lépés után megvizsgálja a függvényértéket, ha , akkor az ellenkező irányban megy tovább ().
Az iteráció befejezésének feltétele: a célfüggvény-érték növekedése, .
Az algoritmus sebességének növelése érdekében a lépésköz változtatásának többféle módszerét dolgozták ki:
-
BEVERIDGE és SCHECHTER (1970) algoritmusa minden esetben, amíg , a lépés nagyságát kétszeresére növeli:, így éri el, hogy a jó irányban egyre gyorsabban haladjon.
-
ROSENBROCK és BERMAN (1960) eljárása minden sikertelen keresés esetén, egy állandóval szorozva, csökkenti a lépés nagyságát, így az optimum közelében lelassít.
-
DIXON (1972) kombinálta a két előző módszert, a lépésközt siker esetén növelte, sikertelenség esetén pedig csökkentette, így az előzőeknél is gyorsabb eljárást kapott.
5.1.2.2.1. Tartományosztó módszerek
Ezek a módszerek a kezdeti keresési tartományt minden lépésben úgy csökkentik, hogy résztartományokra osztják azt, és ezek közül kiválasztva az egyiket, erre ismétlik meg az eljárást. A módszer exponenciálisan közelít a szélsőértékhez.
5.1.2.2.2. Fibonacci sor szerinti keresés
Ezt a tartományosztó eljárást KIEFER mutatta be 1953-ban. A módszer a Fibonacci sor segítségével határozza meg a lépések nagyságát.
A Fibonacci sor :
Ha a keresési intervallum
|
|
(5.3) |
és az osztások száma N, akkor a lépésköz:
|
, ahol: |
(5.4) |
Ez alapján az új pontok:
|
|
(5.5) |
A következő iterációs lépéshez kiválasztunk két pontot ():
|
Ha: akkor: |
(5.6) |
|
|
Ha: akkor: |
(5.7) |
Az eljárást -ig folytatjuk, mert a következő lépésben a pontok már egybeesnének .
5.1.2.2.3. Aranymetszés alapú keresés
Ez a módszer a Fibonacci keresés módosítása úgy, hogy ahol és vagyis az aranymetszés arányával egyenlő (5.4 egyenlet). Így a lépések száma megnő, de nem kell a Fibonacci sort kiszámolni és tárolni.
5.1.2.2.4. Bolzano módszer
Ha van két pontunk (), melyekben a célfüggvény meredeksége ellenkező előjelű, akkor a szélsőérték a pontok által meghatározott tartományon belül van. A következő lépésben megfelezhetjük a tartományt úgy, hogy pontok felezőpontjánál megvizsgálva az értékeket, az közül azt helyettesítjük -val, amelyik meredeksége megegyező előjelű a célfüggvény pontban vett meredekségének előjelével. Így a tartományt határoló pontok meredekségei továbbra is ellenkező előjelűek maradnak, vagyis a szélsőérték az új tartományon is belül esik.
5.1.2.3. Interpolációs módszerek
Ha a célfüggvénynek nemcsak az értékét, hanem a meredekségét is felhasználjuk, akkor az előzőekben bemutatott eljárásoknál gyorsabban konvergáló módszert kaphatunk.
5.1.2.3.1. Regula-falsi iteráció
Míg a Bolzano módszer csak a célfüggvény deriváltjainak előjelét használja fel, addig ez az eljárás a deriváltértékeket is, így gyorsabban képes elérni az optimumot.
Adott két pont: , és az függvények értékei.
Az új pontot a következő egyenlettel kaphatjuk meg:
|
|
(5.8) |
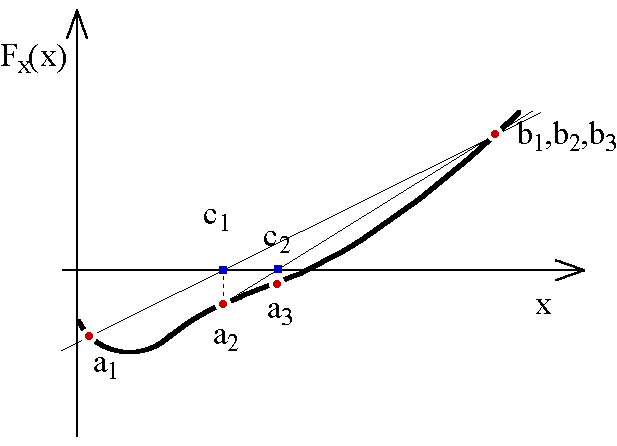
Ha lineáris, akkor , tehát egy lépésben kapjuk meg a megoldást.
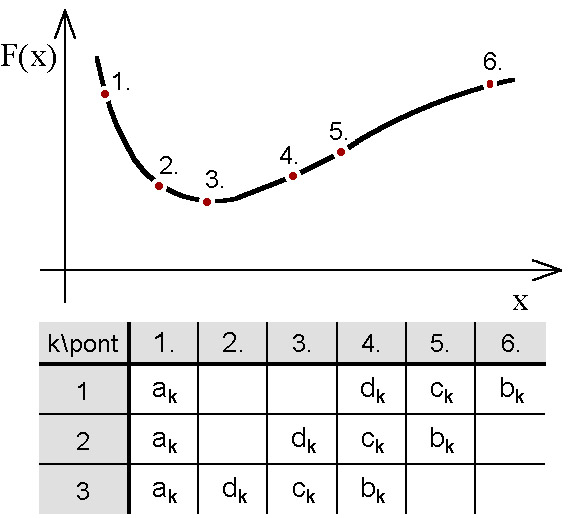
Ha és különböző előjelű, akkor a Bolzano módszernél leírtak alapján választjuk ki az új pontokat. Ha mind a három pontban egyezik a célfüggvény meredekségének előjele, akkor azt helyettesíti amelyiknél nagyobb (5.2. ábra).
Az optimum csak akkor található meg biztosan, ha a kezdőpontokat a minimum közelében vesszük fel, egyébként az iteráció a maximumhoz is vezethet.
5.1.2.3.2. Newton-Raphson iteráció
Ehhez az eljáráshoz szükség van a célfüggvény másodrendű deriváltjainak értékeire is, melyek felhasználásával tovább csökken az iterációs lépésszám. A vizsgált pont, a deriváltak értékei:
A rekurziós formula:
|
|
(5.9) |
Az eljárás hátrányai:
-
Ha a deriváltakat numerikus differenciálás alapján kapjuk, akkor a hatékonyság romlik, különösen a minimum közelében, ahol nagyon kis értékeket vesz fel.
-
A minimumot, maximumot és az inverziós pontot nem tudja egymástól megkülönböztetni.
-
Másodfokúnál nagyobb célfüggvény esetén az iteráció divergens is lehet, a konvergencia feltétele minden x-re.
5.1.2.3.3. Lagrange interpoláció
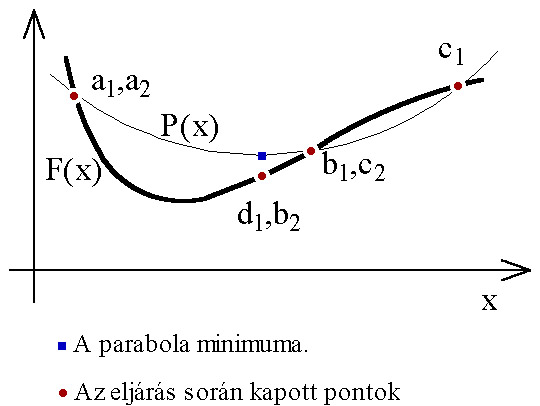
Ennek a módszernek csak a célfüggvény értékekre van szüksége. Az eljárás a függvény három pontjára () egy parabolát illeszt, a negyedik pontot () a parabola minimuma határozza meg. A következő iterációs lépéshez az előző lépés négy pontja közül kiválasztott három pontot használ (). A pontok helyzetüktől és célfüggvény-értéktől függően kerülnek kiválasztásra. Az eljárás a célfüggvény és a parabola hasonlóságát használja ki, így hatékonysága is az egyezés mértékétől függ.
5.1.2.3.4. Hermit interpoláció
Ez az eljárás a Lagrange interpolációhoz hasonlóan működik, de parabola helyett egy harmadfokú függvényt használ próbafüggvényként. Az új pont meghatározásához két pontot, a pontok célfüggvény értékeit és meredekségüket használja fel. A hatékonyság itt is a függvények hasonlóságától függ.
5.1.3. Többdimenziós stratégiák
A többdimenziós keresési esetekben a keresett változók növekedésével a keresési tér nagysága exponenciálisan nő. Ha gyorsítani akarjuk a keresést, akkor azt csak a megbízhatóság rovására tehetjük, vagy olyan módszerek alkalmazásával, melyek a célfüggvény értékein kívül más információkat is felhasználnak.
A különböző módszereket a felhasznált információ jellege alapján csoportosíthatjuk:
-
Direkt keresési eljárások , melyek csak a függvényértékekkel számolnak.
-
A Gradiens módszerek az elsőrendű deriváltakat is felhasználják.
-
A Newton módszereknek a másodrendű deriváltakra is szükségük van.
A többdimenziós eljárások rekurziós formulája általában az alábbi egyenleten alapul, amely a következő vizsgálandó pontot határozza meg:
|
|
(5.10) |
ahol
|
|
|
a paramétervektor, |
|
a lépés nagysága, |
||
|
pedig az iránya. |
Az egyes eljárások a lépés nagyságának és irányának megválasztásában különböznek.
5.1.3.1. Direkt keresési stratégiák
A direkt keresési eljárások nem alkotnak modellt a célfüggvényről, a kereséshez csak a függvényértékeket veszik igénybe. Az irányokat és a lépésnagyságokat heurisztikusan vagy valamilyen más módszerrel határozzák meg. Mivel megvan az esélye, hogy a függvényérték nem fog minden lépésben javulni, az eljárásnak tudnia kell kezelni a hibák előfordulását.
5.1.3.2. Koordináta stratégia
Ez az eljárástípus a legrégibb a többdimenziós keresőeljárások közül, számos variációja létezik, és több elnevezése is van: a változók egymás utáni változtatása; párhuzamos, tengely menti keresés; egy lépés, egy változó módszer; ciklikus, hegymászó koordinátastratégia; Gauss-Seidel stratégia.
A módszer alapötlete eredetileg a lineáris algebrából származik, először itt alkalmazta GAUSS és SEIDEL lineáris egyenletrendszerek megoldására.
Az eljárás az (5.10) egyenlet paramétereit egymástól függetlenül változtatja minden iterációs lépésben. A lépés irányát, azaz hogy melyik koordinátatengely mentén, melyik irányban keressen, akkor változtatja meg, ha a célfüggvény értéke romlik. A lépés nagysága lehet állandó, de alkalmazhatunk Fibonacci keresést, Lagrange interpolációt vagy más egydimenziós keresési módszert is az új pont helyzetének meghatározására.
Abban az esetben, ha csak a koordinátáktól eltérő irányokban érhetünk el eredményt, a módszer nem működik. Gyors megoldást csak akkor kaphatunk, ha a határfelületek koncentrikusak. Kimutatták azt is, hogy egy eredménytelen keresés az egyik irányban, a másik irányú keresést eredményessé teheti, ezt a jelenséget egyes módszerek fel is használják.
A stratégia gyorsításának egyik lehetősége az irányok kiválasztási sorrendjének módosítása. Az irány kiválasztására a ciklikus módszer helyett alkalmazhatjuk például azt a stratégiát, hogy mindig azt az irányt választjuk, amelyik mentén legnagyobb a célfüggvény értékének változása, vagy a legnagyobb lépést tudjuk megtenni.
5.1.3.3. Hook és Jeeves pattern stratégiája
Ezt az eljárást HOOK és JEEVES 1961-ben dolgozták ki, eredetileg automatikus kísérleti alkalmazás céljából, ma már azonban széles körben numerikus paraméter-optimalizáló eljárásként használják.
Az algoritmus kétféle lépésből áll. Az első egy felfedező (explorációs) lépés, amely a koordinátatengelyek irányában lépve (pattern vagy mintavevő lépés) a pont környezetében számítja ki a célfüggvény értékeket. Ha talál egy jobb értékű pontot, akkor innen keres tovább a következő irány mentén. A lépések: (5.4. ábra) a 0. pontból az x-tengely irányában lép az 1. pontba, ami jobb, tehát negatív irányba már nem is kell visszalépnie. Ezután az y-tengely mentén lép a 2. pontba, mivel ez rosszabb mint az 1. ezért a 3.-at is megvizsgálja, ami már jobb lesz. Az explorációs lépések után következik az extrapoláció, ez az iterációs ciklus kezdeti és végső pontja által meghatározott irányban hajt végre egy lépést, a 0. kezdőpont és a 3. utolsó pont alapján lép a 4. pontba.
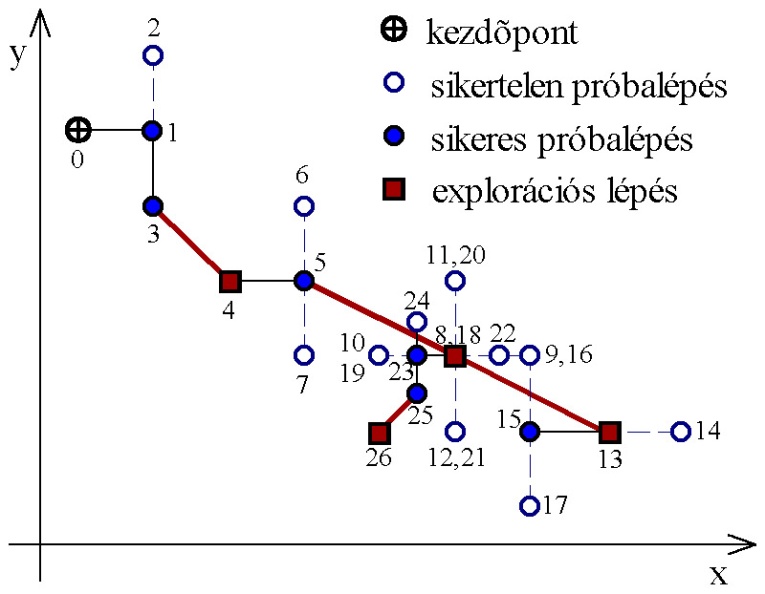
Ezután a következő iterációs ciklus mintavevő lépései jönnek, az 5.-be lépve rögtön eredményt ér el, de az y-irányban nincs további javulás (6.,7.). A 3. és 5. pont közül az utóbbi a jobb, ezért az extrapolációs lépéssel a 8.-ba jutunk. A következő explorációnál nem talál kedvezőbb pontot (9.,10.,11.,12.), de mivel a 8. jobb az 5.-nél a 13. pontba extrapolál. További lépéseken át eljut a 15.-be, de ez rosszabb mint a 8. így vissza kell lépnie ide (18.). Ezután egyik irányban sem talál már jobb pontot, ezért felezi a lépés nagyságát.
Az extrapolációs lépés nagyságát a keresés sebességének növelése érdekében, az eredményektől függően változtatja.
Konvex és folytonosan differenciálható célfüggvény esetén a módszer konvergens. Előnyei az egyszerű számítási műveletek és a kis tárolókapacitás igény.
5.1.3.4. Rosenbrock stratégiája: forgó koordináták
ROSENBROCK a koordinátastratégiát a tengelyek forgatásával egészítette ki, így elérte, hogy a keresési irányok már nem korlátozottak, az algoritmus mégis a tengelyek mentén keres. A módszer lényege, hogy az egyik tengelyt a legkedvezőbb irányba forgatja és az elforgatott koordináta-rendszer tengelyei mentén keres tovább. Egy sikeres lépés után növeli a lépés nagyságát, sikertelen után pedig csökkenti, és az ellenkező irányba fordul. Ezt az eljárást addig folytatja, míg sikert nem ér el mindegyik koordinátairányban. Ezután ismét a tengelyek forgatása következik. Az iteráció befejezésének feltételét a transzformáció elvégzése előtt vizsgálja.
5.1.3.5. Davies, Swann és Campey stratégiája (DSC stratégia)
SWANN 1964-ben ROSENBROCK módszerét kombinálta az egydimenziós kereső eljárásokkal, a stratégiának többféle változata is létrejött.
Az algoritmus a kezdőpontból kiindulva, minden koordináta mentén egy egydimenziós keresést hajt végre, és az így kapott eredmények segítségével határozza meg a következő lépés legkedvezőbb irányát. Ezután a koordinátatengelyek forgatása következik úgy, hogy azok a tengelyek nem változhatnak, melyek mentén nem sikerült egy meghatározott nagyságú lépést megtenni. Ezzel a feltétellel biztosítjuk, hogy az eljárás továbbra is az egész paraméterteret vizsgálja.
5.1.3.6. Nelder és Mead szimplex stratégiája
A szimplex stratégiák az eddig leírt módszerektől nagyban eltérnek, az eljárás alapötlete (SPENDLEY, HEXT és HIMSWORTH, 1962), hogy az egy időben vizsgálandó pontok számát, amennyire csak lehet, csökkentsük le. Ez a szám BROOKS és MICKEY (1961) szerint, n dimenziós esetben n+1.
Az egyszerű szimplex eljárás az n számú paraméter által meghatározott térben n+1 pontot vesz fel egymástól egyenlő távolságban - ezt a csoportot nevezzük szimplexnek. Az iteráció első lépésében a felvett pontokban kiszámoljuk a célfüggvény értékeit, majd a legrosszabb értékű pontot a többi pont középpontjára vett tükörképével helyettesítjük. Az eljárás azon a feltételezésen alapul, hogy az új pont az eddigieknél jobb célfüggvény értéket fog eredményezni.
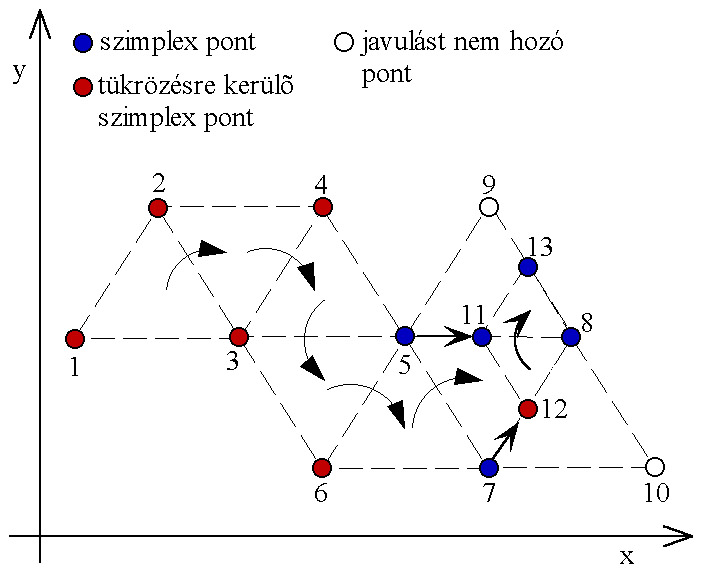
Ha az egyik pont a minimum közelébe esik, akkor az új pont a legrosszabb is lehet - ebben az esetben a második legrosszabbat kell tükrözni. Ha a pontok távolságát nem változtatjuk, akkor az eljárás egy idő után stagnálni kezd, a szimplex a legjobb pont körül forog, ekkor további eredményt a távolság felezésével kaphatunk. NELDER és MEAD módszere abban különbözik az alapötlettől, hogy a szimplex nagyságát és alakját minden lépésben úgy módosítja, hogy az a legjobban illeszkedjen a körülményekhez.
Az eljárást akkor fejezzük be, ha az egyes pontok függvényértékei közötti eltérés egy előre meghatározott érték alá csökken.
Sok változó esetén az eljárás robosztus és megbízható, de ugyanakkor költséges is, n+1 paramétervektort kell tárolni és a paraméterek számának növelésével a számításigény is nő.
5.1.3.7. Box komplex stratégiája
BOX 1965-ben a korlátokkal bővített optimumkeresési esetre módosította a szimplex stratégiát. A fő különbség a két eljárás között a használt pontok nagyobb számában és abban jelentkezik, hogy a pontok halmazát minden tükrözéskor bővíti. Így akadályozza meg, hogy az eljárás, a keresési térnek csak egy résztartományát vizsgálja.
A kezdőpont kijelölése után a többi pontot véletlenszerűen határozza meg. Ha átlép egy korlátot egy új pont létrehozásakor, akkor lépésenként haladva a már létrehozott pontok által meghatározott középpont felé, az első engedélyezett pontra cseréli ki azt.
Ezután tükrözi a legrosszabb pontot, mint a szimplex stratégiánál, de a korlátokat itt is figyelembe veszi.
Mivel az eljárás több pontot használ, így a tárolókapacitás-igénye is nagyobb.
5.1.4. Gradiens stratégiák
A gradiens módszer CAUCHY (1847), KANTOROVICH (1940, 1945), LEVENBERG (1944) és CURRY (1944) munkája nyomán alakult ki, eredetileg egyenletek és egyenletrendszerek megoldására alkalmazták. Az eddigi módszerek vagy csak meghatározott irányokban vizsgálták a célfüggvény értékeit, vagy az előző lépések eredményeiből következtetve határozták meg a következő lépés irányát. A gradiens stratégiák olyan hegymászó algoritmusok, amelyek a döntéshez felhasználják a parciális deriváltakat is, így mindig abban az irányban lépnek tovább, amelyikben a függvény meredeksége a legnagyobb. Ezt az irányt a célfüggvény gradiense határozza meg. Az eljárás az eddigi módszereknél sokkal gyorsabban képes a szélsőértéket elérni, alkalmazhatóságának feltétele a célfüggvény folytonossága és a parciális deriváltak létezése.
Az egyes gradiens stratégiák abban különböznek egymástól, hogy a meghatározott irányban milyen módszerrel lépnek, és mennyire pontosan követik a gradiens által meghatározott útvonalat. Ez alapján rövid- és hosszúlépésű algoritmusokat különböztethetünk meg.
A gradiens stratégiák a lépés nagyságának meghatározására különböző módszereket használnak, a legegyszerűbb esetben alkalmazhatunk állandó lépésközt, de az új pont helyzetének meghatározására bármelyik egydimenziós keresőmódszert is felhasználhatjuk. Ha azt a lépéshosszt választjuk, amelyiknél a függvény értéke a legkedvezőbb, akkor az eljárást a leghosszabb lépés módszerének nevezzük.
Az eljárások egyik hátránya, hogy nem tudják megkülönböztetni a lokális és a globális minimumot. Ennek kiküszöbölésére különböző módszereket kell alkalmaznunk, például több, véletlenszerűen kiválasztott pontból is elindíthatjuk a keresést.
A befejezés feltételét megkaphatjuk az egyes lépések közti függvényérték-eltérések vagy a gradiens vektor hosszának vizsgálatából is.
5.1.4.1. Powell stratégiája: konjugált irányok
A legjelentősebb ötlet a gradiens eljárás konvergenciális nehézségeinek kiküszöbölésére HESTENS-től és STIEFEL-től (1952) származik, a módszert konjugált irányok vagy gradiensek néven ismerjük.
A irányok szempontjából konjugáltak, ha pozitív definit mátrix (az összes sajátértéke pozitív), és minden esetre. A konjugált irányok egymástól lineárisan függetlenek. Ha A-t az I egységmátrixszal helyettesítjük, akkor a vektorok ortogonálisak lesznek. Ha az mátrixot használjuk a irányok meghatározásához, akkor egy négyzetes függvény szélsőértékét ezekben az irányokban végrehajtott egydimenziós keresésekkel kaphatjuk. Iterációhoz jól használható közelítést kapunk abban az esetben is, ha a célfüggvény nem négyzetes. Az eljárás a másodrendű deriváltakat is felhasználja. A konjugált irányok alkalmazásán alapuló eljárásokat azért soroljuk mégis a gradiens módszerek közé, mert nem közvetlenül ugyan, de a gradienst használják fel a kereséshez.
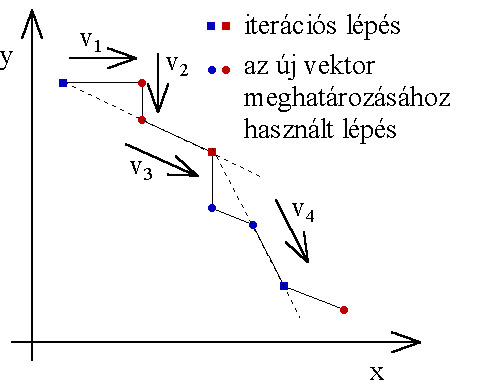
Konjugált vektorokat a másodrendű deriváltak ismerete nélkül is létrehozhatunk, a másodrendű deriváltakra következtethetünk például, a gradiens változásából is.
POWELL módszere kétparaméteres esetre (5.6. ábra) először a koordinátairányokban alkalmazott keresésekkel meghatároz két vektort (), majd a másodrendű deriváltak becslésével vektor mellé kiszámít egy új vektort. A következő iterációban már a irányok mentén keres.
5.1.4.2. Newton stratégiák
A Newton stratégiák azt a tényt használják fel, hogy ha egy függvény számtalanszor differenciálható, akkor egy pontjában az értéke felírható egy másik pontbeli függvény és derivált értékekkel, a következő Taylor-sor szerint:
|
|
(5.11) |
|
|
|
(5.12) |
A módszer analitikus, az egyenlettel a szélsőérték helye egy lépésben kiszámítható. Első ránézésre nagyon egyszerűnek tűnik ez az egy lépésben történő számítás, de tulajdonképpen egy egyenletrendszer megoldását takarja.
Az egyenletrendszer nem oldható meg mindig, és a megoldás lehet minimum, maximum és nyeregpont is, a globális szélsőérték se garantált, megtalálása a kezdőpont kiválasztásától függ.
A Newton stratégiák általában csak a másodrendű deriváltakat használják az iterációs számításban, BIGGS (1971, 1973) kidolgozott egy eljárást, amely magasabb rendű deriváltakat is alkalmaz.
Az iterációs egyenlet másodrendű esetben:
|
|
(5.13) |
vagy más alakban
|
|
(5.14) |
Ezt az eljárást néha másodrendű gradiens módszernek is nevezik, ahol: a keresési irány és a lépéshossz, a valódi lépéshosszt természetesen tartalmazza.
A következő iterációhoz az előzőben kapott pontot használjuk. Az iterációt addig folytatjuk, amíg a célfüggvény értékének változása egy meghatározott érték alá nem csökken. Az eljárás gyorsításához azt az ötletet alkalmazhatjuk, hogy ritkábban számítjuk újra a másodrendű deriváltakat és több iterációhoz is ugyanazt az értéket használjuk.
A módszer továbbfejlesztett változatai az eljárás megbízhatóságának növelését a gyors konvergencia megtartásával együtt érik el.
5.1.4.3. Davidson-Fletcher-Powell módszer (Kvázi Newton stratégia, Variable Metric Strategy)
A kvázi Newton módszerek nem használják a másodrendű deriváltakat, hanem az elsőrendű deriváltak változásából becslik azokat. Az ötlet DAVIDON-től (1959) származik, gyakorlati módszerré FLETCHER és POWELL (1963) alakította.
Az eljárás rekurziós formulája:
|
|
(5.15) |
|
|
|
(5.16) |
|
|
, |
(5.17) |
ahol
|
|
|
az egységmátrix |
|
pedig a korrekciós mátrix: |
|
|
(5.18) |
ahol: , .
5.1.5. Random (véletlenszerű) stratégiák
Az eddigi fejezetekből kimaradtak azok az eljárások, melyek nem determinisztikus, hanem valószínűségi szabályok alapján változtatják a paramétereket.
Általános gyakorlat az optimalizáló módszereknél a véletlen döntések alkalmazása, ha a determinisztikus szabályok nem érik el a kívánt eredményt, vagy zsákutcába vezetnek.
A random módszerekről az általános vélemény az, hogy sokkal költségesebbek, és a gondosan kidolgozott determinisztikus szabályokkal mindig jobb eredményt érhetünk el. Ez nincs így, a véletlenszerűség nem tetszőlegességet jelent, létrehozhatunk olyan véletlenszerű döntéseket, melyek speciális elvárásoknak is megfelelnek. Néhány esetben pedig csak a véletlenszerűség alkalmazásával juthatunk eredményre.
A hegymászó algoritmusokat véletlenszerű döntések alkalmazásával módosíthatjuk, például a keresési irányok kiválasztásánál. Sokszor használják a véletlen döntéseket az eljárások idő előtti befejeződésének kiküszöbölésére is, mert ezek minden esetben alkalmazhatók.
Számos javaslat létezik a globális szélsőérték elérésére, kiegészítő heurisztikus szabályok alkalmazásával, például az intervallum több részre osztásával, és az egyes intervallumokon kapott eredmények összehasonlításával. A másik, és néha az egyetlen, módszer a véletlenszerűen kiválasztott kezdőpontok alkalmazása, majd a kapott szélsőértékek összehasonlítása.
Megfigyelték, hogy egyes determinisztikus eljárásoknál a pontatlanság nemhogy csökkentené, hanem növeli a hatékonyságot, ezért ezt a módszert alkalmazták, ami tulajdonképpen a véletlenszerűség felhasználása.
Az eddigi módszerek mind determinisztikus eljárások módosításai voltak, a tiszta random stratégia létjogosultságát az igazolja, hogy komplikált esetekben még ma is használják egyszerű Monte-Carlo módszer néven. Az eljárás egyenlő valószínűséggel kiválasztja a pontokat, kiszámítja a célfüggvény értékeket és a legkisebb (legnagyobb) értéket választja optimumnak. Ha a módszert összehasonlítjuk a rácsmódszerrel (a paramétertérben egy rács pontjaiban számítja ki a függvényértékeket), akkor azt az eredményt kapjuk, hogy a két eljárás egyenértékű (a felvett pontok száma egyenlő), ha a random keresésnél megelégszünk a szélsőérték megtalálásának 63%-os valószínűségével. Ha azt akarjuk, hogy 90%-os valószínűséggel találjuk meg a szélsőértéket, akkor több mint 2-szer annyi pontot kell felvennünk, mint a rácsos keresésnél. Ez azért van így, mert a véletlenül felvett pontok nagyon közel is eshetnek egymáshoz. Az eljárást javíthatja, ha a tartományt résztartományokra osztva, mindegyikben csak egy pontot veszünk fel (BROOKS). Ha az optimum helyéről valamilyen feltételezésünk van, akkor ott kisebb résztartományokat felvéve sűríthetjük a pontokat (INDELSOHN, 1964).
Javulás érhető el, ha a random eljárást sorrendi működéssel módosítjuk, például az első N pont után a keresést egy kisebb térre szűkítjük. A kúszó (creeping) módszer (BROOKS 1958) másképpen teszi az eljárást szekvenciálissá. Egy pontot felvesz, a többit pedig úgy kapja, hogy a felvett pont koordinátáit valamilyen valószínűségeloszlás-függvény alapján kapott véletlen számmal eltolja. A pontok közül a legkedvezőbb függvényértékűt választja ki, és a következő lépésben ez a pont lesz a véletlenszerűen kiválasztott ponthalmaz középpontja.
Ha az élőlényeket megfigyeljük szembeötlő, hogy mennyire alkalmazkodtak a környezetükhöz, sok esetben a biológiai struktúrák, még a legmodernebb technikai rendszereket is felülmúlják. Ezekből a megfigyelésekből sokan arra a következtetésre jutottak, hogy a természet képes optimális megoldásokat találni a jelentkező problémákra.
A fajok keletkezésének elmélete szerint, minden élőlény egy hosszú fejlődési folyamat eredménye, amit evolúciónak nevezünk. A megfigyelések alapján azt kell feltételeznünk, hogy az optimális, vagy legalábbis egy jól alkalmazkodó organizmus kifejlesztése az evolúció sajátja, vagyis az evolúció rendelkezik egy optimalizáló stratégiával. A természetnek ez a stratégiája hasonlóságot mutat az eddigi optimalizáló eljárásokkal, az evolúcióban a variáció a véletlen változásokban jelenik meg, míg a szelekció a jobban alkalmazkodott egyedeket részesíti előnyben. Ezt a hasonlóságot legtöbbször a random eljárásokkal mutatják ki, mert a mutáció leginkább véletlenszerű változásokkal magyarázható.
Az evolúció hatékonysága azonban nem magyarázható az egyszerű random kereséssel, azt kell feltételeznünk, hogy ez egy sorrendi eljárás, ami az előző esetek eredményeit felhasználva halad az optimum felé.
5.1.6. Evolúciós módszerek
A természetben megfigyelhető struktúrák és folyamatok lemásolásának szándéka, a technikai problémák megoldásának céljából, egyidős a mérnöki tevékenységgel. Az evolúciós módszerek eljövetelét a bionika tudományának megjelenése jelezte, mely a természet problémamegoldó módszereit ülteti át a mérnöki gyakorlatba. Az evolúció által létrehozott megoldásokat a kutatók gyakran találták optimálisnak. Több tudós (ASHBY, 1960; BREMERMANN, 1963; RECHENBERG, 1964; FOGEL, OWENS és WALSH 1965; HOLLAND 1975) is kidolgozott olyan módszereket melyek a természetben megfigyelhető folyamatokat modellezik [21.] .
5.1.6.1. Szimulált hőkezelés
Ez az eljárás is a természetből meríti a keresés alapötletét. A fémek hőkezelését megfigyelve láthatjuk, hogy a kristályszerkezet és ezzel a fizikai tulajdonságok megváltoztatását az anyag felmelegítésével és különböző sebességű lehűtésével érhetjük el. Minél lassabb a lehűlés annál több ideje van az atomoknak, hogy rendezett kristályrácsban helyezkedjenek el, vagyis elérjék az energiaminimumot. Ha túl gyors a folyamat, akkor csak egy lokális energiaminimumú állapot fog létrejönni.
KIRKPATRICK, GELATT, VECCHI (1983) és CERNY (1985) publikáltak ezen a megfigyelésen alapuló optimalizáló módszereket, amelyeket szimulált hőkezelési eljárásoknak nevezzük.
Az algoritmusok - az optimum keresése közben - bizonyos valószínűséggel elfogadnak egy rosszabb lépést is, így az eljárás képes megszökni a lokális szélsőértékekből. Az alkalmazott valószínűséget az idő múlásával csökkentjük, egyre kevesebb hibát engedélyezve, ezzel modellezve a hűtési folyamatot.
A rosszabb állapot elfogadásának valószínűsége:
|
|
(5.19) |
ahol
|
|
a paramétervektor, |
|
|
a valószínűség-eloszlás normalizálására szolgáló állandó, |
||
|
|
a célfüggvény értéke, |
|
|
a Boltzmann állandó, |
||
|
a hőmérséklet. |
A hőmérséklet változtatására különböző terveket alkalmazhatunk, így befolyásolva a keresés folyamatát. [21.]
A szimulált hőkezelő eljárás egy lehetséges algoritmusa:

5.1.6.2. Evolúciós algoritmusok (EA)
Az evolúciós számítás vagy evolúciós algoritmus (evolutionary computation, evolutionary algorithm) elnevezést, a különböző eljárások egységbe foglalására alkották. A módszerek három nagy csoportra oszthatók, ezek a genetikus algoritmusok (genetic algorithms), az evolúciós stratégiák (evolution strategies) és az evolúciós programozás (evolutionary programming). Ezen módszerek közös jellemzői, hogy mindegyik a reprodukciót, a véletlen variációt, a versengést és a kiválasztást alkalmazza a populáció egyedein. Ez a négy művelet az evolúció működésének alapja [25.] .
Az evolúciós algoritmusok közös tulajdonságai:
-
A populációnak, vagyis az egyedek összességének kollektív tanulási mechanizmusát használják fel a kereséshez. Minden egyed egy keresési pontot reprezentál a paramétertérben. Az egyes egyedek által elért eredmények a többiek számára is hozzáférhetők, információt cserélnek egymás közt. Egyéb információkat is szolgáltathatnak, például az algoritmus működési paramétereinek változtatásához.
-
Az egyedek leszármazottjait, véletlenszerűséget felhasználó eljárásokkal hozza létre. A mutáció az egyedek hibás másolása, a rekombináció új egyed létrehozása, két vagy több egyedből nyert részleges információk felhasználásával.
-
Az egyedekhez a populáció többi tagjának felhasználásával egy jellemző, a fitness érték rendelhető. Ezeket az értékeket össze lehet hasonlítani, és döntést lehet hozni arról, hogy melyik egyed életképesebb. Ezen érték alapján a szelekciós eljárás egy jobb egyedet nagyobb valószínűséggel választ az utódok létrehozására vagy a túlélésre, mint egy rosszabbat.
A fitness (fitnesz) fogalma a neo-darwinista evolúciós elméletből származik. Ez a mérőszám mutatja meg, hogy a populáció többi tagjához viszonyítva az egyed mennyire sikeres. Ettől a tulajdonságtól függ a szaporodás esélye és a túlélés sikere. Kiszámításának módja lehet például maximumkeresés esetén, az egyed célfüggvény értékének osztása a populáció célfüggvény értékeinek összegével.
Az evolúciós algoritmusok három csoportja ezeket az elemeket különböző módon és különböző szerkezetben alkalmazza. Az eljárás egy lehetséges általános formája a következő:

5.1.6.2.1. Evolúciós stratégiák (ES=Evolution Strategies)
Az első evolúciós stratégiát 1964-ben RECHENBERG és SCHWEFEL alkotta meg kísérleti optimalizáló módszerként. Az eljárást áramlástani tulajdonságok javításához használták. Létrehozására azért volt szükség, mert az addigi módszerek mindig elakadtak egy lokális minimumban. Ez az eljárás volt a mára kifejlesztett evolúciós stratégiák őse.
5.1.6.2.2. Az egyszerű Evolúciós Stratégia
Az algoritmus csak két egyeddel dolgozik, az utód létrehozásához, rekombinációt nem, csak mutációt alkalmaz. A szelekció determinisztikus, mindig a legjobb egyed a túlélő. A mutáció az egyedek paramétereit egymástól függetlenül, véletlenszerűen változtatja meg egy valószínűségeloszlás-függvény segítségével kapott véletlen szám hozzáadásával.
Az eljárás algoritmusa:

Az algoritmuson különböző változtatásokat végrehajtva, megjelentek a több szülőt és utódot használó, többtagú stratégiák is.
5.1.6.2.3. Az evolúciós stratégiák típusai
Az evolúciós stratégiákat egyaránt csoportosíthatjuk az eljárásban alkalmazott egyed és utódszám valamint a következő generáció egyedeinek kiválasztása alapján
Az algoritmusokat egy rövidített jelöléssel nevezték el. Az egyszerű evolúciós stratégia jelölése például: (1+1) ES, ahol a zárójelben az egyedszám és az egy iteráció alatt létrehozott utódok száma szerepel, a + jel pedig arra utal, hogy a következő generációba az előző generáció egyedei és az utódok közül egyaránt választhat.
Ez alapján létezik (μ+1) ES és (μ+λ) ES, ahol μ az egyedszám, λ pedig az utódok száma. A (μ,λ) ES rövidítésben a + jel helyett egy vessző található, ami arra utal, hogy a következő generáció egyedeit csak az utódok közül választja ki az algoritmus [21.] [25.] .
5.1.6.2.4. Egymásba ágyazott evolúciós stratégiák
Ezek olyan speciális evolúciós stratégiák melyek több algoritmust (szintén evolúciós stratégiák) futtatnak egyszerre, mindegyiket külön populáción, és ezeket az algoritmusokat az eljárás egyedekként kezeli. Az egyes algoritmusok rangsorolásához a populációk egyedeinek átlagértékét veszi alapul. Ez a módszer felhasználható például a belső algoritmusok paramétereinek javítására. Ebben az esetben a külső eljárás által optimalizált paraméterek a belső eljárások futását befolyásoló változók [25.] .
5.1.6.2.5. Genetikus algoritmusok (GA)
Ma a genetikus algoritmusok a leginkább elterjedt és legnépszerűbb evolúciós stratégiák. Az első eljárásokat 1975-ben JOHN HOLLAND és munkatársai fejlesztették ki. Kutatásaik fő célja a természetben található adaptív rendszerek leírása és a természet lényeges mechanizmusait alkalmazó mesterséges rendszerek (programok) fejlesztése volt. Főleg a természetes rendszerek robosztusságát (széles problémakörön való alkalmazhatóságát) kívánták a technikai rendszerekben is megteremteni.
Az első eljárás (HOLLAND eredeti algoritmusa) minden ciklusban csak egy utódot hozott létre, és azt a populációba egy véletlenül kiválasztott egyed helyére illesztette be. Ez a módszer csak a reprodukciónál alkalmazott az egyedek eredményességétől (fitness) függő szelekciót.
A módszernek számos változata alakult ki - az egyes változatok különbözhetnek egymástól az egyedek ábrázolásában (bit, valós, permutációs), a velük dolgozó operátorokban vagy a populáció szerkezetében. Léteznek speciális eljárások is, mint például az egyszerre több szempont szerint optimalizáló és a párhuzamos futású algoritmusok.
A genetikus algoritmus egy lehetséges változata:

A genetikus algoritmusok elterjedésének okai az egyszerű eljárás, a hatékonyság és a széles körben való alkalmazhatóság.
5.1.6.2.6. Evolúciós programozás (EP)
Az evolúciós programozást LAWRENCE FOGEL dolgozta ki 1964-ben, a mesterséges intelligencia megközelítésének új módszereként. A stratégia egyedekként a probléma különböző megoldási módjait, véges állapotú rendszereket (Finite State Machine, FSM), használ. Az eljárás nemcsak a problémát megoldó algoritmusok paramétereit, hanem azok egyéb építőelemeit is módosíthatja.
Az 1980-as évek vége óta az evolúciós algoritmusok elterjedésével az evolúciós programozást több területen is sikeresen alkalmazták: a neurális hálózatok tervezésénél, betanításánál és optimalizálásánál, optimális útvonal meghatározási problémáknál, az automatikus szabályozásoknál, a játékelméletben valamint az interaktív mesterséges intelligenciák területén is [17.] [25.] .
5.1.6.2.7. Genetikus programozás (GP)
Ezt az újfajta eljárást JOHN KOZA alkotta meg 1989-ben. Az ő ötlete az volt, hogy az adott probléma megoldására ne evolúciós programot készítsünk, hanem a lehetséges számítógépprogramok keresési terén alkalmazzunk egy evolúciós algoritmust. Így nemcsak egy már létező algoritmus paramétereinek optimális beállítását kereshetjük, hanem a probléma megoldására alkalmas programok (algoritmusok) között kereshetjük az optimális esetet [17.] .
Mivel a genetikus programozási algoritmus egyedei programok, az alkalmazott mutációs, rekombinációs és szelekciós operátorok is speciálisak, programokként kezelhetők és maguk is fejlődhetnek.
A számítógépprogramok fejlesztésének ezen új módszere azért jelentős, mert megváltoztathatja a problémamegoldásról alkotott képünket, és az eddig emberközpontú módszerek mellé új eszközt ad a fejlesztők kezébe [17.] [25.] .
5.2. Genetikus algoritmusok
5.2.1. Genetikai alapok
A genetikai kód megfejtése és univerzalitásának felismerése óta sokat foglalkoznak a kódrendszer kialakulásának problémáival. Ennek ellenére kérdéses még a keletkezés mechanizmusa és az is, hogy miért éppen ez a típus fejlődött ki.
Ha az evolúciót nemcsak biológiai folyamatként, hanem természeti törvényszerűségek működéseként értelmezzük, és alanyai közé a génekkel még nem rendelkező, egyszerűbb formákat is besoroljuk, akkor magyarázatot találhatunk a genetikai kód kialakulására. A kutatók szerint az egyedek a kémiai körfolyamatok kapcsolódásával keletkeztek, és mivel ezek a folyamatok befolyásolták egymás fennmaradási valószínűségét, verseny alakult ki köztük, ami egyre bonyolultabb szerveződések keletkezését eredményezte. Végül létrejött az egyednek egy olyan funkciója, a replikáció, amely másolással biztosította az elért előnyök fennmaradását és az egyed elterjedését. A szelekció, a fennmaradásért folytatott verseny hatására, a replikáció egyre pontosabbá vált, végül megjelent a közel 100%-os másolást, az identikus replikációt lehetővé tevő genetikai kód. A teljesen megegyező másolatot létrehozó mechanizmus azért nem alakul ki, mert ez már hátrányt jelentene, megakadályozná az új megoldások kialakulását.
Az identikus replikáció következtében lehetővé vált a legkülönbözőbb szelekciós előnyt jelentő változások rögzítése az egyedekben. A nem-identikus replikáció fázisában az egyes egyedek nagyfokú variabilitása miatt az evolúciót elsősorban a divergencia jellemezte, az identikus replikáció megjelenésével csökkent a variabilitás, a szelekció hatására egyfajta szabályozási konvergencia következett be. Ez a konvergencia idézi elő a környezetükhöz alkalmazkodott egyedek kialakulását.
A többsejtűek megjelenésével lehetővé vált az utódok rekombinációval történő létrehozása. Ez a folyamat a szülőegyedek genetikai információinak közös felhasználásával hozza létre az utódot. A rekombináció lehetővé teszi a szülők kedvező tulajdonságainak átörökítését, és így egy mindkét szülőnél sikeresebb egyed létrejöttét.
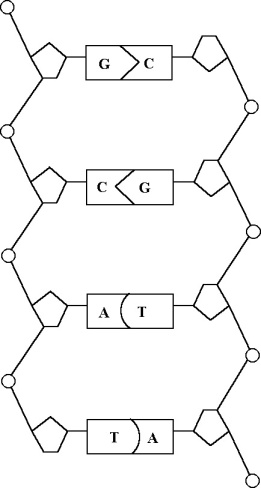
Az egyed felépítéséhez szükséges információt a DNS-lánc kódolja, ez a genotípus, az egyed megjelenési formája pedig a fenotípus. A genotípus és a fenotípus nem határozzák meg egymást egyértelműen, több genotípusnak is lehet ugyanaz a fenotípusa, és egy genotípus több megjelenési formát is eredményezhet, mert egyes tulajdonságok az egyedfejlődéstől is függenek.
A DNS-ben az információt hordozó legkisebb egység a nukleotid, melynek négy típusa a guanin, citozin, adenin és a timin. A nukleotidok 3-as csoportjai alkotják a géneket, melyek a 20-féle aminosav létrehozására szolgáló utasítást kódolják.
A genetikai kód a sejtben kromoszómákba csomagolva található. Kereszteződéskor a két szülő kromoszómája rekombinálódik, így jön létre az utód genotípusa.
A mutáció a kromoszóma megváltozása valamilyen külső hatásra vagy hibás másolás eredményeképpen, például a sejtek osztódásakor.
5.2.2. A genetikus algoritmus
A genetikus algoritmus az egyedeket bitsorokkal ábrázolja, ez a bitsor az egyed genetikai kódja, a genotípusa. A bitek csoportjai - a gének - kódolják a paramétereket, vagyis a fenotípust. A paraméterekkel meghatározható a célfüggvény értéke, melynek segítségével számíthatjuk az egyedek fitness értékeit. A keresést a szelekciós nyomás felhasználásával a kereső operátorok: a keresztezés és a mutáció végzik.
Az algoritmus folyamatábrája:
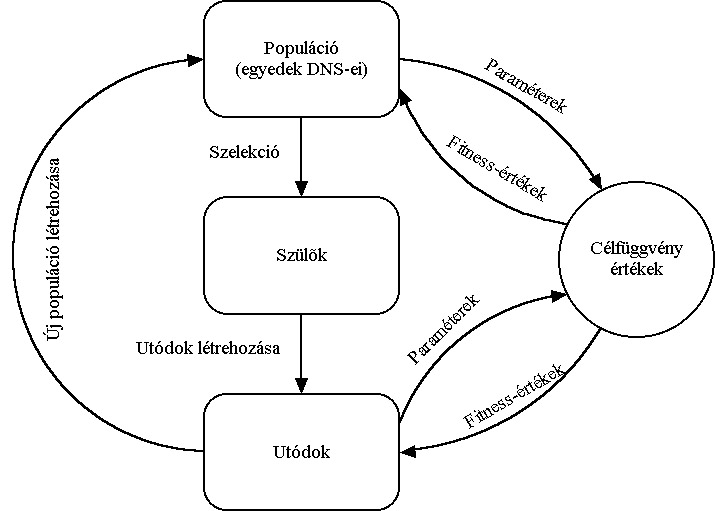
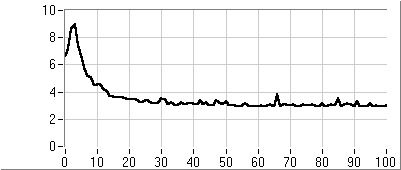
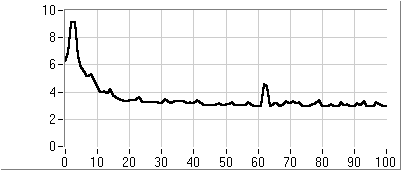
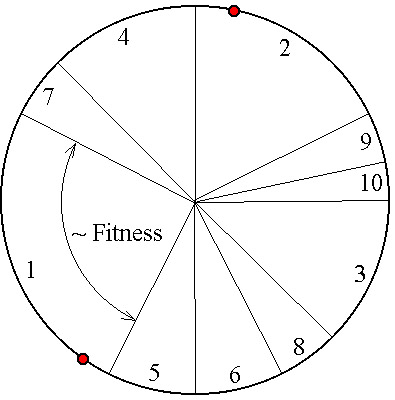
Az eljárás fő lépései az új egyedek létrehozása, a célfüggvény érték és fitness számítása és az új populáció létrehozása. A rulett kerék szelekciós eljárás (5.13. ábra) a populáció egyedeihez, fitness értékükkel arányos nagyságú körcikkeket rendel és azt választja ki, amelyik tartományába esik a kerületen véletlenszerűen meghatározott pont. Az egyedeket a körön összekeverve helyezi el, ezzel is növelve a változatosságot.
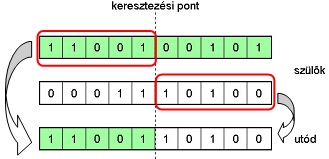
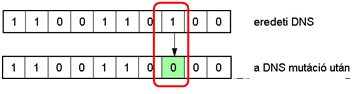
Az egyedek létrehozása a kiválasztott szülők keresztezésével történik (5.14. ábra), majd az utódra alkalmazzuk a mutációs operátort (5.15. ábra).
Ezután kiszámítjuk az új egyedek függvényértékeit, és létrehozzuk az új populációt. Ahhoz hogy az egyedek száma változatlan maradjon, a régi populáció egy részét helyettesítenünk kell az utódokkal.
5.2.3. A genetikus algoritmusok működési mechanizmusa
A genetikus algoritmusok az evolúciót a genetika által leírt folyamatok segítségével modellezik. Megtaláljuk bennük a mutáció, a rekombináció és a szelekció elemeit is. Ezek mellett a fitness fogalmát is felhasználják.
A fitness az egyedek összehasonlítására szolgáló, egyedre jellemző érték, amely alapján döntést lehet hozni arról, hogy melyik egyed jelent kedvezőbb megoldást.
5.2.3.1. A sémaelmélet
A sémaanalízist JOHN HOLLAND 1975-ben dolgozta ki, a genetikus algoritmusok működésének egy lehetséges magyarázataként. Az ő elképzelése szerint a bonyolult problémák legegyszerűbben úgy oldhatók meg, ha részproblémákra bontjuk őket. A genetikus algoritmusoknál jelentkező legkisebb részfeladat a kód legkisebb részének, bitsor esetén egy bitnek, a meghatározása.
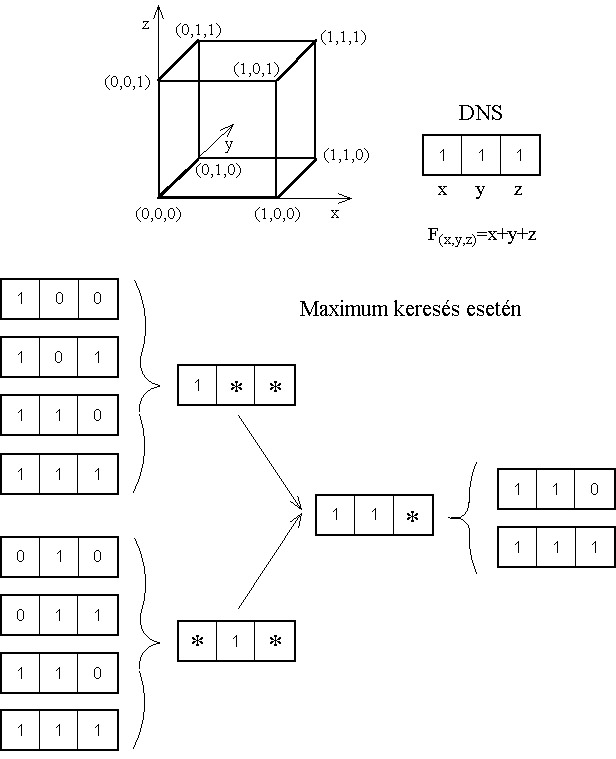
A séma a genetikai kódok olyan halmaza, melyben egyes helyeken azonos bitek vannak, a nem határozott biteket pedig csillaggal jelöljük. A sémaelmélet kimondja, hogy az alacsonyrendű sémák egyre magasabb rendűeket alkotnak, miközben folyamatosan javul a megoldás. Ha az egyik sémával leírható egyedek jobb célfüggvény értékeket adnak, akkor a szelekció ezeket az egyedeket részesíti előnyben, így a séma uralkodóvá válik a populációban, végül az összes egyed egyforma lesz, az optimális megoldást adva.
5.2.3.2. Az építőelem-elmélet
Az építőelem-elmélet azt mondja ki, hogy a genetikus algoritmus az alacsonyrendű sémákból építi fel az egyre magasabb rendűeket, így alkotva meg az elemekből a rekombináció segítségével a megoldást.
A genetikus algoritmusok működésének leírására egyelőre nem létezik egy teljesen kidolgozott elmélet. Egyes kutatók rámutatnak arra, hogy a mutáció és rekombináció együttes alkalmazása befolyásolja egymás eredményességét, és ez nemcsak javulást, hanem romlást is jelenthet.
A működés leírásához további kutatásokra van szükség mind az elméletben, mind a számítógépes kísérletek terén. Egy másik probléma, az ábrázolásmód típusa is megoldásra vár. Ez felveti a kérdést, hogy a binárisan vagy a valósan kódolt génekkel lehet-e nagyobb hatékonyságot elérni.
5.2.4. A genetikus algoritmusok típusai
A genetikus algoritmusok felépítéséből következően, a módszert sokféleképpen módosíthatjuk. Lehetőségünk van az egyes elemeket egymástól függetlenül változtatni, egyszerűbb vagy bonyolultabb szerkezeteket és ezekkel dolgozó eljárásokat alkalmazni.
Ebben a fejezetben sorra vesszük az algoritmus egyes elemeit és bemutatjuk ezek főbb típusait.
5.2.4.1. A gének ábrázolása
A megoldandó probléma paramétereit az algoritmusnak valamilyen formában ábrázolnia kell, és az ábrázolás módját mindig a feladat határozza meg. A lehetséges ábrázolási módok közül azt kell választanunk, amely a paraméterteret úgy képezi le, hogy az algoritmus a lehető leghatékonyabban működhessen.
5.2.4.1.1. Bináris ábrázolásmód
A legtöbb genetikus algoritmus a változókat bitek, 1-esek és 0-ák, sorával ábrázolja, egy kódoló és dekódoló algoritmus felelteti meg egymásnak a paramétertér és a bitek által meghatározott keresési tér pontjait.
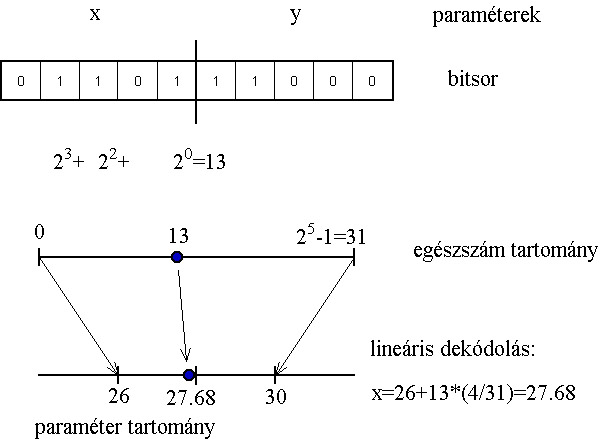
Mivel a bitek tere véges számú pontot ábrázolhat, a dekódoló eljárásnak a paramétertérből ki kell választania ezeket a pontokat. Leggyakoribb a lineáris dekódoló eljárás alkalmazása, amely a pontokat egymástól egyenlő távolságra osztja el egy tartományon belül. Az ábrázolás pontosságát a tartomány nagysága és a bitek száma együtt határozza meg.
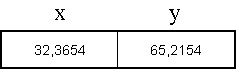
5.2.4.1.2. Valós ábrázolásmód
A valós értékeket alkalmazó eljárások a paramétereket nem bitek soraként, hanem valós értékekkel ábrázolják. Ebben az esetben nincsen szükség kódolásra, viszont speciális mutációs és rekombinációs eljárásokat kell alkalmaznunk.
Az egyes kutatók eltérő véleménnyel vannak a valós és a bináris kódolás előnyeiről és hátrányairól. GOLDBERG (1989) szerint a lehető legkisebb jelkészletet kell használni, mert így jöhetnek létre a legegyszerűbb sémák. A másik vélemény a valós számok alkalmazását részesíti előnyben, FOGEL és STAYTON (1994) szerint a sémák számának növelése nem szükségszerűen hasznos, sőt káros, így nincs értelme valós szám optimalizálási problémánál a paramétervektoron kívüli más ábrázolás alkalmazásának.
MICHALEWITZ (1992) kísérleti példákon keresztül hasonlítja össze a két ábrázolási módot, és azt a következtetést vonja le, hogy a valós ábrázolással nagyobb hatékonyság érhető el.
5.2.4.1.3. Permutációs ábrázolásmód
A kombinatorikai problémáknál a paramétertér pontjainak, véges számú elemek különböző sorrendjei felelnek meg. Ahogyan a kutatók permutációs problémákkal kezdtek foglalkozni, nyilvánvalóvá vált, hogy ezek az eddigi esetektől eltérő ábrázolásmódot és genetikai operátorokat igényelnek.
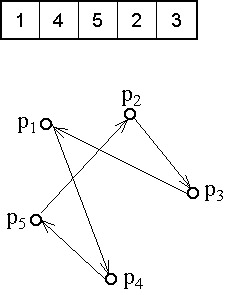
Az ábrázolás egyik lehetősége a permutációk hozzárendelése egy számhoz (bitsorhoz). Ebben az esetben azonban nem tudunk hatékony operátorokat alkalmazni és az ábrázolásmód sem illeszkedik a problémához.
Az egyedek ábrázolásához jobb módszer a permutációban szereplő tagok indexeinek felhasználása - ebben az esetben a DNS egész számokból álló sor.
Kombinatorikai feladatra klasszikus példa az utazó ügynök probléma, ahol meghatározott számú pontot, mindegyiket egyszer érintve, kell körbejárni, és a kiindulási pontba visszatérni.
A permutációs ábrázolásmódot az utazó ügynök probléma segítségével az 5.19. ábra szemlélteti.
5.2.4.1.4. Speciális ábrázolásmódok
-
Mátrix ábrázolásmód: A permutációs ábrázolás olyan változata, amelynél az algoritmus célja nem a sorrend, hanem az egyes elemek egymáshoz képesti elhelyezkedésének meghatározása.
-
Véges állapot ábrázolás: A véges állapotú rendszerek létrehozására használt algoritmusokban alkalmazzák.
-
Vegyes ábrázolás: Valós értékeket és biteket is tartalmazó ábrázolásmód.
-
Intronok alkalmazása: A kód tartalmaz olyan részleteket is (intron), melyeknek nincs jelentése. Ez a módszer az építőelemek keletkezésének megkönnyítését célozza.
-
Összekevert genetikus algoritmusok (Messy genetic algorithms): A paramétereket két változó kódolja, az egyik az értékét, a másik pedig a helyét határozza meg a DNS-en belül.
-
Diploid ábrázolás: Egy paraméter értékét több változó is meghatározhatja, de a domináns változó hatása érvényesül.
5.2.4.2. Fitness számítás
Ahhoz, hogy az algoritmus a populáció fejlődését elő tudja idézni, szükségünk van egy célfüggvényre. A célfüggvény értékét a paraméterek változtatásával, a probléma típusától függően minimalizálni vagy maximalizálni szándékozunk.
A célfüggvény meghatározásakor figyelembe kell venni a következőket:
-
A célfüggvénynek az optimalizálni kívánt mértékeket kell kifejeznie.
-
Valamilyen szabályszerűséget kell mutatnia az ábrázolási térben.
-
Megfelelő információt kell szolgáltatnia a szelekciós nyomás alkalmazhatóságához.
A fitness függvény az egyedeket sikerességük, vagyis a célfüggvény eredménye alapján értékeli. A célfüggvény értékeket egy nemnegatív intervallumra képezi le, gyakran alkalmazva skálázó függvényt is a szelekciós nyomás növelése érdekében.
A fitness függvény:
|
|
(5.20) |
ahol
|
|
|
a célfüggvény, |
|
a skálázó függvény, |
||
|
az i. egyed paramétervektora. |
A leggyakrabban alkalmazott skálázó függvények:
-
Lineáris skálázás alkalmazásakor a következő függvényt használjuk:
(5.21)
ahol , ha maximalizálás , ha minimalizálás a cél, β pedig az aktuális generáció legrosszabb célfüggvény értéke.
-
Szigma skálázás (GOLDBERG 1989) a célfüggvény értékek eloszlásán alapul:
Haakkor , egyébként
(5.22)
ahol
a célfüggvény értékek középértéke,
az átlagos eltérés, c=2 konstans.
Ennél a módszernél a szelekciós nyomást az értékek szórása is befolyásolja.
-
Hatványozáson alapuló fitness számítás :
(5.23)
ahol
k
problémától függő paraméter.
-
Bolzmann számítás olyan hatványozó, skálázó eljárás, amely a szimulált hőkezelésnél alkalmazott módszerrel T-t folyamatosan csökkentve növeli a szelekciós nyomást:
(5.24)
5.2.4.3. Szelekció
A szelekció az evolúciós algoritmusok egyik fő operátora, alkalmazásának két célja lehet, az egyik a szülők kiválasztása az új egyedek létrehozásához, a másik a következő generációba kerülő, túlélő egyedek meghatározása. Egyes eljárások csak az egyik, míg mások mindkét művelethez felhasználják.
A jó és a rossz megoldások megkülönböztetésére a fitness szolgál A szelekció alapötlete, hogy egy jobb fitness értékű egyed kiválasztásának nagyobb legyen a valószínűsége, mint egy rosszabbnak. A rosszabb egyed kiválasztásának is van esélye, ez biztosítja, hogy az eljárás kimozduljon egy lokális szélsőértékből.
5.2.4.3.1. Rulett kerék szelekció
A szelekciós algoritmusok közül ez az eljárás a legegyszerűbb, az egyes egyedekhez fitness értékükkel arányosan rendeli hozzá a rulett kerék kerületének egy részét. A nagyobb fitness értékű egyed arányosan nagyobb helyet kap, ezért amikor véletlenszerűen kiválasztunk egy kerületi pontot, a nagyobb fitness-szel rendelkező egyedet nagyobb eséllyel kapjuk eredményül. A véletlenszerűség növelésének érdekében az egyedeket a keréken összekeverve helyezzük el (5.13. ábra).
A szelekció általános algoritmusa a következő:

5.2.4.3.2. Versenyeztető algoritmus
Ennél az eljárásnál n darab egyedet véletlenszerűen választunk ki, majd ezek részt vesznek egy versenyben, és a győztes lesz az algoritmus kimenete. A versenyeztetés egyik módja a fitness értékek összehasonlítása, vagyis a determinisztikus kiválasztás. Ennél a módszernél az eredmény kialakulására nincs hatással a fitness skálázása és eltolása, ezért ezek alkalmazása szükségtelen.
A módszer további felhasználási lehetősége a párhuzamos genetikus algoritmusoknál jelentkezik. Az eljárás könnyen beilleszthető a párhuzamos struktúrába, mert nincs szüksége globális számításokra, ezért a versenyek egymástól függetlenül folyhatnak.
5.2.4.3.3. Rangsor alapú szelekció
A rangsorba rendezés lehet a megoldás azokban az estekben, amikor a célfüggvény értéke vagy csak pontatlanul, vagy egyáltalán nem határozható meg. Ilyenkor az algoritmus nem a célfüggvény értéket számítja ki, hanem valamilyen más módszer szerint rendezi rangsorba az egyedeket. Ezután az egyes egyedekhez a sorrend alapján rendeli a fitness értékeket, a hozzárendelt értékek változhatnak lineárisan, exponenciálisan vagy más módon is.
5.2.4.3.4. Boltzmann szelekció
Az eljárás a szimulált hőkezelésnél megismert módszer alapján (5.19 egyenlet), határozza meg a kiválasztott egyedet, így adva esélyt egy alacsonyabb fitness értékű egyednek is.
5.2.4.4. Kereső operátorok
A genetikus algoritmus fontos része az új egyedek létrehozása. Ezt a feladatot a genetikus operátorok végzik a már létező egyedek felhasználásával. Ezeknek a műveleteknek két fő típusa van: az egyik a mutáció, a másik a rekombináció. A mutáció a genetikus kód véletlenszerű, általában kismértékű, megváltoztatásával módosítja az egyedet. A rekombináció pedig új egyedet hoz létre több szülő felhasználásával.
A tapasztalatok azt mutatják, hogy az egyedek ábrázolásmódja mellet, az alkalmazott operátorok határozzák meg az algoritmus működésének hatékonyságát. Az operátorok és a reprezentáció között szoros kapcsolat áll fenn, amely meghatározza az alkalmazható elemek típusait.
5.2.4.4.1. Mutáció
Kezdetekben a mutációt a genetikus algoritmusok területén csak a rekombinációt kiszolgáló, háttéroperátorként kezelték, de ma már a kutatók egy önmagában is hatékony keresőműveletnek fogadják el.
A mutáció általános algoritmusa:

5.2.4.4.2. Mutáció bináris ábrázolás esetén
Ha az egyedek ábrázolása bitekkel történik, akkor az eljárás minden bitet egy meghatározott valószínűséggel billent át (5.15. ábra).
5.2.4.4.3. A valós ábrázolás mutációs operátorai
Valós ábrázolásnál minden paramétert egy valós szám ábrázol, ebben az esetben speciális mutációs eljárásra van szükség. A paramétereket egy véletlen számmal módosítjuk, ezt a számot különböző módszerekkel határozhatjuk meg.
5.2.4.4.4. Mutációs operátorok permutációs ábrázolásmód esetén
A permutációs ábrázolásmódú egyedek operátorai az eddigiektől eltérő elveket alkalmaznak. Olyan egyedet kell létrehozniuk, amely szintén permutáció lesz, és a megfelelő mértékű változást kell elérniük.
Ha például az egyedek geometriai pontok sorrendjét határozzák meg, és a gének ezeknek a pontoknak az indexei, akkor két pontot kiválasztva, a köztük lévő pontok sorrendjét megfordíthatjuk, a két kiválasztott pontot felcserélhetjük, vagy egy pontot kivéve a sorból két másik pont közé illeszthetjük. A megfelelő módszer alkalmazásához mindig figyelembe kell venni a probléma sajátosságait, hogy az operátor akkora változást idézzen elő az egyedben, amekkorára szükség van. A különböző problémáknál a permutációk különböző tulajdonságai lényegesek, egy útvonal problémánál a szomszédosság, míg egy sorrendi problémánál a helyzet a fő tulajdonság.
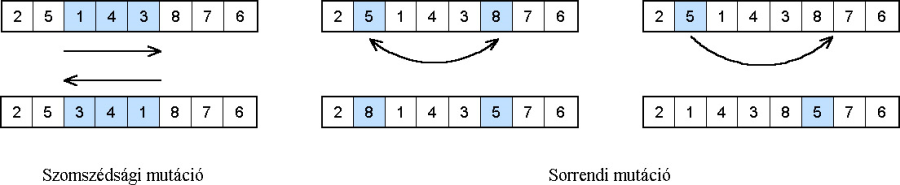
A mutációs operátorok egyéb típusai az egyedek ábrázolási módjaitól függően alakultak ki. Léteznek például véges állapotú rendszereket, faszerkezeteket és egyéb adatszerkezeteket módosító algoritmusok is.
5.2.4.4.5. Rekombináció
A biológiai rendszerekben a kereszteződés két kromoszóma között végbemenő bonyolult folyamat. A kromoszómák azonos helyein törések keletkeznek, és mielőtt ezeket kijavítaná a sejt, a megfelelő kromoszómadarabok helyet cserélhetnek. Ez a genetikai anyag rekombinációját eredményezi, és növeli a populáció változatosságát.
Az evolúciós algoritmusoknál ezt a mechanizmust a keresztező (crossover) eljárások valósítják meg, melyek az egyedeket leíró génsorokból, a megfelelő részsorokat felhasználva, hozzák létre az utódot meghatározó kódot.
5.2.4.4.6. Bináris keresztezés
Az első keresztező eljárást HOLLAND hozta létre, amely három lépésből állt: először kiválasztott két szülőt, majd meghatározta a keresztezési pontokat (keresztezési maszk), végül a szétvágott részekből két utódot hozott létre. Ez a keresztező eljárás csak egy meghatározott valószínűséggel adott a szülőktől eltérő utódokat.
A bináris keresztezés általános algoritmusa:

Az alkalmazott maszk generálására többféle módszert is alkottak, a leggyakoribb algoritmusok a következők:
5.2.4.4.6.1. Egypontos keresztezés:
A szülőket két részre osztja, és ezeket a részeket cseréli fel egymással (5.14. ábra).
A maszkot előállító eljárás:

5.2.4.4.6.2. K-pontos keresztezés:
A szülőket k+1 részre osztja, majd ezekből hozza létre az utódokat (5.26. ábra).
A maszkot előállító eljárás:

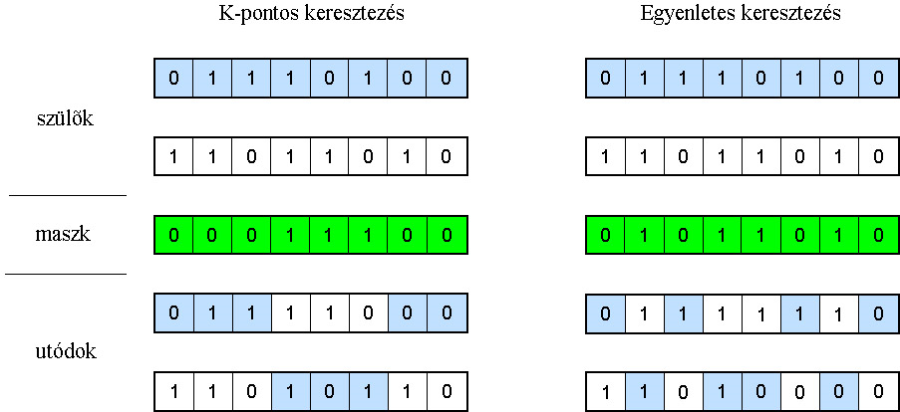
5.2.4.4.6.3. Egyenletes keresztezés (uniform crossover):
Minden pont meghatározott valószínűséggel () származhat, egyik vagy másik szülőtől (5.26. ábra).
Az algoritmus:

5.2.4.4.6.4. A valós ábrázolásmódnál alkalmazott keresztezési módszerek
A valós elemekből álló vektorokat többféle módon is lehet keresztezni. Az eljárások két fő típusa a bináris módszereket és a numerikus műveleteket alkalmazó algoritmusok. A bites ábrázolásnál alkalmazott módszerek könnyen adaptálhatók valós vektorokra is.
Az aritmetikai rekombinációs algoritmusok az előzőektől eltérő elven működnek, az utód génjeit matematikai műveletekkel állítják elő, a szülők génjeiből.
A leggyakoribb aritmetikai keresztező operátorok:
Átlagoló aritmetikus operátorok:
A leszármazott génjeit a szülők génjeinek átlaga határozza meg:
|
|
(5.25) |
|
|
|
(5.26) |
ahol
|
|
az utód paramétervektora, |
|
|
|
a szülők paramétervektorai |
|
|
az alkalmazott súlyozási együtthatók. |
5.2.4.4.6.5. Heurisztikus keresztezés (WRIGHT 1994)
Az eljárás a két szülőt (), melyekre igaz, hogy nem rosszabb mint , egy 0-1 közötti véletlen szám felhasználásával, a következő egyenlet alapján keresztezi:
|
|
(5.27) |
Ez az operátor a célfüggvény értékeket használja fel a keresési irány és lépésnagyság meghatározására.
5.2.4.4.6.6. Szimplex keresztezés (RENDERS és BERSINI 1994)
Az operátor darab szülőt használ fel, melyek közül a legrosszabb fitness értékű. Az eljárás először kiszámolja az pontok középpontját -t, majd erre tükrözi -t. Az egyenlet:
|
|
(5.28) |
|
|
|
(5.29) |
5.2.4.4.6.7. Geometriai keresztezés (MICHALEWITZ 1996)
Az eljárás a szülők megfelelő génjeinek geometriai középértékét számítja.
Két szülő esetére az egyenlet:
|
|
(5.30) |
ahol
|
az n darab génnel rendelkező szülők paramétervektorai. |
5.2.4.4.7. A permutációs ábrázolásmód keresztező eljárásai
Permutációs ábrázolás esetén az eddig megismert módszerek nem alkalmazhatók. Olyan operátorokra van szükségünk, melyek amellett, hogy szintén permutációt adnak eredményül, a probléma megoldását is elősegítik.
Permutációs operátorokat elsőként DAVIS, GOLDBERG és LINGLE definiáltak 1985-ben.
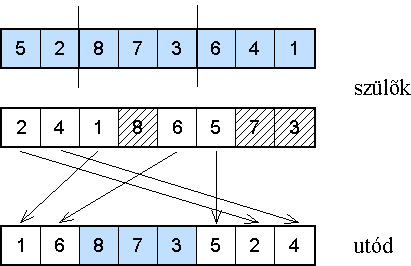
5.2.4.4.7.1. DAVIS sorrendi keresztezése (Order crossover, OX)
Az eljárás menete: vegyünk két permutációt, az egyik a vágandó sor, a másik a kitöltő! Az első permutációból véletlenszerűen válasszunk ki egy szakaszt (8,7,3), és másoljuk át az utód ugyanazon részére! A maradék helyeket a második szülőből töltsük fel a sorrendet betartva, de a már felhasznált pontokat kihagyva (5.28. ábra)!
Az utód az első szülőtől relatív sorrendi, abszolút helyzeti és szomszédsági, míg a másodiktól csak relatív sorrendi információkat örököl.
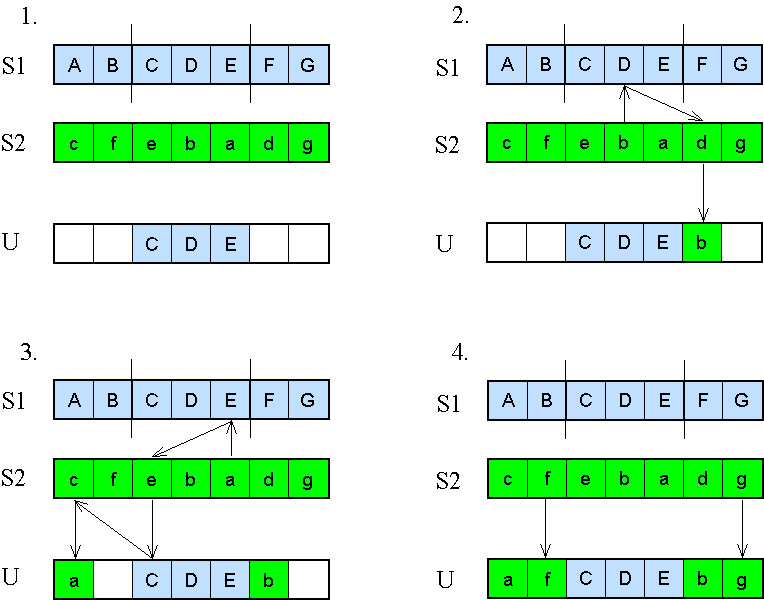
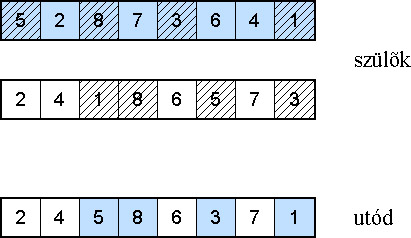
5.2.4.4.7.2. Részleges megfeleltetésű keresztezés (Partially mapped crossover PMX)
Ezt az operátort GOLDBERG és LINGLE alkották meg 1985-ben. Az eljárás a sorrendi keresztezésnél megismert módszertől abban különbözik, hogy a második szülőtől származó pontokat más módon helyezi el (5.29. ábra).
Az S1 szülőtől átmásolt CDE részlet után (5.29. ábra – 1.), először azokat a pontokat helyezi el az U utódban, melyek még nem szerepelnek benne, és az S2 szülőnél azokon a helyeken vannak, melyeket az utódnál már betöltöttünk, ezek a b és az a pontok. A b pont elhelyezése úgy történik, hogy megnézi, melyik pont van az S1-ben a helyén, ez a D pont, ezután arra a helyre teszi a b pontot, amit a d foglal el az S2-ben (5.29. ábra -2.).
Az a pont elhelyezése: a helyén S1-ben E van, de e helyén U-ban már C; ezért tovább kell folytatni a módszert: c helye U-ban még üres, tehát ide kerül a (5.29. ábra – 3.).
A maradék helyeket az S2-ből ugyanazon a helyen található pontokkal tölti fel (5.29. ábra - 4.).
5.2.4.4.7.3. SYSWERDA sorrendi keresztezése (Order crossover-2)
Ez a módszer véletlenszerűen kiválaszt K pontot az első szülőből, megkeresi ezek helyét a másodikban, és a K pontot a második szülőben elfoglalt helyekre, de az első szülőben meghatározott sorrendben, helyezi el az utódban. A maradék pontokat a második szülőből közvetlenül másolja át az utódba.
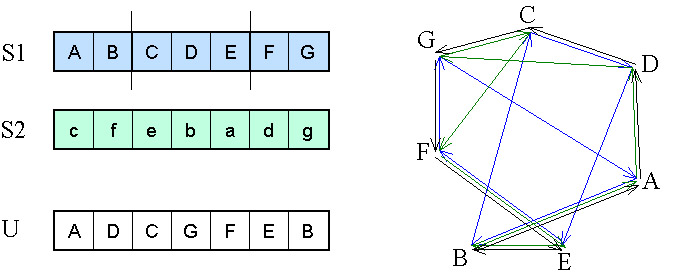
5.2.4.4.7.4. Élkeresztezés
Az élkeresztező eljárás az utazó ügynök problémához készített speciális operátor. Az algoritmus a permutációk szomszédsági tulajdonságait veszi figyelembe, mert ez határozza meg egy útvonal hosszát.
Az eljárás először kifejezi a szülőkből a szomszédsági információkat, és tárolja őket egy táblázatban, tulajdonképpen egy mindkét szülő éleit tartalmazó gráfot rajzol fel. Ezután a táblázat (gráf) alapján egy új egyedet (útvonalat) hoz létre.
Az új egyedet létrehozó eljárás többször is zsákutcába juthat az útvonal keresése közben - az 5.31. ábra egy lehetséges utódot mutat.
5.2.4.5. Korlátkezelési technikák
A korlátok fontos részét képezik minden probléma megfogalmazásának, többféle formában jelentkezhetnek: lehetnek szabályok, algebrai kifejezések, adatösszefüggések és egyéb meghatározások is.
A korlátok határozzák meg a keresési terület azon részét, amelyen belül a megoldások számunkra használhatók, megfelelőek a probléma megoldására.
A következő alfejezetekben a korlátok megvalósításának különböző módszereit mutatjuk be a genetikus algoritmusok területén.
5.2.4.5.1. Büntetőfüggvények
A büntetőfüggvényeket a hegymászó algoritmusok már évtizedek óta alkalmazzák korlátos optimalizálási problémáknál. Alapvetően két típusuk van: a külső büntetőfüggvények a nem-megfelelő megoldásokat, a belső büntetőfüggvények pedig a megfelelőket büntetik. A belső büntetőfüggvények alkalmazásának ötlete onnan származik, hogy korlátos esetekben az optimum gyakran a lehetséges és nem lehetséges megoldások határán van, alkalmazásával pedig gyorsíthatjuk az optimum elérését.
A külső büntetőfüggvényeket alapvetően három csoportra oszthatjuk:
-
A korlát büntetőfüggvények csak a határvonalon található megoldásokat büntetik, az ezen kívül esőket nem.
-
A részleges büntetőfüggvények a megfelelő megoldások határának közelében is alkalmaznak büntetést.
-
A globális büntetőfüggvények a nem megfelelő megoldásokat büntetik.
5.2.4.5.2. Statikus büntetőfüggvények
A legegyszerűbb módszer, a korlátot átlépő megoldást egy konstans értékkel büntetni. Ekkor a büntetett célfüggvény a célfüggvény és a büntetőpont összege lesz (minimumkeresés esetén). Több korlát esetén a büntető függvény:
|
|
(5.31) |
ahol a büntetett célfüggvény, a célfüggvény, m a korlátok száma, C pedig a büntetőpont. Ha az egyed átlépte az i. korlátot, akkor , ha nem akkor .
A módszernek létezik olyan változata is, amely a korláttól való távolság függvényében határozza meg a büntetés nagyságát.
5.2.4.5.3. Dinamikus büntetőfüggvények
A büntetőfüggvények alkalmazásakor a nem megfelelő megoldások megjelenését is megengedjük, de a keresés végén már nem akarjuk, hogy a megoldás is ilyen legyen.
Ezt úgy érhetjük el, ha a keresés közben a büntetőpontok nagyságát folyamatosan növeljük, így kezdetben több, nem megfelelő megoldás jelenik meg, de ezek száma az idő múlásával csökken.
5.2.4.5.4. Adaptív büntetőfüggvények
Az adaptív módszerek a keresőalgoritmus aktuális hatékonyságára jellemző adatokat is használnak a büntetőpontok meghatározásánál. Így a büntetőpontok nagyságát az eljárás hatékonyságától teszik függővé.
5.2.4.5.5. Dekódolók alkalmazása korlátozás céljából
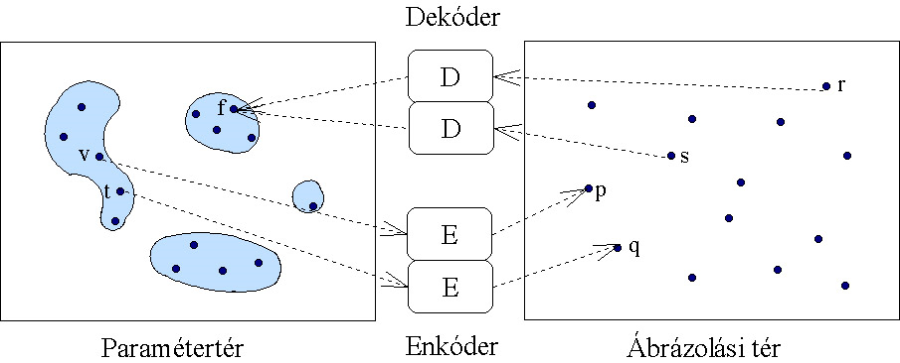
A dekódolók a problémát más módon közelítik meg - a nem megfelelő megoldásokat kizárják a keresési térből úgy, hogy egy másik ábrázolási tér elemeit rendelik hozzá a megengedett megoldások teréhez.
A dekódolónak teljesítenie kell a következő feltételeket:
-
Minden megoldáshoz hozzárendelhető egy pont a dekóder ábrázolási teréből.
-
A dekóder ábrázolási terének minden pontja egy megoldást reprezentál.
-
Minden megoldást azonos számú pont határoz meg a dekóder ábrázolási terében.
A hatékonyság érdekében figyelembe kell venni a következő szempontokat:
-
A transzformációt gyors számításokkal lehessen végrehajtani.
-
A dekóder ábrázolási terében történő kis változások az eredeti ábrázolási térben is kis változásokat jelentsenek.
5.2.4.5.6. Egyéb technikák
5.2.4.5.6.1. Javító algoritmusok
Ezek az algoritmusok az esetlegesen létrejövő hibás megoldásokat egy javító eljárás segítségével alakítják át. A javító algoritmusok alkalmazása nagymértékben megnövelheti a keresés időigényét.
5.2.4.5.6.2. Korlátokat betartó operátorok alkalmazása
Ezek a genetikus algoritmusok olyan speciális operátorokat alkalmaznak, melyek problémafüggő tudást felhasználva tartják meg az egyedek megfelelőségét. Mivel a korlátokat „megértő” eljárások nem hoznak létre hibás egyedeket, a keresés korlátok nélküli esetté alakul.
5.2.5. A populáció szerkezete
A populáció azoknak az egyedeknek a csoportja, melyek között a keresőeljárás kapcsolatokat létrehozva, a populáció egészét felhasználja a megoldáshoz.
Az egyszerű populációs modelltől eltérő egyéb szerkezeteket attól függően csoportosíthatjuk, hogy a genetikus algoritmus milyen kapcsolatokat enged meg az egyes egyedek között.
5.2.5.1. Életfeltételeket alkalmazó módszerek (Niching methods)
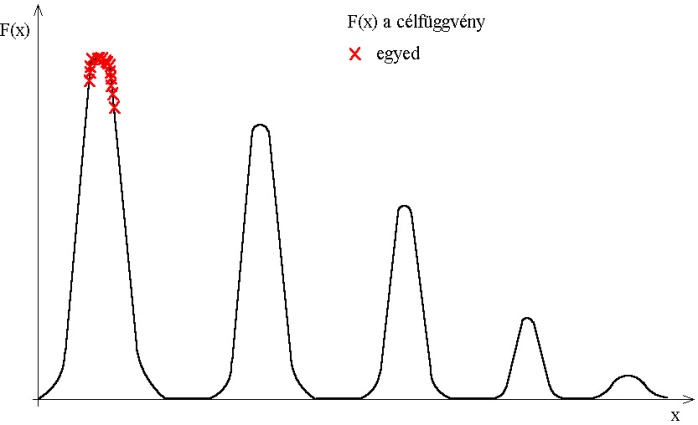
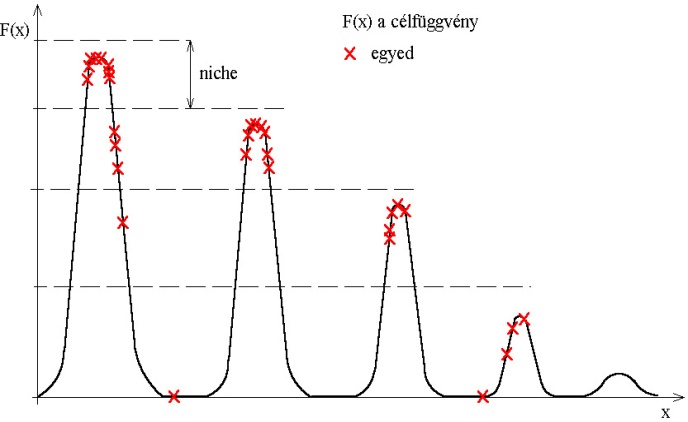
Megfigyelhetjük, hogy a természetben az egyes fajok különböző életkörülményekhez alkalmazkodtak, így a többi fajtól elkülönülve, őket kiszorítva használják fel az erőforrásokat. Ez a kiszorítás nem feltétlenül térbeli jelentésű, az egyes fajok specializálódhatnak egy erőforrás kihasználására vagy problémamegoldó módszer alkalmazására is. Ezeket az egymástól elhatárolt, az egyedek csoportjai által elfoglalt életterületeket nevezi az irodalom niche-nek.
A genetikus algoritmusok területén alkalmazva a niche-ket elérhetjük, hogy az algoritmus a lokális optimumokhoz tartozó megoldásokat is megtalálja. Az eljárás egyik megvalósítási módja a fitness megosztás, amely az egyes egyedek között elosztja egy adott terület fitness értékét. Így limitálja az egyedek számát a megoldások környezetében, ezáltal nem tud az összes egyed a globális szélsőérték köré csoportosulni (5.31. ábra).
5.2.5.2. Fajkialakító módszerek (Speciation methods)
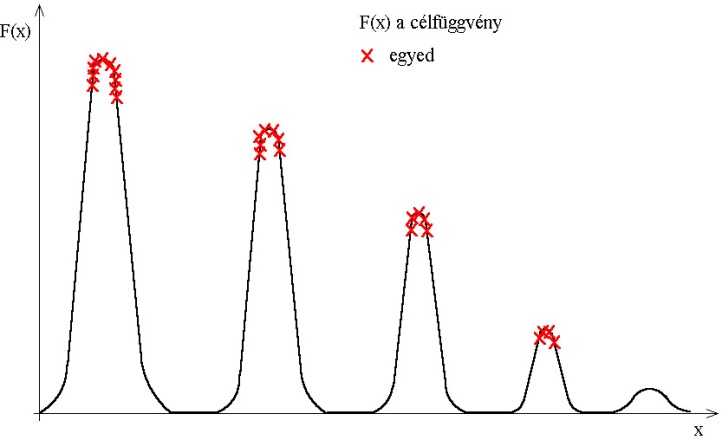
A módszer ötlete abból a megfigyelésből ered, hogy a niche-ket alkalmazó eljárások nem tudnak egyenlő mértékben koncentrálni az egyes lokális optimumokra, és egyenlő hatékonysággal keresni az összes szélsőértéket. Ennek az a magyarázata, hogy az utódok létrehozásához az algoritmus különböző niche-hez tartozó egyedeket is választhat, így mindkét lokális szélsőérték szempontjából rossz egyed jön létre.
A fajkialakító módszerek ezt a problémát úgy küszöbölik ki, hogy csak az egymáshoz hasonló, közeli egyedek hozhatnak létre utódokat. Ha a hasonlóság feltételét megfelelően határozzuk meg, akkor a keletkező egyed is ugyanazon optimum közelében marad (5.35. ábra).
Az életfeltételeket alkalmazó és a fajkialakító modelleket a multikritériumú optimalizálási eseteknél is alkalmazzák. Ezek a feladatok egyidejűleg több célfüggvény szerinti optimalizálást követelnek meg.
A következő modelleket a párhuzamos genetikus algoritmusok területén alkalmazzák. Ezeknél a módszereknél a populáció felosztása az eljárás sebességének növelését célozza.
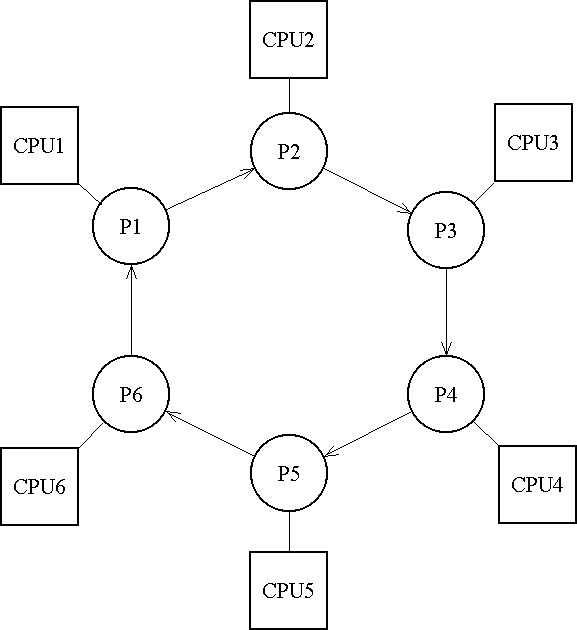
5.2.5.3. Sziget- vagy áttelepedési modellek (Island or Migration modells)
A szigetmodellek a populációt több alpopulációra bontják, és ezek között úgy létesítenek kapcsolatot, hogy bizonyos időközönként az egyedek meghatározott csoportját kicserélik köztük. Az alpopulációkon egymástól függetlenül, általában külön mikroprocesszorok végzik a számításokat (5.36. ábra).
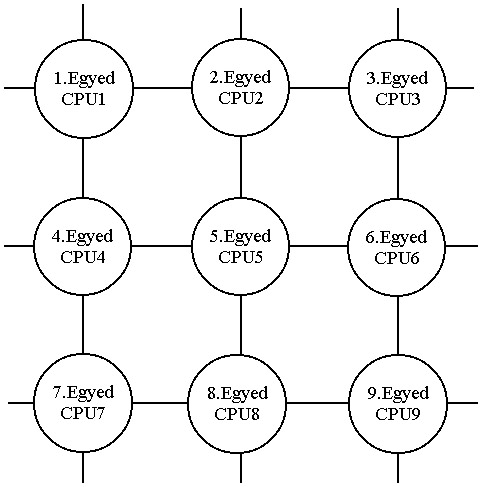
5.2.5.4. Diffúziós vagy celluláris modellek
Mivel az egyedek létrehozása és célfüggvényük kiszámítása egymástól független, ezért párhuzamosan is történhet. A diffúziós modellek esetében az egyes egyedeken végzett műveleteket külön mikroprocesszorok végzik, így még az előzőnél is nagyobb sebességnövekedés érhető el (5.37. ábra).
5.3. A genetikus algoritmusok speciális területei
5.3.1. Multikritériumú optimalizálás
Ha a probléma megoldásához egyszerre több egymással ellentétes célt tűzünk ki, és ezek függvényei az egyedek teljesen eltérő tulajdonságait mérik, akkor multikritériumú optimalizálási feladatról beszélünk. Ebben az esetben a problémának rendszerint nincs egyértelmű megoldása, csak nem alárendelt, alternatív megoldásai, melyet pareto-optimális halmaznak nevezünk.
A multikritériumú optimalizáló eljárásokat alapvetően három csoportba sorolhatjuk:
-
Egyszerű összegző módszerek: a célfüggvények eredményeiből, egy összegző függvény alapján számítják azokat az értékeket, melyekre az optimalizálást végzik.
-
Populáció alapú módszerek: az egyes számítási ciklusokban a célfüggvényeket felváltva alkalmazzák az optimalizáláshoz, vagy a különböző szempontok szerint több rangsort állítanak fel.
-
Pareto-optimumon alapuló módszerek: a pareto-dominancia definíciójának direkt felhasználásával állítanak fel rangsort.
5.3.2. Önadaptációs eljárások
A keresőeljárás hatékonyságát a stratégia paraméterei nagymértékben befolyásolják - ilyenek például a mutációs és a rekombinációs valószínűségek. Az önadaptációt alkalmazó keresőalgoritmusok ezeket a paramétereket a megoldandó probléma paramétereihez hasonlóan optimalizálják az adott keresési feladatra. A stratégia jellemzőit optimalizáló eljárás paramétereit és ezzel a tanulási sebességet a felhasználónak kell meghatároznia.
5.3.3. Metaevolúciós megközelítés
Ez a módszer azt a célt tűzi ki, hogy megtalálja a leghatékonyabb evolúciós algoritmust egy bizonyos feladat megoldásához. Az optimális keresőalgoritmus megtalálásához nemcsak a paramétereket, hanem az operátorok típusait is módosítja.
5.4. A genetikus algoritmusok előnyei és hátrányai
A genetikus algoritmusok áttekintése után, alkalmazásuk szempontjából hasznos, ha megismerjük az előnyeiket és hátrányaikat az egyéb eljárásokhoz viszonyítva.
5.4.1. Robosztusság
Az evolúciós algoritmusok fő tulajdonsága a robosztusságuk, ami azt jelenti, hogy szinte minden probléma megoldására egyformán jó eredménnyel alkalmazhatók.
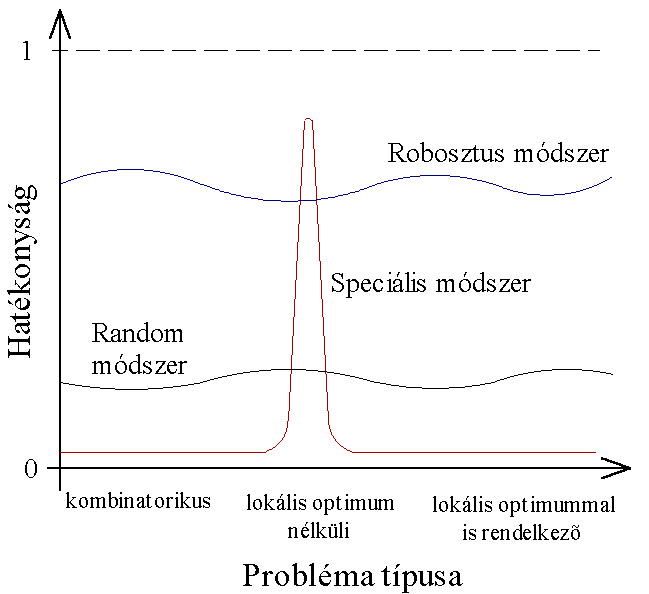
Ennek ellenére egy konkrét feladatra létrehozott speciális keresőeljárással nagyobb hatékonyságot érhetünk el. Abban az esetben, ha ismerünk ilyen optimalizáló módszert, akkor érdemes ezt alkalmaznunk. Ha nem ismerünk, akkor az evolúciós módszerek alkalmazása hatékonyabb megoldás, mint a véletlenszerű keresőeljárások használata.
5.4.2. Lokális és globális szélsőérték
A hegymászó eljárásokkal ellentétben a genetikus algoritmusok a lokális szélsőértékekkel rendelkező célfüggvények esetében is mindig a globális szélsőértékhez tartanak. Egyes típusaikkal egyszerre kaphatjuk meg a globális és lokális szélsőértékeket is.
5.4.3. További előnyök
-
Diszkrét és folytonos problémáknál egyaránt használhatók.
-
A különböző adatreprezentációk segítségével a problémák széles területére alkalmazhatók.
-
Kevés információra van szükségük a problémáról, csak a célfüggvény értékekkel dolgoznak.
-
Egyszerű algoritmusuk miatt könnyen alkalmazhatók minden problémára és könnyen hibridizálhatók.
-
Az eljárások párhuzamos számításokra bonthatók, könnyen párhuzamosíthatók.
-
Egyes problémákra nem ismerünk más megoldást.
5.4.4. Hátrányok
-
A genetikus algoritmusok alkalmazásához nagy gyakorlat szükséges, a hatékonyan működő eljárás paramétereinek beállításához sok kísérletezésre van szükség.
-
A genetikus algoritmusban alkalmazott operátok kiválasztása és a megfelelő algoritmus-szerkezet meghatározása sem könnyű.
-
Az eljárás hátránya még a számítások költségessége, ez a szempont azonban az egyre gyorsabb számítógépek megjelenésével veszít a jelentőségéből.
5.5. A genetikus algoritmus alkalmazásának területei
-
Csomagok összeállítása meghatározott paraméterekkel (pl.: adott térfogattal vagy tömeggel).
-
Útvonal meghatározás: (pl.: több lehetséges útvonal közül a legrövidebb meghatározása.
-
Minimális költségű útvonal meghatározása kommunikációs rendszerekben.
-
Integrált áramköri chip optimális rajzolatának tervezése.
-
Paraméterkeresés tetszőleges alakú görbék közelítéséhez.
-
Ütemezési feladatok megoldása (scheduling problémák).
-
Robotok tanítása (pl.: lépegető robotmozgás tanítása).
-
Aktív zajszűrés, (a szűrő paramétereinek folyamatos hangolása, struktúrájának változtatása).
-
Mesterséges intelligencia: neurális hálók és fuzzy logikák paramétereinek megkeresése.
-
Gazdasági optimumszámítások (pl.: nyereség/erőforrás arány maximalizálása).
-
Beszédfelismerés, alakfelismerés, képfeldolgozás, mesterséges látás (adott minták alapján, tanuló struktúrák paramétereinek meghatározása).
5.6. PI kompenzáció paraméter optimalizálása genetikus algoritmussal
5.6.1. A feladat leírása
A feladat egy szabályozási kör (5.39. ábra) szabályozó paramétereinek beállítása úgy, hogy a szabályozott jellemző () a lehető legpontosabban kövesse az alapjelet ().
A szabályozott szakasz () egy holtidős arányos egytárolós tag (PHT1):
|
|
(5.32) |
A szabályozó () pedig egytárolós integráló tag (PI):
|
|
(5.33) |
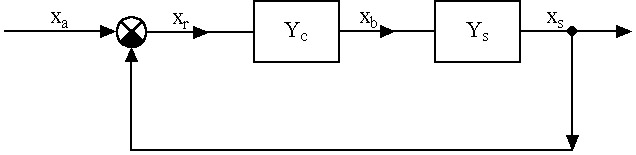
A feladat tehát és meghatározása úgy, hogy és jelek abszolút eltérésének integrálértéke adott időtartamra a lehető legkisebb legyen.
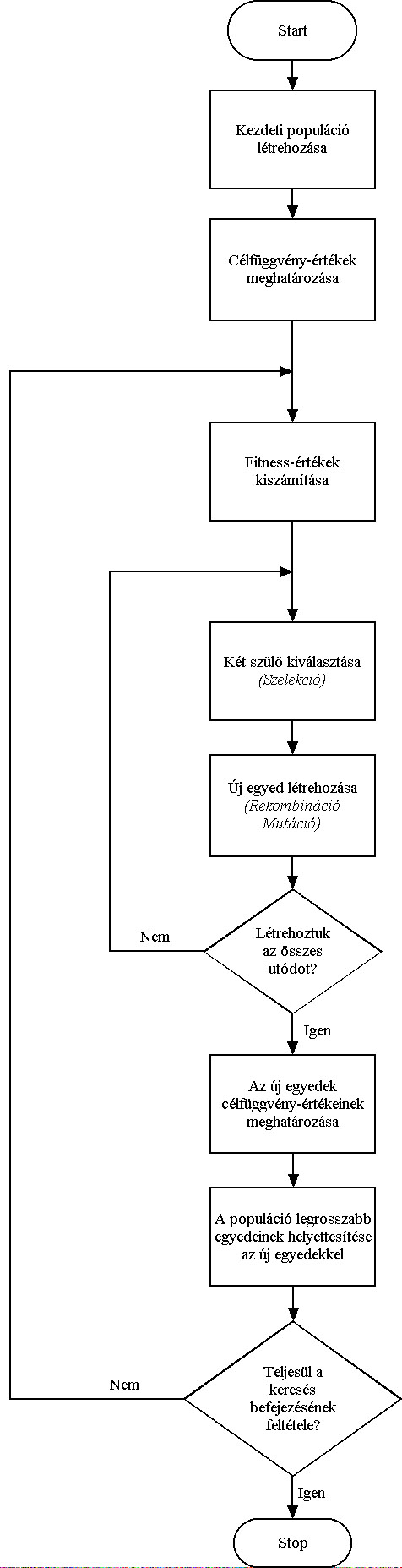
5.6.2. A feladat megoldása
A feladat megoldásához genetikus algoritmust alkalmazunk. Az eljárás a paraméterek (Ap, Ti) optimális értékének meghatározásához célfüggvényként az alapjel és a kimeneti jel abszolút eltérésének integrálértékét használja fel (5.38 egyenlet). Az algoritmus folyamatábrája az előző ábrán (5.41. ábra) látható.
A kezdeti populáció egyedeinek létrehozása és a célfüggvény értékek kiszámítása után kezdődik a keresőciklus. A fitness kiszámítását követően az algoritmus létrehozza az új egyedeket, majd beilleszti őket a populációba, ezután újból a fitness számítás jön.
A programot LabVIEW környezetben fejlesztettük, ami segítette a kezelőfelület kialakítását, míg a számítások egy részét Delphi-ben készített eljárásokkal valósítottuk meg.
5.6.3. Adatreprezentáció
A paraméterek ábrázolása bitsorokkal történik, így egyszerű keresőoperátorokat használhatunk, de a bitek által meghatározott keresési tér és a paramétertér között kódoló eljárást kell alkalmaznunk.
A paramétereket egyenként 16 biten ábrázoljuk, az így elérhető pontosság:
|
-re: , |
(5.34) |
|
|
-re: . |
(5.35) |
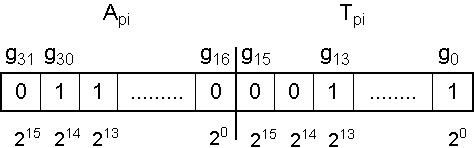
A dekódolás egyenletei:
|
|
(5.36) |
|
|
|
(5.37) |
ahol az egyed i.-edik génje jobbról, pedig a paraméterek minimális és maximális értékei.
5.6.4. Fitness számítás
A megoldások értékeléséhez szükségünk van egy célfüggvényre, ez a (5.38) egyenlettel meghatározott integrálérték. Az integrál nagyságát szimuláció segítségével számítjuk, a TUTSIM modul felhasználásával (genopt.llb → szabszak.vi, 5.43. ábra).
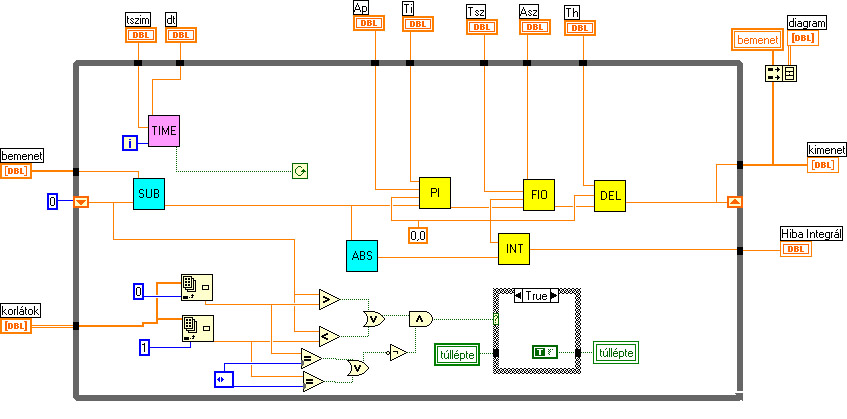
A célfüggvény:
|
|
(5.38) |
Mivel a feladat minimumkeresés, a célfüggvény értékeket ellentettjükre kell változtatnunk és hozzáadnunk a maximális értéket. A szelekciós nyomás növelése érdekében, hatványozáson alapuló, skálázó függvényt alkalmazunk.
A fitness függvény:
|
|
(5.39) |
ahol a populáció legnagyobb célfüggvény értéke, az i. egyed célfüggvény értéke, pedig a programban szabadon megválasztható hatványkitevő.
5.6.5. Az alkalmazott operátorok
A programban az egyedek száma 2-től 100-ig, az utódok száma 1-től 100-ig változtatható, és az egyedeket tömbben tároljuk. Az 5.41. ábra belső ciklusában alkalmazott operátorok végzik a tulajdonképpeni keresést az új egyedek létrehozásával.
5.6.5.1. Szelekció
A szelekciós eljárás a populáció tagjai közül két szülőt választ ki a rulettkerék szelekciót alkalmazva (5.13. ábra). A forráskódban található eljárás (paropt.dll → procedure select) az első szülő meghatározása után egy tőle különböző második szülőt is kiválaszt.
5.6.5.2. Rekombináció
A szülők meghatározása után a keresztező eljárás (paropt.dll → procedure crossover) létrehoz egy utódot. Ehhez k-pontos keresztezést alkalmaz 4 keresztezési ponttal.
5.6.5.3. Mutáció
Az utód létrehozása után a mutációs eljárás (paropt.dll → procedure mutate) az új egyed minden bitjét, egy a programban meghatározható valószínűséggel változtatja meg.
5.6.6. Korlátok kezelése
Az eljárás egy előre meghatározott tartományban keresi a paraméterértékeket. Ezt a tartományt a felhasználónak kell megadnia úgy, hogy a szimulációnak minden esetben legyen megoldása.
Lehetőségünk van a kimeneti jelet egy általunk meghatározott tartományban tartani, amihez statikus büntetőfüggvényt alkalmazunk. A programban a felhasználó egyaránt beállíthatja a korlátokat és a büntető konstans nagyságát.
Korlátos esetben a fitness számításához (5.39 egyenlet) a célfüggvény értékek () helyett a büntetett célfüggvény értéket használjuk:
|
|
(5.40) |
ahol C a büntető konstans.
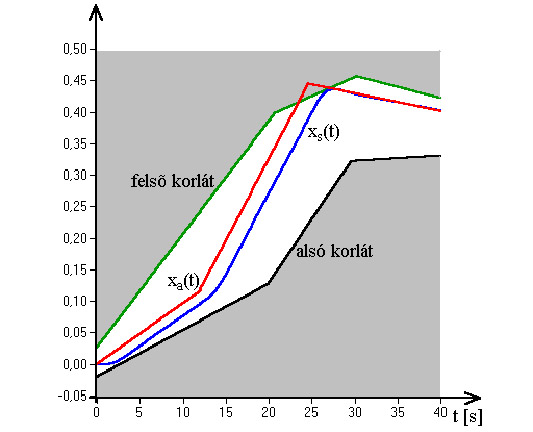
5.6.7. Program kezelési leírása
A programot a LabVIEW alkalmazás segítségével futtathatjuk, a genopt.llb állomány megnyitásával. A kezelőfelületet az 5.45. ábra mutatja.
Az 1. keretben a diagramok a szabályozott jellemző időbeli viselkedését ábrázolják. Az első az éppen létrehozott új egyedet a második pedig az eddigi legjobbat jeleníti meg.
A 2. keretben a grafikonok a generáció sorszámának függvényében ábrázolják a legjobb egyed és a populáció átlagos integrálértékeit.
5.6.8. A program futási eredményei
A program működésének vizsgálatához a következő paramétereket használjuk:
|
As |
Ts [s] |
Th [s] |
tsim [s] |
dt [s] |
|---|---|---|---|---|
|
0,4 |
20 |
1 |
100 |
0,06 |
Az alapjel egységugrás függvény. A szabályozott jellemzőt korlátok segítségével tartjuk az alapjel alatt. A kapott rendszer átmeneti függvénye:
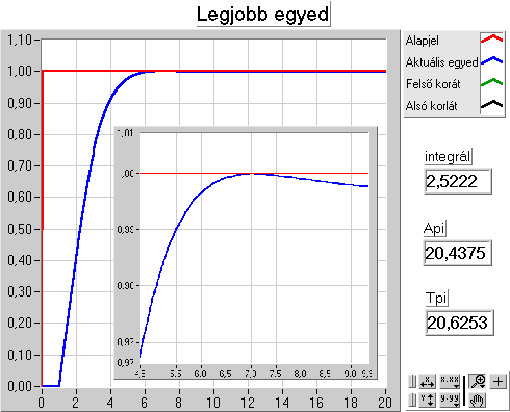
A felnyitott kör átviteli függvénye:
|
|
(5.41) |
A Bode-diagram tiszta integráló jelleget mutat az erősítés diagramon:
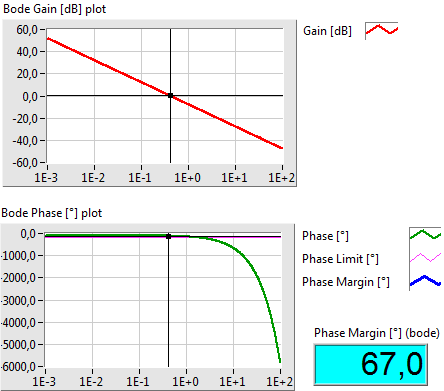
5.6.8.1. A mutációs valószínűség hatása a keresés hatékonyságára
A vizsgálathoz a következő állandó paramétereket vesszük fel:
|
Egyedszám |
Utódszám |
Szelekció hatványa |
[s] |
[s] |
[s] |
[s] |
|
|---|---|---|---|---|---|---|---|
|
16 |
6 |
2 |
0,4 |
20 |
1 |
100 |
0,06 |
A mutáció valószínűségét változtatva a következő eredményeket kapjuk:
|
M: mutáció I: integrál |
A legjobb egyed integrálértéke a generáció sorszámának függvényében |
A populáció átlagos integrálértéke a generáció sorszámának függvényében |
|---|---|---|
|
M=0,01 I=4,07 |
|
|
|
M=0,03 I=2,71 |
|
|
|
M=0,04 I=2,53 |
|
|
|
M=0,05 I=2,69 |
|
|
|
M=0,5 I=2,77 |
|
|
A mutációs valószínűség növelésével az eljárás hamarabb talál jobb megoldásokat, gyorsabb lesz a keresés. Az értékeket egy határon túl növelve a keletkező egyedek nagyobb szórást mutatnak, így csökken az esélye annak, hogy minden lépésben egy jobb egyedet találjon. A túl kicsi és a túl nagy értékek is rontják a hatásfokot.
5.6.8.2. A szelekciós nyomást befolyásoló hatványkitevő hatása a keresésre
Az előző vizsgálatban alkalmazott paramétereket megtartva és a mutációs valószínűséget 0,04-nek választva a szelekciós nyomást változtatjuk:
|
n: kitevő I: integrál |
A legjobb egyed integrálértéke a generáció sorszámának függvényében |
A populáció átlagos integrálértéke a generáció sorszámának függvényében |
|---|---|---|
|
n=1 I=2,87 |
|
|
|
n=2 I=2,9 |
|
|
|
n=2,25 I=2,53 |
|
|
|
n=2,5 I=2,58 |
|
|
|
n=3 I=2,72 |
|
|
A szelekciós nyomás növelése gyorsítja az optimum elérését. Túl nagy érték alkalmazása esetén azonban, már korán leszűkül a keresési terület, így lassulhat az eljárás, különösen lokális optimummal is rendelkező célfüggvény esetén.
A keresés paramétereinek meghatározása nem könnyű feladat, erre az egyik módszer a próbálgatás és a tapasztalatok felhasználása, egy másik érdekes lehetőség az evolúciós algoritmusok alkalmazása.
5.7. Az utazó ügynök probléma megoldása genetikus algoritmussal
5.7.1. A feladat leírása
Az utazó ügynök probléma célja egy olyan útvonal meghatározása, amely az érinteni kívánt koordinátapontok mindegyikén egyszer és csak is egyszer halad keresztül, és a kezdőpontba tér vissza, és eközben a lehető legrövidebb utat járja be. Ez a feladat NP-nehézségű (NP = nem-determinisztikus (nem polinomiális) függvénnyel meghatározható idő), ami azt jelenti, hogy a probléma nem oldható meg pontosan, egy függvénnyel meghatározott időn belül.
A megoldás nemcsak elméleti szempontból jelentős, a gyakorlatban megoldandó feladatok egy része visszavezethető erre a problémára.
Jelen esetben, egy kétdimenziós térben (síkban) elhelyezett pontokat összekötő útvonalat kell meghatároznunk.
5.7.2. A feladat megoldása
A feladat megoldásához genetikus algoritmust alkalmazunk, az útvonalban szereplő pontok optimális sorrendjének meghatározásához, célfüggvénynek pedig az útvonal hosszát használjuk. A keresés folyamatábrája megegyezik az (5.41. ábra) ábrával. A program LabVIEW és Delphi környezetben készült - a kezelőfelület kialakítását a LabVIEW, míg a gyors működés elérését a Delphi segítette.
5.7.3. Adat reprezentáció
A feladat megoldásait a pontok sorrendje adja. Ezt a sorrendet ábrázolja az egyedek DNS-e az egyes pontokat indexeikkel jelölve. A gének így pozitív egész számok lehetnek, minden számnak egyszer és csak egyszer kell szerepelnie a DNS-ben (5.48. ábra).
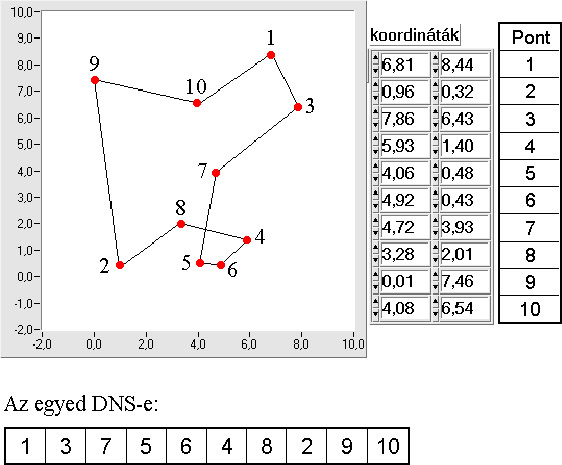
5.7.4. Fitness számítás
A célfüggvény a pontok által meghatározott útvonal élhosszainak összege (5.42 egyenlet).
|
|
(5.42) |
ahol a DNS-ben i-edik helyen található pont indexe, pedig a két pont által meghatározott él hossza.
A célfüggvény alapján számítjuk a fitness értékeket, hatványozó-skálázó függvényt alkalmazva:
|
|
(5.43) |
ahol n értékét a programban szabadon megválaszthatjuk.
A fitness értékeket számító eljárás: Tsp.dll → procedure fitcomp.
5.7.5. Az alkalmazott operátorok
A programban az egyedek száma 2-től 100-ig, az utódok száma 1-től 100-ig változtatható, az ügynök által meglátogatott városok számát 1 és 1000 között adhatjuk meg, és az egyedeket tömbben tároljuk. A keresést az alkalmazott operátorok végzik.
5.7.5.1. Szelekció
A szelekciós eljárás két szülőt választ ki a rulettkerék módszerrel (5.13. ábra). A forráskódban található eljárás: Tsp.dll → procedure select.
5.7.5.2. Rekombináció
A szülők kiválasztása után a keresztező eljárás (Tsp.dll → procedure crossover) létrehozza az utódot. Ehhez sorrendi keresztezést alkalmazunk (5.28. ábra)
5.7.5.3. Mutáció
Az utód létrehozása után a mutációs eljárás (Tsp.dll → procedure mutate) módosítja az új egyedet. Erre a célra szomszédsági mutációt alkalmazunk, két pontot véletlenszerűen kiválasztva a DNS-ben, felcseréljük a köztük levő génszakaszt (5.22. ábra).
5.7.6. Korlátok kezelése
Az algoritmusban alkalmazott operátorok, csak olyan egyedeket hoznak létre, amelyek megfelelnek a megoldásokkal szemben támasztott követelményeknek. Így a korlátokat betartó eljárások nem hoznak létre hibás egyedeket, a keresés korlátok nélküli esetté alakul.
5.7.7. Program kezelési leírás
A programot a LabVIEW alkalmazás segítségével futtathatjuk, a Tsp.vi állományt elindítva. A felhasználói felületet a (5.32. ábra) mutatja.
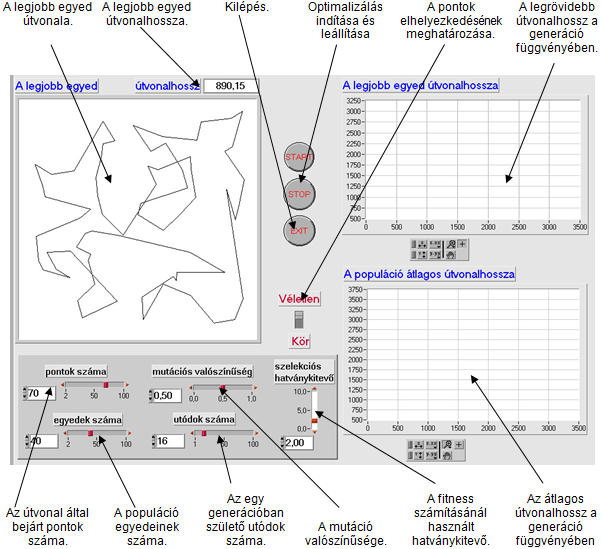
A pontok elhelyezésére kétféle lehetőségünk van, a kör mentén történő elhelyezés a helyes működés megállapítását segíti, a véletlenszerű pedig egy általános feladat megoldásának képességét ellenőrzi.
A beállításokat, a helyes működés érdekében, csak a keresés leállítása után változtathatjuk.
5.7.8. Futási eredmények
A működés vizsgálatához a következő adatokat használjuk:
|
Egyedszám |
Utódszám |
Városok száma |
Mutáció valószínűsége ( m ) |
Hatványkitevő ( n ) |
|---|---|---|---|---|
|
40 |
16 |
70 |
0,5 |
2 |
A pontokat körvonal mentén elhelyezve a következő futtatási eredményeket kapjuk:
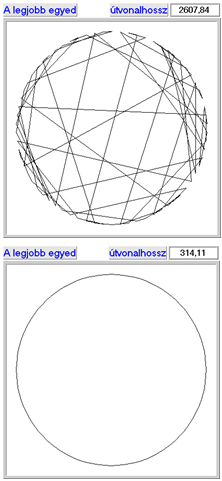
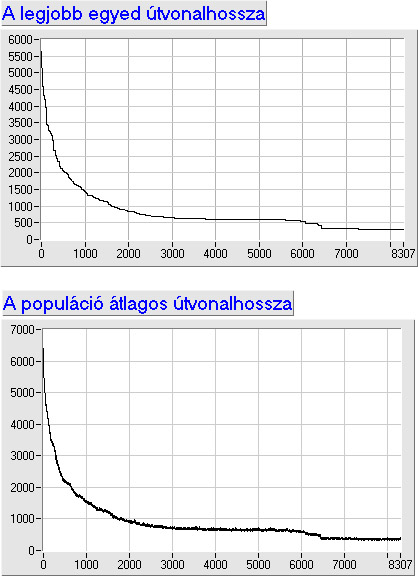
A program 7100 generáció, azaz 113640 egyed létrehozása után találja meg a legrövidebb utat, míg az összes lehetséges egymástól különböző egyed száma darab.
Egy egyed összes meghatározására 1 msec számítási időt feltételezve a teljes számítási idő szükséglet 1,736*1095 sec, amely körülbelül. 0,55 1085 év.
(1 év = 3,1536 107 sec)
5.7.8.1. Véletlenszerű elhelyezés esetén az eredmények:
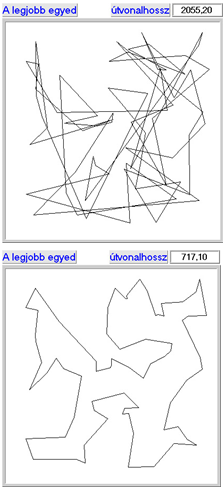
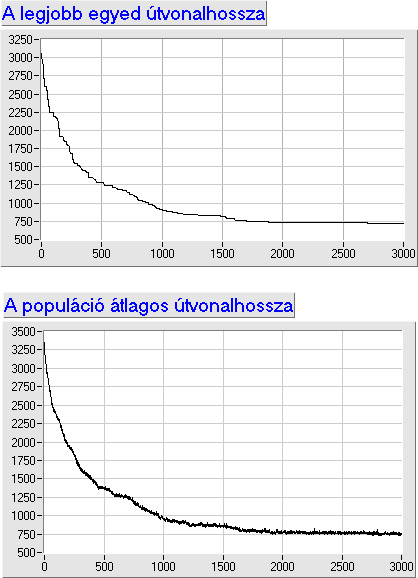
A megoldást 2540 generáció után éri el, a legrövidebb út 717,1 egység, az eljárás szempontjából a véletlenszerű elhelyezés könnyebb feladatot jelent, mint a speciális, körvonal menti esetben.
A legrövidebb útvonalhosszt meghatározó egyed 1000 pont esetén az 50.-ik és a 140000.-ik generációban: