4. fejezet - Lágy számítási módszerek alkalmazása a szimulációban (Soft Computing)
A műszaki (és egyéb területekhez, így biológiához, gazdaságtudományhoz, társadalomtudományhoz stb. tartozó) problémák egy részét analitikusan vagy numerikus módszerek, algoritmusok alkalmazásával meg tudjuk oldani. A megoldáshoz szükségünk lehet (esetleg akár nagy teljesítményű) számítógépre, a beprogramozott algoritmusok futtatására.
A különböző felismerési feladatok (pl. alakfelismerés), a természetes nyelvi szövegek értelmezése vagy akár a komolyabb, rengeteg elágazást kínáló stratégiai játékok algoritmizált, gépesíthető megoldása komoly kihívás. Általános jellemzőjük a megoldás „nehézsége”, amihez az ember szakértelme, tapasztalatai, intelligenciája, intuíciója szükséges, ugyanakkor nem várunk abszolút legjobb megoldást, megelégszünk egy igényeinknek éppen megfelelő „jó” megoldással. Lehetnek ugyan könnyen megfogalmazható problémák, de vagy nincs megoldó algoritmusunk vagy az algoritmus számítási igényeit reálisan nem tudjuk eszközökkel biztosítani, nagyon hosszú ideig (akár a „végtelenségig”) tartana.
Ha nincs hatékony algoritmus, a problémamegoldáshoz a hagyományostól eltérő módszerekre, „intelligens” modellezési és számítási eljárásokra szorulunk. Lágy számítási (soft computing, SC) módszernek nevezzük a hagyományos „kemény” számításnak is nevezhető eljárásokkal ellentétben a határozatlanságot, bizonytalanságot, pontatlanságot, részigazságot és közelítést kezelő, általában biológiai inspirációjú eljárásokat és ezek összekapcsolását.
A „kemény számítások”szabályai szigorúak. A feladat megoldásához szükséges eljárás adott, csakúgy, mint a bemenetek és a kimenetek. A pontos adatok és a jól meghatározott szabályok biztosítják az eredmény pontosságát, nélkülöznek bárminemű bizonytalanságot. A számítás ismétlése mindig ugyanazt az eredményt adja, ha a bemenetek és a számítási szabályok változatlanok.
Ezzel ellentétben a lágy számítások többszöri futtatásra többféle megoldást adnak ugyanarra a feladatra. Ezek közül biztosan lehet a célnak legjobban megfelelőt választani. A soft computing alábbi definícióját L.A. Zadeh – a fuzzy halmazok megálmodója – 1994-ben adta. „A soft computing nem elvek és technikák homogén egysége, hanem különböző – egymástól akár igen távoli – módszerek együttes használata a vezérelvnek megfelelően. A soft computing legfőbb célja (a cikk írásakor) kiaknázni a pontatlanság és bizonytalanság elviselését a kezelhetőség, robosztusság (határozottság, erőteljesség) és alacsony megoldási költség biztosítása érdekében.
A soft computing fő elemei a fuzzy logika, neurális számítások és valószínűségi érvelés, utóbbiba beleértve a genetikus algoritmusokat, a hihetőségi hálókat, kaotikus rendszereket és a tanuláselmélet bizonyos részeit.
A fuzzy logika, neurális számítások és valószínűségi érvelés együttműködésében a fuzzy logika foglalkozik leginkább a pontatlansággal és közelítő érveléssel, a neurális számítások tanulással és görbeillesztéssel, a valószínűségi érvelés pedig a bizonytalansággal és a hihetőség terjesztésével.”
Zadeh definíciója óta jelentősen bővült a soft computing módszerek csoportja, ezt azonban a magyar WikiPedia Lágy számítási modell szócikke az írás pillanatában még nem tükrözi. Az angol Soft computing szócikk sokkal részletesebb csoportosítást ad
-
(mesterséges) neurális hálózatok, angolul (Artificial) Neural networks, rövidítve (A)NN
-
Perceptron
-
-
Support Vector Machines (SVM)
-
fuzzy logika, angolul Fuzzy logic, rövidítve FL
-
evolúciós számítási módszerek, angolul Evolutionary computation, rövidítve, az alábbi részletekkel
-
evolúciós algoritmuosk, angolul Evolutionary algorithms
-
genetikus algoritmusok, angolul Genetic algorithms, rövidítve GA
-
differenciális evolúció, angolul Differential evolution
-
-
metaheurisztikus és raj (például méhraj) intelligencia, angolul Metaheuristic and Swarm Intelligence
-
hangyakolónia optimalizálás, angolul Ant colony optimization
-
részecske-raj alapú optimálás, angolul Particle swarm optimization
-
tűzlégy algoritmus, angolulFirefly algorithm
-
-
valószínűség alapú ötletek, angolul Ideas about probability, beleértve az alábbit:
-
Bayes-hálózat, angolul Bayesian network
-
-
káoszelmélet, angolul Chaos theory
A soft computing módszerek alkalmazási területe igen széles, szimulációban egyebek között komplex rendszerek leírására, rendszerek struktúrájának azonosítására, optimalizálásra használhatók.
4.1. Neurális hálózatok
A (mesterséges) neurális hálózatokat a biológiai neurális hálózatok szerkezete és működése inspirálta. Az emberi agy egymással összekapcsolt neuronjai adták az ötletet, hogy egyszerű számítási egységekből épített hálózatokkal próbáljunk megoldást találni hagyományos algoritmusokkal nehezen vagy egyáltalán nem megoldható feladatokra. Az összetett feladatokhoz, például képfelismeréshez, mozgáskoordinációhoz szükséges „számításokat”, sőt ezt megelőzően a tanulási folyamatot próbáljuk utánozni a szekvenciális működésű számítógépeken mesterséges neurális hálózat építésével és tanításával.
Az emberi (és természetesen állati) agyműködési alapegysége az elektromosan ingerelhető idegsejt (neuron).
Az átlagos idegsejt sejttestből, axonból és dendritekből épül fel. Központi részét, a sejttestet utánozzuk az egyszerű számításokat (súlyozott összegzés és függvényérték számítás) végző mesterséges neuronnal. A neuron egyetlen kimenete az (emberben akár 1 méter hosszú), gyakran százfelé ágazó axon szállítja a „kiszámított” értéket a többi kapcsolódó idegsejt felé. A dendritek is a sejttestből ágaznak ki akár több száz mikrométerre és többször elágazva dendritfákat képeznek. A szinapszisok teremtenek kapcsolatot az idegsejtek között, legnagyobb részük az egyik idegsejt axonját kapcsolja egy másik dendritjéhez. Léteznek különleges kapcsolatok is, így dendrit nélküli neuronok, axon nélküliek, axont axonnal vagy dendritet dendrittel összekötő szinapszisok.
Az emberi agy kb. 85·109 neuronjából hozzávetőleg 20·109 működik a magasabb rendű agykérgi központokban. A felnőtt ember agyában becslések szerint 1-5-ször 1014 szinapszis van. Az agykérgi szinapszisok száma köbcentiméterenként nagyjából 109. Az idegsejt villamos és kémiai jelek segítségével dolgozza fel és továbbítja az információt. A neuronok közötti elektromos jel 100 m/s sebességgel halad, majd az információ általában kémiai, ritkábban elektromos jelek formájában jut a szinapszisokon keresztül a többi idegsejthez. A kémiai jelátvitelű szinapszisokban a pre- és posztszinaptikus (axon-dendrit) rés 30 nanométer körüli, az oda-vissza haladásra képes neurotranszmitter diffúziójával, (csak egy irányban) jut át az információ. Az elektromos szinaptikus kapcsolatban az axon-dendrit távolság hozzávetőleg egy nagyságrenddel kisebb, a jelátvitel sokkal gyorsabb, az ingerület oda-vissza haladhat. A kapcsolatban résztvevő idegsejtek száma szerintmonoszinaptikus (egy idegsejt egy másikat informál) vagy poliszinapsztikus. A szinapszis serkentő és gátló jellegű lehet, előbbin áthalad, utóbbin elakad az ingerület. Serkentő szinapszisra érkező ingerület összeadódik (szummáció) és „erősebbként” halad tovább. Gátló kapcsolat esetén, ha a serkentő mellett gátló neurotranszmitter is képződik, a jelentősebb hatásnak megfelelően „akad el” vagy halad tovább az impulzus. Az ingerület a szinapszisokban divergensen vagy konvergensen haladhat tova. Előbbinél szétterjed, egy preszinaptikus neuron több posztszinaptikusnak adja át az ingerületet. Utóbbi esetben a több neuronról érkező ingerület összeadódik.
A neuronok alapvetően binárisan működnek, a neuron vagy kiad egy impulzsut, szakszóval „tüzel” vagy „nem tüzel”. Tüzelés után mondhatni újra kell töltődnie, a következő jel csak bizonyos – tipikusan 1 milliszekundum – idő után indulhat, vagyis a tüzelési frekvencia 1 kHz vagy kevesebb. A biológiai neurális hálózatok tehát ugyan kisebb órajellel működnek, mint a korszerű számítógépek, azonban hatékonyságuk a párhuzamos, elosztott működésű, (a férgek néhány száz, a patkány ezer körüli, a rovarok milliós, a macska milliárdnyi stb.) elemi egységének és az ezek közötti nagyságrendekkel nagyobb számú kapcsolatnak köszönhetően sokkal nagyobb. Egy neuron átlagosan néhány 100–1000 más neuronhoz kapcsolódva igen összetett rövid– és hosszú hatótávolságú kapcsolatokat és sok visszacsatolást tartalmazó hálózatot alkot.
Ezzel szemben egy digitális számítógép ugyan sokkal nagyobb tempóban, de jellemzően sorban egymás után hajtja végre a műveleteket. A számítógépek műveletvégzését irányító központi órajelhez hasonló, a neuronokat szinkronizáltan „működtető” órajel a természetes neurális hálózatokban nincsen. Az idegsejtek (együtt)működését a szinapszisok határozzák meg. Szinapszisok „eltávolítása” vagy újak „hozzáadása” a hálózat struktúráját és ezen keresztül műveletvégzését változtatja. Gyakran mondjuk, hogy a szinapszisok felelősek az információtárolásért, bár szükséges lehet egyéb szempontok (pl. a jelek közötti időzítés) figyelembevételére is.
Az állatvilág egyik csodálatraméltó jellemzője a tanulás és megjegyzés képessége, emlékezés múltbeli eseményekre és a tapasztalatok alapján a viselkedés változtatása.
A neurális hálózatokat hardverként is próbálták és próbálják utánozni, ám gyakoribb a szoftveres megoldás. A mesterséges neuron több bemenetű, egy kimenetű, egyszerű számítási egység. A mesterséges neurális hálózatok egy vagy több ilyen elemi egységből épülnek fel.
A neuronok között továbbított jelek binárisak, esetleg nulla és egy közötti értéket vehetnek fel. A szinapszisoknak megfelelő kapcsolatot numerikus súlytényezők (connection weight) biztosítják.
Az elemi egységek lehetnek rétegekbe szervezettek vagy alkothatnak laza, észlelhető szervezettség nélküli hálózatot. Ehhez kapcsolódik, hogy a neurális hálózat az elemek összekapcsolása szempontjából lehet egyirányú (feedforward neural network, FFNN) vagy tartalmazhat visszacsatolásokat (recurrent neural network, RNN).
A hálózatműködése időbeli viselkedés alapján a gyakoribb diszkrét (discrete-time neural network, DTNN) vagy folytonos idej ű (continuous-time neural network, CTNN). Előbbi típus kiváló adatok csoportosítására és függvény approximációra, utóbbit például folyamatosan változó jeleket igénylő irányítási rendszerekben alkalmazzák.
A neurális hálózatok tanítására – leggyakrabban a súlytényezők hangolására, ritkábban a struktúra módosítására – is sokféle módszert fejlesztettek (és fejlesztenek), utánozva a biológiai tanulási mechanizmusokat. A tanítási módszerek két nagy csoportja a felügyelt (supervised learning) és az önálló (felügyelet nélküli, unsupervised), bár vannak egyértelműen egyik csoportba sem sorolható eljárások. Felügyelt tanítás (tanárral tanulás) esetén a hálózatba vezetett bemenet vektorhoz kimenet vektor tartozik, azaz adott bemenethez ismert a várt kimenet. Ilyenkor a tanítás célja a hálózat által számított kimenet (a tanuló) és az elvárt (a tanár) közötti különbség (hiba) csökkentése. A felügyelet nélküli tanulás (kritkussal tanulás) folyamán nincs minden bemenet vektorhoz kimenetünk. Az önállóság természetesen ebben az esetben nem teljesen helytálló, hiszen valamiféle visszajelzésre (alkalmankénti kritikára) szükség van a tanulás során. Erre a tanítási módszerre is jellemző az eredmények ellenőrzése, azonban nem minden számítási (idő)lépésben, hanem csak bizonyos tanulási idő elteltével.
4.1.1. Mesterséges neuron, a számítás alapegysége
Ahogyan idegsejt is többféle van, mesterséges neuron modellből is jó néhány készült.
4.1.1.1. McCulloch–Pitts (MCP) neuron
Warren McCulloch és Walter Pitts 1943-ban „A Logical Calculus of Ideas Immanent in Nervous Activity” című cikkükben írták le a róluk elnevezett bináris jelekkel működő McCulloch–Pitts neuront. Ha bemeneteinek súlyozott összege eléri az ingerküszöb értékét, a neuron tüzel, kimenete egy, különben nulla. A neuron n darab bemenetét x k -val jelöljük, ahol k=1, 2, …, n. Az egyes bemenetekhez tartozó, összesen szintén n darab súlytényező jele w k . A w k >0 súlytényező a serkentő, a w k <0 gátló hatást fejez ki, a biológiai analógiát követve. A MCP neuron sajátsága az azonos súlytényező az összes serkentő bemenetnél.
Természetesen ha hálózatba kapcsoljuk az MCP neuronokat, a különböző neuronokhoz vezető ágak nem szükségszerűen azonos súlyúak. A neuron y kimenetét egy ideális relének megfelelő jelleggörbéjű aktiváló függvénnyel határozzuk meg. Az aktiváló függvényben lévő b ingerküszöb (bias) értéke megakadályozza a neuron tüzelését, ha bármely gátló (negatív súlyú) bemenet értéke nem nulla. A b ingerküszöb értékét gyakran egy x 0 =1 értékű fiktív bemenettel és a hozzárendelt w 0 =-b súlytényezővel vesszük figyelembe. A neuron kimenetét egy időlépés alatt számítjuk. Ha az MCP neuron összes bemenete nulla, a küszöbérték határozza meg, hogy a neuron tüzel-e, egy jelenik-e meg a kimenetén. (Az aktiváló függvényt emlegetik „átviteli függvényként” is, ez azonban nem azonos a lineáris rendszerek átviteli függvényével!)
Egy két bemenetű MCP neuron (4.1. ábra) egyenlete
|
|
(4.1) |
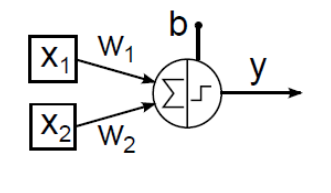
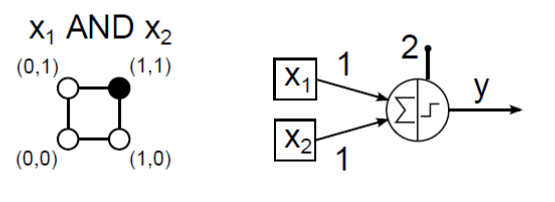
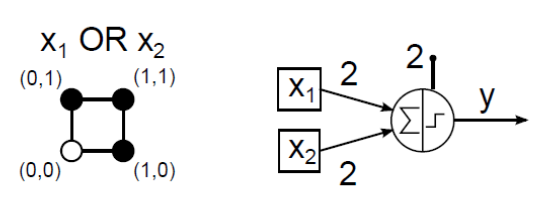
McCulloch–Pitts neuronnal megpróbálhatjuk leképezni a 16 lehetséges két bemenetű (x 1 , x 2 ) logikai függvényt. Az AND (logikai és) kapcsolat (4.2. ábra) és az OR (logikai vagy) függvény (4.3. ábra) MCP neuronos megvalósítása viszonylag egyszerűen meghatározható.
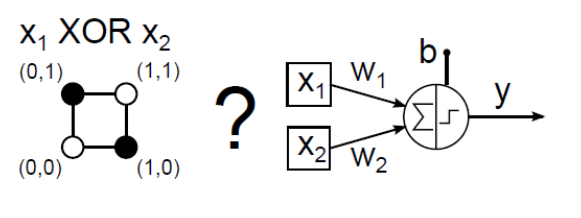
Az XOR (kizáró vagy) kapcsolat egy MCP neuronos utánzása (4.4. ábra) hosszadalmas próbálkozással sem sikerül.
4.1.1.2. Perceptron
A McCulloch–Pitts neuron egyik korlátja az egyszerűsége. Kizárólag bináris bemeneteket és kimeneteket kezel, csak az ideális relé jellegű aktiváló függvényt használja, és nem teszi lehetővé a serkentő bemenetek eltérő súlyozását. 1949-ben Donald Hebb „The Organization of Behavior” című könyvében javasolta a később Hebb–szabálynak nevezett neurális hálózat tanulási módot. Ha egy „A” idegsejt axonja elég közel van a „B” neuron ingerléséhez és ismételten hozzájárul utóbbi tüzeléséhez, valamiféle növekedés vagy metabolikus változás zajlik le egyik vagy mindkét sejtben. E változás „A” hatékonyabb közreműködése a „B” tüzelését kiváltó egyik sejtként. Hebb nem csupán azt gondolta, hogy két neuron együttes tüzelése erősíti kettejük kapcsolatát, hanem ez egyben a tanuláshoz és emlékezéshez szükséges egyik alapművelet.
Hebb ötlete a McCulloch–Pitts mesterséges neuron módosítását igényelte. A változás a bemenetek önálló súlyozása, vagyis az egységnyi bemenet az összes bemenet súlyozott összegében kisebb vagy nagyobb szerepet játszhat.
Frank Rosenblatt a McCulloch–Pitts neuront és Hebb javaslatát alapul véve alkotta meg az első perceptront és mutatta be 1962-es „Principles of Neurodynamics” című könyvében. Ez a Hebbi értelemben, a bemenetek súlyozásával tanulásra képes perceptron lett a későbbi neurális hálózatok alapja.
A perceptron (akár folytonos értékű) bemeneteihez különböző súlyok rendelhetők, sőt a perceptron „megtanulhatja” egyik–másik bemenet a többinél „erősebb” súlyozását. Az n bemenetű perceptron bemeneteinek (akár bemenetenként eltérő súllyal) előállított összege a b (inger)küszöb értékével összegezve
|
|
(4.2) |
A σ aktiváló függvény a küszöbértékkel kiegészített súlyozott összeggel számolja a neuron
kimenetét.
|
|
(4.3) |
A „küszöb–logikát” használó MCP neuron σ aktiváló függvénye a „mindent vagy semmit” biológiai elvet követve ideális relével közelíthető. Mivel a b ingerküszöböt a súlyozott összeg mellett vettük figyelembe (az ott bemutatotthoz képest ellentétes előjellel), a relé a bemenő jel 0 értékénél kapcsol.
|
|
(4.4) |
Hiába a sok változtatás az eredeti McCulloch–Pitts neuronon, egy perceptron sem alkalmas például az XOR-t és a hasonló lineárisan nem szétválasztható függvényeket utánozni. A nehézségeket valamelyest leküzdhetővé tette a neurális hálózatok bevezetése. A perceptront tekinthetjük McCulloch–Pitts neuronok hálózatának is, hiszen egy bemeneti rétegből, és az egy vagy több kimenetet változtatható súlytényezőkkel „összekötő rétegből” áll. A bemenetek asszociációs egységnek nevezett előfeldolgozókon keresztül jutnak a tényleges feldolgozást végző neuronhoz. Az asszociációs egységek a bemenetben bizonyos „mintázatokat” érzékelnek, hasonlóan biológiai ötletadójukhoz (a látóterünkben megjelenő képeken pl. az élek felismerése). Minden asszociációs egység tulajdonképpen MCP neuron, ami a bemenetek bizonyos felismert mintázatára 1 értékű kimenetet ad, egyébként pedig nullát. Az asszociációs egységek a perceptron összes bemenete közül bizonyos számút kapnak, nem feltétlenül az összeset. Valamennyi asszociációs egység kimenete a következő rétegben lévő egyetlen McCulloch–Pitts neuron bemenete. E MCP neuron kimenete pedig a perceptron kimenete. Az említett 16 lehetséges logikai függvény közül az egyetlen MCP neuronnal megvalósítható AND NOT két példánya és az OR (logikai vagy) segítségével kétrétegű MCP neurális hálózattal tudjuk leképezni az XOR függvényt (4.6. ábra).
Az AND NOT az x 1 bemenet AND (logikai és) kapcsolata az x 2 bemenet negáltjával, vagyis ellentettjével (4.5. ábra).
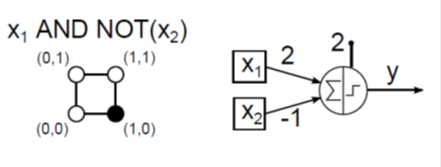
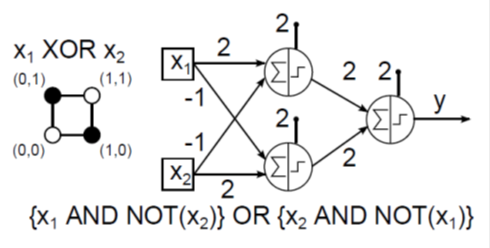
Ha végignézzük a bemutatott logikai függvények (x 1 , x 2 ) számsíkbeli leképezését a logikai igaz (1) értéknek megfeleltetett fekete ponttal és a logikai hamis (0) fehér pontjával, észrevehetjük, hogy a lineárisan szétválaszthatókat egyrétegű MCP neurális hálózattal tudjuk megvalósítani (4.2. ábra, 4.3. ábra és 4.5. ábra). A lineárisan nem szétválasztható ponteloszlást mutató XOR egyrétegű hálózattal (4.4. ábra) nem képezhető le, csak kétrétegűvel (4.6. ábra).
A perceptron tanulási szabállyal az n bemenetű neuron súlytényezőit (a b küszöbértéket állandó 1 értékű bemenet súlytényezőjének tekintve) úgy tudjuk módosítani, hogy a rendelkezésre álló lineárisan szétválasztható minták között lehetséges határvonalak egyikét megkapjuk.
A perceptron tanulási szabályban használt elemek:
-
a neuron bemenetei:
-
a neuron súlytényezői:
-
a súlytényezőhöz tartozó bemenet
-
a neuron által számított súlyozott összeg:
-
a neuron kimenete:
-
a w súlyvektorra merőleges határvonal egyenlete:
-
a t darab tanulási adat párok formájában áll rendelkezésünkre, ahol , az i-edik bemenet vektor és o i az i-edik kimenet
-
a tanulási adatokkal kiszámíthatjuk az i-edik adatnál a neuron kimenete és a tanulandó kimenet különbségét, a hibát: , ahol y i az i-edik tanulási bemenettel számított kimenet
A módosított súlytényezőket és küszöbértéket az i -edik tanuló adatnál a korábbi w és b értékekből az alábbiak szerint számoljuk
|
|
(4.5) |
|
|
|
(4.6) |
Határozzuk meg az AND (logikai és) függvényt leképező két bemenetű perceptron súlytényezőit és küszöbértékét!
A tanító adatok a (Táblázat 4.1) táblázatban szerepelnek. Szemléletes a logikai és leképezése az (x 1 , x 2 ) számsíkon, a logikai igaz (1) értéknek megfeleltetett fekete ponttal és a logikai hamis (0) fehér pontjával (4.7. ábra).
|
sorszám |
bemenet |
kimenet |
|---|---|---|
|
1 |
[0 0] |
0 |
|
2 |
[0 1] |
0 |
|
3 |
[1 0] |
0 |
|
4 |
[1 1] |
1 |
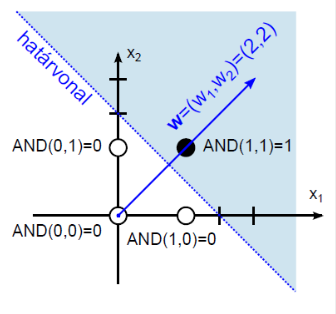
A határoló egyenest válasszuk úgy, hogy a (0; 1,5) és (1,5; 0) ponton menjen át. A határvonal egyenlete így x 2 = -x 1 +1,5. Erre merőleges súlyvektort választunk, például a w =(2; 2) értékűt. A határvonal egy pontját, például az (1,5; 0)-t és a választott súlyvektort használhatjuk a b küszöbérték meghatározására, hiszen a határvonalhoz 0 kimenet tartozik.
|
|
(4.7) |
A w =(2; 2) súlytényezőkkel és a b=-3 küszöbértékkel felírhatjuk a határvonal egyenletét.
|
|
(4.8) |
A logikai igaz értékhez tartozó (a 4.7. ábra ábrán sötéttel jelölt) terület határvonalhoz viszonyított helyzetét egy biztosan ide tartozó pont, például a (2;2) mint bemenet helyettesítésével határozhatjuk meg.
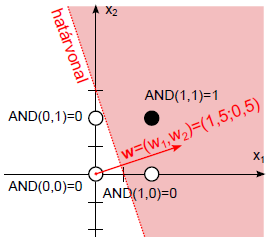
Ha először nem megfelelő határvonalat és erre merőleges súlyvektort választunk, a perceptron tanulási szabállyal eljutunk egy megfelelő megoldáshoz.
Válasszuk a láthatóan (4.8. ábra) rossz, (0; 1,5) és (0,5; 0) ponton áthaladó határvonalat! Az erre merőleges súlyvektor legyen w = (1,5; 0,5)! A (0; 1,5) pontot helyettesítve
|
|
(4.9) |
A relé jelleg ű aktiváló függvény bemenete ezzel
|
|
(4.10) |
A négy tanító adattal végigszámolva az alábbi eredményt kapjuk (Táblázat 4.2). A w = (1,5; 0,5) súlytényezőkkel és a b=-0,75 küszöbértékkel felírhatjuk a határvonal egyenletét.
|
|
(4.11) |
|
sorszám |
bemenet |
kimenet o |
számított z |
számított y |
hiba e=o-y |
|---|---|---|---|---|---|
|
1 |
[0 0] |
0 |
-0,75 |
0 |
0 |
|
2 |
[0 1] |
0 |
-0,25 |
1 |
0 |
|
3 |
[1 0] |
0 |
0,75 |
1 |
-1 |
|
4 |
[1 1] |
1 |
1,25 |
1 |
0 |
A (Táblázat 4.2) táblázatból kiderül, hogy a 3. tanító adatnál hibás eredményt kapunk, e 3 =-1. A perceptron tanítási szabály alkalmazásával a harmadik tanító adatra újraszámoljuk a súlyvektort és a küszöbértéket.
|
|
(4.12) |
|
|
|
(4.13) |
A w = (0,5; 0,5) súlytényezőkkel és a b=0,75 küszöbértékkel felírhatjuk a határvonal egyenletét.
|
|
(4.14) |
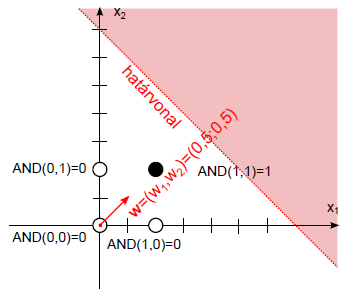
Az újraszámolt értékekkel ellenőrizzük az egyes tanító adatokat (Táblázat 4.3).
|
sorszám |
bemenet |
kimenet o |
számított z |
számított y |
hiba e=o-y |
|
1 |
[0 0] |
0 |
-1,75 |
0 |
0 |
|
2 |
[0 1] |
0 |
-1,25 |
0 |
0 |
|
3 |
[1 0] |
0 |
-1,25 |
0 |
0 |
|
4 |
[1 1] |
1 |
-0,75 |
0 |
1 |
A (Táblázat 4.3) táblázatból kiderül, hogy most a 4. tanító adatnál kapunk hibás eredményt, e 4 =-1. A perceptron tanítási szabály alkalmazásával a negyedik tanító adatra újraszámoljuk a súlyvektort és a küszöbértéket.
|
|
(4.15) |
|
|
|
(4.16) |
A w = (0,5; 0,5) súlytényezőkkel és a b=-0,75 küszöbértékkel felírhatjuk a határvonal egyenletét.
|
|
(4.17) |
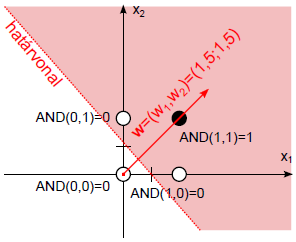
Az újraszámolt értékekkel ismét ellenőrizzük az egyes tanító adatokat (Táblázat 4.4).
|
sorszám |
bemenet |
kimenet o |
számított z |
számított y |
hiba e=o-y |
|---|---|---|---|---|---|
|
1 |
[0 0] |
0 |
-0,75 |
0 |
0 |
|
2 |
[0 1] |
0 |
0,75 |
1 |
-1 |
|
3 |
[1 0] |
0 |
0,75 |
1 |
-1 |
|
4 |
[1 1] |
1 |
2,25 |
1 |
0 |
Ez a súlyvektor és küszöbérték sem jó, a második és harmadik adatra egyaránt hibás eredményt kapunk. Válasszuk ki a második adatsort és alkalmazzuk erre a perceptron tanulási szabályt e 2 =-1 felhasználásával! (Természetesen dolgozhatnánk a harmadik értékkel is.)
|
|
(4.18) |
|
|
|
(4.19) |
Az újraszámolt értékekkel ismét ellenőrizzük az egyes tanító adatokat (Táblázat 4.5).
|
sorszám |
bemenet |
kimenet o |
számított z |
számított y |
hiba e=o-y |
|---|---|---|---|---|---|
|
1 |
[0 0] |
0 |
-1,75 |
0 |
0 |
|
2 |
[0 1] |
0 |
-1,25 |
0 |
0 |
|
3 |
[1 0] |
0 |
-0,25 |
0 |
0 |
|
4 |
[1 1] |
1 |
0,25 |
1 |
0 |
A negyedik lépésben végre hibátlan eredményt kaptunk! A w = (1,5; 0,5) súlytényezőkkel és a b=-1,75 küszöbértékkel felírhatjuk a határvonal egyenletét.
|
|
(4.20) |
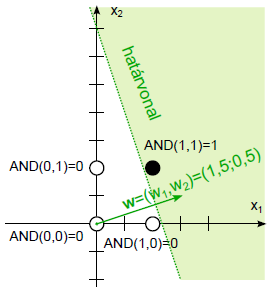
A négy egymást követő lépés eredménye a (4.12. ábra) ábrán látható. Ha a harmadik lépés után a hibát eredményező tanító adatok közül nem a másodikat, hanem a harmadikat választjuk, további lépések szükségesek a megfelelő határvonal meghatározásához.
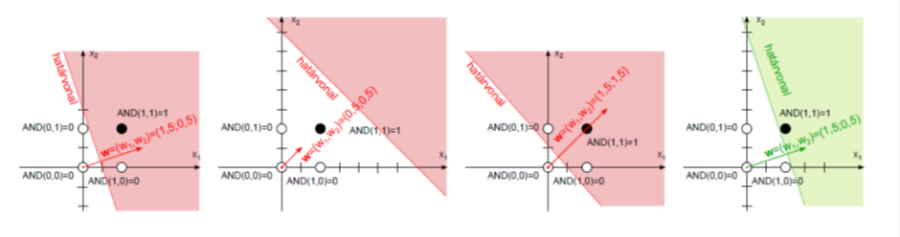
A ma használt neurális hálózatok az MCP neuronból és a perceptronból erednek, azonban sokkal összetettebb feladatok megoldására alkalmasak, mint bármelyik elődjük.
4.1.1.3. ADELINE
Az ADALINE (ADAptive LInear NEuron, adaptív lineáris neuron vagy későbbi nevén ADAptive LINear Element, adaptív lineáris elem) egyrétegű neurális hálózatot Bernard Widrow és Marcian Edward Hoff építette 1960-ban. A McCulloch-–Pitts neuronon alapuló ADALINE súlyokat, ingerküszöböt és összegzést tartalmaz, aktiváló függvényt azonban nem. A súlytényezők módosítása a tanulási fázisban a bemenetek súlyozott összege alapján történik. A perceptronban ez az összeg az aktiváló függvénybe kerül és így adja a neuron súlytényezők módosításához használt kimenetét. A neuron y kimenetét az x bemenet vektor w -vel súlyozott összegéből és a b állandóból kapjuk.
|
|
(4.21) |
A b értéket is tekinthetjük az x 0 =1 állandó értékű bemenet w 0 súlytényezőjének.
|
|
(4.22) |
Az ADALINE tanítása a súlytényezők véletlenszerű felvételével kezdődik. A tanítás epoch nevű (szó szerint fordítva korszak, értelme szerint a teljes tanítási adatsorozaton végighaladó) egységekben zajlik, egy epoch alatt az összes (i=1,2,…, t) tanítási adatot (bemenet vektor–kimenet párt) megkapja a neuron. A súlytényezők módosítása a számított kimenet és a tanítási adatban megadott kimenet különbsége alapján történik. A Widrow-Hoff más néven Delta-szabály a súlyokat a legkisebb négyzetek módszere szerint változtatja.
A tanításhoz használt t bemenet vektorunkkal és a pillanatnyilag érvényes w súlytényezőkkel állítjuk elő a neuron kimenetét az összes (t) tanítási adatra.
Az i-edik (i=1,2,…, t) tanítási adatra felírhatjuk a várt o i és a számított y i kimenet e i különbségét az tanító bemenet vektor segítségével
|
|
(4.23) |
Az összes tanító bemenet hibájából előállíthatjuk a teljes négyzetes hibát
|
|
(4.24) |
A négyzetre emelés pozitívvá teszi a hibát és a nagyobb eltérést jobban hangsúlyozza. Az ½ szorzótényező a későbbi számítást (deriválás) könnyíti meg. A hiba minimalizálásához gradiens módszert használunk. A j+1-edik számítási lépéshez az alábbiak szerint határozzuk meg a súlytényezőket a j pillanatbeli súlyok segítségével
|
|
(4.25) |
Az η tanulási ráta bevezetésével, a hibafüggvény gradiensének megfelelő elemével (parciális deriválttal) írhatjuk fel a súlytényező változását
|
|
(4.26) |
A parciális derivált a fentiek alapján
|
|
(4.27) |
Ezzel a súlytényező változása
|
|
(4.28) |
Így a módosított (a következő, j+1-edik számítási lépésben használt) k -adik súlytényező (k=0, 1, 2, …, n)
|
|
(4.29) |
Az adaptív szűrőkben (pl. zaj eltávolításra) ma is gyakran alkalmazott Delta–szabály (Widrow–Hoff szabály) a súlytényező módosítását a neuron kimenet előírttól eltérése és a súlytényező korábbi értéke alapján, az η tanulási ráta segítségével számolja.
4.1.1.4. Továbblépés, a kimenet számítása
A neuronok működését tovább „finomíthatjuk” a küszöbérték logikánál fokozatosabb átmenetet biztosító aktiváló függvények, így szakaszonként lineáris függvény (telítődés nemlinearitás) és a különböző szigmoid függvények használatával.
Ha a neuron kimenetét a relé be- vagy kikapcsolt állapota között fokozatosan változó (nulla és egy közötti) értékkel szeretnénk inkább megadni, szigmoid jellegű aktiváló függvényt használunk.
A szigmoid korlátos, differenciálható valós függvény, értelmezési tartománya a valós számok halmaza, értékkészlete a valós számok körében értelmezett [0, 1] zárt intervallum. Derivált függvénye harang alakú. Határértéke z→-∞ esetén nulla, z→+∞ -nél egy, mindkét határértéknél vízszintes érintővel. A σ(z) szigmoid függvény kielégíti a
|
|
(4.30) |
differenciálegyenletet, amit peremérték feladatként kezelve harmadik paraméterként c 3 is megjelenik a megoldásban. A differenciálhatóság a neurális hálózat tanításánál kap szerepet.
Néhány jellegzetes szigmoid függvény képlete szerepel a (Táblázat 4.6) táblázatban. A [0; 1] értékkészletre normált aktiváló függvények a (4.13. ábra) ábrán láthatók. (Előfordul természetesen [-1; 1] értékkészlet ű aktivációs függvény is bizonyos neurális hálózatokban.)
|
Képlet |
Elnevezés |
|---|---|
|
ahol c>0 |
logisztikai függvény, bár gyakran ezt hívják szigmoidnak a neurális hálózatokkal foglalkozók |
|
arcus tangens függvény |
|
|
tangens hiperbolicus függvény |
|
|
a (Gauss–féle) hibafüggvény |
|
|
példa algebrai függvényre |
|
|
másik példa algebrai függvényre |
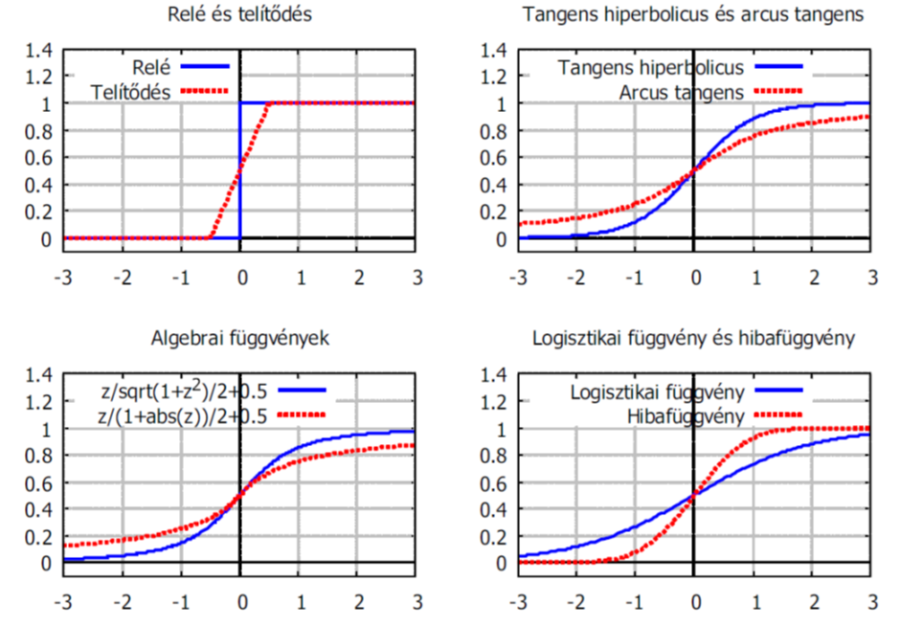
A talán leggyakrabban használt és a neurális hálózatokkal foglalkozók körében szigmoidnak
nevezett (egyébként logisztikai függvény) aktiváló függvény (c>0)
|
|
(4.31) |
A gépi számítás egyszerűsítése érdekében a neuron bemeneteit és a hozzájuk tartozó súlyokat vektorként kezeljük. A b küszöbértéket x 0 =1 állandó értékű, w 0 =b súlytényezőjű bemenetnek tekintve az n bemenetű neuron n+1 bemenetűvé válik.
|
|
(4.32) |
Ha oszlopvektorként kezeljük a bemeneteket ( x ) és a súlytényezőket ( w ), az n bemenetű neuronban képzett z súlyozott összeg tömörebben írható
|
|
(4.33) |
Biológiai analógia értelmezhető, ha a neuron y kimenetét bizonyos időtartam alatti átlagos tüzelési frekvenciának tekintjük, a neuron tényleges kimeneti impulzusával szemben. A bemenetek súlyozott összegét az aktiváló függvényen átvezető neuron modell diszkrét idejű használatra alkalmas, hiszen a kimenet meghatározása egy számítási (idő)lépés alatt történik.
A kimenetre vonatkozó τ időállandóval jellemezhető egytárolós arányos tulajdonság hozzáadásával a neuron modell folytonos idejűvé alakítható.
|
|
(4.34) |
4.1.2. Előrecsatolt neurális hálózat
A többrétegű neurális hálózatok jelölésében a bemeneteket négyzettel (□), a neuronokatkörrel (○) jelöljük. A bemenetek és a kimenetek között lehetnek rejtett rétegek is. A bemenet-neuron és neuron-neuron összeköttetéseket irányított vonalakkal (nyilakkal) kötjük össze. A rétegekbe szervezett, előrecsatolt neurális hálózatban a bemeneteket és az azonos rétegben lévő neuronokat függőlegesen egymás alá rajzoljuk, a nyilak balról jobbra mutatnak (4.14. ábra). (Ha a rétegeket vízszintesen ábrázoljuk, a nyilak természetesen függőleges irányúak.) A rétegek számítása egymás után történik, balról jobbra, a rétegen belüli neuronoké pedig felülről lefelé.
A neuronok (inger)küszöb értékét a korábbiak szerint nulladik (egyértékű) bemenet súlytényezőjeként vesszük figyelembe, ezt az x 0 =1 bemenetet nem mindig tüntetjük fel az ábrán, de a számítások során mindenképpen szerepel. A rejtett rétege(ke)t tartalmazó hálózat minden rétegében hasonlóképpen be kell vezetnünk egy ingerküszöbnek megfelelő, állandó egységnyi kimenetű, fiktív nulladik neuront.
A súlytényezőket a megfelelő nyilak fölé rajzolhatjuk, felső indexük a réteg azonosítója zárójelben (a rejtett réteg sorszáma vagy o a kimeneti rétegnél), az alsó index az adott rétegben lévő neuron sorszáma és a megelőző rétegben lévő neuron sorszáma. A számítás során gondoskodnunk kell arról, hogy a bemeneti és a rejtett rétegek nulladik neuronja mindig egységnyi értékű legyen.
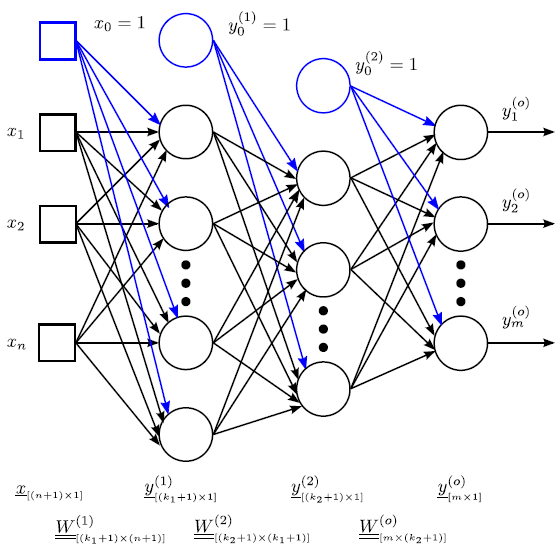
Az első rejtett rétegbeli k 1 neuron bemeneteinek súlyozott összege mátrixos formában
|
|
(4.35) |
Tömörebben
|
|
(4.36) |
Az első rejtett réteg kimenetét az aktiváló függvénnyel határozhatjuk meg
|
|
(4.37) |
A második rejtett rétegbeli k 2 neuron bemeneteinek súlyozott összege mátrixos formában
|
|
(4.38) |
Tömörebben
|
|
(4.39) |
A második rejtett réteg kimenetét is az aktiváló függvénnyel határozzuk meg
|
|
(4.40) |
A kimeneti rétegbeli m neuron bemeneteinek súlyozott összege mátrixos formában
|
|
(4.41) |
Tömörebben
|
|
(4.42) |
A kimeneti réteg neuronjainak kimenetét is az aktiváló függvénnyel határozzuk meg
|
|
(4.43) |
Az i-edik tanító adat x i bemenete a hálózat kimenetén az előzőek alapján meghatározható y i (o) kimenetet eredményezi. A tanító adatban szereplő o i kimenet és a hálózat számított y i (o) kimenete alapján meghatározhatjuk az i-edik tanító adattal kapott hibát. A hiba alapján hangolhatjuk (taníthatjuk) a neurális hálózatot a tanító adatok pontos felismerésére.
|
|
(4.44) |
A kötelező bemeneti réteg és kimeneti réteg között gyakran csak egy rejtett réteget használunk. Több rejtett réteg számítástechnikailag bonyolítja a neurális hálózatot, emellett már egyetlen – természetesen elegendő neuronból álló – rejtett réteg is elegendő bármilyen folytonos függvény közelítésére. A megfelelő számú rejtett rétegbeli neuron rendkívül lényeges, ugyanakkor egyáltalán nem egyszerű meghatározni a szükséges mennyiséget. Túl kevés neuronnal a hálózat nem közelíti megfelelően a megadott kimenetet. Ha viszont a szükségesnél többet használunk, „túltaníthatjuk” a hálózatot, így az csak a néhány tanító mintával működik, más bemenetekkel nem. Általánosan igaz, hogy a rejtett neuronok száma elsősorban a tanító minták számától függ (nyilván több minta több neuront igényel), továbbá a kimeneti függvény bonyolultságától (összetettebb függvény közelítéséhez több neuron szükséges).
4.1.2.1. Backpropagation
A backpropagation (hiba visszavezetés) tanítási módszer a neurális hálózat kimeneti rétegében jelentkező hiba visszajuttatása a rejtett réteg neuronjaihoz, a rejtett neuronok súlytényezőinek módosítása a hiba alapján. Feltehető, hogy a rejtett réteg neuronjai is hibával számolnak, azonban ez a hiba közvetlenül nem érhető el. A backpropagation tulajdonképpen a Delta-szabály általánosítása nemlineáris aktiváló függvényekre és többrétegű hálózatokra.
Egyetlen n bemenetű, aktiváló függvény nélküli neuron egyetlen y kimenete csupán az x bemenet vektortól és a w súlyvektortól függ.
|
|
(4.45) |
Az { x j ; oj} (j=1, 2, …, t) tanító adatokra a várt és számított kimenet négyzetes hibája (ahol x j,i a j-edik tanító adatsor i-edik eleme, i=0, 1, 2, .., n) csupán a súlyoktól függ
|
|
(4.46) |
Az E( w ) hibafüggvény globális minimumát keressük,mert ez azt jelenti, hogy a neuron kimenete a tanító adatban lévő kimenettől a lehető legkevésbé tér el. A gradiens módszerrel határozzuk meg a hibafüggvény ∇E gradiensét.
|
|
(4.47) |
A k-adik parciális derivált kifejtve
|
|
(4.48) |
Az η tanulási ráta bevezetésével a k-adik súlytényező változása
|
|
(4.49) |
A súlytényező módosítás másképpen is felírható, ha nem az egész tanító adatsorozatra ellenőrizzük a kimeneti hibát, hanem külön-külön tanító adatonként (sztochasztikus frissítési szabály). A kifejezés az összegzéstől eltekintve hasonlít az előbbihez
|
|
(4.50) |
(Esetünkben a sztochasztikus és a nem sztochasztikus súlymódosítási szabály ugyanazt eredményezi.)
A aktiváló függvény bevezetésével a hibafüggvény
|
|
(4.51) |
A k-adik parciális derivált kifejtve (a láncszabály alkalmazásával)
|
|
(4.52) |
A aktiváló függvény deriváltja kielégíti az alábbi egyenletet
|
|
(4.53) |
Ezzel
|
|
(4.54) |
Az helyettesítést alkalmazva a j-edik tanító adattal számított kimenetre a sztochasztikus szabály egy neuron súlytényezőinek módosítására
|
|
(4.55) |
A j -edik tanító adattal a neuron kimenetére számított hibáját jelöljük δ j -vel
|
|
(4.56) |
Ha csak a 4.15. ábra ábra kimeneti rétegében van egyetlen neuron, annak hibáját és a súlytényezők módosítását az előzőek alapján tudjuk számolni. Ha viszont a hibát a rejtett hálózat felé szeretnénk visszajuttatni, további összefüggéseket kell felírnunk. A rejtett rétegbeli neuronra ugyanúgy fel kell írnunk az aktiváló függvénnyel és bemenetei súlyozott összegével a kimenet értékét, majd ezt „beágyazva” a hibafüggvénybe, a rejtett rétegbeli neuron súlytényezői módosításához szükséges δ értékeket is ki tudjuk számolni a láncszabály alkalmazásával. A számítás eredményeképpen a kimeneten jelentkező hibával visszafelé haladva, rétegenként tudjuk módosítani a neuronok valamennyi súlytényezőjét.
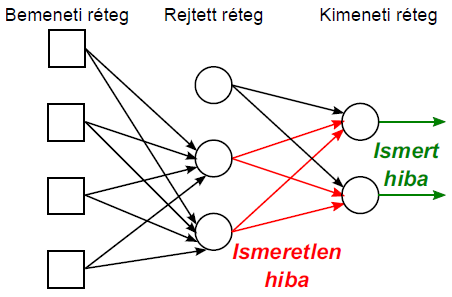
A hibát visszavezető (backpropagation) algoritmus lépései
-
a súlytényezők inicializálása kis véletlen értékekkel
-
az iteráció ismétlése a leállítási feltétel teljesüléséig
-
minden (j=1, 2, …, t) tanító adat x j bemenetét vezessük a neurális hálózatra és határozzuk meg az y j ( o ) kimenetet
-
a kimeneti réteg összes (i=1, 2, …, m) neuronjára számítsuk ki a neuron δ j ( o ) hibáját (rendre az összes tanító adatra, a képletben azonban nem szerepel a tanító adat j indexe az egyszerűség kedvéért)
-
a kimenetet megelőző rejtett réteg összes (h) neuronjára számítsuk ki a neuron δ h ( rejtett réteg ) hibáját (rendre az összes tanító adatra, a képletben azonban nem szerepel a tanító adat j indexe az egyszerűség kedvéért)
-
a további rejtett rétegek neuronjainak hibáját hasonlóan határozzuk meg, az összegzésben a kimeneti helyett a vizsgált réteget követő réteg neuronjainak hibáját és a megfelelő súlytényezőket alkalmazva
-
a módosított súlytényezőket a kifejezéssel számítjuk, ahol w ( a,b ) az előző réteg b-edik neuronját a vizsgált réteg a-adik neuronjával összekötő súlytényező, y b az előző réteg b-edik neuronjának kimenete
-
-
leállítási feltétel lehet az iterációk száma, a tanító adatokra számított összesített hiba adott küszöbérték alá csökkenése vagy ha az egyes iterációk között a hiba nem csökken lényegesen
4.1.3. Radiális bázisfüggvényes hálózat
A radiális bázisfüggvényes (radial basis function, RBF) hálózat a lineáris neurális hálózatok egyik típusa. Az RBF neurális hálózatban (4.16. ábra) egy rejtett réteg van, azonban az előzőektől eltérően a rejtett réteg neuronjainak nincs súlytényezőjük. A rejtett rétegben a megszokott aktiváló függvény helyett radiálisan szimmetrikus bázisfüggvényt használunk, Gauss–, multikvadratikus, inverz multikvadratikus, Cauchy– vagy akár B–spline függvényeket.
A rejtett rétegben az előzőekhez hasonlóan elhelyezhetünk egy állandó kimenetű y 0 ( RBF ) virtuális neuront, hogy a kimeneti neuron ingerküszöbnek megfelelő súlytényezőjét használni tudjuk a vektoros számításban.
A kimeneti réteg a már korábban megismert felügyelt tanulásával szemben a rejtett réteg nem felügyelt tanítású, sőt a backpropagation tanítás globalitásával szemben az RBF hálózat rejtett rétege lokálisan tanul. A globális tanulás a hálózat összes neuronjára kiterjed minden lépésben, a lokális tanulás csak a neuronok bizonyos körzetét érinti minden lépésben. Az RBF hálózat tanítása kétlépéses. Először az RBF függvények paramétereit határozzuk meg valamilyen nem felügyelt tanítási módszerrel, ezután kerül sor a rejtett és a kimeneti réteg közötti súlyok állítására a hibanégyzet minimalizálásával, felügyelt tanítással. Az radiális bázisfüggvények középpontja a bemenet vektorok maximális aktivizáló hatását, a szélességek a középpont körüli sugarakat (a bázisfüggvény területét) jellemzik.
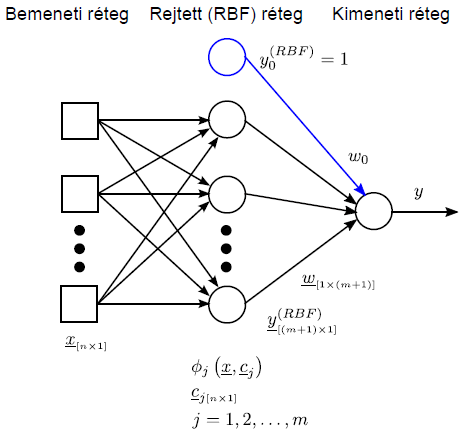
A RBF valós értékű függvény, értéke csak az origótól (esetleg a c középponttól) mért távolságtól függ, a norma általában az Euklideszi távolság.
|
|
(4.57) |
|
|
|
(4.58) |
Az n bemenetű, m radiális bázisfüggvényes rejtett rétegű, egy kimenetű RBF hálózat működését leíró egyenlet
|
|
(4.59) |
ahol φ j a j-edik rejtett neuron radiális bázisfüggvénye, c j a hozzá tartozó középpont, w j a szintén ide tartozó, a rejtett és kimeneti réteg közötti súlytényező, w 0 a rejtett rétegben lévő állandóan egységnyi kimenetű virtuális neuron súlytényezője (mondhatni az y kimenet eltolása).
||⋅|| az Euklideszi norma, az x =[x 1 x 2 … x n ] T bemenet vektorra
|
|
(4.60) |
Néhány tipikus – a szemléltetés érdekében egy változós – radiális bázisfüggvény (4.17. ábra)
|
Függvény |
Leírás |
|---|---|
|
c középpontú, r sugarú Gauss-függvény |
|
|
c középpontú, r sugarú multikvadratikus függvény |
|
|
c középpontú, r sugarú inverz multikvadratikus függvény |
|
|
c középpontú, r sugarú Cauchy-függvény |
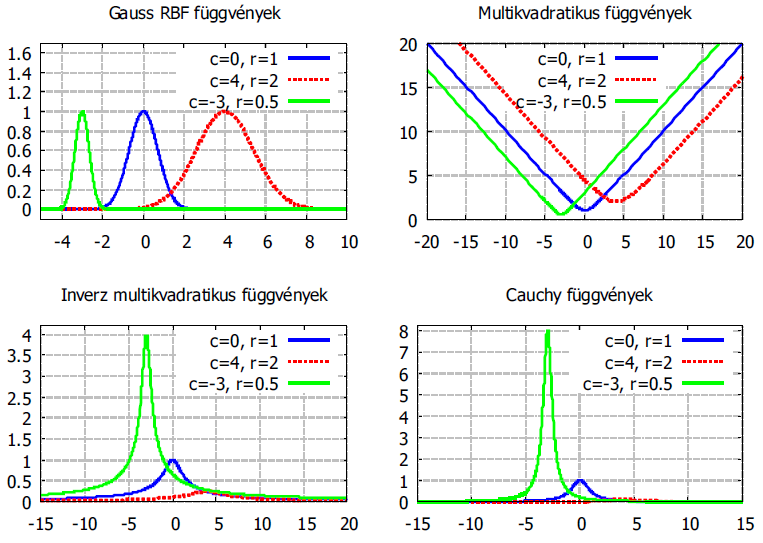
A bázisfüggvények kiválasztása függhet a megoldandó feladattól, de általában tetszőleges.
Talán leggyakoribb a Gauss–függvény használata.
A Gauss-függvényű RBF hálózatot felírhatjuk a klasszikus idősor jelölésekkel
|
|
(4.61) |
ahol a kimeneti neuron m+1 bemenetéhez tartozó súlytényezők vektora
|
|
(4.62) |
a rejtett réteg m (RBF) neuronjának (időfüggőként felírt) kimenete
|
|
(4.63) |
a j-edik Gauss RBF függvény, c j (n elemű) középponttal és r j sugárral
|
|
(4.64) |
Az RBF hálózat t időpillanatbeli bemenete
|
|
(4.65) |
Az RBF hálózat tanításához az { x k (T) , o k } tanító adatokat (k=1, 2, …, T, t helyett, mert azzal most az időt jelöljük) használjuk. A tanítás során meg kell határoznunk a rejtett rétegben lévő RBF neuronok számát, minden egyes bázisfüggvény középpontját és sugarát, valamint a kimeneti réteghez vezető súlytényezőket.
Néhány módszerben ezeket a lépéseket külön hajtjuk végre, másokban egyszerre. A hálózat paramétereinek (középpontok, sugarak, súlytényezők) „hangolására” különböző technikák közül választhatunk.
A tanítás egyik lehetséges módja az alábbi.
-
A tanítás első lépése a rejtett réteg RBF neuronjainak felvétele, m meghatározása. Általános, hogy annyi RBF neuront használunk, amennyi tanuló adat áll rendelkezésünkre, m=T
-
Minden egyes bázisfüggvény középpontját a megfelelő tanító adatnak választjuk, c j = x j (T) , j=1, 2, …, m
-
Kényelmi szempontból választhatjuk az összes bázisfüggvény sugarát egységnyinek, r j =1, j=1, 2, …, m
-
A kimeneti réteg RBF neuronokhoz kapcsolódó súlytényezőit egyenlővé tesszük a tanító adatokban szereplő kimenetekkel. w j =o j , j=1, 2, …, m. Az állandó egy értékű bemenethez tartozó w 0 súlytényezőt nullának választjuk, azaz a kimeneti neuron ingerküszöbét (eltolását) nullára állítjuk.
-
A T tanító adatra kiszámítjuk az RBF hálózat T elemű y oszlopvektorát. Ennek j-edik eleme
-
A súlytényezők meghatározására a korábban már ismertetett hiba (vagyis a várt és a számított kimenet eltérése) négyzetének minimalizálását használhatjuk.
A j-edik súlytényező módosításához az E hiba w j szerinti parciális deriváltját használhatjuk a korábban ismertetett módszerhez hasonlóan.
Ez az alapalgoritmussal értelmezi az RBF hálózatműködését és a tanítás feladatát.
Lehetőségek a rejtett réteg neuronjainak paraméterezésére (számuk, középpontjuk, sugaruk):
-
Az összes tanító adathoz egy-egy RBF neuron választása, a neuron középpontjának a megfelelő tanító bemenetet rendelve. A módszer kis adathalmazokra megfelelő. Több adatnál, különösen online jelfeldolgozási feladatok megoldására, ahol az idő előrehaladtával sokasodnak az adatok, rendszerezettebb megoldás szükséges.
-
A feladattól igencsak függő lehetőség az adathalmaz véletlenszerű mintavételezése, természetesen megfelelő számú adatot választva RBF neuron középpontnak. A probléma jellegéhez illeszkedve több adatot kell választani például a határokon vagy ott, ahol a közelítendő függvény erősen nemlineáris. Mivel általában előre nem ismerjük az adateloszlást, a módszer nem a legjobb, erősen problémafüggő.
-
A mintapéldában szereplő kétlépéses módszerrel (RBF választás, majd súlyok hangolása) szemben egy lépésben is választhatunk RBF neuron középpontokat és a kimeneti réteghez vezető súlytényezőket. A középpontokat egy nagyobb halmazból regresszióval, ortogonális legkisebb négyzetek módszerével határozhatjuk meg, kiejtve a felesleges adatokat. A módszer hasonló a bemutatott legkisebb négyzetek módszeréhez, azaz a hibanégyzet minimalizálásához.
-
A k-közép csoportosítás (k-means clustering) az adatok magas sűrűségű területei (csoportjai) közelébe helyezi a középpontokat. Mivel néhány feladattípusnál egyéb adatterületeken (például a a különböző csoportok közötti, adatokban egyébként ritka határterületeken) is szükségünk van középpontokra, a módszer nem eredményez megfelelő hálózatot.
-
A konstruktív tanulás, más néven az ellenőrzötten növekvő sejtstruktúrák módszere egy kis RBH hálózat inicializálásával és tanításával kezdődik. A tanító adatokból származó hiba alapján döntünk új RBF neuron beillesztéséről. Az új hálózaton is végigfuttatjuk a tanító adatokat és ellenőrizzük a hibát. A neuron beillesztő eljárást addig folytatjuk, amíg a hiba elegendően kicsire nem csökken.
-
Az RBF hálózatok egyik előnye, hogy a rejtett rétegbeli RBF neuronok középpontjának tanításához nincs szükség hiba visszaterjesztésre, a kimeneti réteg súlytényezői egyszerűen a legkisebb négyzetek módszerével módosíthatók. Ennek ellenére felmerülhet a felügyelt tanítás alkalmazása a rejtett RBF neuronok tanítására a kimeneti hiba valamiféle visszavezetésével.
-
A kimeneti réteg súlytényezőinek meghatározása a hálózat többi paraméteréhez képest viszonylag egyszerű. Az kimeneti réteg súlyát offline és online módszerekkel határozhatjuk meg. Az offline módszerek közé tartozik a legkisebb négyzetek módszere. Online megoldás az adaptív legkisebb közép négyzet (Least Mean Square, LMS) algoritmus és a rekurzív legkisebb négyzetek módszere (Recursive Least Squares, RLS).
Az RBF hálózatok egyik alkalmazási területe az idősor modellezés, az F(x): Rn → R funkcionális leképezéssel adott y(t) jel online becslése
|
|
(4.66) |
4.2. Fuzzy halmazok, fuzzy logika
Bizonyos komplex rendszerek leírására és megoldására nincsenek hatékony (számítógépesíthető) algoritmusaink. A komplexitás leginkább a rendszerről rendelkezésünkre álló információ mennyiségéből és minőségéből eredő bizonytalanság miatt jelentkezik. Az emberi felfogóképesség korlátozott mennyiségű információ egyidejű befogadására és feldolgozására képes, mégis képesek vagyunk összetett rendszerekről fogalmat alkotni, következtetéseket levonni. Ennek matematikaileszköze a fuzzy logika módszereit alkalmazó közelítő következtetés (approximate reasoning).
A fuzzy logika, a fuzzy halmazok elmélete a kétértelműségből (ambiguity), pontatlanságból (imprecision) és az információ hiányából adódó bizonytalanság kezelésére alkalmas matematikai eszköz.
Lotfi A. Zadeh 1965-ös „Fuzzy Sets” című cikkében írta le először a nem éles határú halmazokat. A hagyományos (crisp névvel is illetett) halmazok esetén az elem vagy beletartozik a halmazba, vagy nem. A halmazba tartozás mértéke egy, a másik eset nulla értékkel jellemezhető 4.18. ábra), vagy a klasszikus logika fogalmait kölcsönözve igaz és hamis adja meg, hogy egy elem az adott halmazba tartozik--e vagy sem. A színek közül a fehér jelezheti a halmazba tartozást, fekete pedig a halmazon kívüliséget.
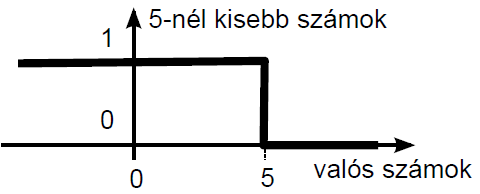
A fuzzy halmazokba tartozás számszerű mértékét a nulla és egy közötti értéket felvehető tagsági függvénnyel adjuk meg (4.19. ábra). A logika fogalmaival a fuzzy halmazba tartozás mértéke az igaz és hamis között részleges igazságként adható meg teljesen, kevésbé, közepesen, alig, egyáltalán nem jellegű fogalmakkal. A fehér és fekete színek között a különböző szürke árnyalatokat feleltethetjük meg a fuzzy halmazba tartozás mértékének.
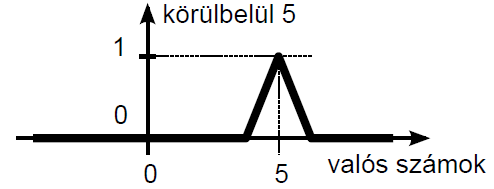
A (4.19. ábra) ábrán a hagyományos halmaz Venn-diagramja mellett két fuzzy halmaz szerepel. A hagyományos halmaz elemeit az alaphalmazon értelmezett halmazba tartozás mértékét diagramon ábrázolva 0 vagy 1 értékű, négyszögimpulzus jellegű a függvény. Fuzzy halmazokat a halmazba tartozás [0,1] intervallumba eső mértékét leképező szakaszonként lineáris vagy folytonos függvénnyel ábrázolunk.
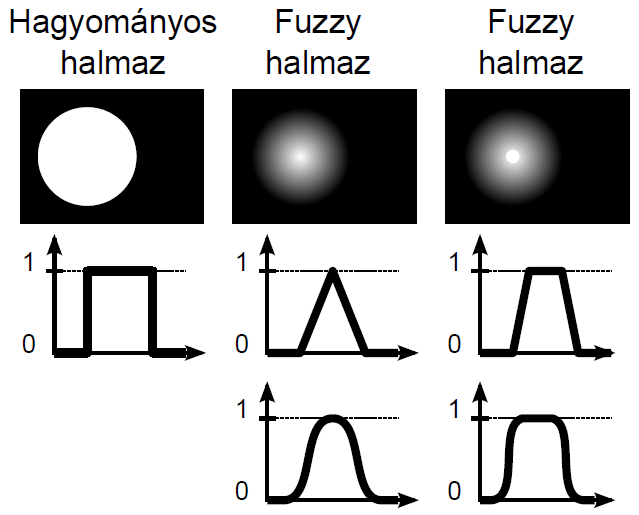
Az X alaphalmazon értelmezett A: X → {0 ; 1}, más jelöléssel A = {x | x ∈ A } hagyományos halmaz karakterisztikus („tagsági”) függvénye
|
|
(4.67) |
Az X alaphalmazon értelmezett A: X → [0 ; 1] fuzzy halmaz tagsági függvénye
|
|
(4.68) |
Zadeh 1965-ös áttörést jelentő cikkétől az elmélet gyorsan és folyamatosan fejlődik. Az 1970-es évek közepétől Japánban megjelentek a fuzzy logikához kapcsolódó szabadalmak és gyakorlati alkalmazások. Ehhez kicsit később csatlakoztak az alapvetően az arisztotelészi kétértékű logikán nevelkedett szakemberek, így Európában, az Amerikai Egyesült Államokban és a világ más részein is egyre több a fuzzy alkalmazás. Nagyon összetett, teljesen esetleg nem is érthető vagy szubjektív megítélésű rendszerek modellezése és az emberi érékelést, következtetést, döntést mindenképpen igénylő folyamatok a fuzzy logika fő alkalmazási területei.
A fuzzy halmazok és fuzzy logika ismertetése előtt tekintsük át a klasszikus kétértékű logika és a hagyományos halmazok alapfogalmait.
4.2.1. Klasszikus logika, hagyományos halmazok
A klasszikus kétértékű logikában (Boole-algebra) a logikai változó igazságértéke 0 (hamis) vagy 1 (igaz), az igazságértékek halmaza két elemű: {0,1}. Egy unáris és két bináris alapműveletet értelmezünk (p és q jelű logikai változókkal)
-
az egy logikai változóra értelmezhető negálás: ¬p
-
a két logikai változó közötti VAGY kapcsolat (diszjunkció): p ∨ q
-
a két logikai változó közötti ÉS kapcsolat (konjunkció): p ∧ q
A logikai összefüggéseket gyakran igazságtáblán (Táblázat 4.8) szemléltetjük.
|
p |
q |
¬ p |
p ∨ q |
p ∧ q |
|---|---|---|---|---|
|
0 |
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
0 |
|
1 |
0 |
0 |
1 |
0 |
|
1 |
1 |
0 |
1 |
1 |
A fenti három alapművelet felhasználásával a többi kétváltozós logikai alapművelet (implikáció, ekvivalencia stb.) előállítható. Bármely logikai állítás értéke igaz vagy hamis lehet, számokkal 0 vagy 1.
Az állítás lehet
-
egy logikai változó (pl. p)
-
egy logikai változó negáltja (pl. ¬p)
-
VAGY kapcsolatban lévő két logikai változó: p ∨ q
-
ÉS kapcsolatban lévő két logikai változó: p ∧ q
-
a fentiek kombinációjából felépített összetett logikai kifejezés (pl. (¬p) ∧ (p ∨ q)
Összetett logikai kapcsolat (állítás) igazságértékét az alkotó logikai változók igazságértékén keresztül értékeljük ki a logikai műveletek alkalmazásával, a „belülről kifelé” szabály betartásával.
A klasszikus logikai műveletek tulajdonságai (p, q és r jelű logikai változókkal)
-
kommutativitás: p∧q = q∧pés p∨q = q∨p
-
asszociativitás: p∧(q∧r) = (p∧q)∧r és p∨(q∨r) = (p∨q)∨r
-
disztributivitás: p∧(q∨r) = (p∧q)∨(p∧r) és p∨(q∧r) = (p∨q)∧(p∨r)
-
egységelem: p∧1 = p
-
nullelem: p∨0 = p
-
elnyelési tulajdonság: p∧0 = 0 és p∨1 = 1
-
idempotencia: p∧p = p és p∨p = p
-
involució: ¬(¬p) = p
-
De Morgan azonosságok: ¬(p∧q) = ¬p∨¬q és ¬(p∨q) = ¬ p∧¬q
-
a harmadik kizárásának elve: p∨¬ p = 1
-
az ellentmondás elve: p∧¬p = 0
A hagyományos halmazok esetén a halmazba tartozás egyértelműen eldönthető, igennel vagy nemmel. Bármilyen (pl. az A) halmazt mindig valamilyen (X) alaphalmazon értelmezhetünk (4.18. ábra és 4.19. ábra). Az x ∈ X alaphalmazbeli elem (X alaphalmazon értelmezett) A halmazba tartozását x ∈ A-val jelöljük. Ha az x ∈ A elem nem tartozik az A halmazba, jele x ∉ A.
Szükségünk van az üres halmaz, a halmazok egyenlősége, a részhalmaz és a hatványhalmaz fogalmára.
Az üres halmaznak (∅) nincs eleme.
Az A és B halmaz egyenlő (A = B), ha elemeik azonosak. Ha ez nem teljesül, a két halmaz nem egyenlő: A ≠ B.
A és B tetszőleges halmazok esetén A részhalmaza B-nek, ha B tartalmazza A összes elemét: A ⊆ B = { ∀ x ∈ X | ha x ∈ A ,akkor x ∈ A}.
Ha A ⊆ B, de A ≠ B (B-nek van legalább egy eleme, ami nem eleme A-nak), akkor A halmaz a B valódi részhalmaza A ⊂ B).
X hatványhalmaza tartalmazza X összes részhalmazát: ℘ (X) = { A | A ⊆ X }.
Hagyományos halmazokon értelmezhető műveletek
-
negálás, komplemensképzés (jele felülvonás vagy aposztróf): A’!Szintaktikai hiba, { = { x | x ∉ A }
-
két halmaz metszete, ÉS kapcsolat, konjunkció (jele ∩): A ∩ B = { x | x ∈ A ∧ x ∈ B}
-
két halmaz uniója, VAGY kapcsolat, diszjunkció (jele ∪): A ∪ B = { x | x ∈ A ∨ x ∈ B}
-
két halmaz különbsége (jele \): A\B = { x | x ∈ A ∧ x ∉ B}
A halmazműveletek tulajdonságai (az X alaphalmazon értelmezett A, B és C halmazokkal)
-
kommutativitás: A ∩ B = B ∩ A és A ∪ B = B ∪ A
-
asszociativitás: A ∩ (B ∩ C) = (A ∩ B) ∩ C és A ∪ (B ∪ C) = (A ∪ B) ∪ C
-
disztributivitás: A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C ) és $ A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
-
egységelem: A ∩ X = A
-
nullelem: A ∪ ∅ = A
-
elnyelési tulajdonság: A ∩ ∅ = ∅ és A ∪ X = X
-
idempotencia: A ∩ A = A és A ∪ A = A
-
involució: (A’)’ = A
-
De Morgan azonosságok: (A ∩ B)’ = A’ ∪ B’ és (A ∪ B)’ = A’ ∩ B’
-
a harmadik kizárásának elve: A ∪ A’ = X
-
az ellentmondás elve: A ∩ A’ = ∅
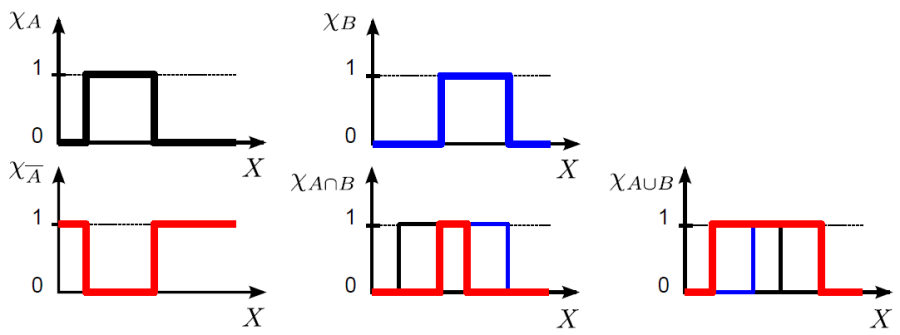
A klasszikus logika és a hagyományos halmazok közötti kapcsolatot a halmazok definiáló összefüggésében és karakterisztikus egyenletükben találjuk, ahol a klasszikus logika írásmódját alkalmazzuk.
A χ A (x) és χ B (x) karakterisztikus függvénnyel matematikai összefüggésként (többféleképpen is) le tudjuk írni a halmazműveleteket (4.21. ábra).
-
negálás, komplemensképzés (jele felülvonás vagy aposztróf): χ A’ (x) = 1 - χ A (x) vagy χ A’ (x) = (1 – (χ A (x))2)½
-
két halmaz metszete, ÉS kapcsolat, konjunkció (jele ∩): χ A (x) ∩ χ B (x) = min (χ A (x), χ B (x)) vagy χ A (x) ∩ χ B (x) = χ A (x)·χ B (x)
-
két halmaz uniója, VAGY kapcsolat, diszjunkció (jele ∪): χ A (x) ∪ χ B (x) = max (χ A (x), χ B (x)) vagy χ A (x) ∪ χ B (x) = χ A (x) + χ B (x) - χ A (x)·χ B (x)
A ⊆ B is kifejezhető a karakterisztikus függvényekkel: A ⊆ B ⇔ χ A (x) ≤ χ B (x)
4.2.2. A fuzzy halmazok tulajdonságai
A hagyományos halmaz [0,1] értékkészletű karakterisztikus függvényét terjeszti ki a fuzzy halmazokon értelmezett tagsági függvény a {0,1} intervallumra. Az X alaphalmazon értelmezett A fuzzy halmaz tagsági függvénye
|
|
(4.69) |
Fuzzy halmaz megadási lehetőségei különböző jellegű halmazok esetén (a leggyakrabban használtak)
-
x 1 , x 2 , … , x n ∈ X n diszkrét elemből álló A fuzzy halmaz két jelölése
-
szakaszonként lineáris, trapéz alakú tagsági függvény (és speciális esete a háromszög)ahol a < b < c < d a trapéz négy csúcsának vízszintes koordinátája (háromszögnél b=c) és 0 < λ ≤1 a tagsági függvény maximális magassága
-
szakaszonként exponenciális tagsági függvény, a trapéz (és háromszög) „legömbölyített” változata
-
az intervallum fuzzy halmazt két (akár „szögletes”, akár „gömbölyded”) tagsági függvény adja meg úgy, hogy a fuzzy halmazba tartozó minden alaphalmazbeli értékhez két tagsági érték, egy alsó és egy felső tartozik
-
singleton vagyis egyetlen x 0 ∈ X pontban egy, máshol nulla értékű tagsági függvénnyel adott fuzzy halmaz
A fuzzy halmaz magassága (az angol height rövidítéséből) a μ A tagsági értékek legnagyobbika (supremum), egy szám
|
|
(4.70) |
A fuzzy halmaz normális, azaz magassága egy, hgt(A) = 1, ha létezik x ∈ A elem, hogy μ A (x)=1.
A szubnormális fuzzy halmaz magassága hgt(A) < 1.
A szubnormális fuzzy halmaz normalizálható, ha az összes tagsági értéket elosztjuk a halmaz hgt(A) magasságával.
|
|
(4.71) |
A fuzzy halmaz tartójának vagy hordozójának (support) nevezzük az alaphalmaz hagyományos részhalmazát, ahol a fuzzy halmaz tagsági érték nem zérus
|
|
(4.72) |
A fuzzy halmaz magjának (core vagy kernel) nevezzük az alaphalmaz hagyományos részhalmazát, ahol a fuzzy halmaz tagsági értéke egy
|
|
(4.73) |
A fuzzy halmaz α-vágatának (α-cut) nevezzük az alaphalmaz hagyományos részhalmazát, ahol a fuzzy halmaz tagsági értéke legalább α ∈ [0,1]
|
|
(4.74) |
Érvényes a core(A) = 1 - cutα(A) összefüggés, a supp(A) = 0 - cutα(A) viszont nemmindig igaz.
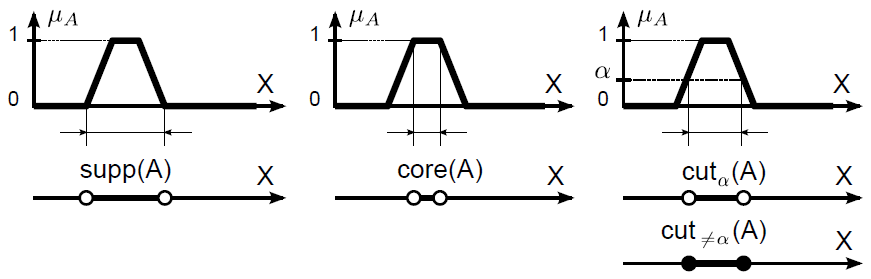
A fuzzy halmaz erős vagy szigorú α-vágatának (strict α-cut) nevezzük az alaphalmaz hagyományos részhalmazát, ahol a fuzzy halmaz tagsági értéke nagyobb α-nál.
|
|
(4.75) |
Szinthalmaznak nevezzük az A fuzzy halmaz összes lehetséges egymástól különböző α-vágatát tartalmazó halmazt valamely x ∈ X -re
|
|
(4.76) |
Felbontásnak (decomposition) nevezzük az A fuzzy halmaz megadását összes lehetséges α -vágatával. Az α -vágatok α -szorosának uniójaként definiált felbontás
|
|
(4.77) |
A μ A tagsági függvény unimodális ha pontosan egy globális vagy lokális maximuma van.
A fuzzy halmaz konvex, ha μ A tagsági függvénye unimodális. Másképpen
|
|
(4.78) |
Még ha a fuzzy halmaz konvex is, tagsági érték függvénye nem feltétlenül konvex.
A fuzzy halmaz nem konvex, ha μ A tagsági függvénye multimodális, azaz több lokális maximuma van.
Fuzzy számnak (fuzzy number) nevezzük a valós számok halmazán értelmezett folytonos tagsági függvényű, konvex, normalizált fuzzy halmazt.
A fuzzy halmaz (skaláris) számosságának (cardinality) nevezzük a halmazelemek tagsági függvény értékének összegét
|
|
(4.79) |
A hagyományos halmaz számossága elemeinek számával egyenlő, amit a karakterisztikus függvénnyel is felírhatunk a fuzzy halmaz számosságához hasonlóan
|
|
(4.80) |
A fuzzy számosság a skalár számossághoz hasonlóan értelmezhető, értéke azonban az fcard(A) fuzzy szám. Az A fuzzy halmaz Λ A szinthalmazában megtalálható valamennyi α értékre az α-vágat (hagyományos) halmaz számosságához rendeli α értékét
|
|
(4.81) |
Fuzzy részhalmaz (A ⊆ B)
|
|
(4.82) |
Az X alaphalmaz tagsági függvénye μX(x) = 1, az ∅ üres halmazé μ∅(x) = 0 $. A hagyományos halmazokhoz hasonlóan ∅ ⊆ A és A ⊆ X.
Fuzzy halmazok egyenlősége (A = B, a hagyományos halmazokhoz hasonlóan, vagyis A ⊆ B és A ⊆ A)
|
|
(4.83) |
4.2.3. Fuzzy halmazműveletek
4.2.3.1. Hagyományos halmazműveletek kiterjesztése
A hagyományos halmazok karakterisztikus függvénnyel definiált egyik matematikai művelet megfeleltetését terjesszük ki fuzzy halmazokra az alábbiak szerint (ezeket nevezzük szokványos fuzzy halmazműveleteknek)
-
negálás, komplemensképzés (jele felülvonás vagy aposztróf): μ A’ (x) = 1 – μ A (x)
-
két halmaz metszete, ÉS kapcsolat, konjunkció (jele ∩): μ A’ (x) ∩ μ B’ (x) = min(μ A’ (x), μ B’ (x))
-
két halmaz uniója, VAGY kapcsolat, diszjunkció (jele ∪): μ A’ (x) ∪ μ B’ (x) = max(μ A’ (x), μ B’ (x))
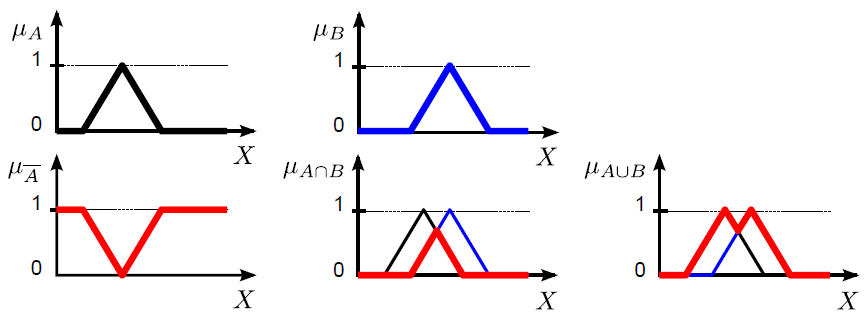
A De Morgan azonosságok teljesülnek
|
|
(4.84) |
A harmadik kizárásának elve nem teljesül minden esetben
|
|
(4.85) |
A levezetés alapján kiderül, hogy a harmadik kizárása csak akkor teljesül, ha A hagyományos halmaz és μA’(x) = ∅ (üres halmaz) vagy μA’(x) = X (az alaphalmaz).
Az ellentmondás elve sem teljesül minden esetben
|
|
(4.86) |
A levezetés alapján kiderül, hogy az ellentmondás elve csak akkor teljesül, ha A hagyományos halmaz és és μA’(x) = ∅ (üres halmaz) vagy μA’(x) = X (az alaphalmaz).
4.2.3.2. Fuzzy halmazművelet csoportok
Fuzzy halmazokkal kapcsolatos művelteket a hagyományos halmazokon definiált három alapművelet kiterjesztéseként az alábbi függvények segítségével értelmezzük.
-
negálás: N: [0,1] → [0,1], függvénnyel
-
metszet: T: [0,1] × [0,1] → [0,1], függvénnyel
-
unió: S: [0,1] × [0,1] → [0,1], függvénnyel
Negálás a klasszikus kétértékű komplemensképzés kiterjesztése.
Ha teljesül az első két feltétel, az N függvényt negálásnak nevezzük, ha a harmadik és negyedik feltétel is teljesül, a negálás szigorú, az ötödik feltételt is kielégítőt pedig erősnek nevezzük.
-
N(0)=1 és N(1)=0 (a hagyományos negálás)
-
Minél nagyobb egy elem tagsági értéke az A halmazban, annál kisebb legyen A’-ban. Emiatt N nem növekvő függvény: x 1 ≤ x 2 N(x 1 ) ≥ N(x s )
-
N szigorúan csökkenő
-
N folytonos
-
N involutív: N(N(x)) = x $
Néhány gyakori fuzzy negálás
-
szokványos, egyből kivonással
-
szigorú, de nem erős
-
θ küszöbértékes
-
cos függvényes
-
Sugeno-féle parametrikus osztály, λ > -1
-
Yager-féle parametrikus osztály, λ ∈ (0,∞)
Metszet (konjunkció), fuzzy t-norma (trianguláris norma) a klasszikus kétértékű konjunkció kiterjesztése.
Ha teljesülnek az alábbi feltételek, a T függvényt konjunkciónak nevezzük.
-
a hagyományos halmazoknál az egységelemre vonatkozó X ∩ A = A megfelelője T(μ X (x), μ A (x)) = T(1, μ A (x)) = μ A (x)
-
a hagyományos halmazoknál értelmezett A ∩ B = B ∩ A kommutativitás megfelelője T(μ A (x), μ B (x)) = T(μ B (x), μ A (x))
-
a hagyományos halmazoknál értelmezett „Ha A ⊆ B, akkor A∩C ⊆ B∩C” monotonitás megfelelője, hogy T nem csökkenő függvény, vagyis T(μ A (x), μ C (x)) ≤ T(μ B (x), μ C (x)), ha μ A (x) ≤ μ B (x)
-
a hagyományos halmazoknál értelmezett A∩(B∩C) = (A∩B)∩C asszociativitás megfelelője T(μ A (x), T(μ B (x), μ C (x))) = T(T(μ A (x), μ A (x)), μ C (x))
Néhány gyakori t-norma
-
minimum (Gödel--norma)
-
szorzat
-
Łukasiewicz t-norma
-
drasztikus t-norma
-
nilpotens minimum (nilpotens jelentése: ∀ μ A (x) ∈ (0,1) esetén ∃ μ B (x) ∈ (0,1), hogy μ A (x) és μ B (x) ∈ (0,1) t-normája nulla értékű)
-
Hamacher-szorzat
-
Schweizer-Klar t-norma, λ ∈ R \{0}
-
Yager t-norma, λ ∈ (0, ∞)
Unió (diszjunkció), fuzzy s-norma vagy t-konorma (trianguláris norma konormája) a klasszikus kétértékű diszjunkció kiterjesztése.
Ha teljesülnek az alábbi feltételek, az S függvényt diszjunkciónak nevezzük.
-
a hagyományos halmazoknál az üres halmazra vonatkozó ∅ ∪ A = A megfelelője S(μ ∅ (x), μ A (x)) = S(0, μ A (x)) = μ A (x)
-
a hagyományos halmazoknál értelmezett A ∪ B = B ∪ A kommutativitás megfelelője S(μ A (x), μ B (x)) = S(μ B (x), μ A (x))
-
a hagyományos halmazoknál értelmezett „Ha A ⊆ B, akkor A∪C ⊆ B∪C” monotonitás megfelelője, hogy S nem csökkenő függvény, vagyis S(μ A (x), μ C (x)) ≤ S(μ B (x), μ C (x)), ha μ A (x) ≤ μ C (x)
-
a hagyományos halmazoknál értelmezett A∪(B∪C) = (A∪B)∪C asszociativitás megfelelője S(μ A (x), S(μ B (x), μ C (x))) = S(S(μ A (x), μ B (x)), μ C (x))
Néhány gyakori s-norma (másnéven t-konorma)
-
maximum (a minimum konormája)
-
valószínűségi összeg (a szorzat konormája)
-
korlátos összeg (a Łukasiewicz t-norma konormája)
-
drasztikus t-konorma
-
nilpotens maximum
-
Hamacher-szorzat konormája
-
Schweizer-Klar t-konorma, λ ∈ R \{0}
-
Yager t-konorma, λ ∈ (0, ∞)
De Morgan hármasnak nevezzük azt a {T,S,N} hármast, ahol T t-norma, S t-konorma, N szigorú negálás és fennáll a két De Morgan azonosság.
-
Zadeh-féle:
-
szorzat:
-
Łukasiewicz-féle:
Duális t-norma pár T és S normája a szokványos „1-”negálással kielégíti a De Morgan azonosságokat.
|
∩: t-norma |
∪ : t-konorma (s-norma) |
|---|---|
Az intervallum értékű fuzzy halmazokra, a μA(x)=[ μA,alsó(x), μA,felső(x)] és a μB(x)=[ μB,alsó(x), μB,felső(x)] intervallum tagsági függvénnyel adott A és B halmazra külön kell értelmeznünk a halmazműveleteket (pl. a {min, max, 1-} hármassal)
-
metszet
-
unió
-
negálás
4.2.4. Relációk
Először a hagyományos halmazokon értelmezhető relációkat tekintjük át, majd ezeket kiterjesztjük fuzzy halmazokra.
Két halmaz Descartes-szorzata (direkt szorzata) az összes olyan rendezett pár halmaza, ahol a pár első eleme az egyik, második eleme a másik halmaz eleme.
|
|
(4.87) |
Több halmaz Descartes-szorzata az összes olyan rendezett szám n-es halmaza, ahol az első elem az első, a második elem a második, …, az n-edik elem az n-edik halmaz eleme.
|
|
(4.88) |
Ha az összes halmaz azonos, X 1 = X 2 = … = X n = X, akkor Descartes-szorzatuk jele X n .
Reláció két halmaz között (bináris reláció) a két halmaz X×Y Descartes-szorzatának R X×Y ⊆X×Y részhalmaza. x ∈ X és y ∈ y relációját kétféleképpen jelöljük (x,y) ∈ R X×Y vagy x(R X×Y )y.
|
|
(4.89) |
A véges n-elemű X = {x 1 , x 2 , …, x n } és a véges m-elemű Y = {y 1 , y 2 , …, y m } halmaz X×Y Descartes-szorzatán értelmezett R X×Y , röviden R részhalmazt, a két halmaz közötti bináris relációt n×m méretű, r ij ∈ {0,1} elemekből álló mátrix adja meg
|
|
(4.90) |
ahol i=1, 2, …, n és j=1, 2, …, m.
A reláció inverze az Y×X Descartes-szorzaton értelmezett R -1 ⊆ Y×X reláció, karakterisztikus függvénnyel
|
|
(4.91) |
Relációk kompozíciója két bináris reláció, PX×Y ⊆ X×Y és QY×Z ⊆ Y×Z kapcsolata, az X×Z Descartes-szorzaton értelmezett RX×Z ⊆ X×Z reláció, ha létezik y ∈ Y, amire (x,y) ∈ PX×Y és (y,z) ∈ QY×Z
|
|
(4.92) |
A kompozíció tulajdonságai
|
|
(4.93) |
|
|
|
(4.94) |
|
|
|
(4.95) |
Véges sok halmaz közötti reláció megadja, hogy az egyes halmazok elemei kapcsolatban vannak-e egymással vagy sem.
A halmazok közötti reláció az n halmaz X 1 × X 2 × … × X n Descartes-szorzatának RX1×X2×…×Xn ⊆ X 1 × X 2 × … × X n részhalmaza. x 1 ∈X 1 , x 2 ∈X 2 , …, x n ∈X n (x1, x2, …, xn) ∈ RX1×X2×…×Xn -el jelöljük. Használhatjuk még a reláció karakterisztikus függvényét is
|
|
(4.96) |
Bináris (két halmaz közötti) fuzzy reláció véges halmazok esetén az n-elemű X = {x1, x2, …, xn} és a véges m-elemű Y = {y1, y2, …, ym} halmaz X×Y = {x1, x2, …, xn}×{y1, y2, …, ym} Descartes-szorzatán értelmezett RX×Y, röviden R részhalmaz. Az R relációt az n×m méretű tagsági mátrix adja meg
|
|
(4.97) |
ahol r ij = μ R (xi, yj) ∈ [0,1], i=1, 2, …, n és j=1, 2, …, m. Szokás még páros gráfként ábrázolni a véges halmazok között értelmezett bináris fuzzy relációt.
A bináris fuzzy reláció tekinthető a függvényfogalom kiterjesztésének, megadhatjuk az értelmezési tartománynak, értékkészletnek és inverz függvénynek megfelelő fogalmakat.
A reláció értelmezési tartománya (domain) a dom(R) ⊆ X fuzzy részhalmaz, tagsági függvénye az x∈X értékekre
|
|
(4.98) |
A reláció értékkészlete (range) a ran(R) ⊆ Y fuzzy részhalmaz, tagsági y∈Y értékekre
|
|
(4.99) |
A reláció inverze az Y×X Descartes-szorzaton értelmezett R -1 ⊆ Y×X fuzzy reláció, tagsági függvénye
|
|
(4.100) |
A véges halmazok közötti bináris fuzzy reláció tagsági mátrixát invertálva kapjuk az inverz reláció tagsági mátrixát.
Minden R bináris fuzzy relációra igaz, hogy (R-1)-1 = R.
Két fuzzy reláció kompzíciójához többféleképpen rendelhetünk tagsági függvényt.
A PX×Y ⊆ X×Y és QY×Z ⊆ Y×Z fuzzy reláció kompozíciója az X×Z Descartes-szorzaton értelmezett RX×Z ⊆ X×Z reláció, ha létezik y ∈ Y, amire (x,y) ∈ PX×Y és (y,z) ∈ QY×Z
Az egyik legelterjedtebb módszer a Zadeh-féle max-min kompozíció.
|
|
(4.101) |
A max-prod kompozícióban a min helyett szorzás szerepel
|
|
(4.102) |
Gyakran használjuk a max-average kompozíciót is, ahol az eredeti min helyett átlag (average) szerepel
|
|
(4.103) |
A fuzzy kompozíció általános alakját a T t-norma és az S s-norma (t-konorma) segítségével így írhatjuk fel
|
|
(4.104) |
Véges sok halmaz közötti fuzzy reláció az egyes halmazok elemei közötti összerendeltség mértékét adja meg.
Az n darab X 1 , X 2 , …, X n halmaz közötti fuzzy reláció a μ R (x1, x2, …, xn) tagsági függvénnyel jellemzett fuzzy halmaz
|
|
(4.105) |
Az R (pontosabban R X1 × X2 ×…× Xn ) fuzzy reláció bármelyik cutα(R) α-vágata „hagyományos” reláció ugyanezen halmazok között.
Vetület (projekció), vagyis az n-dimenziós tér (információvesztéssel járó) vetítése n-nél kisebb dimenziós térre.
Jelöljük az X 1 × X 2 × … × X n alaphalmazok Descartes-szorzataként értelmezett alaphalmaz elemeit vektorral
|
|
(4.106) |
magát az alaphalmazt pedig X × vektorral (a felső indexben a Descartes-szorzat szimbólumával)
|
|
(4.107) |
Az m<n dimenziós térre vett, hasonlóképpen vektorként jelölt y vetületet a sorozatként értelmezett x vektor részsorozatának nevezzük és y ⊲ x -el jelöljük, ha x elemeinek csak egy részét tartalmazza.
Ha például a k-adik elemet hagyjuk el a vetítés során
|
|
(4.108) |
Ekkor a csökkentett dimenziójú alaphalmazt X × mintájára az X × vektorral jelöljük
|
|
(4.109) |
Az fuzzy reláció fuzzy relációra vett vetületét (projekcióját) az -on értelmezett szintén fuzzy relációval jellemezzük, tagsági függvénye
|
|
(4.110) |
Véges számosságú X × esetén sup helyett max is használható.
Hengeres kiterjesztés, vagyis az m-dimenziós tér kiterjesztése m-nél nagyobb dimenziós (korábban nem definiált dimenziókat tartalmazó) térre.
Az előző példa szerint (ahol a k-adik elem hiányzik) az X ×-ban megtalálható, de az X ×\ Y ×-ből hiányzó dimenzió az X k alaphalmazzal jellemezhető.
Az fuzzy reláció fuzzy relációra vett hengeres kiterjesztésének nevezzük az jelölésű, X ×-en értelmezett, szintén fuzzy relációt minden x vektorra, amire y ⊲ x -el. A hengeres kiterjesztés fuzzy reláció tagsági függvénye
|
|
(4.111) |
A hengeres kiterjesztés eredménye a vizsgált RY× projekcióval kompatibilis legnagyobb fuzzy reláció. Ez a hengeres kiterjesztés az adott projekcióval kompatibilisek között a legkevésbé specifikus.
Egy fuzzy relációt közelíthetünk az egyes dimenzióira vett vetületei hengeres kiterjesztésének metszetével. Ez az összes vetület ismeretében is általában csak közelítheti a vizsgált relációt.
Kompozíció alkalmazásával határozhatjuk meg a B ∈ Y fuzzy halmazt az R ⊆ X×Y fuzzy reláció és az A ∈ X fuzzy halmaz ismeretében. Fuzzy szabályalapú rendszerekben a következmény (B) meghatározására a szabályt (R reláció) és a megfigyelést (A) használjuk.
Az A és R kompozíciójaként előállítható a B = A ◦ R fuzzy halmaz.
-
Első lépés A kiterjesztése az X×Y Descartes-szorzatra
-
Ezután a reláció és a kiterjesztés metszetét állítjuk elő
-
Végül az eredményt $ Y $-ra vetítjük
Így az A ∈ X fuzzy halmaz és az R ⊆ X×Y reláció ismeretében a kompozícióval meghatározott B fuzzy halmaz
|
|
(4.112) |
A B fuzzy halmaz tagsági függvénye, min metszet művelettel és a vetítés max (sup) műveletével
|
|
(4.113) |
Aggregációs operátorokra is szükségünk lesz a fuzzy szabályrendszerek kiértékelésénél.
Az függvényt aggregációs operátonak nevezzük, ha
Aggregációs operátor
-
a T(a)=a feltételt kielégítő T(a,b) t-normák
-
az S(a)=a feltételt kielégítő S(a,b) S-normák
-
a súlyozott számtani közép
-
a súlyozott mértani közép
-
az (x 1 , x 2 , …, x n ) szám n-es csökkenő sorrendbe rendezésével előállított vektor, ahol i=1, 2, …, n és , valamint a w = [w 1 , w 2 , …, w n ] súlyvektor skaláris szorzata adja a w súlyvektorhoz tartozó rendezett súlyozott átlagot (ordered, weighted average, owa)
4.2.5. Fuzzy szabályalapú rendszerek
A fuzzy szabályalapú rendszerek szabályait természetes nyelvi kifejezésekkel fogalmazzuk meg ha-akkor kapcsolatokként. Az emberi tudásból nyert, fuzzy halmazként kezelt nyelvi változókkal (pl.nagyon gyors, hideg, közepesen erős) leírt szabályokat fuzzy relációkként dolgozzuk fel. A szabálybázisban lévő szabályok alapján következtetéssel határozzuk meg a bemenetekhez (megfigyelésekhez) tartozó kimeneteket (következtetéseket).
Fuzzy szabályalapú rendszereket igen gyakran használunk irányítási feladatok megoldására is. Az első fuzzy következtető algoritmust a kompozíciós következtetést (Compositional Rule of Inference, CRI) L.A.Zadeh készítette 1973-ban. Az első működő fuzzy logikai irányítást (erősen nemlineáris gőzgép irányítása) E.H.Mamdani és S.Assilian szintén 1973-ban közölte. Azóta egyre több helyen találkozunk fuzzy elveket követő irányítási rendszerekkel (pl. mosógép, fényképezőgép, földalatti, lift, hogy csak néhányat említsünk.)
Zadeh 1973-as következtető módszere a nagy bonyolultságú rendszereket nyelvi változókkal (fuzzy halmazok) és „HA-AKKOR” szabályokkal írja le. A szabályok értékelése magas dimenziójú fuzzy relációkkal, bonyolult, számításigényes módszerrel történik. Ezt egyszerűsítette Mamdani 1975-ös modelljében. A Zadeh-féle n-dimenziós relációként leképezett szabályok helyett Mamdani n darab egydimenziós relációból indul ki. A reláció-vetületek hengeres kiterjesztésének metszetét használja, ezzel erősen csökken a számításigény.
A fuzzy szabályalapú (irányítási) rendszerek egységei:
-
a tudásbázis a fuzzy szabályokba foglalt (emberi megfigyelésen alapuló) „tudással” és a fuzzifikáláshoz, defuzzifikáláshoz szükséges adatokkal
-
a numerikus bemeneteket fuzzy halmazokra leképező fuzzifikáló egység az illeszkedés vagyis halmazba tartozás mértékét határozza meg
-
a döntéshozó vagy következtető modul határozza meg a szabályok alapján a kimenet(ek)hez tartozó fuzzy halmaz(oka)t
-
a defuzzifikáló a következtetés eredményeképpen kapott fuzzy halmazokat az itányítandó folyamat számára kezelhető numerikus értékekké alakítja
4.2.5.1. Nyelvi változók, módosítók
A fuzzy szabályalapú rendszerekben használt nyelvi kifejezések az ember (szakértő, üzemeltető) által megfogalmazott, jó értelemben bizonytalan kifejezéseket az általában számítógépen megvalósított fuzzy rendszer számára értelmezhetően írják le. A nyelvi kifejezésekben lévő nyelvi változókat nyelvi módosítókkal és műveletekkel kapcsoljuk össze. A nyelvi (lingvisztikai) változókat az alaphalmazra vonatkoztatott fuzzy halmazokként definiáljuk. Egy nyelvi változó több értéket vehet fel, mindegyiket egy fuzzy halmaz képez le (pl. a hőmérséklet mint nyelvi változó lehetséges értékei hideg, hűvös, kellemes, meleg, forró).
A V (variable) nyelvi változót öt jellemzője határozza meg, V = (N, G, T, X, M):
-
N (name) a V nyelvi változó neve
-
G (grammar) a nyelvtan
-
T(N) (terms) a nyelvi értékek nevéből a nyelvtan alapján képzett halmaz
-
X az alaphalmaz
-
M (mapping) leképezés, a nyelvi érték és a fuzzy halmaz összerendelésének szemantikai szabálya
Példa nyelvi változóra a (4.24. ábra) ábrán szereplő hőmérséklet: N=hőmérséklet, T(N)={hideg, hűvös, kellemes, meleg, forró}, X=[0°C, 100°C] és a hőmennyiség: N=hőmennyiség, T(N)={ negatív nagy, negatív kics, nulla, kicsi, nagy}, Y = [-100 %, 100 %].
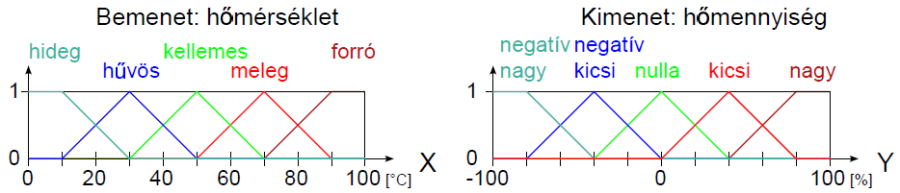
Nyelvi módosító például a legalább és legfeljebb, ezekkel – és társaikkal – a fuzzy halmazokat módosíthatjuk, ezt szemléltetik a (4.25. ábra) ábrán szereplő legalább hűvös és legfeljebb meleg módosított nyelvi értékek.
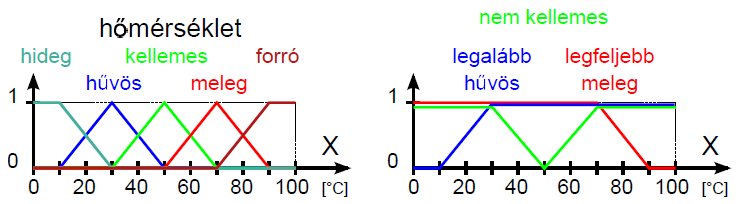
A nagyon módosítóval a kis tagsági értékeket tudjuk tovább csökkenteni, a összefüggéssel, „szűkítjük”, koncentráljuk a fuzzy halmazt (concentrate).
A kis tagsági értékeket növeli a összefüggésű, fuzzy halmazt „szélesítő” módosító, ritkíto (dilute), a többé-kevésbé.
Az értékkészlet felénél, 0,5-nél nagyobb tagsági értékeket (kontrasztot) erősítő, a kisebbeket gyengítő összefüggés (intensify) afokozottan módosító
|
|
(4.114) |
Nyelvi módosítónak tekinthetjük tulajdonképpen a komplemensképzéssel (negálással) leképezhető nem fuzzy halmazműveletet is, az 1- művelettel például (4.25. ábra).
Nyelvi változókat határozunk meg a bemenetekhez (megfigyelésekhez) és kimenetkehez (következtetésekhez). A nyelvi változóhoz tartozó alaphalmazt nyelvi értékekre (és a hozzájuk tartozó tagsági függvényre) kell bontanunk tapasztalataink vagy a rendszermodell alapján. E fuzzy felosztás eredményét elsődleges fuzzy halmazoknak nevezzük.
Az egyes bemenetekhez és kimenetekhez tartozó elsődleges fuzzy halmazok száma határozza meg a maximálisan kialakítható fuzzy szabályok számát. (Például egy öt nyelvi értékű bemenettel és egy három nyelvi értékkel adott kimenettel jellemzett SISO rendszerben ötször három, azaz tizenöt szabályt írhatunk fel.) Minél több részre osztjuk az egyes nyelvi változókat, annál több szabályt írhatunk fel. A szabályok számának növelése persze emeli a számítási igényt, bár nem feltétlenül szükséges az összes lehetséges szabályt használni.
A kompozíciós következtetéshez (CRI) az alaphalmazokat teljesen lefedő ún. „fedő” fuzzy felosztás szükséges, hogy biztosíthassuk a minden lehetőséget lefedő „sűrű” fuzzy szabályrendszert.
A nyelvi módosítókkal a nyelvi változóhoz tartozó nyelvi értékek jellegét (és esetleg számát) befolyásolhatjuk.
4.2.5.2. Fuzzifikálás
A fuzzifikálás tulajdonképpen „életlenítés”, a szabálybázis számszerű (akár egyelemű hagyományos halmaznak is tekinthető) bemenő változóit fuzzy tagsági értékké alakítja, elmossa a halmaz éles határát. A fuzzifikáló az érkező bemenő változót összekapcsolja a megfelelő fuzzy nyelvi változóval és megkeresi, hogy a bemenő jel érték a változó melyik fuzzy halmazába tartozik (eredményez pozitív tagsági értéket). Természetesen ha a bemenet bizonytalansággal nem terhelt, egyértékű fuzzy halmazzá alakíthatjuk (csak az adott bemeneti értékhez tartozik egy tagsági érték, a többi alaphalmazbeli értékhez pedig nulla). Ha a zajos adatról statisztikai információnk van, a zajt sűrűségfüggvényével jellemezhetjük, egyszerűbb azonban a görbe helyett háromszögesített tagsági függvénnyel dolgozni.
Például a (4.24. ábra) ábrán látható hőmérséklet nyelvi változóra leképezve a 14°C értéket, megállapíthatjuk, hogy mind a hideg, mind a hűvös fuzzy halmazba nullától különböző tagsági értékkel tartozik.
A (4.26. ábra) ábráról le tudjuk olvasni az egyes halmazokba tartozás mértékét a választott 14°C hőmérsékletnél
-
μ hideg (14°C) = 0.8
-
μ hűvös (14°C) = 0.2
-
μ kellemes (14°C) = 0
-
μ meleg (14°C) = 0
-
μ forró (14°C) = 0
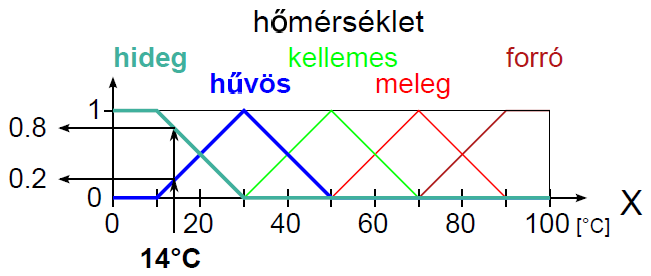
A megfigyelések (bemenetek) és következtetések (kimenetek) alaphalmazát szükség esetén normalizálhatjuk. A folytonos alaphalmaz diszkretizálása („mintavételezése”) a számítási igényt csökkentheti, ha ezzel nem csökkentjük a fuzzifikálás pontosságát. A mintavételezés lehet a lényeges tartományokban sűrűbb, az adatok szempontjából kevésbé informatív részeken ritkább.
4.2.5.3. Fuzzy szabálybázis, fuzzy következtetés
A deduktív következtetésben a szabályokat logikai deduktív szabálynak, implikációnak tekintjük. A hozzárendelési megközelítésben a szabályokat feltételes hozzárendelésként (conditional assignment) kezeljük, fuzzy függvényekkel dolgozunk, hasonlóan a procedurális programozási nyelvekhez. Mindkét módszerben először a kimeneti (következmény) fuzzy halmazt minden egyes szabályra, majd ezek aggregálásával egyetlen globális következmény (kimenet) fuzzy halmazt állítunk elő.
Elképzelhető, hogy egy bemenet bizonyos értéke két vagy esetleg több szabály teljesülését (elterjedt szóhasználattal tüzelését) váltja ki. Az is lehet, hogy ebben a két vagy több szabályban egymástól eltérő, szélsőséges esetben ellentmondó következmények szerepelnek – ez nem feltétlenül jelent problémát a végső eredmény meghatározásánál.
Feltétel azonban, hogy minél nagyobb az adott bemenetre a szabályból meghatározható illeszkedési mérték, a szabály annál erősebben hat a kimenetre.
A fuzzy szabálybázisban HA – AKKOR (IF – THEN) szabályokban foglaljuk össze a bemenetek (megfigyelések) és kimenetek (következtetések) nyelvi változókkal és esetleg módosítókkal adott kapcsolatait.
A fuzzy szabályokat fuzzy reláció formájában is megfogalmazhatjuk. Jelölje X a példában (4.24. ábra) szereplő hőmérséklet bemenet alaphalmazát, Y a hőmennyiség kimenetét, a köztük definiálható R i relációkat az X×Y Descartes-szorzaton értelmezhetjük.
A példában szereplő fuzzy halmazzal adott hőmérséklet nyelvi változó bemenet öt, a szintén öt fuzzy halmazzal adott hőmennyiség nyelvi változó kimenet (4.24. ábra) elméletileg összesen 5⋅5 = 25 szabállyal kapcsolható össze.
|
{A1 = hideg, A2 = hűvös, A3 = kellemes, A4 = meleg, A5 = forró} |
(4.115) |
|
|
{B1 = nagy, B2 = kicsi, B3 = nulla, B4 = negatív kicsi, B5 = negatív nagy} |
Ezek közül a hőmérsékletet és a rendszerbe juttatandó hőmennyiséget összekapcsoló értelmes szabályok
-
HA a hőmérséklet hideg, AKKOR a hőmennyiség nagy
R 1 : IF x ∈ A 1 THEN y ∈ B 1
-
HA a hőmérséklet hűvös, AKKOR a hőmennyiség kicsi
R 2 : IF x ∈ A 2 THEN y ∈ B 2
-
HA a hőmérséklet kellemes, AKKOR a hőmennyiség nulla
R 3 : IF x ∈ A 3 THEN y ∈ B 3
-
HA a hőmérséklet meleg, AKKOR a hőmennyiség negatív kicsi
R 4 : IF x ∈ A 4 THEN y ∈ B 4
-
HA a hőmérséklet forró, AKKOR a hőmennyiség negatív nagy
R 5 : IF x ∈ A 5 THEN y ∈ B 5
Minden fuzzy szabály (reláció) felírható R i : (X×Y) → [0,1] alakban, ahol i = 1, 2, …, n a fuzzy szabály sorszáma, x ∈ X egy hőmérséklet érték, y ∈ Y egy hőmennyiség érték, A3 az X, B i az Y alaphalmazon értelmezett nyelvi értéknek megfelelő (nem feltétlenül i-edik) fuzzy halmaz, $ I : ([0,1]× [0,1]) → [0,1] fuzzy következtetés (implikáció) vagy t-norma.
|
|
(4.116) |
|
|
|
(4.117) |
Fuzzy következtetést (implikációt) használunk A-ból következik B, másképpen A ⇒ B, HA A, AKKOR B esetben.
Klasszikus kétértékű logikában a HA p, AKKOR q implikáció kétváltozós logikai függvény igazságtáblája (Táblázat 4.10) és néhány ekvivalens felbontás logikai alapműveletekkel (∧, ∨ és ¬)
|
|
(4.118) |
|
p |
q |
p ⇒ p |
|---|---|---|
|
0 |
0 |
1 |
|
0 |
1 |
1 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
A fuzzy implikációk nem ekvivalensek egymással, négy nagy családba tartozhatnak, ezeket T(a,b) jelű t-normával, S(a,b) s-normával és N(a) negálással írjuk fel:
-
fuzzy leképezése
-
fuzzy leképezése, ahol a max mögött lévő (p∧x) és q a logikai kifejezés értéke számként (0 vagy 1)
-
fuzzy leképezése
-
fuzzy leképezése
Néhány gyakori fuzzy implikáció az R5: IF x ∈ A THEN y ∈ B szabályra
-
Zadeh implikáció
-
Łukasiewicz implikáció
-
Kleene-Dienes implikáció
Az A∧B (A és B egyidejű teljesülése) esetén használhatjuk a t-normás implikációkat, például az alábbiakat.
Mamdani (min) implikáció (4.27. ábra)
|
|
(4.119) |
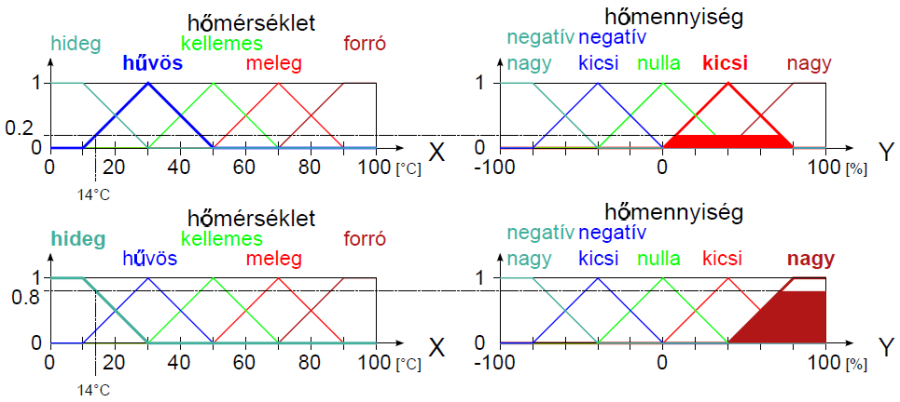
Larsen (prod) implikáció (4.28. ábra)
|
|
(4.120) |
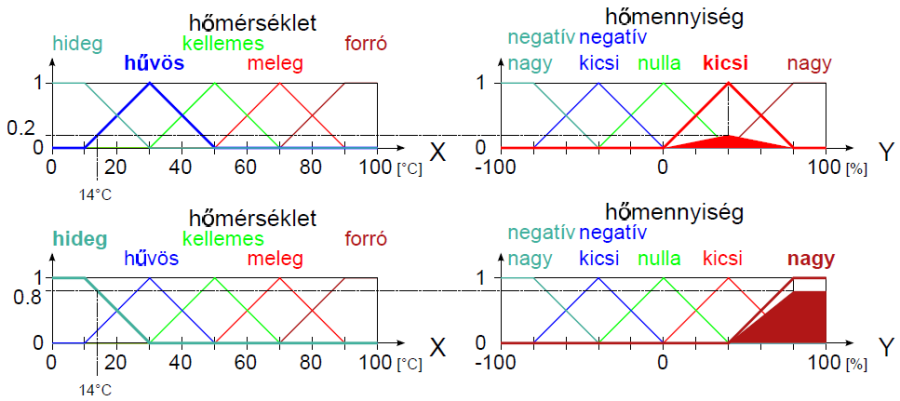
Több bemenet vagy több szabály egyidejű teljesülése esetén szükség lehet az aggregációs (összekapcsolási) műveletekre. Ezzel több bemenet esetén a szabályok lehetséges maximális száma ugrásszerűen nőhet, a kiértékelés mindkét esetben számításigényesebb lehet.
Ha ismerjük az IF x ∈ A i THEN y ∈ B i fuzzy szabályt és tudjuk, hogy x ∈ A’, kompozícióval megtalálhatjuk azt a B’ fuzzy halmazt, amire y ∈ B’ kielégíti a szabályt (az R relációt)
|
|
(4.121) |
Több (n) szabály egyidejű teljesülése esetén az implikáció relációkat egyesítjük, célszerűen metszet (t-norma) felhasználásával
|
|
(4.122) |
Tagsági függvénye a max t-normával
|
|
(4.123) |
Konjunkciós kapcsolat esetén az aggregált relációt unióval állítjuk elő
|
|
(4.124) |
Tagsági függvénye a max s-normával
|
|
(4.125) |
A 4.27. ábra és 4.28. ábra ábrán a hőmérséklet-hőmennyiség kapcsolatú mintapéldában két egyszerre „tüzelő” fuzzy szabály kiértékelése látható. A Mamdani-módszerben (4.27. ábra) az összetartozó bemenet (fuzzy halmaz) és a megfelelő szabály (reláció) kompozíciója alapján a szabályban szereplő kimenet megfelelő módosítását a min t-normával határozzuk meg (4.29. ábra) külön-külön mindkét tüzelő szabálynál.
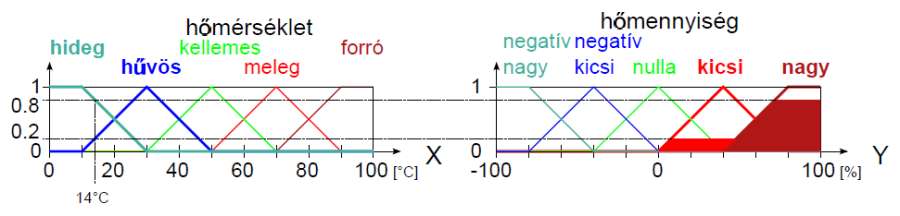
A Larsen-módszerben (4.28. ábra) min helyett a prod t-norma szerepel, a szabályban szereplő kimenet fuzzy halmaz „tetejének levágása” helyett „összenyomása” történik. (4.30. ábra).
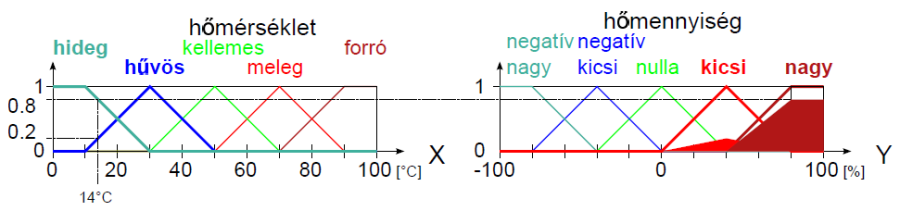
Mindkét módszerben közös az egyszerre érvényes szabályok kimenetének aggregációja, erre a max s-normát használják (4.29. ábra és 4.30. ábra).
A többi következési, szabálykiértékelési módszer is hasonló elveket követ. Az aktuális bemenet és a megfelelő fuzzy szabály megfigyelés részéhez illeszkedés mértékével általában t-normával mintegy súlyozza a következmény fuzzy halmazt. A több szabály együttes tüzeléséből származó eredményt aggregációval, általában s-normával kapcsoljuk össze. A következtető egység aggregált kimenete általában nem konvex és nem normált fuzzy mennyiség.
A Takagi-Sugeno-Kang fuzzy modell célja, hogy adott bemenet-kimenet adathalmazból szisztematikusan generálhassunk fuzzy szabályokat. A Takagi-Sugeno-Kang módszer kombináció művelete az előzőekhez képest más elvű, nem fuzzy mennyiséget eredményez, közelebb áll a neurális hálózatoknál megismert elvekhez, hiszen a szabály kiértékelése során közvetlenül egy crisp függvényt állítunk elő.
A Mamdani- és Larsen módszernél a szabályok kiértékelésének eredménye fuzzy mennyiség. A példákban (4.29. ábra és 4.29. ábra) szereplő következmény terület több módosított („levágott tetejű” vagy „összenyomott”) fuzzy halmaz összetétele. Ebből kell sokszor egyetlen (crisp) értéket, vagyis egy jelelmző számot előállítanunk.
4.2.5.4. Defuzzifikálás
Bizonyos esetekben, például amikor az emberi kezelőt kell tájékoztatnunk, elegendő a nyelvi változó nyelvi értéke mint kimenet. Sokszor azonban egyetlen számmá kell alakítanunk a következtetés után kapott, esetenként összetett fuzzy mennyiségeket. Ezt a számot úgy kell kiválasztanunk, hogy a lehető legjobban jellemezze az eredményt. A defuzzifikálás, vagyis az életlen határúság megszüntetése számos módszerrel lehetséges.
Az alábbi képletekben jelölje μ OUT (y) az Y kimeneti alaphalmazon értelmezett összetett eredményhalmzt, y* ∈ pedig pedig a defuzzifikálással kapott crisp értéket!
Tipikus defuzzifikáló eljárások
-
a maximális értékkel kapcsolatos módszerek (4.31. ábra)
-
a maximális érték (amennyiben csak egy ilyen van), vagyis az eredményhalmaz „legmagasabb” pontjáthoz tartozó érték (Height)
a maximumok (a maximális értéknek megfelelő α-vágat) első értéke (First of Maxima, FOM)
-
a maximumok (a maximális értéknek megfelelő α-vágat) utolsó értéke (Last of Maxima, LOM)
-
a maximumok (a maximális értéknek megfelelő α-vágat) középső értéke, számtani közepe (Mean of Maxima vagy Middle of Maxima, MOM)
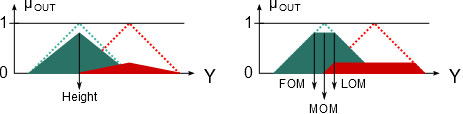 4.31. ábra - A kimeneti összetett fuzzy halmaz maximális értékével kapcsolatos deffuzifikációs módszerek
4.31. ábra - A kimeneti összetett fuzzy halmaz maximális értékével kapcsolatos deffuzifikációs módszerek
-
-
a kapott összetett tagsági függvény alatti területtel kapcsolatos módszerek (4.32. ábra)
-
a terület súlypontjának megfelelő érték a vízszintes tengelyen, vagyis a területet két egyenlő részre osztó függőleges (Center of Area, COA, Centroid módszer)
-
legalább két konvex részterület esetén ha az összetett halmaznak legalább két konvex az eredmény fuzzy halmazokból mint egyes lemezterületekekből előállított egyesített tömegközéppont (Center of Gravity, COG)
-
szimmetrikus elemi fuzzy halmazokból álló összetett halmaznál az egyes összetevők y a középső maximális értékét az illető halmaz magasságával súlyozzuk és ezek átlaga adja a defuzzifiált értéket (Weighted Average, WA)
-
az eredményben szereplő fuzzy halmazok algebrai összegén alapuló gyors módszer az összegek közepe (Center of Sums, COS), itt az n darab kimeneti halmaz (n=1, 2, .., k) uniója helyett algebrai összeget képzünk (az a módszer a metsző területeket többször veszi figyelembe)
-
legalább két konvex részterület esetén a μ OUT. max (y) tagsági függvénynel jellemzett legnagyobb konvex részterület tömegközéppontja (Center of Largest Area, COLA)
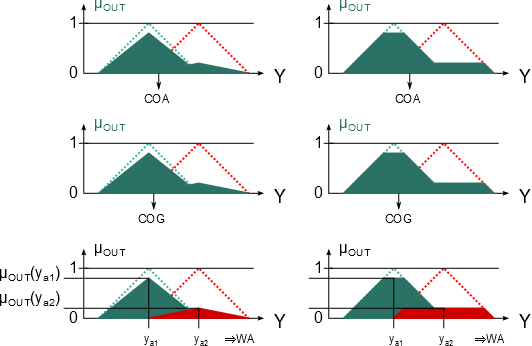 4.32. ábra - Néhány kimeneti összetett fuzzy halmaz alatti területtel kapcsolatos deffuzifikációs módszer
4.32. ábra - Néhány kimeneti összetett fuzzy halmaz alatti területtel kapcsolatos deffuzifikációs módszer
-
4.3. Komplex rendszerek
A lágy számítási módszerek mindegyike más területen hatékony. Fuzzy modellt gyakran használunk, ha a rendszer matematikai modelljét nem vagy csak igen nehezen tudjuk előállítani. A fuzzy logikán alapuló szabályalapú vagy következtető rendszerek a jó értelemben bizonytalan, nem teljes információt hordozó adatokon alapuló érvelésben és következtetésben erősek. A neurális hálózatok előnyös tulajdonsága az adaptivitás. A paraméterek (legtöbbször súlytényezők) automatikus hangolásával mintafelismerési, döntési, szabályozási, (állapot)becslői feladatukat optimálisan hajtják végre. Alkalmazkodóképességük a rendszer vagy a környezeti körülmények változását is képesek követni.
Viszont ezek a módszerek – saját erősségük mellett – nem rendelkeznek a másik nyújtotta előnyökkel, így célszerű kombinálni őket, mindegyiket arra használva, amire a legalkalmasabb. A fuzzy rendszerek bizonytalan információk alapján vonnak le következtetéseket, de az ehhez szükséges szabályokat nem tudják automatikusan előállítani és finomítani. A neurális hálózatok mintafelismerést biztosító működésüket nem tudják „megmagyarázni”, algoritmizálni, szabályokként megadni. Az egyes módszerek korlátai megfelelő kombinációjukkal leküzdhetők.
Az adott feladat szempontjából fontos technikák ötvözetének elnevezése tükrözi összetevőiket, így neurális fuzzy rendszerekről (Neuro-Fuzzy System, NFS), valamint fuzzy neurális hálózatokról (Fuzzy Neural Network, FNN) beszélünk a módszerek kombinálásakor. Ezek a rendszerek szinergikusan ötvözik a fuzzy rendszerek emberihez hasonló következtetési képességeit a neurális rendszerek hálózatos felépítésével és tanulási képességével.
A neuro-fuzzy rendszerek tulajdonképpen univerzális approximátorok, közvetlenül értelmezhető HA-AKKOR (IF-THEN) szabályokkal. A lingvisztikai fuzzy modellezés neuro-fuzzy rendszerekben a fuzzy komponensek neurális támogatottságú előállításával és hangolásával foglalkozik. Ez igen gyakran a Mamdani modellnek megfelelő fuzzy rendszer pontosítását jelenti. A másik neuro-fuzzy megközelítés a pontosságot részesíti előnyben, főképpen a Takagi-Sugeno-Kang (TSK) modell felhasználásával.
Az egyik – talán legáltalánosabb – megközelítés szerint a neuro-fuzzy rendszer alapja a neurális hálózatok elméletéből ismert tanulási algoritmussal tanított fuzzy szabályalapú rendszer. A tanítási eljárást lokális információkra alkalmazzák, a teljes fuzzy rendszerben is csak lokális módosításokat eredményezve (pl. fuzzy nyelvi változóhoz tartozó tagsági függvények hangolása).
E felfogás szerint a neuro-fuzzy rendszer háromrétegű, előrecsatolt neurális hálózat. Az első rétegben vannak a fuzzy rendszer bemeneti változói, a rejtett réteg képezi le a fuzzy szabályokat, a harmadik rétegben találjuk a fuzzy kimeneti változókat. A fuzzy halmazok (fuzzy) súlytényezőkként jelennek meg. Tulajdonképpen ez nem más, mint a fuzzifikáció, fuzzy következtetés (szabály kiértékelés) és defuzzifikáció megvalósítása többrétegű előrecsatolt hálózatokkal. Ez a felépítés persze nem kötelező ahhoz, hogy a fuzzy rendszerben/rendszerhez tanuló algoritmust alkalmazzunk, de mindenképpen kényelmes, hiszen követi az adatok hagyományos fuzzy rendszerbeli útját, kiegészítve a modellen belüli tanulás képességével. (Előfordulnak ötrétegű hálózatok is, ahol a második és az utolsó előtti réteg neuronjai felelnek meg a tagsági függvényeknek.)
A neuro-fuzzy rendszer a tanulás előtt, közben és utána is fuzzy szabályok rendszere. A modell (szabálybázis) létrehozása lehetséges teljességgel a tanító adatok alapján vagy a fuzzy szabályok előzetes ismeretével.
A neuro-fuzzy rendszer egy n dimenziós, a tanító adatokkal részben definiált, tulajdonképpen ismeretlen függvényt közelít. A fuzzy szabályok a tanító adatok prototípusainak tekinthetők, hiszen csak bizonyos bemenet-kimenet kapcsoaltokat képeznek le a lehetségesek közül.
Neuro-fuzzy jelzővel illethejük az előbb ismertetett összekapcsolt hálózatként megvalósított fuzzy szabályalapú rendszerek mellett egyebek között az alábiakat.
-
Tanított radiális bázisfüggvényes (RBF) hálózatból származó fuzzy szabályok.
-
A neurális hálózat tanító paramétereinek fuzzy logika alapú beállítása.
-
A hálózat méretének növelése fuzzy kritériumok alapján.
-
A fuzzy tagsági függvények létrehozása neurális hálózatokkal.