1. fejezet - A Végeselem módszer elméleti alapjai
Vissza		Előre

1. fejezet - A Végeselem módszer elméleti alapjai

Tartalom

Megfelelő matematikai apparátussal a végeselem módszer egyszerűen megfogalmazható, áttekinthető számítási metodika. Az egyszerű megfogalmazáshoz azonban szükséges néhány alapfogalom tisztázása. Az alábbiak elsősorban Karátsony János [1.] előadásaira alapozottak. Nem tartalmazzák azonban a funkcionál analízis összes rejtélyét, csak azokat az alapfogalmakat, melyek a végeselem módszerről való plasztikus – a numerikus részletek kidolgozási metódusait elfedő – kép kialakításához szükségesek.

1.1. Alapfogalmak

A módszer matematikai értelmezéséhez tekintsünk át először a fent említett néhány alapfogalmat!

1.1.1. Az algebrai test

Definíció: Az algebrai test egy olyan struktúra (alapelemek, relációk és műveletek halmaza) ahol értelmezettek + és a ∗ műveletek.

F = (T, + , ∗)

(1.1)

ahol T kommutatív csoportot alkot az összeadás (+) műveletre és a szorzás (∗) műveletre.

Létezik 0 elem, azaz

Minden a ∈ T, a+0 = a

a,b ∈ T, a+b = b+a ∈ T,

(1.2)

Létezik 1 elem, azaz

Minden a ∈ T, a∗1 = a

(1.3)

A szorzás kommutatív

a,b ∈ T, a∗b = b∗a ∈ T

(1.4)

A szorzás asszociatív

a,b,c ∈ T a ∗ (b∗c)=(a∗b)∗c∈T

(1.5)

Minden nem 0 elemnek létezik inverze (a^-1 ∈ T)

a ∈ T, a≠0 a∗a^-1 = 1

(1.6)

A ∗ szorzás disztributív az összeadásra nézve, azaz

a,b,c ∈ T (a+b) ∗c=(a∗c)+(b∗c)

(1.7)

Ha jól végiggondoljuk a definíciót, akkor láthatjuk, hogy a valós számok, a komplex számok egyaránt testet alkotnak. Szokás is beszélni a valós számtestről, illetve a komplex számtestről. A későbbiekben ez a két test alapvető szerepet játszik.

1.1.2. A vektortér

Definíció: Egy V nem üres halmazt vektortérnek nevezünk egy F test felett, ha V halmaz elmei között értelmezett az összeadás művelete, azaz bármely két elemhez értelmezett egy + függvény úgy, hogy

u,v ∈ V akkor u+v ∈V vagy másképp

+:V×V→V

(1.8)

F és V között értelmezve van a skalárral való szorzás művelete (∗) azaz

λ ∈ F és v ∈V akkor λ∗v ∈V vagy másképp

∗:F×V→V

(1.9)

úgy hogy V az összeadásra nézve kommutatív csoport, és a skalárral való szorzásra igaz, hogy

λ ∈ F és u,v ∈V akkor λ∗ (u+v)= λ∗u+λ∗v

λ,μ ∈ F és u ∈V akkor (λ+μ) ∗u= λ∗u+μ∗u

λ,μ ∈ F és u ∈V akkor λ∗ (μ∗u)=(λ∗μ) ∗u

minden u ∈V akkor 1∗u=u, ahol 1 a test egysége

(1.10)

Ha a térbeli vektorokra gondolunk, akkor könnyen meggyőződhetünk arról, hogy azok vektorteret alkotnak az összeadásra és a valós skalárral való szorzásra. De vektortér a folytonos függvények tere is, ha a függvények közötti összeadásra és a függvény skalárral való szorzására gondolunk. A függvények tere különösen fontos szerepet játszik majd, hiszen a differenciálegyenletek megoldásai függvények.

1.1.3. A metrikus tér

Metrikus térnek nevezünk egy olyan halmazt (X), melyen értelmezett egy olyan d függvény, amely a halmaz bármely két eleméhez hozzárendel egy nem negatív valós számot. Legyen

d:X×X→R^+,

(1.11)

amelyre igazak az alábbiak:

1.) d(x,y)=0 akkor és csak akkor,ha x=y,

2.) d(x,y)=d(y,x),

3.) d(x,z)≤d(x,y)+d(y,z).

(1.12)

Ez megfelel a távolság fogalmunknak, például a térben két pont távolsága csak akkor 0, ha azonos pontokról van szó (ez éppen az első feltétel), x pont távolsága y-tól ugyanannyi, mint y-nak x-től (a második feltételnek megfelelően) a távolság szimmetrikus. Végül igaz a háromszög-egyenlőtlenség (pontosan a harmadik feltétel írja le).

1.1.4. Norma, normált tér

Definíció: Legyen X vektortér K felett, ahol K = C (a komplex számok halmaza) vagy R (a valós számok halmaza). A norma X vektortéren értelmezett függvény, mely a vektortér elemeihez nem negatív egész számot rendel

‖ ⋅ ‖:X→R^+,

(1.13)

és

1.) minden x∈X-re ‖x‖≥0 és ‖x‖=0 akkor és csak akkor,ha x=0,

2.) minden λ∈K és x∈X-re ‖λ∗x‖= |λ|∗‖x‖,

3.) minden x,y∈X-re ‖x+y‖≤‖x‖+‖y‖.

(1.14)

A |λ| a komplex szám abszolút értéke

A háromdimenziós vektorok (x,y,z) ∈ R³ között értelmezett az euklideszi norma

$‖ \cdot ‖_{2} : R^{3} \to R^{+}, ‖ (x, y, z) ‖_{2} = \sqrt[2]{x^{2} + y^{2} + z^{2}} .$

(1.15)

Könnyen meggyőződhetünk arról, hogy norma az úgynevezett maximum-norma is

$‖ \cdot ‖_{m a x} : R^{3} \to R^{+}, ‖ (x, y, z) ‖_{m a x} = m a x (| x |, | y |, | z |)$ ,

(1.16)

hiszen a definícióban megfogalmazott összes feltételt teljesíti.

Az (X, ‖⋅‖) vektorteret és az azon értelmezett normából képzett párt normált térnek hívjuk. Az R valós számok halmaza az abszolút értékkel normált tér, a háromdimenziós vektorok szintén normált teret alkotnak az euklideszi normával. A normált terek egyúttal metrikus terek is, hiszen a ρ(x,y)=‖x-y‖ metrika értelmezhető.

1.1.5. Sorok és sorozatok normált térben

Definíció: Legyen (X, ‖⋅‖) normált tér, x_n⊂X a tér elemeiből alkotott sorozat és x∈X egy vektor! Azt mondjuk, hogy a x_n sorozat határértéke x, ha az ‖x_n-x‖ számsorozat határértéke 0, azaz

$lim_{n \to \infty} x_{n} = x$ , ha $lim_{n \to \infty} ‖ x_{n} - x ‖ = 0$ .

(1.17)

Azt mondjuk, hogy a $\sum_{i = 0}^{\infty} x_{i}$ sorösszeg x, ha a részösszegekből alkotott sorozat tart x-hez, azaz

$\sum_{i = 0}^{n} x_{i} = x$ , ha $s_{n} = \sum_{i = 0}^{n} x_{i}$ sorozatra $lim_{n \to \infty} s_{n} = x$

(1.18)

Tehát a normált terekben minden ugyanúgy működik, mint a valós számoknál.

Definíció: Egy vektortér elemeiből képzett sorozatot Cauchy sorozatnak hívunk, ha minden ε>0 számhoz létezik olyan – ε-tól függő – N egész, hogy minden n>m>N(ε) számra

‖x _n -x _m ‖<ε

(1.19)

Ez azt jelenti, hogy ha a sorozat elejét levágjuk, akkor a maradék tagok közel vannak egymáshoz.

A sorok és sorozatok segítségével a határérték és a Cauchy sorozat pontosan úgy definiálható normált terekben, mint a valós számok esetében.

Tétel: A norma folytonos függvény, azaz ha vektorok egy sorozata (x_n) közeledik a vektortér egy vektorához, akkor a sorozat elemeinek normái is közelítenek a határérték normájához.

1.1.6. A Banach-tér

Definíció: Egy normált teret Banach-térnek nevezünk, ha minden Cauchy sorozata konvergens, azaz a tér teljes.

Ez is azt jelenti, hogy a Banach-tér elemei úgy viselkednek, mint a valós számok. Az Rⁿaz n elemű valós vektorok is az euklideszi normával Banach teret alkotnak. Minden véges dimenziós normált tér Banach-tér. A intervallumon folytonos függvények C_[a,b] a maximum normával (‖f‖_max=max_[a,b]f) szintén Banach-teret alkotnak.

Tétel: Legyen (X, ‖⋅‖) normált tér, X₀ ⊂ X véges dimenziós altér és x ∈ X tetszőleges vektor. Ekkor létezik y₀ ∈ X₀, amelyre d = min(x, y₀ ∈X₀) =‖x-y₀ ‖=dist(x,X₀).

Ez azt jelenti, hogy egy véges-dimenziós altérnek a tér bármelyik eleméhez van legközelebbi eleme. Ezt nevezzük a vektor és az altér távolságának. Ha a háromdimenziós térben gondolkodunk, akkor annak például a sík altere. Bármely térbeli vektor sík altérre vetett merőleges vetülete a kétdimenziós sík altér legközelebbi eleme.

1.1.7. Lineáris leképezések, funkcionálok, korlátos leképezések

Azonos test felett definiált vektorterek között leképező függvényt lineárisnak nevezzük, ha

két vektor összegének képe a két vektor képének összege, és
egy vektor számszorosának képe a vektor képének ugyanezen számszorosa.

Ugyanez definíciószerűen megfogalmazva:

Definíció: Legyenek X és Y vektorterek a T számtest felett. Az

L:X→Y

(1.20)

leképezés lineáris, ha L értelmezési tartománya a H altér, és bármely u, v ∈ H valamint λ ∈T-re igaz, hogy

L(u+v)=L(u)+L(v) és

L(λ ∗ u)=λ ∗ L(u).

(1.21)

A lineáris leképezéseket szokták lineáris operátoroknak is hívni. Lineáris operátoroknál el szokták hagyni a () jeleket, és mintha mátrix-szorzás lenne Ax –szel jelölik. A definícióból egyértelmű, hogy A0=0.

A linearitás definíciója pontosan megfelel az egyváltozós lineáris függvényeknek, illetve a vektorok mátrixszal való szorzásának és eltolásának. (Ax+b).

Definíció: Legyen X vektortér a T alaptest felett! Funkcionálnak nevezzük a

F:X→T

(1.22)

leképezéseket.

A funkcionál tehát egy olyan leképezés, ami a vektortér elemeit az alaptest „számaira” képezi.

Definíció: Normált térben korlátosnak nevezünk egy L leképezést, ha létezik olyan M állandó, hogy

‖Lx‖≤M ∗ ‖x‖

(1.23)

minden L értelmezési tartományában lévő x esetén.

Tétel: Egy lineáris leképezés akkor és csak akkor folytonos, ha korlátos.

A továbbiakban legyen X normált tér. A fenti tétel funkcionálokra is érvényes, így egy

ϕ : X → K

(1.24)

lineáris funkcionál pontosan akkor folytonos, ha korlátos, azaz ha van olyan M ≥ 0 állandó, hogy minden x ∈ X esetén |ϕx| ≤ M∥x∥.

Tétel: Ha X normált tér és K az alaptest, akkor az X-n értelmezett korlátos lineáris funkcionálok halmaza Banach-tér.

1.1.8. A skalárszorzás vektorterekben

A vektorterek skaláris szorzata is általánosítható.

Definíció: Legyen X vektortér T (valós vagy komplex számok) felett! Egy olyan <,>-nal jelölt leképezést, amelyre

< ,>X×X→T

(1.25)

skalár szorzatnak nevezünk, ha

lineáris funkcionál, azaz minden x,y,z ∈ X-re és λ∈T-re, igaz, hogy

<x,λ y+z >= λ <x,y>+<x,z>
hermitikus, azaz <x,y>= $\bar{< y, x >}$ , ahol a felülvonás a komplex konjugáltat jelöli. Természetesen valós számok esetén ez szimmetriát jelent.
pozitív definit, azaz <x,x>≥0, és <x,x>=0 akkor és csak akkor, ha x=0.

A térbeli valós számtest feletti vektorok skaláris szorzata ilyen értelemben is skaláris szorzat. Hasonlóan igaz ez a komplex számtest felett értelmezett vektorokra.

Például az intervallumon folytonos függvények (C_[a,b]) esetében az integrál alaptulajdonságai miatt skaláris szorzat lehet a

$< f, g > \int_{a}^{b} f (x) * g (x) d x$

(1.26)

Bizonyítható, hogy az X vektortér $‖ x ‖ = \sqrt[2]{< x, x >}$ skalárszorzata (x ∈ X esetén) norma.

Definíció: Az X vektortérben a skalár szorzat

$‖ x ‖ = \sqrt[2]{< x, x >}$

(1.27)

kifejezését (x ∈ X) a skalárszorzat által indukált normának nevezzünk.

A valós vektorok körében a szokásos skaláris szorzat az euklideszi normát indukálja.

1.1.9. A Hilbert-tér

Definíció: Egy teljes (minden Cauchy sorozat konvergens) normált (Banach) teret

(H, <,>)

(1.28)

Hilbert-térnek nevezünk, ha a norma a skaláris szorzat által indukált $\sqrt[2]{< x, x >}$ norma.

A véges-dimenziós vektorterek Hilbert-terek, a szokásos skalárszorzással az euklideszi normára.

A Ω ⊂ Rⁿ négyzetesen integrálható függvények ( $\int_{Ω} {| f |}^{2} d x < \infty$ ) Hilbert-teret alkotnak a

$< f, g > = \int_{Ω} f * \bar{g} d x$

(1.29)

normára.

Definíció: Azt mondjuk, hogy az x, y ∈ H (Hilbert-tér) vektorok ortogonálisak (vagy merőlegesek x ⊥ y) egymásra, ha <x,y> = 0.

A síkban és a térben jól ismert a merőleges vektorok ilyen tulajdonsága a szokásos skaláris szorzásra nézve.

Bizonyíthatók az alábbi állítások:

Tétel: Legyen H Hilbert-tér, K ⊂ H nem üres, konvex, zárt halmaz. Ekkor bármely x ∈ H esetén van egyetlen olyan y ∈ K, melyre ‖x - y‖ = min(x,y)=dist(x,K) (vagyis az x-nek K-tól vett távolsága).

Tétel: (Riesz reprezentációs tétele). Legyen H Hilbert-tér. Ekkor minden ϕ : H → C folytonos, lineáris funkcionálhoz létezik egyetlen olyan y ∈ H, hogy

ϕx = 〈 x,y 〉 minden x∈H

(1.30)

Tehát minden folytonos, lineáris funkcionál leírható a Hilbert-tér egy elemével való skalárszorzással. Más szavakkal minden folytonos lineáris funkcionál azonos a tér valamely elemével való skalárszorzással.

1.1.10. Szimmetrikus operátorok

Definíció. Legyen H Hilbert-tér, A lineáris operátor! Az

A : H → H

(1.31)

lineáris operátor szimmetrikus, ha

< Ax,y> = <x,Ay>

(1.32)

teljesül minden x, y-ra A értelmezési tartományán.

Egy mátrixot akkor nevezünk szimmetrikusnak, ha elemei a főátlóra szimmetrikusak. Bizonyítható, hogy a szimmetrikus mátrixok is definiálhatók a fenti módon.

Tétel: Ha H komplex Hilbert-tér, az A : H→H operátor akkor és csak akkor szimmetrikus ha

< Ax,x> ∈ R ∀x ∈ H

(1.33)

1.1.11. Adjungált és önadjungált operátorok

Amennyiben a skaláris szorzatokban operátorok által leképzett elemeket is használunk, szükséges néhány fogalom tisztázása.

Tétel: Ha A Hilbert-téren értelmezett korlátos lineáris operátor, akkor létezik egyetlen olyan A^∗ korlátos lineáris operátor, melyre

〈 Ax,y 〉 = 〈 x,A^ ∗ y 〉 minden x,y∈H

(1.34)

Ezt az A^∗ operátort az A adjungáltjának nevezzük.

Az adjungált operátorra bizonyíthatóak az alábbi állítások

Tétel: Ha A és B korlátos lineáris operátorok, és λ komplex szám, akkor

	${(A + B)}^{} = A^{} + B^{*}$	(1.35)
	${(λ * A)}^{} = λ A^{*}$	(1.36)
	${(A * B)}^{} = B^{} * A^{*}$	.37)
	${‖ A ‖}^{2} = ‖ A^{} A ‖$	(1.38)

Definíció: Egy A korlátos és lineáris operátor önadjungált, ha

A ^* =A

(1.39)

Az önadjungált operátor definíciója alapján írhatjuk, hogy

〈 Ax,y 〉 = 〈 x,Ay 〉 minden x∈H

(1.40)

Ha A korlátos és lineáris operátor akkor és csak akkor önadjungált, ha

〈 Ax,x 〉 valós minden x∈H

(1.41)

Hiszen fennállnak a (1.42) egyenlőségek.

$A x, x = x, A^{*} x = x, A x = \bar{A x, x}$ minden x∈H

(1.42)

1.1.12. Pozítív, szigorúan pozitív, egyenletesen pozitív önadjungált operátorok, koercív operátorok

Definíció. Egy H Hilbert-téren értelmezett A lineáris korlátos operátor pozitív, ha

〈 Ax,x 〉 ≥ 0 ( ∀ x ∈ H);

(1.43)

szigorúan pozitív, ha

〈 Ax,x 〉 > 0 ( ∀ x ∈ H,x≠ 0);

(1.44)

egyenletesen pozitív, ha létezik

m > 0 úgy,hogy 〈Ax,x〉≥ m∥x∥² (∀x ∈ H).

(1.45)

Definíció: Legyen A korlátos lineáris leképezés! Az A operátort koercívnek hívjuk, ha létezik m > 0, hogy

Re 〈 Ax,x 〉 ≥m ∗ ‖x‖ ², minden x∈H

(1.46)

Valós Hilbert-térben, illetve önadjungált esetben elhagyható a valós rész képzés Re operátora.

Ha H komplex Hilbert-téren értelmezett, önadjungált, egyenletesen pozitív, korlátos operátor, akkor <Ax,x> valós, így (1.41) miatt önadjungált. Ha A valós Hilbert-téren értelmezett egyenletesen pozitív operátor, akkor ugyancsak (1.41) miatt önadjungált kell, legyen, és létezik m > 0, hogy (1.46) fennáll.

Tétel: Összefoglalva tehát, egy operátor akkor és csak akkor egyenletesen pozitív, ha koercív és önadjungált.

1.1.13. Monoton és Lipschitz-folytonos operátorok

Definíció: Legyen H Hilbert-tér! Azt mondjuk, hogy F : H → H operátor

monoton operátor, ha

〈Fx-Fy,x-y〉≥0 minden x,y∈H

(1.47)

szigorúan monoton operátor, ha

〈 Fx-Fy,x-y 〉 >0 minden x,y∈H

(1.48)

egyenletesen monoton operátor, ha létezik m > 0, hogy

〈 Fx-Fy,x-y 〉 >m ∗ ‖x-y‖ ² minden x,y∈H

(1.49)

Definíció: Legyen H Hilbert-tér! Az F : H → H operátror Lipschitz-folytonos, ha létezik M > 0, hogy

〈 Fx-Fy,x-y 〉 ≤M ∗ ‖x-y‖ minden x,y∈H

(1.50)

A monotonitás és a Lipschitz feltétel is megfelel a függvényeknél megismerteknek.

1.1.14. Operátorok bihemi-folytonossága

Definíció. Legyenek X, Y és Z normált terek! Legyen A leképezés, ami a X ről, az Y-ról Z-re képező korlátos és folytonos leképezések halmazára (ez is vektortér) képez. Azt mondjuk, hogy

a kérdéses A leképezés hemi-folytonos, ha minden u, v ∈ X és minden w ∈ Y, valamint t∈R esetén a

t → A(u+tv)w

leképezés folytonos;

A bihemi-folytonos, ha minden u, v,w ∈ X, z ∈ Y valamint s,t∈R esetén az

(s, t) → A(u + tv + sw)z

leképezés folytonos.

A hemi- és a bihemi-folytonosság valami olyasmit takar, hogy ha egy egyenes mentén, vagy két paraméterrel, két egyenessel meghatározott módon változtatjuk egy leképezés független változóját, akkor a leképezések a paraméterek függvényében folytonosan változnak.

1.1.15. Az energianorma

Definíció. Legyen H Hilbert-téren értelmezett A operátor folytonos, korlátos, lineáris és szigorúan pozitív (A:H→H) . Ekkor az

〈 x,y 〉 _A = 〈 Ax,y 〉

(1.51)

skalárszorzatot az A operátorhoz tartozó energia-skalárszorzatnak, az indukált

$∥ x ∥_{A} = \sqrt[2]{〈 A x, x 〉}$

(1.52)

normát pedig energianormának nevezzük.

Tétel: Ha A:H→H egyenletesen pozitív (1.1.12. szakasz) operátor, akkor H Hilbert-tér a < , >_A skalárszorzat által generált ∥x∥_A normával is Hilbert-tér lesz.

1.1.16. Bilineáris formák

Definíció. Egy B : H × H → K (ahol K a komplex vagy a valós számtest) leképezés

bilineáris, ha mindkét változójában lineáris;

konjugáltan bilineáris, ha első változójában lineáris, második változójában konjugáltan lineáris, azaz

$\begin{array}{l} B (x_{1} + x_{2}, y) = B (x_{1}, y) + B (x_{2}, y) \\ B (c * x, y) = c * B (x, y) \\ B (x, y_{1} + y_{2}) = B (x, y_{1}) + B (x, y_{2}) \\ B (x, c * y) = \bar{c} * B (x, y) \end{array}$

(1.53)

szimmetrikus, ha

$B (x, y) = B (y, x)$

(1.54)

konjugáltan szimmetrikus, ha

$B (x, y) = \bar{B (y, x)}$

(1.55)

korlátos, ha létezik M > 0, hogy

|B(x,y)|≤M ∗ ‖x‖ ∗ ‖y‖ minden x,y ∈H

(1.56)

koercív, ha létezik m > 0, hogy

Re B(x,x)≥m ∗ ‖x‖ ² minden x ∈H

(1.57)

Tétel (korlátos formák Riesz-reprezentációja). Legyen H valós (komplex) Hilbert-tér, és B : H × H → K korlátos, (konjugáltan) bilineáris forma. Ekkor létezik pontosan egy olyan A korlátos, lineáris operátor, melyre

B(x,y)= 〈 Ax,y 〉 minden x,y ∈H

(1.58)

A tétel állítása emlékeztet a 1.1.9. szakasz fejezet (1.30) állítására. Minden korlátos, konjugált, bilineáris forma reprezentálható lesz korlátos, lineáris operátorral.

Tétel. Legyen H valós (komplex) Hilbert-tér, B : H × H → K korlátos, (konjugáltan) bilineáris forma, és A korlátos és lineáris operátor, a B forma Riesz-reprezentánsa.

B akkor és csak akkor (konjugáltan) szimmetrikus, ha A önadjungált.
B akkor és csak akkor koercív, ha A koercív.

Látható tehát, hogy a bilineáris formák az operátorokhoz hasonlóan viselkednek. Kapcsolat is teremthető köztük.

Tétel: (Lax_Milgram-lemma, koercív változat).

(1) Legyen H valós Hilbert-tér, B : H × H → R korlátos, koercív, bilineáris forma. Ekkor minden ϕ:H→R korlátos lineáris funkcionálhoz létezik egyetlen olyan x ∈ H, melyre

B(x,y)=ϕy minden y ∈H

(1.59)

(2) Legyen H komplex Hilbert-tér, B : H × H → C korlátos, koercív, konjugáltan bilineáris forma. Ekkor minden ϕ:H→C korlátos, lineáris funkcionálhoz létezik egyetlen olyan x ∈ H, melyre

B(y,x)=ϕy minden y ∈H

(1.60)

Tétel (Lax_Milgram-lemma, általános változat). Legyen H valós Hilbert-tér, B :H × H → R korlátos és létezik m>0 úgy, hogy

|B(x,x)|≥m ∗ ‖x‖ ² minden x ∈H

(1.61)

akkor a valós tér esetén minden ϕ : H → R korlátos, lineáris funkcionálhoz létezik pontosan egy olyan x ∈ H, melyre

B(x,y)=ϕy minden y ∈H

(1.62)

Illetve, ha H komplex Hilbert-tér, B :H × H → C esetén

B(y,x)=ϕy minden y ∈H

(1.63)

Az alapfogalmak eddigi tisztázása után kezdhetünk foglalkozni célunkkal az operátoregyenletek megoldásával.

1.2. Operátoregyenletek megoldása

Mielőtt a numerikus megoldásokra koncentrálnánk célszerű néhány szót ejteni az

Ax=f

(1.64)

operátoregyenlet megoldásáról, a megoldás létezéséről és egyértelműségéről.

1.2.1. Lineáris, korlátos operátoregyenletek

Tétel. Legyen A a H Hilbert-téren értelmezett, korlátos, lineáris és egyenletesen pozitív operátor, azaz A koercív és önadjungált. Ekkor bármely f ∈ H esetén az Ax = f egyenletnek létezik pontosan egy x^∗ ∈ H megoldása.

Szokás ezt az első megoldhatósági tételnek is nevezni.

Tétel. Legyen A a H Hilbert-téren értelmezett, korlátos, lineáris és koercív. Ekkor bármely f ∈ H esetén az Ax = f egyenletnek létezik pontosan egy x^∗ ∈ H megoldása.

Láthatóan ez az előző tétel kiterjesztése - nem kell, hogy az operátor önadjungált legyen, elég, ha csak koercív. Szokás ezt a tételt második megoldhatósági tételnek is nevezni.

Tétel. Legyen A a H Hilbert-téren értelmezett, korlátos, lineáris. Ha

|Ax,x|≥m ∗ ‖x‖ ² minden x∈H

(1.65)

akkor bármely f ∈ H esetén az (1.64 egyenletnek létezik pontosan egy x^∗ ∈ H megoldása.

Még a koercivitás sem feltétel, elég a pozitívságot biztosító feltétel.

1.2.2. Lineáris nem korlátos operátoregyenletek

A nem korlátos operátoregyenletekre nem mondható ki egzisztencia és unicitás jellegű állítás, ezért bevezetjük a gyenge megoldás fogalmát.

1.2.2.1. Szimmetrikus operátoregyenletek gyenge megoldása

Tekintsük a (1.64) egyenletet! Legyen A szimmetrikus operátor!

Definíció. Legyen H Hilbert-tér, f ∈ H adott vektor és A szimmetrikus operátor! Az x ∈ H vektort az Ax = f feladat gyenge megoldásának nevezzük, ha

〈 x,y 〉 _A = 〈 f,y 〉 (minden y ∈ H)

(1.66)

Ha x az A operátor értelmezési tartományában található, akkor a gyenge megoldás egyúttal megoldás is. Tehát a gyenge megoldás arra az esetre vonatkozik, ha f nincs A képterében.

Tétel. Ha A egyenletesen pozitív, nem korlátos, akkor minden f ∈ H esetén az Ax = f egyenletnek egyértelműen létezik x^* ∈ H gyenge megoldása.

〈 x ^* ,y 〉 _A = 〈 f,y 〉 (minden y ∈ H)

(1.67)

1.2.2.2. Nem szimmetrikus operátoregyenletek gyenge megoldása

Tekintsük a (1.64) egyenletet! Ha A nem szimmetrikus operátor, akkor azzal nem definiálhatunk energia-skalárszorzatot (1.52), mert nem egyenletesen pozitív, így, ha a gyenge megoldást szeretnénk értelmezni, akkor egy másik, alkalmas S szimmetrikus operátor energiaterére vezetjük vissza a feladatot.

Definíció: Legyen S : H → H egyenletesen pozitív operátor, melynek értelmezési tartománya H altere (H_s). Azt mondjuk, hogy az A : H → H lineáris operátor, melynek értelmezési tartománya szintén H altere S -korlátos és S -koercív, ha

A értelmezési tartománya részhalmaza H_S–nek, és az értelmezési tartomány sűrű H_S-ben (a lezártja H_s az energianormában)

Létezik M > 0 állandó, hogy

| 〈 Ax,y 〉 |≤M ∗ ‖x‖ _s ∗ ‖y‖ _s minden x,y∈A ért.tartományára

(1.68)

Létezik m > 0 állandó, hogy

| 〈 Ax,x 〉 |≤m ∗ ‖x‖ _s ² minden x∈A ért.tartományára

(1.69)

Ezzel az A operátort mintegy becsültük az S operátor és energianormája segítségével.

Definíció. Legyen az A : H → H leképezés S-korlátos és S-koercív, ahol az A értelmezési tartománya H altere (H_S)! Ekkor A_S a H_S-ről H_S–re képező korlátos, lineáris operátor, melyre

〈 A_S x,y 〉 _S = 〈 Ax,y 〉 minden x,y ∈A ért.tartományára

(1.70)

Tétel: Az A_S operátor jól definiált.

Ez az állítás belátható, hiszen (1.68) miatt <Ax,y> bilineáris forma folytonos a S operátorhoz tartozó normára. A bilineáris formának létezik pontosan egy reprezentánsa a Riesz-féle reprezentációs tétel miatt (1.58).

Definíció: Legyen A : H → H S-korlátos és S-koercív ahol A értelmezési tartománya H altere,. Az x∈H_S vektor a (1.64) egyenlet gyenge megoldása, ha

〈 A_S x,y 〉 _S = 〈 f,y 〉 minden y ∈H_s

(1.71)

Tétel. Nem szimmetrikus S-korlátos és S-koercív A esetén bármely f ∈ H esetén az (1.64) egyenletnek egyértelműen létezik gyenge megoldása.

Ezzel, a gyenge megoldást használva a nem szimmetrikus operátorok esetére is kimondhattunk egzisztencia és unicitás jellegű állítást. Kérdés, hogy mit tegyünk nem lineáris esetben.

1.2.3. Nem lineáris operátoregyenletek

Nemlineáris esetben F a H valós Hilbert-térről H valós Hilbert-térre képező operátorra vonatkozó

F(x)=f

(1.72)

egyenlet megoldását keressük.

Tétel. Legyen H valós Hilbert-tér és F : H → H adott operátor. Tegyük fel, hogy F egyenletesen monoton és F Lipschitz-folytonos, ekkor bármely b ∈ H esetén az F(x) = b egyenletnek létezik pontosan egy x^∗ ∈ H megoldása.

A Lipschitz-folytonosság – az implicit függvényrendszerekhez hasonlóan – ebben az esetben is biztosítja az egyértelmű megoldás létezését.

Ahhoz, hogy potenciál függvényt használva az operátoregyenlet helyett variációs elvet használjunk a megoldás keresésére szükségünk van a derivált fogalom általánosítására. Operátorok között is értelmezhető derivált jellegű kifejezés.

1.2.4. Gâteaux-derivált, potenciál operátor

Definíció: Legyenek X, Y normált terek! Egy F:X → Y (nemlineáris) operátorról azt mondjuk, hogy Gâteaux deriválható az x∈X pontban, ha

Bármely d∈X -hez létezik

$\partial_{d} F (x) = \lim_{λ \to 0} \frac{F (x + λ * d) - F (x)}{λ}$

(1.73)

A d→∂_d F(x) hozzárendelés folytonos, lineáris operátor, melynek jele F’(x)

F’(x)=∂ _d F(x)

(1.74)

A ∂ _dF(x) Gâteaux derivált (F’(x)) a d irányú iránymenti derivált, az operátor pedig a definíció szerint d irányhoz rendeli az iránymenti deriváltat, tehát X-ből Y-ba képező operátor

Definíció: Legyen X Banach-tér! Egy A: X → X (nemlineáris) operátort potenciáloperátornak nevezünk, ha létezik olyan J : X → R Gâteaux-deriválható funkcionál, melyre J’= A, azaz J’(x) = A(x) minden x ∈ X. Ekkor a J funkcionált A potenciáljának hívjuk.

1.2.5. A variációs elv

Ha egy A operátor potenciáloperátor, akkor az A(x) = b egyenletek megoldása helyett egy funkcionál minimalizálására vezethetjük vissza az egyenlet megoldását.

Legyen X Banach-tér és A:B→B potenciáloperátor és J:B→R a potenciálja! Azaz

J’(x)=A(x) (x ∈ B)

(1.75)

Legyen

E ∶ X→R

(1.76)

funkcionál a következő!

E(x)=J(x)- 〈 b,x 〉

(1.77)

Akkor E potenciáloperátora az x→A(x)-b leképezésnek

E'(x)=A(x)–b (x ∈ X)

(1.78)

hiszen J’=A és <b,x>’=b.

Tehát az A(x)–b=0 egyenlet megoldása megegyezik E funkcionál stacionárius értékével. Az E funkcionál sokszor energia jellegű mennyiség, és ilyenkor az energiaminimumot keressük.

1.3. Variációs elven alapuló közelítő módszerek

A következőkben variációs elven alapuló módszerekkel foglalkozunk.

1.3.1. Lineáris, szimmetrikus operátoregyenletek funkcionáljai

Legyen H komplex Hilbert-tér, A : H → H szimmetrikus, szigorúan pozitív, lineáris operátor, amelynek értelmezési tartománya altér, és f∈ H adott vektor!

Definíció. Az

Ax = f

(1.79)

egyenlethez tartozó kvadratikus funkcionál az alábbi Φ : H → R funkcionál:

Φ(x)= 〈 Ax,x 〉 - 2 ∗ Re 〈 f,x 〉

(1.80)

Tétel: Ha létezik A (szigorúan pozitív) operátor értelmezési tartományában x^∗, amelyre Ax^∗ = f, akkor Φ-nek pontosan egy minimumhelye van, és ez éppen x^∗.

Egyszerűen meggyőződhetünk a tétel igazságáról, hiszen bármely x≠ x^*esetén írjuk át a fenti egyenletet úgy, hogy „ketté írjuk” a (1.80) jobb oldalán álló kifejezés második tagját!

Φ(x)= 〈 Ax,x 〉 - 〈 f,x 〉 - 〈 x,f 〉 =

(1.81)

(1.81)-ban f helyébe írhatjuk az Ax^* kifejezést

Φ(x)= 〈 Ax,x 〉 - 〈 Ax ^* ,x 〉 - 〈 x,Ax ^* 〉

(1.82)

(1.82) első két tagját összevonva

Φ(x)= 〈 A(x-x ^* ),x 〉 - 〈 x,Ax ^* 〉

(1.83)

(1.83) egyenlet jobb oldalát bővítsük a -<A(x-x^*),x^*>+<A(x-x^*),x^*> azonosan 0 kifejezéssel!

Φ(x)= 〈 A(x-x ^* ),x 〉 - 〈 A(x-x ^* ),x ^* 〉 + 〈 A(x-x ^* ,x ^* 〉 - 〈 x,Ax ^* 〉

(1.84)

összevonva az első két tagot

Φ(x)= 〈 A(x-x ^* ),x-x ^* 〉 + 〈 A(x-x ^* ),x ^* 〉 - 〈 x,Ax ^* 〉

(1.85)

kihasználva A szimmetrikus voltát, és összevonva az utolsó két tagot

Φ(x)= 〈 A(x-x ^* ),x-x ^* 〉 - 〈 Ax ^* ,x ^* 〉

(1.86)

<Ax^*,x^*> helyébe (1.80) alapján írhatjuk,

〈 Ax ^* ,x ^* 〉 =Φ(x ^* )+2 ∗ Re 〈 f,x ^* 〉

(1.87)

Mivel x^* megoldás, így f=Ax^* és így Re(Ax^*, x^*) A szimmetriája miatt valós

Φ(x ^* )+2 ∗〈 Ax ^* ,x ^* 〉 = 〈 Ax ^* ,x ^* 〉

(1.88)

azaz

〈 Ax ^* ,x ^* 〉 =-Φ(x ^* )

(1.89)

(1.89)-t (1.86)-be helyettesítve

Φ(x)= 〈 A(x-x ^* ),x-x ^* 〉 +Φ(x ^* )>Φ(x ^* )

(1.90)

Tehát ha létezik az x^* megoldás, akkor az a Φ funkcionál stacionárius értéke. Kérdés létezik-e megoldás?

Ha A egyenletesen pozitív és korlátos, akkor 1.2.1. szakasz első tétele szerint (1.79) egyenletnek létezik pontosan egy megoldása.

Ha A egyenletesen pozitív, de nem korlátos, akkor 1.2.2. szakasz tétele szerint egyértelműen létezik az u^∗ ∈ H gyenge megoldás.

Gyenge megoldás esetén a variációs elvet úgy tudjuk használni, hogy (1.80) egyenlet helyett áttérünk az energiatérre, azaz Φ-t kiterjesztjük a H értelmezési tartományról a teljes X-re. Legyen Ψ:X→R olyan, hogy

Ψ(x)=‖x‖ _A ² -2 ∗ Re<f,x> x∈X

(1.91)

Ha H valós Hilbert-tér, A : H → H szimmetrikus, szigorúan pozitív operátor, melynek értelmezési tartománya H altere, f ∈ H adott vektor. A (1.80) egyenlethez tartozó eredeti, ill. kiterjesztett kvadratikus funkcionál ekkor az alábbi Φ és Ψ funkcionálokra is érvényes a (1.92) eredmény.

ϕ(x)= 〈 Ax,x 〉 -2 ∗ <f,x> Ψ(x)=‖x‖_A²-2∗<f,x> x∈X

(1.92)

1.3.2. Nemlineáris egyenletek funkcionáljai

Legyen H valós Hilbert-tér. Ha az A : H → H nemlineáris operátor potenciáloperátor, akkor az

A(x)=f

(1.93)

egyenlethez, mint a 1.2.4. szakasz fejezetben láttuk, bizonyos feltételek esetén van minimalizáló funkcionál

Φ:X→R, Φ(x)=J(x)-〈f,x〉

(1.94)

ahol X Banach-tér, J egy potenciálja A-nak. Itt ugyanis A(x^*) = f pontosan akkor áll fenn, ha Φ′(x^*) = 0.

Arról, hogy a nemlineáris egyenletnek létezzék megoldása a következő tétel feltételeivel gondoskodhatunk.

Legyen a (1.93) egyenlet A operátora

Gâteaux-deriválható, és A′ bihemi-folytonos,
minden u ∈ H esetén A′(u) ∈ B(H) önadjungált,
létezik m > 0, hogy

〈 A(u)h,h 〉 ≥m‖h‖ ², minden h∈H

(1.95)

Legyen J egy potenciálja A-nak! Ekkor bármely f ∈ H esetén J funkcionálnak egyértelműen létezik minimumhelye, és ez az A(u) = f egyenlet megoldása.

1.4. Ritz-Galjorkin módszer

A Ritz-Galjorkin módszer az egyik legelterjedtebben használt variációs módszer [2.] .

1.4.1. A Ritz-Galjorkin módszer szimmetrikus lineáris egyenletekre

A Ritz-Galjorkin módszer hasonlóan működik más variációs módszerekhez. Legyen H Hilbert-tér, A:H→H egyenletesen pozitív leképezés és A értelmezési tartománya altér! Ekkor az

Ax = f

(1.96)

egyenlet megoldása a

Ψ(x)=‖x‖ _A ² -2 ∗ <f,x>, x∈H

(1.97)

funkcionál minimuma, hiszen a (1.80)-(1.90) egyenletekkel jellemzett – Φ-re elvégzett bizonyítást –végigvezethetjük Ψ-re is.

Ψ(x)=‖x-x ^* _A -‖x ^* ‖ _A ² =‖x-x ^* ‖ _A +Ψ(x ^* )>Ψ(x ^* )

(1.98)

és (1.90) egyenlet helyett (1.98) adódik.

Legyenek ϕ₁, ϕ₂, . . . ∈H elemek halmaza olyan, hogy H Hilbert-tér összes belső pontja kifejezhető ϕ_i elemekből képzett, lineáris kombináló sorok összegével. Ekkor a {ϕ₁, ϕ₂,… ϕ_n } elemek a H_n altér egy bázisát adják. Ha definiálnánk is ilyen {ϕ_i} végtelen elemű halmazt, a variációs egyenletek megoldása nyilván lehetetlen végtelen számú ϕ_i-re.

Keressük a megoldás közelítését egy véges-dimenziós altéren! Legyen n rögzített egész és H_n a ϕ₁, ϕ₂,… ϕ_n elemek (vektorok) által kifeszített altér! Ritz-Galjorkin módszere szerint a közelítő megoldást, a Ψ minimumát csak a H_n altéren keressük.

Keressük a minimumot H_n altéren

$x_{n} = \sum_{i = 1}^{n} c_{i} * ϕ_{i}$

(1.99)

formában!

Itt x_n egyértelműsége ugyanúgy következik, mint x^∗-é (1.3.1. szakasz)-ban, hiszen a kvadratikus funkcionálnak a H_n végesdimenziós téren is egyetlen minimumhelye van.

Mondhatjuk, hogy (1.97) egyenletbe helyettesítve a (1.99) kifejezést,

$\tilde{Ψ} (c) = \sum_{i = 1}^{n} c_{i} * ϕ_{i}, \sum_{j = 1}^{n} c_{j} * ϕ_{j}_{A} - 2 * f, \sum_{i = 1}^{n} c_{i} * ϕ_{i}$

(1.100)

adódik. Ekkor

$\tilde{Ψ} : R^{n} \to R$

(1.101)

azaz

$\tilde{Ψ} (c_{1}, c_{2}, \dots c_{n}) = Ψ (\sum_{i = 1}^{n} c_{i} * ϕ_{i})$

(1.102)

funkcionál, és ennek keressük a minimumát. Bizonyítható, hogy a minimum a parciális deriváltak 0 helyén található. Jelöljük a c_i-kből képzett vektort c-vel!

$\tilde{Ψ} (\underline{c}) = {〈 \sum_{i = 1}^{n} c_{i} * ϕ_{i}, \sum_{j = 1}^{n} c_{j} * ϕ_{j} 〉}_{A} - 2 * 〈 f, \sum_{i = 1}^{n} c_{i} * ϕ_{i} 〉$

(1.103)

Átrendezve

$\tilde{Ψ} (\underline{c}) = {〈 \sum_{i = 1}^{n} \sum_{j = 1}^{n} c_{i} * c_{j} * ϕ_{i}, ϕ_{j} 〉}_{A} - 2 * \sum_{i = 1}^{n} c_{i} f, ϕ_{i}$

(1.104)

A minimum feltétele tehát

$\frac{\partial \tilde{Ψ} (\underline{c})}{\partial c_{k}} = 2 * \sum_{i = 1}^{n} c_{i} * {〈 ϕ_{i}, ϕ_{k} 〉}_{A} - 2 * 〈 f, ϕ_{k} 〉 = 0$

(1.105)

A (1.105) lineáris egyenletrendszer az ismeretlen c_i-kre.

Jelöljük az egyenletrendszer együtthatóit g_ik-val!

g _ik = 〈 ϕ _i ,ϕ _k 〉 _A = 〈 ϕ _k ,ϕ _i 〉 _A =g _ki

(1.106)

A (1.106) egyenletek g_ik elemeiből alkotott szimmetrikus mátrixot Gram mátrixnak, a végeselem rendszerek pedig merevségi mátrixnak hívják. Vezessük be a (1.107) jelölést!

b _k = 〈 f,ϕ _k 〉

(1.107)

Az egyenlet tehát

$\sum_{i = 1}^{n} g_{i, k} * c_{k} = b_{k}$ k=1..n

(1.108)

azaz

[g _i,k ] ∗ [c _k ]=[b _k ]

(1.109)

Tétel: Az egyenletrendszer megoldásaként adódó összeg A norma szerint tart a tényleges megoldáshoz, ha n tart a végtelenhez, azaz

$\lim_{n \to \infty} {‖ \sum_{i = 1}^{n} c_{i} * ϕ_{i} - x^{*} ‖}_{A} = 0$

(1.110)

Ha egy konkrét problémát szeretnénk megoldani, azt háromféleképpen is megtehetjük az alábbi tétel szerint:

Tétel. A Ritz-Galjorkin módszerrel kapott (1.99) szerinti x_n-re az alábbi tulajdonságok teljesülnek:

(a) Közelítő minimalizálás: kereshetjük a fenti (1.108) egyenletrendszerrel a minimumot.

(b) Vetületi egyenlet:

〈 x _n ,y 〉 _A = 〈 f,y 〉, minden y∈H_n

(1.111)

〈 x _n -x ^* ,y 〉 _A =0, minden y∈H_n

(1.112)

Két utóbbi (1.111), (1.112) tulajdonság azt jelenti, hogy x_n éppen x^∗ vetülete H_n-re.

A tétel (a) állítása éppen a Ritz-Galjorkin módszer definíciója.

A (1.111) kifejezést elég, ha minden Φ_k-ra igazoljuk, hiszen akkor lineáris kombinációjukra (v) is igaz lesz.

${〈 x_{n}, ϕ_{k} 〉}_{A} = {〈 \sum_{i = 1}^{n} c_{i} * ϕ_{i}, ϕ_{k} 〉}_{A} = \sum_{i = 1}^{n} c_{i} * {〈 ϕ_{i}, ϕ_{k} 〉}_{A}$

(1.113)

a (1.113) kifejezés jobb oldala viszont (1.105) miatt éppen

$\sum_{i = 1}^{n} c_{i} * {〈 ϕ_{i}, ϕ_{k} 〉}_{A} = 〈 f, ϕ_{k} 〉$

(1.114)

a (1.113) és (1.114) egyenletek összevetéséből viszont (1.111) igaz minden Φ_k-ra.

A (1.112) állítást igazolhatjuk, ha az (1.111) vetületi egyenletet x_n-re és x^*-ra alkalmazva

〈 x _n ,y 〉 = 〈 f,y 〉

(1.115)

és

〈 x ^* ,y 〉 = 〈 f,y 〉

(1.116)

(1.115) és (1.116) egyenleteket egymásból kivonva

〈 x _n ,y 〉 - 〈 x ^* ,y 〉 = 〈 f,y 〉 - 〈 f,y 〉 =0

(1.117)

adódik.

Szemléletessé tehetjük a fenti tétel (b) és (c) állítását, ha a normál háromdimenziós térre és annak egy síkjára, mint kétdimenziós altérre gondolunk. Egy tetszőleges térbeli vektorhoz legközelebbi altérbeli vektor meghatározható, mint a térbeli vektor altérre vetett vetülete (b), vagy az altérbeli közelítő és a térbeli vektor távolságának minimalizálása (a merőleges az eltérés) (c).

1.4.2. A Ritz-Galjorkin módszer általánosítása

Ahogy a fenti gondolatmenetben növeltük az altér dimenzióját, a közelítő megoldás úgy közelítette a tényleges megoldást (1.110), vagyis a módszer konvergens volt. Az altér dimenziójának megnövelésekor a választott Φ_i bázishoz mindig új elemet választottunk. A módszert úgy általánosíthatjuk, hogy minden egyes lépésben az altér teljes bázisát lecseréljük.

A dimenziószám növelése során x_n (1.99) szerinti közelítésében minden egyes lépésben választhatunk az altérben új bázisfüggvényeket. Az n. lépésben a bázisfüggvények Φ_i,n, amelyek kifeszítik (span) az aktuális alteret.

H _n =span{Φ _1,n ,Φ _2,n ⋯ Φ _n,n }

(1.118)

Az x_n közelítést minden lépésben ugyanúgy állíthatjuk elő, mint a szimmetrikus esetben, az x_n együtthatóit a (1.109) lineáris algebrai egyenletrendszer megoldásával kapjuk, azonban most ezek származtatása esetén nem használhatjuk fel az eggyel kisebb dimenzióra meghatározott Gram-mátrixot. Érvényesek a (1.110), (1.111), (1.112) tulajdonságok is, és a nem használtuk ki a H_n alterek egymásba ágyazottságát.

Ebben az esetben a konvergenciához plusz feltételre van szükség a szimmetrikus esethez képest (1.110). Legyen igaz bármely x∈H_Aesetén, hogy

dist _A (x,H _n )=min{‖x-x _n ‖ _A : x _n ∈ H _n }→0,ha n→∞

(1.119)

Olyan sorozatot kell keresnünk, ahol a sorozat n. tagja H_n-ből való, azaz bármely x esetén az kifejezhető Φ_i,n lineáris kombinációjával. A (1.119) feltétel és (1.112 miatt x^*-x_n éppen merőleges H_n-re, tehát az van a legközelebb, így

‖x ^* -x _n ‖ _A =min{‖x-x _n ‖ _A : x _n ∈ H _n }→0,ha n→∞

(1.120)

azaz olyan sorozattal közelítjük x^*-t, amelynek n. tagja éppen Hn-ben van.

1.4.3. A Ritz-Galjorkin módszer nem szimmetrikus lineáris egyenletekre

Most a nem szimmetrikus operátorok esetén megvizsgáljuk a Ritz-Galjorkin módszer lehetőségeit! Legyen H valós Hilbert-tér, A: H →H, nem szimmetrikus, lineáris operátor és gϵH. Ebben az esetben a

Ax=f

(1.121)

operátoregyenlettel kell foglalkoznunk. Módszerünk szerint megvizsgáljuk, hogyan lehet a problémát visszavezetni egy szimmetrikus operátorra. Mivel az energianormához szimmetrikus operátor szükséges, mi az A helyett egy másik S szimmetrikus operátorra vezetjük vissza a feladatot.

Az 1.2.2.2. szakasz fejezet szerint ennek egyértelműen létezik gyenge megoldása, azaz x^* ∈ H_S, melyre igaz, hogy

〈 A _s x ^* ,y 〉 _s = 〈 f,y 〉, minden y∈H_s

(1.122)

Bázisfüggvényeket rögtön válasszuk az általánosított (1.118) szerint!

A (1.119)-hez hasonlóan itt is legyen feltétel, hogy bármely x∈H_sesetén

dist (x,H _n )=min{‖x-x _n ‖ _S : x _n ∈ H _n }→0,ha n→∞

(1.123)

Legyen ebben az esetben is

$x_{n} = \sum_{i = 1}^{n} c_{i} * ϕ_{i}$

(1.124)

Most azonban a szimmetria hiánya miatt nem használhatunk kvadratikus funkcionált. A közelítő megoldást keressük

〈 A _s x _n ,y 〉 _s = 〈 f,y 〉 minden y∈H_s

(1.125)

alakban. Ez egyértelműen létezik 1.2.2. szakasz fejezet szerint.

Az x_n együtthatóit ugyanúgy számíthatjuk, mint szimmetrikus esetben, ha (1.124)-t (1.122) – be helyettesítjük, és az y helyett a Φ_k-kat használjuk, akkor egy lineáris algebrai egyenletrendszer adódik.

Gc=b

(1.126)

Az egyenletrendszer együtthatómátrixának elemei g_ik-k és jobb oldala b_k.

g _k i= 〈 A _s ϕ _i ,ϕ _k 〉 _s, b_k=〈f,ϕ_k〉, i,k=1,2,…n

(1.127)

(A reziduális hiba ortogonalitása.) Ez esetben a Galjorkin féle ortogonalitás nem az x_n − x^∗, hanem az A_S(x_n−x^∗) vektorra teljesül. A (1.122) és (1.125) egyenleteket kivonva egymásból

〈 A _s (x _n -x ^* ),y 〉 _s =0, minden y∈H_s

(1.128)

azaz L_Sx_n − L_Sx∗ ⊥H_n–re. Ha b ∈ H_S jelöli (1.122) jobb oldalának Riesz-reprezentánsát, azaz

〈 b,y 〉 s= 〈 f,y 〉 _s ,minden y∈H_s

(1.129)

akkor mivel Ax^*=f, (1.128) miatt

A _s x _n -b ⊥ H _n

(1.130)

Bizonyítható, hogy ha (1.123) fennáll, akkor

x _n →x ^* ‖⋅‖s normában, ha n→∞

(1.131)

azaz a módszer konvergens.

1.4.4. A Ritz-Galjorkin módszer nemlineáris egyenletekre

Tétel: Legyen tehát H valós Hilbert-tér, F : H → H adott nemlineáris operátor, amelyre fennáll, hogy létezik olyan m≥0 valós szám, hogy F egyenletesen monoton és Lipschitz-folytonos operátor, akkor létezik olyan M ≥m>0, hogy bármely x, y ∈ H esetén

〈 A(x)-A(y),x-y 〉 ≥m ∗ ‖x-y‖ ² és

‖A(x)-A(y)‖≤M ∗ ‖x-y‖ , minden x,y ∈H

(1.132)

Legyen tehát H valós Hilbert-tér, F : H → H adott nemlineáris, egyenletesen monoton, Lipschitz-folytonos operátor, akkor 1.2.3. szakasz szerint a (1.133) egyenletnek létezik pontosan egy megoldása.

F(x)=b

(1.133)

Ekkor írhatjuk, hogy

〈 F(x ^* ),y 〉 = 〈 b,y 〉, minden y∈H

(1.134)

Legyenek (1.118)-hez hasonlóan H_n Φ_i,n lineárisan független elemek által kifeszített alterek!

H _n =span{Φ _1,n ,Φ _2,n ⋯ Φ _n,n }

(1.135)

és (1.119)-hoz hasonlóan

dist _F (x,H _n )=min{‖x-x _n ‖ : x _n ∈ H _n }→0,ha n→∞

(1.136)

Most is x_n ∈ H_n közelítést keressük az (1.124) alakban

$x_{n} = \sum_{i = 1}^{n} c_{i} * ϕ_{i}$

(1.137)

A (1.137) egyenletet (1.134)-be helyettesítve, és y helyett Φ_k,n-t használva adódik, hogy

$〈 F (\sum_{i = 1}^{n} c_{i} * ϕ_{i}), Φ_{k, n} 〉 = 〈 b, Φ_{k, n} 〉$ , k=1,2,…n

(1.138)

A (1.138) c_i-re nézve nemlineáris egyenletrendszer megoldásával kaphatjuk a keresett közelítő megoldást.

A lineáris esethez hasonlóan a (1.134) és (1.138) egyenleteket kivonva egymásból következik, hogy

〈 F(x ^* )-F(x _n ),y 〉 =0, minden y∈H_n

(1.139)

azaz a hiba merőleges H_n-re. A lineáris esethez hasonlóan (1.131) állítás fennáll, azaz a módszer konvergens, ha n→∞

1.5. A végeselem-módszer háttere

A végeselem módszer (Finite Element Method) a fent leírt Ritz-Galjorkin módszer differenciálegyenletek megoldására szolgáló speciális alkalmazása. Általában függvények Hilbert-terén dolgozunk, ahol a független változók terét, amelyen az ismeretlen függvényt keressük, véges számú elemre bontjuk. Síkbeli esetben az elemek lehetnek háromszögek, négyszögek stb., a térben hasábok tetraéderek stb. A modellben az elemek csak sarokpontjaikon (csomópontjaikon) csatlakoznak egymáshoz. Ekkor az ismeretlen függvény az elemeken olyan a csomópontok által meghatározott polinomokkal közelíthető, hogy azok megfelelő számban folytonosan differenciálhatók legyenek.

Példaként tekintsük az alábbi egyszerűen megoldható (a rugalmas szál lehajlásának megfelelő) egydimenziós esetet!

$\frac{d^{2} y}{d x^{2}} = f (x)$ x∈(0,1)

(1.140)

ahol f(x) ismert (rugalmas szál esetén a nyomatéki ábra által meghatározott M/I/E függvény) legyenek a peremfeltételek

y(0)=0 és y(1)=0

(1.141)

a fenti (1.140)-(1.141) peremérték probléma gyenge megoldására (1.111) egyenlet szerint igaz, hogy ha bármilyen folytonos z peremértékeket kielégítő függvényre (z(0)=z(1)=0) akkor

$\int_{0}^{1} \frac{d^{2} y}{d x^{2}} z (x) d x = \int_{0}^{1} f (x) z (x) d x$

(1.142)

Parciális integrálással

$\int_{0}^{1} \frac{d^{2} y}{d x^{2}} z (x) d x = {[\frac{d y}{d x} z (x)]}_{0}^{1} - \int_{0}^{1} \frac{d y}{d x} \frac{d z}{d x} d x$

(1.143)

mivel az z függvény a peremeken 0, (1.143) jobb oldalának első tagja eltűnik, így a (1.122) szerinti operátoregyenlet (1.143) alapján

$- \int_{0}^{1} \frac{d y}{d x} \frac{d z}{d x} d x = \int_{0}^{1} f (x) z (x) d x$

(1.144)

Keressük a (1.144) egyenlet megoldásait a (0,1) intervallumon a peremeket kielégítő szakaszonként lineáris függvények halmazán (1.1. ábra)!

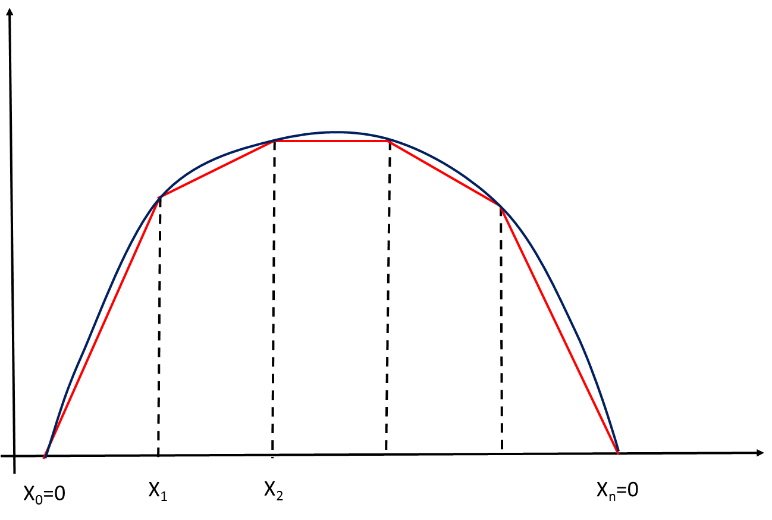
1.1. ábra - A (0,1) intervallumok szakaszonként folytonos függvény

Bontsuk fel a (0,1) intervallumot n részre, x₀=0 és x_n=1 között x_k=k/n osztópontokkal! Ki kell választanunk az szakaszosan lineáris függvények egy n-1 elemű bázisát. A folytonos bázisfüggvények legyenek olyanok, hogy minden belső osztóponthoz egy olyan függvény tartozzon, amely az osztópontban egy, az osztópontot tartalmazó két szakaszon lineáris, egyébként 0! (1.2. ábra)

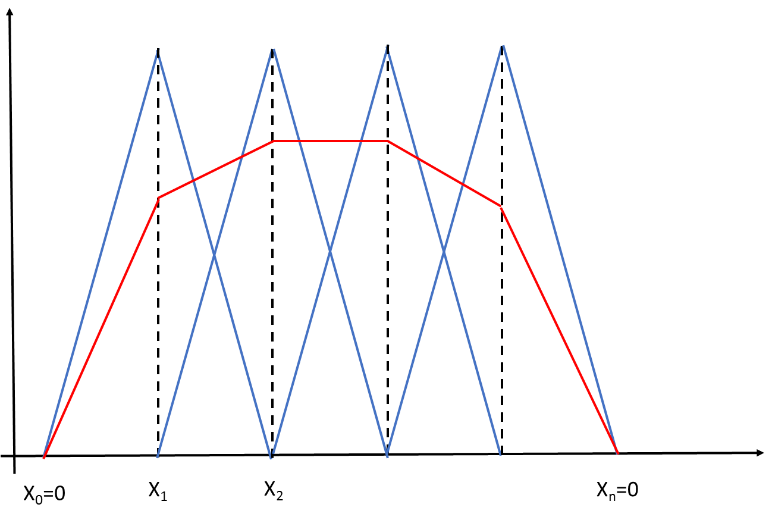
1.2. ábra - A választott bázisfüggvények

A bázisfüggvények ekkor a 1.2. ábra jelöléseivel:

$ϕ_{k} (x) = {\begin{array}{l} \frac{x - x_{k - 1}}{x_{k} - x_{k - 1}}, & x \in [x_{k - 1}, x_{k}] \\ \frac{x_{k + 1} - x}{x_{k + 1} - x_{k}}, & x \in [x_{k}, x_{k + 1}] \\ 0, & e g y é b k é n t \end{array}$

(1.145)

A (1.145) bázisfüggvényeket a (1.144) operátoregyenletbe helyettesítve (1.114)-nak megfelelően a tetszőleges z függvény helyett ϕ_k-kra felírva:

$- \sum_{u = 1}^{n} c_{i} \int_{0}^{1} \frac{d ϕ_{i}}{d x} \frac{d ϕ_{k}}{d x} d x = \int_{0}^{1} f (x) ϕ_{k} (x) d x$ , k=1,2,…n

(1.146)

Tegyük fel a példa egyszerűsítése kedvéért, hogy a vizsgált diszkrét intervallumok egyenlő hosszúak, azaz

x _k -x _k-1 =h, k=1,2,…n

(1.147)

Ha i=k, akkor a

$\int_{0}^{1} \frac{d ϕ_{i}}{d x} \frac{d ϕ_{i}}{d x} d x = [{(\frac{d}{d x} (\frac{x - x_{i - 1}}{h}))}^{2} + {(\frac{d}{d x} (\frac{x_{i + 1} - x}{h}))}^{2}] \cdot h = \frac{2}{h}$ , i=1,2,…n

(1.148)

Ha |i-k|=1, akkor a

$\int_{0}^{1} \frac{d ϕ_{i}}{d x} \frac{d ϕ_{i + 1}}{d x} d x = (\frac{d}{d x} (\frac{x_{i + 1} - x}{h}) \frac{d}{d x} (\frac{x - x_{i + 1}}{h})) \cdot h = - \frac{1}{h}$ , i=1,2,…n

(1.149)

Egyébként

$\int_{0}^{1} \frac{d ϕ_{i}}{d x} \frac{d ϕ_{k}}{d x} d x = 0$ i,k=1,2,…n ,|i-k|>1

(1.150)

A merevségi mátrix tehát

$[\begin{matrix} \begin{matrix} 2 / h & - 1 / h \\ - 1 / h & 2 / h \end{matrix} & \begin{matrix} 0 & \dots \\ - 1 / h & \dots \end{matrix} & \begin{matrix} 0 & 0 \\ ⋮ & 0 \end{matrix} \\ \begin{matrix} 0 & - 1 / h \\ 0 & \dots \end{matrix} & \begin{matrix} ⋱ & ⋱ \\ ⋱ & ⋱ \end{matrix} & \begin{matrix} ⋮ & ⋮ \\ - 1 / h & 0 \end{matrix} \\ \begin{matrix} 0 & \dots \\ 0 & 0 \end{matrix} & \begin{matrix} \dots & - 1 / h \\ \dots & 0 \end{matrix} & \begin{matrix} 2 / h & - 1 / h \\ - 1 / h & 2 / h \end{matrix} \end{matrix}]$

(1.151)

Legyen például az f(x)≡1 függvény!

$b_{k} = \int_{0}^{1} f (x) ϕ_{k} (x) d x = {[\frac{x^{2}}{2 h} - \frac{x_{k - 1} * x}{h}]}_{x_{k - 1}}^{x_{k}} + {[\frac{x_{k + 1} * x}{h} - \frac{x^{2}}{2 h}]}_{x_{k}}^{x_{k + 1}}$ , k=1,2,…n

(1.152)

azaz

$b_{k} = \frac{x_{k}^{2}}{2 h} - \frac{x_{k - 1} * x_{k}}{h} - \frac{x_{k - 1}^{2}}{2 h} + \frac{x_{k - 1} * x_{k - 1}}{h} + \frac{x_{k + 1}^{2}}{h} - \frac{x_{k + 1}^{2}}{2 h} - \frac{x_{k + 1} * x_{k}}{h} + \frac{x_{k}^{2}}{2 h}$

(1.153)

azaz

$b_{k} = \frac{x_{k - 1}^{2}}{2 h} + \frac{x_{k}^{2}}{2 h} - \frac{2 x_{k} * x_{k - 1}}{2 h} + \frac{x_{k + 1}^{2}}{2 h} + \frac{x_{k}^{2}}{2 h} - \frac{2 * x_{k + 1} * x_{k}}{2 h}$

(1.154)

azaz

$b_{k} = \frac{{(x_{k} - x_{k - 1})}^{2}}{2 h} + \frac{{(x_{k + 1} - x_{k})}^{2}}{2 h}$

(1.155)

helyettesítsük x_k+1-x_k= x_k-x_k-1 = h-val!

b _k =h

(1.156)

Amit akár a kis háromszögek területéből is kiszámíthattunk volna.

1.5.1. A végeselemes technika

Ha egy valós problémával találjuk magunkat szemben, akkor a fentiekhez hasonlóan a keresett, ismeretlen függvény értelmezési tartományát elemekre kell bontanunk. Tényleges mérnöki modellek esetén az ismeretlen függvényeink egy, két illetve háromváltozósak attól függően, hogy vonalmenti, síkbeli vagy térbeli feladatot oldunk meg. Az ismeretlen függvényt úgy keressük, hogy az elemeken kitüntetett pontokat (csomópontokat) veszünk fel. Az elem alakja a csomópontok függvényében közelíthető. A véges elemekre bontott geometriához csatlakozóan az ismeretlen függvényt sem a teljes (végtelen dimenziós) téren keressük, hanem annak egy olyan közelítésén, amelyet a csomóponti értékek határoznak meg. A csomópontjaikban egymáshoz kapcsolódó elemeken az ismeretlen függvények megfelelő rendben folytonosan csatlakoznak egymáshoz. Természetesen meg kell követelnünk azt, hogy a közelítő megoldás is a megfelelő rendben folytonos és fizikailag megvalósulható legyen. (Például, rugalmasságtani feladatoknál az ismeretlen elmozdulásmező kinematikailag lehetséges legyen.)

1.5.1.1. Koordináta-rendszerek

Az adott mérnöki probléma megfogalmazása sokszor egyszerűbb az elemhez csatlakoztatott koordináta-rendszerben. Az egyes, véges elemekre vonatkozó összefüggések levezetéséhez gyakran célszerű az elemeken lokális koordináta-rendszert használni. A lokális rendszerből a globális rendszerbe egyszerű, kölcsönösen egyértelmű koordináta-transzformációval térhetünk át. Használhatunk paraméteres – akár görbevonalú – koordináta-rendszert, melynek jellemző pontjai a -1, 0, 1 koordináta-értékek. Bármely térbeli pont globális koordinátái (x,y,z) származtathatók a lokális koordinátákból (ξ,η,ζ) egy lineáris transzformációval ( $\underline{\underline{T}}$ ) és egy eltolással.

$[\begin{matrix} x \\ y \\ z \end{matrix}] = \underline{\underline{T}} * [\begin{matrix} ξ \\ η \\ ζ \end{matrix}] + [\begin{matrix} x_{0} \\ y_{0} \\ z_{0} \end{matrix}]$

(1.157)

illetve fordítva

$[\begin{matrix} ξ \\ η \\ ζ \end{matrix}] = {\underline{\underline{T}}}^{- 1} * [\begin{matrix} x - x_{0} \\ y - y_{0} \\ z - z_{0} \end{matrix}]$

(1.158)

1.5.1.2. Bázisfüggvények

Az elem alakját és az ismeretlen függvényt azonos módon bázisfüggvényekkel közelítjük, például 3D-ben az elem (ξ,η,ζ) lokális koordinátarendszerben értelmezett pontjához az (x,y,z) ontok tartoznak az alábbiak szerint:

$\begin{array}{l} x = \sum_{i = 1}^{N} B_{i} (ξ, η, ζ) * x_{i} \\ y = \sum_{i = 1}^{N} B_{i} (ξ, η, ζ) * y_{i} \\ z = \sum_{i = 1}^{N} B_{i} (ξ, η, ζ) * z_{i} \end{array}$

(1.159)

ahol az elemnek N pontja van, és az i. pont globális koordinátái (x_i, y_i, z_i). Az elem egy pontjának lokális koordinátái (ξ,η,ζ), és a megfelelő pont globális koordinátái (x,y,z).

A feladat ismeretlen függvényének értékeit csak a kitüntetett pontokban határozzuk meg, úgy hogy a teljes ismeretlen mező a koordinátafüggvényekhez hasonló

$f = \sum_{i = 1}^{N} B_{i} (ξ, η, ζ) * f_{i}$

(1.160)

legyen.

1.5.2. Egyváltozós bázisfüggvények

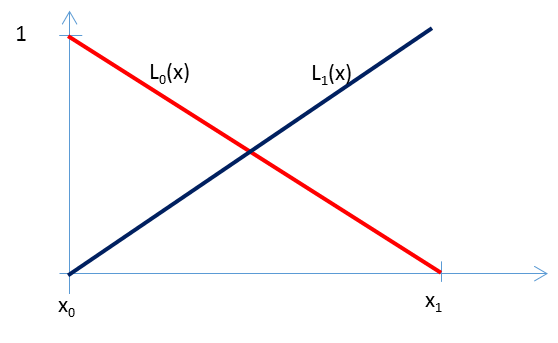
Ha vonalszerű alkatrészen egyváltozós lineáris függvénnyel közelítünk (1.3. ábra),

1.3. ábra - A C0 folytonos vonali bázisfüggvények akkor az L0

$L_{0} (x) = \frac{(x_{1} - x)}{(x_{1} - x_{0})}$

(1.161)

és az

$L_{1} (x) = \frac{(x - x_{0})}{(x_{1} - x_{0})}$

(1.162)

súlyfüggvényeket használhatjuk az (x₀,x₁) intervallum által jellemzett kétpontos vonalelemen. Ha az (1.4. ábra) ábrát megnézzük, akkor azt látjuk, hogy az L₀(0)=1 és L₀(1)=1, illetve az L₁(0)=0 és L₁(1)=1. Ha x₀=0, és x₁=1, akkor a függvények ξ lokális változót is használhatjuk a szakasz saját koordináta-rendszerében.

Ha vonalszerű alkatrészek ismeretlen függvényét közelítjük, akkor ha n csomópontunk van az elemen, akkor az ismeretlen függvény folytonos (C⁰), így használhatjuk a Lagrange-féle interpolációs polinomokat. Ezek bázisfüggvényei n csomópont esetén (n-1)-ed fokúak

1.4. ábra - A C0 folytonos vonali bázisfüggvények

$L_{i} () = \frac{(x - x_{0}) * (x - x_{1}) * \dots * (x - x_{i - 1}) * (x - x_{i + 1}) * \dots * (x - x_{n})}{(x_{i} - x_{0}) * (x_{i} - x_{1}) * \dots * (x_{i} - x_{i - 1}) * (x_{i} - x_{i + 1}) * \dots * (x_{i} - x_{n})}$

(1.163)

Ha megfigyeljük a Lagrange súlyfüggvényeket, akkor azt látjuk, hogy az L_i mindegyik csomópontban 0, kivéve az i. csomópontot, ahol az értéke 1. Ez a tulajdonság biztosítja, hogy a bázisfüggvények (1.158)-nek megfelelő lineáris kombinációja éppen a kívánt függvényértékeket veszi fel.

A fenti példában a (1.140) bázisfüggvények választásánál gyakorlatilag ezt használtuk.

Ha folytonosan deriválható függvényeket szeretnénk használni (C¹), akkor alkalmazhatjuk a (1.159) alapján felírt Hermite-féle interpolációt [3.] . Az interpoláció alapgondolata szerint az elem szélső közös pontjában a függvényértékek mellett a deriváltak azonossága is biztosított.

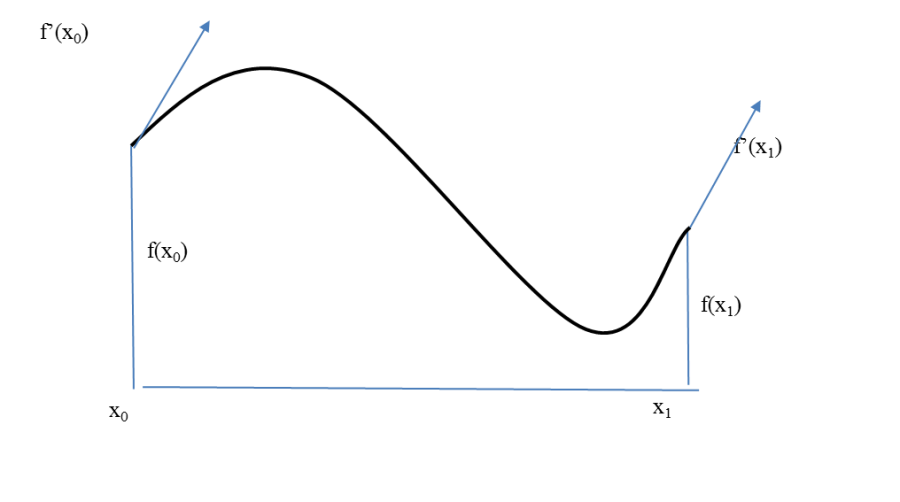
1.5. ábra - Hermite-féle görbeszakasz

Ekkor az

$\begin{array}{l} L_{0} (x) = 2 * {[\frac{(x - x_{0})}{(x_{1} - x_{0})}]}^{3} - 3 * {[\frac{(x - x_{0})}{(x_{1} - x_{0})}]}^{2} + 1 \\ L_{1} (x) = - 2 * {[\frac{(x - x_{0})}{(x_{1} - x_{0})}]}^{3} + 3 * [\frac{(x - x_{0})}{(x_{1} - x_{0})}] \\ L_{0}^{'} (x) = {[\frac{(x - x_{0})}{(x_{1} - x_{0})}]}^{3} - 2 * {[\frac{(x - x_{0})}{(x_{1} - x_{0})}]}^{2} + [\frac{(x - x_{0})}{(x_{1} - x_{0})}] \\ L_{1}^{'} (x) = {[\frac{(x - x_{0})}{(x_{1} - x_{0})}]}^{3} - {[\frac{(x - x_{0})}{(x_{1} - x_{0})}]}^{2} \end{array}$ , x∈[x₀,x₁]

(1.164)

A ξ ∈ [0,1] intervallumra transzformált bázisfüggvények az (1.6. ábra) ábrán láthatók.

$ξ = \frac{(x - x_{0})}{(x_{1} - x_{0})}$

(1.165)

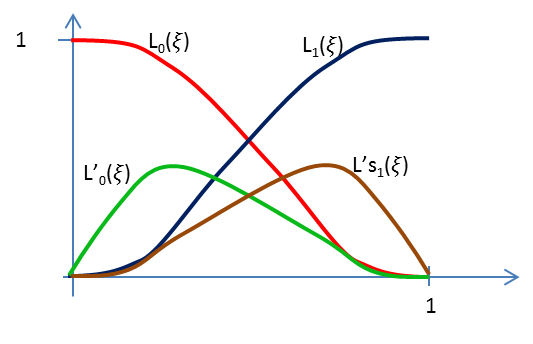
1.6. ábra - A C1 folytonos vonali bázisfüggvények

Többpontos C¹ folytonos bázisfüggvények esetén több belső pontban megadott függvényértéket (akár derivált értéket is) előírhatunk. A szélső, csatlakozó pontokban a függvényértékek és a derivált értékek azonossága biztosíthatja a folytonosságot. A bázisfüggvények felírásához meg kell határoznunk azokat a függvényeket, amelyek csak az adott pontban vesznek fel 1 értéket és az összes többi helyen 0-t, továbbá az adott pontban a derivált értéke 0, illetve a pontban, ahol derivált kényszert írunk elő, a derivált értéke 1, a függvény 0 és az összes többi pontban a függvényérték és a derivált érték egyaránt 0. A bázispolinomok fokszáma a felírt kényszerek számánál eggyel kisebb. Az együtthatókra a kényszerek alapján egyenletrendszereket írhatunk fel.

1.5.3. Kétváltozós bázisfüggvények

Legyen egy háromszög elemünk az (1.7. ábra) ábrának megfelelően a síkban! Bármely (x,y) síkbeli pont kifejezhető , mint a lokális (ξ,η) koordináták függvénye. [4.]

$[\begin{matrix} x \\ y \end{matrix}] = [\begin{matrix} x_{0} \\ y_{0} \end{matrix}] + [\begin{matrix} x_{1} - x_{0} & x_{2} - x_{0} \\ y_{1} - y_{0} & y_{2} - y_{0} \end{matrix}] [\begin{matrix} ξ \\ η \end{matrix}]$

(1.166)

illetve

$[\begin{matrix} ξ \\ η \end{matrix}] = {[\begin{matrix} x_{1} - x_{0} & x_{2} - x_{0} \\ y_{1} - y_{0} & y_{2} - y_{0} \end{matrix}]}^{- 1} * [\begin{matrix} x - x_{0} \\ y - y_{0} \end{matrix}]$

(1.167)

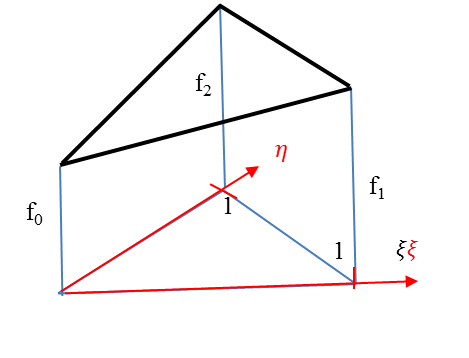
1.7. ábra - Lineáris függvény háromszög elemen

A bázisfüggvények a lokális koordináta-rendszerben (1.8. ábra)

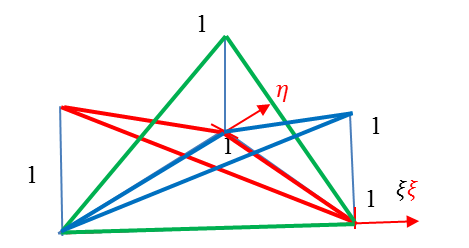
1.8. ábra - A kétdimenziós bázisfüggvények háromszög elemen

$\begin{array}{l} L_{0} (ξ, η) = 1 - ξ - η \\ L_{1} (ξ, η) = ξ \\ L_{2} (ξ, η) = η \end{array}$

(1.168)

Négycsomópontú lineáris elemet is készíthetünk (1.9. ábra)

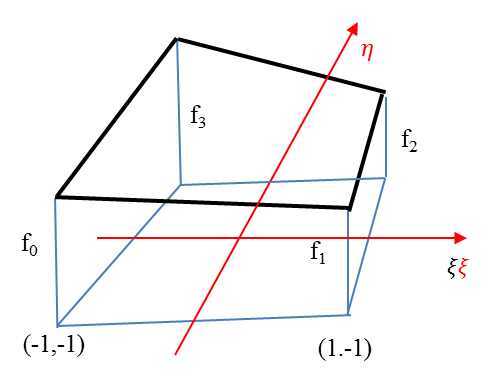
1.9. ábra - A négycsomópontú lineáris elem

A bázisfüggvények a lokális koordinátarendszerben

$\begin{array}{l} L_{0} (ξ, η) = \frac{1}{4} (1 - ξ) * (1 - η) \\ L_{1} (ξ, η) = \frac{1}{4} (1 + ξ) * (1 - η) \\ L_{2} (ξ, η) = \frac{1}{4} (1 + ξ) * (1 + η) \\ L_{3} (ξ, η) = \frac{1}{4} (1 - ξ) * (1 + η) \end{array}$

(1.169)

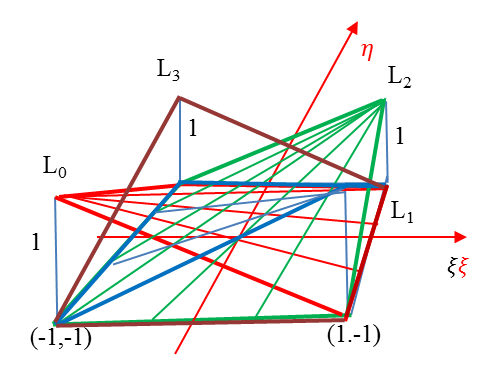
1.10. ábra - A kétdimenziós bázisfüggvények négyszög elemen

1.5.4. Háromváltozós bázisfüggvények

Az izoparametrikus térbeli elemek a tégla vagy tetraéder topológiájúak. Az élek lehetnek egyenesek ilyenkor a függvények paramétereikben lineárisak, ha a görbültek az élek, akkor a függvények legalább kvadratikusak.

Egy térbeli tégla topológiájú elem nyolc paraméterfüggvénye:

$L_{0} (ξ, η, ζ) = \frac{1}{8} (1 - ξ) * (1 - η) * (1 - ζ)$

$L_{1} (ξ, η, ζ) = \frac{1}{8} (1 + ξ) * (1 - η) * (1 - ζ)$

$L_{2} (ξ, η, ζ) = \frac{1}{8} (1 + ξ) * (1 + η) * (1 - ζ)$

$L_{3} (ξ, η, ζ) = \frac{1}{8} (1 - ξ) * (1 + η) * (1 - ζ)$

$L_{4} (ξ, η, ζ) = \frac{1}{8} (1 - ξ) * (1 - η) * (1 + ζ)$

$L_{5} (ξ, η, ζ) = \frac{1}{8} (1 + ξ) * (1 - η) * (1 + ζ)$

$L_{6} (ξ, η, ζ) = \frac{1}{8} (1 - ξ) * (1 + η) * (1 + ζ)$

$L_{7} (ξ, η, ζ) = \frac{1}{8} (1 + ξ) * (1 + η) * (1 + ζ)$

(1.170)

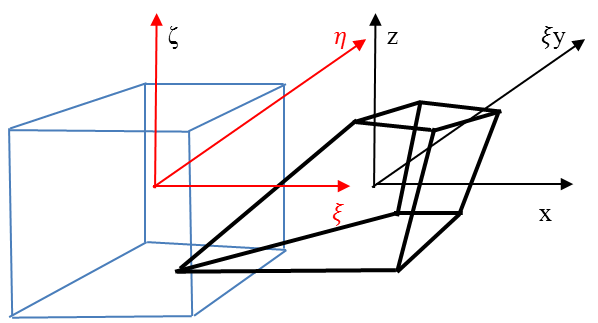
1.11. ábra - A háromdimneziós lineárisan módosított elem

hasonlóan a görbült tertraéder-forma:

$\begin{array}{l} L_{0} (ξ, η, ζ) = 4 * ξ * (1 - ξ - η - ζ) \\ L_{1} (ξ, η, ζ) = 4 * ξ * η \\ L_{2} (ξ, η, ζ) = 4 * η * (1 - ξ - η - ζ) \\ L_{3} (ξ, η, ζ) = 4 * ξ * ζ \\ L_{4} (ξ, η, ζ) = 4 * η * ζ \\ L_{5} (ξ, η, ζ) = 4 * ζ * (1 - ξ - η - ζ) \\ L_{6} (ξ, η, ζ) = 1 - ξ - η - ζ - \frac{1}{2} * (L_{0} + L_{2} + L_{5}) \\ L_{7} (ξ, η, ζ) = ξ - \frac{1}{2} * (L_{0} + L_{1} + L_{3}) \\ L_{8} (ξ, η, ζ) = η - \frac{1}{2} * (L_{1} + L_{2} + L_{4}) \\ L_{9} (ξ, η, ζ) = ζ - \frac{1}{2} * (L_{3} + L_{4} + L_{5}) \end{array}$

(1.171)

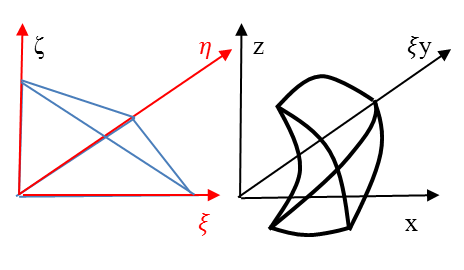
1.12. ábra - A háromdimneziós kvadratikus

1.5.5. Végeselemek használata térbeli rugalmasságtani feladatokon

Tekintsünk egy V térfogatú lineárisan rugalmas térbeli testet, melyet A határoló felület vesz körül! Az A felület egy részén (A_u) elmozdulás kényszer adott, míg másik részét (A_p) terheljük. A test bármely r pontjának elmozdulása ( u ) leírható a koordináta-rendszer e _i egységvektorainak lineáris kombinációjával.

$\underline{u} (\underline{r}) = u_{x} * {\underline{e}}_{x} + u_{y} * {\underline{e}}_{y} + u_{z} * {\underline{e}}_{z}$

(1.172)

Ekkor az alakváltozási tenzor

$\underline{\underline{ε}} (\underline{r}) = [\begin{matrix} ε_{x} & γ_{x y} & γ_{x z} \\ γ_{x y} & ε_{y} & γ_{y z} \\ γ_{x z} & γ_{y z} & ε_{z} \end{matrix}] = [\begin{matrix} \frac{\partial u_{x}}{\partial x} & \frac{1}{2} * (\frac{\partial u_{x}}{\partial x} + \frac{\partial u_{y}}{\partial y}) & \frac{1}{2} * (\frac{\partial u_{x}}{\partial x} + \frac{\partial u_{z}}{\partial z}) \\ \frac{1}{2} * (\frac{\partial u_{x}}{\partial x} + \frac{\partial u_{y}}{\partial y}) & \frac{\partial u_{y}}{\partial y} & \frac{1}{2} * (\frac{\partial u_{y}}{\partial y} + \frac{\partial u_{z}}{\partial z}) \\ \frac{1}{2} * (\frac{\partial u_{x}}{\partial x} + \frac{\partial u_{z}}{\partial z}) & \frac{1}{2} * (\frac{\partial u_{y}}{\partial y} + \frac{\partial u_{z}}{\partial z}) & \frac{\partial u_{z}}{\partial z} \end{matrix}]$

(1.173)

ennek független elemeit hatelemű vektorba szervezhetjük.

$\underline{ε} = {[\begin{matrix} \begin{matrix} ε_{x} & ε_{y} & ε_{z} \end{matrix} & \begin{matrix} γ_{x y} & γ_{y z} & γ_{x z} \end{matrix} \end{matrix}]}^{T}$

(1.174)

A hatelemű vektor és az elmozdulásmező kapcsolata operátorszimbólumokkal tehát

$\underline{ε} = [\begin{matrix} \begin{matrix} \frac{\partial}{\partial x} & 0 & 0 \\ 0 & \frac{\partial}{\partial x} & 0 \\ 0 & 0 & \frac{\partial}{\partial x} \end{matrix} \\ \begin{matrix} \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & 0 \\ 0 & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ \frac{\partial}{\partial x} & 0 & \frac{\partial}{\partial z} \end{matrix} \end{matrix}] * [\begin{matrix} u_{x} \\ u_{y} \\ u_{z} \end{matrix}] = \underline{\underline{\partial}} * \underline{u}$

(1.175)

Közelítsük egyetlen elemen az elmozdulásmezőt a megismert bázisfüggvények segítségével!

$\begin{array}{l} u_{e} = \sum^{} u_{i} L_{i} \\ v_{e} = \sum^{} v_{i} L_{i} \\ w_{e} = \sum^{} w_{i} L_{i} \end{array}$

(1.176)

Ekkor az n csomópont alapján egyetlen elemen

${\underline{u}}_{e} = [\begin{matrix} u_{e} \\ v_{e} \\ w_{e} \end{matrix}] = [\begin{matrix} \begin{matrix} L_{1} & 0 & 0 \\ 0 & L_{1} & 0 \\ 0 & 0 & L_{1} \end{matrix} & \begin{matrix} \dots \\ \dots \\ \dots \end{matrix} & \begin{matrix} L_{n} & 0 & 0 \\ 0 & L_{n} & 0 \\ 0 & 0 & L_{n} \end{matrix} \end{matrix}] * [\begin{matrix} \begin{matrix} u_{1} \\ v_{1} \\ w_{1} \end{matrix} \\ ⋮ \\ \begin{matrix} u_{n} \\ v_{n} \\ w_{n} \end{matrix} \end{matrix}] = {\underline{\underline{L}}}_{e} * {\underline{q}}_{e}$

(1.177)

(1.175) és (1.176) egyenletek alapján

${\underline{ε}}_{e} = \underline{\underline{\partial}} * {\underline{u}}_{e} = \underline{\underline{\partial}} * {\underline{\underline{L}}}_{e} * {\underline{q}}_{e} = {\underline{\underline{B}}}_{e} * {\underline{q}}_{e}$

(1.178)

Kifejezhetjük tehát az elmozdulás tenzor független elemeit a csomóponti elmozdulásokkal.

A feszültségtenzor

$\underline{\underline{σ}} (\underline{r}) = [\begin{matrix} σ_{x} & τ_{x y} & τ_{x z} \\ τ_{x y} & σ_{y} & τ_{y z} \\ τ_{x z} & τ_{y z} & σ_{z} \end{matrix}]$

(1.179)

melynek független elemeit is hatelemű vektorba szervezhetjük.

$\underline{σ} = {[\begin{matrix} \begin{matrix} σ_{x} & σ_{y} & σ_{z} \end{matrix} & \begin{matrix} τ_{x y} & τ_{y z} & τ_{x z} \end{matrix} \end{matrix}]}^{T}$

(1.180)

Rugalmas test esetén rugalmassági modulus (E) és a Poisson állandó (ν) segítségével kapcsolatot írhatunk fel a feszültségtenzor és az alakváltozási tenzor elemei között. Legyen

$\begin{array}{l} c_{1} = E \frac{1 - ν}{(1 + ν) (1 - 2 ν)} \\ c_{2} = E \frac{ν}{(1 + ν) (1 - 2 ν)} \\ c_{3} = \frac{E}{2 (1 + ν)} \end{array}$

(1.181)

Ekkor

$\underline{σ} = [\begin{matrix} \begin{matrix} c_{1} & c_{2} & c_{2} \\ c_{2} & c_{1} & c_{2} \\ c_{2} & c_{2} & c_{1} \end{matrix} & \begin{matrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{matrix} \\ \begin{matrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{matrix} & \begin{matrix} c_{3} & 0 & 0 \\ 0 & c_{3} & 0 \\ 0 & 0 & c_{3} \end{matrix} \end{matrix}] * \underline{ε} = \underline{\underline{D}} * \underline{ε}$

(1.182)

(1.178)-t felhasználva az elemen, a feszültségtenzor elemei az elemen

${\underline{σ}}_{e} = \underline{\underline{D}} * {\underline{\underline{B}}}_{e} * {\underline{q}}_{e}$

(1.183)

Rugalmas test esetén a csomóponti elmozdulásokkal a feszültségtenzor elemei is kifejezhetők.

Az egyensúlyi egyenlet a feszültségtenzorral és a $ρ * \underline{k}$ megoszló terheléssel

$\underline{σ} * [\begin{matrix} \frac{\partial}{\partial x} \\ \frac{\partial}{\partial y} \\ \frac{\partial}{\partial z} \end{matrix}] + ρ * \underline{k} = 0$

(1.184)

Ezeket az egyenleteket egészítik ki az

$\underline{u} = {\underline{u}}_{0}$ az A_u peremen előírt elmozdulás,

$\underline{σ} * \underline{u} = {\underline{p}}_{0}$ az A_p peremen előírt terhelés

(1.185)

peremfeltételek.

A differenciálegyenlet-rendszer megoldása helyett, a (1.184) egyenletek és a kapcsolódó (1.185) peremelőírások helyett a teljes potenciális energia (Π_e) minimumát keressük az aktuális elemen (ezt választjuk skaláris szorzatnak).

$П_{e} = \frac{1}{2} * \int_{V_{e}} {\underline{ε}}_{e}^{T} * \underline{\underline{D}} * {\underline{ε}}_{e} * d V - \int_{A_{e}} {\underline{u}}_{e}^{T} * {\underline{p}}_{0} d A - \int_{V_{e}} {\underline{u}}_{e}^{T} * ρ * \underline{k} * d V$

(1.186)

Felhasználva a (1.178) összefüggést,

$П_{e} = \frac{1}{2} * \int_{V} {\underline{q}}_{e}^{T} * {\underline{\underline{B}}}_{e}^{T} * \underline{\underline{D}} * {\underline{\underline{B}}}_{e} * {\underline{q}}_{e} * d V - \int_{A} {\underline{q}}_{e}^{T} * {\underline{\underline{B}}}_{e}^{T} * {\underline{p}}_{0} d A - \int_{V} {\underline{q}}_{e}^{T} * {\underline{\underline{B}}}_{e}^{T} * ρ * \underline{k} * d V$

(1.187)

Írhatjuk tehát, hogy egyetlen elemre vonatkozóan

$П_{e} = \frac{1}{2} * {\underline{q}}_{e}^{T} * {\underline{\underline{K}}}_{e} * {\underline{q}}_{e} - {\underline{q}}_{e}^{T} * {\underline{f}}_{e}$

(1.188)

ahol az elemi merevségi mátrix

${\underline{\underline{K}}}_{e} = \int_{V} {\underline{\underline{B}}}_{e}^{T} * \underline{\underline{D}} * {\underline{\underline{B}}}_{e} * d V$

(1.189)

az elemi terhelés.

${\underline{f}}_{e} = \int_{A} {\underline{\underline{B}}}_{e}^{T} * {\underline{p}}_{0} d A + \int_{V} {\underline{\underline{B}}}_{e}^{T} * ρ * \underline{k} * d V$

(1.190)

(1.189) alapján a térfogati integrálást lokális ξ,η,ζ koordinátákra transzformálva bekerül a képletbe a Jacobi mátrix determinánsa

${\underline{\underline{K}}}_{e} = \int_{V} {\underline{\underline{B}}}_{e}^{T} * \underline{\underline{D}} * {\underline{\underline{B}}}_{e} * d V = \int_{V} {\underline{\underline{B}}}_{e}^{T} * \underline{\underline{D}} * {\underline{\underline{B}}}_{e} * \det ([\begin{matrix} \frac{\partial x}{\partial ξ} & \frac{\partial y}{\partial ξ} & \frac{\partial z}{\partial ξ} \\ \frac{\partial x}{\partial η} & \frac{\partial y}{\partial η} & \frac{\partial z}{\partial η} \\ \frac{\partial x}{\partial ζ} & \frac{\partial y}{\partial ζ} & \frac{\partial z}{\partial ζ} \end{matrix}]) * d ξ d η d ζ$

(1.191)

A szerkezet több elemből áll, a szerkezet potenciálos energiája (1.188) alapján, az elemek (N_e darab) energiája mellett az elemektől független csomóponti erők (W) munkáját kell figyelembe venni.

$П = \sum_{e = 1}^{N_{e}} \frac{1}{2} * {\underline{q}}_{e}^{T} * {\underline{\underline{K}}}_{e} * {\underline{q}}_{e} - {\underline{q}}_{e}^{T} * {\underline{f}}_{e} - W$

(1.192)

Ha a terhelés vektorokat és az elmozdulás vektorokat összegyűjtjük, akkor az Ncs csomópontra

${\underline{q}}^{T} = [{\underline{q}}_{1}^{T}, {\underline{q}}_{2}^{T}, \dots, {\underline{q}}_{N_{c s}}^{T}]$

${\underline{f}}^{T} = [{\underline{f}}_{1}^{T}, {\underline{f}}_{2}^{T}, \dots, {\underline{f}}_{N_{c s}}^{T}]$

(1.193)

Legyen ${\underline{\underline{K}}}_{e, i j}$ az i és j csomópontot egyaránt tartalmazó elem merevségi mátrixa. Összegezzük az összes olyan elem merevségi mátrixát, amely tartalmazza az i,j pontokat!

${\underline{\underline{K}}}_{i, j} = \sum_{i, j ϵ e} {\underline{\underline{K}}}_{e, i j}$

(1.194)

Az így adódó ${\underline{\underline{K}}}_{i, j}$ a $\underline{\underline{K}}$ merevségi mátrix i,j csomópontokhoz tartozó almátrixa.

(1.192) és (1.193) és (1.194) egyenletek alapján a külső erők munkáját is csomópontra bontva

$П = \frac{1}{2} * {\underline{q}}^{T} * \underline{\underline{K}} * \underline{q} - {\underline{q}}^{T} * \underline{f}$

(1.195)

Ha az energiaminimumot keressük, akkor annak szükséges és elégséges feltétele

$\underline{\underline{K}} * \underline{q} = \underline{f}$

(1.196)

lineáris egyenletrendszer teljesülése.

Az egyenletrendszer ismeretlenjeinek nagy száma mellett vigasztalhat minket az, hogy az együttható mátrixnak csak azok az i,j indexű elemei különböznek zérustól, ahol egy elemen belül szerepel az i és a j indexű csomópont is. A csomópontok megfelelő számozásával elérhető, hogy az együttható mátrix sávszerkezetű legyen, hiszen a sáv szélességét az egy elemen belül lévő indexek maximális különbsége szabja meg.

Vissza		Előre
Végeselem módszerek	Főoldal	2. fejezet - A végeselem rendszerek működésének alapjai