2. fejezet - A végeselem rendszerek működésének alapjai
Vissza		Előre

2. fejezet - A végeselem rendszerek működésének alapjai

Tartalom

2.1. Bevezetés: A végeselem analízis alapvető lépései

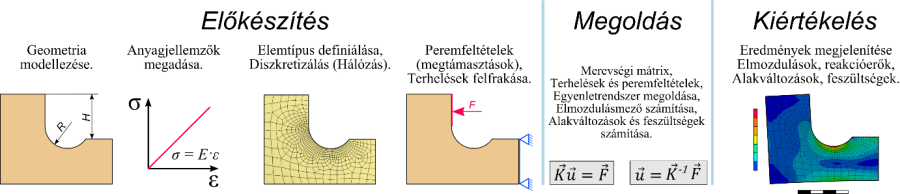
A végeselemes analízis a fizikai szerkezet matematikai modelljét képviseli, ami magában foglalja az elemeket, anyagmodelleket, peremfeltételeket és mindazon tulajdonságokat, amelyek a fizikai valóságot modellezik. A módszer lényege a vizsgált geometria véges kis részekre (véges elemekre) bontása, és az elemeket összekapcsoló csomópontokra ható csomóponti terhelések és a hatásukra létrejövő kimenő mennyiség közötti kapcsolatot leíró egyenletrendszer megoldása. A végeselemes analízis folyamatát három jól elkülöníthető részre, előkészítés (Preprocess) , megoldás (Process) és kiértékelés (Posztprocess) szokás osztani, amit meg kell, hogy előzzön a döntési szakasz.

2.1. ábra - A végeselem szimuláció folyamatának legfontosabb lépései, (statikai példán bemutatva).

Döntési szakasz – a probléma jellegének meghatározása és a megoldásához használt eljárás kiválasztása.
- A fizikai probléma jellege (mechanikai, hőtani, elektromágneses, stb.)
- Az analízis típusa (statikai, modal, harmonikus, tranziens, stb.)
- Milyen közelítéssel akarjuk vizsgálni a valóságot (Lineáris/nemlineáris)?
- Az alkalmazott modell típusa (3D-s testmodell vagy egyszerűsített 2D-s, héj, rúd, stb.)
- Szimmetria feltételek alkalmazhatósága (fél, negyed modell, tengelyszimmetria, ciklikusság, stb.).
- Elemtípus (alakjuk vagy fokszámuk szerint).
- Hálósűrűség (globális elemméret), részletesség (lokális hálósűrítés mértéke).
- Peremfeltételek megfelelő alkalmazása (alkatrészek kiváltása kényszerekkel).
Előkészítés (Preprocessing) – a végeselem modell előkészítését jelenti, amely az alábbi lépéseket tartalmazza:
- Geometria létrehozása, (modellezés, importálás).
- Anyagmodell kiválasztása, (anyagparaméterek megadása, görbeillesztés anyagvizsgálati adatokra.).
- Hálózás, (elemtípus, hálózási eljárás, elemméret, stb. megadása).
- Peremfeltételek, kezdeti feltételek és terhelések definiálása, (Megtámasztások, kényszerek, alkatrészkapcsolatok, koncentrált és megoszló erők, nyomatékok, hőterhelés, inerciális terhelések, stb. definiálása).
Megoldás (Solution) – lényegében a megoldó futtatását jelenti. Ez a szakasz az, amely a felhasználó elől leginkább rejtve marad.
- Transzformációs mátrix (lineáris statikai esetben merevségi mátrix) létrehozása az egyes elemekre, majd ezekből a teljes szerkezetre.
- Csomóponti terhelések és peremfeltételek felvétele.
- Egyenletrendszer megoldása, az elemek szabadságfokának megfelelő mennyiségek (mechanikai esetben elmozdulás) kiszámolásával.
- A kívánt származtatott mennyiségek számolása a fenti eredményből (pl. mechanikai feszültség és alakváltozás számítása az elmozdulásmezőből).
Kiértékelés (Post-processing) – az eredmények lekérdezését és kiértékelését jelenti. A jelenlegi modern végeselem szoftverek számos olyan eszközzel rendelkeznek, amely segítségünkre van ebben a munkában.
- Az eredmény megjelenítése a testmodellen színsávok vagy vektormező ábrázolásával.
- A deformált test megjelenítése és testmodellként való kimentése, animálása, stb.
- Diagramok, szöveges kimenet, maximum / minimum helyek lekérdezése, stb.

[5.] , [6.]

2.2. Geometria modellezés

2.2.1. Geometriai modellek és előállításuk

A végeselem analízisben vizsgált fizikai test digitális reprezentációja a számítógépes geometriai modell. A modellt felépítő elemek lehetnek pontok, görbék (egyenes, körív, paraméteres polinomok, Spline-ok, Bezier görbék, stb.), felületek (analitikus és parametrikus felületek) és szilárd testek. A testmodellek leírása zárt felületekkel határolt, anyaggal kitöltött objektumként történik. A testmodellek előállításának legelterjedtebb megvalósítási módját az alábbiakban foglaljuk össze, a teljesség igénye nélkül. A lent leírtakhoz hasonló eljárásokkal hozhatók létre a térbeli felületmodellek is, de ez esetben nem követelmény a generálógörbe és a létrejött felületmodell zárt szerkezete.

2.2.1.1. Testmodell előállítása primitívekkel (Primitives)

Halmazműveletek segítségével (unió, különbség és metszet képzésével) elemi testekből, un. primitívekből hozható létre a teljes geometria. Primitíveknek azokat az előre definiált alaptesteket nevezzük, melyekből a kívánt geometria épül fel (kúp, gúla, henger, gömb, tórusz, ék, téglatest). A modellezés során a primitívek helyzetét, méretét és a velük végzett halmazműveleteket (boolean) definiáljuk. Az így végrehajtott műveletek sora, vagyis a primitívek kombinálása vezet a kívánt geometria kialakulásához. A primitívekkel való művelet ma már elavultnak számít, mivel nem támogatja az iteratív parametrikus alkatrész-modellezést.

2.2.1.2. Alaksajátosságra (Features) épülő parametrikus modell

Az alaksajátosságokon alapuló modellezés a primitívekhez hasonlóan szintén a modell jellemző geometriai adottságainak kombinálásával építkezik, de ebben az esetben az alaksajátosságok lényegesen szabadabb építőelemei a modellnek. Csoportosításuk sokféle szempont szerint történhet, de legcélszerűbb talán a létrehozás módja szerint osztályozni. E szerint beszélhetünk vázlatra épülő és elhelyezett alaksajátosságról.

A vázlatra épülő alaksjátosságot mint a neve is mutatja valamilyen (az alaksajátosság típusától függően tetszőleges bonyolultságú is lehet) vázlat egy pálya mentén történő elmozdításával generáljuk. A vázlat (ok) és a pálya(k) alakjától függ a létrehozott geometria. A leggyakrabban használt vázlatra épülő alaksajátosságok: kihúzás (Extrude), megforgatás (Revolve), pásztázás (Loft), söprés (Sweep), borda (Rib), spirál (Coil), domborítás (Emboss), szelés (Slice). Az elhelyezett alaksajátosságoknál éppúgy értelmezhetőek a boolean műveletek, mint a primitíveknél.

Az elhelyezett alaksajátosságok csak meglévő geometriára lehet érvényesíteni, önmagukban nem értelmezhetőek. Általában gyakran ismétlődő, szabványos technológiai lépéseket foglalnak magukban, mint a furat (Hole), lekerekítés (Fillet), letörés (Chamfer), kilökési ferdeség (Draft), menet (Thread), héj (Shell), különféle kiosztások (Pattern), tükrüzés (Mirror), stb.

A szilárdtest részét nem képező, de a megalkotásához nélkülözhetetlen elemeket munka alaksajátosságnak nevezzük, mint a munkasík (Plane), tengely (Axis), stb.

Az alaksajátosságra épülő modell jellemző tulajdonsága a modelltörténet (modellfa), vagyis, hogy a modellalkotás folyamata visszatekinthető és bármely eleme utólag módosítható, paraméterezhető. Jelenleg ez az általánosan elterjedt modellezési eljárás a korszerű CAD rendszerekben.

2.2.1.3. Explicit modellezési eljárás (Explicit or Direct 3D)

Az explicit modellezési eljárás lehetőséget biztosít a modellfa nélküli geometria létrehozására és módosítására. Közvetlen modellezésel, ha egy vázlat segítségével hozunk létre geometriát, akkor az beépül a geometriába és a továbbiakban a vázlat nélkül, közvetlenül a geometriát módosíthatjuk. A parametrikus modellezéshez hasonlóan lehetőséget ad az egyes geometriai elemek közötti kényszerek definiálására. A módszer rugalmassága nagyobb mozgásteret enged a szabad formájú organikus felületek modellezése során. A modellezési gyakorlat elkövetkező fejlődési fokát látják benne és számos fejlett modellezőrendszer már beépítette az eszköztárába a parametrikus modellezés mellett.

2.2.1.4. Testmodell előállítása határfelületekkel (Boundary Representation)

A határfelületekkel való testmodell definiálás alapkövetelménye egy térrészt elkülönítő zárt felületmodell megléte. A felületelemek normálvektora határozza meg, hogy a felület melyik oldalán van az anyag (a vektor általában kifelé mutat). A határoló felületmodell előállítása történhet a fenti módszerek bármelyikével, primitív felületek kombinálásával, alaksajátosság alapú felületmodellek definiálásával vagy a felületet leíró vezérgörbék, kontrolpontok, stb. közvetlen megadásával.

[7.] , [8.] , [9.] , [10.] .

2.2.2. Geometria importálása

A végeselem (VEM) és a geometriai modellező (CAD) szoftverek együttműködésének, integrációjának különböző szintjei vannak. A szoftverek fejlődése során a tendencia a minél nagyobb mértékű integráció felé mutat. A kezdeti teljesen különálló működés során a két szoftver együttműködése biztosította a kapcsolatot. Részleges együttműködés esetén a még mindig különálló VEM szoftver a CAD program részeként teljesíti a feladatát. Az integráció legmagasabb fokának a CAD rendszerbe szakmodulként teljesen beépülő VEM rendszert tekintjük. A két program között súlypont gyakran eltolódik valamelyik javára. Ennek megfelelően a véges elemes szoftverek között találunk olyat, amely egy főként tervezésre használt CAD rendszer beépülő modulja, de olyat is, amely függetlenül működő VEM program saját geometriai modellezővel. Az utóbbi esetben is tartalmaz a véges elemes szoftver a geometria megalkotására alkalmas modellező modult, de az képességeiben és szolgáltatásaiban általában nem éri el egy korszerű CAD rendszer tulajdonságait.

Egyszerű geometria esetén általában a véges elemes szoftver részeként működő geometriai modellezővel készítjük el a geometriát. Ebben az esetben a két rendszer közti átmenet gyorsan és dinamikusan valósul meg, nem kell a geometria importálásával külön foglalkoznunk, a paraméterek átöröklődnek a véges elemes rendszerbe/modulba.

Természetesen, ha különálló geometriai modellező és véges elemes szoftvert használunk, akkor is mód van a geometria importálására illetve legtöbbször a CAD és a VEM rendszer dinamikus együttműködésére (paraméterek, koordináta rendszerek, anyagtulajdonságok, stb. átvitelére). A geometria véges elemes szoftverbe történő importálására a szabványos file-formátumok (pl. IGES, Parasolid, ACIS, STEP, stb.) biztosítanak lehetőséget, de számos esetben a fejlettebb végeselem szoftverek kezelik a legelterjedtebb CAD rendszerek saját formátumát is. Általában test, felület, 2D-s modellek és vonalak is importálhatóak.

Ha a tervezési folyamat különböző szakaszaiban végzünk véges elemes analíziseket, akkor úgy érdemes a beállításokat megtenni, hogy a geometria változása érvényesüljön a véges elemes rendszerben is. Amennyiben optimalizációra is sor kerül a geometriai paramétereket általában abban a CAD rendszerben kell definiálni, amelyben a geometria készült. Bizonyos egyszerűsítéseket (pl. szimmetriasíkok definiálása) a véges elemes rendszerben is elvégezhetünk.

[5.] , [6.] , [11.]

2.2.3. Egyszerűsítések

Véges elemes analízisek esetében a geometriai modell előkészítése nagymértékben befolyásolja a szimuláció lefutásának időtartamát illetve a kapott eredmény helyességét, ezért különösen fontos, hogy a lehetséges egyszerűsítéseket elvégezzük, de semmiképp ne éljünk olyan geometriai modell-egyszerűsítéssel, amely az analízis szempontjából jelentősen befolyásolná a vizsgált modell viselkedését, vagy a modellezett feltételeket.

Amennyiben az analízis tárgyát képező geometria tartalmaz olyan alaksajátosságokat, amelyekről biztosan el tudjuk dönteni, hogy elhagyása nincs befolyással az analízis eredményére, azt mellőzhetjük. Ugyanígy több testből álló geometriai modellek esetén (pl. több alkatrészből álló szerelt összeállítás) elhagyhatók akár bizonyos alkatrészek is.

A legfontosabb geometriai egyszerűsítés a szimmetria feltételek alkalmazásával (fél, negyed, ciklikus, stb.) használatával és a 2D-s modellek (sík alakváltozás, sík feszültség, tengelyszimmetrikus) alkalmazásával érhető el.

2.2.3.1. Szimmetria feltételek alkalmazása

Előnyös lehet a szimmetria feltétel alkalmazása abban az esetben, ha a geometriai modell, a peremfeltételek és a terhelések, valamint az anyagmodell valamilyen szimmetriát mutat, mivel így a teljes geometria helyett csak annak egy reprezentatív részével számolunk, így csökkentve a szimuláció időigényét. Természetesen ennek az egyszerűsítésnek alapfeltétele, hogy a geometriának, a terheléseknek, a megtámasztásoknak és az anyagmodellnek egyaránt tartalmazni kell az adott szimmetriát. Csak akkor használható szimmetria, ha az anyagmodell nem tartalmaz olyan irányfüggő tulajdonságot, amely nem összeegyeztethető az adott szimmetriával. (Megjegyzés: érdemes ellenőrizni, hogy koncentrált terheléseknél a terhelés a teljes- vagy a szimmetria szerinti részterhelés megadása szükséges, mivel ez programonként eltérő lehet.) A részmodellek alkalmazása különösen fontos abban az esetben, ha optimalizációt végzünk, mert ilyenkor a sok optimalizációs lépés miatt egy kisebb időnyereség is jelentősen gyorsítja az optimalizációs folyamatot.

Hátránya lehet az esetleges megjelenési limitáltság, mely prezentációs anyagokban való felhasználásoknál nem mindig szerencsés, illetve ha nem kellő körültekintéssel alkalmazzuk az egyszerűsítéseket, akkor egy esetleges figyelembe nem vett az egyszerűsítésnek ellentmondó tényező könnyen okozhat hibás eredményt.

Alkalmazható szimmetriák:

Tengelyszimmetria (Axisymmetry) – Forgásszimmetrikus geometria jellemzi, 2D tengelyszimmetrikus, 3D-s fél és negyedmodell alkalmazható,
Ciklikus (Rotational symmetry) - A szerkezet tengelyszimmetrikus tulajdonsággal rendelkezik, melyet a tengelyvonal körül ismétlődően kiosztott szegmensek egészítenek ki (pl. turbinalapátok).
Tükörszimmetria (Planar, reflective symmetry) – fél, negyed vagy nyolcad modell alkalmazható a szimmetriasíkok számától függően.
Ismétlődés (Repetitive, translational symmetry) – egyenes mentén kiosztott ismétlődő geometriai elem jellemzi.

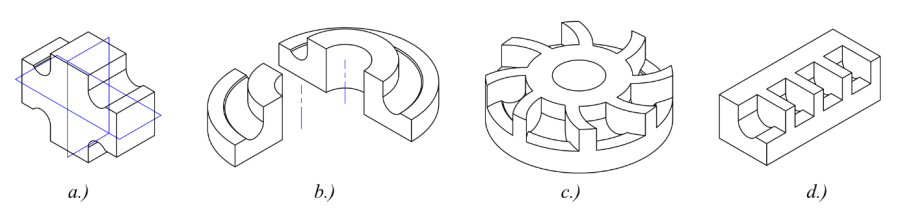
a.) Tükörszimmetria, b.) Tengelyszimmetrikus alkatrész negyed vagy félmodellel, c.) Körkörös ciklikusság, d.) Egyenes menti ismétlődés.

2.2. ábra - Testmodelleken alkalmazható szimmetriák.

2.2.3.2. 2D-s és 3D-s modellek alkalmazása

A geometria kiterjedésétől és a mechanikai feladat jellegétől függően választhatunk a térbeli vagy síkbeli analízis között, de lehetőség van térbeli analízisek elvégzésére alacsonyabb dimenziójú topológiával rendelkező elemekkel. Ezeket a lehetőségeket a legtöbb végeselemes rendszer támogatja. Az adott egyszerűsítés előfeltétele az analízis típushoz illeszkedő geometria létrehozása. A különböző geometriai típusokat és a kapcsolódó analízis típusát az Táblázat 2.1 szemlélteti.

2.1. táblázat - Különböző geometriai egyszerűsítések áttekintése, mechanikai példán keresztül.

Geometria	Analízis / Elem	Mechanikai eset	Az alkalmazás jellemzői
Testmodell	3D / 3D	Térbeli	Mindhárom irányú kiterjedése azonos nagyságrendű. Térbeli terhelés.
Térbeli Felületmodell	3D / 2D	Héj, membrán, lemez	Vékony térbeli szerkezetek. Térbeli terhelés és deformáció. (pl. lemezalkatrészek, karosszériaelemek, membránok)
Sík Felületmodell	2D / 2D	Sík feszültség	Vékony, sík szerkezetek. Csak a szerkezet síkjában fellépő feszültség. A keresztmetszet síkjába eső terhelés. (pl. Húzott lemezszerkezetek.)
	Sík alakváltozás	hosszú és állandó keresztmetszetű alkatrészek. A 2D-s geometria a szerkezet egy keresztmetszetét jelenti. Csak a keresztmeszet síkjában van alakváltozás. Keresztmetszettel párhuzamos terhelés és deformáció. (pl. Csővezetékek, zártszelvények, profilok)
	Tengely-szimmetrikus	Tengelyszimmetrikus szerkezet, melynek (fél) keresztmetszete a 2D-s modell (+XY síkon). A terhelések és a deformációk értéke állandó a kerület mentén. A kerület mentén állandó radiális és axiális komponensű terhelés. (pl. Forgástestek, nyomástartó edények.)
Térbeli vonalmodell	3D / 1D	Rúd, Gerenda	Állandó keresztmetszetű, vékony, hosszú elemekből álló térbeli szerkezetek. Vékony térbeli szerkezetek. Térbeli terhelés. (pl. Rácsos tartó, gerendaszerkezet.)

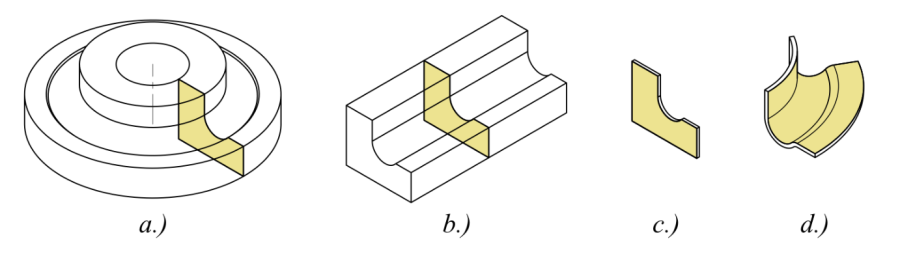
a.) Tengelyszimmetrikus, b.) Sík Alakváltozás, c.) Sík feszültség, d.) Héjmodell.

2.3. ábra - Térbeli testek felületmodellel történő modellezése.

A fenti táblázatból látható, hogy a geometriai modellek dimenzió szerinti osztályozása több szempont szerint is történhet, attól függően, hogy a vizsgált mechanikai probléma (feszültség vagy alakváltozási állapot, terhelések iránya, peremfeltételek, stb.) vagy az alkalmazott elemek, ill. a geometria topológiájának dimenzióját vesszük figyelembe. Az alábbiakban a geometriai modellek szerint soroljuk fel azok jellemzőit és alkalmazásukat.

2.2.3.2.1. Testmodell

A valós test geometriáját megközelítő tömör testmodelleket (3D-s testmodell), akkor alkalmazzuk, ha a test kiterjedése a tér minden irányába közel azonos nagyságrendű. Alkalmazásuk a legáltalánosabb és szinte minden probléma megoldásánál használható.

2.2.3.2.2. Térbeli felületmodell

Az olyan felületmodellek soroljuk ide, melyek 2 dimenziós topológiával, de 3 dimenziós kiterjedéssel vagy terhelési állapottal rendelkeznek, (pl.: héj, membrán vagy lemezmodell). A 3 dimenziós felületmodellek akkor használhatók, amikor a modellezett szerkezet vastagsága sokkal kisebb, mint a más irányú kiterjedése. Alakja lehet sík (lemezmodell) vagy térbeli kiterjedésű alakzat (héj). Fontos, hogy csak olyan igénybevételek esetén használhatók, ahol a vastagság irányában nincs olyan deformáció, amely befolyásolná a szerkezet viselkedését (pl. nyírási igénybevétel).

Modellezésük egy vastagság nélküli felület létrehozásával történik. Vastagságot a hálózáskor kapnak a megfelelő elemek hozzárendelésével. A modellezett felület általában a véges vastagságú szerkezet középfelülete, de általában lehetőség van az alsó vagy felső felületével modellezni a szerkezetet. Tipikus példa erre a fajta geometriai típusra a gépkocsik karosszériájának elemzése.

2.2.3.2.3. Sík felületmodellek

2 dimenziós modellek a 3 dimenziós modellek egyszerűsítésével hozhatóak létre a következő esetekben:

Sík feszültség - Amennyiben a tér egyik irányába fellépő feszültség elhanyagolható a másik két irányhoz képest. A geometria kiterjedése abba az irányba, amelybe a feszültség elhanyagolható sokkal kisebb, mint a másik két irányba. Tipikus példa erre az esetre egy a síkjában terhelt lemezszerű geometria vizsgálata, vagy például egy rugózó horog típusú pattanó kötés elemzése.
Sík alakváltozás - Amennyiben a tér egyik irányába fellépő deformáció elhanyagolható a másik két irányhoz képest. A geometria kiterjedése abban az irányban, amelyben a deformáció elhanyagolható sokkal nagyobb, mint a másik két irányban. Tipikus példa erre az esetre a zárszelvények bizonyos terhelési esetei, vagy például egy vonatsín terhelésének vizsgálata.
Tengelyszimmetrikus - Amennyiben a geometria és a peremfeltételek tengelyszimmetrikusak. A harmadik esetbe olyan geometriák tartoznak, amelyek tengelyszimmetrikusak, a terhelési és megfogási viszonyok is tengelyszimmetrikusak és a használt anyagmodell nem tartalmaz olyan irányfüggő tulajdonságot, amely ellentmondana a tengelyszimmetriának.

A fenti esetekben elegendő a geometriának azt a 2 dimenziós metszetét vizsgálni, amely a feszültség és deformáció szempontjából releváns (2.3. ábra). Természetesen csak akkor használhatók ezek az egyszerűsített geometriai modellek, ha a terhelések, megfogások és az esetleges irányfüggő anyagtulajdonságok ezt megengedik.

2.2.3.2.4. Vonalmodellek

Speciális eset az úgynevezett rúd, vagy gerendamodell használata, mely vonalakkal közelíti a terhelt szerkezetet. Ezt a megoldást akkor érdemes alkalmazni, amikor a geometria vonalak mentén azonos keresztmetszettel rendelkezik és az egyes geometriai szakaszok határán lévő kapcsolatot elhanyagolhatjuk, vagy későbbi vizsgálat során fogjuk annak viselkedését vizsgálni. Tipikus példa erre az esetre egy hegesztett, zártszelvényekből álló rácsszerkezet vizsgálata.

[12.]

2.3. Hálókészítés

A végeselem szimuláció alapvető lépése az adott geometria véges kis elemekre való felosztása, amit hálózásnak nevezünk. A végeselem modell létrehozásához ki kell választani a megfelelő elemtípust és a hálózás sűrűségét, figyelembe véve a kívánt pontosságot és a szükséges futásidőt. A legtöbb végeselem program a hálózást automatikus elvégzi, de lehetőség van a kézi beállításra is.

A végeselem modell elemeit (elements) és az elemeket összekapcsoló csomópontjait (nodes) a geometriai modell hálózásával (Solid modelling) vagy közvetlenül (Direct generation) hozhatjuk létre. A geometriai modell létrehozható a VEM programon belül vagy importálható külső CAD programból. A végeselemes háló közvetlen létrehozásakor (Direct generation) az egyes csomópontok helyét és az elemek tulajdonságait külön-külön kell megadni. Bár a direkt módszer több lehetőséget ad az elemek számának, eloszlásának, alakjának és más tulajdonságainak szabad befolyásolására, nagyobb elemszámnál nem hatékony és növeli a hiba lehetőségét. A két módszer tulajdonságait az alábbiak szerint foglalhatjuk össze [6.] :

2.2. táblázat - A direkt és az automatikus hálózás összehasonlítása.

	CAD modell hálózása (Solid Modelling)	Közvetlen hálógenerálás (Dirct generation)
Előnyök	Elsősorban nagy bonyolultságú, főleg 3D-s testmodellek hálózására alkalmas.	Elsősorban kis és egyszerű modellek hálózására alkalmas.
	Kisszámú paraméter kezelését teszi szükségessé.	Teljes felügyeletet biztosít a csomópontok és elemek száma, eloszlása, alakja, stb. felett.
	Az adaptív hálózáshoz ajánlott.
	Lehetővé teszi a geometria módosítását.
Hátrányok	Nagy a szimuláció futásideje.	A kis és egyszerű modelleket kivéve, időigényes az előállítása.
	Kis és egyszerű modelleknél több paraméter kezelését teszi szükségessé, mint a direkt módszer.	Nem használható adaptív hálózásra.
	Egyes esetekben a program nem tudja legenerálni a végeselemes hálót.	A háló módosítása túl bonyolult.
		A monoton művelet során könnyű hibát véteni.

2.3.1. Elemtípusok

Megjegyzendő, hogy a felsorolt elemek és azok tulajdonságának leírása közel sem teljes, mivel az meghaladná a jegyzet kereteit, csak a jegyzet témaköreiben ismertetett feladatok tárgykörébe tartozó kategóriákra szorítkozunk. Teljesebb áttekintésért és mélyebb ismeretekért érdemes használni a felhasznált és ajánlott irodalmakat és a használni kívánt végeselem szoftver súgóját, mivel azok teljes körű leírást tartalmaznak a rendelkezésre álló elemkészletről.

2.3.1.1. Kiterjedésük szerint

Bizonyos feltételek teljesülése mellett lehetőség van a 3D-s esetek síkbeli (sík feszültség, sík alakváltozás és tengelyszimmetrikus) vizsgálatára, vagy egyszerűsített térbeli, de 1 vagy 2 dimenziós topológiával rendelkező (rúd, héj, stb.) modellek alkalmazására. Mivel az 1D-s, ill. 2D-s modellek elemszáma jóval kisebb, mint ugyanannak a szerkezetnek a 3D-s modelljének, ezért futtatásuk sokkal gyorsabb és a szimuláció beállítása is egyszerűbb. Az analízisben használt elemek az alkalmazott geometriától függően kiterjedésük szerint dimenzió nélküli pont, 1D-s vonal, 2D-s felületi vagy 3D-s térfogati elemek lehet (2.3. ábra).

A pont elemeket (point element) egy csomópont (node) definiál, (pl., mint tömegpont vagy csomópont-felület kontaktelem).
A vonal elemeket (line element) két vagy három csomópontot összekötő egyenes, vagy ív definiál. A vonalelem lehet rúd (trust) , gerenda (beam) , cső (pipe) és tengelyszimmetrikus héj (axisymmetric shell) .
A felületelemek háromszög (triangular) , vagy négyszög (quadrilateral) alakúak, ill. 2D-s sík modell (2-D sík feszültség, sík alakváltozás, vagy tengelyszimmetrikus), vagy héj (shell) elemek lehetnek.
A térfogati elemek tetraéder (tetrahedral), gúla (piramid), prizma (wedge) vagy tégla (brick, hexahedron) alakú, 3D-s szilárdtest (3-D solid) elemek lehetnek.
A peremfeltételek definiálására (kontaktok, rugó elemek, tömegpont, stb.) speciális tulajdonságokkal rendelkező elemeket használunk. [6.] ).

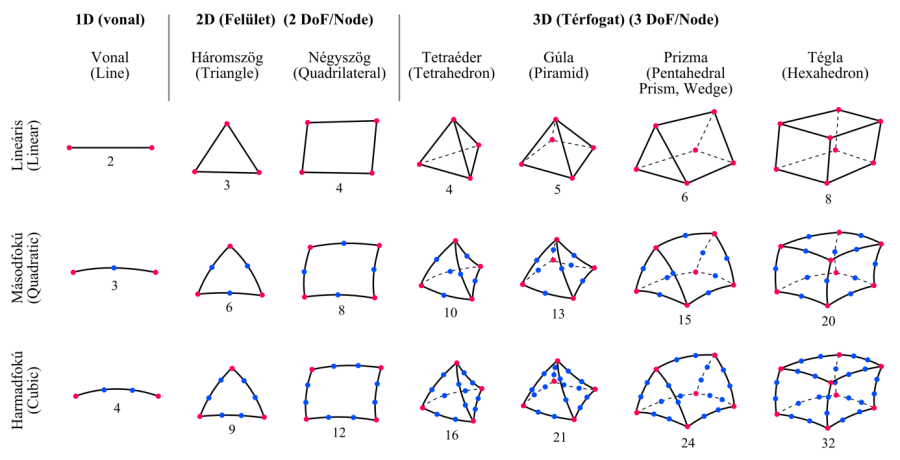
Az egyes elemek alatt a csomópontok száma van feltüntetve. (Az egy csomópontból álló és a belső csomópontokkal rendelkező elemek az ábrán nincsenek feltüntetve.)

2.4. ábra - Elemek csoportosítása alakjuk és fokszámuk szerint.

2.3.1.2. Az elemek fokszámuk szerint

A végeselem szimulációban használt elemek a geometriájuk és az alkalmazott interpolációs függvényük fokszáma szerint lineárisak (linear, first-order), másodfokúak (second-order, quadratic, parabolic) vagy harmadfokúak (third-order, cubic) lehetnek. Például egy lineáris háromszög (triangle) elem 3 csomóponttal (node) és 3 egyenes éllel van definiálva. A magasabb rendű háromszög elemnél a 3 csúcsnál lévő csomóponton felül a görbe vonalú éleken köztes csomópontok is (1 vagy 2) találhatóak.

A lineáris vagy magasabb rendű elemek választásakor az alábbiakra kell figyelemmel lenni. Alapvetően elmondható, hogy ugyanolyan hálósűrűség mellett a magasabb rendű elemek adnak pontosabb eredményt, mivel jobb matematikai közelítést használnak, és az íves élekkel / felületekkel határolt geometriát pontosabban követik. Viszont szem előtt kell tartani, hogy nagyobb teljesítményt, vagyis több számolási időt igényelnek.

Jacobi pontok (Jacobian Points). Magasabb rendű elemek esetén egy éles vagy erősen görbült perem olyan torzult elem generálását eredményezheti, melynek élei keresztezik egymást. A Jakobi vizsgálat esetén, az elem belsejében felvett pontok segítségével megállapítható a hiba, ugyanis ilyen extrém mértékben torzult elem esetén a Jakobi determináns értéke negatív lesz. (statikai feladatnál alkalmazott p-eljárás esetén célszerű a Jakobi vizsgálat elvégzése) [11.] .

2.3.1.3. Az elemek szabadságfoka

Az elemek szabadságfoka határozza meg, hogy melyik elem milyen típusú analízisre alkalmazható (pl.: szerkezeti, hő, áramlástani, elektromos, mágneses vagy kapcsolt terű analízisre.) Egy térbeli szerkezeti analízisben használt elem csomópontjainak 3 (U_x, U_y, U_z) szabadságfoka van, ezzel szemben egy hőtani szimulációban csak egy, a hőmérséklet. A megfelelő szabadságfokú elemtípus választása jellemzi a modell válaszát. Az elemek fölösleges szabadságfoka növeli a szimuláció memóriafoglalását és futási idejét. Hasonlóképpen a szükségtelen elemtulajdonságokkal rendelkező elem (pl. plasztikus tulajdonságok egy rugalmas szimulációban) alkalmazása szintén növeli a futásidőt.

2.3.1.4. Az elemtulajdonságok

Általános esetben az elemek koordinátarendszereire, bemeneteire (csomópontok, szabadságfok, anyagtulajdonságok, terhelések, stb.), és a szimuláció eredményeire (a csomópontok elmozdulása, feszültség, reakcióerő, stb.), oszthatók. Az alábbiakban nézzük meg az elemek főbb tulajdonságait a felhasználásuk szerinti csoportosításban.

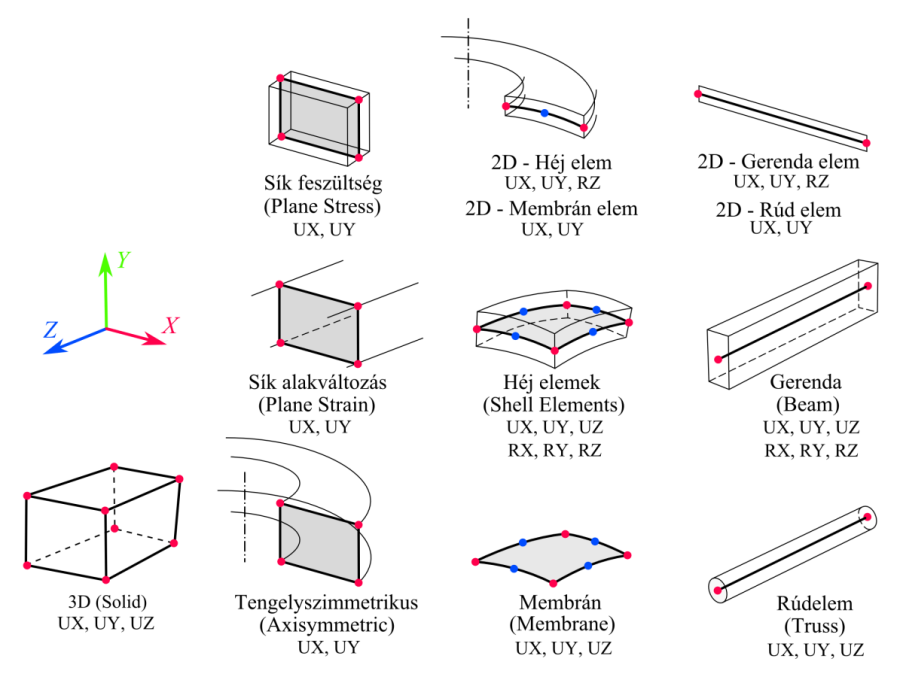
2.5. ábra - Gyakori mechanikai elemtípusok és a csomópontok szabadságfoka.

2.3.1.4.1. A feszültséganalízis elemei

az alábbiak szerint csoportosíthatók (2.5. ábra):

Kontinuum feszültségű elemek (Continuum Stress Elements) - az adott térfogatelem deformáció és feszültséganalízisére alkalmazhatóak. NEM tartoznak ide a héj, felület, kontakt, rúd és egyéb speciális elemek. Bármilyen strukturális analízishez használhatók. Nem hatékony az alkalmazása olyan esetekben, amikor a modell egy vagy két mérete sokkal kisebb a harmadiknál (pl.: membrán, lemez vagy rúdszerű modellek). Az elemek lehetnek 2, ill. 3 dimenziósak attól függően, hogy sík vagy térfogati modell hálózására használjuk. 2D-s változataik:
- Sík feszültség (Plane Stress) – olyan, csak X és Y irányokban változó feszültségi állapotoknál alkalmazzuk, amelynél a Z irányú normál, ill. az XZ és YZ nyíró feszültség nulla. Általában vékony, sík szerkezetek szimulációjára alkalmazzuk, melyeknél feltételezzük, hogy csak a szerkezet síkjában van deformáció.
- Sík alakváltozás (Plane Strain) – olyan, csak X és Y irányokban változó feszültségi állapotoknál alkalmazzuk, amelynél a Z irányú megnyúlás, ill. az XZ és YZ nyíró alakváltozás nulla. Tipikusan hosszú és állandó keresztmetszetű alkatrészek vizsgálatára alkalmazzuk, ahol a 2D-s geometria a szerkezet egy keresztmetszetét jelenti. (Az általánosított sík feszültség szimulációnál a Z irányú alakváltozás nem nulla.)
- Tengelyszimmetrikus (Axisymmetric) – A modell geometriai paraméterei, anyagjellemzői, a terhelések és a deformációk értéke állandó a kerület mentén. (Az általánosított, ill. harmonikus tengelyszimmetrikus szimulációk esetében a deformáció, ill. a terhelés lehet nem tengelyszimmetrikus.). A tengelyszimmetrikus szimulációk geometriáját az XY síkon, a +X térfélen kell elhelyezni, amely az Y forgástengelyű test keresztmetszetét jelenti [6.] vagy definiálni kell a metszősíkot és a forgástengelyt [11.] .
Héj elemek (Shell Elements) – Vékony térbeli szerkezetek szimulációjára alkalmas, melyeknél az egyik méret sokkal kisebb, mint a másik kettő. A héj elem a deformációt a felület szerinti normál és felületi irányokra bontja, ami egyszerű és hatékony szimulációt tesz lehetővé. Az elem felvehet membrán és hajlító terheléseket, ezért a csomópontok 6 szabadságfokkal (3 elmozdulás, 3 elfordulás) rendelkeznek. Az eredményként kapott eredő feszültség lekérdezhető a héj elem felső (top) ill. alsó (bottom) oldalán, továbbá a hajlító (bending) és a felület síkjába eső (membrane) feszültségkomponensek külön-külön is lekérdezhetőek. Általában lehetőség van a héj elemek membrán elemként való alkalmazására, melynél deformáció csak a felület mentén történik és a feszültség állandó a vastagság mentén.

A végeselem szoftver automatikusan héj elemeket rendel a térbeli (3D-s) felületmodellekhez vagy az olyan síkbeli felületmodellekhez, melyeknél a modell típusát 3D-re állítjuk [6.] . Egyes szoftvereknél az állandó vastagságú lemezalkatrészek (sheet metal) is héj elemekkel lesznek behálózva [11.] .
Vonal elemek (Line) – Állandó keresztmetszetű, vékony, hosszú elemekből álló szerkezetek szimulációjára alkalmas, melyeknél az egyik méret sokkal nagyobb, mint a másik kettő. A vonal elemekből álló rácsszerkezet szimulációja lényegesen egyszerűbb és gyorsabb, mint a szilárdtest-modellé. Az elemek egyenesek vagy ívek felosztásával (hálózásával) jönnek létre. A vonal elemek az alábbiak lehetnek.
- A rúdelem (Truss) csomópontjai nyomatékot nem adnak át, tehát csak tengelyirányú erőt képes átvinni, amely a rúd teljes hossza mentén állandó értékű és a keresztmetszetben egyenletesen megoszló feszültséget hoz létre. A rúdelem nulla feszültséget és alakváltozást feltételez az elem tengelyétől eltérő irányokban. Csak transzlációs mozgást enged elfordulást nem (3 DoF). Fő alkalmazási területe a rácsos tartók szimulációja. (A „link” elem a nyírófeszültséget és a feszültség gradienst szintén figyelmen kívül hagyja.)
- A gerenda (Beam) elem fel tud venni hajlító, csavaró és nyíró terhelést, ezért az elem keresztmetszetét is definiálni kell. A rúd hossza mentén és a keresztmetszet síkjában is változhat a feszültség értéke. Az elemek tengely körüli orientációja is definiálva van, tehát az elmozdulás mellett elfordulásra is képes (6 DoF), [6.] .
Speciális elemeket alkalmazunk a peremfeltételek, terhelések vagy különleges anyagtulajdonságok megadásához. Néhány példa a teljesség igénye nélkül:
- Kapcsolatot biztosító elemek - több alkatrészes összeállítás esetén az egyes alkatrészek közötti kapcsolatot lehet velük definiálni. Az alapvető kontakt elemek által biztosított kapcsolat lehet teljesen merev (Bonded), ideálisan érdes (Rough), ideálisan súrlódásmentes (frictionless), az érintkezésbenmaradó súrlódásmentes (no separation) és súrlódásos (frictional). Az alkatrészek közé lehet definiálni különböző szabadságfokokat megtestesítő csuklókat valamint rugalmas és csillapító elemeket.
- Cső (Pipe) elemek definiálására is lehetőség van egyes végeselem programokban, melyek egyenes, vékony vagy mérsékelten vastag csőszerkezetek szimulációjára alkalmas. A csőelem egy speciális rúdelem, melynek keresztmetszete tengelyszimmetrikus, külső és belső nyomás definiálható és nemlineáris anyagmodelleket is tartalmazhat [6.] .
- Felületi elemek (Surface Elements) – a szilárdtest elemek felületéhez csatlakozva lehet felruházni a modellünket speciális felületi tulajdonságokkal, mint pl. a nyomás, hidrosztatikus nyomás, sugárzás, kontakt felületek definiálása, stb.
- Erősítő elemek (Reinforcing Elements) – a kompozit anyagok vizsgálatára szolgáló elemtípus. Az erősítő szál rendszerek szimulációja egyirányú merevséggel rendelkező membrán rétegekkel történik (pl.: Szénszál erősítésű polimer kompozit). Egy rétegben lévő erősítő szálaknak egyforma keresztmetszettel, anyagtulajdonsággal, orientációval és távolsággal kell rendelkezniük. Lehetőség van az egyedi tulajdonságokkal (pl.: keresztmetszet, anyag, távolság, és a tájolás.) rendelkező ritkán elhelyezett erősítő szálak egyedi számolására (pl.: acél armatúra vasbeton szerkezetben). Alkalmazható rúd, héj vagy szilárdtest elemekhez [6.] .

2.3.1.4.2. A termikus analízis elemei

A termikus analízisekhez hőmérsékleti szabadságfokkal rendelkező elemeket használunk. A szilárd testek részeit, 2D-s vagy 3D-kontinuum elemekkel hálózhatjuk. A különböző területek közötti kapcsolat megvalósítására 1D-s elemek szolgálnak. A 0D-s pont elemet a koncentrált tömeg modellezésére lehet használni.

A szilárdtestben alkalmazható termikus elemtípusok:

3D – homogén vagy rétegezett szerkezetű szilárd testek modellezésére.
2,5D – vékony szerkezetek, mint a lemezek vagy héjak síkban történő hőmérséklet-eloszlásának vizsgálatára szolgál. A felület irányában és a vastagságon keresztüli hővezetés szimulációjára alkalmas.
2D – sík vagy tengelyszimmetrikus testek, ill. sík vagy görbe határfelületek modellezésére alkalmas.
1D - különböző területek közötti hővezetés (Conduction), hőátadás (Convection) és hősugárzás (Radiation) modellezésére szolgál.
0D – egy test hőkapacitásának (thermal capacitance) koncentrált paraméterrel történő modellezésére szolgáló termikus tömegpont. Nem rendelkezik hőmérsékleti gradienssel.

A hőterhelés közlésének két módja, a felületi hőterhelés megadásával, vagy az elem-kontaktokon keresztül történő hőátadással lehetséges.

A termikus modellben a felületi hőterhelés a konvekciót (convection), hőáramot (heat flux), vagy a hősugárzást (radiation) tartalmazhatja. A hőterhelést közvetlenül a kontinuum elemekre is lehet alkalmazni, sokkal kényelmesebb az azokat elfedő felületi elemek segítségével.

A felületi elemeken kívül a hőterhelés kontakt-elemekkel is megvalósítható. Ha két vagy több egymás közvetlen közelében lévő vagy érintkező szerkezeti régió van a modellben, kell számolni a köztük lévő hőátadással (konvekció, hővezetés, vagy a hősugárzás). Az érintkező felületek közötti súrlódási erő is lehet a hőtermelés forrása [6.] .

2.3.1.4.3. Az elektromos és mágneses analízis elemei

Az elektromágneses problémák analízisében alkalmazott elemeket a következő csoportokra bonthatjuk:

Kontinuum elemek (Continuum). Lehetnek 2, vagy 3 dimenziósak.
- Elektrosztatikus (Electrostatic) - töltés alapú, elektromos potenciál (Volt) szabadságfokú elemek.
- Elektromos (Electric) – áram alapú, elektromos potenciál (Volt) szabadságfokú elemek.
- Mágneses, elektromágneses (Magnetic, Electromagnetic) elemek – szabadságfoka mágneses skalár vagy vektor potenciál (magnetic scalar / vector potential), idő-integrált elektromos skalár potenciál (time-integrated electric scalar potential), elektromos áram (electric current) és elektromotoros erő (electromotive force) lehet.
- Végtelen tartomány (Infinite) – egy határtalan mező hatásának nyitott határfelületeken történő modellezésére szolgáló elemek. Segítségével a távoli tér (elektromos, mágneses) hatása modellezhető peremfeltételeken és testeken.
Forrás (Source) – Az elektromágneses analízisben a mágneses térerősséget létrehozó áram forrása. Az elemekben az áram iránya meghatározott, általában az áramvezető alakja is előre definiált. A vezetőben folyó áram által keltett mágneses tér (H) kiszámításához a Biot-Savart törvényt alkalmazó numerikus integrálással történik.
Áramkör (Circuit) – Az áramköri elemek modellezésére szolgál, mint az ohmnikus ellenállás (resistor), kapacitás (capacitor), induktivitás (inductor), dióda (diode) áram és feszültségforrás (current / voltage source), 2 és 3D-s tekercsek (stranded / massive coil), kölcsönös induktivitás (mutual inductor) és vezérelt forrás (controlled source), stb. Alapvetően elektromos áramkörök szimulációjára szolgál, de lehetőség van kapcsolt Elektromos-Mágneses analízis során a mágneses teret létrehozó áram közvetett megadására a segítségével.
Kontakt (Contact) – az alkatrészek közötti kapcsolatot, ill. a mágneses vektor és skalár mennyiségek kapcsolatát teremti meg.

2.3.1.4.4. Csatolt-tér elemek

A csatolt-tér (Coupled-Physics) elemek különféle fizikai jelenségek együttes vizsgálatát teszik lehetővé. Ezek az elemek mindazon szabadságfokokkal rendelkeznek, amelyek az adott típusú fizikai viselkedésre jellemzőek. A csatolt-tér elemek alkalmazásával a különböző fizikai jelenség szimulációja szimultán történik, (egyazon analízisben és egyazon végeselemes modell (háló) felhasználásával). A csatolt-tér elemek alkalmazása a szoros kapcsolatban álló fizikai jelenségek esetében ajánlott.

Főbb típusai:

Szerkezeti - termál (Structural-thermal),
Elektroelasztikus (Electroelastic),
Piezoelektromos (Piezoelectric),
Piezorezisztív (Piezoresistive),
Mágneses – szerkezeti (Magneto-structural),
Szerkezeti – elektromágneses (Structural-electromagnetic),
Elektromágneses (electromagnetic),
Termo-elektromos (thermo-electric),
Áramköri – elektromágneses (Circuit-coupled electromagnetic),
Akusztikus folyadék – szerkezeti (Acoustic fluid-structure),
Termál – folyadék (Thermal-fluid),
Porózus - nyomás (Pore-pressure),
Termál – diffúziós (Thermo-diffusion),
Szerkezeti – diffúziós (Structural-diffusion).

További általános vagy többszörösen összetett elemek is használatosak a fenti párosítások kombinációjaként [6.] .

2.3.2. A hálózás lépései

Az automatikus hálókészítés alapvetően a háló attribútumainak (attributes) beállításából, a kontrollok (mesh controls) megadásából és a hálógenerálásból áll. Lépései:

Fizikai elv kiválasztása (Mechanikai, elektromágneses, fluid, stb.),
Hálózási eljárás beállítása (Automatikus, söpréses, tetraéder/tégla, háromszög/négyszög),
Globális hálózási tulajdonságok beállítása,
Lokális hálótulajdonságok definiálása,
Előnézet és hálógenerálás,
A háló ellenőrzése.

[13.]

2.3.2.1. Attribútumok és kontrollok beállítása (mesh controls)

A hálógenerálás előtt szükség van a háló tulajdonságait meghatározó attribútumok és kontrollok beállítására. Választhatjuk az alapbeállított értékeket, ebben az esetben a program kiválasztja az adott szimulációhoz megfelelő beállításokat. A globális elemméret automatikus beállítása a modell térfogata, felülete és egyéb geometriai méretek figyelembevételével történik. Viszont lehetőség van azok egyéni, lokális beállítására is a hálógenerálás előtt. Az attribútumok és kontrollok által lehetőség van az alábbi tulajdonságok beállítására:

Attribútumok:

Elemtípus kiválasztása,
Geometriai tulajdonságok megadása (pl.: vastagság, keresztmetszet),
Anyagtulajdonságok hozzárendelése (pl.: Rugalmassági modulus, Poisson-tényező, hővezetés, stb.),
Elemkoordináta-rendszer megadása.

Kontrollok:

Az elem mérete – A globális (a teljes modellre kiterjedő) elemméret méretmegadása történhet automatikusan vagy manuálisan. A manuális elemméret megadható közvetlenül vagy a háló finomságának beállításával, valamint az elemszám, vagy az elem élhosszak minimumának és maximumának megadásával.
A háló lokális finomítása – Olyan helyeken ahol a szerkezet fizikai tulajdonságai miatt az alapértelmezett elemméret nem alkalmas (ilyenek lehetnek például a feszültséggyűjtő, vagy szinguláris helyek), szükség van a lokális hálófinomításra.
Az elem alakja - Ha olyan elemtípust kívánunk alkalmazni, amely több alakot is felvehet, akkor meg kell adnunk az alkalmazható elemalakokat. Például sok 2D-s területelem egyaránt lehet háromszög és négyszög alakú ugyanazon a behálózott területen. A térfogati elemek gyakran lehetnek hatlapú (tégla) vagy tetraéder alakúak, de a két alakzatot keverve ugyanabban a modellben nem ajánlott alkalmazni. (Kivétel ez alól átmeneti piramiselemek használata, [6.] ).
Strukturálatlan vagy rendezett háló (Free or Mapped Mesh) – A szabad vagy strukturálatlan háló esetében nincs korlátozás az elemformák tekintetében, és nincs meghatározott minta alkalmazva. A rendezett vagy strukturált háló (Mapped) esetében az elem formájára és a háló mintájára is vannak korlátozások. A rendezett felületháló csak négyszög vagy csak háromszög elemeket tartalmazhat, míg a rendezett térfogati háló csak tégla elemeket tartalmazhat. A rendezett háló mintázatát a sorbarendezett elemek alkotják, melynek előfeltétele a geometria megfelelő előkészítése [6.] .
A köztes csomópont elhelyezése (az elem fokszáma) – Kvadratikus elemekkel való hálózáskor meghatározható a köztes csomópont elhelyezése vagy annak eltávolítása. Amikor egy kvadratikus elem a határfelületen van, akkor a köztes pont követi a határfelület görbületét.

A modellépítés e szakaszának az egyik legfontosabb lépése, mivel ezek a tulajdonságok alapvetően befolyásolják az egész analízis pontosságát és munkaigényét.

[6.] , [14.] .

2.3.2.2. Automatikus hálózási eljárások

A hálógeneráló algoritmusok szempontjából a végeselem háló egyik legfontosabb tulajdonsága, az elem típusa mellett, a strukturáltsága. Vagyis, hogy a háló lehet strukturált vagy strukturálatlan. A strukturált háló lokálisan ortogonális vonalak rendezetett hálózata alkotja. A háló vonalai a geometria határához illeszkednek. A strukturálatlan hálót rendezetlen poligonok sokasága alkotja.

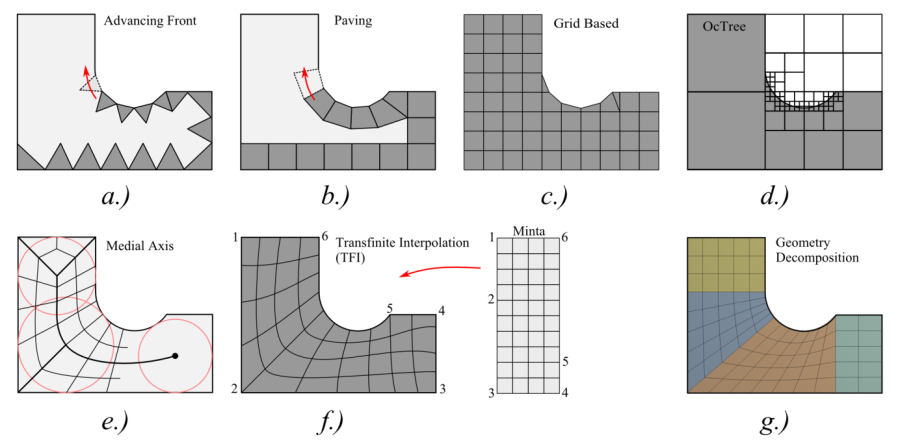
a-d.) Strukturálatlan, e-g .) strukturált háló létrehozása

2.6. ábra - Automatikus és részben automatikus hálógenerálási eljárások.

2.3.2.3. Strukturálatlan háló létrehozása

2.3.2.3.1. Topológia felosztása (Topology decomposition)

A geometriát alkotó pontok (vertex) felhasználásával a komplex geometriát minimális számú, nem átfedő háromszögekre bonjuk, az így létrejött háló torz és durva, analízisre alkalmatlan. A felosztás eredményeként létrejött háromszögek további elemekre bontásával finomítjuk a hálót.

2.3.2.3.2. Csomópont csatlakozás (Node connection)

Első lépésben a csomópontokat hozzuk létre, majd ezeket kapcsolják össze az elemek. A fenti utólagos hálósűrítés elkerülhető, ha a végső háló sűrűségének megfelelően osztjuk szét a csomópontokat. A következő lépésben az így létrejött ponthálót kell megfelelő módon összekötni, hogy a lehető legjobb elemek jöjjenek létre.

2.3.2.3.3. Mozaik (Advancing front, Paving)

A „Front” módszer háromszög elemeket a határoló éltől kiindulva befelé hozza létre (2.6. ábra, a.). A Paving eljárás a „Front” technika négyszögelemre kidolgozott változata, a háromszögelem kiváltására. (2.6. ábra, b.), (csak 2D-ben) [15.] .

2.3.2.3.4. Négy-fa (Octree)

Négyzetes háló, melynek finomítása a határvonalra eső négyzet-elem négyfelé osztásával érhető el. A kívánt felbontásig több lépcsőben ismételve a háló topológiája fa struktúrájú lesz, innen az elnevezés (2.6. ábra, d.).

2.3.2.3.5. Rács alapú (Grid-based)

Valamilyen előre generált minta adaptálásával jön létre a háló. A minta egy végtelen négyzetes vagy háromszög rács, amely a geometriára kerül ráhelyezésre. A geometria határán kívülre kerülő elemek eltávolítódnak. Azok az elemek, amelyek metszik a geometria határát elmetsződnek vagy hozzáillesztődnek a határvonalhoz. A létrejött háló belseje kitűnő tulajdonságú (2.6. ábra, c.). A 3D-s hálógenerálás egyik legelterjedtebb eljárása.

2.3.2.4. Strukturált háló létrehozása

A strukturált háló létrehozása kiváló minőségű kellően egyszerű geometriához és ezáltal hatékonyabb analízishez vezet. Jobb kontrollt biztosít a háló paraméterei felett, pl. anizotrópia esetén. Valósághű geometriák is vizsgálhatóak a „multiblock” hálózási eljárás segítségével.

2.3.2.4.1. Minta leképezéses eljárások (Mapped element)

A minta egy a paramétersíkon lévő egységoldalú elemekből álló négyszögháló, amelyet ráképezünk a hálózandó 4 oldalú felületre a minta megfelelő torzításával (2.6. ábra, f.). Ezzel a módszerrel rendezet négyszögelemmel kirakott hálót hozhatunk léte, olyan szabálytalan felületeken is, melyek topológiája visszavezethető egy 4 oldalú felületre (TFI-Transfinite Interpolation, Elliptic), vagy szétválasztható azokra (Geometry Decomposition).

2.3.2.4.2. Geometria szétválasztás (Geometry decomposition, Sub-maping)

Az eljárás a hálózás során konvex „map”-elhető részekre bonja a geometriát, majd csomópontokat helyez el ezek határán. Végül a különálló tartományokat hállózza be (2.6. ábra, g.). Az eljárás figyelembe veszi az elem alakját és méretét mialatt felosztja a geometriát. Számos eljárás rekurzív, mások iteratívak. A Multiblock-Decomposition eljárás bonyolultabb, strukturálatlan alkatrészek (négyszög oldalú) tartományokra osztása, melyek külön-külön már automatikusan „map”-elhetőek. A Medial Object Decomposition egy maximális sugarú kör / gömb végiggörbítésével jelöli ki a nyomvonalát a közép-objektumnak (középvonal, középfelület) (2.6. ábra, e.). A közép-objektum felhasználása a geometria automatikus szétválasztására, kisebb „map”-elhető részekre.

2.3.2.4.3. Söprés (Sweeping)

Prizmaszerű alaktrészek alapfelületen generált 2D-s háló végigsöprése a teljes test mentén. A véglapokon struktúrálatlan 2D-s hálót, a palást mentén struktúrált hálót generál. Követelmény, hogy a kiinduló (source) és a célfelület (target) topológiailag hasonló és az öszekötő palástfelület „map”-elhető legyen (2.8. ábra).

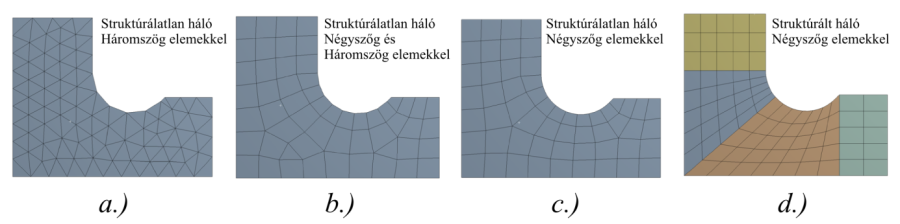
2.7. ábra - 2D-s hálókialakítások.

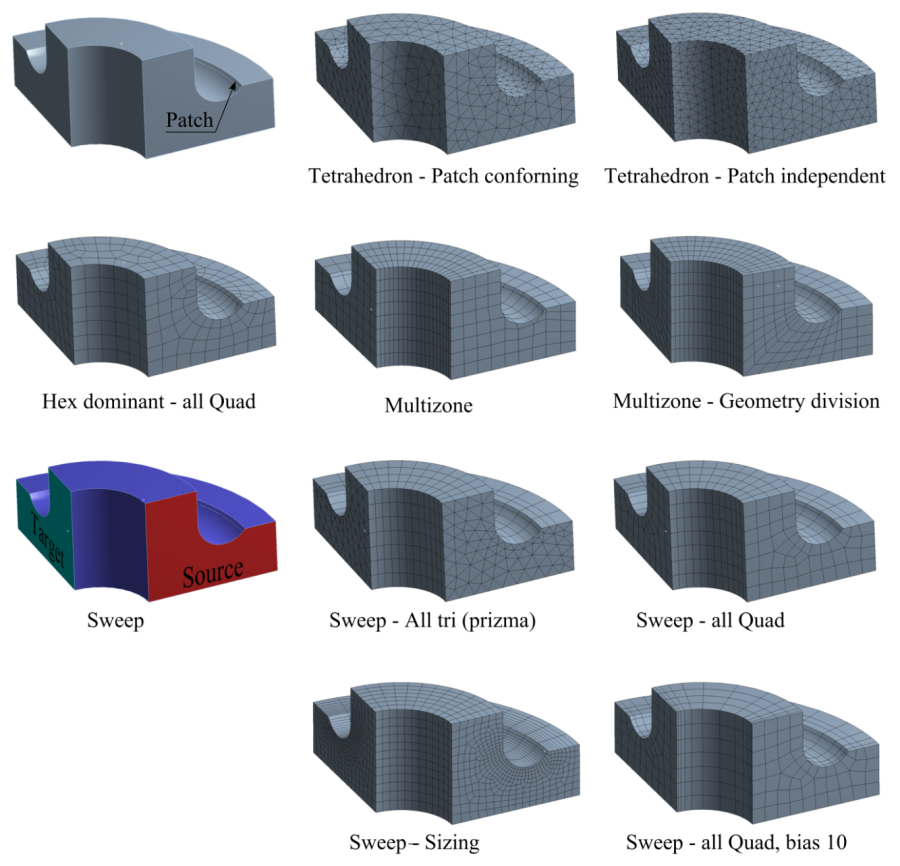
2.8. ábra - 3D-s testek hálózása különféle eljárásokkal.

[16.] , [17.] , [18.] , [19.] .

2.3.2.5. A háló illeszkedése

Több alkatrészből álló modell esetén célszerű a hálót úgy kialakítani, hogy a csomópontok illeszkedjenek, ugyanis az elemre ható terheléseket a csomópontok közvetítik.

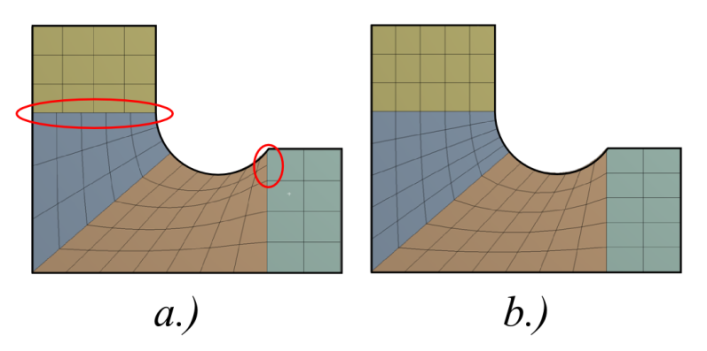
a.) Nem illeszkedő csomópontok (Non-conformal interface), b.) Illeszkedő csomópontok (Matching interface).

2.9. ábra - Különálló felületek vagy testek határán lévő csomópontok illeszkedése.

2.3.3. Konvergencia módszerek

A tervezés kezdeti stádiumában a gyors futás érdekében érdemes lehet nagyobb elemméret és lineáris elemek alkalmazása, a későbbiekben a pontosabb eredményhez pedig finomabb hálózás és vagy magasabbrendű elemek alkalmazása. A konvergencia javításának és az elérhető számítási pontosság növelésének ez a két lehetséges módját h és p konvergencia módszernek nevezik.

H – eljárás: a háló finomítás, elemméret csökkentés,

P – eljárás: az elemek fokszámának növelése,

HP – eljárás: H és P módszer együttes alkalmazása.

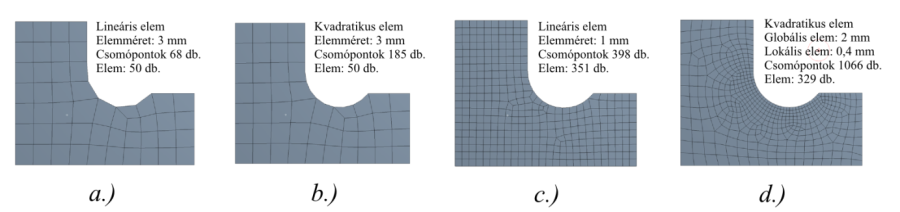
a.) Kiindulási háló, b.) P – eljárás: az elemek fokszámának növelése, c-d.) H – eljárás: elemméret csökkentés, c.) Globális elemméret beállítás, d.) Lokális hálófinomítás.

2.10. ábra - Konvergenciát elősegítő eljárások.

2.3.3.1. Hálósűrítés, hálósimítás

Az egész modellre kiterjedő globális elemparaméterek, főként az elemméret általában nem megfelelő. Olyan helyeken, ahol a vizsgált fizikai mennyiség megváltozása nagyobb (nagyobb gradiens), mint a modell többi részén (pl. feszültséggyűjtő helyek), akkor ott a háló sűrítése indokolt. A háló sűrítése történhet az adott geometria finomítási lépcsőinek megadásával (Refinement, az elemek felezési számának), adott számú elemre történő felosztásával (Number of division, éleknél alkalmazható), vagy az elemméret közvetlen megadásával (element size).

A lokális hálófinomítás során ügyelni kell az átmenet, vagyis az elemméret növekményének intenzitására, a kisméretű lokális elemek és a nagyobb globális beállítású háló között. Ugyanis túl nagy növekmény rossz minőségű, pl. nagy oldalarányú (aspect ratio) vagy torzult elemeket hozhat létre. Az átmenet mértékének (Growth Rate) kezelésére általában van lehetőség a végeselem szoftverekben.

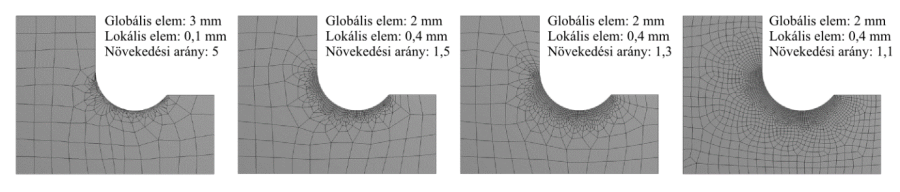
2.11. ábra - Elemátmenetek különböző mértékű növekedési arány (Growth Rate) megadásával.

További segítséget nyújt a megfelelő minőségű elemek létrehozásában a háló simítás (Mesh Smoosing) funkció. A hálósimítás egy már meglévő háló csomópontjainak eloszlását módosítja több iterációban, úgy hogy az elemek alakja minél egyenletesebb legyen. Természetesen ezt a felhasználó nem érzékeli, mert a hálógenerálás egy lépésben történik. Többféle eljárás létezik (Lapalce, Isoparametrikus, centroid, stb.), de előfordulhat, hogy a végeselem szoftverben csak a minőségre utaló értékeket tudunk kiválasztani (low, medium, high).

2.3.3.2. Adaptív hálózás

Abban az esetben, ha a nagy alakváltozások következtében a háló annyira torzul, hogy a szimuláció nem konvergál, szükséges lehet a geometria adaptív újrahálózására (adaptive remeshing). Az eljárás során, amikor a háló eltorzult, a szimuláció leáll. A torzult geometriát a szoftver újrahálózza és érvényesíti rá a korábbi hálón számolt eredményeket, perem és kontakt feltételeket és az analízis folytatódik. [20.]

2.3.4. A hálózásnál előforduló hibák

Elvékonyodó vagy túl éles geometria – a túlságosan elvékonyodó vagy éles geometria hibát okoz a tetraéderes háló generálásában a csúcsoknál (élek mentén).
Extrém elemméret átmenet – a hirtelen átmenet az elemméretben rossz minőségű tetraéder hálót eredményez.
Túl nagy elem görbület – Célszerű lineáris elemet használni, ha nincs szükség pontos feszültség meghatározásra a görbület mentén, vagy kvadratikus elem esetén növelni a háló sűrűségét, hogy egy elem ne fogjon át 15°-nál nagyobb szöget.

Tetraéderhálózási hiba – Elkerüléséhez célszerű előzetesen megvizsgálni a modellt, hogy háromszög elemmel hálózva a test egyes felületeit, tartalmazza-e a fenti hibák valamelyikét, ugyanis azok elősegíthetik a tetraéderes hálózás hibáját.

Kivonóan hálózott részek – A már hálózott elemeken végzett kivonásos boolean művelet esetében jelentkező hibát a hálózás törlésével és újra definiálásával szüntethetjük meg.

Magas és alacsonyrendű elemek szomszédos részeken – Az alacsonyabb rendű hálózást kell először létrehozni majd a magasabb rendűt [6.] .

A háló minőségének vizsgálatára többféle módszer is rendelkezésre áll a végeselemes programokban. A vizsgálatok eredményét szövegesen, statisztikai adatok formájában, hisztogramon, vagy közvetlenül a geometrián szemléltetve közli a szoftver. Az alábbiakban ez utóbbira láthatunk példát (SolidWorks), az elemek oldalarányának (Aspect ratio) és a Jakobi determináns értékének szemléltetésével [6.] , [11.] .

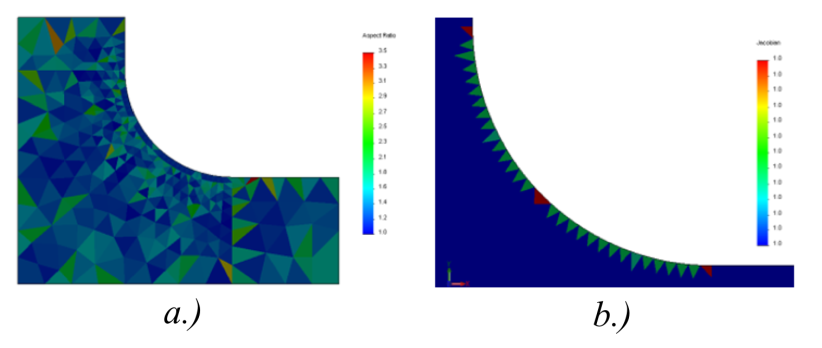
a.) Oldalarány (Aspect ratio) vizsgálata. b.) Jakobi determináns vizsgálat.

2.12. ábra - Elemtulajdonságok vizuális megjelenítése.

2.4. Anyagmodellek létrehozása

Az anyagmodell nem más, mint egy anyag az alkalmazott terhelés hatására adott válaszának matematikai ábrázolása, amely a fizikai változók (mechanikai feszültség, hőáram, villamos áram, stb.) és más fizikai mennyiségek (mint pl. alakváltozás, hőmérséklet eloszlás, villamos feszültség, stb.) között teremtenek kapcsolatot [21.] . A tipikus anyagmodell osztályok a feszültség-alakváltozás, a hőáram-hőmérsékleti gradiens, valamint a villamos áram-feszültség között teremtenek kapcsolatok, de egyéb olyan általános fizikai viselkedést, (mint például a súrlódás, hőtágulás, piezoelektromos és mágneses hatások, stb.) is az anyagmodellek segítségével írhatunk le [6.] .

2.4.1. Általános anyagtulajdonságok

a.) Nyíltcellás polimerhab, b.) szálas szerkezetű anyag, c.) koncentrikusan rétegelt struktúra, d.) szálerősítéses polimer kompozit.

2.13. ábra - Példa az inhomogén és anizotróp anyagokra.

2.4.1.1. Linearitás

Az anyagmodelleket aszerint csoportosíthatjuk, hogy miként teremtenek kapcsolatot a bemenő és kimenő mennyiségek, (vagyis mechanikai esetben a feszültség és az alakváltozás) között. Ez a kapcsolat lehet lineáris (linear), vagy nemlineáris (non-linear). Lineáris esetben a kimenő mennyiség egyenesen arányos a bemenettel és az arányossági tényező valamilyen anyagjellemző.

2.4.1.2. Homogenitás

Az anyag szerkezetét tekintve lehet homogén (homogeneous), vagy inhomogén (non-homogeneous). Az inhomogén anyagok tulajdonságainak (pl. sűrűség, szilárdsági tulajdonságok, stb.) térbeli eloszlása nem egyenletes. Mikroszkopikus szinten gyakorlatilag az összes anyag inhomogén, (kristályokra, molekulára majd atomokra tagolódik), de a szimuláció szempontjából lényeges makroszkopikus szintű inhomogenitást az anyag nagyobb strukturáltsága jelenti, amely méreteiben összevethető a teljes modell méretével (mint pl. a szivacsos csontszövet struktúrája, polimer vagy fém habok, porózus, szemcsés anyagok, stb.).

2.4.1.3. Irányfüggőség

Egy anyag iránymenti viselkedését az alábbi három modellel írhatjuk le.

2.4.1.3.1. izotróp anyagmodell (Isotropic model)

Izotróp anyagról beszélünk, ha az anyagi tulajdonságok (pl. rugalmassági modulus, Poisson-tényező, termikus tulajdonságok, stb) minden irányban megegyeznek. Mikroszerkezetük lehet homogén vagy inhomogén.

2.4.1.3.2. Ortotróp modell (Orthotropic model)

Ortotróp anyagmodell esetén az anyagtulajdonságok három, egymásra merőleges tengely mentén eltérőek és egymástól függetlenek. Tipikus példa az ortotróp anyagra a fa, melynek természetes szerkezete miatt mechanikai tulajdonságai axiális, radiális és tangenciális irányokban különböző. De további ortotrópiát okoznak a szerkezeti anyagainkban egyes technológiai lépések is, mint pl. a polimer szálak húzása, vagy az acéllemezek hengerlése, stb.

2.4.1.3.3. izotrópAnizotróp modell (Anisotropic model)

Az izotrópanizotróp anyag az irányfüggő viselkedés teljesen általános esete, melynél az anyagtulajdonságok különböző irányokban, (nem derékszögű koordináták mentén) eltérő viselkedést mutatnak.

2.4.2. Az anyagmodellek csoportosítása szabadságfokuk alapján

Az anyagmodellek a szabadságfokuk alapján az alábbiak lehetnek, amely közvetlenül vagy közvetve megadják a modell terhelési módját, vagyis az anyagmodell bemenetét:

Elmozdulás,
Hőmérséklet,
Elektromágneses,
Csatolt

2.4.3. Mechanikai, vagyis elmozdulás szabadságfokú anyagmodellek

Az elmozdulás szabadsági fokkal rendelkező elemzésekben szerepelnek, melyekben a bemenet egy deformációs függvény, mint például az alakváltozás vagy az elmozdulás, és az adott válasz valamilyen erő típusú mennyiség, mint például feszültség, vagy a normális és tangenciális erők.

2.4.3.1. A mechanikai anyagmodellek csoportosítása fesz-nyúlás karakterisztikájuk szerint

A mechanikai anyagmodelleket a feszültség-alakváltozás karakterisztikájukkal jellemezzük, amely lehet lineáris, vagy nemlineáris, ill. rugalmas, képlékeny vagy viszkoelasztikus.

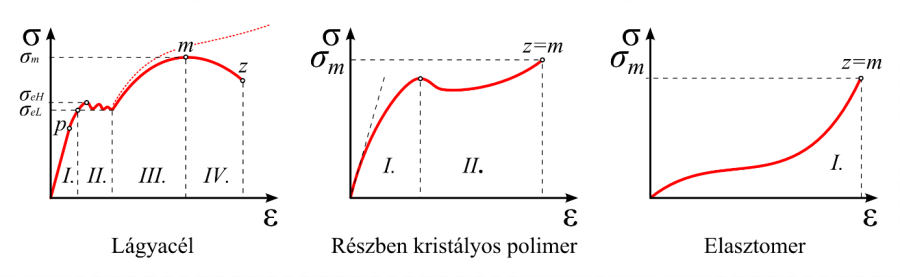
p – lineárisan rugalmas tartomány, I.- Rugalmas tartomány (reverzibilis), II.- Folyási tartomány, III.- Keményedési tartomány, IV. – Kontrakciós tartomány.

2.14. ábra - Néhány gyakran alkalmazott szerkezeti anyag jellemző feszültség-nyúlás karakterisztikája.

Az anyagok mechanikai viselkedése rendkívül változatos és rendszerint összetett (2.14. ábra). De általában kiemelhető olyan eleme, ami az adott analízis szempontjából lényeges. A felhasználástól függően ugyanannak az anyagnak különböző lehet a modellje. Például az acélt a konstruktőr egy lineárisan rugalmas anyagmodellel (2.14. ábra, I./p szakasz), a képlékeny alakítás vizsgálatához a technológus egy képlékeny anyagmodellel (2.14. ábra, I és II. szakaszok) definiálja (2.27. ábra).

2.15. ábra - Az anyagok mechanikai viselkedését leíró főbb anyagmodelleket jellemző feszültség - nyúlás karakterisztikák [22.] .

Tisztán rugalmasnak akkor nevezzük az anyagot, ha a felterhelést követő tehermentesítés során visszanyeri eredeti alakját és sem maradó sem pedig késleltetett alakváltozást nem szenved. Tehát ha a feszültség-alakváltozás diagram terhelési és a tehermentesítési görbéje egybeesik, reverzibilis és útfüggetlen. Feszültség – nyúlás karakterisztikájuk lehet lineáris, vagy nemlineáris.

Lineárisan rugalmas (Linear elastic) anyagmodellről akkor beszélünk, ha a feszültség-alakváltozás karakterisztikája egy egyenesre esik, vagyis a feszültség egyenesen arányos az alakváltozással, ellenkező esetben nemlineáris anyagmodellről beszélünk. A terhelés megszüntetésével az anyag teljes mértékben visszanyeri az eredeti alakját. Izotróp anyagok esetében a Hooke törvény, anizotróp esetben az általánosított Hooke törvény írja le az anyag viselkedését. A legtöbb szobahőmérsékletű fém viselkedésére alkalmazható kis alakváltozások esetén.

A nemlineáris anyagi viselkedés jellemzője, hogy a feszültség és fajlagos nyúlás közötti kapcsolat nem lineáris, tehát nem érvényes rá a Hook törvény. A modellezés során gyakran közelítjük a nemlineáris karakterisztikát két vagy több szakaszból álló lineáris anyagmodellel (bilinear, multilinear material models). Nemlineáris Feszültség-alakváltozás tulajdonsággal rendelkező plasztikus (plastic), multilineáris rugalmas (multilinear elastic), és a nagyrugalmas (hyperelastic) anyagmodellek különböző terhelési szinteken és hőmérsékleten a szerkezet különböző merevségét eredményezik. A kúszás (Creep), viszkoplasztikus (viscoplasticity), és viszkoelasztikus (viscoelasticity) anyagmodellek nemlinearitása lehet idő, sebesség, hőmérséklet, és a feszültségből adódó.

A nemlineáris statikus szerkezeti analízisekben leggyakrabban alkalmazott anyagmodellek az alábbiak:

Nemlineárisan rugalmas (Nonlinear Elasticity Models),
- Multilineáris rugalmas (Multilinear Elasticity Material Model),
- Hiperelasztikus vagy nagyrugalmasságú (Hyperelasticity Material Model),
Viszkoelasztikus (Viscoelasticity),
Plasztikus (Plasticity Material Model),
Viszkoplasztikus (Viscoplasticity),

Hiperelasztikus (Hyperelastic) anyagmodellek viselkedését az alkváltozási-energia potenciál, vagyis a deformált anyagban tárolt energia definiálja. A matematikai megfogalmazás lehetővé teszi a nagy alakváltozások leírását. A hiperelasztikus modelleket gyakran használják olyan anyagok esetében, amelyek nagyrugalmas alakváltozásnak vannak kitéve, mint az elasztomerek és a biológiai anyagok.

Sebesség és időfüggés (Rate effects and time dependency) olyan anyagi viselkedések, amelyek függenek a deformáció sebességétől és az eltelt időtől. Ilyenek például a viszkoelaszticitás, viszkoplaszticitás, kúszás és a csillapítás. A polimerek és magas hőmérsékletű fémötvözetek jelentős kúszást mutatnak. Az anyagmodell alkalmazható a sebesség függő fémmegmunkáló technológia, az alakváltozási sebesség-függő polimerek (tipikusan merevebbé válnak nagyobb sebességeken), és dinamikusan terhelt struktúrák frekvenciafüggő csillapításának vizsgálatára.

Viszkoelasztikus anyagmodell viszkózus és rugalmas komponenseket tartalmaz. A feszültség - nyúlás karakterisztika fel és leterhelési szakasza eltérő pályán mozog és a kezdőpontba tér vissza, vagyis visszanyeri eredeti alakját. A két görbe egy hiszterézis-hurkot ír le, és közöttük lévő terület nagysága az alakváltozás során disszipált energiával egyenlő.

A viszkoplasztikus anyagmodell egy ideálisan képlékeny, és egy ideálisan viszkózus tagból áll, így a szilárdtestek sebesség-függő rugalmatlan viselkedését írja le. A feszültség az alakváltozás sebességével arányos (a newtoni folyadékokhoz hasonlóan ideálisan viszkózus), de az alakváltozás csak egy bizonyos határfeszültség elérése után indul meg [23.] .

Plasztikus vagy elaszto-plasztikus (Plastic, elastic-plastic) anyag deformációja tartalmaz egy rugalmas és egy maradó vagy plasztikus komponenst. A terhelés megszűnésével a tehermentesítés nem a felterhelés görbéjén történik és nem tér vissza a kiindulási állapotba. Ebben az esetben a képlékeny alakváltozás nem az idő vagy a sebesség függvénye, hanem a feszültségi állapoté, a képlékeny alakváltozás egy határfeszültség elérése után indul meg. Képlékeny alakváltozás megfigyelhető a fémek, ötvözetek, a talaj, kőzetek, beton és kerámia anyagok esetében.

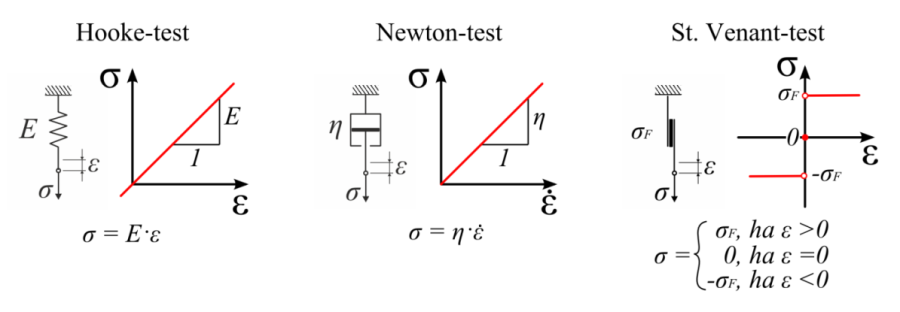
Hooke-test – ideálisan rugalmas (elasztikus), Newton-test – ideálisan viszkózus, St. Venant-test – ideálisan képlékeny (plasztikus).

2.16. ábra - A reológiai anyagmodelleket alkotó alapvető modellek.

A fenti anyagmodelleken kívül, esetleg azok kiterjesztése, vagy speciális eseteként további számos anyagmodell áll rendelkezésre a végeselemes programokban. A valós anyagi viselkedés jobb közelítésének érdekében a végeselemes szoftverekben gyakran van lehetőség ezek kombinációinak alkalmazására, (pl. viszkoelasztikus és hiperelasztikus anyagmodell). Végeselem szoftvertől függően további lehetőségek vannak a speciális anyagi tulajdonságok definiálására:

Tágulás és duzzadás (Expansion and swelling) . Némely anyag strukturális viselkedése megváltozik a fizikai környezet hatására. Ilyen például az anyag hőtágulása (térfogatváltozás a hőmérsékletváltozás hatására), vagy a duzzadás (vízmegkötés hatására), ragasztott anyagok eltérő hőtágulása, és a vizet felszívó talaj viselkedése, stb.

Kölcsönhatás (Interaction). Ennek a modellnek a válasza a struktúrák kölcsönhatásán alapul (pl.: Tömítő és ízületi anyagok, valamint ragasztott és elválasztó felületek közötti kölcsönhatások.

Alakemlékező-fém (Shape memory alloy) . Egy belső fázisátalakulással rendelkező rugalmas anyagmodell. A fázisátalakulás függ a feszültségtől és a hőmérséklettől, melyek hatására a belső átalakulási feszültség jön létre.

Kúszás (Creep), Mullin effektus (Mullins Effect). A polimerek esetében általában és gumiszerű anyagok ideális nagyrugalmas (reverzibilis) viselkedése mellett a gyakorlatban megjelennek viszkoelasztikus tulajdonságok, mint a kúszás (Creep), Mullin effektust (Mullins Effect) jelensége. A viszkoelasztikus anyag definiálásán kívül néha lehetőség van ezeket az anyagtulajdonságokat külön is definiálni.

2.4.3.2. Lineárisan rugalmas anyagmodell (Linear elastic)

Lineáris és izotróp esetben a feszültség és a fajlagos nyúlás közötti kapcsolat egyenes arányosság, és a rugalmassági (Young) modulus E az arányossági tényező, vagyis anyagmodellt a Hook törvény írja le (egytengelyű feszültségi állapot esetén: E=σ/ε). Számos anyagra jellemző a lineáris viselkedés kis alakváltozásoknál, és csak nagyobb alakváltozás után válik nemlineárissá (pl. fémek). Más anyagok egészen kis alakváltozásnál is nemlineáris tulajdonságot mutatnak (pl. polimerek). A lineáris anyagmodell lehet izotróp. ortotróp vagy izotrópanizotróp.

Izotróp esetben az anyagban ébredő feszültség és az alakváltozás közötti összefüggés megadása két paraméter megadásával lehetséges. Leggyakrabban a rugalmassági modulust (Young's modulus, E) és a Poisson-tényezőt (Poisson’s ratio, ν) alkalmazzuk, de alkalmazható a nyírási és a térfogatváltozási modulus is. Térbeli feszültségi állapot esetén az általános Hook törvény tenzoros alakja a feszültségre

$\underline{\underline{σ}} = \frac{E}{1 + ν} [\underline{\underline{ε}} + \frac{ν}{1 + 2 ν} \cdot ε_{I} \cdot \underline{\underline{I}}]$

(2.1)

és az alakváltozásra felírva

$\underline{\underline{ε}} = \frac{1 + ν}{E} [\underline{\underline{σ}} - \frac{ν}{1 + ν} \cdot σ_{I} \cdot \underline{\underline{I}}]$

(2.2)

Ahol:

$\underline{\underline{σ}}$ – a feszültségtenzor,

$\underline{\underline{ε}}$ – alakváltozási tenzor,

σ _I , ε _I – a megfelelő tenzorok első skalár invariánsa, (a főátló összege),

E – rugalmassági, (Young) modulus,

ν – Poisson-tényező,

$\underline{\underline{I}}$ – egységmátrix.

A Poisson-tényezővel adjuk meg az anyag keresztirányú alakváltozásának mértékét. A Poisson-tényező a terhelés irányára merőleges (ε_k) és azzal párhuzamos irányú fajlagos nyúlások arányát adja meg, (ν=−ε_k/ε=−ε₂₂/ε₁₁=−ε₃₃/ε₁₁). Elméleti értéke −1 és 0,5 között lehet. A 0 értéknél a terhelés hatására nincs keresztirányú méretváltozás, a negatív előjel pedig azokra az anyagokra jellemző, melyek keresztirányú nyúlása a terhelés irányába esővel azonos értelmű (pl. egyes speciális szerkezetű habok mutatják ezt viselkedést). Összenyomhatatlan anyagok esetében, amikor a deformáció hatására nem történik térfogatváltozás, csak alaktorzulás, a Poisson tényező elméleti értéke 0,5 (ezt a közelíti az elasztomerek viselkedése, a valóságban 0,49 körüli értékkel, és ilyen az emberi szervezetben lévő lágy szövetek Poisson-tényezője is [21.] ).

A nyírási modulus (Shear modulus) a tiszta nyírás (τ=σ₁₂=σ₂₁) és a hatására létrejött alaktorzulás kapcsolatát adja meg (G=τ/γ₁₂=σ₁₂/2ε₁₂). Kifejezhető a rugalmassági modulus és a Poisson-tényező segítségével(E=2G(1+ν)), ezért megadása opcionális, kiváltható vele valamelyik fenti paraméter megadása. Értéke mindig pozitív és megegyezik a második Lamé állandóval (G=µ).

A térfogat-változási modulus (Bulk modulus) a hidrosztatikus nyomás (p=σ₁₁=σ₂₂=σ₃₃=σ_I/3) hatására bekövetkezett térfogatváltozás kapcsolatát adja meg (K=p/ε_I). Ahol ε_I az alakváltozási invariáns. Kifejezhető a rugalmassági modulus és a Poisson-tényező segítségével (E=3K(1-2ν)), ezért megadása opcionális, kiváltható vele valamelyik fenti paraméter megadása. Értéke mindig pozitív.

Ha az anyagmodell izotróp akkor a fenti anyagparaméterekből elég kettőt megadni (pl. rugalmassági modulust és a Poisson tényezőt) a többi ezek lineáris kombinációjaként számítható.

További anyagállandók, az ellenállási modulus (M), és a Lamé állandók (λ, µ) leírását lásd a felhasznált irodalomban [21.] .

Ortotróp anyag esetén a rugalmassági modulus, a Poisson-tényező és a nyírási modulus együttes megadása szükséges a szimuláció dimenziója szerinti tengelyek mentén.

(3D-s szimuláció esetén: E_X, E_Y, E_Z, ν_XY, ν_YZ, ν_XZ, G_XY, G_YZ, G_XZ;

Tengelyszimmetrikus esetben, ha a tengelyek jelölése radiális (R), axiális (Z), és tangenciális irányban (θ), ekkor az anyag paraméterei: E_X = E_R, E_Y = E_Z, E_Z = E_θ. Oszlop-normalizált esetben (column-normalized) ν_XY = ν_RZ, ν_YZ = ν_Zθ = (E_θ/E_Z) ν_θZ, ν_XZ = ν_Rθ. Sor-normalizált esetben (row-normalized) ν_XY = (E_Z/E_R)ν_RZ, ν_YZ=(E_θ/E_Z)ν_θZ, ν_XZ=(E_θ/E_R)ν_Rθ.

2D-s szimuláció, pl. sík alakváltozás esetén: E_X, E_Y, ν_XY, G_XY;

Anizotróp anyag esetén a rugalmassági együttható mátrixot (elastic coefficient matrix, $\underline{\underline{D}}$ ) kell definiálni, mely ebben az esetben 36 ill. az ideálisan rugalmas anyagban tárolt energia reverzibilitásának figyelembevételével 21 független paraméter megadását jelenti.

Az anyagok mechanikai tulajdonságai a hőmérséklet függvényében változnak, melyek megadására különböző hőmérsékleti szinteken lehetséges a végeselemes szoftverekben. A hőmérsékletfüggő anyagmodell lineárisnak tekinthető, amennyiben a szimuláció konstans hőmérsékleten zajlik, de nemlineáris probléma megoldásról beszélhetünk ugyanakkor, ha hőtani szimulációt folytatunk ugyanezzel az anyaggal [24.] , [21.] , [25.] , [26.] .

2.4.3.3. Viszkoelasztikus anyagmodellek (Viscoelastic Material Model)

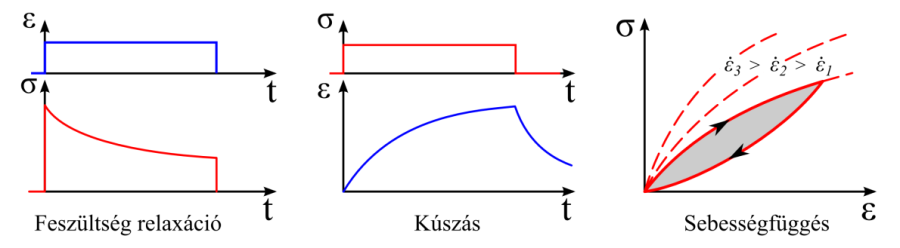
A viszkoelasztikus anyagokat jellemző jelenségek az állandó alakváltozás alatt bekövetkező feszültségrelaxáció, az állandó feszültség alatt bekövetkező kúszás, a feszültség – nyúlás karakterisztika sebességfüggése és a hiszterézis.

2.17. ábra - A viszkoelasztikus anyagokat jellemző jelenségek az állandó alakváltozás alatt bekövetkező feszültségrelaxáció, az állandó feszültség alatt bekövetkező kúszás, a feszültség – nyúlás karakterisztika sebességfüggése és a hiszterézis.

A viszkoelasztikus anyagok jellemzője, hogy a terhelés hatására az anyag válasza függ az eltelt időtől és a terhelés sebességétől. Ugrásszerűen ráadott majd állandó értéken tartott erőterhelésre az anyag időben egyre növekvő deformációval válaszol, vagyis kúszik (Creep). Ha ugrásszerűen ráadott időben állandó deformációt kényszerítünk az anyagra, akkor a reakcióerő értéke időben csökken, vagyis a feszültség relaxál (Stress relaxation). Időben változó terhelés a terhelés sebességével arányos választ produkál. Ezt a viselkedést elasztikus (rugalmas) és viszkózus elemek kombinációjával modellezzük (2.16. ábra, a, b). A modell rugalmas eleme (Hook-test) a deformáció során energiát tárol, viselkedése sebességfüggetlen és a mechanikai terhelés megszűnésével az anyag visszanyeri eredeti alakját. A viszkózus eleme (Newton-test) a deformáció folyamán energiát disszipál, viselkedése sebességfüggő és a terhelés hatására maradó deformációt okoz. Ezek különböző kombinációjaként előálló viszkoelasztikus anyagmodellek deformációját pillanatnyi rugalmas (ε_r), késleltetett rugalmas (ε_k) és maradó (plasztikus) (ε_m) alakváltozásra bonthatjuk.

A viszkoelasztikus viselkedés a polimerek jellemző tulajdonsága, de a gyakorlatban az anyagok nagy része mutat viszkoelasztikus tulajdonságot, mint az üvegszerű anyagok, a talaj, a biológiai szövetek és a textilek.

2.4.3.3.1. A leggyakrabban alkalmazott viszkoelasztikus anyagmodellek

Kis alakváltozások leírására az alábbi rugók és csillapítások segítségével felépített lineáris modelleket használják [27.] , [28.]

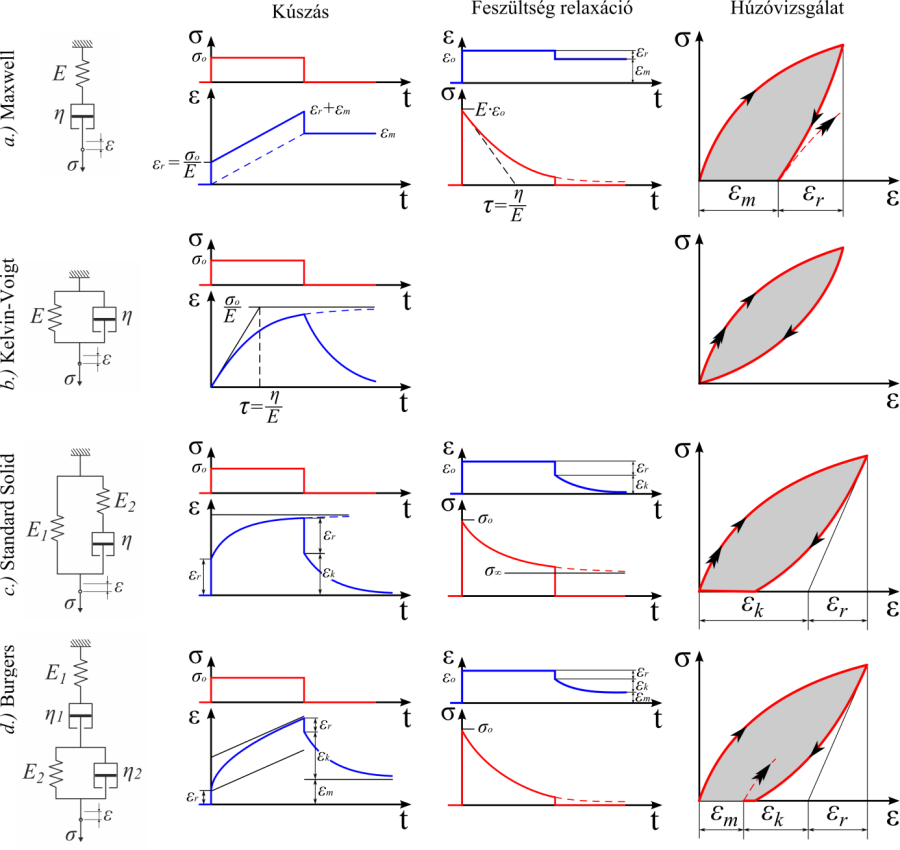
2.4.3.3.2. Maxwell modell

Rugó és csillapítás soros kapcsolása az un. Maxwell modell, mely a feszültségrelaxáció modellezésére szolgál (2.18. ábra, a.). Ugrásszerűen ráadott elmozdulás hatására a rugóelem szintén ugrásszerűen azonnal deformálódik, és a benne ébredő kezdeti feszültség σ₀=E·ε₀. A rugó által tárolt energiát a csillapító elem disszipálja így a Maxwell elemben ébredő feszültség idővel csökken vagyis relaxál, értéke 0-hoz konvergál. Ugrásszerűen ráadott feszültség (erő) gerjesztésre a rugóelem azonnali és a csillapító elem időben lineárisan növekvő deformációjával válaszol.

A Maxwell modellt leíró differenciálegyenlet:

$\dot{ε} = \frac{\dot{σ}}{E} + \frac{σ}{η}$

(2.3)

2.4.3.3.3. Kelvin-Voigt modell

A Kelvin-Voigt modell párhuzamosan kapcsolt rugó és csillapító elemből áll. A késleltetett rugalmas deformációkomponens vagyis egy véges értékű kúszás modellezésére szolgál (2.18. ábra, b.). Ugrásszerűen ráadott feszültségterhelés hatására a nyúlás időben fokozatosan növekszik és a végtelenben a rugó merevsége által definiált értékhez konvergál, ε_∞=σ₀/E. A terhelés megszüntetésével a deformáció idővel csökken, értéke 0-hoz konvergál (az eredeti alakot veszi fel), miközben a rugó által felhalmozott energiát a csillapítóelem disszipálja. A Kelvin-Voigt modell ugrásszerű deformációval való vizsgálata nem értelmezhető, mivel ekkor végtelen nagy feszültség ébredne.

A Kelvin-Voigt modellt leíró differenciálegyenlet:

$σ = E \cdot ε + η \cdot \dot{ε}$

(2.4)

2.4.3.3.4. Standard-Solid modell

A Standard-Solid modell egy párhuzamosan kapcsolt rugó és Maxwell elemből áll (2.18. ábra, c.). Ezzel a modellel már modellezhető a viszkoelasztikus anyagok pillanatnyi rugalmas (ε_r), késleltetett rugalmas (ε_k) alakváltozása. Mivel az elasztomerek esetén a maradó deformációkomponens általában elhanyagolható mértékű, ezért előszeretettel alkalmazzák modellezésükre a Standard-Solid modellt.

Ugrásszerűen ráadott feszültségterhelés hatására egy azonnal bekövetkező rugalmas (ε_r), és időben fokozatosan növekvő késleltetett (ε_k) alakváltozással válaszol. A végtelenben a Maxwell testel párhuzamos rugó merevsége által definiált értékhez konvergál, (ε_∞=σ₀/E₁). A terhelés megszüntetésével a deformáció idővel csökken, értéke 0-hoz konvergál (az eredeti alakot veszi fel).

Ugrásszerűen ráadott elmozdulás hatására a rugóelemek szintén ugrásszerűen azonnal deformálódnak, a kezdeti feszültség így σ₀=(E₁+E₂)·ε₀. A Maxwell tag rugója által tárolt energiát a csillapító elem disszipálja tehát a Maxwell elemben ébredő feszültség idővel 0-hoz konvergál, így a teljes modellben a feszültség a párhuzamosan kapcsolt rugó merevsége által meghatározott szinthez közelít (σ_∞=E₁·ε₀).

A Standard-Solid modellt leíró differenciálegyenlet:

$\dot{ε} (\frac{E_{1}}{E_{2}} + 1) + ε \cdot \frac{E_{1}}{η} = \dot{σ} \frac{1}{E_{2}} + σ \frac{1}{η}$

(2.5)

2.4.3.3.5. Burgers modell

A Burgers modell egy sorosan kapcsolt Kelvin-Voigt és Maxwell elemből áll (2.18. ábra, d.). Ezzel a viszkoelasztikus anyagok pillanatnyi rugalmas (ε_r), késleltetett rugalmas (ε_k) és maradó (plasztikus) (ε_m) alakváltozás egyidejű jelenléte is modellezhető (termoplasztikus polimerekre jellemző viselkedés).

Ugrásszerűen ráadott feszültségterhelés hatására egy azonnal bekövetkező rugalmas (ε_r), és időben fokozatosan növekvő késleltetett (ε_k) és maradó (ε_m) alakváltozással válaszol, ami az idő múlásával a végtelenbe tartó deformációt jelent. A terhelés megszüntetésével a deformáció idővel csökken, de a maradó alakváltozás miatt értéke nem éri el a 0-át.

Ugrásszerűen ráadott elmozdulás hatására a sorosan kapcsolt Maxwell elem, (pontosabban annak csillapítás eleme) miatt a feszültség 0-hoz konvergál.

A Burgers modellt leíró differenciálegyenlet:

$\ddot{ε} \frac{η_{1} \cdot η_{2}}{E_{2}} + \dot{ε} \cdot η_{1} = \ddot{σ} \frac{η_{1} \cdot η_{2}}{E_{2} \cdot E_{2}} + \dot{σ} (\frac{η_{1} + η_{2}}{E_{2}} + \frac{η_{1}}{E_{1}}) + σ$

(2.6)

2.18. ábra - Viszkoelasztikus anyagmodellek és válaszfüggvényeik.

2.4.3.3.6. Általánosított modellek

A fenti modellek alkalmasak a viszkoelasztikus anyagok viselkedésének minőségi leírására, de mennyiségi szempontból nem megfelelőek, mivel csak durván közelítik az anyag időbeli viselkedését. A kúszás és a feszültségrelaxáció időbeli lefutásának pontos időbeli leírására az általánosított modellek szolgálnak (2.19. ábra). A kúszás leírására az Általánosított Kelvin-Voigt modellt (sorba kötött Kelvin-Voigt elemek), a feszültségrelaxáció leírására pedig az Általánosított Maxwell modellt (Párhuzamosan kapcsolt Maxwell elemek) használják. A továbbiakban ez utóbbi lesz érdekes számunkra mivel a végeselem programok többnyire ezt alkalmazzák a viszkoelasztikus anyagtulajdonságok modellezésére. Az összetett modelleke (azok időbeli viselkedését) nem csak egy időállandó (τ = E/η) jellemzi, hanem a modellt alkotó elemek számának megfelelő számú.

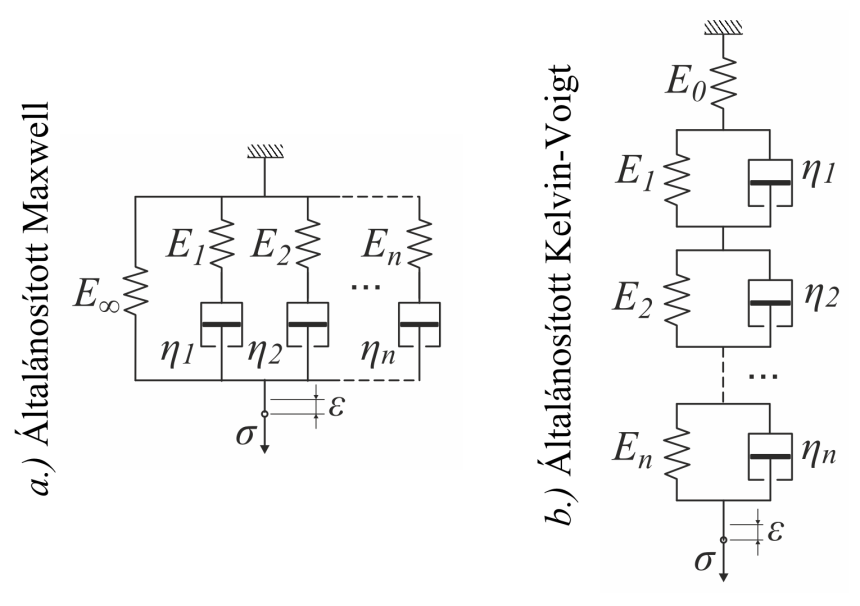
2.19. ábra - Általánosított modellek.

2.4.3.3.7. A viszkoelasztikus modellek VEM-es alkalmazása

Kis deformációk esetén az általánosított Maxwell modellel írhatjuk le az anyag viselkedését.
Nagy alakváltozás esetére az általánosított Maxwell modell, egy hiperelasztikus modellel kiegészített (a rugók helyett) változatát használjuk.

A feszültségállapot leírására az alábbi egyenletet használjuk

$\underline{\underline{σ}} = \int_{0}^{t} 2 G (t - τ) \frac{\partial {\underline{\underline{ε}}}_{d}}{\partial τ} d τ + \underline{\underline{I}} \int_{0}^{t} K (t - τ) \frac{\partial ε_{v}}{\partial τ} d τ$

(2.7)

Ahol:

$\underline{\underline{σ}}$ = Cauchy feszültség (Cauchy stress),

${\underline{\underline{ε}}}_{d}$ = Az alakváltozás deviátoros (vagy alaktorzító) része (deviatoric part of the strain),

ε _v = Az alakváltozás hidrosztatikus (vagy gömbi) része (volumetric part of the strain),

G(t) = A nyíró modulus relaxációs függvénye (shear relaxation function),

K(t) = A térfogat-változási modulus relaxációs függvénye (bulk relaxation function),

t = jelen időpillanat (current time),

τ = az elmult idő (past time),

$\underline{\underline{I}}$ = egységtenzor (unit tensor),

A relaxációs függvények az általánosított Maxwell modellel történő leírásához a modulusok Prony sorát használjuk. A nyíró és térfogat-változási moduluszok egymástól függetlenül megadhatók.

	$G (t) = G_{\infty} + \sum_{i = 1}^{N_{G}} G_{i} \cdot e^{- t / τ_{i}^{G}}$	(2.8)
	$K (t) = K_{\infty} + \sum_{i = 1}^{N_{k}} K_{i} \cdot e^{- t / τ_{i}^{K}}$	(2.9)

Ahol:

G _∞ – A teljesen relaxált anyag nyírómodulusa (t = ∞)

K _∞ – A teljesen relaxált anyag térfogat-változási modulusa (t = ∞)

	$G_{0} = G_{\infty} + \sum_{i = 1}^{N_{G}} G_{i}$	(2.10)
	$K_{0} = K_{\infty} + \sum_{i = 1}^{N_{k}} K_{i}$	(2.11)

Ahol:

G ₀ = E / 2(1+ν) – A kezdeti nyírómodulus (t = 0)

K ₀ = E / 3(1-2ν) – A kezdeti térfogat-változási modulus (t = 0)

Alkalmazva a g_i = G_i/G₀ és a k_i = K_i/K₀ relatív modulusokat, az alábbi formában írhatjuk fel

	$G (t) = G_{0} (g_{\infty} + \sum_{i = 1}^{N_{G}} g_{i} \cdot e^{- t / τ_{i}^{G}})$	(2.12)
	$K (t) = K_{0} (k_{\infty} + \sum_{i = 1}^{N_{K}} k_{i} \cdot e^{- t / τ_{i}^{K}})$	(2.13)

Így az anyagmodell merevsége csak egy paraméter a kezdeti modulus megadásával megváltoztatható, skálázható. Ezzel az anyagmodell definiálásához az időbeli viselkedést leíró k_i vagy g_i és a hozzájuk tartozó relaxációs idő τ_i mellett meg kell adnunk a merevségi tulajdonságokat leíró paramétereket is. (pl. lineárisan rugalmas anyag esetén a nyíró (G) és térfogat-változási (K) modulust vagy a rugalmassági modulust (E) és a Poisson-tényezőt (ν), ill. nagy deformációk esetén alkalmazott hiperelasztikus anyagmodell esetén pedig a megfelelő (C_ij, d, stb.) konstansokat).

Mivel a k és g konstansok relatív értékek összegük nem haladhatja meg az 1,0-et. A k_∞ és g_∞konstansok határozzák meg az anyag merevségét végtelen idő elteltével. Értéküket nem kell közvetlenül megadni ugyanis a k_∞ + Σk_i =1 és g_∞ + Σg_i =1 összefüggések szerint számolódik. Ezek szerint, ha Σk_i ill. Σg_i egyenlő 1,0-el, akkor az anyag merevsége „végtelen” idő elteltével 0-ra csökken [29.] , [6.] , [11.] .

2.4.3.3.8. A viszkoelasztikus anyagok hőmérsékletfüggése

A viszkoelasztikus anyagok lényeges tulajdonsága a hőmérsékletfüggés. Jellemzően a hőmérséklet emelkedésével csökken az anyag merevsége, vagyis a relaxáció gyorsabbá válik. A különböző hőmérsékleten felvett merevségi görbék között az eltolási (Shift) függvények teremtenek kapcsolatot. Ez lehetővé teszi, hogy csak egy hőmérsékletfüggő Proni sorral megadott relaxációs görbével definiáljuk az anyag idő és hőmérsékletfüggő viselkedését.

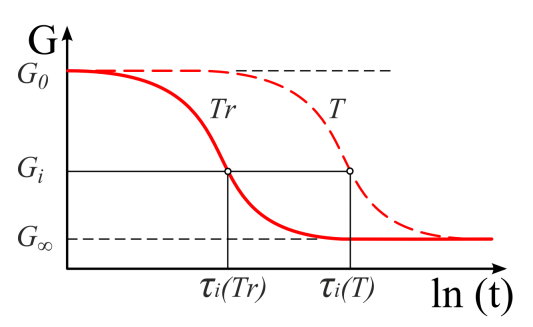
2.20. ábra - Az eltolási függvények értelmezése.

Az eltolási függvény a merevségi görbét az időtengellyel párhuzamosan tolja el. A leggyakrabban alkalmazott eltolási függvény a William-Landel-Ferry (WLF)

$l o g A (T (τ)) = \frac{c_{1} (T - T_{r})}{c_{2} + T - T_{r}}$

(2.14)

és a Tool-Narayanaswamy (TN)

$l n A (T (τ)) = d_{1} (\frac{1}{T_{r}} - \frac{1}{T})$

(2.15)

Ahol:

T _r – a referencia hőmérséklet,

τ – a látszólagos idő (pseudo time),

c ₁ , c ₂ , d ₁ – anyagállandók.

2.4.3.4. Sebességfüggetlen plasztikus anyagmodellek (rate-independent plasticity)

Az elasztoplasztikus modellek az anyag irreverzibilis viselkedését modellezi egy bizonyos feszültségérték elérése után. A képlékeny alakváltozás jellemzője, hogy azonnal végbemegy, vagyis a modell viselkedése az időtől független, irreverzibilis (maradó alakváltozás) és útfüggő (függ a terhelési előélettől). A sebességfüggetlen képlékeny anyagmodellek elméletnek két lényeges eleme van, a folyási feltétel (yield criterion) és a felkeményedési szabály (hardening rule).

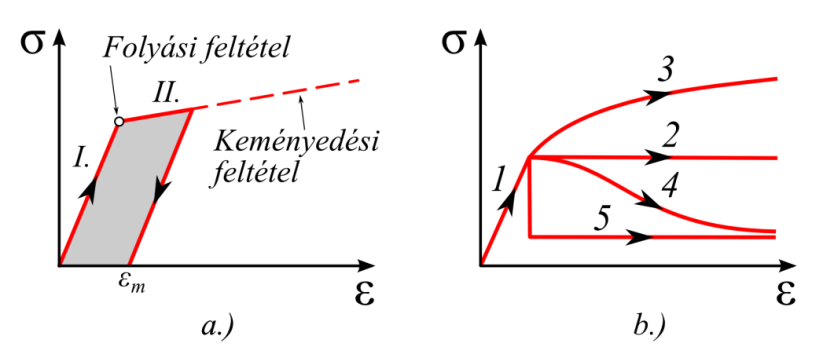
(a.) Lineáris elasztoplasztikus modell főbb részei I.) Lineárisan rugalmas szakasz, II.) folyási szakasz. (b.) Az elasztoplasztikus modellek főbb típusai: 2.) ideálisan képlékeny, 3.) nemlineárisan felkeményedő, 4.) nemlineárisan lágyuló, 5.) ridegen lágyuló.

2.21. ábra - (a.) Lineáris elasztoplasztikus modell főbb részei I.) Lineárisan rugalmas szakasz, II.) folyási szakasz. (b.) Az elasztoplasztikus modellek főbb típusai: 2.) ideálisan képlékeny, 3.) nemlineárisan felkeményedő, 4.) nemlineárisan lágyuló, 5.) ridegen lágyuló.

2.4.3.4.1. A folyási feltétel

A folyási feltétel azt a feszültségszintet (σ_y) jelenti, melynél az anyag elkezdi a plasztikus alakváltozást, ez alatt viselkedése rugalmas. Értéke többtengelyű feszültségi állapot esetén a feszültségi vektor függvénye, melyet a folyási felületdiagram segítségével ábrázolunk. A folyási felületen belüli feszültségi állapot rugalmas alakváltozáshoz tartozik, a felületen következik be a plasztikus deformáció.

Homogén és izotróp anyag esetén, amennyiben a hidrosztatikus hatás elhanyagolható (a legtöbb fém ilyen) a folyási felület a hidrosztatikus egyenessel meghatározott vezérgörbéjű mindkét végén nyitott felület. Ha a hidrosztatikus hatás nem hagyható el (Kőzetek, talaj, beton, stb.) a folyási felület legalább egyik végén zárt.

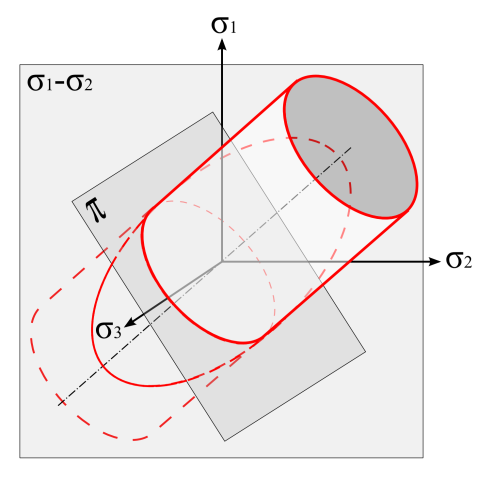
A henger alakú (HMH) folyási felület metszete a fősíkokkal (σ ₁ -σ ₂ ) ellipszis, a deviátoros síkkal (π) kör alakú.

2.22. ábra - A folyási felület értelmezése.

A Huber-Mises-Hencky modellben a felület egy mindkét végén nyitott henger, melynek metszetei a deviátoros síkon kört, az egyes főfeszültségi síkokon ellipsziseket alkotnak. A fémek, kompozitok és lágy polimerek esetében leggyakrabban használt modell.
A Tresca féle modellt melyben a folyási felület egy hatszög alapú palástfelület, lágyabb fémek (pl. alumínium, rézötvözetek) még ma is alkalmazzák.
A Rankine modell geometriai megjelenése a főfeszültségi térben a hidrosztatikai hatás figyelembevételére is alkalmas, egyik csúcsa felől zárt téglatest felület. Az eredetileg talajok képlékenységi felületeként megadott modell ma inkább rideg anyagok törési feltételeként alkalmazzák.
A Mohr-Coulomb szintén figyelembe veszi a hidrosztatikus hatásokat. A felület egyik végén zárt hatoldalú gúla. A talajmechanika leírásokra előszeretettel alkalmazott.
A Prager-Drucker -modell a Huber-Mises-Hencky modell hidrosztatikai hatást is figyelembe vevő általánosításának tekinthető. A folyási felület alakja a főfeszültségi térben a húzás irányában zárt kúp.

Általános anizotróp modellt a mérési nehézségek miatt nem hoztak létre, hanem több olyan modell is van, amely valamely izotróp modell ortotróppá általánosításával kaptak, (pl.: Mises-Hill és a Kubik - Mielniczuk modell (HMH-feltétel kiterjesztése), Sawczuk - Iwlin (Tresca-feltétel általánosítása).

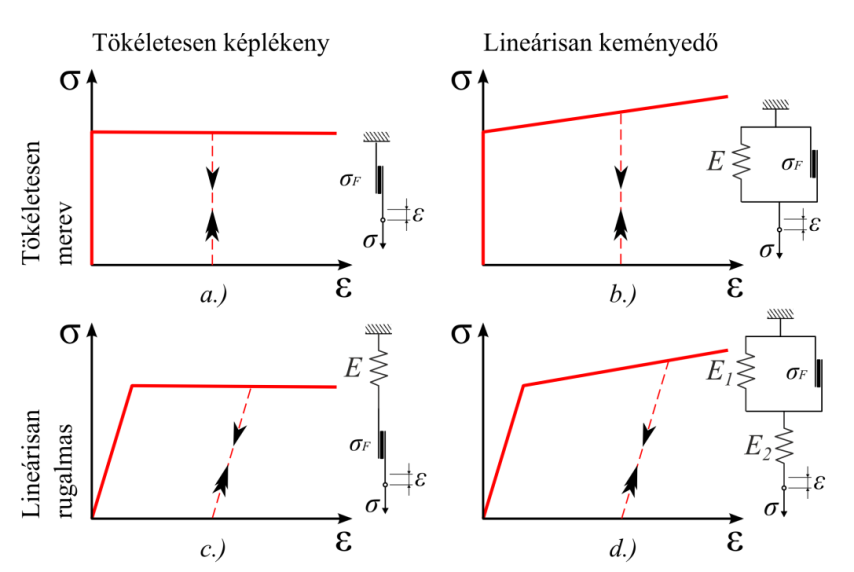
2.23. ábra - Lineáris tagokból álló egyszerű elasztoplasztikus modellek.

2.4.3.4.2. Keményedési szabály (hardening rule).

Abban az esetben, amikor a képlékenységi szakaszba lépő anyag alakváltozása a feszültség további növelése nélkül folytatódik, tökéletesen képlékeny alakváltozásnak nevezzük. Ez a modell egy erősen leegyszerűsített modellje a képlékeny anyagok valós viselkedésének. Ha a képlékeny alakváltozás szakaszában csak a feszültség további növelésével folytatódik az alakváltozás, felkeményedő anyagokról beszélünk. Tökéletesen képlékeny anyag esetén a folyási felület a feszültségi térben fix, míg felkeményedő anyagnál elmozdulhat, és/vagy az alakját változtathatja. Ezek alapján a keményedést leíró modell lehet:

izotróp (a folyási felület alakja nem, csak mérete változik minden irányban arányosan),
kinematikus (a folyási felület mérete nem, csak a helyzete változik), vagy
vegyes (a valóságot jobban modellező kombinációk, pl. izotróp-kinematikus, lokálisan változó alakú, stb.).

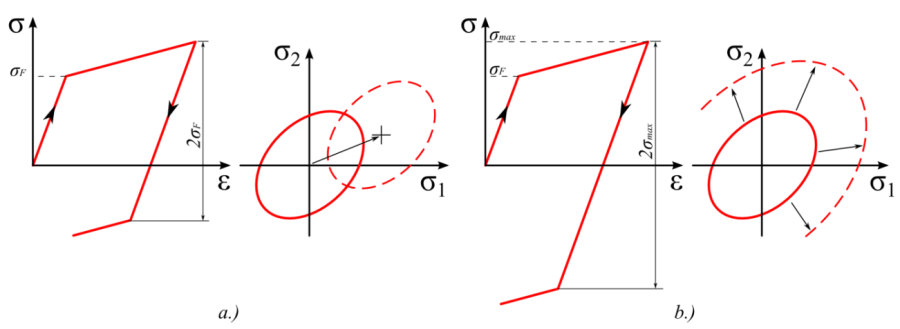
A kinematikus (a.) és izotróp (b.) keményedésű elasztoplasztikus anyagok feszültség-nyúlás jelleggörbéje és a folyási felület megváltozásának módja.

2.24. ábra - A kinematikus (a.) és izotróp (b.) keményedésű elasztoplasztikus anyagok feszültség-nyúlás jelleggörbéje és a folyási felület megváltozásának módja.

2.4.3.5. Viszkoplasztikus anyagmodellek

A viszkoplasztikus anyagmodellek a képlékeny anyagok sebességfüggő rugalmatlan viselkedését írják le. Ami azt jelenti, hogy az anyagban ébredő feszültség az alakváltozási sebesség függvénye. Az anyagmodell egy ideálisan képlékeny (St. Venant-test), és egy ideálisan viszkózus tagból (Newton-test) áll. A viszkózus elemnek köszönhetően a feszültség az alakváltozás sebességével arányos, de az alakváltozás csak egy bizonyos határfeszültség elérése után indul meg (σ_F) a plasztikus elem jóvoltából. A fő különbség a sebességfüggetlen plasztikus vagy elasztoplasztikus és a viszkoplasztikus anyagok között, hogy ez utóbbi alakváltozása nem csak maradó alakváltozást mutat, hanem a deformáció az idő elteltével folytatódik a terhelés alkalmazása után is, vagyis kúszik. Főként a rugalmatlan fémek (mint pl. a forrasztóón, ólom), kerámia szuszpenziók, Zagyok, paszták leírására alkalmazzák. [30.] , [23.] .

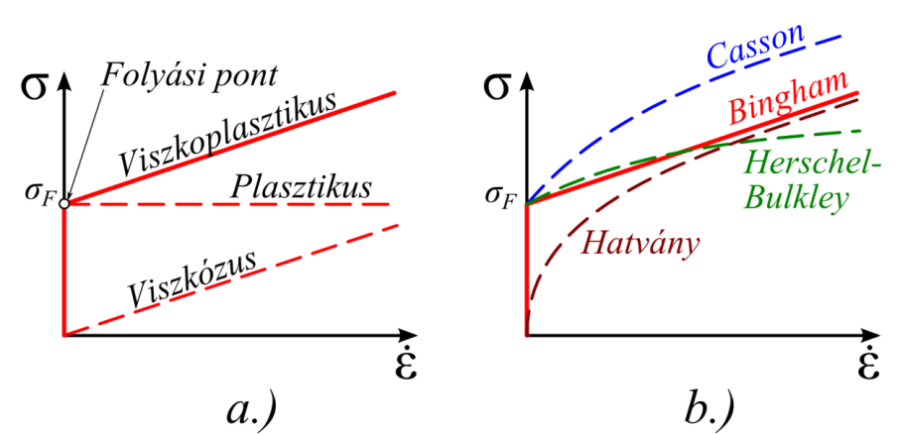
A viszkoplasztikus, az ideálisan viszkózus (Newtoni) és az ideálisan képlékeny (St. Venant) modellek Feszültség - alakváltozási sebesség karakterisztikája (a.). A legismertebb viszkoplasztikus anyagmodellek (b.).

2.25. ábra - A viszkoplasztikus, az ideálisan viszkózus (Newtoni) és az ideálisan képlékeny (St. Venant) modellek Feszültség - alakváltozási sebesség karakterisztikája (a.). A legismertebb viszkoplasztikus anyagmodellek (b.).

2.4.3.5.1. Bingham modell

A viszkoplasztikus anyagok jellemzésére szolgáló egyik legismertebb anyagmodell.

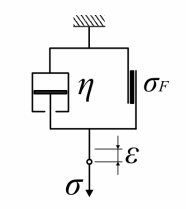
2.26. ábra - Bingham modell - párhuzamosan kapcsolt viszkózus és súrlódó elem.

A Bingham modellt leíró differenciálegyenlet:

$σ = σ_{F} + η \cdot \dot{ε}$

(2.16)

Ahol:

η – viszkozitás,

σ _F – a folyási feszültség,

ֹ ε – az alakváltozási sebesség.

2.4.3.5.2. Herschel-Bulkley modell

	$σ = σ_{F} + K \cdot {\dot{ε}}^{n}$	(2.17)
	$\frac{d σ}{d \dot{ε}} = n \cdot K \cdot ε^{(n - 1)}$	(2.18)

Ahol:

K – a látszólagos viszkozitás,

n – a folyási szám. n=1 estén a Bingham modellt kapjuk, n<1 esetén a feszültség degresszív növekedését, (szerkezeti viszkózus; nyírásra vékonyodó - shear thinning) és n>1 esetén a feszültség progresszív növekedését (dilatáns; nyírásra vastagodó - shear thickening) eredményezi.

A nyíró-határfeszültség elhanyagolásával az Ostwald-de Waele hatványtörvényhez jutunk.

2.4.3.5.3. Hatványtörvény, (Ostwald-de Waele egyenlet)

$σ^{m} = \frac{\dot{ε}}{Φ}$

(2.19)

Ahol:

m és Φ – anyagi függvények, Φ(T) a „fluiditás” hőmérsékletfüggő.

A fluiditás helyett gyakran alkalmazzák a K konzisztencia faktort, K = Φ ^-1/m .

2.4.3.5.4. Casson

$\sqrt{σ} = \sqrt{σ_{F}} + \sqrt{η \cdot \dot{ε}}$

(2.20)

[31.] .

2.4.3.5.5. Módosított Bingham,

A lineáris Bingham modell egy másodrendű taggal kiegészített változata.

$σ = σ_{F} + η \cdot \dot{ε} + c \cdot {\dot{ε}}^{2}$

(2.21)

Ahol:

c – a nemlineáris viselkedést befolyásoló állandó, c/η=0 estén a lineáris Bingham modellt kapjuk, c/η<0 esetén a feszültség degresszív növekedését (szerkezeti viszkózus; nyírásra vékonyodó – shear thinning) és c/η>0 esetén a feszültség progresszív növekedését, (dilatáns; nyírásra vastagodó – shear thickening) eredményezi.

2.4.3.5.6. Perzyna

$\dot{\hat{ε}} = η {(\frac{σ}{σ_{F}} - 1)}^{\frac{1}{m}}$

(2.22)

2.4.3.5.7. Peirce

$\dot{\hat{ε}} = η [{(\frac{σ}{σ_{F}})}^{\frac{1}{m}} - 1]$

(2.23)

2.4.3.5.8. EVH (Exponential visco-hardening)

Az exponenciálisan viszkoelasztikus keményedő (EVH) modell lehetőséget ad nemlineáris kinematikai keményedésre a von Mises vagy Hill plaszticitás alkalmazásával.

	$\dot{ε} = η {(\frac{σ - σ_{F}}{K})}^{\frac{1}{m}}$	(2.24)
	${\bar{σ}}_{F} = K_{0} + R_{0} \cdot \bar{ε} + R_{\infty} (1 - e^{- b \cdot \bar{ε}})$	(2.25)

Ahol:

Ko, Ro, R _∞ , b – alakváltozás-keményedési (strain hardening) paraméter,

m – alakváltozási sebesség-keményedési (strain rate hardening) anyagparaméter,

K – viszkozitási (viscosity) paraméter.

2.4.3.5.9. Anand

Az Anand plasztikus modell egy teljes értékű anyagmodell, amely nem igényli más anyagmodellekkel való kombinálását. Fémek képlékenyalakításának modellezésére hozták létre. A magas hőmérsékleten fémek fizikai viselkedése nagyban függ az alakítás sebességétől, a hőmérséklettől, az alakváltozás sebességi és hőmérsékleti előélettől, és az alakváltozási keményedéstől vagy lágyulástól. Mindezen tulajdonságokat figyelembe veszi az Anand viszkoplasztikus anyagmodell.

$\underline{\underline{\dot{ε}}} = \dot{\hat{ε}} (\frac{3}{2} \cdot \frac{\underline{\underline{S}}}{q})$

(2.26)

Ahol:

ֹ << eqn0033.wmf >> - az alakváltozási sebesség tenzor,

ε ֹ ˆ - a halmozott egyenértékű fajlagos nyúlás sebessége

S – a Cauchy feszültségtenzor deviátoros része,

q – egyenértékű feszültség.

[6.] , [32.] , [31.] , [23.] .

2.4.3.6. Összetett reológia anyagmodellek

A fenti kétkomponensű modellek mellett, az anyagok valós fizikai viselkedésének leírására számos összetett, mindhárom reológiai alaptestet (rugalmas, viszkózus, súrlódó) tartalmazó modellt alkottak. Dinamikai vizsgálatok leírásához ezek kiegészülnek a „tömeg-elemmel”, amely az anyag tehetetlenségét hivatott modellezni. A végeselemes anyagmodellben ez az anyag sűrűségének (fajsúly) megadásával kerül definiálásra. A teljesség igénye nélkül néhány összetett reológiai modell:

Kiterjesztett Bingham,
3 elemű modell,
BingMax modell,
Bouc-Wen modell.

[33.]

2.4.3.7. Hiperelasztikus anyagmodellek

A hiperelasztikus anyagmodell (Hyperelastic Material Model) viselkedését az alkváltozási-energia sűrűség, vagyis az egységnyi térfogatú deformált anyagban tárolt potenciális energia alapján írja le. A matematikai megfogalmazás lehetővé teszi a nagy alakváltozásokat. A hiperelasztikus, vagy Green féle anyagmodelleket gyakran használják olyan anyagok esetében, amelyek nagyrugalmas alakváltozásnak vannak kitéve, mint a gumiszerű anyagok és egyes biológiai szövetek.

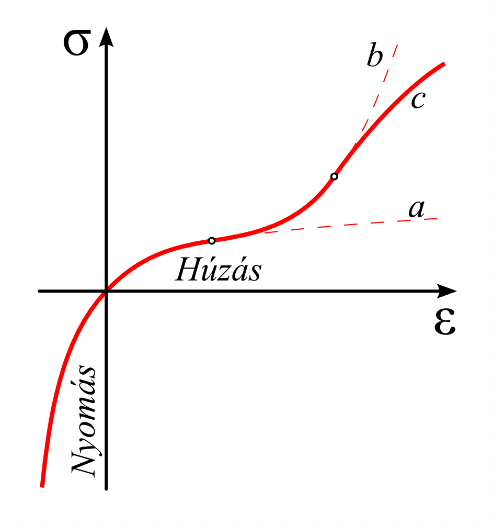
Hiperelasztikus anyagok jellemző feszültség-nyúlás karakterisztikája. 0 (a.), 1 (b.) ill. 2 inflexiós ponttal rendelkező húzókarakterisztika (c.).

2.27. ábra - Hiperelasztikus anyagok jellemző feszültség-nyúlás karakterisztikája. 0 (a.), 1 (b.) ill. 2 inflexiós ponttal rendelkező húzókarakterisztika (c.).

A gumiszerű anyagokra jellemző

a nagymértékű alakváltozási képesség, amely általában több 100% de akár 1000% fölé is emelkedhet,
a döntően rugalmas deformáció (recoverable),
erősen nemlineáris feszültség-nyúlás karakterisztika, (általában húzás esetén először lágyul, majd felkeményedik, nyomás esetén felkeményedés tapasztalható),
a deformáció során bekövetkező kis- vagy elhanyagolható mértékű térfogatváltozás (összenyomhatatlan, ν ~ 0,5.)

Az alkalmazott hiperelasztikus anyagokra nemlineárisan rugalmas, izotróp, izotermikus és teljesen, vagy közel összenyomhatatlan (térfogat-állandóságot, ν ~ 0,5) tulajdonságokat feltételezünk.

Mivel a hiperelasztikus anyagmodellek az alakváltozási energia alapján vannak felírva, ezért kielégítik a termodinamika főtételeit, reverzibilisek és útfüggetlenek. Viszont a hőmérséklet és az idő hatását nem veszik figyelembe.

$σ_{i j} = \frac{\partial Π}{\partial ε_{i j}}$

(2.27)

Ahol:

Π - az anyag egységnyi térfogatára vonatkozó alakváltozási energia, alakváltozási energiasűrűség, (strain energy per unit reference volume),

σ _ij - a Cauchy (valódi) feszültség,

ε _ij – a rugalmas alakváltozás.

A megnyúlás definíciója, az i. irányba eső főnyúlás (stretch ratio / stretch):

$λ_{i} = \frac{l}{l_{0}} = \frac{l_{0} + Δ l}{l_{0}} = ε_{i} + 1$

(2.28)

Ahol:

l ₀ – a kezdeti hossz,

l – a pillanatnyi hossz,

Δl – a hosszváltozás.

A főnyúlásokkal felírt deformációgradiens tenzor, (elastic deformation gradient tensor):

$\underline{\underline{F}} = [\begin{matrix} λ_{1} & 0 & 0 \\ 0 & λ_{2} & 0 \\ 0 & 0 & λ_{3} \end{matrix}]$

(2.29)

A jobboldali Cauchy-Green alakváltozási tenzor főnyúlások segítségével felírva:

$\underline{\underline{C}} = {\underline{\underline{F}}}^{T} \underline{\underline{F}} = [\begin{matrix} λ_{1}^{2} & 0 & 0 \\ 0 & λ_{2}^{2} & 0 \\ 0 & 0 & λ_{3}^{2} \end{matrix}]$

(2.30)

A Cauchy-Green féle alakváltozási tenzor invariánsai:

	$I_{1} = λ_{1}^{2} + λ_{2}^{2} + λ_{3}^{2}$	(2.31)
	$I_{2} = λ_{1}^{2} \cdot λ_{2}^{2} + λ_{1}^{2} \cdot λ_{3}^{2} + λ_{2}^{2} \cdot λ_{3}^{2}$	(2.32)
	$I_{3} = λ_{1}^{2} \cdot λ_{2}^{2} \cdot λ_{3}^{2}$	(2.33)

A térfogatváltozás definíciója, (a deformációgradiens tenzor determinánsa):

$J = \det (\underline{\underline{F}}) = λ_{1} \cdot λ_{2} \cdot λ_{3} = \frac{V}{V_{0}}$

(2.34)

Látható, hogy ha az anyag teljesen összenyomhatatlan, akkor I₃ = 1.

A térfogat-változási komponenst különválasztva a deviátoros nyúlás:

(i= 1, 2, 3)

${\bar{λ}}_{i} = λ_{i} \cdot J^{- \frac{1}{3}}$

(2.35)

A deviátoros alakváltozási invariáns:

${\bar{I}}_{i} = I_{i} \cdot J^{- \frac{2 i}{3}}$

(2.36)

A fenti mintára az alakváltozási energiafüggvényt deviátoros (Π_d) és a térfogat-változási (Π_V) komponensekre bonthatjuk, és ez utóbbit felírhatjuk a deformációgradiens tenzor determinánsával (J=det( $\underline{\underline{F}}$ )) segítségével.

$Π = Π_{d} (I_{1}, I_{2}) + Π_{V} (J)$

(2.37)

Izotróp anyag esetén az alakváltozási energiát az alakváltozási skalár invariánsok, vagy közvetlenül a főnyúlások segítségével írjuk fel, (melyek függetlenek a koordinátarendszer megválasztásától).

Összenyomhatatlan anyag esetében az alakváltozási munka csak deviátoros vagyis alaktorzító komponensből áll, és a három alakváltozási invariánsból csak kettő független (I₃=1). Ebben az esetben a jobboldali Cauchy-Green alakváltozási tenzorral a modell az alábbi alakban írható fel [21.] , [6.] .

$σ_{i j} = - p δ_{i j} + 2 \frac{\partial Π}{\partial I_{1}} C_{i j} - 2 \frac{\partial Π}{\partial I_{2}} C_{i j}^{- 1}$

(2.38)

Ahol:

p - a hidrosztatikus nyomás,

δ _ij - a Kronecker delta,

[21.] , [34.] , [6.] , [35.] .

A hiperelasztikus anyagmodellek néhány széles körben használatos energiafüggvényét az alábbiakban ismertetjük. Az adott modell tárgyalásánál csak fent definiáltaktól és az alábbiakban felsorolt jelölésektől eltérőt ismertetjük.

Megjegyzés: Mivel a modellek a hőmérséklet hatását nem veszik figyelembe, hőtágulással járó vizsgálat esetén a modellekben szereplő teljes deformációgradiens tenzor determinánsa (J) helyettesítésre kerül, annak hőtágulástól megtisztított rugalmas részével (J_el=J/J_th). Ahol a J_th=(1+αΔT)³;

α – a lineáris hőtágulási együttható, J_th – a referencia hőmérséklethez viszonyított hőmérsékletkülönbség.

Alkalmazott jelölések:

μ – Az anyag kezdeti nyírómodulusa (initial shear modulus),

d – az anyag összenyomhatatlanságra jellemző paraméter, 0 ha összenyomhatatlan, mivel d=2/K, ahol K – a kezdeti térfogat-változási modulus (initial bulk modulus).

2.4.3.7.1. Arruda-Boyce

Az Arruda-Boyce (vagy eight-chain) egy statisztikus mechanikára épülő modell. Főleg polimereknél használt, nyúlási korláttal (λ_L) definiált hiperelasztikus anyagmodell, amely általában 300%-os nyúlásig alkalmazható.

A Yeoh modell N=5 fokú eseteként értelmezhető a nyúlási korlát függvényekén definiált együtthatókkal. Végtelen nyúlási korlát (λ_L = ∞) esetén a Neo-Hooke modellel egyenértékű lesz.

$Π = μ [\frac{1}{2} ({\bar{I}}_{1} - 3) + \frac{1}{20 λ_{L}^{2}} ({\bar{I}}_{1}^{2} - 9) + \frac{11}{1050 λ_{L}^{4}} ({\bar{I}}_{1}^{3} - 27) + \frac{19}{7000 λ_{L}^{6}} ({\bar{I}}_{1}^{4} - 81) + \frac{519}{673750 λ_{L}^{8}} ({\bar{I}}_{1}^{5} - 243) + \frac{1}{d} (\frac{J^{2} - 1}{2} - l n J)]$

(2.39)

Ahol:

λ _L – nyúlási korlát, (melynél a feszültség felkeményedési szakaszba, vagyis határtalan növekedésbe kezd),

2.4.3.7.2. Neo-Hooke

Ez a legegyszerűbb hiperelasztikus modell mely konstans nyírómodulust használ. Viszont alkalmazhatósága 30-40%-os egytengelyű húzásig vagy 80-90%-os tiszta nyírásig terjed.

A Neo-Hooke modell egy mikromechanikai modell, ami az elasztomerek anyagszerkezeti vizsgálatán alapszik és a klasszikus Hooke anyagmodell kiterjesztését jelenti nagy deformációkra. A μ = 2·C₁₀; C₁₀ = 0 és N=1 esetén a polinomiális modell speciális eseteként áll elő. Eszerint az energiafüggvény:

$Π = \frac{1}{2} μ ({\bar{I}}_{1} - 3) + \frac{1}{d} {(J - 1)}^{2}$

(2.40)

2.4.3.7.3. Saint Venant–Kirchhoff model

A legegyszerűbb hiperelasztikus modell, amely a lineárisan rugalmas anyagmodell kiterjesztése a nagyrugalmasságú tartományba. Főleg kis alakváltozások és nagy elfordulások esetén alkalmazzuk (pl. horgászbot).

$Π (E_{i j}) = \frac{λ}{2} {(E_{k k})}^{2} + μ {(E_{k k})}^{2}$

(2.41)

Ahol:

µ és λ – a Lamé állandók.

E – Lagrange Green nyúlás

2.4.3.7.4. Mooney-Rivlin

A Mooney-Rivlin modell nagy deformációkra jó eredményt ad. A leggyakrabban 2, 3, 5, esetleg 9 paraméteres változatát használják, A kétparaméteres változat energiafüggvénye:

$Π = C_{10} ({\bar{I}}_{1} - 3) + C_{01} ({\bar{I}}_{2} - 3) + \frac{1}{d} {(J - 1)}^{2}$

(2.42)

Ahol:

C ₁₀ és C ₀₁ – anyagra jellemző konstansok, (A kezdeti nyírási modulus értéke: μ =2(C ₁₀ +C ₀₁ ).

Az anyag feszültség-nyúlás görbéjén lévő inflexiós pontok száma alapján választhatunk a megfelelő paraméterszámú anyagmodellt. A 2 paraméteres MR modell 90-100%-os nyúlásig alkalmazható. A modellnek nincs inflexiós pontja, így nem jelentkezik a felkeményedési szakasz, ezért az összenyomás modellezésére nem alkalmas (2.27. ábra, a.). Nagyobb alakváltozás modellezésére (100-200%) magasabbrendű modellek, mint az 5, ill. 9 paraméteres MR lehet alkalmas (2.27. ábra, b ill. c.).

2.4.3.7.5. Ogden

Az Ogden egy fenomenológiai megközelítésű anyagmodell, melyben közvetlenül a főnyúlások segítségével van felírva az energiafüggvény. Ebből kifolyólag pontosabb és jobban leírja a nagyobb alakváltozásokat, akár 700%-ig is.

$Π = \sum_{i = 1}^{N} \frac{μ_{i}}{α_{i}} ({\bar{λ}}_{1}^{α_{i}} + {\bar{λ}}_{2}^{α_{i}} + {\bar{λ}}_{3}^{α_{i}} - 3) + \sum_{k = 1}^{N} \frac{1}{d_{k}} {(J - 1)}^{2 k}$

(2.43)

Ahol:

α _i és μ _i – anyagjellemző konstansok, a kezdeti nyírómodulus μ ₀ = (Σ α _i μ _i )/2

N elvileg korlátlan, a gyakorlatban 3-nál nagyobb értéket nem szoktak használni.

2.4.3.7.6. Polinomiális

A polinomiális modellben az 1. és 2. alakváltozási invariáns segítségével van felírva az energiafüggvény. Általában ritkán használnak 3-nál magasabb fokú (N) polinomot.

$Π = \sum_{i + j = 1}^{N} C_{i j} {({\bar{I}}_{1} - 3)}^{i} {({\bar{I}}_{2} - 3)}^{j} + \sum_{k = 1}^{N} \frac{1}{d_{k}} {(J - 1)}^{2 k}$

(2.44)

Ahol: μ = 2(C ₁₀ +C ₀₁ ) – Az anyag kezdeti nyírómodulusa (initial shear modulus).

2.4.3.7.7. Yeoh

A Yeoh modell a polinomiális modell, csak az 1. alakváltozási invariánsra épülő, redukált változata. Közel összenyomhatatlan nemlineárisan rugalmas anyagok modellezésére alkalmazzák, pl. gumi. Általában az N=3 értékkel használatos, amivel jól modellezhetők a nagy alakváltozások.

$Π = \sum_{i = 1}^{N} C_{i 0} {({\bar{I}}_{1} - 3)}^{i} + \sum_{k = 1}^{N} \frac{1}{d_{k}} {(J - 1)}^{2 k}$

(2.45)

Ahol:

μ = 2·C ₁₀ – Az anyag kezdeti nyírómodulusa (initial shear modulus).

Gent

Mikromechanikai alapokon nyugvó (Hibrid) modell, mely az Arruda-Boyce modellhez hasonlóan a nyúlások határértékét (J_m) alkalmazza.

$Π = \frac{μ \cdot J_{m}}{2} l n (1 - \frac{{\bar{I}}_{1} - 3}{J_{m}}) + \frac{1}{d} (\frac{J^{2} - 1}{2} - l n J)$

(2.46)

Ahol:

J _m – a (I ₁ – 3) határértéke. J _m = ∞ esetén a Neo-Hooke modellel egyenértékű lesz.

2.4.3.7.8. Marlow modell

$Π = Π_{d} ({\bar{I}}_{1}) + Π_{V} (J)$

(2.47)

2.4.3.7.9. Van der Waals

$Π = μ [- (λ_{m}^{2} - 3) (l n ((1 - η) + η)) - \frac{2}{3} a {(\frac{\tilde{I} - 3}{2})}^{\frac{3}{2}}] + \frac{1}{d} (\frac{J^{2} - 1}{2} - l n J)$

(2.48)

Ahol:

	$\tilde{I} = (1 - β) {\bar{I}}_{1} - β {\bar{I}}_{2}$	(2.49)
	$η = \sqrt{\frac{\tilde{I} - 3}{λ_{m}^{2} - 3}}$	(2.50)

λ _m – záróparaméter, (nyúlási korlát),

α - globális kölcsönhatási paraméter,

β – invariáns keverési paraméter.

2.4.3.7.10. Összenyomható hiperelasztikus modellek habok modellezésére

Ezen anyagok fő tulajdonsága az előzőekkel ellentétben, hogy nagymértékben összenyomható anyagot modelleznek, ezért az energiafüggvény deviátoros és volumetrikus része között szoros összefüggés van.

Odgen habmodell (Hiperfoam)

$Π = \sum_{i = 1}^{N} \frac{μ_{i}}{α_{i}} (J^{α_{i} / 3} \cdot ({\bar{λ}}_{1}^{α_{i}} + {\bar{λ}}_{2}^{α_{i}} + {\bar{λ}}_{3}^{α_{i}}) - 3) + \sum_{k = 1}^{N} \frac{μ_{i}}{α_{i} \cdot β_{i}} (J^{α_{i} \cdot β_{i}} - 1)$

(2.51)

Ahol:

μ ₀ = (Σ α _i μ _i )/2 - az anyag kezdeti nyírási modulusa,

K =Σ α _i μ _i ((1/3)+ β _i ) - a kezdeti térfogat-változási modulus.

2.4.3.7.11. Blatz-Ko habmodell

Az összenyomható Poliuretán gumi hab modellezésére lett létrehozva.

$Π = \frac{μ}{2} (\frac{I_{2}}{I_{3}} + 2 \sqrt{I_{3}} - 5)$

(2.52)

K =µ 5/3 - a kezdeti térfogat-változási modulus.

2.4.3.7.12. Varga-modell

$Π = \frac{μ}{2} (λ_{1} + λ_{2} + λ_{3})$

(2.53)

2.4.3.7.13. További hiperelasztikus modellek biológiai szövetek modellezésére

Fung energiafüggvénye

Holzapfel modellje

2.3. táblázat - Hiperelasztikus anyagmodellek csoportosítása összefoglalása [36.] , [21.] , [37.] , (nincs adat: „-”).

	Anyagmodell	Alapja	Alkalmazás, max. ε
Összenyomhatatlan vagy közel összenyomhatatlan, (ν ~ 0,5)	Arruda-Boyce	I ₁	300 %
	Neo-Hooke	I ₁	30-40 %
	Gent	I ₁	-
	Van der Waals	I ₁ , I ₂	-
	Mooney-Rivlin	I ₁ , I ₂	MR2 = 90-100 % MR5/9 = 100-200 %
	Ogden	λ ₁ , λ ₂ , λ ₃	700 %
	Polinomiális	I ₁ , I ₂	300 %
	Yeoh	I ₁	-
	Saint Venant–Kirchhoff	µ, λ (Lamé)	kis alakváltozások és nagy elmozdulás
	Marlow	I ₁ , I ₂	-
	Fung	Q(E _ij )	érfalak vizsgálatára
	Holzapfel	$\underline{\underline{C}}, {\underline{\underline{A}}}_{1}, {\underline{\underline{A}}}_{2}$	emberi artéria vizsg.
Összenyomható (0 < ν < 0,5)	Ogden habmodell	λ ₁ , λ ₂ , λ ₃	Összenyomható habok vizsgálatára
Összenyomható (0 < ν < 0,5)	Blatz-Ko habmodell	I ₂ , I ₃	Összenyomható habok vizsgálatára

[38.] , [21.] , [6.] , [35.] .

2.4.3.8. Anyagparaméterek megadása

Mivel az anyagmodell a matematikai kapcsolatot testesíti meg a terhelés és a válasz között, szükséges a bemenő anyagparaméterek megadása, azért hogy a modell illeszkedjen az anyag valós viselkedéséhez. Egyes esetekben a paraméterek függhetnek a fizikai környezet tulajdonságaitól, úgy mint a hőmérséklet, frekvencia vagy az idő, illetve különböző mennyiségek kölcsönhatásától, mint pl. a normál nyomás, relatív távolság, vagy relatív sebesség.

2.4.3.8.1. Mechanikai anyagvizsgálati adatok

Az anyagmodellek meghatározása történhet az anyag mikroszintű vizsgálatával (mikromechanikai modell), vagy makromechanikai vizsgálatok útján (fenomenológiai modell). A jegyzetben ez utóbbiról adunk rövid áttekintést.

Példaként nézzük a mechanikai anyagmodellek létrehozásához az egyik leggyakrabban alkalmazott anyagvizsgálati eljárását, a szakítóvizsgálatot. A vizsgálat során a próbatestre állandó sebességű egytengelyű megnyúlást kényszerítünk és mérjük a fellépő reakcióerőt. Ezeket a kiinduló paraméterekkel (keresztmetszet, hossz) fajlagos mennyiségekké konvertáljuk, így kapjuk meg a szóban forgó anyag (mérnöki) feszültség-nyúlás karakterisztikáját, melyet bemenő adatként használhatunk egy anyagmodell definiálásához. Hasonló elvek szerint végezhetünk nyomó, nyíró vagy többtengelyű vizsgálatokat. Az alábbiakban nézzük meg a leggyakrabban használt anyagvizsgálati eljárásokat.

2.4.3.8.1.1. A mechanikai anyagvizsgálatok főbb típusai

A lineáris vagy lineáris szakaszokkal közelíthető (pl. ideálisan rugalmas – tökéletesen képlékeny) anyag esetén elég megadni az anyagvizsgálatból származtatott anyagjellemzőket (pl. a rugalmassági modulus és a Poisson-tényező) vagy a karakterisztika jellemző pontjait (pl. folyási pont). Nemlineáris esetben görbe-illesztés segítségével határozzuk meg a megfelelő anyagjellemzőket, (pl. kúszás, hiperelasztikus, viszkoelasztikus, és néhány plasztikus anyagmodell esetén). Az anyagmodell felállításához és az anyagvizsgálati adatok feldolgozásához a legtöbb végeselem program beépített megoldást nyújt. Ebben az esetben az importált adatokra a kiválasztott anyagmodellnek megfelelő görbét illeszthetjük.

A mechanikai anyagmodellek felállításához általában az alábbi vizsgálati eljárásokból származó adatokat használhatjuk:

Egytengelyű (Uniaxial)
(Egyen-) Kéttengelyű (Equibiaxial)
Tiszta nyírás (Pure shear / planar tension)
Térfogati vizsgálat (Volumetric)
Egyszerű nyírás (Simple shear)
Egytengelyű húzás (Uniaxial tension)
Egytengelyű nyomóvizsgálat (Uniaxial compression)
Nyírómodulus (Shear modulus)
Térfogat-változási modulus (Bulk modulus)
Húzó (rugalmassági) modulus (Young’s / Tensile modulus)
Poisson-tényező (Poisson's ratio)

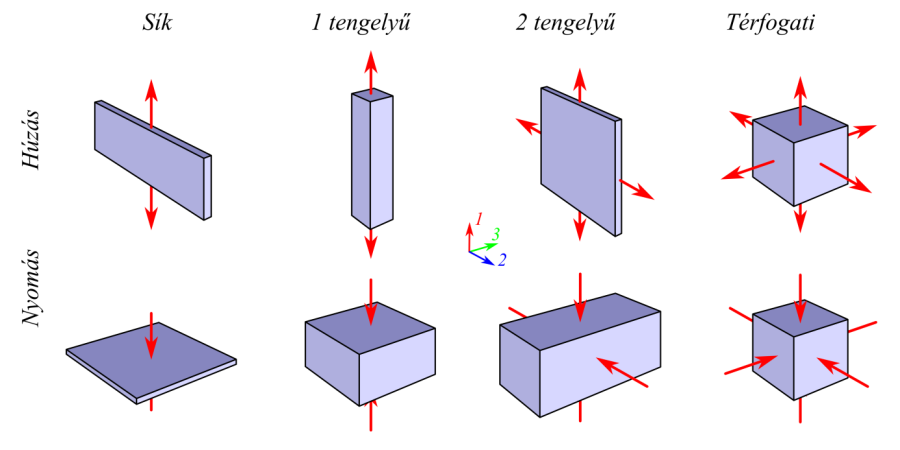
2.28. ábra - A modellalkotáshoz leggyakrabban használt anyagvizsgálatok értelmezése.

Az alábbiakban bemutatott anyagvizsgálatok alakváltozási és feszültségi állapotai homogén, izotróp és összenyomhatatlan (I₃=1) hiperelasztikus anyagmodellre vonatkoznak.

Egytengelyű (Uniaxial) anyagvizsgálat magában foglalja az egytengelyű húzás (Uniaxial tension) és/vagy az egytengelyű nyomóvizsgálat (Uniaxial compression) adatait.

Térfogatállandóságot feltételezve az alakváltozási állapot:

λ ₁ =λ – A terhelés irányába eső nyúlás,

λ ₂ =λ ₃ =λ ^-1/2 – A keresztirányú nyúlás.

Az alakváltozási invariánsok:

I ₁ =λ ² +2λ ^-1

I ₂ =2λ+2λ ^-2

A feszültségi állapot főfeszültségei:

	$σ_{11} = 2 λ^{2} \frac{\partial Π}{\partial I_{1}} + 2 λ^{- 2} \frac{\partial Π}{\partial I_{2}}$	(2.54)
	$σ_{22} = σ_{33} = 2 λ^{- 1} \frac{\partial Π}{\partial I_{1}} + 2 λ \frac{\partial Π}{\partial I_{2}} = 0$	(2.55)

A σ₁₁ – σ₂₂ egyenletek különbségét képezve a terhelés irányába eső főfeszültség:

$σ_{11} = 2 (λ^{2} - λ^{- 1}) (\frac{\partial Π}{\partial I_{1}} + \frac{1}{λ} \frac{\partial Π}{\partial I_{2}})$

(2.56)

A terhelt keresztmetszet pillanatnyi (a) és kezdeti (A) területének viszonya, az alakváltozási állapot alapján (a/A=1/ λ). Így a terhelés irányú mérnöki (σ_E) és a valós Cauchy (σ₁₁) feszültség közötti összefüggés:

$σ_{11} = λ \cdot σ_{E}$

(2.57)

A Kéttengelyű (Equibiaxial) anyagvizsgálat szintén magában foglalja a húzás és/vagy a nyomóvizsgálat adatait.

Térfogatállandóságot feltételezve az alakváltozási állapot:

λ ₁ =λ ₂ =λ – A terhelés irányába eső nyúlás,

λ ₃ =λ ^-2 – A keresztirányú nyúlás.

Az alakváltozási invariánsok:

I ₁ =2λ ² +λ ^-4

I ₂ =λ ⁴ +2λ ^-2

A feszültségi állapot főfeszültségei:

	$σ_{11} = σ_{22} = 2 λ^{2} \frac{\partial Π}{\partial I_{1}} + 2 λ^{- 2} \frac{\partial Π}{\partial I_{2}}$	(2.58)
	$σ_{33} = 2 λ^{- 4} \frac{\partial Π}{\partial I_{1}} + 2 λ^{4} \frac{\partial Π}{\partial I_{2}} = 0$	(2.59)

A σ₁₁ – σ₃₃ egyenletek különbségét képezve a terhelés irányába eső főfeszültség:

$σ_{11} = σ_{22} = 2 (λ^{2} - λ^{- 4}) (\frac{\partial Π}{\partial I_{1}} + λ^{2} \frac{\partial Π}{\partial I_{2}})$

(2.60)

A fentiek alapján a terhelés irányú mérnöki és a valós feszültség közötti összefüggés:

$σ_{11} = λ \cdot σ_{E}$

(2.61)

Tiszta nyírás (Pure shear / planar tension)

Térfogatállandóságot feltételezve az alakváltozási állapot:

λ ₁ =λ – A terhelés irányába eső nyúlás,

λ ₂ =1 – A keresztirányú nyúlás (a próbatest szélessége mentén – nincs nyúlás),

λ ₃ =λ ^-1 – A keresztirányú nyúlás (a próbatest vastagsága mentén – nem ébred feszültség).

Az alakváltozási invariánsok:

I ₁ =λ ² +λ ^-2 +1

I ₂ =λ ² +λ ^-2 +1

A feszültségi állapot főfeszültségei:

	$σ_{11} = σ_{22} = 2 λ^{2} \frac{\partial Π}{\partial I_{1}} + 2 λ^{- 2} \frac{\partial Π}{\partial I_{2}}$	(2.62)
	$σ_{33} = 2 λ^{- 2} \frac{\partial Π}{\partial I_{1}} + 2 λ^{2} \frac{\partial Π}{\partial I_{2}} = 0$

A σ₁₁ – σ₂₂ egyenletek különbségét képezve a terhelés irányába eső főfeszültség:

$σ_{11} = 2 (λ^{2} - λ^{- 2}) (\frac{\partial Π}{\partial I_{1}} + \frac{\partial Π}{\partial I_{2}})$

(2.63)

A fentiek alapján a terhelés irányú mérnöki és a valós feszültség közötti összefüggés:

$σ_{11} = λ \cdot σ_{E}$

(2.64)

Térfogati vizsgálat (Volumetric test)

Az alakváltozási állapot:

λ ₁ =λ ₂ =λ ₃ =λ=J ^1/3 ,

J=V/V ₀ ;

Térfogatállandóságot feltételezve:

λ≈1;

A feszültségi állapot:

$σ = \frac{\partial Π}{\partial J} = - p = (\frac{σ_{1} + σ_{2} + σ_{3}}{3})$

(2.65)

[6.] , [35.] .

2.4.3.8.1.2. Az anyagvizsgálati adatok formátuma

Fontos tisztában lenni azzal, hogy amíg a végeselem programok által kiszámított eredmények a valós feszültség (Cauchy) és a valós (logaritmikus vagy Hencky féle) nyúlás értékeit mutatják (beállítástól és szoftverről függően: ha be van kapcsolva a nagy alakváltozások opció, akkor logaritmikus nyúlás a kimenet, egyébként mérnöki nyúlás), addig az anyagmodell típusától függően a bemenetnek általában az anyagvizsgálatokból származó mérnöki (engineering, nominal) vagy az ezekből számolható valós értékeket kell betáplálni.

Például egy hiperelasztikus anyagmodell létrehozásához az ANSYS és az Abaqus végeselem programban a mérnöki (Engineering, nominal) feszültséget és fajlagos nyúlást, a SolidWorks CAD szoftver szimulációs moduljában a mérnöki feszültséget (Engineering Stress) és a megnyúlást (Stretch ratio) kell megadni. Ezért a vizsgálati adatok betáplálása előtt mindenképen szükséges informálódni az adatok elvárt formájáról, mert azok szoftverenként és anyagmodellenként változó lehet.

Anyagvizsgálatból származó adatok megadásának formátuma hiperelasztikus anyaghoz:

	ANSYS és ABAQUS:	σ _E – ε _E
	SolidWorks:	σ _E – λ

Egy anyagvizsgálat során a mérnöki feszültség és fajlagos nyúlás értéke a kezdeti geometria alapján kerül kiszámításra (σ_E=F/A₀, ε_E=ΔL/L₀), ellenben a valós érték a pillanatnyi geometria függvénye. Mivel a vizsgálat közben a pillanatnyi geometria mérése nehézkes lenne, ezért a mérnöki gyakorlatban a mérnöki feszültség alkalmazása terjedt el. Tekintve, hogy a legtöbb szerkezeti anyag normál igénybevétele során csak kis alakváltozást szenved (<5%), e két érték jó közelítéssel megegyezik. Nagy alakváltozásra képes (pl. elasztomerek) vagy képlékeny anyagok esetén viszont már jelentős különbséggel kell számolnunk. Nagyrugalmasságú elasztomerek esetén, ha a Poisson-tényezőt 0,5 közelinek feltételezzük, így a térfogatállandóság miatt a mérnöki és valós feszültség között a σ_T=λ·σ_Eösszefüggés teremt kapcsolatot. A valós fajlagos nyúlás értékét a logaritmikus (természetes vagy Hencky féle) nyúlással adjuk meg, ε_ln=ln(λ), ahol λ=L/L₀=ε_E+1 a terhelés irányába eső megnyúlás (Stretch ratio).

2.4.3.8.1.3. Görbeillesztés

A végeselem programok általában automatikusan elvégzik az anyagparaméterek meghatározását a betáplált vizsgálati adatok (pl. szakítódiagram) alapján. A görbeillesztés (curve fitting) a legkisebb négyzetek módszerével történik, mely az illesztett és a mért adatok közötti hibát minimalizálja. Választhatunk a normalizált (S=Σ(1-σ/σ_E)²) vagy az abszolút (S=Σ(σ_E-σ)²) hibaszámítás között. Ahol S - a relatívhiba, σ és σ_E– az illesztett és mért feszültségértékek [6.] .

Az alábbiakban a mechanikai analízis során alkalmazott további anyagparamétereket soroljuk fel, melyek többnyire konstans értékként szerepelnek a szimulációban.

2.4.3.8.2. Sűrűség (Density)

Az anyag sűrűsége vagy más néven fajsúlya azt adja meg, hogy egységnyi térfogatú anyagnak mennyi a tömege (ς=m/V), mértékegysége [kg/m³]. Alkalmazásának a dinamikai szimulációk (modál, harmonikus, tranziens analízis), az inerciális terhelésekkel (szögsebesség, gyorsulás, gravitáció) végzett statikai vagy kihajlás analízisekben, illetve termikus vizsgálatokban van szerepe.

2.4.3.8.3. Hőtágulási együttható (Coefficient of thermal expansion)

A lineáris hőtágulási együttható az anyag 1°C hőmérsékletváltozás hatására bekövetkező fajlagos nyúlását adja meg (α=Δl/l·ΔT), mértékegysége [1/K] vagy [1/°C].

2.4.3.8.4. Anyagcsillapítási tényező (Material Damping Ratio)

Anyagcsillapítás lehetővé teszi az anyag belső csillapításának modellezését a dinamikai szimulációkban. Az anyagfüggő tömeg és merevségi csillapítás (α, β, - Rayleigh Damping), hasznos eszköze a dinamikai analíziseknek olyan esetben, amikor az egyes alkatrészek különböző csillapítással rendelkeznek. Az anyagcsillapítási állandó (Constant material damping coefficient) egy anyagfüggő csillapítási együttható, amely a harmonikus analízis gerjesztési frekvenciáin állandó értékű és a modell egyes alkatrészei különböző értékű anyagcsillapítással rendelkezhetnek. A csillapítási együtthatók hőmérsékletfüggetlenek.

2.4.3.8.5. Az anyag szilárdsági határa (Material Strength Limits)

Az anyag szilárdsági határai azt a feszültséget vagy alakváltozást jelentik, amit az anyag még képes elviselni. Megadása történhet pl. a szakító, ill. nyomó folyáshatár (Tensile Yield Strength) vagy az anyag szakítószilárdságának (Tensile Ultimate Strength) megadásával. A megadott érték az analízis eredményében, mint tájékoztató érték (pl. a színskálán bejelölve) jelenik meg, vagy felhasználásra kerül a biztonsági tényező számításához.

2.4.4. Hőmérsékleti szabadságfokkal rendelkező anyagok

A hőmérséklet szabadsági fokkal rendelkező elemzésekben szerepelő hővezetési anyagmodellek megadják a hőmérséklet gradiens hatására kialakuló hőáramot (heat flux), valamint a testek közötti kölcsönhatásnál, a felületi hőmérséklet-különbségek hatására kialakuló sugárzásos hőátadást (radiative heat transfer). A termikus szimuláció anyagmodelljében az alábbi tulajdonságokat kell definiálni:

2.4.4.1. Hővezető képesség (Thermal Conductivity)

Egy anyag hővezetési képességét a hővezetési együtthatójával definiáljuk. Az együttható azt adja meg, hogy egységnyi vastagságú anyagon milyen hőáram keletkezik, ha a két oldalán egységnyi hőmérsékletkülönbség van (λ=q/A⋅ΔT), mértékegysége [W/mK].

2.4.4.2. Fajhő (Specific Heat)

A fajhő vagy más néven fajlagos hőkapacitás értéke azt mondja meg, hogy milyen hőmennyiségre van szükség egységnyi tömegű anyag hőmérsékletének egy fokkal való megnöveléséhez (c=dQ/dT·m), mértékegysége [J/kgK].

2.4.4.3. Sűrűség (Density)

Az anyag sűrűsége vagy más néven fajsúlya azt adja meg, hogy egységnyi térfogatú anyagnak mennyi a tömege (ς=m/V), mértékegysége [kg/m³]. Alkalmazásának a dinamikus szimulációk (modál, harmonikus, tranziens analízis), az inerciális terhelésekkel (szögsebesség, gyorsulás, gravitáció) végzett statikai, vagy kihajlás analízisekben, illetve termikus vizsgálatokban van szerepe.

A fenti anyatulajdonságok lehetnek konstansak, vagy hőmérsékletfüggőek. Ez utóbbi esetben a paraméterek megadása különböző hőmérsékleti szinteken lehetséges a végeselemes szoftverekben. Egy mechanikai analízisben a hőmérsékletfüggő anyagmodell lineárisnak tekinthető, amennyiben a szimuláció konstans hőmérsékleten zajlik, de nemlineáris probléma megoldásról beszélhetünk ugyanakkor, ha hőtani szimulációt folytatunk ugyanezzel az anyaggal.

A hővezetési tényező lehet izotróp (minden irányban azonos) vagy ortotróp (egymásra merőleges tengelyek mentén eltérő) is.

2.4.5. Elektromágneses szabadságfokú anyagok

Az elektromágneses szabadsági fokkal rendelkező elemzésekben szerepelő anyagmodellek az alábbiak lehetnek:

Mágneses, (Magnetic) - a mágneses fluxus (magnetic flux) hatására megadja a mágneses erőt (magnetomotive force).

Vezetőképesség, (Conductivity) - az elektromos és mágneses áramvezető képesség modellezi egy adott mező és annak fluxusa közötti kapcsolatot.

Permittivitás és Permeabilitás, (Permittivity, Permeability) - egy elektromágneses mező hatására megadja az anyag energiatároló képességét.

Veszteség, (Loss) - Az elektromágneses anyagok és dielektrikumok elektromágneses mező változásának hatására bekövetkező energiaveszteségét képviseli.

2.4.5.1. Az anyagok mágneses tulajdonságai

2.4.5.1.1. Mikroszkopikus modell.

Az anyagok mágneses tulajdonságait az atomszerkezetre lehet visszavezetni. Az atommag körül keringő elektron egy elemi köráramnak tekinthető, így egy mágneses dipólussal modellezhető. Az elemi dipólus dipólus-momentumát a d m =I⋅d A összefüggésből, az elektron pályája által meghatározott A felület és az I áram szorzataként kapjuk.

2.4.5.1.2. Makroszkopikus modell.

Mérnöki szempontból nem az egyes dipólusok, hanem azok sokaságának a modellezésére van szükség. Egy dV térfogatban, N darab mágneses dipólus helyezkedik el. Az egyes dipólusok mágneses dipólus-nyomatékát tekintsük közel azonosnak. Így m _i≈α⋅ H , ahol: α kölcsönhatási tényező. Az anyag mágnesezettségét az egységnyi térfogatban elhelyezkedő dipólus-momentumok sűrűsége határozza meg.

$\underline{M} = \lim_{d V \to 0} \frac{\sum_{i = 1}^{N} {\underline{m}}_{i}}{d V} \approx \frac{N \cdot \underline{m}}{d V} = \frac{N}{d V} \cdot α \cdot \underline{H} = n_{m} \cdot α \cdot \underline{H} = κ \cdot \underline{H}$

(2.66)

Ahol:

n _m = N/dV - a dipólus sűrűség,

κ=α⋅n_m - a mágneses szuszceptabilitás,

M - az anyagra jellemző mágnesezettség.

Sok esetben a µ ₀⋅ M mágneses polarizációt alkalmazzák az anyag mágneses tulajdonságainak jellemzésére.

$\underline{B} = μ_{0} (\underline{H} + \underline{M}) = μ_{0} \cdot \underline{H} (1 + κ) = μ_{0} \cdot μ_{r} \cdot \underline{H}$

(2.67)

Ahol az μ _r =1+κ a relatív mágneses permeabilitás.

2.4.5.2. Mágneses anyagok típusai

A tapasztalat azt mutatja, hogy ha valamilyen anyagot mágneses térbe helyezünk, akkor megváltozik a mágneses indukció értéke. Ugyanis megváltozik a tér mágneses vezetőképessége, vagyis a permeabilitása. Az anyagok, permeabilitásuk alapján, három csoportba sorolhatók. Ami tovább bontható a mikromágneses viselkedésük alapján.

Az anyagok makromágneses viselkedése alapján:

Diamágneses anyagok
Parramágneses anyagok
Ferromágneses anyagok

Az anyagok mikromágneses viselkedése alapján:

Rendezetlen mágneses anyagok
- Diamágneses anyagok
- Paramágneses anyagok
Rendezett mágneses anyagok
- Ferromágneses anyagok
- Ferrimágneses anyagok
- Antiferromágneses anyagok

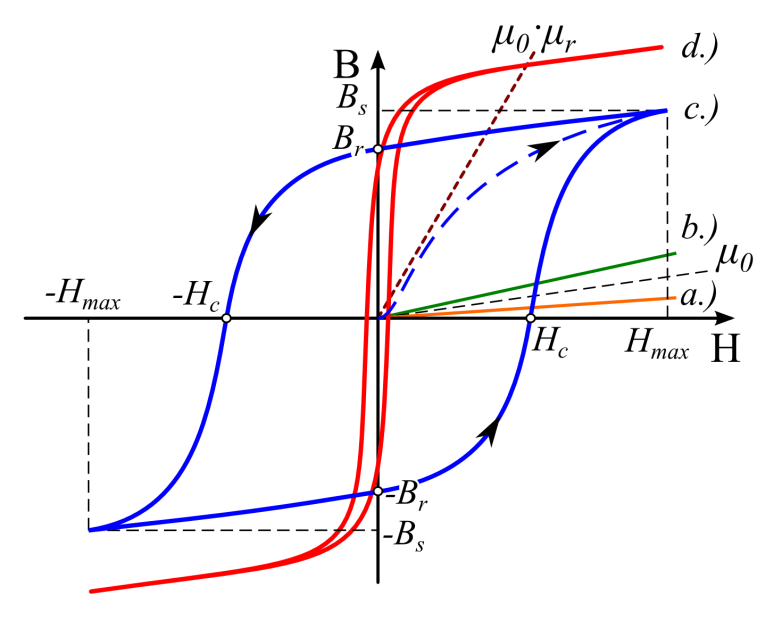
a.) Diamágneses anyag; b.) Paramágneses anyag; c.) "Kemény" ferromágneses anyag (állandómágnes); d.) "Lágy" ferromágneses anyag; µ ₀ – a vákuumpermeabilitás egyenese; µ ₀ ⋅ µ _r – lineáris mágneses anyagmodell;

2.29. ábra - Mágneses anyagok jellemző B-H görbéje

[39.] , [40.] .

2.4.5.2.1. A diamágneses anyagok

κ ≈−10^-5; μ_r=1+κ<1;

(H₂, H₂O, Si, P, S, Cu, Zn, Ge, Hg, Bi, C, Ag, Au, Pb, Zn fa, paraffin, pirolitikus grafit, gyémánt, szerves vegyületek,)

A diamágneses anyagok egynél kisebb permeabilitásuak, ami azt jelenti, hogy a mágneses vezetőképességük rosszabb a vákuuménál (2.29. ábra, a.). Szemléletesen úgy képzelhetjük el, hogy az ilyen anyagok kis mértékben taszítják a mágnest. Persze ez a taszítóerő olyan kis értékű, hogy nem tudjuk érzékelni. A diamágneses anyagok ilyen viselkedésének az az oka, hogy két ellentétes irányú mágneses momentumú vegyértékelektronnal rendelkeznek, amelyek külső mágneses tér hatására beállnak a térrel párhuzamos irányba, és a térrel ellentétes irányú mágneses momentum megnő, míg az azonos irányú lecsökken

A diamágneses anyagok mágneses szuszceptibilitása ill. permeabilitása nem függ a hőmérséklettől.

Szupravezető állapot κ=−1; μ=1+κ= 0;

A szupravezetők ideális diamágnesekként viselkednek. Úgy is szokás fogalmazni, hogy a szupravezetőből a mágneses tér "kiszorul", tehát az anyag belsejében a mágneses indukció értéke zérus [39.] .

2.4.5.2.2. A paramágneses anyagok

κ≈10^-5; μ_r=1+κ>1;

(O₂, Al, Bi, Pb, Pt, Mg, Ti, Cr, Mn, Mo,W, Cr, K, Na)

A paramágneses anyagok permeabilitása egynél kicsit nagyobb, ami azt jelenti, hogy az ilyen anyagok kis mértékben vonzzák a mágnest (2.29. ábra, b.). Persze ez a vonzóerő olyan kis értékű, hogy nem tudjuk érzékelni. A paramágneses anyagok ilyen viselkedésének az az oka, hogy egy vegyértékelektronnal rendelkeznek, amely mágneses momentuma külső mágneses tér hatására beáll a mágneses tér irányába.

Mágneses szuszceptibilitásuk fordítottan arányos hőmérséklettel. κ=C/T, ahol C anyagi minőségtől függő ún. Curie-állandó [39.] .

2.4.5.2.3. Ferromágneses anyagok

κ ≈10³-10⁶; μ_r=1+κ>>1;

(Fe, Ni, Co, Gd), doménszerkezetük: ↑↑↑↑

A ferromágneses anyagokban lévő elemi térfogatokban (doménekben) a mágneses dipólusok, külső tér nélkül is, egy irányba rendeződnek, a közöttük lévő erős kölcsönhatás miatt. A ferromágneses anyagok mágneses szuszceptibilitása nagyon nagy pozitív érték. Ha az anyag még nem volt kitéve mágneses térnek a domének statisztikus elrendeződése olyan, hogy az anyag kifelé nem mutat mágneses tulajdonságokat. Az első felmágnesezés során a B - H görbe az un. szűzgörbén halad (2.29. ábra, c.- kék szaggatott vonal), mely során a domének befordulnak a mágneses térrel párhuzamos irányába, majd a mágneses tér irányába mutató domének térfogata növekszik, az ellentétes irányúaké csökken, végül minden domén befordul a mágneses tér irányába, ahol a görbe telítési szakaszba ér. Tovább növelve a H mágneses térerősség értékét B indukció értéke nem változik.

A térerősség csökkentésével az indukció nem a szűzgörbén fog visszatérni, a domének átrendeződésére fordított energiaveszteség miatt fölötte fog haladni, a térerősség nulla értékénél marad egy B _r remanens mágneses indukció. A mágneses indukció megszüntetéséhez ellenkező irányú, - H _c koercitív mágneses térerősségre van szükség. Tovább növelve az ellenkező irányú térerősség értékét ismét eljutunk a telítési pontba. Majd megfordítva a gerjesztés irányát - B _r majd H _c pontokon keresztül záródik a hiszterézis karakterisztika.

Keskeny hiszterézis görbével (kis ± H _c érték) az un. lágy mágneses anyagok rendelkeznek (2.29. ábra, d.), ezeknél kicsi a domének átrendeződéséhez szükséges energiaveszteség. Ilyen anyag pl. a transzformátorlemez és dinamólemez.

Széles hiszterézis görbével (nagy ± H _c érték) az un. kemény mágneses anyagok rendelkeznek (2.29. ábra, c.), ezeknél nagy a domének átrendeződéséhez szükséges energiaveszteség. Ilyen anyagok pl. az állandó-mágnesként használt alnico és nipermag ötvözetek.

A ferromágneses anyagok mágneses szuszceptibilitása az ún. Curie-hőmérsékletig (T_C) rendkívül nagy, majd e hőmérséklet felett a paramágneses anyagokhoz hasonlóan csökken. A paramágneses tartományban

κ=C/(T−T _C ), ahol C a Curie-állandó, (T_C értéke vasra 768°C, kobaltra 1130°C, nikkelre 360°C).

[Sályi István: Pattantyús II.]

2.4.5.2.4. Ferrimágneses anyagok

(Fe3O4, CrO2, ErO, …), doménszerkezetük: ⇑↓⇑↓

Mágneses viselkedésű kerámiák, melyek elektromos viselkedésüket tekintve szigetelők. Telítési pontjuk alacsonyabb, mint a ferromágneses anyagoknak. Szupceptibilitás hőmérsékletfüggése a ferromágneses anyagokéhoz hasonló.

2.4.5.2.5. Az antiferromágneses anyagok

κ=0, μ_r≈1

(Cr, Mn, ausztenites acélok), doménszerkezetük: ↑↓↑↓

Az antimágneses anyagokban a mágneses tér irányába és azzal ellentétesen beálló domainek mennyisége megegyezik, ezért nem változtatják meg a mágneses teret.

Az antimágneses anyagok κ–T görbéje két szakaszra osztható: Néel-hőmérsékletig (T_N) tartó szakasz az antiferromágneses tartomány, felette pedig paramágneses hatás κ≈C/(T-T_N), érvényesül. Ahol C a Curie-állandó.

2.4. táblázat - Az anyagok csoportosítása mágneses tulajdonságuk szerint.

Anyag / állapot	Hiszterézis	B -függés	Hőmérséklet-függés	Példa (μ=1+κ)
Diamágneses anyagok	Nincs	Nincs	Nincs	Víz: κ=−9.0×10^-6
Paramágneses anyagok	Nincs	Nincs	κ=C/T	Al: κ=2.2 ×10^-5
Ferro-és ferrimágneses anyagok	Van	Van	κ=C/(T−T _C )	Vas: κ=3000
Antiferromágneses anyagok	Van	Van	κ≈C/(T−T _N )	Terbium: κ=2500

[41.] .

A mágneses anyagokat relatív permeabilitásuk ill. mágneses szuszceptibilitásuk szerint a fenti csoportokba lehet sorolni. Azonban a dia, paramágneses valamint antiferromágneses anyagok mágneses szuszceptibilitása |κ|=|μ_r−1|≈10^-5nagyságrendű, tehát gyakorlati szempontból a mágneses anyagokat ferromágneses és nem ferromágneses csoportokba sorolhatjuk [40.] .

2.4.5.3. A mágneses szimuláció során definiálható mágneses anyagtípusok

Lineáris "lágy" (soft) mágneses anyag

Ebben az esetben a permeabilitás (az indukció és a térerősség hányadosa, μ= B / H ) konstans érték, nem függ a térerősségtől és a mágnesezési előélettől (2.29. ábra, μ_o⋅μ_r). A relatív permeabilitást (μ_r) kell definiálni, μ=μ_o⋅μ_r, ahol a vákuumpermeabilitás értéke: μ₀=4π⋅10^-7 H/m. Általában a nem mágneses anyagok esetén használjuk (pl. levegő, réz), vagy olyan mágneses anyagok közelítésére, melyeknek nem ismerjük a mágnesezési (B-H) görbéjét. Előfordulhat olyan eset, hogy a permeabilitás nem izotróp, ilyenkor általában lehetséges ortotróp anyagmodell definiálása is. (Mivel ilyenkor globális vagy lokális koordináta rendszerben kell definiálni a relatív permeabilitás irányonkénti értékét célszerű az adott alkatrészhez saját, releváns koordinátarendszert meghatározni. Fontos továbbá megjegyezni, hogy ortotróp anyagmodellek estén a többi anyagtulajdonságot is irányonként kell megadni.)

Nemlineáris "lágy" (soft) mágneses anyag

Ebbe a kategóriába tartoznak azok az anyagok, amelyek nemlineáris viselkedést mutatnak. Ilyenkor a B-H görbe pontos megadásával tudjuk definiálni a fő mágneses tulajdonságokat (2.29. ábra, d.). Egyetlen B-H görbét lehet megadni ebben az esetben. A B-H görbe definiálása történhet a görbe pontjainak megadásával, vagy az adott szoftver anyag adatbázisaiból kiválasztásával (a leggyakoribb anyagok B-H görbéi általában elérhetőek). Ha az adott anyag ortotróp viselkedést mutat, akkor itt is megadható irányonként a relatív permeabilitás és a többi anyagjellemző is, így akár a B-H görbe is megadható irányonként is. Ortotróp anyagmodell esetén is érdemes az alkatrészhez saját koordinátarendszert definiálni. A B-H görbe megadásakor az alábbi alapszabályokat mindenképpen érdemes betartani:

A görbe legyen sima és folytonos.

A görbe nyúljon túl a működési tartományon, tartalmazza a telítődés szakaszát is. (A telítődési szakasz aszimptotikusan közelít a vákuumpermeabilitás egyeneséhez, tehát a program ez alapján tud extrapolálni ha szükséges.)

A szimuláció során a B-H görbe az origó közelében a 0,0 értékhez tart, egy ettől eltérő közeli pont megadása konvergencia problémát okozhat.

Lineáris "kemény" (hard) mágneses anyag

A keménymágneses anyagok, jellemző tulajdonsága a nagy koercív erővel jellemezhető (széles hiszterézishurokkal rendelkező) B-H karakterisztika (2.29. ábra, c.). Ebbe a kategóriába tartoznak pl. a permanens mágnesek. Ennél az anyagmodellnél a lemágnesezési görbét lineárisnak feltételezzük. Így két értéket kell csak megadni; ahol az egyenes metszi a B-H görbe H (mágneses térerősség) tengelyét azt nevezzük koercív erőnek (Coercive Force), mely azt a mágneses térerősség értéket jelenti, amely elégséges az adott anyag lemágnesezésére, tehát ahol B (mágneses indukció) nulla (Ansys programban ezt abszolút értékben kell megadni, tehát pozitív értékként). A második megadandó érték a lemágnesezési egyenes metszéspontja a B tengellyel, melyet remanens, vagyis maradó mágnesezettségnek vagy remanenciának nevezünk (Residual Induction). Az anyagtulajdonságok mellett definiálni kell a mágnes polaritását is. (Ansys programban mindig a globális, vagy egy alkatrészhez meghatározott lokális koordinátarendszer X tengelye mutatja meg a polaritás irányát, alapértéken az északi pólus a koordinátarendszer X tengelyének pozitív irányába mutat, ezt természetesen át lehet állítani. Mivel nem csak Descart-féle, hanem poláris koordinátarendszert is definiálhatunk akár radiális irányú mágnesezettséget is tudunk szimulálni.

Nemlineáris "kemény" (hard) mágneses anyag

A nemlineáris keménymágneses anyagot a B-H karakterisztika 2. síknegyedbe eső pontjaival adjuk meg. Az első adatpár a B=0, H=−H_c kell, hogy legyen. Az állandómágnes mágnesezése egy tengely mentén történik, amely egy célszerűen megválasztott modellkoordináta rendszer X tengelye lehet (a +X irány jelenti az állandómágnes északi pólusát). Ellenkező esetben a mágnesezettség iránya az alapértelmezett Globális Koordinátarendszer X tengelye lesz. A választott koordinátarendszer lehet derékszögű (Cartesian) vagy hengeres (cylindrical). Hengeres koordinátarendszer alkalmazásával létrehozhatunk radiálisan mágnesezett modellt is. A B-H görbe megadásakor az alábbi alapszabályokat mindenképpen érdemes betartani:

A görbe legyen sima és folytonos.

A görbe megadása a 2. síknegyedben történik, de kiterjedhet az 1. síknegyedbe is.

2.4.5.4. Elektromos anyagmodellek

2.4.5.4.1. Elektromos vezető

Az anyag elektromos vezetési tulajdonságát a fajlagos ellenállás (Resistivity) (ς [Vm/A=Ωm]) vagy a fajlagos vezetőképesség (Specific conductivity) (γ=1/ς [A/Vm=S/m]) megadásával definiálhatjuk, amely lehet izotróp vagy ortotróp. Ez utóbbi esetben célszerű lokális koordinátarendszert definiálni az adott alkatrészhez. Az ellenállás lehet a hőmérséklettől függő is melyet különböző hőmérsékleti szinteken megadott ellenállás értékekkel definiálhatunk.

2.4.5.4.2. Dielektrikum

A nagy fajlagos ellenállású (ς>10⁸ Ωm)anyagokat szigetelőknek, vagyis dielektrikumoknak hívjuk. Jellemzésükre a relatív permittivitást (ε_r) használjuk. A mágneses permeabilitás analógiájára a permittivitás vagyis a dielektromos állandó (ε=ε₀⋅ε_r) teremti meg a kapcsolatot az elektromos térerőség (E) és az eltolási vektor (D) között: D =ε E ; (ε₀=8,854⋅10−12 As/Vm).

2.4.6. Csatolt anyagmodellek

Számos modell alkalmazható csatolt termikus, elektromágneses és elmozdulás szabadsági fokokkal rendelkező elemzésekhez. Bár a modellek kapcsolva vannak, azok továbbra is önállóak és így az egyéni terhelés-válasz viselkedéssel rendelkeznek. A piezoelektromos anyagok azonban elektromechanikusan csatolt modellek, amelyek villamos feszültség bemenetre alakváltozást adnak válaszul, valamint deformáció hatására villamos feszültséget generálnak.

A csatolt tér analízisek típusai, mint már az elemtípusoknál láthattuk, rendkívül sokfélék lehetnek. Jellemzően a mechanikai, villamos, mágneses, termikus, és áramlási hatások páronkénti vagy többszörösen összetett modelljei alkotják, de léteznek akusztikus, dífúziós, stb. elemei is. Az alábbiakban az elektro-mechanikus analízis anyagaira hozunk két példaként.

2.4.6.1. Piezorezisztív anyag

A piezorezisztív anyagok fő jellegzetessége, hogy mechanikai feszültség, (vagyis közvetlenül az alakváltozás) hatására megváltozik az ellenállásuk. Egy deformált test ellenállás-változása tenzometrikus és piezorezisztív komponensekből áll. A tenzometrikus komponens csak a geometria változásától függ, így a Poisson-tényező és az alakváltozási állapot ismeretében könnyen számolható (fémekre jellemző). A piezorezisztív hatásként oka az, hogy az anyag a fajlagos ellenállása megváltozik (félvezetőkre jellemző).

Piezorezisztív anyagmodell végeselemes definiálásához az anyag fajlagos ellenállásának (ς), a rugalmassági együtthatók (pl. rugalmassági modulus E, Poisson-tényező ν) és a piezorezisztív mátrix megadása szükséges. Ez utóbbi a mechanikai feszültség, vagy alakváltozás (megadástól függ, hogy melyik) hatására bekövetkező ellenállás-változás mértékét adja meg [42.] .

2.4.6.2. Piezoelektromos anyagmodell

A piezoelektromos anyag egy elektromechanikusan csatolt anyag, melynek jellemzője, hogy villamos feszültség hatására alakváltozással válaszol, valamit fordított helyzetben deformáció (vagy mechanikai feszültség) hatására villamos feszültséggel, pontosabban töltésszétválasztással reagál.

Piezorezisztív anyagmodell az anyag permittivitásának (dielektromos állandójának), a rugalmassági együttható mátrixának (pl. rugalmassági modulus E, Poisson-tényező ν) és a piezoelektromos együttható mátrixának megadásával definiálható. A piezoelektromos együttható mátrix a mechanikai feszültség vagy alakváltozás (megadástól függ, hogy melyik) és az elektromos térerősség kapcsolatát adja meg.

2.5. Terhelések, perem- és kezdeti feltételek

A geometriai modell elemeire (térfogat, felület, él, pont) vagy közvetlenül a végeselem háló csomópontjaira peremfeltételeket és terheléseket írhatunk elő.

2.5.1. Kezdeti feltételek

Egy időben változó analízis során lehetőségünk van a szimulációt egy előre definiált kezdeti feltétellel indítani. A feltétel megadja a t₀=0 időpillanatban az adott konfiguráció valamely paraméterének értékét. Tranziens folyamatoknál ez lehet pl. egy geometriai elem sebessége, hőmérséklete, stb. Homogénnek nevezzük a peremfeltételt, ha értéke 0; inhomogénnek, ha 0-tól különböző értékű, [43.] .

Típusa az adott szimuláció típusától függ, pl. lehet egy előzőleg futtatott szimuláció eredménye, valamilyen kapcsolódó környezet vagy egy kezdeti hőmérséklet.

Kezdeti feltétel (Initial State Loading) - Statikai, tranziens, modál, harmonikus és kihajlás típusú szerkezeti analízisek esetén alkalmazható a kezdeti feltétel, melyet az első lépésben kell definiálni.

2.5.2. Peremfeltételek

A peremfeltételek a fizikai valóság azon részeinek hatását jelentik, amelyeket elhagyunk a modellezés során. Ezért rendkívül körültekintően kell eljárnunk akkor, amikor ezeket a külső hatásokat modellezzük, mivel a modell helyessége fejti ki az egyik legnagyobb hatást a teljes végeselem modell jóságára [5.] .

A peremfeltételek származhatnak közvetlenül az adott modellre definiált kényszerekből (megtámasztás, elmozdulás kényszer, szimmetriafeltétel) vagy más alkatrésszel való érintkezésből (kontaktokból). Általános esetre megfogalmazva az adott szimulációnak megfelelő szabadságfokot korlátozó feltételről beszélünk. Például mechanikai, (vagyis elmozdulás szabadságfokú) rendszer esetén, kinematikai kényszerről; termikus (hőmérséklet szabadságfokú) szimuláció esetén megadott hőmérséklet-kényszer, stb. Az alábbiakban láthatjuk a jegyzet témaköreit érintő analízistípusokban definiálható peremfeltételek:

Szerkezeti analízis (Structural) - elmozdulás, elfordulás, sebesség kényszer vagy szimmetriafeltétel.
Hőtani analízis (Thermal) - előírt hőmérséklet.
Mágneses (Magnetic) - párhuzamos-fluxus, Vektor vagy skalár potenciál.
Elektromos (Electric) – Feszültség.

Homogénnek nevezzük a peremfeltételt, ha értéke 0 (pl. fix megtámasztás); inhomogénnek, ha 0-tól különböző értékű (pl. elmozduláskényszer).

[43.] , [6.] .

A különféle típusú feladatok megoldásánál alkalmazott peremfeltételeket az adott analízis fejezetében részletesebben tárgyaljuk.

2.5.3. Terhelések

Egy végeselemes analízis elsődleges célja annak meghatározása, hogy egy szerkezet, hogyan reagál bizonyos terhelésekre. Ezért a megfelelő terhelési feltételek definiálása kulcsfontosságú a szimuláció szempontjából. A jegyzet témaköreit érintő analízistípusokban definiálható terhelések:

Szerkezeti analízis (Structural) - elmozdulás (displacements), sebesség (velocities), gyorsulás (accelerations), gravitáció (gravity), erő (forces), nyomás (pressures), hőmérséklet (temperatures) [hőtágulásnál].
Hőtani analízis (Thermal) - hőmérséklet, hőáram sűrűség (heat flow rates), konvekció (convections), belső hőtermelés (internal heat generation), végtelen felület (infinite surface).

Mágneses (Magnetic) - mágneses potenciálok (magnetic potentials),mágneses fluxus (magnetic flux), mágneses áramszegmensek (magnetic current segments), áramsűrűség (source current density), végtelen felület (infinite surface).

Elektromos (Electric) - elektromos potenciál (feszültség), (electric potentials (voltage)), elektromos áram (electric current), elektromos töltések (electric charges), töltéssűrűség (charge densities), végtelen felület (infinite surface).

A terhelés lehet a vizsgált test külső, határoló entitásaira (felület, él, pont) ható koncentrált vagy megoszló terhelés (mint az erő, nyomaték, nyomás), vagy a test teljes térfogatára ható test, vagy inerciális terhelés, (mint a gravitációs gyorsulásból eredő súlyerő, vagy a rotációs vagy transzlációs gyorsulásból származó tehetetlenségi erő). A terhelések, a terhelt testen való eloszlásuk szerint, az alábbi kategóriákba sorolhatók:

Erők (Forces / concentrated loads) – egy csomópontra (node) ható koncentrált terhelés. Például egy erő, vagy egy nyomaték a szerkezeti analízisben; hőáramsűrűség a hőtani szimulációban; vagy gerjesztőáram egy mágneses mező vizsgálatnál.
Felületi terhelés (Surface loads) – egy felület mentén megoszló erő. Például nyomás a szerkezeti analízisben; konvekció és a hőáram a termikus analízisben.
Test terhelés (body loads) – térfogati vagy mező jellegű terhelés. Pl.: a hőmérséklet a szerkezeti analízisben; belső hőtermelés sűrűség a hőtani szimulációban; áramsűrűség a mágneses vizsgálatban.
Inerciális terhelés (Inertia loads) – a test tehetetlenségének (tömeg mátrix) tulajdonítható terhelések, mint a gravitációs gyorsulás, szögsebesség és a szöggyorsulás a szerkezeti analízisben.
Csatolt tér terhelések (coupled-field loads) – a fenti terhelések speciális esete, amikor is egy szimuláció eredménye szolgál egy más típusú analízis terheléseként. Például a mágneses szimulációban kiszámolt erő, mint terhelés egy szerkezeti analízisben; vagy egy hőtani szimuláció eredménye, mint bemenet egy szerkezeti analízisben a hőtágulásból eredő deformációk számításához.

A fentiek szerint a terheléseket a geometriai modell entitásaira (pontok, élek, felületek) vagy a végeselem modell csomópontjaira lehet érvényesíteni. A terhelés megadásának módjától függetlenül, a megoldó (solver) áthelyezi a terheléseket a végeselemes modell csomópontjaira, és úgy futtatja a számolást. A terhelések alkalmazásának szempontjai:

A szilárdtest modellre alkalmazott terhelések függetlenek a végeselem hálótól, (a háló módosítható a terhelés változtatása nélkül.
A szilárdtest modell lényegesen kevesebb elemet tartalmaz, mint a végeselem modell, ezért a kijelölés egyszerűbb, (grafikus kijelölés).
A szilárdtest és a végeselem modellnek általában eltérő a koordinátarendszere, így a terhelés iránya is eltérő lehet a különböző kijelölés esetén.
Az egyszerűsített szimulációkat egyszerűvé teszik a terhelések végeselem modellre történő közvetlen alkalmazása, mivel a terheléseket közvetlenül a csomópontokra helyezhetjük.

2.5.3.1. Terhelési lépések (Load steps)

A terhelési lépés (load step) – a terhelés egy konfigurációja melyre megkapjuk a megoldást. A lineáris statikai (linear static) vagy a stacionárius (steady-state) analízisekben különböző terhelési lépésekben állíthatunk be különböző terhelési konfigurációkat (pl. erőterhelés az első lépésben, nyomás a másodikban, mindkét terhelés és megváltoztatott rögzítés a harmadik lépésben.). Tranziens analízisben több lépésben adhatjuk meg a terhelés időbeni lefutását.

Nincs szükség több időlépés beállítására akkor, ha csak a terhelés mértékét akarjuk változtatni az idő függvényében. Erre a célra a terhelési lépések allépésekre való felosztása szolgál.

Allépések (Substeps) – a terhelési lépések közötti lépések. Az allépések sűrűségét megadhatjuk a lépések számával vagy a köztük eltelt idővel (A statikai szimuláció esetén ez csak egy követési paraméter). Alkalmazásuknak az alábbi okai lehetnek:

Egy nemlineáris statikai (nonlinear static) vagy a stacionárius (steady-state) analízisben, allépések alkalmazásával, a terhelés fokozatos ráadásával pontosabb eredmény érhető el.
Egy lineáris, vagy nemlineáris tranziens analízis esetén alkalmazzuk az idő integráció feltételeinek kielégítése érdekében (ami egy minimális integrálási időt ír elő a pontos eredmény érdekében).
Harmonikus analízisben használunk allépéseket a frekvenciatartományokon belüli számos frekvencián való megoldásért.

A terhelések alkalmazása az allépésekben történhet ugrásszerűen (stepped) vagy fokozatosan emelkedő (ramped) módon. Az ugrásszerű megoldásnál az egy lépésen belüli allépések mind egyazon terhelési szinten vannak, míg az emelkedő eljárással fokozatosan változtatva, csak a lépés végén éri el a beállított szintet a terhelés [6.] .

Egyensúlyi iteráció (Equilibrium iterations) – Nemlineáris analízisek során a konvergencia elősegítése miatt, egy adott allépésen belül további iteratív megoldások számolódnak. Gyakori eljárás a nemlineáris analíziseknél, hogy a pontos eredmény érdekében a terhelést két lépésben adják rá a szerkezetre, az első lépés több (5-10) allépésre van osztva, allépésenként egy egyensúlyi iterációval; a második lépés viszont csak egy allépésből áll, ami több (10-20) egyensúlyi iterációt tartalmaz. Az első lépés a végső terhelési szint stabil elérését hivatott biztosítani, a második lépés pedig a pontos eredményeket adó konvergenciát szolgálja.

2.5.4. Szimmetriafeltételek

A 2.2.3.1. szakasz fejezetben láthattuk a geometria lehetséges szimmetriáit. Ezeket a végeselem modellen a megfelelő kényszer és terhelés felrakásával, vagy a végeselem programban előre definiált szimmetriafeltételekkel tudjuk érvényesíteni. Ez utóbbi megoldás esetén is a program a megfelelő szabadságfok kényszert (DOF constraints) hozza létre, valamint a szimmetriasíkban lévő csomópontok koordinátarendszerét befordítja a szimmetriasíkba.

Beszélhetünk szimmetrikus és antiszimmetrikus peremfeltételekről. Például egy szerkezeti analízisben a szimmetria peremfeltétel esetén a szimmetriasíkra merőleges elmozdulások és azzal párhuzamos tengelyű elfordulás értéke lesz nulla, az antiszimmetria esetén a síkban történő elmozdulás és a síkra merőleges tengelyű elfordulás lesz zérus értékű.

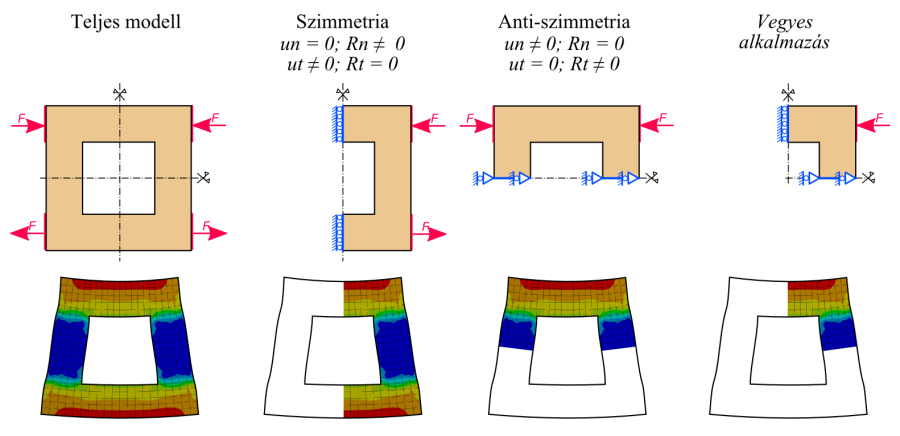
Az „u” - az elmozdulást, az „R” - az adott tengely körüli elfordulást jelenti, ahol az „n” index a normális a „t” a tangenciális irányt jelöli.

2.30. ábra - Szimmetria és anti-szimmetria értelmezése.

2.5.4.1. Tengelyszimmetrikus (Axisymmetric) terhelések

A kényszerek, felületi és volumetrikus erők, valamint a tengelyirányú gyorsulásokat úgy kell definiálni, mint egy nem tengelyszimmetrikus modell esetén. A koncentrált erőket és a számítások eredményeit a teljes kör mentén (360°) kell értelmezni, vagyis a modellen koncentrált erőként definiált terhelés a valóságban vonalmentén megoszló terhelésnek felel meg. Például egy cső végére alkalmazott tengelyirányú megoszló terhelés q [N/mm], a tengelyszimmetrikus végeselem modellen F=2Rπq [N] értékű koncentrált erőként szerepel.

2.6. Alkatrészek közötti kapcsolatok

Az egyes alkatrészek közötti kapcsolatot nevezzük kontaktoknak, melyek az alkatrészek közötti terhelés és kényszerek átadását biztosítják. Ennek a kapcsolatnak a tulajdonságai határozzák meg az egyes geometriai elemek egymáshoz képesti viselkedését. Nagyon fontos, hogy olyan kontaktot definiáljunk, amely leginkább megfelel az adott szerkezet valós viselkedésének. A kontaktok definiálása az olyan mechanikai esetekben a legfontosabb, ahol az alkatrészek elmozdulást, deformációt szenvednek. Ennél fogva a legtöbb kontaktok jelentős nemlinearitást visznek a feladatba.

a kontaktproblémák két fő nehézsége abból adódik, hogy nehéz megjósolni az analízis előtt, hogy pontosan milyen területek fognak részt venni a kontaktban. A másik probléma a kontaktokkal átadott mennyiségek (súrlódó erő, hő, elektromos áram, stb.) nemlineáris jellegében van. Olyan esetekben, ahol nem történik deformáció (pl. bizonyos elektromágneses, hőtani szimulációk) ott nem szükséges a kontaktok beállításaira különösebb figyelmet fordítani.

A mechanikai analízis kontaktproblémájának két lényeges típusa a merev – rugalmas és a rugalmas – rugalmas kapcsolat. A merev – rugalmas kapcsolat esetén a kapcsolatban lévő testek egyike rugalmas, a másik pedig merev test (vagy sokkal merevebb, mint a másik). Tipikus példa lehet erre a fém - polimer kapcsolat vagy a fémek képlékenyalakítási eljárásainak szerszámai és munkadarabja közötti kapcsolat. A rugalmas – rugalmas kapcsolat minden alkatrésze deformálható (vagy hasonló merevségű).

A kontaktok csoportosítása kapcsolódó geometria szerint a következő lehet:

Csomópont – csomóponttal (node-to-node), – a két elem egymáshoz képest csak kis elmozdulásra képes.
Csomópont – felülettel (node-to-surface),
Él – éllel kapcsolódik (line-to-line),
Él – Felülettel (line-to-surface),
Felület – felülettel (surface-to-surface).

Az analízis típusa szerint az alábbiak lehetnek a kontaktok [6.] :

Szerkezeti analízis (Structural)
- Súrlódásos (Frictional) – a valós fizikai kapcsolatot a legjobban modellező kontakt. A felületek eltávolodhatnak és a súrlódási erő ellenében elcsúszhatnak egymáson.
- Súrlódásmentes (Frictionless) – Idealizált csúszó kontakt. A felületek akadálymentesen elcsúszhatnak egymáson és eltávolodhatnak egymástól.
- Síkban maradó (No-separation) – A súrlódásmentes speciális esete, amikor a felületek akadálymentesen elcsúszhatnak egymáson, de nem eltávolodhatnak el egymástól.
- Tapadó (Rough) – Idealizált csúszásmentes kontakt. A felületek nem csúszhatnak el egymáson, de eltávolodhatnak egymástól.
- Ragasztott (Bonded) – minden szabadságot megkötő, a kapcsolódó felületeket egymáshoz fixen rögzítő kontakt.
Hőtani analízis (Thermal) – a termikus analízisben szereplő kontakt a kapcsolódó felületek közötti hőellenállást vagy hővezető képességet definiálja. Egy összeállításban a testek közötti hőátadáshoz elengedhetetlen a fenti kontaktok megléte és a testek érintkezése vagy közelsége. Nem érintkező, de közel (pinball region) lévő felületek hőátadása csak a bonded, vagy a no-separation kényszerrel valósul meg. A pinball régión kívül eső felületelemek között már nem jön létre hőátadás [44.] .
Elektromos (Electric) – az elektromos vagy elektromágneses analízisben szereplő villamos vezetők közötti elektromos ellenállást vagy vezetőképességet definiálja. A hőtani analízishez hasonlóan, két test közötti áramvezető képesség megléte a testek érintkezésének, vagy egymáshoz közel lévő felületek esetén a köztük lévő távolság függvénye, amit a pinball opcióval állíthatunk be.

2.7. A szimuláció főbb beállításai és futtatása

2.7.1. Az analízis típusának kiválasztása

A szerkezeti analízis a mechatronikai feladatok talán az egyik leggyakrabban alkalmazott végeselemes vizsgálati módszere. A kifejezés magában foglalja az építészetben előforduló szerkezetek, (úgy, mint a hidak, épületek, stb.), valamint a gépészetben előforduló mechanikus elemeket, (mint pl.: közlekedési eszközök, gépalkatrészek, stb.). A szerkezeti analízis egyre nagyobb teret nyer a bimechanikában és az orvostudományban is (biológiai szövetek, implantátumok, orvosi eszközök vizsgálatában.). A szerkezeti analízisek során az elsődlegesen kiszámolt ismeretlen az elmozdulás, az összes többi mennyiség (megnyúlás, feszültség, reakcióerők) ebből vannak származtatva. A szerkezeti analízisek főbb típusai:

Statikai analízis (Static Analysis) – Statikai (tehát időfüggetlen) terhelés hatására kialakuló állandósult deformáció, feszültség, stb. meghatározására szolgál. Figyelmen kívül hagyja a tehetetlenséget és csillapítást, vagyis az időfüggő terheléseket okozó elemeket. Tartalmazhat viszont időben állandó inerciális terheléseket, mint pl. a gravitáció vagy a szögsebesség, vagy időben lassan változó hatásokat, mint a terhelés lassú megváltozása, vagy az anyag időfüggő viselkedése (pl. kúszás). A statikai analízis lehet lineáris, vagy nemlineáris. A nemlineáris oka lehet az anyagi nemlinearitás, nagy alakváltozás (large deflection / large strain), vagy a terhelési, ill. peremfeltételek megváltozása.
Modál analízis (Modal Analysis) – A modál vagy alaki analízis az adott szerkezet rezgési karakterisztikájának meghatározására, vagyis a sajátfrekvenciáinak kiszámolására és a lengésképek bemutatására használjuk. A modál analízis kiindulási pontja lehet részletesebb dinamikai vizsgálatoknak, mint a tranziens dinamikai, harmonikus, vagy a spektrum analízis. Lehetőség van előfeszített szerkezetek modál analízisére, mint pl. nagy sebességgel forgó, rezgésre hajlamos alkatrészek (turbinalapát).
Harmonikus analízis (Harmonic Analysis) – Egy szerkezet időben ciklikusan változó, (harmonikus) gerjesztésre adott állandósult válaszának meghatározására használjuk. Tehát az eredmény nem tartalmazza a terhelés elején fellépő tranziens rezgéseket. Az analízis segítségével előrejelezhető a szerkezet hosszú távú dinamikai viselkedése harmonikus gerjesztés hatására. Ezáltal vizsgálható a szerkezet rezonanciája vagy kifáradása. A vizsgálat eredményeként, a vizsgált mennyiséget (leggyakrabban elmozdulást) kapjuk a frekvencia függvényében. A lineáris harmonikus vizsgálatban a nemlineáris elemek figyelmen kívül maradnak.
Tranziens dinamikai analízis (Transient Dynamic Analysis / Time-history Analysis) –Egy szerkezet tetszőleges, időben változó terhelésre (statikus, tranziens, harmonikus) adott válaszának meghatározására használjuk. Minden fajta nemlinearitás alkalmazható, ami a statikus szimulációban. A tranziens analízis időbeli lefolyása szempontjából a szerkezet tehetetlenségének és csillapításának van fontos szerepe. Amennyiben ezek hatása nem fontos, akkor a statikus analízis alkalmazható helyette.
Spektrum analízis (Spectrum Analysis) – A modál analízis kiterjesztett változata, amely a válaszspektrum vagy véletlenszerű rezgés bemenetre adott feszültséget vagy alakváltozást számolja ki.
Kihajlás vizsgálat (Buckling Analysis) – A kihajlást előidéző terhelés (az a kritikus terhelés, amelynél a szerkezet elveszti stabilitását) és a kihajlási alak meghatározására szolgál. Lineáris és nemlineáris kihajlás egyaránt vizsgálható.
Explicit dinamikai analízis (Explicit Dynamic Analysis) – Az explicit dinamika gyors számolást nyújt rövid idejű feladatok, nagy alakváltozások, összetett érintkezési problémák, valamint nagy alakváltozásokkal és összetett nemlinearitásokkal rendelkező kvázistatikus problémák megoldásához.
Többtest dinamikai szimuláció (Multibody simulation) – Több összekapcsolt merev vagy rugalmas testből álló rendszer dinamikai szimulációja alkotja. Az egyes testeket kinetikailag megengedett kényszerek láncolata, mint pl. csuklók kötik egymáshoz. A komponensek így nagy elmozdulásra, nagy elfordulásra és véges alakváltozásra képesek.

Termikus analízisek (Thermal Analysis)

Állandósult termikus analízis (steady-state thermal analysis) – A hőmérsékleteloszlás vagy egyéb hőtani mennyiségek meghatározására szolgál állandósult terhelési feltételek mellett. A szimuláció során a hőtároló hatás időbeli változása figyelmen kívül hagyható. Eredményül a hőtani folyamat állandósult állapotát adja.
Tranziens termikus analízis (transient thermal analysis) - A hőmérsékleteloszlás vagy egyéb hőtani mennyiségek, az idő függvényében történő meghatározására szolgál.

Elektromágneses analízis (Electromagnetic Analysis)

Nagyfrekvenciás elektromágneses analízis (High-Frequency Electromagnetic Analysis)–adott szerkezetben terjedő, nagyfrekvenciás elektromágneses tér és hullámok szimulációjára szolgál. Olyan esetekben célszerű az alkalmazása, amikor a hullámhossz hasonló nagyságrendű vagy kisebb, mint a vizsgált szerkezet mérete. A vizsgálati frekvenciatartomány néhány száz MHz-től néhány száz GHz-ig terjedhet.
Alacsony frekvenciás elektromágneses analízis (Low-Frequency Electromagnetic Analysis) – A szimuláció során a mágneses tér az elektromos áram, állandómágnes vagy külső tér hatására jöhet létre. A szimulációban résztvevő anyagokat villamos szempontból nem vezető és vezető (örvényáram vagy a nélküli) ill. mágneses tulajdonságaik szempontjából nem mágneses, lágy és kemény mágneses anyagok lehetnek.

Folyadék analízis (Fluids Analysis) [6.]

Noha a folyadékszimulációk nem tartoznak a jegyzet témakörébe, említés szinten érdemes róluk szót ejteni, mivel nagy fontossággal bírnak a végeselemes analízisek terén. Főbb típusaik:

Numerikus folyadékdinamika (Computational Fluid Dynamics (CFD))–(FLOTRAN, CFX, FLUENT, POLYFLOW). A CFD folyadékáramlást, hőátadást, kémiai reakciókat és egyéb kapcsolódó fizikai jelenségeket szimulációjára szolgáló eszköz. A szimuláció megoldása egy meghatározott régióra korlátozódik, amely a meghatározott peremfeltételekkel rendelkezik. A CFD analízisben lehetőség van Lamináris vagy turbulens, termál vagy adiabatikus, Szabad felület, Összenyomható vagy összenyomhatatlan, Newtoni vagy nem Newtoni, és többfajta áramlás szimulációkra vagy ezek kombinációjára.

Akusztikus (Acustics) – Az akusztikus analízis a rezgések, hanghullámok keletkezését (generation), terjedését (propogation), abszorpcióját (absorption) és visszaverődését (reflection) vizsgálja valamilyen fluidumban.

Vékony réteg (Thin Film) –A szimuláció mozgó felületek közötti vékony folyadékréteget vizsgálja, amely megváltoztatja a szerkezet viselkedését, merevség és csillapítás hozzáadásával. A felületek a résre merőleges elmozdulása a folyadék préselését, érintő irányú elmozdulása a folyadék csúszását eredményezi.

2.7.2. A megoldó kiválasztása (Selecting a Solver)

A szimuláció futtatása előtt az alábbi megoldók közül választhatunk a feladat elvégzésére [6.] .

Ritka közvetlen, (sparse direct solution) – Közvetlen elimináció, (direct elimination). Alkalmazása olyan esetben célszerű, ahol a robusztus megoldás és a számolási idő a követelmény (nemlineáris), és olyan lineáris számolásnál, ahol az iteratív megoldók túl lassúak a konvergáláshoz. Ideális modellméret: 0,1 - 5 millió szabadságfok.
Előkezelt konjugált gradiens, (Preconditioned Conjugate Gradient (PCG)) - Iterációs megoldó, (iterative solver). A direkt megoldóhoz képest relatíve kis I/O követelmény. Nagy szilárdtest elemeket és finom hálót tartalmazó modelleknél a legelőnyösebb az alkalmazása. [A legrobosztusabb iteratív megoldó az Ansys-ban] Ideális modellméret: 0,5 - 20 millió szabadságfok.
Jacobi-konjugált gradiens, (Jacobi Conjugate Gradient (JCG)), - Iterációs megoldó. Egyszeres terek (termikus, mágneses, akusztikus) megoldására a legalkalmasabb. Gyors és egyszerű előkészítőt (preconditioner) használ, minimális memóriaigénnyel. Nem olyan robusztus, mint a PCG. Ideális modellméret: 0,5 - 20 millió szabadságfok.
Befejezetlen Cholesky-konjugált gradiens, (Incomplete Cholesky Conjugate Gradient (ICCG)) - Iterációs megoldó. Kifinomultabb előkészítővel rendelkezik, mint a JCG. A legalkalmasabb olyan bonyolultabb problémák megoldására, melyeknél a JCG már hibázik, mint például aszimmetrikus termál analízis. Ideális modellméret: 0,05 – 1 millió szabadságfok
Kvázi-minimális maradék (QMR) megoldás,(Quasi-Minimal Residual (QMR) solution) - (Iterációs megoldó) Nagyfrekvenciás elektromágneses analízis. Ideális modellméret: 0,05 - 1 millió szabadságfok.

A Direkt megoldó speciális változata, a PCG és a JCG megoldók alkalmasak párhuzamosan (klaszterekbe) rendezett hardveren történő futtatásra is.

2.8. Az eredmények lekérdezése és kiértékelése (posztprocesszálás)

A szimuláció futtatása után választ akarunk kapni azokra a kérdésekre, amelyek információt szolgáltatnak a szerkezet működéséről, ill. működőképességéről. Például, hogy milyen feszültség ébred az adott szerkezet egyes részein, mi a szerkezet maximális alakváltozása, milyen elmozdulást végez a szerkezet egy pontja adott terhelés hatására, milyen lesz a szerkezet hőmérséklet-eloszlása, vagy hogy milyen a mágneses tér az adott szerkezetben, stb. A szimuláció eredményeinek feldolgozása és a kívánt mennyiség bemutatása (postprocessing) érdekében definiálnunk kell, hogy mire is vagyunk kíváncsiak.

2.8.1. Lekérdezett mennyiségek

A lekérdezett mennyiségek helyes értelmezése döntő fontosságú, mivel egy jól összeállított és helyes eredményeket hozó szimulációról is kiolvashatunk fals eredményeket a helytelenül értelmezett lekérdezések miatt. A helyes kiértékelés érdekében tekintsük át a legfontosabb fizikai mennyiségeket.

Elsődleges adatok – Az elsődlegesen kiszámolt mennyiségek az egyes csomópontok szabadságfokainak megoldása (nodal solution), úgy mint az elmozdulás, hőmérséklet, mágneses potenciál, stb.

Származtatott adatok – Az elsődlegesen kiszámolt adatokból számolt, úgy mint a feszültség és alakváltozás, hőmérsékleti gradiens, mágneses fluxus, stb. A származtatott mennyiségek megoldása az elemekre (element solution) vagy a csomópontokra vonatkozhat (nodal solution). Az alábbiakban táblázatosan mutatjuk be néhány analízis típushoz tartozó elsődlegesen és másodlagosan kiszámolt mennyiségeket.

2.5. táblázat - Néhány analízis típushoz tartozó elsődleges és másodlagos mennyiségek.

Analízis típus

(Discipline)

Elsődleges adat

(Primary Data)

Származtatott adatok

(Derived Data)

Szerkezeti

(Structural)

Elmozdulás (Displacement)

Feszültség, fajlagos nyúlás, reakcióerő, stb.

(Stress, strain, reaction, etc.)

Termikus

(Thermal)

Hőmérséklet (Temperature)

Hőáram, hőmérsékleti gradiens, stb.

(Thermal flux, thermal gradient, etc.)

Mágneses

(Magnetic)

Mágneses potenciál (Magnetic Potential)

Mágneses fluxus, áramsűrűség, stb.

(Magnetic flux, current density, etc.)

Elektromos

(Electric)

Elektromos potenciál (Electric Scalar Potential)

Elektromos térérősség, indukció, stb.

(Electric field, flux density, etc.)

Folyadék

(Fluid)

Sebesség, nyomás (Velocity, Pressure)

Nyomásgradiens, hő fluxus, stb.

(Pressure gradient, heat flux, etc.)

2.8.2. Az eredmények megjelenítési formái

Az eredmények megjelenítése történhet grafikus vagy szöveges formában. Az alábbiakban bemutatunk néhány általánosan használt eljárást egy statikus szerkezeti analízis példáján keresztül. A grafikus megjelenítés történhet a modellen szilárdtest vagy vektoros formában, ill. diagramon.

Valamely számolt mennyiség (pl. feszültség, alakváltozás, stb.) a szilárdtestben való eloszlását a színsávokkal ábrázoljuk. Az egyes színekhez tartozó értéket a képernyőn megjelenő színskála segítségével olvashatjuk le. Alkalmasan elhelyezett címkék segítségével a számolás lokális eredményeit, vagy annak minimum és maximum helyeit közvetlenül a testmodellen is lekérdezhetjük.

Vektormennyiségek bemutatása történhet vektoros formában is. Némely esetben ezek hossza vagy sűrűsége változtatható az adott mennyiség intenzitása szerint.

Diagramban számos mennyiség ábrázolható és lekérdezhető a végeselem programokon belül. Például statikus szerkezeti analízisnél, a lekérdezett mennyiség eloszlása egy él mentén vagy tranziens dinamikai szimulációnál az időbeli változása.

a.) testmodellen színsávok segítségével, b.) a testmodellen vektorok segítségével, c.) diagramon.

2.31. ábra - Az eredmény megjelenítésének lehetséges módjai.

A szilárdtest megjelenítése történhet a deformáció ábrázolásával, ill. a nélkül, valamint a két állapotot együttesen ábrázolva. A deformáció megjelenítés mértéke skálázható, így az esetlegesen kis valós (True scale) deformáció is látványossá tehető annak nagyításával. Természetesen ebben az esetben csak a képi megjelenítés változik, a színsávok értéke továbbra is a valós értéket mutatja. Általában lehetőség van az elemek kontúrjának kirajzolására is a látványosabb megjelenítés érdekében.

a.) deformálatlan drótváz, b.) deformálatlan átlátszó, c.) csak deformált test, d.) háló megjelenítése.

2.32. ábra - Az eredmény megjelenítésének módjai.

A színsávok megjelenítése történhet éles és lágy átmenettel, vagy csak az egyenértékű határvonalak (isolines) kirajzoltatásával a modell felületén. A színsávok nélküli deformált modell ábrázolása is lehetséges.

a.) kontrasztos, b.) "lágy" átmenet, c.) Egyenértékű vonalak, d.) csak a szilárdtest megjelenítése.

2.33. ábra - Egyenértékű színsávok megjelenítési módjai.

A belső helyeken lévő eredmények megtekintése érdekében lehetőség van a modell metszésére sík vágófelületekkel vagy az egyenértékű felületek mentén nyitott vagy zárt formában egyaránt.

a.) Metszősíkokkal feldarabolt térfogat, b.) egyenértékű felületekkel határolt zárt térfogat, c.) egyenértékű felületek.

2.34. ábra - Metszési módok.

2.9. Ellenőrző kérdések a 2. fejezethez.

Milyen alapvető lépései vannak egy végeselemes analízisnek?
1. Hálókészítés, anyagmodell hozzárendelés, posztprocesszálás, eredmények kiértékelése.
2. Geometria elkészítése, hálózás, anyagmodell hozzárendelés, peremfeltételek és terhelések megadása, megoldás, eredmények kiértékelése.
3. Geometria elkészítése, hálózás, elemek hozzárendelése, terhelőerők definiálása, preprocesszálás, posztprocesszálás.
Hány szabadságfokkal rendelkezik egy 2D-s statikai analízisben használt lineáris háromszögelem?
1. 3,
2. 6,
3. 9,
4. 12.
Hány szabadságfokkal rendelkezik egy hőtani analízisben használt lineáris tetraéder elem?
1. 4,
2. 6,
3. 8,
4. 12.
Milyen típusú analízist alkalmazna egy kivágásokat tartalmazó sík lemez vizsgálatához, ha ismert, hogy a lemezt terhelő erők a lemez síkjában hatnak?
1. 2D – Sík alakváltozás,
2. 2D – Sík feszültség,
3. 2D – tengelyszimmetrikus,
4. 3D – héj modell,
5. 3D – testmodell.
Milyen típusú analízist alkalmazna egy forgásszimmetrikus nyomástartó edény vizsgálatához?
1. 2D – Sík alakváltozás,
2. 2D – Sík feszültség,
3. 2D – tengelyszimmetrikus,
4. 3D – héj modell,
5. 3D – testmodell.
Milyen típusú analízist alkalmazna egy hosszú, állandó keresztmetszetű alkatrész vizsgálatához, ha az alkatrészt a hossza mentén állandó nagyságú és a keresztmetszetével párhuzamos irányú megoszló erő terheli?
1. 2D – Sík alakváltozás,
2. 2D – Sík feszültség,
3. 2D – tengelyszimmetrikus,
4. 3D – héj modell,
5. 3D – testmodell.
Milyen típusú szimulációt alkalmazna egy lemezalkatrész vizsgálatához, ha a lemezt terhelő erők a lemez síkjára merőlegesek?
1. 2D – Sík alakváltozás,
2. 2D – Sík feszültség,
3. 2D – tengelyszimmetrikus,
4. 3D – héj modell,
5. 3D – testmodell.
Az alábbi feltételek melyike okozhatja a szimuláció nemlinearitását? (Több válasz is megjeleölhető.)
1. Nagy deformáció,
2. Változó terhelési feltételek,
3. „Ragasztott” (Bonded) kontaktok,
4. Nemlineáris anyagmodell.
Mi a különbség az ortotróp és izotróp anyagmodell között?
1. Az ortotróp anyag viselkedése nemlineáris, míg az izotrópé igen.
2. Az ortotróp anyag tulajdonságai a derékszögű vagy polár koordinátarendszer tengelyei mentén különbözőek lehetnek, míg az izotrópé minden irányban megegyezik.
3. Az ortotróp anyag tulajdonságai a tetszőleges irányban különbözőek lehetnek, míg az izotrópé csak a Descartes koordináta rendszer tengelyei mentén lehetnek eltérőek.
Lineárisan rugalmas, homogén és izotróp anyag statikus szerkezeti analízise esetén milyen anyagparaméterek megadása szükséges (elégséges)?
1. Rugalmassági modulusz és a sűrűség,
2. Rugalmassági modulusz, a Poisson-tényező és a nyíró modulusz,
3. Rugalmassági modulusz és a Poisson-tényező,
4. Rugalmassági modulusz, a Poisson-tényező és a folyáshatár.
Melyik az HAMIS állítás az alábbiak közül?
1. A Poisson-tényező az anyag összenyomhatóságát jellemzi.
2. A Poisson-tényező a terhelés irányába eső és az arra merőleges alakváltozás különbsége.
3. A Poisson-tényező elméleti értéke – 1 és 0,5 közötti lehet.
Milyen esetekben van szükség az anyag sűrűségének megadására? (Több válasz is megjelölhető.)
1. Statikus szerkezeti analízis esetén ha időben állandó inerciális jellegű terhelés van megadva.
2. Tranziens jelenségek dinamikai szimulációjánál.
3. Modás és harmonikus analízis esetén.
4. Statikus szerkezeti analízis esetén, ha terhelési lépésenként változó erő van megadva.

Megoldások

Milyen alapvető lépései vannak egy végeselemes analízisnek?
1. Hálókészítés, anyagmodell hozzárendelés, posztprocesszálás, eredmények kiértékelése.
2. Geometria elkészítése, hálózás, anyagmodell hozzárendelés, peremfeltételek és terhelések megadása, megoldás, eredmények kiértékelése.
3. Geometria elkészítése, hálózás, elemek hozzárendelése, terhelőerők definiálása, preprocesszálás, posztprocesszálás.
Hány szabadságfokkal rendelkezik egy 2D-s statikai analízisben használt lineáris háromszögelem?
1. 3,
2. 6,
3. 9,
4. 12.
Hány szabadságfokkal rendelkezik egy hőtani analízisben használt lineáris tetraéder elem?
1. 4,
2. 6,
3. 8,
4. 12.
Milyen típusú analízist alkalmazna egy kivágásokat tartalmazó sík lemez vizsgálatához, ha ismert, hogy a lemezt terhelő erők a lemez síkjában hatnak?
1. 2D – Sík alakváltozás,
2. 2D – Sík feszültség,
3. 2D – tengelyszimmetrikus,
4. 3D – héj modell,
5. 3D – testmodell.
Milyen típusú analízist alkalmazna egy forgásszimmetrikus nyomástartó edény vizsgálatához?
1. 2D – Sík alakváltozás,
2. 2D – Sík feszültség,
3. 2D – tengelyszimmetrikus,
4. 3D – héj modell,
5. 3D – testmodell.
Milyen típusú analízist alkalmazna egy hosszú, állandó keresztmetszetű alkatrész vizsgálatához, ha az alkatrészt a hossza mentén állandó nagyságú és a keresztmetszetével párhuzamos irányú megoszló erő terheli?
1. 2D – Sík alakváltozás,
2. 2D – Sík feszültség,
3. 2D – tengelyszimmetrikus,
4. 3D – héj modell,
5. 3D – testmodell.
Milyen típusú szimulációt alkalmazna egy lemezalkatrész vizsgálatához, ha a lemezt terhelő erők a lemez síkjára merőlegesek?
1. 2D – Sík alakváltozás,
2. 2D – Sík feszültség,
3. 2D – tengelyszimmetrikus,
4. 3D – héj modell,
5. 3D – testmodell.
Az alábbi feltételek melyike okozhatja a szimuláció nemlinearitását? (Több válasz is megjeleölhető.)
1. Nagy deformáció,
2. Változó terhelési feltételek,
3. „Ragasztott” (Bonded) kontaktok,
4. Nemlineáris anyagmodell.
Mi a különbség az ortotróp és izotróp anyagmodell között?
1. Az ortotróp anyag viselkedése nemlineáris, míg az izotrópé igen.
2. Az ortotróp anyag tulajdonságai a derékszögű vagy polár koordinátarendszer tengelyei mentén különbözőek lehetnek, míg az izotrópé minden irányban megegyezik.
3. Az ortotróp anyag tulajdonságai a tetszőleges irányban különbözőek lehetnek, míg az izotrópé csak a Descartes koordináta rendszer tengelyei mentén lehetnek eltérőek.
Lineárisan rugalmas, homogén és izotróp anyag statikus szerkezeti analízise esetén milyen anyagparaméterek megadása szükséges (elégséges)?
1. Rugalmassági modulusz és a sűrűség,
2. Rugalmassági modulusz, a Poisson-tényező és a nyíró modulusz,
3. Rugalmassági modulusz és a Poisson-tényező,
4. Rugalmassági modulusz, a Poisson-tényező és a folyáshatár.
Melyik az HAMIS állítás az alábbiak közül?
1. A Poisson-tényező az anyag összenyomhatóságát jellemzi.
2. A Poisson-tényező a terhelés irányába eső és az arra merőleges alakváltozás különbsége.
3. A Poisson-tényező elméleti értéke – 1 és 0,5 közötti lehet.
Milyen esetekben van szükség az anyag sűrűségének megadására? (Több válasz is megjelölhető.)
1. Statikus szerkezeti analízis esetén ha időben állandó inerciális jellegű terhelés van megadva.
2. Tranziens jelenségek dinamikai szimulációjánál.
3. Modás és harmonikus analízis esetén.
4. Statikus szerkezeti analízis esetén, ha terhelési lépésenként változó erő van megadva.

Vissza		Előre
1. fejezet - A Végeselem módszer elméleti alapjai	Főoldal	3. fejezet - Lineáris statikai analízis