14. fejezet - Komplex mechatronikai projektfeladat
Vissza		Előre

14. fejezet - Komplex mechatronikai projektfeladat

Tartalom

A feladat egy egyszerű nyúlásmérő bélyeges gyorsulásérzékelő tervezése. A legegyszerűbb konstrukció, egy mozgó házban konzolosan rögzített lemez, melynek a befogással ellentétes végén egy tehetetlen tömeg teremti meg a gyorsulás és a rúdvégre ható erő közötti kapcsolatot. A lemez alakját egyenszilárdságúra célszerű kialakítani, hogy a fajlagos nyúlás értéke állandó legyen a deformálódó lemez hossza mentén. Így kevésbé lesz érzékeny a nyúlásmérő bélyegek elhelyezésére. Az állandó vastagságú egyenszilárdságú tartó előkövetelménye, hogy a befogás helyétől a terhelés (az elhelyezett tömeg) támadáspontjáig lineárisan csökkenjen a szélessége. Tehát egy háromszög alakú lemezre van szükség, melynek oldalai a tömeg rögzítésnek középpontjában metszik egymást. Természetesen a kész jelátalakító geometriája ettől bonyolultabb, a rögzítési helyek megfelelő kialakítása miatt, de a vizsgálat szempontjából, elég az egyszerűsített modellel dolgozni.

14.1. Numerikus megoldás

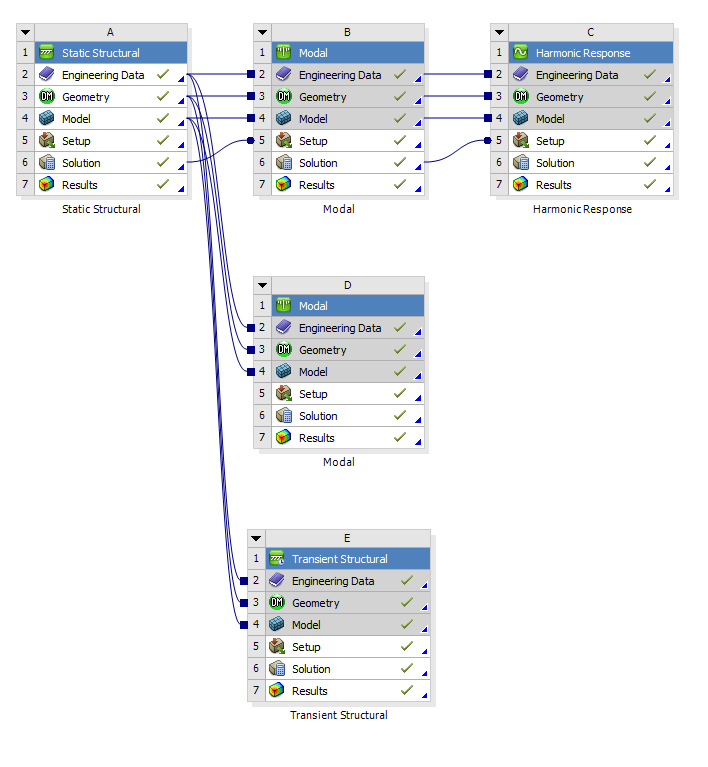
A feladat megoldására az ANSYS Workbench végeselem programot fogjuk használni. A projektszervező felületen látható, hogy statikai (jelátalakító statikus jelleggörbéjének a meghatározásához), modál, harmonikus és tranziens mechanikai analízist (a dinamikai átviteli tulajdonságok meghatározásához) fogunk végezni.

14.1. ábra - A projektfelületen elhelyezett analízisek.

14.1.1. Statikai analízis

A következőekben egy statikai analízissel vizsgáljuk, hogy az egyik oldalán befogott egyenszilárdságú tartó, mekkora Z tengely irányú lehajlást és Y tengely menti fajlagos nyúlást szenved a Z irányú gyorsulás hatására.

Kiinduló adatok:

Méretek: B=10mm, L=20mm, vastagság: h=0,2mm;

Anyag: Rugóacél – E=200GPa, ν=0,3;

Tömeg a tartó végén: m=0,02kg;

Terhelés: a=1G, (9,8066m/s ² ).

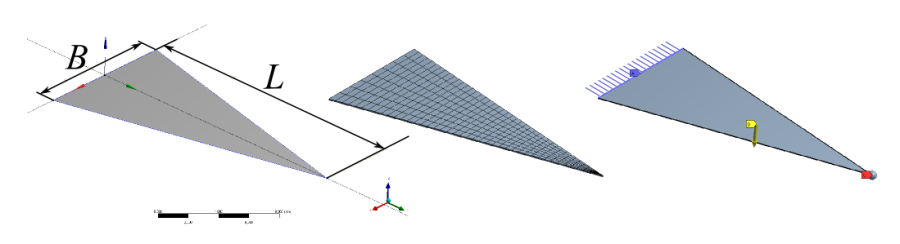
14.2. ábra - Az egyenfeszültségű tartó geometriája, Hálózása és perem, ill. terhelési feltételei.

A geometriát célszerű felületmodellként létrehozni, így héjelemeket használhatunk a hálózás során. A rendezett háló érdekében célszerű a felület felosztása (14.3. ábra).

A lemez megtámasztása a széles végénél történik egy Fix kényszerrel (Fix Support) . A háromszög csúcsánál elhelyezünk egy tömegpontot (Point Mass) , és terhelésként a földi gravitációt (Standard Earth Gravity) alkalmazzuk.

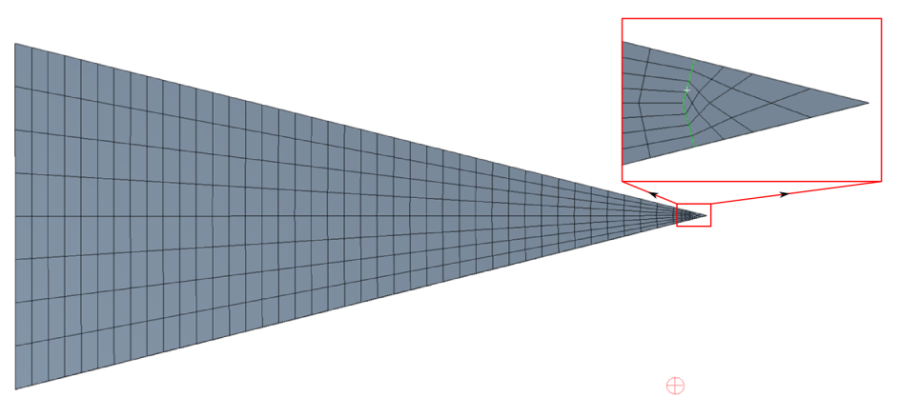
14.3. ábra - Strukturált háló létrehozása háromszög felületen.

A lehajlás számszerű lekérdezéséhez helyezzünk el egy konstrukciós vonalat (Path) , a lemez hossztengelye mentén.

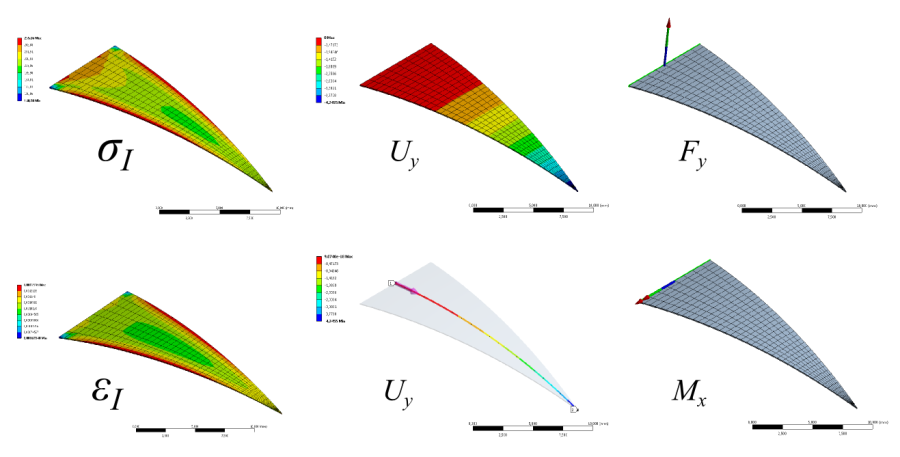
A futtatás után kérdezzük le az Z irányú lehajlás (Directional Deformation), valamint a főfeszültségek (Maximum Principal Stress) és főnyúlások (Maximum Principal Strain) értékeit. És ellenőrzésképpen lekérdezhetjük a befogás helyén ébredő reakcióerő (Force Reaction) és nyomaték (Reaction Moment) értékét (14.4. ábra).

Megjegyzés: Amennyiben nem, vagyunk biztosak az alakváltozási főirányokkal, célszerű ellenőrizni a helyi tenzorok megjelenítésével ( Strain/Vector Principal ). Ennek megfelelően célszerű lehet egy alkalmasan elhelyezett koordinátarendszer, valamely tengelye szerint lekérdezni a normálfeszültségek, ill. alakváltozások értékét (Normal Elastic Strain) , (pl. esetünkben, az hossztengely irányában (Y)). Nagy alakváltozások esetén, a kezdetben párhuzamos tengely nem követi a deformált alakot, ezért célszerűbb lehet a főnyúlás lekérdezése.

14.4. ábra - Az egyenfeszültségű tartó analízisének eredményei.

14.1.2. Modal analízis

Egy gyorsulásérzékelő esetében nélkülözhetetlen a dinamikai tulajdonságok vizsgálata. Első lépésben határozzuk meg a szerkezet sajátfrekvenciáit (első 6-ot), és a hozzájuk tartozó lengésképeket. Megjegyzés: Valójában elég lenne az első sajátfrekvencia vizsgálata, mivel a jelátalakító működési tartománya ez alatt kell, hogy legyen. A többi csak a példa kedvéért mutatjuk meg.

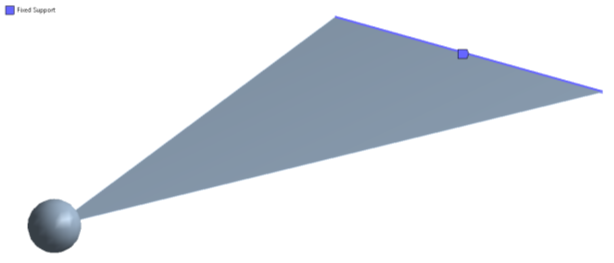
14.5. ábra - Megtámasztás a terheletlen modál analízis esetén.

A modál analízis során lehetőség van terheletlen és az előterhelt vizsgálat elvégzésére. Előfeszített, vagy előterhelt analízishez egy előzetesen lefuttatott statikai analízis jelenti terhelési és peremfeltételeket. Ehhez a projekt felületen, létrehozásakor a modál analízis panelt rá kell húzni a már meglévő statikai (Static Structural) megfelelő sorára. A megoldásra (Solution) húzva az előterhelt esetet, a végeselem modellre (Modell) húzva csak a beállításokkal ellátott terheletlen analízist hozzuk létre. A terheletlen analízisnél csupán a megfogást (Fix Suppoert) kell definiálni (14.5. ábra), a pontszerű tömeget, anyagmodellt és a hálózási beállításokat megörökli a végeselem modell a statikai analízistől. Figyeljük meg, hogy melyik analízisbe milyen elemek vannak bekötve (14.1. ábra).

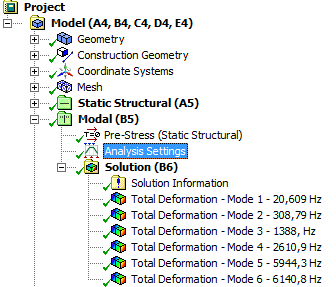
14.6. ábra - A modellfában megjelenő előterhelés.

A beállítások elvégzése után futtassuk mindkét analízist és hasonlítsuk össze az eredményeket.

14.1. táblázat - A jelátalakító első 6 sajátfrekvenciája terheletlen és terhelt állapotban.

Módus	Terheletlenül f [Hz]	Előterheléssel f [Hz]
1.	20,575	20,609
2.	315,85	308,79
3.	1877,1	1388,
4.	1937,5	2610,9
5.	5933,1	5944,3
6.	6019,1	6140,8

Mivel sem a sajátfrekvenciák értékében, sem pedig a lengésképek alakjában nincs jelentős különbség a kétfajta terhelési állapot során, itt csak a terhelt szerkezet lengésképeit mutatjuk.

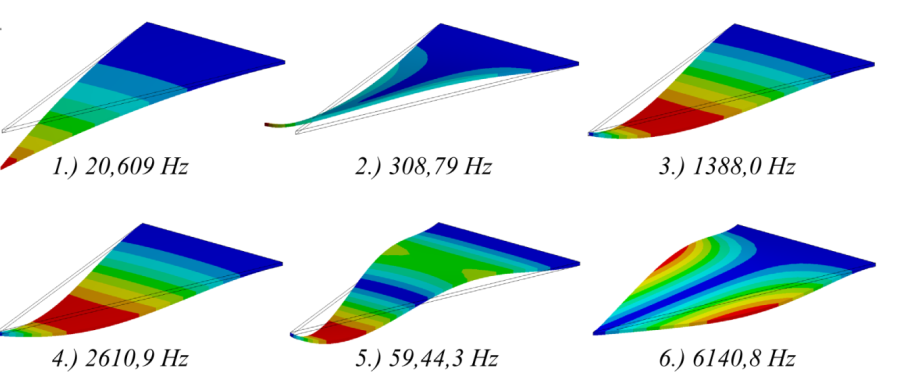
14.7. ábra - A jelátalakító földi gravitációval terhelt modelljének első 6 sajátfrekvenciája és lengésképe.

Mint már említettük számunkra az 1. sajátfrekvencia a lényeges, mert mint ahogy a hozzá tartozó lengésalak is mutatja, ez az első lengés, amelyik a mérés irányába esik.

14.1.3. Harmonikus

Hogy megvizsgáljuk a jelátalakító átviteli tulajdonságait a frekvenciatartományban, el kell végezni egy harmonikus válasz analízist (Harmonic Response) , amely a harmonikusan gerjesztett rendszer válaszát (kimeneti amplitúdóját) adja meg egy megadott frekvenciatartományon. Amint a 14.1. ábra mutatja, lehetőség van a modál analízis eredményeinek (Solution) felhasználására a harmonikus analízis során, a (Mode Superposition) beállítás alkalmazásával.

Az analízis beállításai során meg kell adni a vizsgálat frekvenciatartományát. Esetünkben az előzetes modál analízis eredményei alapján (f₀=20,6Hz), ezt 0-50Hz tartományra állítjuk. Így csak, a számunkra érdekes, 1 rezonanciahely fog szerepelni a frekvenciadiagramon.

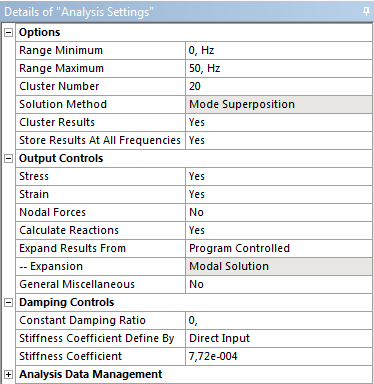
14.8. ábra - A harmonikus analízis beállításai.

Ahhoz, hogy a számolási pontok, a frekvenciatartományon ne egyenletesen, hanem a számunkra fontos helyeken, a sajátfrekvenciák környékén, sűrűbben legyenek elosztva, be kell kapcsolnunk a Cluster Result opciót. Ez szükségessé teszi csillapítás megadását, mivel e nélkül a végtelenhez tartana az amplitúdó értéke ezen a helyen.

A csillapítást (Damping) definiálhatjuk a csillapítási fok (ξ=0,05; Constant Damping Ratio ), vagy a Rayleigh féle anyagcsillapítás merevségi tagjának (β_R=2⋅ξ/ω= 0,0007746s; Stiffness Coefficient ) megadásával.

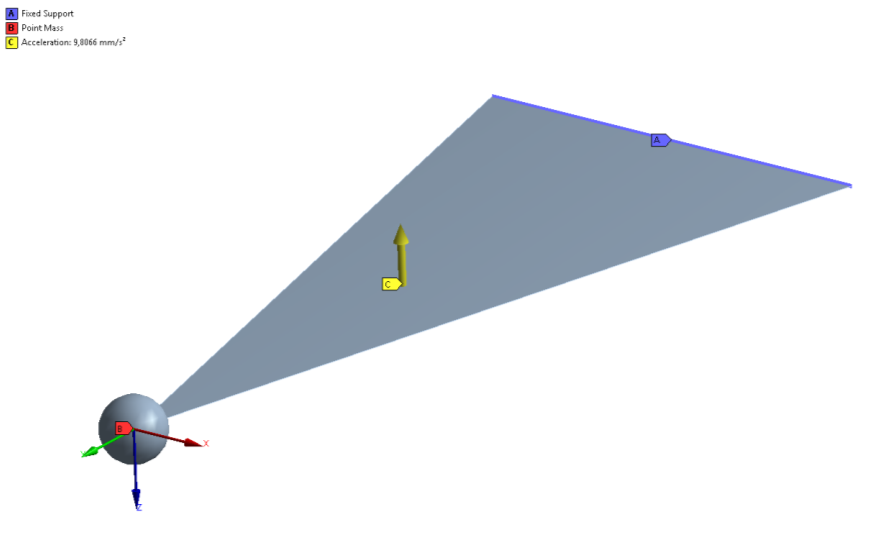
Ha a modál analízist felhasználtuk bemenetként, akkor a megtámasztást, anyagot, hálózást nem, csak a terhelést kell definiálnunk. Összességében az alábbi ábrán szereplő megtámasztásnak, gravitációs gyorsulásnak és egy koncentrált tömegpontnak kell szerepelnie a modellen (14.9. ábra). A terhelés amplitúdója megegyezik a statikai analízisnél alkalmazott földi gravitációs gyorsulás értékével (9,8066m/s²), de egy általános célú gyorsulással (Acceleration) kell megadni. Mivel a harmonikus analízis során szinuszosan változik a terhelés értéke és előjele, tehát a földi gravitáció nem jöhet szóba mint terhelés.

14.9. ábra - A harmonikus analízis során alkalmazott megtámasztás, gyorsulás és tömegpont.

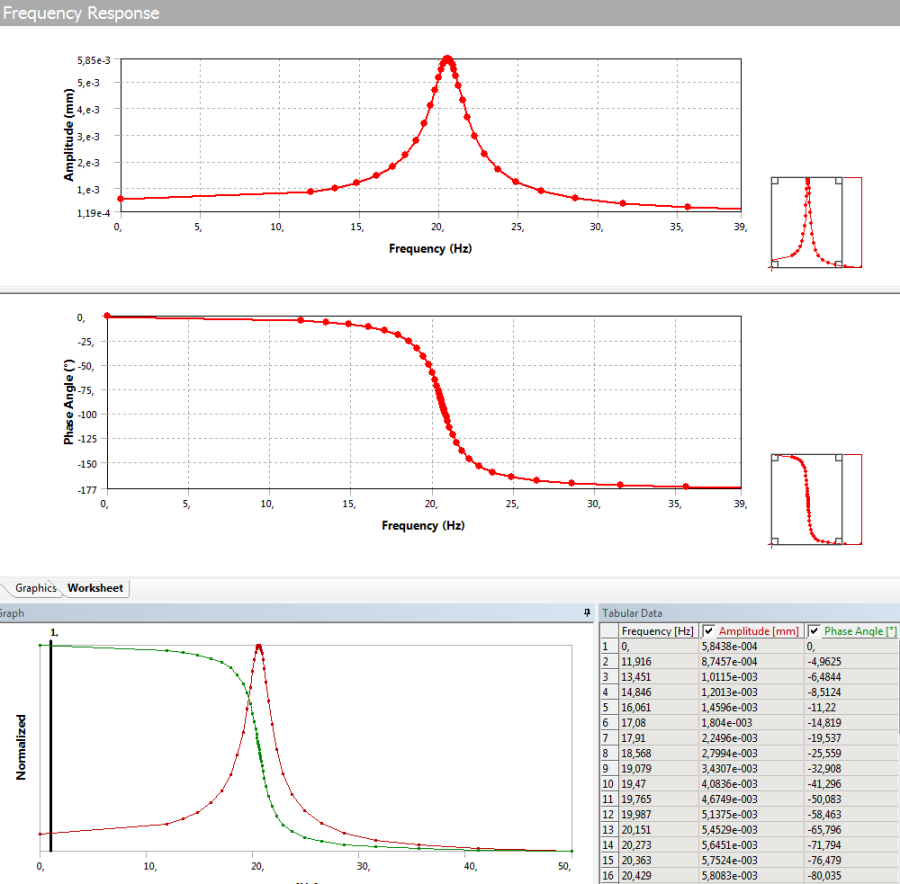
A beállítások elvégzése után futtassuk az analízist és kérdezzük le a konzolvég lehajlásának amplitúdóját és fázisát a frekvencia függvényében, vagyis egy Bode-diagramot. Ehhez a Frequency Response/Deformation parancs kiválasztása után jelöljük ki a konzol végpontját (a tömegpont közepén), és állítsuk át Z–re az irányt. A megjelenítés típusa alapértelmezetten Bode-diagram. Az adatokat a Tabular Data táblázatból egyszerűen vágólapra helyezve átvihetünk más programba adatfeldolgozás céljából.

14.10. ábra - A jelátalakító végének elmozdulása a gerjesztő gyorsulás hatására, Bode-diagramon ábrázolva.

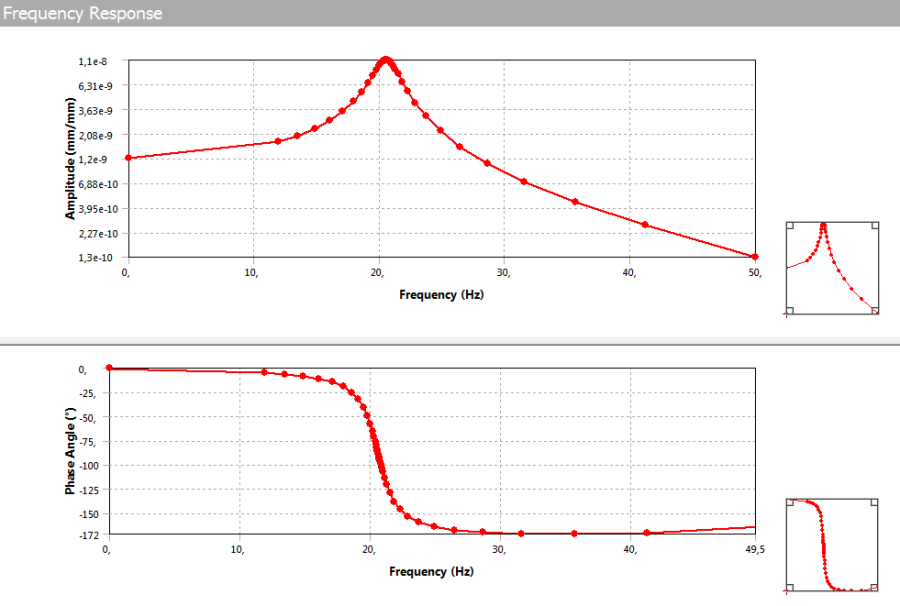
14.11. ábra - A jelátalakító felületén ébredő fajlagos nyúlás értéke a gerjesztés frekvenciájának függvényében (Bode).

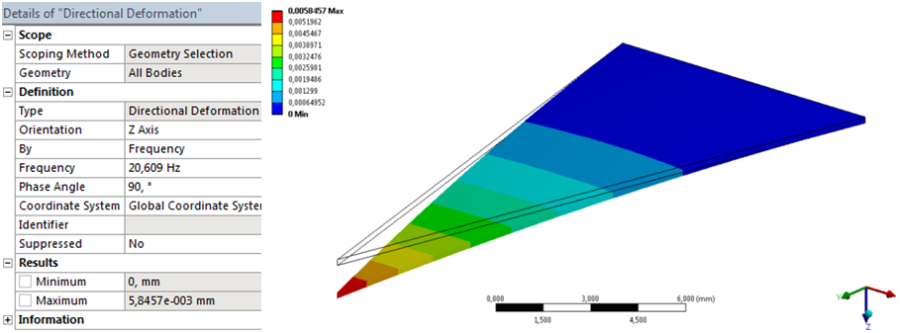
A statikai analízishez hasonlóan, itt is le tudjuk kérdezni a feszültség, alakváltozás és deformáció értékeit a teljes, vagy a kiválasztott geometriára vonatkoztatva, annyi kiegészítéssel, hogy a harmonikus analízis esetén a lekérdező parancsokban definiálnunk kell, hogy melyik frekvencián és milyen fázisszögben akarjuk tudni az adott mennyiséget (14.12. ábra).

14.12. ábra - Maximális elmozdulás lekérdezése a 20,609Hz frekvencián, 90°-os fázisnál.

14.1.4. Tranziens

A műszerünk időtartománybeli viselkedését, vagyis tranziens hatásokra adott időbeni válaszát a tranziens szerkezeti analízissel (Transient Structural) vizsgálhatjuk. A harmonikushoz hasonlóan a tranziens analízisnek is lehet bemenete egy modál analízis, de példánkon csak a geometriát, anyagot és hálózást tartalmazó végeselem modellt örökítettük át a statikai analízisről (14.1. ábra). Tehát a megtámasztást és a terhelést létre kell hoznunk az analízisen belül.

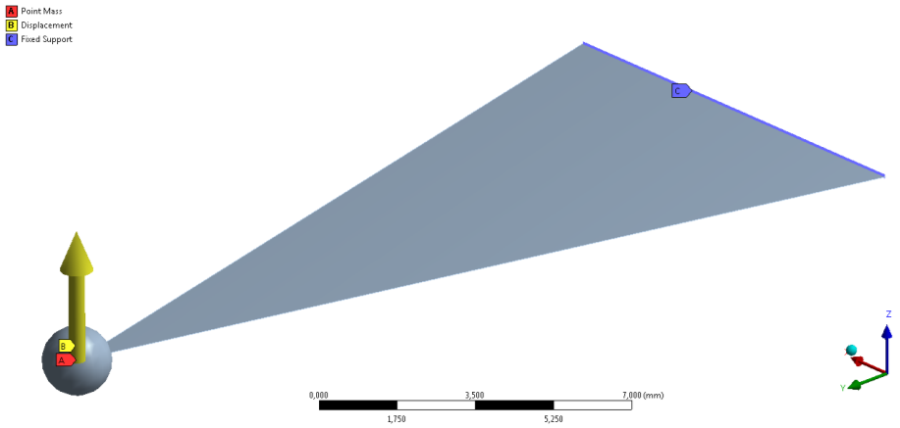
14.13. ábra - A tranziens szerkezeti analízis során alkalmazott perem és kezdeti feltételek.

A megtámasztás továbbra is a tartó széles végének fix megfogása jelenti, de a terhelés most nem a gyorsulás lesz. Azt az esetet szeretnénk szimulálni, amikor bizonyos mértékig (1mm), meghajlított tartót elengedjük, és az csillapodó lengésbe kezd., vagyis az z₀=1mm, és v₀=0m/s, kezdeti feltétellel megadott, magára hagyott rendszer viselkedését szeretnénk vizsgálni.

Ehhez definiálni kell a megtámasztást (Fix Support) és egy Z irányú, 1mm-es elmozdulás kényszert (Displacement), amit az 1mm elérésese után kikapcsolunk. Ezt 2 terhelési lépés (Step) beállításával oldjuk meg úgy, hogy az elmozdulás kezdeti értéke

az 1. lépés elején, t=0s időpillanatban z=0mm;

az 1. lépés végén t=0,5s időpillanatban z=1mm; és

a 2. lépésben kapcsoljuk ki a kényszert.

Ezt az elmozdulás mértékét jelző grafikonon (Graph), a 2. lépésben a terhelés vonalára jobb gombbal kattintva, majd az Activate/Deactivate… opciót választva tehetjük meg (14.14. ábra).

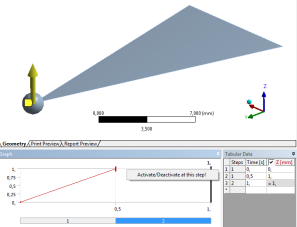
14.14. ábra - Az elmozdulás kezdeti feltétel beállítása, mint az 1. lépésben létrehozott elmozdulás.

A következő fontos lépés a lépések felosztásának, vagyis az al-lépések időtartamának (Time Step) megadása. Egy rezgő rendszernél a rezonancia periódusideje, amit az (előzetes modál analízisből megkaptunk, Tp=1/f≈0,05s) nyújt támpontot az időlépések beállításában. Az elmozdulásfüggvény alakhű reprodukálásához a periódusidőtől legalább egy nagságrendel kisebb időlépést célszerű venni, de nemlineáris problémák esetén a konvergencia elősegítése érdekében további csökkentésre is szükség lehet. Így a példánkban szereplő szerkezet analízise során az 1. lépés 0,01s-os és a 2. lépés 0,0001-0,001s-os beállítása volt szükséges (14.15. ábra).

Az analízis beállításainál a numerikus csillapítás (Numerical Damping Value) és/vagy a Rayleigh féle merevségi csillapítás (Stiffness Coefficient) értékét tudjuk megadni. Ez utóbbi értékét a harmonikus analízishez hasonlóan állítsuk β_R=2⋅ξ/ω= 0,0007746s-ra, és a numerikus csillapítást állítsuk 0-ra.

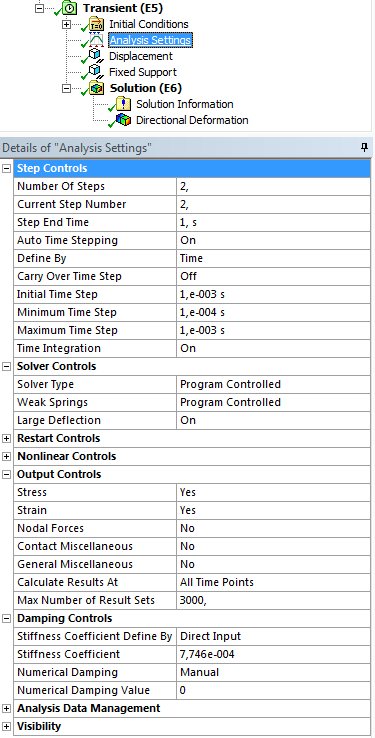
14.15. ábra - Az analízis beállításai.

A nagy lehajlások (Large Deflections) bekapcsolása után indítsuk az analízist, majd kérdezzük le a végpont Z tengely menti elmozdulását (Directonal Displacement).

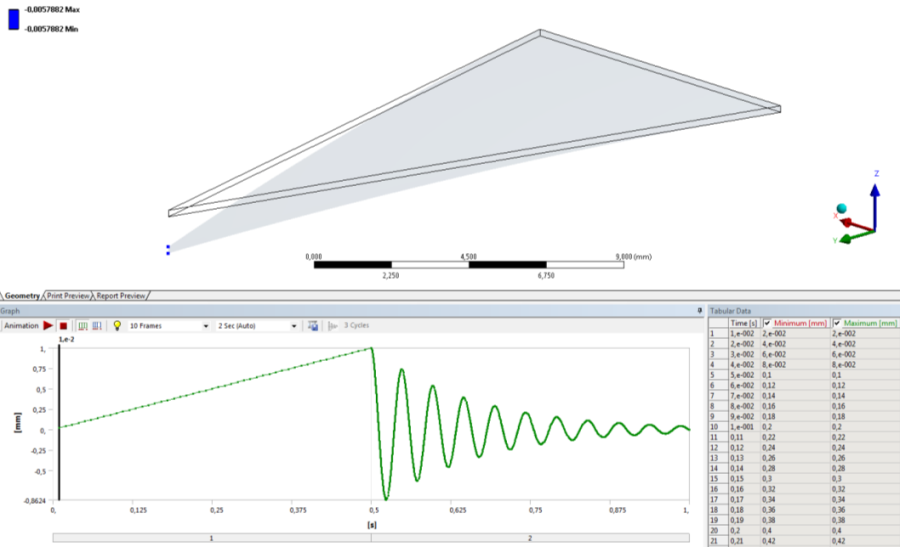
14.16. ábra - A végpont csillapodó lengését szemléltető eredmény.

14.2. A komplex feladat analitikus megoldása

A végeselemes programok eredményének ellenőrzéseként oldjunk meg a feladatot a rugalmasságtan és a dinamika módszereivel. Kiindulásnak adva van egy az egyik oldalán befogott egyenszilárdságú tartó melynek másik oldalán koncentrált tömeget helyezünk el. A lemez síkjára merőlegesen hat a gravitációs gyorsulás, melynek hatását vizsgáljuk első lépésben.

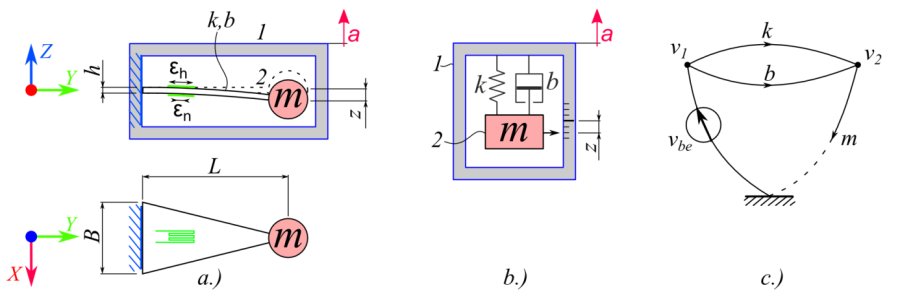
14.17. ábra - A gyorsulásérzékelő különböző szintű absztrakciói: a.) egyszerűsített szerkezeti ábra, b.) szabadtest ábra, c.) Struktúra gráf.

Kiinduló adatok:

Méretek: B=10mm, L=20mm, vastagság: h=0,2mm;

Anyag: Rugóacél – E=200GPa, ν=0,3;

Tömeg a tartó végén: m=0,02kg;

Terhelés: a _z =1G, (9,8066m/s ² ).

14.2.1. Statikus lehajlás számolása

Mivel a tartó szélessége a befogástól távolodva lineárisan csökken (14.1), ezért a keresztmetszetet jellemző mennyiségek is a hely (z) függvényei.

	$b (z) = B \cdot \frac{(L - z)}{L}$	(14.1)
	$I (z) = \frac{h^{3} \cdot B \cdot (L - z)}{12 \cdot L}$	(14.2)
	$K (z) = \frac{h^{2} \cdot B \cdot (L - z)}{6 \cdot L}$	(14.3)

Ahol:

I – a másodrendű nyomaték,

K – a keresztmetszeti tényező,

h – a tartó vastagsága,

L – a tartó teljes hossza,

B – a tartó szélessége a „z=0” helyen,

b(z) – a tartó szélessége a „z” helyen,

A tartó egész térfogatára és a végén elhelyezett koncentrált tömegre ható Y irányú gyorsulás hatására a tartót M_x(z) nyomaték terheli.

$M_{x} (z) = a (m \cdot (L - z) + \frac{ρ \cdot B \cdot h}{6 \cdot L} {(L - z)}^{3})$

(14.4)

Ennek hatására a külső szálakban σ_z=M_x(z)/K(z) normál feszültség,

és lineáris anyagmodellt feltétételezve, ε_z=σ_z/E fajlagos nyúlás ébred.

Ahol: E – az anyag rugalmassági modulusa.

A lehajlásfüggvényt a rugalmas szál differenciál egyenletéből számoljuk ki [25.] .

$\frac{d^{2} y}{d z^{2}} = - \frac{M_{x} (z)}{I_{x} (z) \cdot E}$

(14.5)

Az egyenletet z szerint kétszer integrálva kapjuk a lehajlásfüggvényt,

$y (z) = - \frac{1}{E} \iint^{} \frac{M_{x} (z)}{I_{x} (z)} d z^{2} = - \frac{a}{E} (\frac{6 L m}{B h^{3}} [z^{2}] + \frac{2 ρ}{h^{2}} [\frac{L \cdot z^{2}}{2} - \frac{L \cdot z^{3}}{3} + \frac{z^{4}}{12}] + C_{1} \cdot z + C_{2})$

(14.6)

Mivel a befogás zérus elfordulás és elmozdulás peremfeltételeket jelent, ezért a C₁ és C₂ értéke szintén nulla. Ezzel a lehajlás Értéke a z=L helyen:

$y_{z = L} = - \frac{6 \cdot a \cdot m \cdot L^{3}}{E \cdot B \cdot h^{3}} - \frac{a \cdot ρ \cdot L^{4}}{2 \cdot E \cdot h^{2}}$

(14.7)

Koncentrált tömeggel modellezve a (14.7) egyenletnek csak az 1. tagja marad meg:

$y_{z = L} = - \frac{6 \cdot a \cdot m \cdot L^{3}}{E \cdot B \cdot h^{3}}$

(14.8)

A konzol végének lehajlása	y _z [mm]
Elosztott tömeggel számolva	-0,5892
Koncentrált tömeggel számolva	-0,5884

Látható, hogy a kétféle számolás eredménye nagy pontossággal megegyezik, ami azt jelenti, hogy a továbbiakban elegendő a koncentrált paraméterű modell alkalmazása. Persze ezt az egyszerűsítést csak akkor tehetjük meg, ha az elmozduló mérőtest tömege elhanyagolható a koncentrált tömeghez képest.

✎ A fenti egyenletek alapján rajzoltassuk ki diagramban a tartó szélső szálaiban ébredő feszültséget, fajlagos nyúlást és a rúd lehajlását. Hasonlítsuk össze a végeselemes programok eredményeivel.

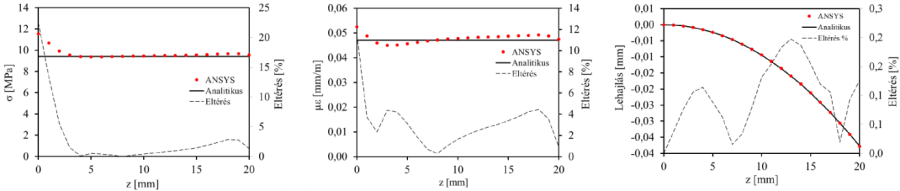
14.18. ábra - Az egyenfeszültségű tartó eredményei kis lehajlás esetén (h=0,5).

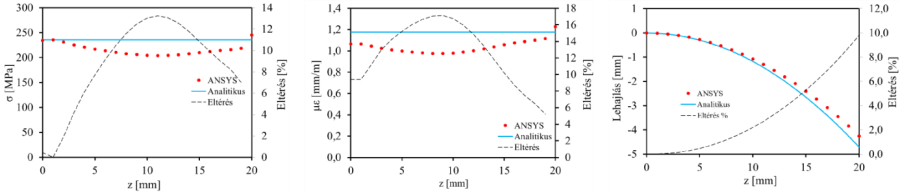
14.19. ábra - Az egyenfeszültségű tartó eredményei (főfeszültség és főnyúlás) nagy lehajlás esetén (h=0,1).

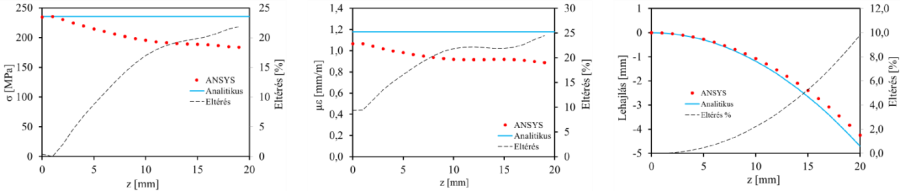
14.20. ábra - Az egyenfeszültségű tartó eredményei (z irányú normál feszültség és fajlagos nyúlás) nagy lehajlás esetén (h=0,1).

14.2.2. Dinamikai számítás

A szenzor dinamikai vizsgálatához szükségünk lesz a koncentrált paraméterű modell paramétereinek meghatározására, ami esetünkben a rugómerevséget (k [N/m]), a csillapítási tényezőt (b [Ns/m]), és a tömeget (m [kg]) jelenti.

A tömeg értéke adott, mint a fenti számolásban láthattuk, ebben az esetben elegendő a tömeg koncentrált paraméterként történő modellezése.

Ami esetünkben a pontszerű tömeg: m=0,02kg.

A rugómerevség értékét a mérőtest végén ható tehetetlenségi erő (F) és fenti számolás (14.8) eredményeként kapott lehajlás (f_y) hányadosaként áll elő.

$k = \frac{F}{y_{z = L}} = \frac{E \cdot B \cdot h^{3}}{6 \cdot L^{3}}$

(14.9)

A csillapítási tényező meghatározására nem mindig állnak rendelkezésére megfelelő adatok, mivel rendkívül összetett jelenség. Értékét jelen esetben az anyagcsillapítás, a terhelési állapot és a mozgó lemez körül áramló levegő által okozott csillapítás egyaránt befolyásolja, ezért pontos értékét csak kísérleti úton tudnánk meghatározni. A koncentrált paraméterű lineáris vizsgálat során a csillapítást is lineáris viszkózus csillapítással modellezzük. Jó közelítést jelent az irodalomban fellelhető csillapítási fok értéke, amely meghatározza az egész rendszer csillapítását [49.] .

Acél szerkezetre:

a csillapítási fok: ξ=0,00143; [49.] ,
a logaritmikus dekrementum: δ =0,009; [49.] ,
a csillapítási tényező: b=2 ⋅ ξ ⋅ (k ⋅ m) ^1/2 =0,007384Ns/m
a Rayleigh féle merevségi csillapítás, β_R=2⋅ξ/ω=0,00002215s; (a sajátfrekvencia értékére számolva, a Rayleigh féle tömegcsillapítás α_R figyelmen kívül hagyásával).

Megjegyzés: Az eredmény és a csillapítás hatásának szemléletes megjelenítése miatt közel egy nagyságrenddel nagyobb értékkel mutatjuk be a példát, mint az irodalmi adat:

a csillapítási fok: ξ=0,05;
a csillapítási tényező: b=2 ⋅ ξ ⋅ (k ⋅ m) ^1/2 = 0,2582Ns/m
a Rayleigh féle merevségi csillapítás, β_R=2⋅ξ/ω= 0,0007746s; (a sajátfrekvencia értékére számolva, a Rayleigh féle tömegcsillapítás α_R figyelmen kívül hagyásával).

A fenti struktúra gráf (14.17. ábra) segítségével felírhatjuk a rendszer csomóponti egyenletét. Mivel az 1-es csomópont (Ház) sebessége megegyezik a sebesség gerjesztéssel, egy ismeretlenünk marad így elég csak a 2. csomópontra (a mozgó tömegre) felírni az egyenletet. Az 1-es és a 2-es csomópont sebesség különbségéből számított elmozdulás jelenti majd a kimenő mennyiséget számunkra.

$k \int^{} (v_{1} - v_{2}) d t + b (v_{1} - v_{2}) - m \frac{d v_{2}}{d t} = 0$

(14.10)

Amelynek Laplace transzformálásával, a t időtartományból átlépve az s operátor tartományba jutunk. Végül a fizikai paramétereket (k,b,m) megfelelően összevonva, és bevezetve a rendszertechnikában szokásos jelöléseket, a másodrendű lengő rendszer átviteli függvényét kapjuk (14.14).

	$v_{1} (\frac{k}{s} + b) + v_{2} (\frac{k}{s} + b + m) = 0$	(14.11)
	$v_{2} = v_{1} (\frac{\frac{k}{s} + b}{\frac{k}{s} + b + m})$	(14.12)
	$v_{k i} (s) = v_{1} - v_{2} = v_{1} (1 - \frac{\frac{k}{s} + b}{\frac{k}{s} + b + m})$	(14.13)
	$Y (s) = \frac{y_{k i} (s)}{a_{b e} (s)} = \frac{v_{k i} (s)}{s^{2} \cdot v_{b e} (s)} = \frac{\frac{m}{k}}{s^{2} \cdot \frac{m}{k} + s \cdot \frac{b}{k} + 1} = \frac{A}{s^{2} \cdot T^{2} + s \cdot 2 ξ T + 1}$	(14.14)

ahol:

A=m/k – a rendszer erősítése,

T=(m/k) ^1/2 – a rendszer időállandója, (ω ₀ =1/T, - a rendszer saját-körfrekvenciája),

ξ= b/2(k ⋅ m) ^1/2 – a csillapítási fok, (definíció szerint: ξ=b/b _k ; ahol: b _k =2(k ⋅ m) ^1/2 – a kritikus csillapítási tényező).

Az így felírt átviteli függvény nevezőjében szereplő karakterisztikus polinom megoldásával jutunk el a rezonanciafrekvencia meghatározásához.

	$s^{2} \cdot T^{2} + s \cdot 2 ξ T + 1 = 0$	(14.15)
	$s_{1,2} = - \frac{2 ξ T}{2 T^{2}} \pm \frac{1}{2 T^{2}} \sqrt{4 T^{2} ξ^{2} - 4 T^{2}} = - \frac{ξ}{T} \pm \frac{1}{T} \sqrt{ξ^{2} - 1}$	(14.16)

A megoldáson látható, hogy csak ξ értékétől függ, hogy valós, vagy komplex gyököt kapunk.

Ha ξ>1, tehát nagy csillapítás esetén (b>b_k), az átviteli függvény két egytárolós tag szorzataként írható fel. A túlcsillapított rendszer rezgésre nem képes.
Ha ξ=1, (b=b_k), Ez az aperiodikus határesetet jelenti. Az egyenletnek egy valós gyöke van (s₁=s₂).
Ha 0<ξ<1, tehát kis csillapítás esetén (b<b_k), Az egyenletnek egy konjugált komplex gyökpár a megoldása. A magára hagyott, alulcsillapított rendszer csillapodó rezgést végez.
Ha ξ=0, tehát nincs csillapítás. Az előző speciális esete (gyakorlatban nincs ilyen), melynél a magára hagyott, csillapítatlan rendszer, nem csillapodó rezgést végez.

Esetünkben a 3. esetnek van jelentősége, mivel 0<ξ<1értékű. Ebben az esetben az (14.16) egyenletet komplex összetevőivel felírva az alábbi összefüggést kapjuk.

$s_{1,2} = - \frac{ξ}{T} \pm j \frac{1}{T} \sqrt{1 - ξ^{2}}$

(14.17)

Az s operátor definíció szerinti komplex összetevői az s=σ+jω, innen a rezonancia körfrekvencia:

$ω_{r} = \frac{1}{T} \sqrt{1 - ξ^{2}} = ω_{0} \sqrt{1 - ξ^{2}} = \sqrt{ω_{0}^{2} - β^{2}}$

(14.18)

ahol: ω ₀ =1/T=(k/m) ^1/2 – a sajátkörfrekvencia értéke, és β= ω ₀ ⋅ ξ =b/2m – a csillapítási kitevő.

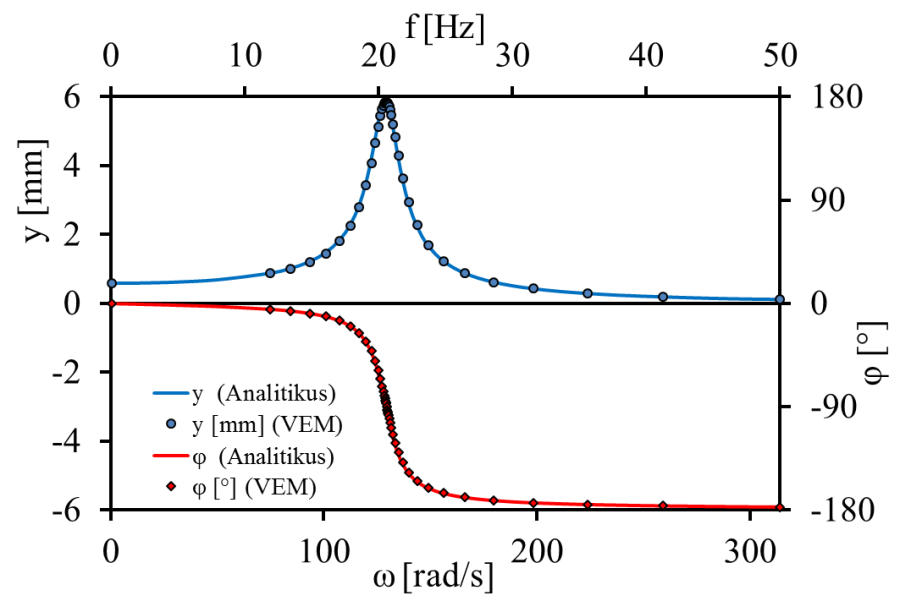
A Bode diagramon, frekvenciatartományban való ábrázoláshoz végezzük el a s=jω, helyettesítést a (14.14) egyenleten, majd rendezzük át az alábbi (14.19) egyenleten látható formában, a valós és a képzetes tagok csoportosításával a nevezőben. A gerjesztés hatására a kimenet amplitúdójának (14.20) és fáziskésése (14.21) az átviteli függvény komplex vektorának abszolút értékével és állásszögével adható meg.

	$Y (j ω) = \frac{y_{k i} (j ω)}{a_{b e} (j ω)} = \frac{A}{(1 - {(T ω)}^{2}) + j (2 ξ T ω)}$	(14.19)
	$\| Y (j ω) \| = \| \frac{x_{k i} (j ω)}{a_{b e} (j ω)} \| = \frac{A}{\sqrt{{(1 - {(T ω)}^{2})}^{2} + {(2 ξ T ω)}^{2}}}$	(14.20)
	$φ = 0 - a r c t g (\frac{2 ξ T ω}{1 - {(T ω)}^{2}})$	(14.21)

✎ A fenti egyenletek alapján számítsuk ki a jelátalakító sajátfrekvenciáját, és rezonancia frekvenciáját, a gyorsulás érzékelő végén lévő tömeg minimális és maximális elmozdulását. Továbbá, rajzoltassuk ki Bode-diagramban az elmozdulás amplitúdóját és fáziskésését a körfrekvencia függvényében. Hasonlítsuk össze a végeselemes programok eredményeivel.

A jelátalakító frekvenciadiagramja (az összehasonlíthatóság kedvéért, a szokásos Bode-diagramtól eltérően, abszolút értékekkel megadva).

14.21. ábra - A jelátalakító frekvenciadiagramja (az összehasonlíthatóság kedvéért, a szokásos Bode-diagramtól eltérően, abszolút értékekkel megadva).

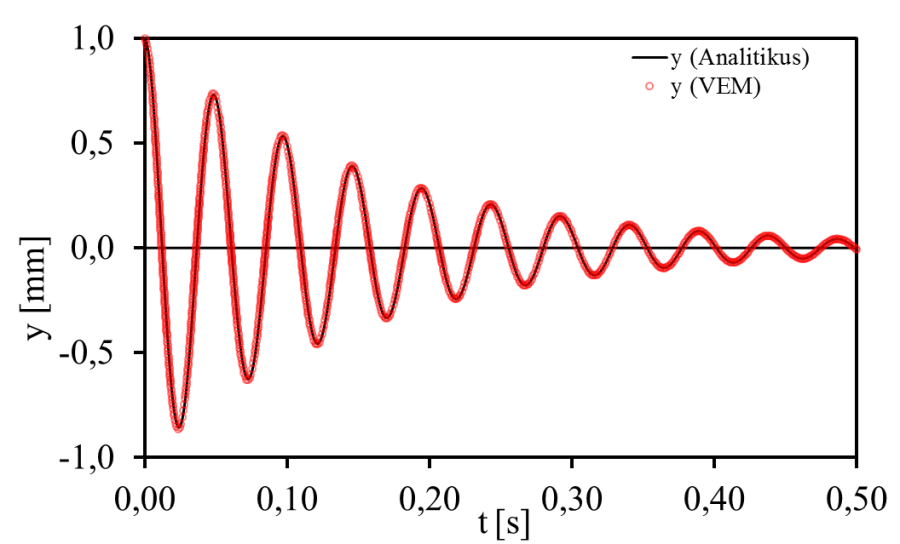
A szerkezet időtartománybeli tranziens viselkedésének vizsgálatához írjuk fel a gerjesztetlen, csillapított másodrendű rendszer differenciálegyenletének általános megoldását.

$y_{k i} (t) = e^{- ξ t ω_{r}} (A \cdot s i n (t \cdot ω_{r}) + B \cdot c o s (t \cdot ω_{r}))$

(14.22)

Melynek A és B állandóinak a t=0, időpillanatban vett y(0)=y₀, v(0)=0; kezdeti feltételekre megoldva kapjuk az alábbi alakot.

$y_{k i} (t) = y_{0} \cdot e^{- ξ t ω_{r}} \cdot c o s (t \cdot ω_{r})$

(14.23)

✎ A fenti egyenletek alapján rajzoltassuk ki az y ₀ =1, kezdeti feltételű, tranziens rezgést időtartományban. Hasonlítsuk össze a végeselemes eredménnyel.

14.22. ábra - A deformált és magára hagyott („megpendített”) tartó tranziens viselkedése.

14.2. táblázat - Az analitikus és VEM eredmények összehasonlítása.

Mennyiség	Jelölés	m.e.	VEM	Analitikus, kontinuum tömeggel	Eltérés [%]	Analitikus, pontszerű tömeggel	Eltérés [%]
Hajlítónyomaték a befogásnál	M(z=0)	Nmm	3,93	3,93	0,06	3,92	0,21
Normálfeszültség a külső szálban	σ	MPa	58,09	58,88	1,53	58,84	1,27
Fajlagos nyúlás a külső szálban	ε	-	2,936E-04	2,944E-04	0,28	2,942E-04	0,22
Lehajlás a tartó végénél	y(z=L)	mm	-0,586	-0,588	0,36	-0,589	0,49
Rugómerevség	k	N/m	337	336	0,51	333	1,16
Saját-körfrekvencia	ω ₀	rad/s	129,28			129,10	0,14
Sajátfrekvencia	fo	Hz	20,58			20,55	0,14

Vissza		Előre
13. fejezet - Termikus szimuláció	Főoldal	15. fejezet - Korszerű végeselelem rendszerek áttekintése