13. fejezet - Termikus szimuláció
Vissza		Előre

13. fejezet - Termikus szimuláció

Tartalom

Hőtani szimulációk során a rendszerre, vagy annak egy komponensére ható hőtani terhelés hatására létrejött állapotot vizsgálunk.

13.1. Áttekintés

A hőtani szimulációknak két nagy csoportját különböztethetjük meg; az állandósult hőtani szimulációkat (Steady-state Thermal Analysis) , és az időben változó hőtani szimulációkat (Transient Thermal Analysis) . Előbbi esetében állandó értékű hőterhelés hatására (elvileg végtelen idő eltelte után) kialakuló állandósult állapot szimulálható, tehát a folyamatot nem tudjuk áttekinteni, csak az egyensúlyi végállapotot. Utóbbi esetében azonban a hőterhelés, (ami lehet időben változó is) hatására kialakuló folyamat is nyomon követhető, és a meghatározott idő múlva fennálló aktuális állapot megtekinthető. A hőtani terhelések és peremfeltételek meghatározása gyakorlatilag ugyanúgy történik, csak a végeredmény esetében van különbség abban, hogy a kialakult egyensúlyi állapot, vagy a kérdéses időpillanatban fennálló állapot kerül megjelenítésre. A két típus számítási igénye természetesen eltérő, az időben változó szimuláció hosszabb idő alatt fut le.

A két fajta szimulációt sok esetben egymás után futtatjuk le. Egyik jellemző eset, hogy egy állandósult termikus analízist felhasználunk egy utána következő tranziens hőtani szimuláció kezdeti feltételeként. Másik eset, mikor egy tranziens hőtani szimuláció utolsó lépéseként alkalmazunk egy állandósult hőtani analízist, ezzel csökkentve az összes tranziens hőtani terhelés hatását.

Az állandósult termikus analíziseket olyan hőtani terhelések hatására kialakuló állapot meghatározására használjuk, amelyek időben nem változnak. A következő típusú terheléseket használhatjuk (ha megfelelnek a fenti kritériumnak): hőmérséklet, hőáramlás, hősugárzás, hővezetés, hőáram-sűrűség illetve állandó belső hőfejlődés.

Állandósult termikus analízisek esetén használhatunk lineáris és nem lineáris hőtani anyagtulajdonságokat is. Előbbi esetében konstans anyagtulajdonságokat használunk az anyagmodell definiálásához, míg utóbbi esetben ezek a tulajdonságok hőmérsékletfüggőek. Legtöbb esetben azonban az anyagtulajdonságok függenek a hőmérséklettől, így a nemlineáris anyagmodell a jellemző.

A tranziens termikus szimulációk felhasználási területe igen széles. Elemezhető a segítségével például egy elektromos eszköz használat közbeni hő fejlődése során kialakuló hőmérsékleti eloszlása, a hűtőbordák működése, vagy akár egy oltási folyamat hatása.

A hőtani szimulációkat, de főként a tranziens termikus analíziseket nagyon jól lehet használni olyan statikai szimulációk kezdeti feltételeként, ahol a hőmérséklet, vagy a hőmérséklet változása befolyásolja a szerkezet viselkedését. Különösen fontos ez olyan esetekben, ahol a hőmérséklet változása nagy mértékű, és a használat során olyan esetek is előfordulnak, amikor extrém terhelés lép fel (pl. műszaki probléma miatt). Ahogyan az állandósult termikus analíziseknél is itt is lehet lineáris és nemlineáris anyagmodelleket alkalmazni. A termikus anyagtulajdonságok, mint pl. a hővezetési tényező (Thermal Conductivity) , fajhő (Specific Heat) , hőátadási tényező (Convection Coefficient) hőmérsékletfüggő viselkedése nemlinearitást okoz, amely esetén a pontos eredmény eléréséhez olyan iteratív megoldásra van szükség.

13.2. A termikus szimulációk beállításai

Hőtani szimuláció esetében első lépésként definiálni kell a megfelelő anyagtulajdonságokat.

Az alábbi anyagjellemzőket szükséges megadni:

hővezetési tényező (Thermal Conductivity) ,
sűrűség (Density) ,
fajhő (Specific Heat) .

A hővezetési tényező lehet izotróp (minden irányban azonos), vagy ortotróp (merőleges koordinátarendszerben irányonként eltérő), valamint minden érték lehet konstans, vagy hőmérsékletfüggő.

A geometria kialakításában nincsenek különleges kritériumok a hőtani szimulációk esetén, 3 és 2 dimenziós geometria alkalmazására is van lehetőség.

Alkatrészek közötti kapcsolatok közül csak a kontakt típusú kapcsolatok használhatók, az esetlegesen definiált csukló jellegű (Joint) és rugó típusú (Spring) kapcsolatok nem fognak részt venni a szimulációban. A hőtani szimulációk során az alkatrészek közötti kontakt nem változik, tehát a zárt érintkező felületek zártak maradnak, a nyitott felületek nyitottak maradnak. Az egymáshoz zártan illeszkedő felületek között (ha a hővezetési tényező kellően nagy) a hőtani ellenállás minimális. Amennyiben nem így van, kézzel is be lehet állítani a hővezetést a két felület között.

Termikus analíziseknél általában nem kell semmiféle specifikus hálózási módot használni, ebben az esetben ugyanis kevesebb jelentősége van a háló finomságának, mint például egy jelentősebb alakváltozással járó statikai analízisnél. Arra azonban mindenképpen érdemes figyelni, hogy ha a termikus analízisünk egy későbbi statikai analízis kezdeti feltétele lesz, akkor olyan hálót használjunk, amely megfelel a későbbi szimulációnak. (Ansys programban ugyanazt a hálót lehet csak használni.)

Tranziens termikus szimulációk esetén az Ansys programban a következő szabályozókat (Controls) érdemes beállítani:

Lépések (Step Control) – ezt a beállítást a következőkre használhatjuk:
- tranziens analízis időintervallumának beállítására,
- az egyes lépésközök nagyságának beállítására,
- több lépcsőből álló terhelések definiálásához, amennyiben erre szükség van.
A több lépcsőben megadott terhelésre abban az esetben van különösen szükség, amikor az anyagtulajdonságok hőmérsékletfüggése gyorsan változik. Ilyenkor a terhelést kis lépésekkel növelve biztosítható, hogy a szimuláció konvergens legyen. Akkor is szükséges a több lépcsős terhelés-definiálás, amikor az eredményeket kis időtartományokban szeretnénk lekérdezni.
Kimeneti beállítások (Output Controls) - ezek a beállítások lehetőséget adnak arra, hogy beállítsuk, a folyamat mely időpillanataiban szeretnénk az eredményeket vizsgálni, azonban nem lehetséges az összes közbülső időpontra lekérdezni az eredményeket. A túl sok időpontra lekérdezett eredmények irreális mértékben megnövelik az eredményfile méretét, így nehezen kezelhetővé válik a szimuláció. Ha mégis előfordul ez az eset mindenképpen érdemes a lekérdezési időpontokat jelentősen csökkenteni.
Nemlinearitás szabályozói (Nonlinear Controls) – itt van lehetőségünk változtatni a konvergencia kritériumokon (Convergence Criteria) és néhány a megoldási folyamathoz kapcsolódó beállítást.
Adatkezelési beállítások (Analysis Data Management) – lehetőséget ad arra, hogy bizonyos eredmény fájlokat kimentsünk, így más szimulációkban is felhasználhatók.
Szükséges kezdeti feltétel (Initial Condition) tranziens termikus analízisek során, hogy definiáljuk a 0. időpillanatban a hőmérséklet-eloszlást. Az ANSYS-ban a kezdeti feltétel alapértelmezetten 22°C (71.6°F) értékű egyenletes hőmérséklet. Ha nem szobahőmérséklet a kezdeti állapot, akkor ezt itt kell beállítani. Pl. ha egy felhevített tárgy hűlési folyamatát szeretnénk vizsgálni hideg vízben. Kezdeti feltételként természetesen nem csak egy egyenletes hőmérsékletet lehet megadni, hanem egy korábban elvégzett állandósult termikus analízis végeredményét is. Pl. egy öntőformában lévő olvadt fém megszilárdulási folyamatának elemzése, melyet előzetesen állandósult termikus analízissel vizsgáltunk.

13.3. Terhelések tranziens termikus analízisek során

A következő alapvető terheléseket alkalmazhatjuk az időfüggő hőtani szimulációk során:

Hőmérséklet (Temperature) ,
Hőátadás (Convection) ,
Hősugárzás (Radiation) ,
Hőáramlás (Heat Flow) ,
Hőáramsűrűség (Heat Flux) ,
Belső hőtermelés (Internal Heat Generation,)
Tökéletes szigetelés (Perfectly Insulated) .

Minden terhelés definiálható konstans értékként, időben változókként, amit akár táblázatosan akár függvény szerint is megadhatunk. Az alábbiakban bemutatjuk ezeknek a terheléseknek a lehetőségeit:

13.3.1. Hőmérséklet kénszer

Használható 3 és 2 dimenziós szimulációk során is, annyi megkötéssel, hogy 2D-ben csak síkfeszültség (Plane Stress) és tengelyszimmetrikus (Axisymmetric) típusú modelleknél alkalmazható. Hőmérsékletterhelést definiálhatunk egy, vagy több felületre, élre, pontra, vagy akár egész testekre. Ha egy hőmérsékletterhelésen belül definiáljuk a különböző területeket (akár kapcsolódnak egymáshoz akár nem) azonos és egyenletes eloszlású hőmérséklet lesz minden kijelölt területen. Lehet azonban definiálni olyan hőmérsékletterhelést is, amely helytől függően változik, ebben az esetben pl. egy koordináta rendszer tengelye mentén, akár egy függvény szerint is meghatározhatjuk a nem egyenletes eloszlást.

13.3.2. Hőátadás

Olyan hőátadást jelent, amely egy, vagy több (sík, vagy ívelt) felület és a környező közeg (levegő, folyadék) között valósul meg. Ugyanazon geometriai típusok esetében használható, mint a hőmérséklet kényszer. Meg kell határozni a közeg és a felületek hőmérsékletét, valamint a kettő közötti hőátadási tényezőt. A környezeti közeg (folyadék) hőmérséklete egyenletes eloszlású, és a kapcsolódó felülettől távolabbi pontra vonatkozik. A hőátadási tényező a külső környezetnek (folyadék) a kapcsolódó felületre vonatkozó értéke, mely függ a felület nagyságától és geometriájától, valamint a környező közeg áramlási viszonyaitól. Lehetőség van idő- és hőmérsékletfüggő hőátadási tényező definiálására is. A környezet hőmérsékletét is definiálhatjuk időfüggő tényezőként.

A hővezetés során bekövetkező hőátadást a következőképpen számíthatjuk ki (Newton törvény szerint): q/A=h(t_s-t_f), ahol q/A a hőáram sűrűség a felületen, h a hőátadási tényező, t_s a felület hőmérséklete és t_f a környezet (folyadék) hőmérséklete.

Amikor a környezet hőmérséklete meghaladja a felület hőmérsékletét, akkor a tárgy felé energia áramlás következik be, amikor a felület hőmérséklete meghaladja a környezet hőmérsékletét akkor a test energiát veszít. Egyszerre több felület és a környezet között is végbemehet a hőáramlás (függetlenül attól, hogy a felületek kapcsolódnak-e egymáshoz).

13.3.3. Hősugárzás

A hősugárzás elektromágneses hullámokkal megvalósuló energiaátvitel, melyhez nem szükséges közvetítő közeg jelenléte. Mivel a sugárzás által okozott hőáram a hőmérséklet 4. hatványának függvénye, ezért a hősugárzást tartalmazó analízis erősen nemlineáris. Az analízisben a hősugárzás vonatkozhat egy 3D-s modell felületére, vagy egy 2D-s modell élére. Ilyen terhelés esetén meg kell határozni a sugárzó képességet (Emissivity) , amely a felület által kibocsátott sugárzást az ideális fekete test azonos hőmérsékleten kibocsátott sugárzásának arányaként határozza meg. Emellett definiálni kell a környezet hőmérsékletét.

13.3.4. Hőáram

A hőáram adott geometrián időegység alatt áthaladó energiamennyiséget határoz meg. Csak 3D-s szimulációk és 2D-s tengelyszimmetrikus és síkfeszültség típusú analíziseknél használható. A geometria típusa szerint 3 csoportra oszthatjuk a hőáramlási terheléseket:

Felületen ható hőáramlás (Face Heat Flow Rate),
Élen ható hőáramlás (Edge Heat Flow Rate),
Pontszerűen ható hőáramlás (Vertex Heat Flow Rate).

Egy adott felületen áthaladó hőáramlást határoz meg. A felület lehet sík, vagy ívelt. Pozitív hőáramlásnak tekintjük a felület felé irányuló hőáramlást. Energia per időegységként definiálhatjuk. Amennyiben több felületet választunk ki, a megadott hőáramlás érték megoszlik ezek között. Amennyiben a felület a szimuláció közben növekszik a teljes terhelés változatlan marad, azonban a hőáram-sűrűség (mely tulajdonképpen a hőáramlás felületre vonatkoztatott mennyisége) természetszerűleg csökkenni fog. Ha olyan felületeket választunk ki a hőáramlás definiálásához, amely különböző testekhez tartozik, akkor az értelmezhetetlen lesz, és a véges elemes szoftver figyelmen kívül fogja hagyni.

Élen ható hőáram: Gyakorlatilag ugyanazok vonatkoznak erre a terhelésre, mint a felületre vonatkoztatott esetében, annyi különbséggel, hogy itt egy élen hat az áramlás, tehát a hőáram sűrűséget az adott hosszra kell vonatkoztatni, nem pedig a felületre.

Pontszerűen ható áramlás: Szintén ugyanazok vonatkoznak rá, mint a fenti 2 geometrián ható háramlásra, annyi különbséggel, hogy ebben az esetben a hőáram sűrűség nem definiálható a pontszerű geometria miatt.

13.3.5. Hőáramsűrűség

A hőáram-sűrűség egységnyi geometrián időegység alatt áthaladó energiamennyiséget határoz meg. 3D-s szimulációk és 2D-s tengelyszimmetrikus és síkfeszültség típusú analízisek esetében használható. Egy, vagy több sík, vagy ívelt felületre lehet definiálni. A hőáramsűrűség akkor pozitív irányú, ha a test belseje felé mutat. Ekkor a test energiát vesz fel. A hőáramsűrűséget energia per időegység per felületként adjuk meg. Ha több felületet jelölünk ki, akkor mindegyik esetében ugyanaz az érték valósul meg. Ha a meghatározott felület növekszik a szimuláció folyamán, akkor a teljes terhelés (hőáramlás) növekszik, de a hőáramsűrűség állandó marad.

13.3.6. Belső hőtermelés

Egyenletes eloszlású hőtermelést határoz meg a testben. 3D-s szimulációk és 2D-s tengelyszimmetrikus és síkfeszültség típusú analízisek esetében alkalmazható. Pozitív hőtermelésről akkor beszélünk, ha a test energiája növekszik (tehát a hőmérséklete is növekszik). A hőtermelést energia per idő per térfogatként határozhatjuk meg. Ha több testet jelölünk ki a hőtermeléshez, akkor mindegyik test ugyanazzal a hőtermelési értékkel fog rendelkezni. Amennyiben a test térfogata növekszik a szimuláció során a teljes termelt energia mennyisége is növekszik, (mivel az térfogategységre vonatkozik).

13.3.7. Tökéletes szigetelés

Ez a lehetőség gyakorlatilag a „nincs terhelés” feltételt jelenti. 3D-s szimulációk és 2D-s tengelyszimmetrikus és síkfeszültség típusú analízisek esetében alkalmazható. A kiválasztott geometriai elemekre (elsősorban felületekre) nem hatnak a szimuláció során megadott hőterhelések. A szigeteléssel ellátott felületeken 0 hőáramlás megy végbe. Akkor hasznos ez az opció, amikor egy geometriai modell adott hőterheléséből csak néhány felület van kivonva (Pl. egy földelt terület).

Ha egy geometrián belül több, akár különböző testekhez tartozó felületre van definiálva a szigetelés, természetesen mindegyik rendelkezik majd ezzel a tulajdonsággal.

13.4. Példa hőtani szimulációra –hűtőborda hőmérsékleti viszonyainak vizsgálata

Az alábbi egyszerű példában egy 100mm*10mm*2mm nagyságú hasáb, mint hűtőborda hőtani szimulációját láthatjuk. Ennél a példánál állandósult hőtani szimulációt (Steady-State Thermal) használunk.

Mivel kizárólag hőtani szimulációt végzünk nincs szükség a hűtőborda anyagának mechanikai tulajdonságira. Egyedül az izotróp hővezetési tényező (Isotropic Thermal Conductivity) megadása szükséges: 60,5W/mC°.

A geometria felépítése után egy olyan konstrukciós geometriát (Path) definiáltunk, mely hosszirányban végigfut a rúd tengelye mentén (13.1. ábra).

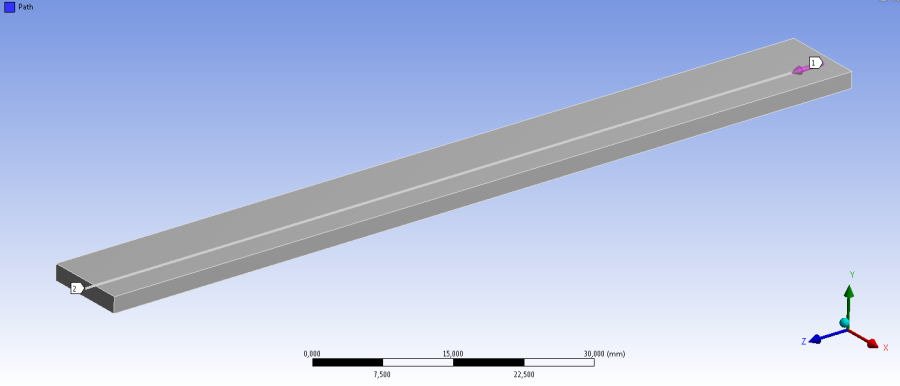
13.1. ábra - Konstrukciós geometria a hőmérséklet-eloszlás hossz menti lekérdezéséhez.

A háló elkészítésénél 4mm-es elemméretet használtunk, így a véges elemek száma összesen 40 db. A hálózott modell a 13.2. ábra mutatja.

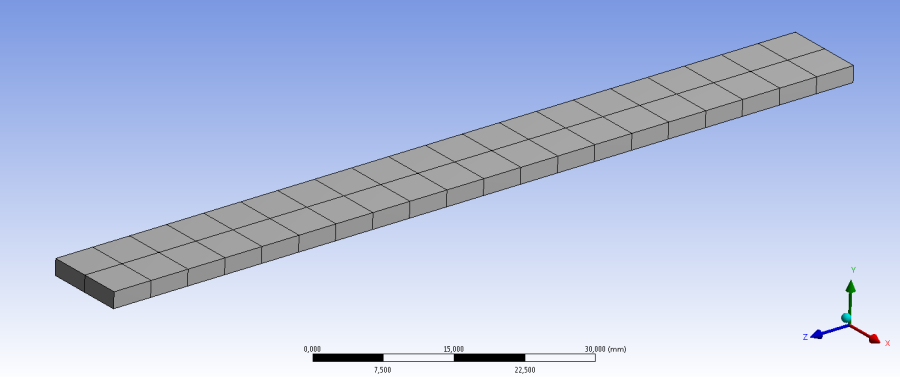
13.2. ábra - Véges elemes háló a hőtani példa esetén

Kezdeti feltételként 20˚C-os környezeti hőmérsékletet határoztunk meg. (Ez a modelltérben lévő testekre is érvényes.)

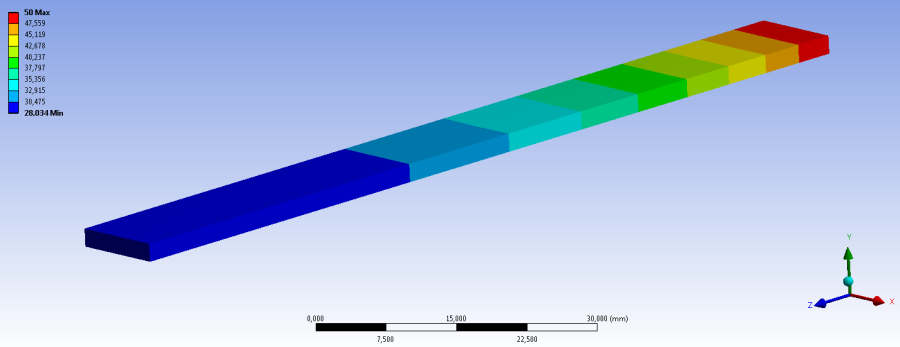
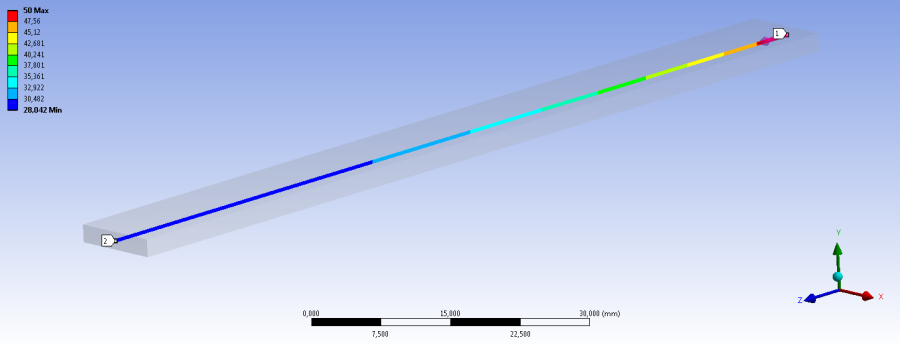
Az alkalmazott peremfeltételek: 50˚C-os hőmérséklet kényszer (Temperature) , a rúd egyik végén (13.3. ábra „A” jellel jelölt kisméretű felületen), valamint a hosszanti oldalakon (4 hosszú oldal) hőátadási tényezővel (film coefficient: 0,0002W/mm²C˚) definiált hőátadás (Convection), mely a 20˚C-os környezett felé történő hőközlést definiálja. A hőmérséklet kényszert táblázatosan adjuk meg, amiben 2 lépést definiáltunk, az első lépésben 20, a második lépésben pedig 50˚C-os a felület.

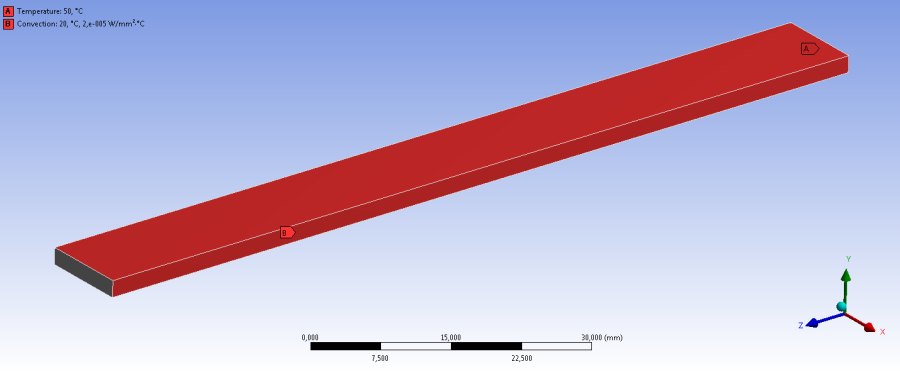
13.3. ábra - A hőtani analízisperem feltételei.

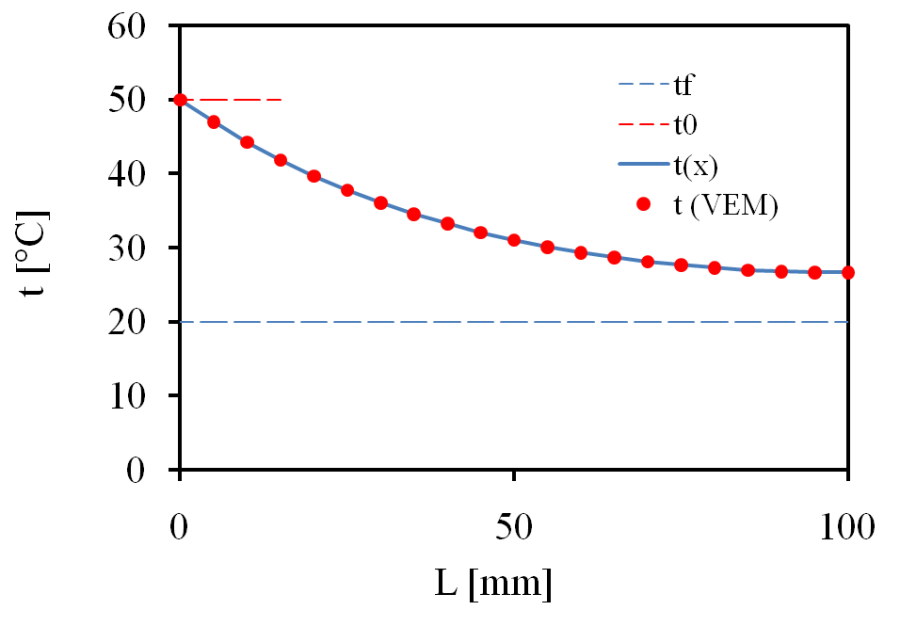
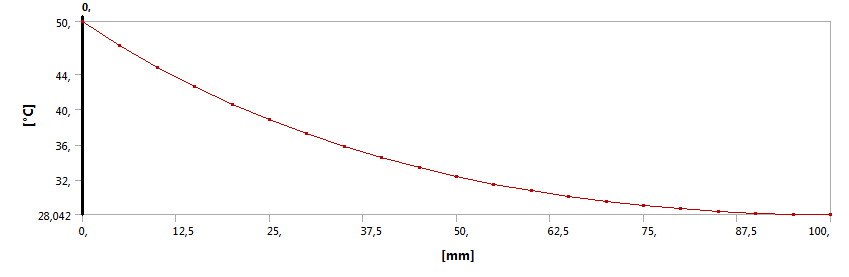
Az alábbi ábrákon láthatóak az állandósult hőmérsékleti viszonyok. A hőmérsékleti terheléssel ellentétes oldalon kialakuló hőmérséklet nagyjából 28˚C. A teljes test eredményeit bemutató 13.4. ábra is mutatja, hogy a hőmérsékleti eloszlás nem egyenletes. Ezt megerősíti a konstrukciós geometria mentén lekérdezett grafikonban ábrázolt hőmérséklet (13.5. ábra és 13.6. ábra).

13.4. ábra - Az állandósül hőmérsékleti viszonyok a teljes test felületén

13.5. ábra - Állandósult hőmérsékleti viszonyok a konstrukciós geometria mentén

13.6. ábra - Állandósult hőmérsékleti viszonyok a konstrukciós geometria mentén grafikon formátumban

13.5. Analitikus megoldás

Egy homogén rúd (hűtőborda) hőmérsékletének állandósult állapotbeli eloszlását a hővezetés és a palástján történő hő leadás ismeretében számolhatjuk ki. Oldjuk meg a feladatot arra az esetre, ha ismerjük a rúd egyik végének hőmérsékletét és a környezeti hőmérsékletet. [48.]

A rúd hossza: L = 100 mm; keresztmetszetének méretei: a = 2 mm, b = 10mm,

Az egyik rúdvég hőmérséklete: t₀ = 50 °C, a környezeti hőmérséklet: t_f = 20 °C.

Anyaga – acél, hővezetési tényező: λ = 50 W/mm·K; a hőátadási tényező közelítő értéke (levegő közeg és természetes konvekció esetén) α= 20 W/mm²·K.

Határozzuk meg a rúd (hűtőborda) állandósult állapotbeli hőmérséklet eloszlását,

A rúdban lévő hőáram a hely függvényében írható fel, mivel a hőmérséklet eloszlás és a hőmérséklet gradiens is változik a rúd hossza mentén.

$\dot{Q} (z) = λ \cdot A \cdot \frac{d t (z)}{d z}$

(13.1)

Felhasználva, hogy a palást elemi felületén leadott hőmennyiség megegyezik a hővezetés hőáramának ezen elemi hosszra eső növekményével, a paláston történő hőleadást a rúd hosszának elemi részére az alábbi módon írhatjuk fel.

$d \dot{Q} (z) = α \cdot U \cdot d z \cdot (t (z) - t_{f})$

(13.2)

Ahol: az U·dz jelenti a palást felültének elemi részét,

A – a keresztmetszet területe,

U – a keresztmetszet kerülete,

λ - hővezetési tényező,

α - a hőátadási tényező becsült értéke.

Két egyenlet rendezése után kapjuk,

$\frac{d \dot{Q} (z)}{d z} = \frac{d (λ \cdot A \cdot \frac{d t (z)}{d z})}{d z} = α \cdot U \cdot (t (z) - t_{f})$

(13.3)

Az egyenletet rendezve, állandó keresztmetszetű rúd esetén

$B^{2} = \frac{α \cdot U}{λ \cdot A}$

(13.4)

helyettesítéssel, a

$\frac{d^{2} t (z)}{d z^{2}} - B^{2} \cdot t (z) = - B^{2} \cdot t_{f}$

(13.5)

másodrendű differenciálegyenletet kapjuk, melynek általános megoldása

$t (z) = t_{f} + e^{z \cdot A} \cdot C_{1} + e^{- z \cdot A} \cdot C_{2}$

(13.6)

Ahol: C₁, C₂ – a peremfeltételektől függő állandók. t(0)=t₀ peremfeltétel esetén, ha a véglap hőleadását elhanyagoljuk

$t (z) = (t_{0} - t_{f}) \frac{cosh (B (L - z))}{cosh (B \cdot L)} + t_{f}$

(13.7)

ahol: L – a rúd teljes hossza.

Az analitikus és numerikus eredmények összehasonlítását az alábbi ábrán láthatjuk.

13.7. ábra - Az analitikus és numerikus eredmények összehasonlítása.

Vissza		Előre
12. fejezet - Elektromos és mágneses szimulációk	Főoldal	14. fejezet - Komplex mechatronikai projektfeladat