12. fejezet - Elektromos és mágneses szimulációk
Vissza		Előre

12. fejezet - Elektromos és mágneses szimulációk

Tartalom

12.1. Bevezetés

Mágneses tér jöhet létre áramjárta vezető, vagy állandó mágnes hatására is. Mikor véges elemes szoftver segítségével mágneses szimulációról beszélünk legtöbbször egy, vagy több árammal átjárt vezető, vagy egy, vagy több állandó mágnes által létrehozott mágneses tér analízisét végezzünk. A szimuláció célja többféle lehet, pl. a szenzortechnika területén, induktív elven működő érzékelők tervezésekor a mozgó alkatrész által létrehozott induktivitás-változás detektálása, elektromágneses aktuátorok által kifejtett erő, vagy nyomaték analízise, stb. Mágneses szimulációk esetén különösen fontos szerepe van a megfelelő anyagmodellek definiálásának. Lényegi kérdés az állandó mágnesek, mágnesezhető anyagok (pl. vasmag anyaga egy tekercsben), vezetők (pl. réz kábel), valamint a rendszer elemeit körbevevő levegő modellezésének helyessége. Mágneses szimulációk során általában a kontaktok modellezése elhanyagolható tényező. A mágneses szimulációk tipikus felhasználási területei a következők:

Elektromos motorok
Transzformátorok
Indukciós hőfejlesztés
Mágnesszelep
Nagy mágneses térrel rendelkező mágnesek felhasználása
Roncsolásmentes anyagvizsgálat modellezése
Mágneses keverés
Elektrolizáló cellák
Részecske gyorsító
Orvosi és geofizikai eszközök

Mivel mágneses szimulációk során az alkatrészek közötti és körüli levegő (vagy egyéb közeg) is modellezésre kerül különösen fontos a szimmetria- feltételek használata. Ellenkező esetben a nagy elemszám meglehetősen megnöveli a számítási időt. A szimuláció során az alábbi mennyiségeket számoltathatjuk ki:

Mágneses indukció (Magnetic flux density)
Teljesítményveszteség (Power loss)
Mágneses térerősség (Magnetic field intensity)
Fluxus szivárgás (Flux leakage)
Mágneses erők és nyomatékok (Magnetic forces and torques)
S-paraméterek (S-parameters)
Impedancia (Impedance)
Minőségi tényező (Quality factor)
Induktív ellenállás (Inductance)
Visszirányú csillapítás (Return loss)
Örvényáramok (Eddy currents)
Sajátfrekvenciák (Eigenfrequencies)

12.2. Példa elektromágneses szimulációra – solenoid tekercs szimulációja

A következő példában egy árammal átjárt, vasmag nélküli, hengeres (solenoid) tekercs mágneses terét fogjuk megvizsgálni az ANSYS Workbench -ben végzett szimuláció segítségével.

A mágneses szimulációknál a testeket körülvevő környezet modellezése miatt különösen fontos a geometria egyszerűsítése, amire a legcélravezetőbb módszer a 2D-s, fél-, negyed- és nyolcad modellek alkalmazása.

A tekercset egy 19mm belső és 21mm külső átmérőjű, 50mm magasságú szilárd henger nyolcadával modelleztük.

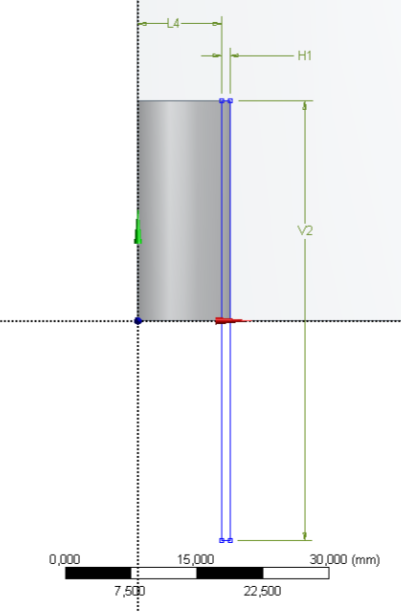
12.1. ábra - Tekercs modellezése.

A teljes tekercs megrajzolása után, a hengert körülvevő 100mm-es vastagságú környezet-modellt (levegő) kell definiálni, amelynek alakja szintén hengeres (Tools/Enclosure => Details/Shape: Cylinder) .

Ezután darabolhatjuk csak szét a modellt a szimmetriasíkok mentén. Mivel a tekercset 1/8 modellként valósítjuk meg, az elkészült teljes tekercset mindhárom fősíkkal elmetszük (Tools/Symmetry => Number of Planes: 3).

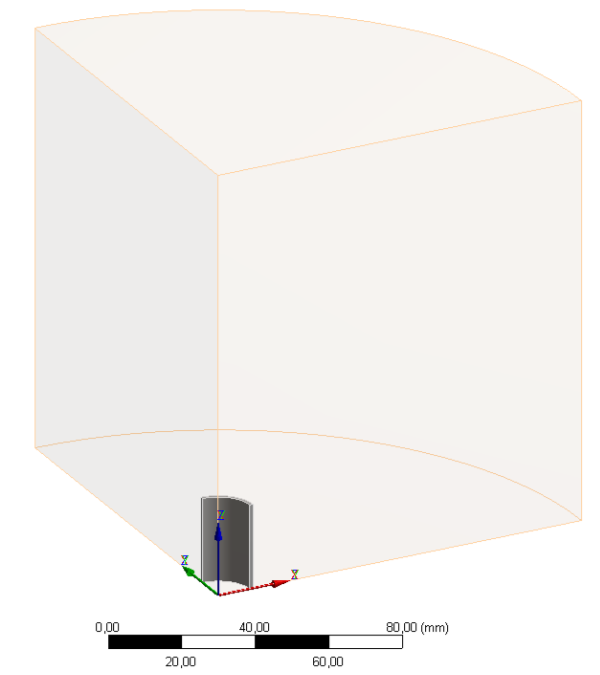
12.2. ábra - A geometriai modell a környezettel.

Mivel itt az alkatrészek közötti mechanikai kontaktok nem játszanak szerepet, a geometriában lévő alkatrészeket egybe kell kapcsolni. Ezt a modellfa utolsó, testek (Body) sorában lévő alkatrészek kijelölésével, és a jobb gombos menü egy alkatrészbe tömörítés (Form new Part) parancsával lehet elérni (12.3. ábra).

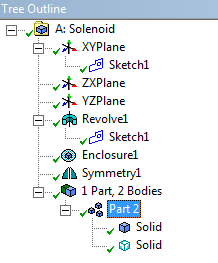
12.3. ábra - A testek egy alkatrésszé alakítása.

A geometria elkészítése után lépjünk át az anyagkönyvtárba és rendeljük hozzá a szimulációnkhoz egy Copper Alloy anyagmodellt. A levegő (Air) anyagmodell, alapértelmezetten a szimulációs könyvtár része.

A szimulációs környezetbe való belépés után rendeljük hozzá az előre definiált anyagmodelleket az egyes testmodellekhez. Ellenőrizzük, hogy a környezethez alapértelmezetten hozzá van-e rendelve a levegő.

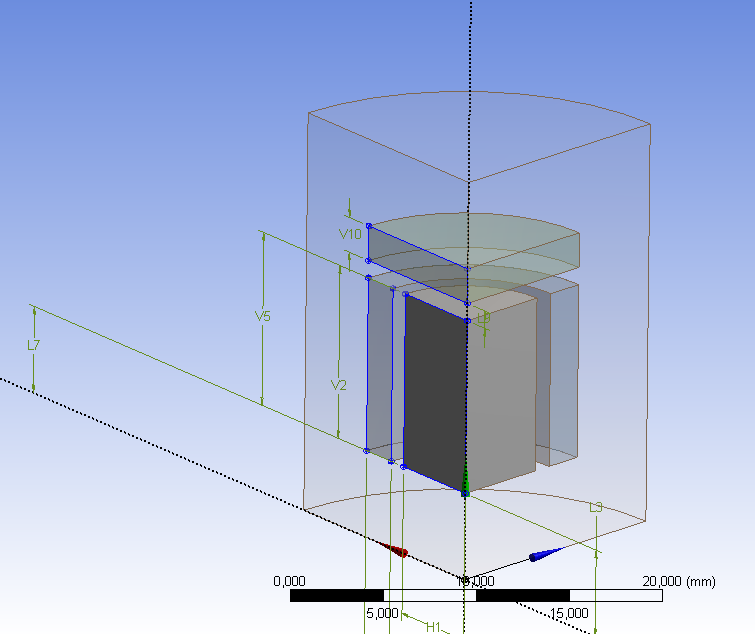
Az eredmények megjelenítéséhez szükséges egy konstrukciós vonal (Path) definiálása. Ezt a tekercs tengelyében hozzuk létre, amely túllóg a tekercs magasságán (összesen 50mm hosszú). Az 1. és 2. címke között futó konstrukciós vonalat szemlélteti 12.4. ábra.

12.4. ábra - Konstrukciós geometria definiálása solenoid tekercs tengelyében

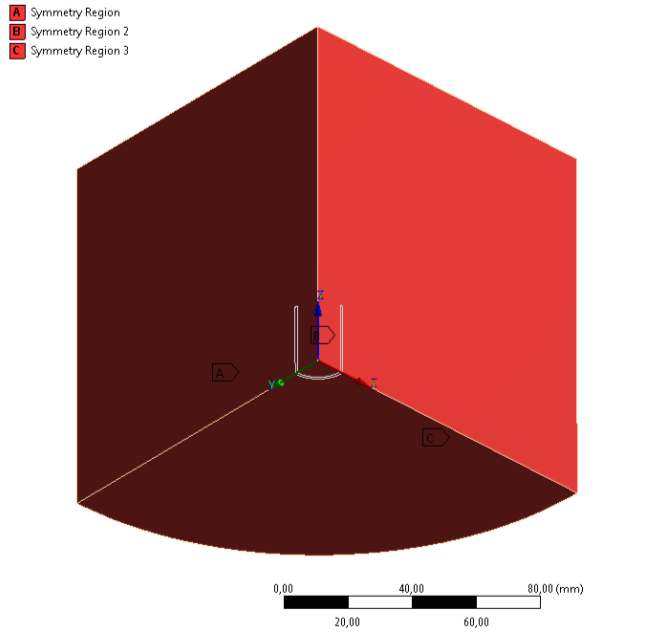
A 3 definiált szimmetria síkot a 12.5. ábra szemlélteti.

12.5. ábra - Szimmetria síkok a solenoid tekercs esetében

A hálózásnál fontos, hogy a tekercs és közvetlen környezete megfelelően kicsi elemméretet tartalmazzon a pontos eredmény érdekében. Ennél a példánál három hálósűrítési beállítást használtunk. A globális beállításokat, egy a tekercsen alkalmazott elemméret meghatározást (Sizing) és egy gömbfelületen belüli (Sphere of influence) hálósűrítést (12.6. ábra).

A globális beállításokat az (Outline/…/Mesh => Details/Sizing/Use Advanced Size Function/On:Fixed) opció bekapcsolásával, az elemméret alsó (Min Size: 0,5mm ) és felső (Max Face Size: 10mm ) korlátjával és a növekményi faktorral (Growth Rate: 1,1 ) adjuk meg.

A tekercset jelentő testmodell elemméretét, egy Sizing funkció hozzáadásával állítjuk 0,5mm-re.

A levegő modelljének lokális hálósűrítését egy újabb Sizing parancs hozzáadásával, és a Sphere of influence opció beállításával érjük el. A gömb sugarát 30mm-re, a benne található elemek méretét 1mm-re állítjuk.

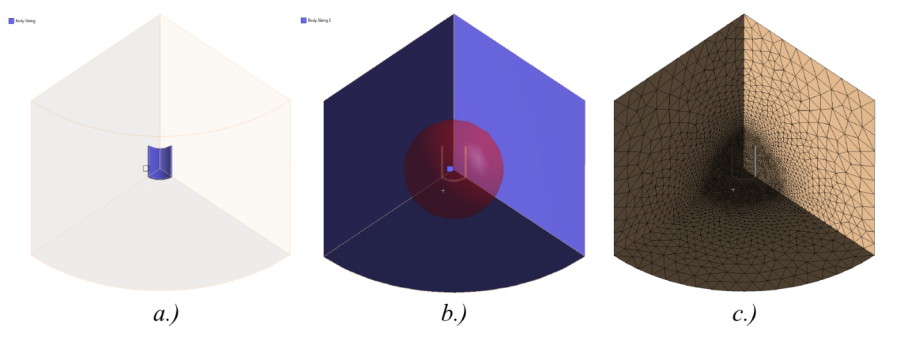
12.6. ábra - Hálósűrítési beállítások a solenoid tekercs szimulációja során

A beállításoknak köszönhetően a véges elemes háló mérete egyenletesen csökken a tekercstől a környezet széle felé. A háló a környezet esetén tetra elemeket, míg a tekercsként szolgáló test esetén hexa elemekből áll.

A szimuláció során az alábbi peremfeltételek megadása szükséges (12.7. ábra):

Mágneses fluxus párhuzamossága (Magnetic Flux Prallel) - a mágneses fluxussal párhuzamos falak megadása a külső felületeken (Open Domain) és az oldalsó szimmetriasíkok mentén ( Symmetry:XYPlane , és Symmetry:YZPlane , amennyiben Y a tengelyvonal). Az alsó szimmetriasíkot nem kell kijelölni, mivel arra merőlegesek az erővonalak. Megjegyzés: a felületek kijelölésénél, használjuk a modellfában lévő előre definiált kiválasztásokat (Named Selections) .
Vezető test (Source Conductor) – az áramvezető anyag, a tekercset modellező test kijelölése.
Áramerősség (Current) - a vezető tekercsen átmenő áram (500mA) belépési felületének kijelölése a tekercs egyik végén.
Potenciál (Voltage) – A tekercs másik, (az árambevezetéssel ellentétes) végén a potenciál (föld-pont: 0mV) megadása szükséges.

12.7. ábra - Peremfeltételek a solenoid tekercs szimulációja során.

A szimuláció futtatása után, kérdezzük le a teljes mágneses térerősséget (Magnetic Field Intensity) a teljes testre vonatkoztatva (12.9. ábra), és az Y irányú (tehát tengely irányú) mágneses térerősség értékét a tekercs tengelyében definiált konstrukciós egyenes mentén, (12.8. ábra).

Ha az erővonalak irányát is szeretnénk látni a tekercs környezetében, a mágneses térerősséget vektorosan célszerű megjeleníteni (12.9. ábra, b, c). Ahogy az alábbi ábrákon látható a térerősség eloszlása és a vektorok eloszlása megfelel a várakozásainknak és előzetes ismereteinknek.

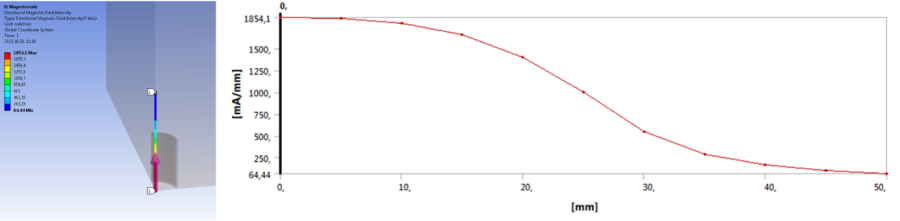
12.8. ábra - A mágneses térerősség alakulása a konstrukciós geometria mentén

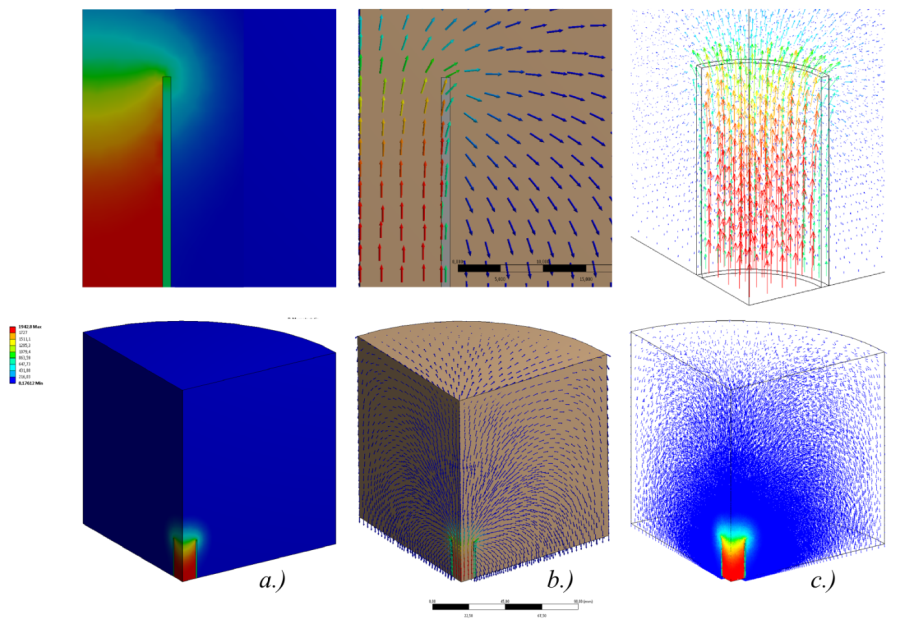
12.9. ábra - A mágneses térerősség bemutatása a tekercs környezetében: a.)színsávokkal, b, c.) vektorokkal.

Hasonló módon kérdezzük le a mágneses indukció (Magnetic Flux Density) értékét a teljes modellre és a konstrukciós vonal mentén. Látható, hogy a mágneses indukció nagysága a vonal mentén hasonló jelleggel változik, mint a mágneses térerősség esetében, mivel a légmagos tekercsben a permeabilitás értéke konstans, a két diagram csak a skálázásában tér el egymástól.

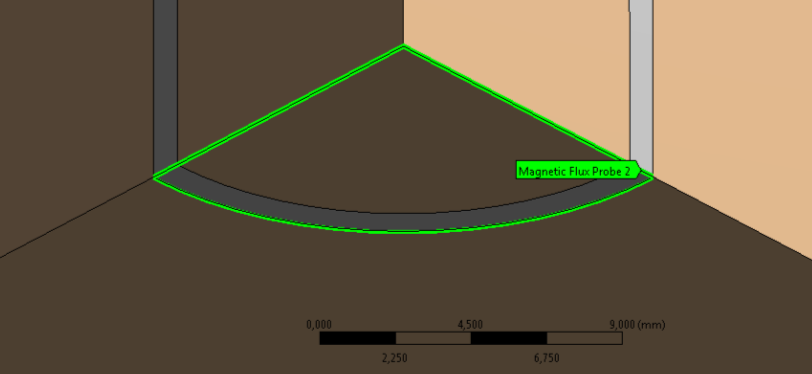
Lehetőségünk, van egy felületen áthaladó fluxus lekérdezésére (Magnetic Flux Probe) . A tekercs negyed keresztmetszetére kapott eredmény: 1,82⋅10^-4 mWb, (12.10. ábra).

A tekercs induktivitását (Inductance) egy egyszerű lekérdezéssel kapjuk meg. Ez jelen példában 0,032mH.

12.10. ábra - Egy felületen áthaladó fluxus lekérdezése.

12.2.1. Analitikus megoldás

Határozzuk meg egy homogén közegben lévő hengeres tekercsben (Szolenoid) folyó állandó áram által keltett mágneses térerősséget, a tér valamely P pontjában. Oldjuk meg a feladatot a tekercs tengelyére, az alábbi adatokkal.

A tekercs hossza: L = 50 mm, sugara: R = 10 mm, menetszáma: N = 100.

A tekercsen átfolyó áram erőssége: I = 1 A.

Első lépésben, határozzuk meg egy menet által keltett térerősség H értékét a tekercs tengelye mentén a menettől mért távolság függvényében a Biot-Savart törvény segítségével.

$\overset{⇀}{H} (r) = \frac{I}{4 π} \oint_{l} \frac{d \overset{⇀}{l} \times \overset{⇀}{r}}{r^{3}}$

(12.1)

A tengelyvonalon fekvő ponthoz tartozó r helyvektor merőleges az elemi vezetékhossz d l érintő vektorával, tehát a szorzatuk abszolút értékére felírhatjuk:

$| d \overset{⇀}{l} \times \overset{⇀}{r} | = | d \overset{⇀}{l} | \cdot | \overset{⇀}{r} | \cdot \sin ϑ = | d \overset{⇀}{l} | \cdot | \overset{⇀}{r} |$

(12.2)

Ezzel a térerősség abszolút értéke:

$H (r) = \frac{I}{4 π} \oint_{l} \frac{d l}{r^{2}}$

(12.3)

A térerősség-vektor radiális komponensei kioltják egymást, így a tengelyirányú komponens

$H_{a} (r) = \sin (α) \cdot \frac{I}{4 π} \oint_{l} \frac{d l}{r^{2}} = \frac{I}{4 π} \cdot \frac{R}{\sqrt{x^{2} + R^{2}}} \oint_{l} \frac{d l}{x^{2} + R^{2}} = \frac{I \cdot R^{2}}{2 {(x^{2} + R^{2})}^{3 / 2}}$

(12.4)

Hengeres tekercs esetén ezt kell összegeznünk a tekercs teljes hosszára, ahol az elemi hosszra n = N⋅dx/L számú menet jut.

$d H = \frac{I \cdot R^{2} \cdot N}{2 {(x^{2} + R^{2})}^{3 / 2} \cdot L} d x$

(12.5)

A tekercs tengelye mentén a mágneses térerősség abszolút értéke

$H = \frac{I \cdot R^{2} \cdot N}{2 \cdot L} \int_{- L / 2}^{L / 2} \frac{1}{{(x^{2} + R^{2})}^{3 / 2}} d x = \frac{I \cdot R^{2} \cdot N}{2 \cdot L} {[\frac{1}{R^{2}} \cdot \frac{x}{{(x^{2} + R^{2})}^{1 / 2}}]}_{- L / 2}^{L / 2} = \frac{I \cdot N}{L} \cdot \frac{1}{2} \cdot (\frac{\frac{L}{2} - x}{\sqrt{R^{2} + {(\frac{L}{2} - x)}^{2}}} - \frac{- \frac{L}{2} - x}{\sqrt{R^{2} + {(- \frac{L}{2} - x)}^{2}}})$

(12.6)

Ahhol az I⋅N/L szorzat a szolenoid tekercsek belsejében lévő mágneses tér közelítő képlete.

[47.]

12.2.2. Összefoglalás

Az alábbi diagramon (12.11. ábra) láthatjuk a numerikus, valamint a közelítő és pontos analitikus számolás eredményét. A diagram csak a tekercs felét mutatja, amely 25mm-nél ér véget, az origó pedig a tekercs közepét jelenti.

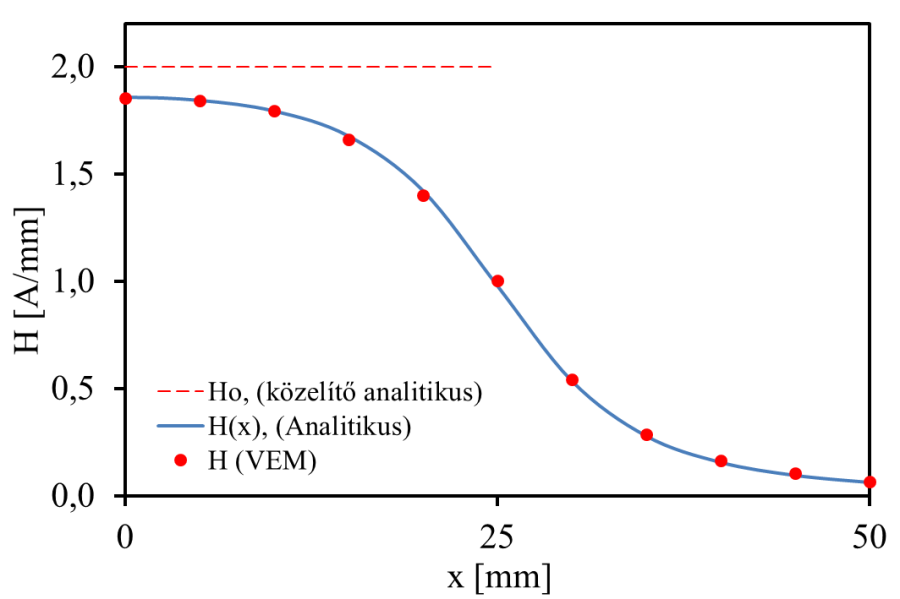
Az analitikus H(x) és végeselem H (VEM) számolás eredményeinek összehasonlítása. Ho=IN/L közelítő értéket mutatja, (a tekercs széléig jelölve).

12.11. ábra - Az analitikus H(x) és végeselem H (VEM) számolás eredményeinek összehasonlítása. Ho=IN/L közelítő értéket mutatja, (a tekercs széléig jelölve).

Az analízis elvégezve a környezet (levegő) különböző vastagságaival, azt találjuk, hogy jelentősen befolyásolja az eredményt. A tekercs sugarával azonos nagyságrendű levegőburok esetén a numerikus analízis hibája 30% feletti, (Táblázat 12.1).

12.1. táblázat - A környező levegőréteg vastagságának hatása a tekercs középpontjában számolt mágneses térerősségre.

Környezet vastagsága [mm]	H [A/mm]	Hiba [%]
5	1,166	37,2
25	1,777	4,3
40	1,839	1,0
100	1,854	0,2
Analitikus megoldás: 1,857 A/mm

12.3. Alkalmazási példa elektromágneses szimulációra

Az alábbiakban egy árammal átjárt tekercs és a benne lévő vasmag mágneses terének szimulációját mutatjuk be. A 3D-s negyed-modellként elkészített feladatban meg tudjuk majd figyelni a létrejövő mágneses tér jellemzőit, illetve a tekercs feletti tárcsára ható erő nagyságát. Az analízist az ANSYS Workbench végeselem programban végezzük el, melynek Magnetostatic szimulációját kell hozzáadnunk a projektünkhöz.

Minden elektromágneses és mágneses szimuláció estén különösen figyelni kell a geometria felépítésénél arra, hogy megfelelő méretű környezetet építsünk fel az alkotó alkatrészek köré, hogy a levegőben futó mágneses erővonalak is számításra kerüljenek.

12.12. ábra - Az elektromágnes geometriai modellje.

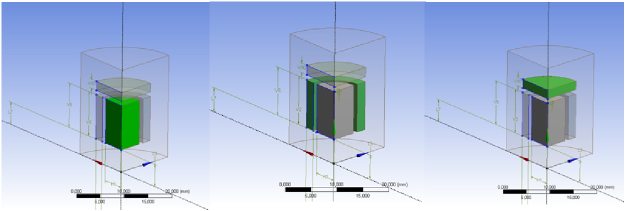
A vasmag, tekercs és a fedőlap geometriáját 90˚-os forgatással hoztuk létre, ahogy a 12.13. ábra is mutatja, (zöld színnel jelölt testek). Így egyből negyed modellt kapunk. (Megjegyzés: mivel több testet tartalmazó geometriát modellezünk, az újonnan létrehozott testeket „fagyasztott módban” (Add Frozen) kell elkészíteni.

12.13. ábra - A geometriai modell alkotói. Balról jobbra haladva: belső vasmag, tekercs, felső vasmag.

A környezetet egy olyan testtel kell modellezni, amely adott (lehetőleg egyenletes) távolsággal túlnyúlik a szimulációban részt vevő többi test szélétől, nem tartalmazza a többi test térfogatát és a levegő fizikai és elektromos-mágneses jellemzőivel rendelkezik.

A tekercset körülvevő környezetet (Tools/Enclosure) a többi test szélétől 5mm-es túlnyúlással hozunk létre, ugyanazokkal a szimmetria síkokkal, amik már definiálva vannak. Természetesen a szimmetria síkok irányában nincs túlnyúlása a környezetnek. A környezetet modellező geometria alakja hengeres.

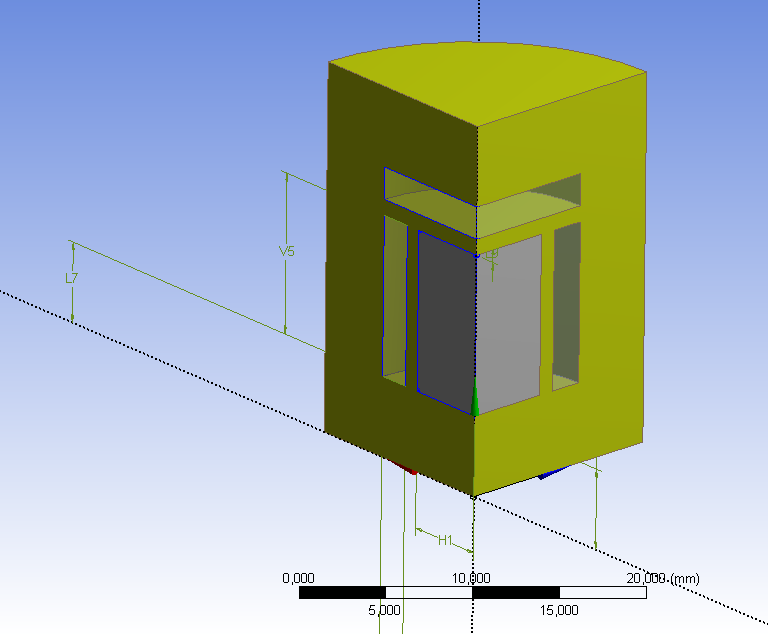
12.14. ábra - A környezetet geometriai modellje (sárga színű test)

Az elektromos-mágneses szimulációknál fontos, hogy a szilárd testek (Solid Bodies) egy alkatrészbe (Part) legyenek összefogva. Ezt a testek modellfában történő kijelölése után, a jobbgombos menüből elérhető új alkatrész készítése (Form New Part) paranccsal végezhetjük el. Ebben az esetben a testek közötti kapcsolatok (Contacts) nem kerülnek számításra.

A szimuláció során 3 féle beépített anyagot használunk, (Új anyag definiálása esetén csak az elektromágneses tulajdonságaikat kell definiálni). A felhasznált három anyag, és azok elektromágneses tulajdanoságaik a következők:

levegő (Air)
- Izotróp relatív permeabilitás (Isotropic Relative Permeability) : 1 [-],
réz ötvözet (Copper Alloy)
- Izotróp relatív permeábilitás (Isotropic Relative Permeability) : 1 [-],
- Izotróp fajlagos ellenállás (Isotropic Resistivity) : értéke hőmérséklettől függően megadva a következő:
  - 0˚C-on 1,548·10 ^-7 Ohm·m,
  - 20˚C-on 1,694·10 ^-7 Ohm·m,
  - 100˚C-on 2,277·10 ^-7 Ohm·m,
szerkezeti acél (Structural Steel)
- Izotróp relatív permeábilitás (Isotropic Relative Permeability): 10000 [-],
- Izotróp fajlagos ellenállás (Isotropic Resistivity): 1,7·10^-7 Ohm·m.

Az anyagkönyvtárba (Engineering Data) belépve, rendeljük ezeket a szimulációnkhoz, majd átlépve a szimulációs környezetbe, rendeljük hozzá őket a megfelelő testekhez. A levegő anyagot a környezethez, a szerkezeti acélt a belső vasmag és a fedőlap modellezésénél, míg a réz ötvözetet a tekercs modellezésénél használjuk.

A végeselemes háló elkészítésekor 1mm-es elemméretet alkalmaztunk, a környezet esetén tetra (tetraéder) elemeket, míg a vasmag, tekercs és fedőlap esetén hexa (tégla) elemeket használunk. A hálózott modellt a 12.15. ábra mutatja.

12.15. ábra - A véges elemes háló.

A szimuláció során alkalmazott terheléseket és peremfeltételeket a 12.16. ábra mutatja. Ezek alapján a környezeti levegő külső határaira olyan kényszert alkalmaztunk, mely definiálja, hogy a kijelölt felületekkel csak párhuzamos erővonalak húzódhatnak (Magnetic Flux Parallel) . A réz tekercset modellező testet vezető forrásként (Source Conductor) definiáltuk és 1000mA nagyságú áram (Current) átvezetését írtuk elő. (Megjegyzés, az áram be- és kivezetését nem szükséges külön definiálni.) Valamelyik pont potenciálját (Voltage) meg kell adni, esetünkben az árambevezetés helyén adjunk meg 0V-ot.

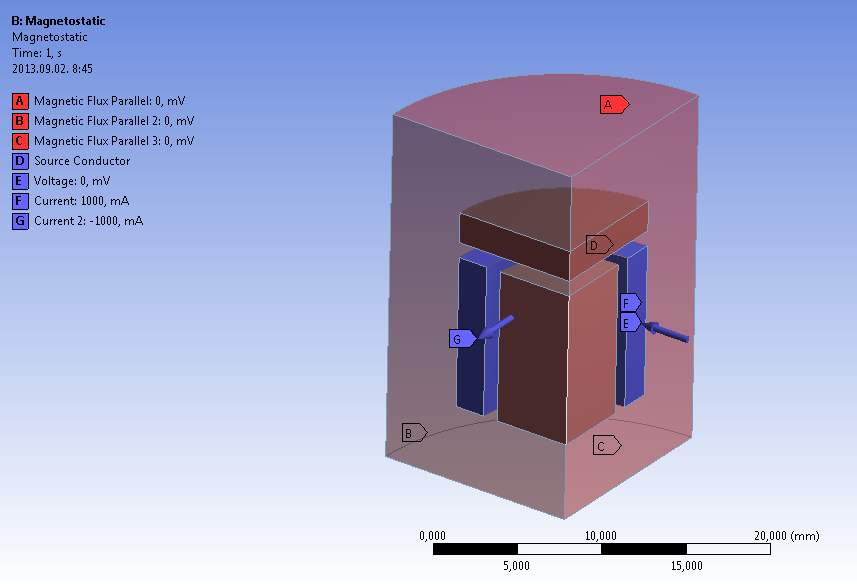
12.16. ábra - A terhelési modell komponensei elektromágneses szimuláció esetén

Az eredményeket tekintve láthatjuk, hogy a mágneses erővonalak a várakozásainknak megfelelő irányba haladnak. Ezt szemlélteti a 12.17. ábra és a 12.18. ábra, ahol a mágneses indukció (Magnetic Flux Density) és a mágneses térerősség (Magnetic Field Intensity) látható. Ebben az esetben érdemes az eredmények megjelenítését vektoros formában értékelni.

12.17. ábra - A mágneses indukcó eredményei vektoros formában

12.18. ábra - A mágneses térerősség eredménye vektoros formában

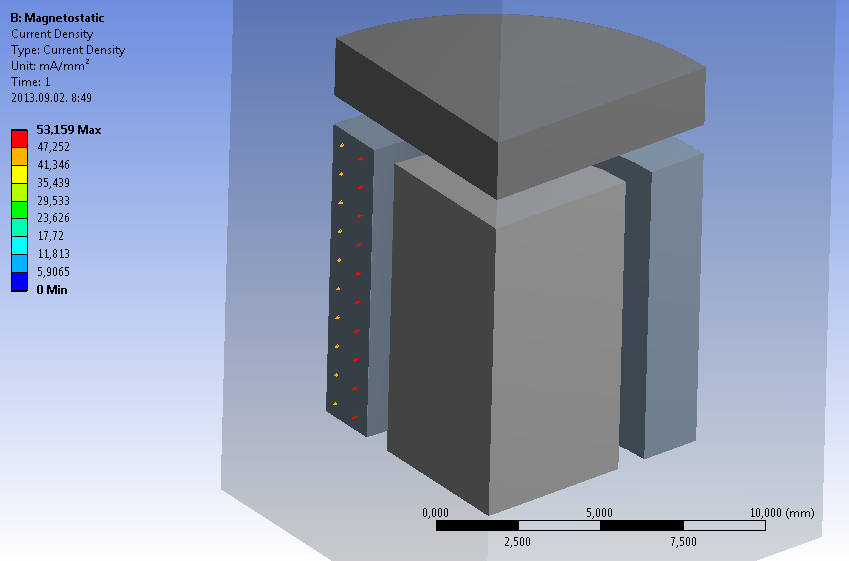
A következő, 12.19. ábra mutatja az áramsűrűséget (Current Density) szintén vektoros formában. Az eredmény mA/mm² mértékegységben látható.

12.19. ábra - Az áramsűrűség vektoros formában

A következő ábrán megfigyelhetjük az áramjárta tekercs erőhatását a szerkezeti acél fedőlapra (12.20. ábra). Mivel a fedőlapra –Y irányú vonzóerő lép fel, az eredmény negatív előjelű, tehát a fedőlap tekercshez közelebb eső részén nagyobb az erőhatás abszolút értéke (kb. 2 nagyságrenddel), mint a fedél tekercstől távolabb lévő részén.

12.20. ábra - Y irányú erőhatás a fedőlapra [N]

Vissza		Előre
11. fejezet - Harmonikus terhelések vizsgálata	Főoldal	13. fejezet - Termikus szimuláció