11. fejezet - Harmonikus terhelések vizsgálata
Vissza		Előre

11. fejezet - Harmonikus terhelések vizsgálata

Tartalom

11.1. Áttekintés
11.2. Példa harmonikus analízisre
11.3. Analitikus megoldás

11.1. Áttekintés

Mechanikai rendszereket gyakran ér tartósan ciklikus, ill. harmonikus terhelés, melynek hatására a szerkezet szintén harmonikus válasszal reagál. A harmonikus válasz analízis egy lineáris szerkezet időben szinuszosan változó terhelés(ek) hatására bekövetkező egyensúlyi válaszát adja meg (tranziens rezgések vizsgálatára nem alkalmas). Ez segít feltárni a gerjesztett rezgéseknek kitett szerkezet viselkedését (kifáradás, rezonancia, stb.). Mechatronikai rendszereknél, mérőműszereknél, szenzoroknál, a működési tartomány és az átviteli tulajdonságaik megállapításához különösen fontos, hogy vizsgálni tudjuk a szerkezet frekvenciafüggő dinamikus viselkedését. Az alábbiakban nézzük meg a harmonikus analízis speciális beállításait az ANSYS Workbench példáján keresztül.

Anyagmodellek.

Az analízis lineáris jellegéből adódóan a nemlineáris anyagtulajdonságok figyelmen kívül maradnak. Definiálnunk kell az anyag merevségét (pl.: rugalmassági modulus és Poisson-tényező) és a tömegét valamilyen formában (pl.: sűrűség, vagy ponszerűen megadott tömeg, stb.). Az anyag lehet izotróp, vagy ortotróp, állandó, vagy hőmérsékletfüggő.
Alkatrész viselkedés.

A statikai szimulációnál leírtak a mérvadóak.

Pontszerű tömeg alkalmazható. Csukló definiálására viszont nincs lehetőség a harmonikus analízisben. A rugóelemek csillapítása a csak a Teljes (Full) eljárásban használható, a módus szuperpozíciónál figyelmen kívül marad.
Alkatrészkapcsolatok, Kontaktok.

A nemlineáris kontaktok, mint pl. a súrlódásos kontakt (Frictional Contact) , a kezdeti értéküket kapják meg. A kontaktfelületek között definiált merevség a kezdeti feltételt veszi fel és a szimuláció alatt nem változik.
Hálózás.

A statikai analízisnél leírtak alkalmazhatók.
A szimuláció beállításai

A legfontosabb beállítás a vizsgált frekvenciatartomány kijelölése és a számítási pontok számának megadása. Ez utóbbi fogja meghatározni a frekvencia függvényében megadott eredménygörbe részletességét.

Az ANSYS esetében két számítási eljárást választhatunk a Teljes-et (Full) és a Módus Szuperpozíciót (Mode Superposition) . A Teljes módszer a szimultán mozgásegyenletek direkt megoldásával működik. A Módus Szuperpozíció esetében a harmonikus gerjesztésre adott válasz a modál analízisből származó sajátvektorok lineáris kombinációiból számolódik. Ez utóbbi esetben előnyös egy meglévő modál analízis eredményeinek felhasználása. (Mivel a sajátvektorok számítása a leg időigényesebb, ezért gyorsabban létrehozhatunk akár több harmonikus analízist, eltérő terhelési esetekkel, ugyanarra a modál analízisre építkezve.) A Módus Szuperpozíció általában gyorsabb eredményt ad, mint a Teljes eljárás. (Viszont nem alkalmazható akkor, ha (nem nulla) elmozdulást írunk elő.)

A fent már említett számítási pontokat egyenletes osztásközzel, vagy a rezonancia frekvenciák köré csoportosítva (Cluster Results) lehet kiosztani. Egyenletes kiosztásnál, ritkán felvett számolási pontok esetén, rezonanciacsúcsok maradhatnak ki. A rezonancia frekvenciák köré csoportosított pontok simább eredménygörbét adnak, viszont a módszer szükségessé teszi csillapítás definiálását, mivel a csillapítatlan rendszer csomópontjai a végtelenhez tartó rezonancia körül csoportosulnának. Ez utóbbi csak Módus Szuperpozíció esetén alkalmazható.

11.1. ábra - a.) Egyenletes eloszlású számolási pontok és b.) a pontok besűrítése a sajátfrekvenciáknál (Cluster result).

A vizsgált rendszer csillapításának definiálására az ANSYS végeselem rendszerben az alábbi lehetőségek állnak rendelkezésünkre: A csillapítási fok ( Constant Damping Ratio ) segítségével definiálhatjuk a legegyszerűbben a csillapítást. Béta csillapítás (Beta Damping) a merevségi mátrix szorzóját határozza meg. Segítségével közvetlenül adhatunk meg frekvenciafüggő csillapítást. Az anyagcsillapítást az anyagmodell definiálásánál kell megadnunk, ( ANSYS -ban kétféle: Material Dependent Damping, Constant Material Damping Coefficient ). Valamint alkalmazhatunk még elemcsillapítást (Element Damping), mint a rugóelem csillapítása. Többféle csillapítás definiálásakor hatásuk halmozódik.
Kezdeti és hőmérsékleti feltételek nem alkalmazhatók.
Peremfeltételek / Terhelések

A legtöbb mechanikai terhelés alkalmazható, melyek időben szinuszosan változó amplitúdójúak. Több terhelés megadásánál a jellegük, amplitúdójuk és fázisuk különböző lehet, de a frekvenciájuk azonos kell, hogy legyen. A terhelések fázisa a legtöbb esetben tetszőlegesen megadható, viszont a külpontos erő (Remote Force) , a nyomaték (Moment) és a gyorsulás (Acceleration) esetében csak nulla lehet. A terhelések szinuszos változása által csak az erővektor hossza és iránya változik támadáspontja nem ANSYS-ban. Ezért olyan terheléseket, amelyek támadáspontja irányfüggő, pl. csapágyterhelés (Bearing Loads) , nem célszerű alkalmazni.

11.2. ábra - Csapágyterhelés szinuszos váltakozása ANSYS-ban, Forrás: [6.] .

A lineáris kényszerek alkalmazhatók, viszont a nemlineáris kényszerek, mint a Csak nyomó (Compression Only) , vagy a Súrlódásmentes kényszer (Frictionless Support) viselkedése lineárissá válik a harmonikus szimuláció alatt.
Az eredmény bemutatása.

Az eredmények bemutatásának két lényeges módja lehetséges. Az egyik a modellen színsávok segítségével szemléltetett feszültség, alakváltozás, vagy elmozdulás, stb. Ebben az esetben definiálni kell, hogy az adott eredményt milyen frekvencián és fázisszög mellett szeretnénk megtudni.

A másik lehetőség az eredmények diagramon való ábrázolása, mely lehet Bode, vagy a reális és imaginárius részeket bemutató diagram.

11.2. Példa harmonikus analízisre

Harmonikus analízis esetén harmonikus gerjesztésre adott rendszerválaszt tudunk szimulálni. Ebben a példában kezdeti feltételként a korábban ismertetett modál analízis lett definiálva, mely tartalmazza a konzol megfogását az egyik végén (10.4. ábra). (Abban az esetben, ha nincs előzetes analízis, amelyben definiálva van a megtámasztás, akkor a terheléssel átellenes oldalon egy fix megfogást (Fix Support) kell alkalmaznunk.) A harmonikus terhelés a konzol másik végén, 8N nagyságú, +Y irányú erő (Force) .

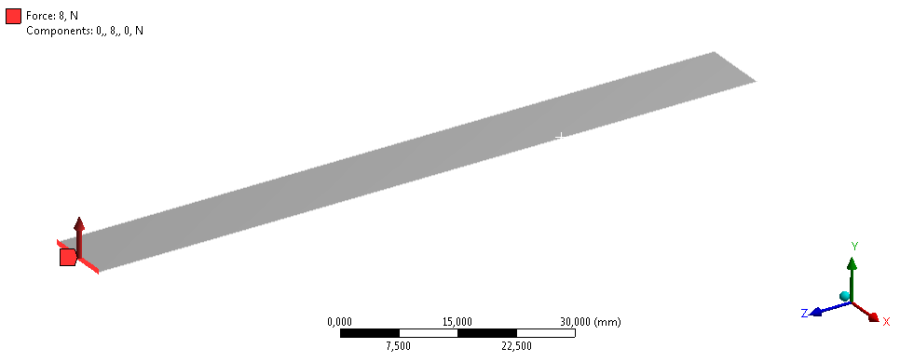
11.3. ábra - A harmonikus erőterhelés helye

A vizsgálat frekvenciatartományát 0-500Hz-re választjuk, az előzetes modál analízis alapján (1. sajátfrekvencia 164Hz), (Outline/Analysis Settings => Details/Options/Range Minimum: 0; Range Maximum: 500 Hz) .

A számolási pontok, a sajátfrekvencia környékén történő besűrítéséhez kapcsoljuk be a Cluster Result opciót, (a pontok száma: 10 (Cluster Number) ). Ehhez definiálni kell a rendszer csillapítását, amit a merevségi mátrix csillapítás (Details/Damping Control/Stiffness Coefficient) , értékének 0,0001 –re állításával adunk meg.

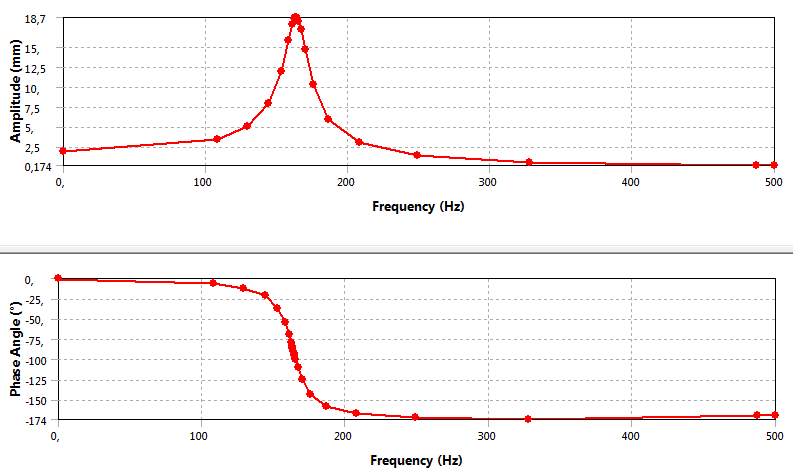
A szimuláció futtatása után, az eredményeket Bode-diagramon tudjuk megtekinteni, a Frequency Response/Deformation lekérdezés hozzáadásával. A lekérdezett, vagyis kimenő paraméter az erővel terhelt rúdvég Y irányú elmozdulása. A Bode diagram, így a rúdvég elmozdulásának amplitúdóját (felső, amplitúdó görbe), és a gerjesztő erőhöz viszonyított fáziskésését (alsó, fázisszög) mutatja a frekvencia függvényében.

Megjegyzés: A rendszertechnikában alkalmazott (az itt használatossal ellentétben), Bode diagram vízszintes tengelye logaritmikus osztású, melyen a körfrekvencia értékek megadása viszont lineáris. Így nagyobb tartományok átfogására is kitűnően alkalmas. Valamint az amplitúdómenettel a ki és bementi mennyiségek hányadosának hússzoros logaritmusát ábrázoljuk lineáris osztású tengelyen.

A Bode-diagramot elemezve láthatjuk, hogy a diagramon lévő rezonanciacsúcs helye megegyezik a korábbi példánál számított első sajátfrekvenciájával (10.8. ábra).

11.4. ábra - Harmonikus terhelés esetén a Bode-diagram

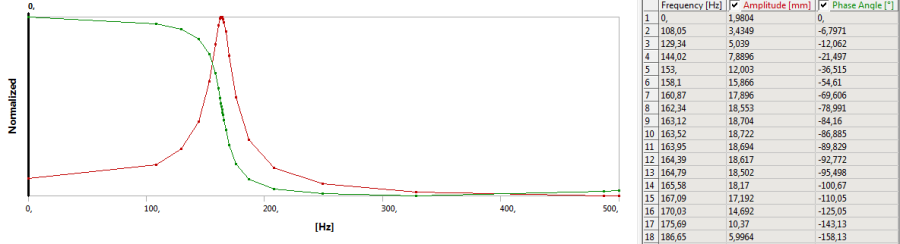
A normált megjelenítésnél egy diagramban láthatjuk az amplitúdó és fázismenetet. Mellette táblázatos formában találhatjuk a görbe pontjait, melyeket vágólapra másolva kimenthetünk további feldolgozás céljából (11.5. ábra).

11.5. ábra - Amplitúdó és fázismenet normált diagram

11.3. Analitikus megoldás

Az előző fejezetben már vizsgáltuk a rudak szabad rezgéseit. Most vizsgáljuk meg az egyik oldalán befogott rúd gerjesztett rezgését. A végeselemes harmonikus analízis eredményének ellenőrzéseként oldjunk meg a feladatot analitikusan is [46.] . Kiindulásnak adva van egy téglalap keresztmetszetű, homogén és izotróp rúd, az alábbi paraméterekkel.

Gerjesztő erő: F ₀ = 8N.

A hasáb méretei – hossza: L=100mm, magassága: h=2mm, szélessége: b=10mm;

Anyaga – acél, Rugalmassági modulus: E=200GPa, Poisson-tényező: ν=0,3.

Határozzuk meg a rúd rezgésének nagyítási (vagy Bode) diagramját és feszültségét.

Az egyik oldalán befogott állandó keresztmetszetű prizmatikus rudat a rúd tengelyére merőleges harmonikus erő gerjeszti, amit az F=F₀⋅sin(ωt) egyenlettel írhatunk le. A rúd anyagának belső csillapítása és a levegő ellenállása csillapítják a rezgést. Így a rúd rezgését leíró (10.3) egyenlet időfüggő része (u(t)), az alábbi formában adható meg, (állandósult csillapított kényszerrezgés).

$u (t) = A_{i} (ω) \cdot s i n (ω \cdot t - φ_{i} (ω))$

(11.1)

Az i. módus amplitúdója, (i=1,2,3…):

$A_{i} (ω) = \frac{A_{i 0}}{\sqrt{{(ω_{i o}^{2} - ω^{2})}^{2} + {(2 ξ \cdot ω_{i 0} \cdot ω)}^{2}}}$

(11.2)

Az egyes módusokhoz tartozó saját-körfrekvencia:

$ω_{0 i} = {(\frac{λ_{i}}{l})}^{2} \cdot \sqrt{\frac{E \cdot I}{ρ \cdot T}}$

(11.3)

Ahol λ az alkalmazott peremfeltételektől függő tényező. Az egyik végén befalazott rúd (y(0)=0, y’(0)=0, y”(l)=0) esetén λ értéke az első 3 sajátfrekvencia esetén rendre λ=1,875; 4,694; 7,855.

Az amplitúdó maximuma a rezonancia-körfrekvencia értékénél van:

	$A_{i, m a x} = \frac{A_{i 0}}{2 ξ \cdot ω_{i o}^{2} \sqrt{1 - ξ_{i}^{2}}}$	(11.4)
	$ω_{r i} = ω_{i 0} \cdot \sqrt{1 - 2 ξ_{i}^{2}}$	(11.5)

A csillapítás hatására létrejövő fáziseltérést a gerjesztő erő és a rúd rezgése között a fáziskésés értékével adjuk meg:

$φ_{i} (ω) = a r c t g \frac{2 ξ \cdot ω_{i 0} \cdot ω}{ω_{i o}^{2} - ω^{2}}$

(11.6)

Ahol:

A _0i – A gerjesztés mértékétől függő amplitúdó-állandó,

ω _0i –az egyes módusokhoz tartozó saját-körfrekvencia,

ω _ri –az egyes módusokhoz tartozó rezonancia-körfrekvencia,

φ – a fáziskésés szöge,

ξ – a csillapítási fok (0,05),

I – a keresztmetszeti tényező, (téglalap esetén I = b·h ³ /12),

E – az anyag rugalmassági modulusa,

ρ– az anyag sűrűsége,

T– a keresztmetszet területe,

A fenti egyenletek segítségével diagramon adhatjuk meg a rezgő rúd amplitúdó és fáziskésés értékét a körfrekvencia függvényében.

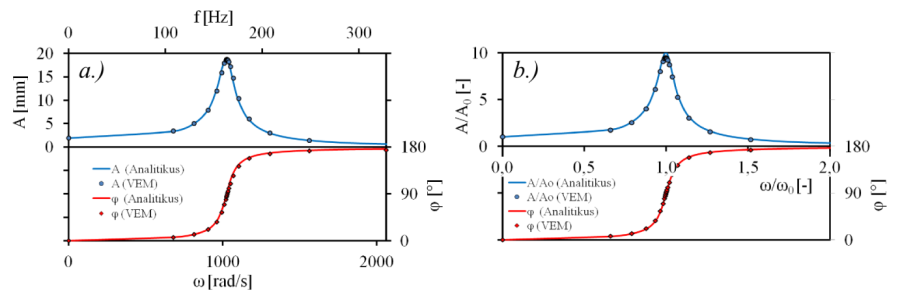
a.) abszolút értékekkel és b.) normált formában. (Csillapítási fok: 0,05)

11.6. ábra - Az analitikus és a numerikus eredmények összehasonlítása.

Vissza		Előre
10. fejezet - Modális analízis	Főoldal	12. fejezet - Elektromos és mágneses szimulációk