10. fejezet - Modális analízis
Vissza		Előre

10. fejezet - Modális analízis

Tartalom

10.1. Áttekintés

A modál (Modal) , vagy alaki analízis segítségével határozhatjuk meg egy szerkezet rezgésének karakterisztikáját, tehát a rezgési sajátfrekvenciáit és a hozzájuk tartozó lengésképeket. Ezek fontos paraméterei egy dinamikusan igénybevett szerkezet tervezésének. A modál analízis eredményeit kiindulópontként használhatjuk más, részletesebb vizsgálathoz, (mint pl.: a tranziens dinamikus, harmonikus válasz, vagy a spektrum analízis).

Előfeszített (Prestressed) szerkezetek analízisére is lehetőség van, mint pl.: nagy centripetális gyorsulásnak kitett turbinalapát, előfeszített szerkezeti elem, stb.

Csillapított szerkezeti elem esetén a szimuláció csillapított, a sajátfrekvenciák és a lengésalakok komplexek lesznek.

Forgó szerkezet esetén a szögsebességből fakadó giroszkópikus hatás bekerül a modál analízisbe, ami hatással van a rendszer csillapítására. A sajátérték változását különböző szögsebességnél a Campbell diagramon vizsgálhatjuk.

Anyagmodellek.

A modál analízis jellegéből adódóan csak a lineáris anyagtulajdonságokkal dolgozhatunk. Meg kell adnunk az anyag merevségét (pl.: rugalmassági modulus és Poisson-tényező) és a tömegét valamilyen formában (pl.: sűrűség, vagy pontszerűen megadott tömeg, stb.).
Alkatrész viselkedés, kontaktok.

A statikai szimulációnál leírtak vonatkoznak ide is. A 2D-s és szimmetriakényszerek alkalmazásánál figyelembe kell venni, hogy az aszimmetrikus módusok nem kerülnek bele az eredménybe.

Megoldótól függően csuklók, rugó és csillapító elemek valamint pontszerű tömegek alkalmazhatók [6.] .
Hálózás.

A statikai szimulációnál leírtak szerint.
A szimuláció beállításai.

Az egyik legfontosabb beállítás a módusok számának megadása, vagyis, hogy az első hány db. sajátfrekvenciát és a hozzátartozó lengésképet akarjuk kiszámoltatni (minimum 1).

Beállítható a megoldó típusa és, hogy a rendszer csillapított, vagy nem. Kétféle csillapítás, a merevségi együttható (Stiffness Coefficient) és a tömeg együttható (Mass Coefficient) segítségével adható meg.
Kezdeti feltételek

Előfeszített szerkezetek szimulációjára használhatunk statikai analízist a modál analízis bemeneteként. Olyan esetekben célszerű az alkalmazása, amikor egy szerkezet tipikus üzemi feltételei olyan mértékű deformációt, vagy feszültséget okoznak, ami jelentősen befolyásolja a rezgési karakterisztikáját, vagyis elhangolja azt. Előfeszített szerkezet szimulációjakor a modál analízis peremfeltételeit nem kell külön megadnunk, mert azt a statikus terhelési esetből (előfeszítés) származtatjuk.
Peremfeltételek / Terhelések

Terhelésként csak szögsebesség adható, egyéb mechanikai terhelést előfeszítésként kell megadni. A szabadságfokok megkötésére szolgáló kinematikai kényszerek alkalmazhatók, kivéve a nem nulla elmozdulás kényszereket (Ansysban: Non-zero Displacement, Remote Displacement, Velocity boundary condition) . Nemlineáris jellege miatt a csak nyomóhatást kifejtő kényszerek (Compression Only Supports) kerülendőek.
Az eredmény bemutatása.

A modál analízis eredménye alapvetően a szerkezet sajátfrekvenciái és a hozzájuk tartozó lengésképek. Egyes esetekben lekérdezhető a feszültség és a fajlagos nyúlás is, de abszolút értékük nem valós, (az elmozduláshoz hasonlóan), helyes információt csak a relatív eloszlásukról ad. Az eredményt animálhatjuk, ami a relatív elmozdulások időbeni lefolyásával szemléletesen mutatja a rezgés módját.

Forgó szerkezet esetén a sajátérték változását különböző szögsebességnél a Campbell diagramon vizsgálhatjuk.

10.2. Konzolos lemez modal analízise előfeszítés nélkül és előfeszítéssel

Ebben a fejezetben egy egyszerű konzol előfeszítés nélküli és előfeszített modál analízisét mutatjuk be ANSYS Workbench végeselem programmal. A következő fejezetekben pedig a harmonikus terhelésre adott válaszát és tranziens viselkedését vizsgáljuk.

A konzol geometriája mindhárom szimulációnál, a már korábban alkalmazott 100x10x2mm nagyságú hasáb, amelyet felületként modelleztünk. Ez látható a következő ábrán. (A lemez vastagságát a szimuláció során definiáltuk.)

10.1. ábra - A konzol felületmodellje.

A test anyaga minden szimuláció során szerzeti acél (Structural Steel) . A modell hálózásánál 2,5mm-es hexa elemeket használjunk. Így a teljes modell 160 elemet tartalmaz (10.2. ábra).

10.2. ábra - A hálózott végeselem modell.

Az eredmények lekérdezéséhez egy a lemez hosszanti irányában végig futó konstrukciós geometria (Path) is definiáljunk (10.3. ábra).

10.3. ábra - A konstrukciós vonal helye.

10.2.1. Modal analízis előfeszítés nélkül

Az előfeszítés nélküli modal analízis megmutatja a rendszer saját frekvenciáját abban az esetben, ha nincs semmilyen terhelő erő. Ekkor csak a rögzítést kell megadni. Jelen példában ez egy fix megfogás (Fix Support) a lemez egyik végén (10.4. ábra).

10.4. ábra - A fix megfogás helye a lemezen - kék címkével jelölve.

Ezután állítsuk be a keresendő sajátfrekvenciák számát (6 az alapértelmezett), (Outline/…/Analysis Settings => Details/Options/Max Modes to Find: 6).

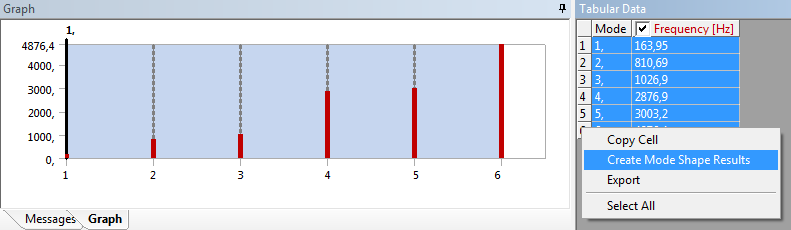
Futtassuk a szimulációt, majd kérdezzük le a lengésképeket. A lengésalakok lekérdezésénél eljárhatunk a hagyományos módon a deformáció (Total Deformation) parancs kiadásával. Ekkor lekérdezésenként a vizsgálni kívánt módus számának manuális beállítása szükséges (Details/Definition/Mode: 1, 2, ...) . Több módus vizsgálata esetén egyszerűbb, ha az eredményeket tartalmazó táblázat (Outline/Solution => Tabular Data) , minden sorát kijelölve, a jobbgombos menüből a Creat Mode Shape Results parancsot alkalmazzuk (10.5. ábra). Ekkor minden kijelölt frekvenciához automatikusan létrejön a lengésképeket bemutató teljes deformációs eredményt. Ismételt futtatás után megjelennek a lengésképek.

10.5. ábra - Lengésképek lekérdezése a sajtfrekvenciák eredményei alapján.

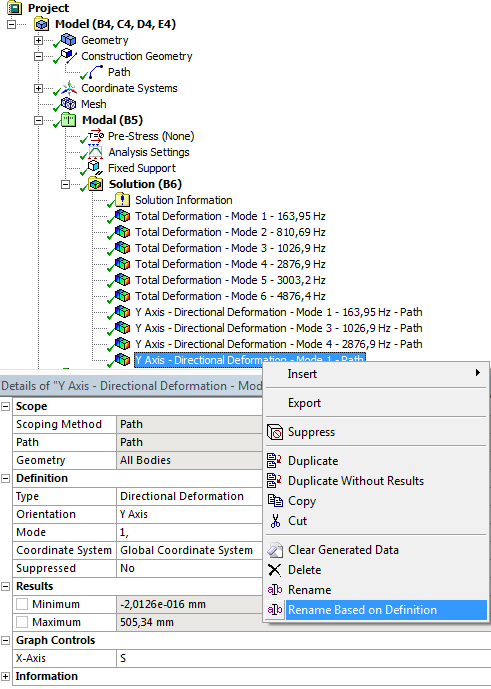
A teljes deformáció képe alapján, az eredmények nélkül duplikáljuk (Duplicate Without Results) azokat az eredményeket, amelyek csak Y irányú lengést végeznek. Majd a kijelölést (Scoping Methode) állítsuk át a konstrukciós vonalra (Path) , és a típusát pedig (Y) irány menti deformációra (Type: Directional Deformation; Orientartion: Y Axis) . Ismételt futtatás után megjelennek az eredmények, az ábra alatt grafikon és táblázatos formában is.

Az eredmények jobb áttekinthetősége végett, a modellfában átnevezhetjük az eredményeket tartalmazó sorokat, a rájuk vonatkozó sajátfrekvencia alapján. Ehhez jelöljük ki az összes eredménysort a Shift billentyű lenyomásával az elsőre és utolsóra kattintva), majd jobbgombos menüből válasszuk a Rename Based On Definition parancsot (10.6. ábra).

10.6. ábra - Automatikus átnevezés a definíció alapján.

10.2.2. Modal analízis előfeszítéssel

A következő példa ugyanannak a konzolnak a saját frekvenciáit keresi, mint az előző példában, annyi különbséggel, hogy itt egy statikus előfeszítést alkalmazunk. A fix befogás (jelen példában egy egyszerű megtámasztást (simply supported) használtunk 0 elmozdulással) a konzol ugyanazon oldalán található, az ellentétes oldalon pedig egy 0,5 [mm] nagyságú, pozitív z irányú elmozdulás típusú terhelés található. Jelen példában egy külpontos elmozdulást (remote displacement) alkalmaztunk. A statikus előfeszítés terhelési modellje a következő ábrán látható.

10.7. ábra - A statikus előfeszítés terhelési modellje.

Eredmények:

A terheletlen szerkezet modál analízisének eredményeit a 10.8. ábra és a 10.9. ábra tartalmazza.

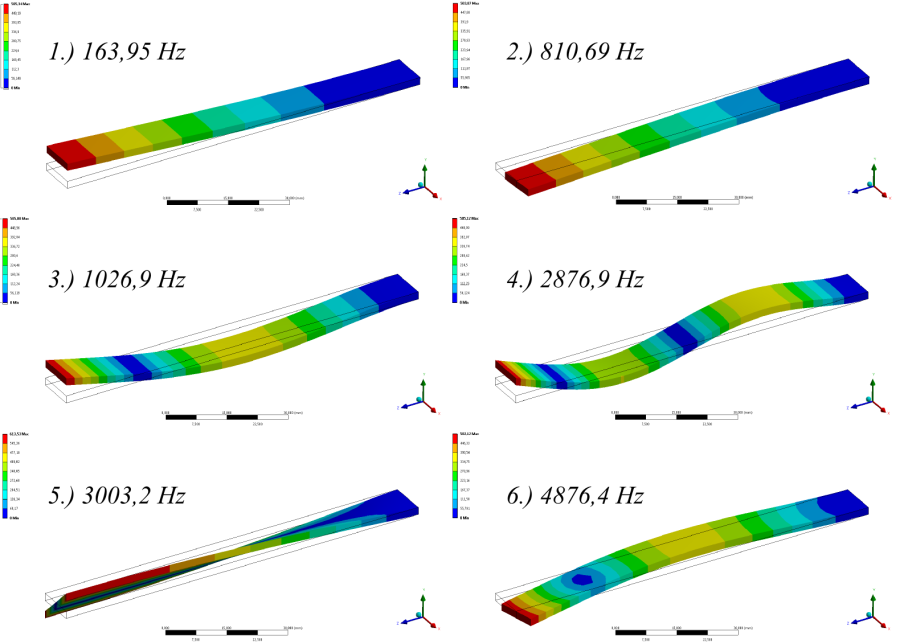
10.8. ábra - A terheletlen szerkezet lengésképei és sajátfrekvenciái.

Az Y irányú konstrukciós geometria mentén lekérdezett saját frekvenciák természetesen csak az Y irány mentén változó lengésképen mutat értelmezhető eredményt. Ezeket a következő táblázat tartalmazza.

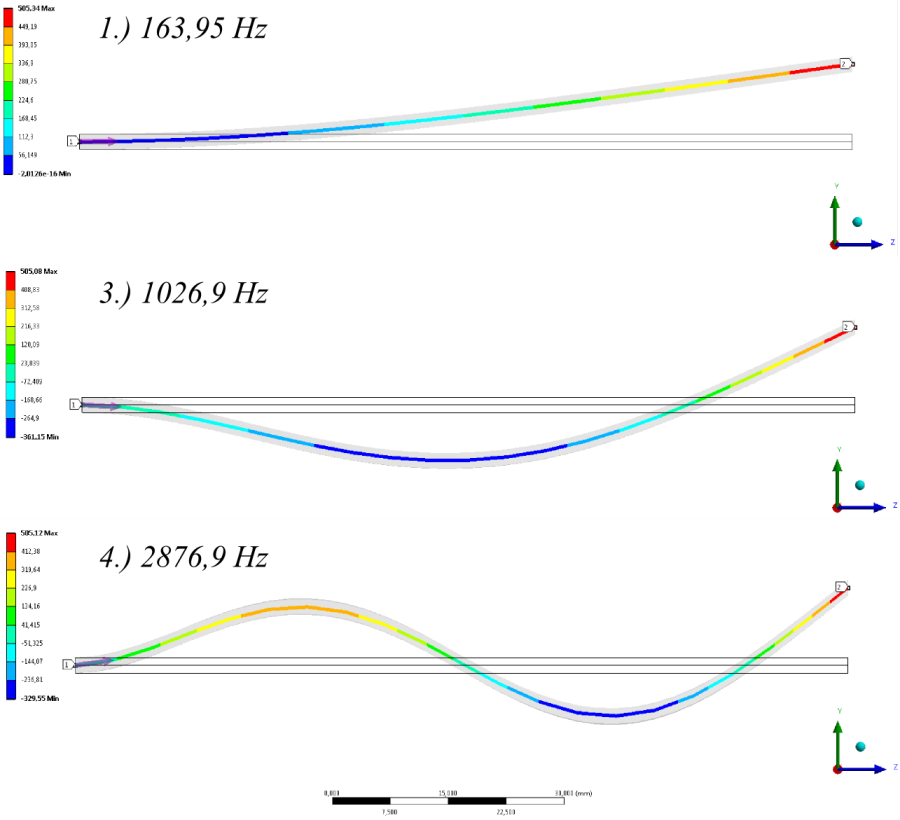
10.9. ábra - A terheletlen szerkezet Y irányú jellemző lengéssel rendelkező módusainak vonal menti eredménye.

Az előfeszített konzol saját frekvenciái, ahogy az várható volt, nőttek (Táblázat 10.1), a saját frekvenciák lengésképe lényegesen nem változott.

10.1. táblázat - A terheletlen és az előfeszített szerkezet első 6 sajátfrekvenciájának összehasonlítása.

Módus	A jellemző lengés iránya	Terheletlen f ₀ [Hz]	Terhelt f ₀ [Hz]
1.	Uy	163,95	979,87
2.	Ux	810,69	1611,1
3.	Uy	1026,9	3088,7
4.	Uy	2876,9	3130,1
5.	Rz	3003,2	5612,6
6.	Ux	4876,4	7155,9

10.2.3. Analitikus megoldás

A végeselemes eredményének ellenőrzéseként oldjunk meg a feladatot analitikusan is [25.] , [46.] . Kiindulásnak adva van egy téglalap keresztmetszetű homogén és izotróp rúd, az alábbi paraméterekkel.

A hasáb méretei – hossza: L=100mm, magassága: h = 4 mm, szélessége: b = 10 mm;

Anyaga – acél, Rugalmassági modulus: E = 200 GPa, Poisson tényező: ν = 0,3.

Határozzuk meg a rúd első sajátfrekvenciáját és a meghajolt rúd alakját.

Egy állandó keresztmetszetű prizmatikus rúd hajlító rezgéseit, idő és a keresztmetszet helye szerint az alábbi parciális differenciálegyenlet írja le:

$E \cdot I \frac{\partial^{4} f (z, t)}{\partial z^{4}} + ρ \cdot A \frac{\partial^{2} f (z, t)}{\partial t^{2}} = 0$

(10.1)

Bevezetve a

$λ = \sqrt[4]{\frac{ω_{0}^{2} \cdot ρ \cdot A}{E \cdot I}}$

(10.2)

az egyenlet megoldása az

$y (z, t) = u (t) \cdot y (z)$

(10.3)

alakban várható, melynek helyfüggő, v(z) tagjának általános megoldása az alábbi:

$y (z) = A \cdot c o s (\frac{λ \cdot z}{l}) + B \cdot s i n (\frac{λ \cdot z}{l}) + C \cdot c h (\frac{λ \cdot z}{l}) + D \cdot s h (\frac{λ \cdot z}{l})$

(10.4)

ahol:

y(z) – az egyenestől való kitérés mértéke,

I – a keresztmetszeti tényező, (téglalap esetén I = b·h ³ /12),

E – az anyag rugalmassági modulusa,

ρ – az anyag sűrűsége,

A – a keresztmetszet területe,

ω ₀ – a sajátkörfrekvencia.

Az A, B, C és D tagok a rúdvégeken alkalmazott peremfeltételektől függő állandók.

A mindkét végén csuklós megfogást választva (y(0)=0, y(l)=0, y”(0)=0, y”(l)=0), A=C=D=0 és B⋅sin(λ⋅z/l)=0. Ebből B=0 triviális megoldás az y(z)=0-t eredményezné, ezért λ=n⋅π adódik (n=1,2,3… a sajátfrekvenciák sorszámának megfelelően.)

Visszahelyettesítés után kapjuk a rezgő rúd sajátfrekvenciáit és a lengésképet leíró függvényt.

	$ω_{0} = {(\frac{λ}{l})}^{2} \cdot \sqrt{\frac{E \cdot I}{ρ \cdot A}}$	(10.5)
	$y (z) = B \cdot s i n (\frac{n \cdot π \cdot z}{l})$	(10.6)

Az egyik végén befalazott rúd (y(0)=0, y’(0)=0, y”(l)=0) esetén λ értéke az első 3 sajátfrekvencia esetén rendre λ=1,875; 4,694; 7,855. A lengésképet leíró függvény (Rayleigh féle függvényekből kifejezve):

$y (z) = \frac{1}{2} (c h (\frac{λ \cdot z}{l}) - c o s (\frac{λ \cdot z}{l})) + \frac{D_{4}}{2} (s h (\frac{λ \cdot z}{l}) - s i n (\frac{λ \cdot z}{l}))$

(10.7)

ahol: D4 állandó értéke az első 3 sajátfrekvencia esetén rendre: D₄=-0,734; -1,018; -0,999.

Mindkét végén befalazott rúd (y(0)=0, y’(0)=0, y(l)=0, y’(l)=0) esetén λ értéke az első 3 sajátfrekvencia esetén rendre λ = 4,7301; 7,8532; 10,9956. A D₄ állandó értéke az első 3 sajátfrekvencia esetén rendre: D4=-0,9826; -1,0008; -0,9999.

✎ A fenti egyenletek alapján határozzuk meg a rúd első 3 sajátfrekvenciáját és rajzoltassuk ki diagramban a rezgő rúd alakját különböző peremfeltételek alkalmazása mellett. Hasonlítsuk össze a végeselemes programok eredményeivel.

10.2. táblázat - Az analitikus és numerikus eredmények összehasonlítása az első 3, Y irányú lengés esetében.

Módus	fo [Hz] (Analitikus)	fo [Hz] (VEM)	Hiba [%]
1	163,95	163,06	0,55
2	810,69	-	-
3	1026,9	1021,94	0,49
4	2876,9	2861,75	0,53

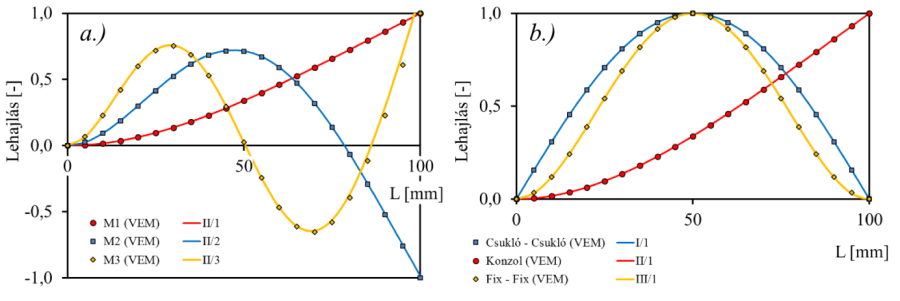
a.) Egy oldalon befogott tartó első 3, Y irányú lengésképe. b.) Mindkét végén megtámasztott tartó első lengésképe, különféle típusú megtámasztásokkal.

10.10. ábra - Terheletlen rúd lengésképei különféle peremfeltételek esetén.

Vissza		Előre
9. fejezet - Dinamikus, tranziens mechanikai analízis	Főoldal	11. fejezet - Harmonikus terhelések vizsgálata