9. fejezet - Dinamikus, tranziens mechanikai analízis
9.1. Áttekintés
A dinamikus, vagy más néven tranziens mechanikai analízis (Transient Structural Analysis, time-history analysis) során adott szerkezet időfüggő terhelés hatására bekövetkező dinamikus válaszát vizsgáljuk. Az analízis során meghatározhatjuk az elmozdulások, fajlagos nyúlás, feszültség, stb. időbeli változását a tranziens terhelés hatására. A szimuláció időbeli lefutását főként a szerkezet tehetetlensége és csillapítása befolyásolja. Amennyiben ezek hatása nem fontos, használhatunk statikai analízist a probléma megoldására.
( ANSYS -ban a Mode Superposition eljárás segítségével lehetőség van a tranziens analízis terhelési feltételeinek, a Modal analízis sajátvektorainak lineáris szuperpozícióval való számolására.)
A tranziens mechanikai analízis lehet lineáris, vagy nemlineáris (nagy alakváltozás, plasztikus, vagy hiperelasztikus anyagi viselkedés, nemlineáris kontaktok, stb.).
A tranziens analízis lényegesen számolásigényesebb, mint a statikai szimuláció, ezért az erőforrások gazdaságos felhasználása érdekében az alkalmazó mérnöknek tisztában kell lenni a probléma fizikai hátterével:
-
A szimulációban lévő nemlinearitások statikai vizsgálata segítségével eldönthetjük, hogy szükséges-e alkalmazásuk a dinamikai analízis során.
-
Előzetes modál analízis segítségével képet kaphatunk a szerkezet viselkedéséről adott frekvencián és a sajátfrekvenciák segítségével beállíthatjuk a megfelelő integrációs időt a tranziens analízisben.
-
Egy egyszerűsített modell vizsgálata gazdaságosan adhat képet a szerkezet viselkedéséről.
-
A tranziens szerkezeti analízis esetében alkalmazható anyagmodellek.
A statikai analízisben alkalmazott anyagmodellek itt is használhatók (lineáris, vagy nemlineáris, izotróp, vagy ortotróp, állandó, vagy hőmérsékletfüggő), de az inerciális terhelés miatt az anyag sűrűségét is meg kell adni.
-
Alkatrész viselkedés.
Egy összeállítás dinamikai analízisében gyakran szerepelnek olyan alkatrészek, melyek deformációjára és feszültségi állapotára nem, vagyunk kíváncsiak, csupán a terhelések átadásában van szerepük. Ezeket merevtestként (Rigid Parts) definiáljuk a szimulációban.
Lehetőség van pontszerű tömeg (Point Mass) megadására, amelynek általában a tehetetlenségi nyomatéka is megadható.
A statikai analízishez hasonlóan, itt is célszerű a modell egyszerűsítése (2D-s geometria, vagy szimmetriafeltételek alkalmazásával).
-
Alakatrészkapcsolatok, Kontaktok.
Némely végeselem szoftverben (pl. ANSYS) a hagyományos kontaktok mellett csukló (joint), vagy csillapítással ellátott rugóelemek (Spring) is alkalmazhatók.
-
Hálózás.
Egy dinamikus analízis esetében, a statikai analízisnél leírtak figyelembevételén túl, a hálónak elég finomnak kell lennie, hogy képes legyen bemutatni a vizsgált legnagyobb módushoz tartozó alakot.
-
A szimuláció beállításai.
A dinamikus szerkezeti analízisben (a statikaihoz hasonlóan), karcsú szerkezetek nagy lehajlásai, vagy hiperelasztikus anyagmodellek alkalmazása esetén szükség lehet a nagy lehajlások (Large Delection) funkció alkalmazására. (Bővebben lásd a „Statikai analízis” fejezetben leírtakat.)
A dinamikai szimulációnál kap igazi jelentőséget az időlépések (Time Steps) beállítása, ugyanis az időben lefutó tranziens jelenségről csak akkor kapunk megfelelő képet, ha a számolási pontok időbeni sűrűsége megfelelő. Az időlépések (Time Steps) definiálásánál több lépés is megadható, aminek segítségével lépésenként változó beállításokat, vagy terheléseket definiálhatunk. Megadható az al-lépések (Substeps) száma, vagy időintervalluma, mellyel egy lépés felosztását definiáljuk. A tranziens analízisnél beállított időlépések a valós időt jelentik (Time Integration = ON) .
Egy mechanikai szerkezet időbeni viselkedésének egyik fontos meghatározója a szerkezeti elemek csillapítása, aminek a definiálására a csillapítás beállításánál (Damping Controls) van lehetőségünk. (Az ANSYS VEM szoftverben Béta, numerikus, anyag és a rugóelemek csillapítása definiálható.)
Nemlineáris analízis esetében számolni kell a konvergencia problémák felmerülésével. A problémát okozhatják merevtest szerűen elmozduló alkatrészek, túl nagy terhelés-növekmény, anyagi instabilitások, vagy a nagy deformáció okozta elemtorzulások. A megoldást, a probléma okától függően, az elemméret, ill. az időlépések optimális megválasztása, a konvergencia kritériumok módosítása, vagy a megoldó megfelelő megválasztása jelentheti.
-
Kezdeti feltételek
Tranziens szerkezeti analízis során a terhelések az idő függvényei, melynek első lépésében a kezdeti feltételek (tehát a nulladik időpillanatban érvényes kondíciók) érvényesülnek. Az alapértelmezett kezdeti feltételként a szerkezet nyugalomban van, tehát mind az elmozdulások, mind pedig a kezdeti sebesség értéke nulla. A szerkezet egy, vagy több alkatrészére definiálható konstans sebesség kezdeti feltételként, a többi alkatrészen nyugalmi kezdeti feltétel marad.
-
Peremfeltételek / Terhelések
Alkalmazható minden, a statikai analízisnél használható szerkezeti kényszer és terhelés, valamint inerciális terhelés. A terhelések mértéke lehet állandó, vagy időben változó. Az időben változó terhelést definiálhatjuk az egyes lépések terhelésszintjének megadásával direkt módon (táblázatosan), az al-lépések növekményével (lineárisan növekvő – ramped, vagy egy lépésben stepped), vagy függvény megadásával. Az egyes terhelések, vagy peremfeltételek hatása adott lépésnél ki, ill. bekapcsolható.
-
Az eredmény bemutatása.
Az eredmények lekérdezése és bemutatása hasonlóan történik, mint a statikai analízisnél, de itt az eredmény az idő függvényében értelmezendő. Az eredmény animálásánál az időskála a valós időt mutatja, de a lejátszás sebessége általában ettől eltérő. Egy lengő, vagy rezgő mozgást végző szerkezet esetében a képkockák sűrűségének beállításánál (Frame/s) ügyelni kell a rezgés frekvenciájára, ugyanis a túl ritkán felvett képkockák nem a valós tranziens jelenséget fogják bemutatni.
9.2. Példa tranziens szimulációra
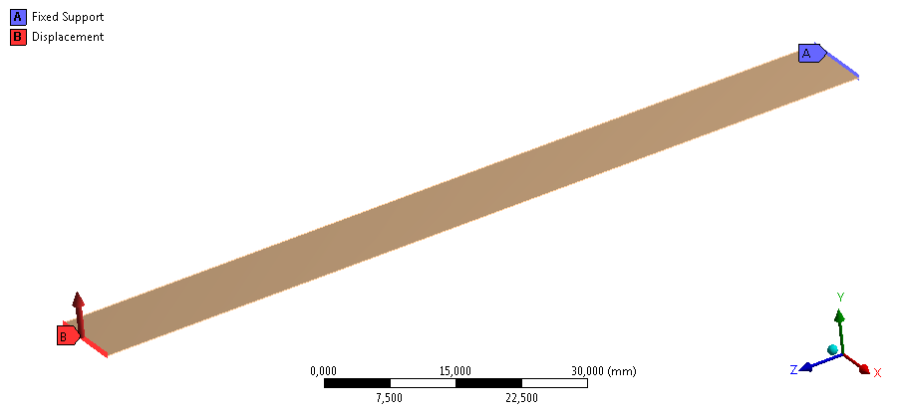
Ebben a tranziens dinamikus szimulációban, (a korábbi statikai feladatokból ismert) konzol adott terhelésre adott válaszának időbeni lefutását szimuláljuk. A terhelési modell egy fix befogást (Fix Support) tartalmaz a konzol egyik végén, míg a másik oldalán egy olyan elmozdulás (Displacement) típusú terhelést, melyben +Y irányban 2mm elmozdulás van definiálva, míg a másik két tengely (X és Z) irányában a szabad elmozdulás megengedett (9.1. ábra). A szimulációnál kezdeti feltételként a modál analízis eredményeit használtuk fel.
A beállításoknál nagyon fontos a lépések és a lépések időtartamának beállítása. Ebben az esetben a szimuláció 2 lépést tartalmazott, az első lépés időtartama 0,0001s, míg a második lépés vége 0,1s. Fontos az al-lépések időtartamának helyes beállítása, ugyanis ez határozza meg a tranziens jelenség számolása során az időbeni eredménypontok sűrűségét. Ha túl ritkán vesszük fel az időlépéseket az helytelen eredményhez vezet, ha túl sűrűn, akkor nagy számolási idő és tárolókapacitás igényű lesz az analízisünk. Ezért érdemes valamilyen módszerrel (előzetes modál analízis, közelítő analitikus számolás, stb.) a rendszer vizsgálandó legnagyobb sajátfrekvenciájának, vagy becslése, mert ez jó támpontot ad az időlépések sűrűségének beállításához. Ha ez ismert, akkor az időlépéseket úgy érdemes felvenni, hogy a rezgés periódusidejétől legalább egy nagyságrenddel kisebbek legyenek az időlépések.
Mivel esetünkben a rúd 1. sajátfrekvenciája: f=163Hz, periódusideje: T≈0,006s, ezért érdemes az időlépések felosztását dt<0,0006s –ra választani.
A tranziens jelenség kialakulásának oka a rugalmasan deformált, (meghajlított) konzol elengedésekor létrejövő rezgés. Ehhez nem elég a rúd végének Y irányú 2mm-es elmozdítása, de el is kell engedni azt. Ezt úgy tehetjük meg, hogy a modellfán kijelölt elmozdulás kényszert (Displacement) , az idődiagramján, a második időlépésben ki kell kapcsolni ( Graph fülön a munkatér alatt, az elmozdulást jelképező vízszintes vonalra való jobb egérgombos kattintással, majd Deactivate ).
Megjegyzés: A kikapcsolással (Deactivate) nem egyenértékű a 0 érték megadása, mert míg az előző magára hagyja a rendszert, addig a második megoldás 0 elmozdulást kényszerít rá, vagyis rögzíti az eredeti helyzetben.
A nagy alakváltozások miatt, a Large Deflection opciót alkalmazni kell. Mivel minden tranziens szimulációnál alapvető a csillapítás definiálása, itt is adjuk meg az értékét a modellfa szimulációs beállítások elemével (Outline/…/Analysis Settings => Outline/Damping Control/…) . A csillapítást jelen esetben merevségi együttható (Stiffness Coefficient) megadásával határozzuk meg, melynek értéke 0,0001[-]. A numerikus csillapítási érték (Numerical Damping Value) 0,1 [-].
![Deformáció [mm] a tranziens szimuláció 2. időpillanatának végén](images/image_IX_2.png)
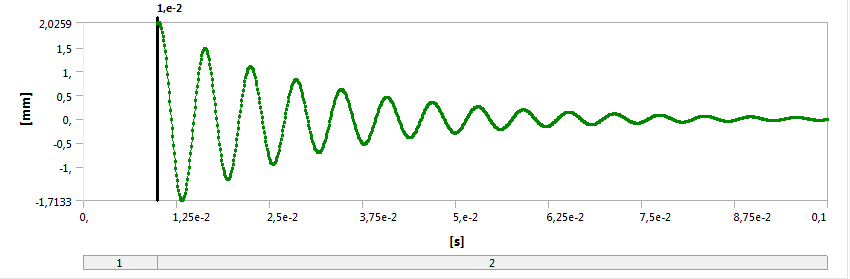
A szimuláció lefutása után látható az eredményen, hogy a 2. időintervallum végén a deformáció már jóval alatta marad a megadott 2mm nagyságú elmozdulásnak. Az egy pillanatra vonatkozó deformációs értékek azonban nem sokat árulnak el a folyamat lényegéről, vagyis az időbeli lefolyásáról. Ezért a tranziens szimulációknál elengedhetetlen az időbeli eredmény grafikus megtekintése. A konzol terhelt véglapjának Y irányú deformációjának (Directional Deformation) időbeli lefutását mutatja be a 9.3. ábra. Látható, hogy a konzol a terhelés kikapcsolása után, a beállított csillapítás hatására, pár lengés után visszaáll kiinduló helyzetébe.