8. fejezet - Kihajlás vizsgálat
8.1. Áttekintés
Az alábbiakban az ANSYS Workbench végeselem programban elvégezhető lineáris kihajlás vizsgálatot mutatjuk be. A lineáris kihajlás vizsgálat (Linear Buckling Analysis) , (vagy más néven sajátérték kihajlás (Eigenvalue Buckling) ), egy ideálisan rugalmas szerkezet elméleti kihajlási merevségét határozza meg, (pl. egy rugalmas oszlop kihajlásának Euler féle megoldását adja meg.). Bár a valóságban az anyagszerkezet hibái és nemlinearitásai megakadályozzák, hogy a szerkezet elérje az elméleti kihajlási merevségét, mégis hasznos lehet az (nem konzervatív) eredmény gyors becslésére. Az instabilitás előrejelzésére sokkal pontosabb megoldást ad a nemlineáris kihajlás vizsgálat, amely magában foglal egy statikai analízist, bekapcsolt „nagy lehajlások” (Large Deflection) effektussal. Ebben a vizsgálatban fokozatosan növekedő terhelést használunk az instabillá válás terhelési szintjének megtalálásához. Nemlineáris technika alkalmazásakor lehetőségünk van kezdeti tökéletlenségek, plasztikus viselkedés, hézagok, nagy lehajlások alkalmazására a modellben.
-
Anyagmodellek.
Az anyagmodell csak lineáris lehet, továbbá izotróp, vagy ortotróp, állandó, vagy hőmérsékletfüggő. Az anyag nemlineáris tulajdonságai figyelmen kívül maradnak. Meg kell adnunk az anyag merevségét (pl.: rugalmassági modulus és Poisson-tényező).
-
Alkatrész viselkedés, Kontaktok, Hálózás.
A statikai szimulációnál leírtak vonatkoznak rá.
-
A szimuláció beállításai.
Meg kell adni a módusok számát, (általában az 1., vagyis a legalacsonyabb az érdekes).
-
Kezdeti és Peremfeltételek / Terhelések
A lineáris kihajlás vizsgálatot egy statikai analízisnek kell megelőznie, ami a lineáris kihajlás vizsgálat kezdeti feltételét fogja jelenteni. A kihajlás vizsgálatban nem lehet terheléseket és peremfeltételeket definiálni. Ezek és a feszültségi állapotok a statikai analízisből kerülnek felhasználásra.
Nem nulla értékű kényszerek is alkalmazhatók.
-
Az eredmény bemutatása.
A lineáris kihajlás vizsgálat eredménye a kihajlási terhelés faktora és a hozzá tartozó kihajlási alakok. A kihajlási terhelés faktora a statikai analízisben megadott terheléssel szorozva adja meg az instabil viselkedéshez tartozó kritikus terhelést értékét. (Kihajlási terhelés = Kihajlási terhelés faktora * Statikus terhelés). A kihajlási terhelés faktora az összes alkalmazott terhelésre vonatkozik. Egy szerkezet elvileg végtelen sok kihajlási terhelési faktorral rendelkezhet, és minden faktor egy instabilitási mintához tartozik. De számunkra általában a legalacsonyabb az érdekes.
Az eredményként kapott módusok hasznos segítséget nyújtanak a kihajlás alakjának szemléltetésében, de a deformáció abszolút értéke nem ad valós eredményt. Lekérdezhető a feszültség és a fajlagos nyúlás is, de abszolút értékük nem valós, (az elmozduláshoz hasonlóan), helyes információt csak a relatív eloszlásukról ad. Az eredményt animálhatjuk, ami a relatív elmozdulások időbeni lefolyásával szemléletesen mutatja a kihajlás módját.
8.2. Kihajlás vizsgálat VEM példa
Az alábbi példában, ugyanazt a geometriai modellt felhasználva, többféle megtámasztási esettel vizsgáljuk a szerkezet kihajlását. A geometria minden esetben egy, a korábbi példákban alkalmazott, 100mm hosszú és 10x2mm-es négyszög keresztmetszetű gerendamodell (Line Body/Beam Element).
A szimuláció mindig két részből áll, először az adott befogási feltételekkel egy statikai vizsgálatból, majd egy erre épülő (kezdeti feltétel a megelőző statikai analízis) lineáris kihajlás vizsgálat (Linear Buckling) . Tehát a geometria létrehozása után egy statikai (Static Structural) analízist kell létrehoznunk, melyben definiáljuk az anyagmodellt, a hálózást, valamint a perem és terhelési feltételeket. A feladatban eltekintünk a statikai analízis eredményeinek bemutatásától, csak a kihajlási eredményeket tekintjük át az egyes befogási eseteknél.
Az anyaghoz használjunk szerkezeti acélt (E=200GPa, v=0,3). A hálózáshoz 2mm-es elemméretet használtunk, így a teljes elemszám 50 lett. A geometriát és a véges elemes hálót a 8.1. ábra szemlélteti.
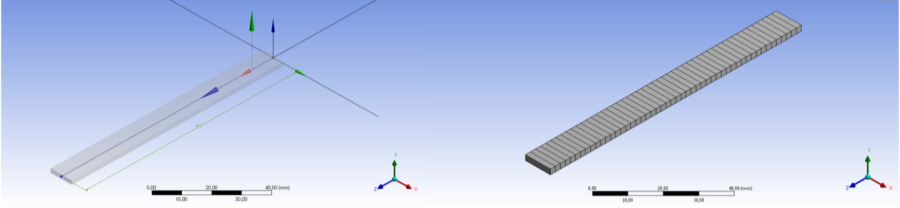
A szerkezeti analízisben egy alapterhelést kell beállítanunk, amelynek a szorzóját a kihajlás vizsgálat fogja megadni. A négyszög keresztmetszetű rudat mindegyik esetben 100N nagyságú –Z tengely irányú erővel terheljük az egyik végén, úgy, hogy a rúd nyomva legyen.
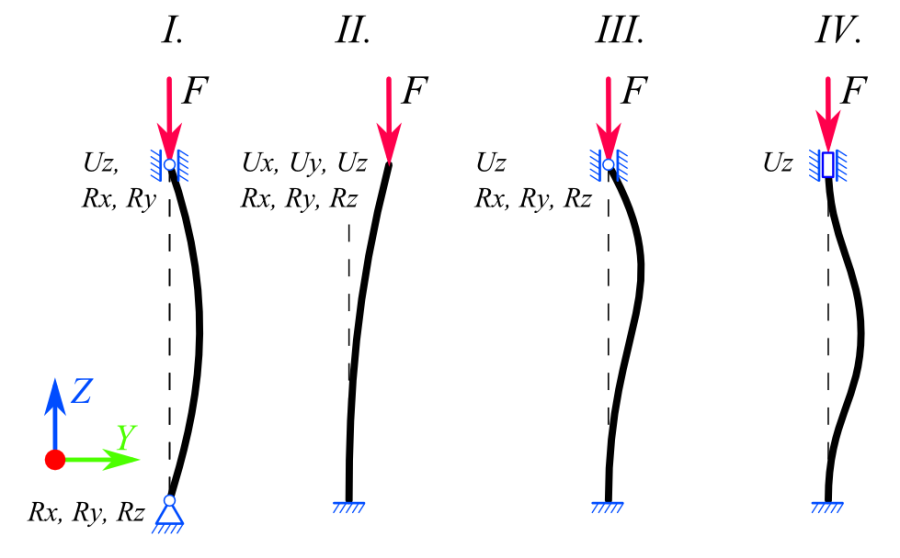
A vizsgálatot a peremfeltételek, vagyis a két rúdvég megtámasztásának különböző eseteivel végezzük el. A befogási esetek megegyeznek a karcsú rúd analitikus kihajlás vizsgálata során használt, és jól ismert 4 modellel:
-
befogási eset (8.2. ábra, I.):
Az első esetben az erőterhelési oldalon egy külpontos megfogás (Remote Displacement) típusú kényszerrel definiáljuk ennek a végpontnak a viselkedését. Ezzel az adott pont elmozdulását és elfordulását is beállíthatjuk. (Jelen esetben a végpont elmozdulása oldalirányban (X és Y) gátolva van, azonban tengelyirányban (Z) szabadon elmozdulhat, az elfordulás X és Y tengely körül megengedett, Z tengely körül azonban 0˚, tehát e tengely mentén nincs elfordulás.)
A terhelőerővel ellentétes oldalon egy egyszerű megtámasztás típusú (Simply Supported) befogást definiáltunk, amely azt jelenti, hogy a rögzített pont elmozdulása minden irányban gátolt, azonban az elfordulás minden tengely mentén megengedett.
Kihajlás vizsgálat eredménye az első befogási viszonyokkal:
A kihajlás nagyságát az középvonal mentén kérdeztük le, X és Y irányban megfigyelve a deformációt. Látható, hogy a kihajlás Y irányba, (vagyis a keresztmetszet kisebb másodrendű nyomatékának tengelyére merőleges irányban) történt, az X irányban a deformáció elhanyagolható. A kihajlott alak megfelel a peremfeltételek mellett várt alaknak, a konzol közepe kihajlik.
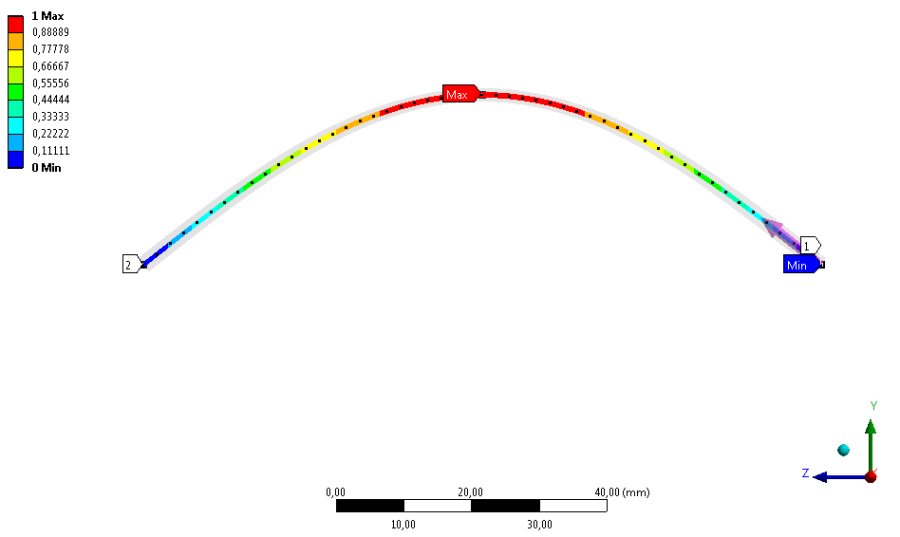 8.3. ábra - Y irányú deformáció az első megfogási esetben.
8.3. ábra - Y irányú deformáció az első megfogási esetben.
-
befogási eset, (8.2. ábra, II.):
Ebben a megfogási esetben a terheléssel ellentétes oldalon egy fix megfogás (Fix Support) típusú megtámasztás található. Tehát ennek a pontnak minden szabadságfokát elimináltuk, se elmozdulás, se elfordulás nem lehetséges. A terhelés támadáspontjánál nem definiáltunk kényszereket, ez a pont szabadon elmozdulhat és elfordulhat minden irányban.
Kihajlás vizsgálat eredménye a második befogási esetnél:
Az deformációs eredményen jól látható, hogy a kihajlott alak megfelel az előzetes várakozásainknak, a terhelés támadáspontja az Y irányba, (vagyis a keresztmetszet kisebb másodrendű nyomatékának tengelyére merőleges irányban) mozdul el (8.4. ábra).
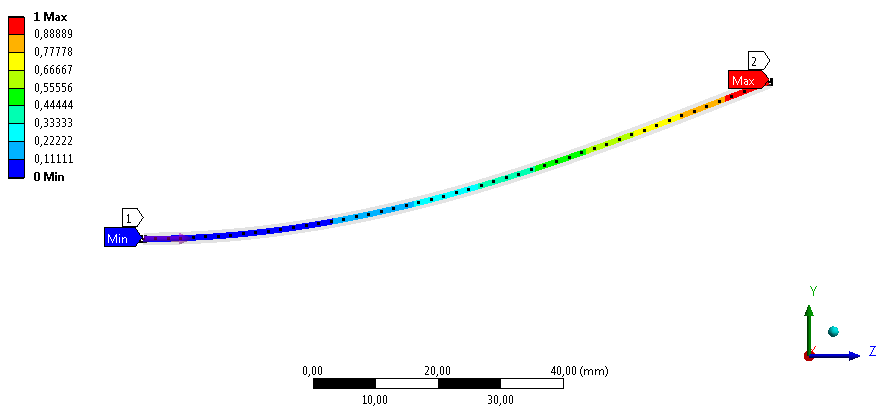 8.4. ábra - Y irányú deformáció a második megfogási esetben.
8.4. ábra - Y irányú deformáció a második megfogási esetben.
-
befogási eset, (8.2. ábra, III.):
Ebben az esetben a konzol befogásánál fix megfogást (Fix Support) definiálunk, míg a terhelési pontnál egy külpontos megfogást (Remote Displacement) alkalmazunk, a következő beállításokkal: X és Y irányú elmozdulás megkötése, a Z irányú elmozdulás, valamint az X, Y és Z tengely körüli elfordulás szabadon hagyása. Mivel az elfordulást egyik tengely mentén sem kell megkötni, használhatunk Displacement kényszert is.
Kihajlás vizsgálat eredménye a harmadik befogási esetnél:
Az alábbi ábrán látható, hogy a kihajlott deformált alak megfelel a várakozásoknak, a konzol egy része az Y irányba kihajlik (8.5. ábra).
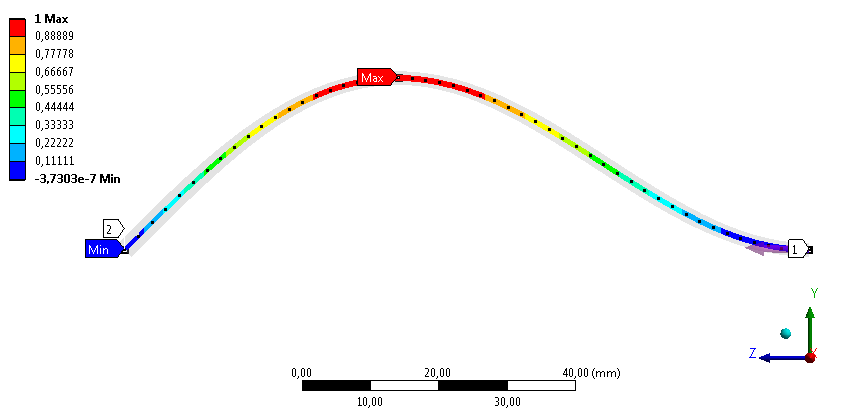 8.5. ábra - Y irányú deformáció a harmadik megfogási esetben.
8.5. ábra - Y irányú deformáció a harmadik megfogási esetben.
-
befogási eset, (8.2. ábra, IV.):
Utolsó esetben a terhelési oldalon egy olyan külpontos megfogást (Remote Displacement) alkalmazunk, amely csak a Z irányú elmozdulást enged meg, a többi irányú elmozdulás és minden tengely menti elfordulás gátolva van. A befogási pont fixen van rögzítve (Fix Support) . (8.2. ábra, I.)
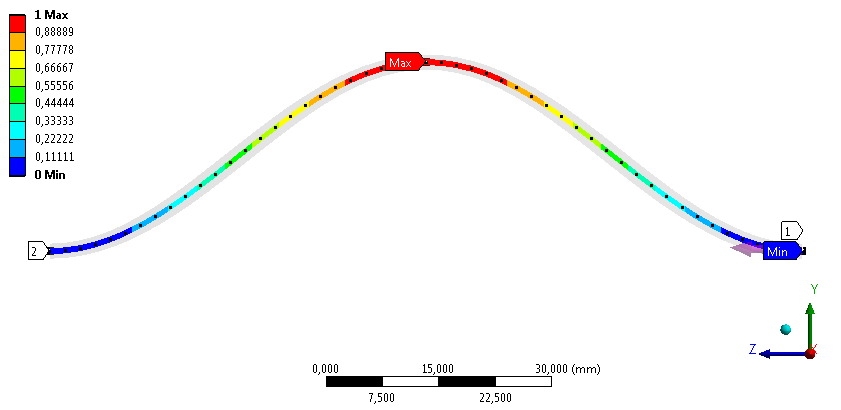 8.6. ábra - Y irányú deformáció a negyedik megfogási esetben.
8.6. ábra - Y irányú deformáció a negyedik megfogási esetben.
8.3. Analitikus megoldás
A végeselemes programok eredményének ellenőrzéseként oldjunk meg a feladatot Euler és Tetmajer módszerével. Kiindulásnak adva van egy téglalap keresztmetszetű rúd, az alábbi paraméterekkel. Feltételezzük, hogy a rúd anyaga homogén és izotróp és a terhelés a keresztmetszet súlypontjában, rúdirányban hat. [25.] .
Kiinduló adatok:
A hasáb méretei – hossza: L = 100 mm, magassága: h = 2 mm, szélessége: b = 10 mm;
Anyaga – Szénacél [25.] , Rugalmassági modulus: E = 200 GPa, Poisson tényező: ν = 0,3;
A Tetmajer egyenes állandói a = 308, b = 1,14; Folyáshatár: σ eH = 240 MPa.
Határozzuk meg a rúd kritikus (törő) feszültségét és a meghajolt rúd alakját.
A rudat terhelő kritikus erő hatására a rúdvégtől számított (z) távolságú helyen M(z)=F t ·y(z) nyomaték hat, amely a rúd alakváltozását okozza.
Ahol:
M(z) – a rúdba ébredő hajlítónyomaték,
F t – a kritikus terhelőerő,
y(z) – az egyenestől való kitérés mértéke.
A kihajlás egyenletét a rugalmas szál differenciál egyenletéből származtatjuk.
|
|
(8.1) |
ahol:
I – a keresztmetszeti tényező, (téglalap esetén I = b·h 3 /12),
E – az anyag rugalmassági modulusa.
|
|
(8.2) |
helyettesítéssel az y”+α 2 ⋅y=0 másodrendű homogén differenciálegyenletet kapjuk, melynek általános megoldása adja a rúd alakját leíró függvény.
|
|
(8.3) |
Az A és B tagok a rúdvégeken alkalmazott peremfeltételektől függő állandók. Mindkét végén csuklós megfogást választva ( y(0)=0, y(l)=0), B=0 és A⋅sin (α⋅l)=0, ebből A=0 triviális megoldás a y(z)=0 -t eredményezné ezért α=n⋅π/l adódik (n=1 -nek van gyakorlati jelentősége). Visszahelyettesítés után kapjuk a kritikus erő számításának Euler féle egyenletét, ahol az l 0 a peremfeltételektől függő működő rúdhossz (lásd: 8.2. ábra).
|
|
(8.4) |
|
|
|
(8.5) |
állandók bevezetésével kapjuk a gépészeti tervezésben szokásos összefüggést.
|
|
(8.6) |
ahol:
σ t – a kritikus törőfeszültség,
λ – karcsúsági tényező.
Az Euler féle összefüggés csak karcsú rudak rugalmas kihajlására érvényes. A zömök rudak képlékeny kihajlására a Tetmajer összefüggés ad megoldást.
|
|
(8.7) |
ahol:
a, b– anyagtulajdonságtól függő állandók.
A képlékeny szakaszra számos más megoldás is létezik, de példánkban a Tetmajer egyenest vesszük fel mivel ez a legismertebb eljárás.
✎ A fenti egyenletek alapján rajzoltassuk ki diagramban a kritikus feszültség értékét a karcsúsági tényező függvényében és a kihajlott rúd alakját különböző peremfeltételek alkalmazása mellett. Hasonlítsuk össze a végeselemes programok eredményeivel.
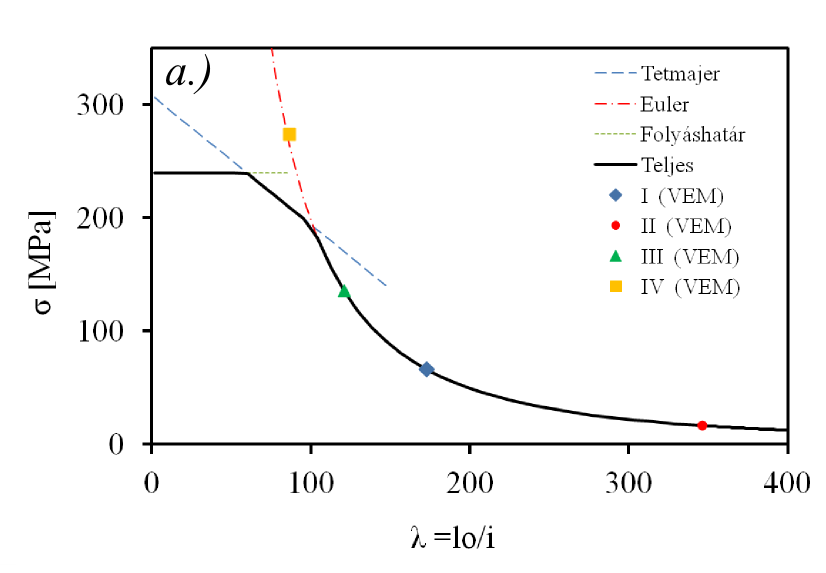
Ismét felhívnánk a figyelmet az eredmények körültekintő alkalmazására. Látható, hogy a IV. megfogási eset végeselem megoldása már a képlékeny tartományba esik, tehát a kapott eredményt felül kell bírálni az adott anyagra érvényes karcsúsági határ (λ 0 ) szerint.