7. fejezet - Több alkatrészes, statikai analízis
Vissza		Előre

7. fejezet - Több alkatrészes, statikai analízis

Tartalom

Az összeállítások, vagyis a több alkatrészes modellek analízisénél az un. kontaktok testesítik az egyes alkatrészek közötti kapcsolatokat, vagyis a csomóponti elmozdulások és erők átadását az alkatrészek kapcsolódó felületein keresztül. Mivel így az egyes alkatrészek terhelési és peremfeltételét a kontaktok adják, nagy jelenetősséggel bírnak az analízis eredményét illetően. A valós fizikai kontaktok bonyolult viselkedésének leírására számos modellt dolgoztak ki, de a jegyzetünk csak a valóságot lényegesen leegyszerűsítő, a végeselemes programokban beépített megoldások bemutatására szorítkozik. Az alábbiakban nézzük meg a statikai analízisben használatos kontaktok csoportosítását.

7.1. A kontaktok csoportosítása

Az alap kontaktokat könnyen átláthatjuk, ha a szerint csoportosítjuk őket, hogy a két kapcsolódó alkatrész a kapcsolódó felületre (vagy élre) merőlegesen (normális irányban), és azzal párhuzamos, vagy érintő (tangenciális) irányban milyen elmozdulásokat tehet. Az előbbi jelentése, hogy a két kapcsolódó elem el tud-e távolodni, esetleg egymásba hatolni, vagy az érintkező elemek mindig egy felületbe (vonalba) esnek. A felülettel párhuzamos, vagy tangenciális elmozdulást gyakorlatilag a súrlódási tényezővel definiálhatjuk. Ez alapján a következő csoportokba sorolhatjuk az idealizált kontaktokat:

7.1. táblázat - A kontaktok csoportosítása a normális és tangenciális irányú viselkedésük alapján.

	Az érintkező felületek
A súrlódási tényező:	eltávolodhatnak egymástól	nem távolodhatnak el egymástól
µ=0	Ideális súrlódásmentes	Elválás nélküli kapcsolat
0<µ<∞	Súrlódásos	-
µ=∞	Ideálisan érdes, tapadó	Ragasztott

Súrlódásos (Frictional) – a valós fizikai kapcsolatot a legjobban modellező kontakt. A felületek eltávolodhatnak és a súrlódási erő ellenében elcsúszhatnak egymáson. A két geometria között idealizált súrlódásos kapcsolat van, ekkor definiálni kell a súrlódási tényezőt. Ebben az esetben a két felület/él között tapadás van, mely a súrlódási tényezőből adódó feszültséget elérve megszűnik és a két felület/él egymáson elcsúszik, eközben azonban súrlódási veszteség lép fel.
Súrlódásmentes (Frictionless) – Idealizált csúszó kontakt. A kacsolódó felületek/élek egymáson súrlódás nélkül, akadálymentesen (tehát veszteség nélkül) elcsúszhatnak egymáson és eltávolodhatnak egymástól. Ilyen kontakt alkalmazása esetén különös figyelmet kell fordítanunk a megfogások és terhelések definiálásánál, hogy ne jöjjön létre olyan eset, amikor a súrlódásmentes elcsúszás végtelen elmozdulást eredményezhet.
Elválás nélküli kapcsolat (No-separation) – A súrlódásmentes speciális esete, amikor a felületek/élek akadálymentesen elcsúszhatnak egymáson, de nem eltávolodhatnak el egymástól.
Tapadó (Rough) – Idealizált csúszásmentes kontakt. A súrlódási tényező végtelennek tekinthető, tehát a felületek nem csúszhatnak el egymáson, de a kontaktfelületre merőleges irányban eltávolodhatnak egymástól, (pl. egy dörzshajtás modellezése).
Ragasztott (Bonded) – minden szabadságot megkötő, a kapcsolódó felületeket egymáshoz fixen rögzítő kontakt. A súrlódási tényező végtelennek tekinthető, de a két felültet egymástól nem tud elmozdulni semmilyen irányba. Ezt nevezhetjük ragasztott, vagy hegesztett kontaktnak is. Használhatjuk abban az esetben is, mikor a két geometria külön modellezésének csak az az oka, hogy más anyagminőséggel rendelkezik, és ezt szükséges volt definiálni. Több esetben, mikor több alkatrészből álló geometriákat modellezünk és a kontaktok milyensége elhanyagolhatóan befolyásolja a szimuláció végeredményét, akkor pl. a csavarkötések helyett is lehetséges csupán ragasztott kontaktot használni. Természetesen az ilyen esetekben körültekintően meg kell vizsgálni, hogy valóban nem befolyásolja-e ez az egyszerűsítés a végeredményt.

A legtöbb véges elemes szoftver a kapcsolódó felületeket automatikusan felismeri, de általában mód van a kontaktok kézi definiálására is. Ez utóbbi esetnek akkor van kiemelt jelentősége, amikor az alkatrészek egymáshoz képesti elmozdulása viszonylag nagy, és olyan felületek is kontakt kapcsolatba kerülnek a szimuláció közben, amelyek az elején még egymástól távolabb helyezkednek el. Ilyenkor a későbbi helyzetet ismeretében mindenképp érdemes az összes szimuláció során érintkező felület közötti kontakt beállítása már a szimuláció előtt. (Természetesen, ha nem látható előre a terhelés hatására fellépő geometriai helyzet, akkor egy előzetes szimuláció után is finomíthatóak a beállítások.)

7.2. Példa - kontaktfeladat az alkatrészek közötti alapvető kapcsolat típusok bemutatására

Az alábbi példában egy egyszerű geometrián fogjuk bemutatni az alkatrészek közti kapcsolatok típusait. A két alkatrészből álló összeállítás és a terhelési és anyagmodellek minden esetben ugyanolyanok, így egyedül a két alkatrész közötti fizikai kapcsolat lesz más és más. Annak érdekében, hogy az eredmény látványosabb legyen két egymástól eléggé eltérő anyagot definiálunk az alkatrészek anyagának. A modell egy hosszú, az egyik végén befogott szerkezeti acél konzolból és egy rajta lévő lekerekített szélű polietilén téglatestből áll.

Kiinduló adatok.

A konzol méretei:

Hossz (X irányban): 50mm,

Vastagság (Y): 2mm,

Szélesség (Z – a szimulációnál kell megadni): 10mm,

A konzolon lévő test méretei:

10mm élhosszúságú kocka (a 2D-s modellben négyzet),

Saroklekerekítés sugara 2mm,

Konzol anyaga: Structural Steel,

A lévő lekerekített szélű négyzet anyaga: Polyethilene.

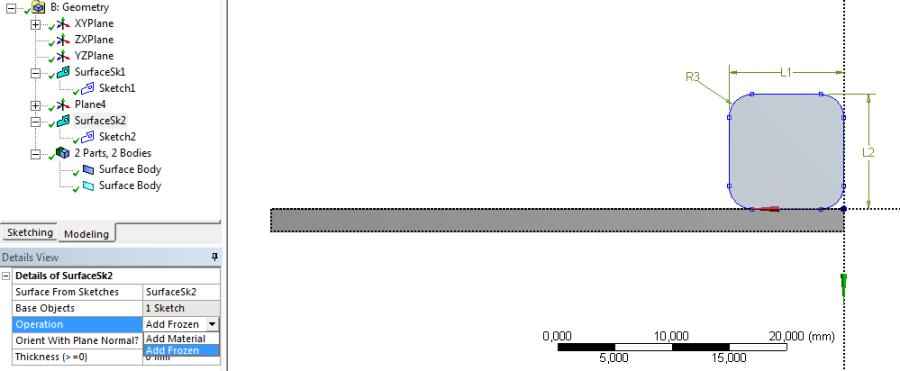
A feladatot 2D-s analízissel oldjuk meg, a geometriát tehát az ANSYS Design Modeller moduljában az XY síkra kell rajzolni, és a projektfelületen a geometria tulajdonságai között, a geometria típusát 2D-re kell átállítani az analízis hozzácsatolása előtt. A geometria elkészítésénél ügyeljünk arra, hogy a két alkatrész külön vázlattal legyen létrehozva. A második alkatrész vázlatának rajzolásakor a téglalap parancs kiadásakor bejelölhetjük az automatikus lekerekítés opciót (Draw/Rectangle/Auto-Fillet) , így később ezzel nem kell külön foglalkoznunk. A második felület létrehozásakor (Concept/Surfces From Sketches) , a „fagyasztott hozzáadása” művelet (Details/Operation/Add Frozen) legyen kiválasztva. Ennek hatására a két felület, mint két különálló alkatrész szerepel majd a modellfa utolsó sorában. Tehát így hozhatunk létre összeállításokat a Design Modeller –ben, (7.1. ábra).

Megjegyzés: Kontakt feladatok esetén fontos lehet az alkatrészeken található lekerekítés is, így ilyen feladatok esetén nem szabad a geometria egyszerűsítésekor a kontakt szempontjából releváns lekerekítéseket mellőzni.

7.1. ábra - 2D-s Geometria.

A geometria elkészítése után lépjünk át az anyagkönyvtárat tartalmazó Engineering Data felületre és rendeljük hozzá az analízisünkhöz a fentebb definiált anyagmodelleket. Majd átlépve a szimulációs környezetbe rendeljük hozzá őket a megfelelő geometriához.

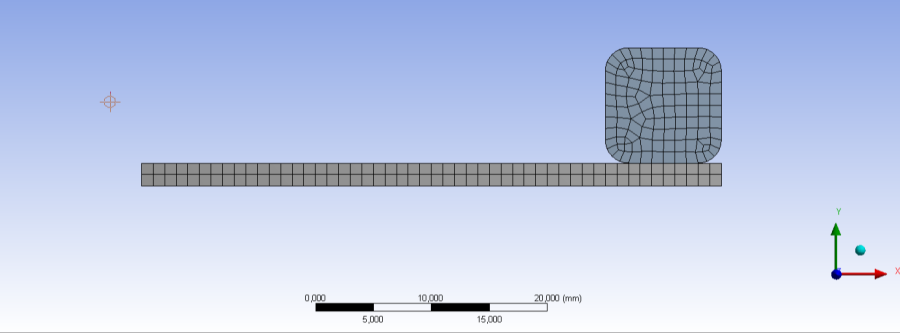
A hálózáskor 1mm-es elemméretet használva végezzük el, így a teljes modell 219 véges elemet tartalmaz. A hálózott modellt a következő 7.2. ábra szemlélteti.

7.2. ábra - Kontakt feladat - hálózott modell.

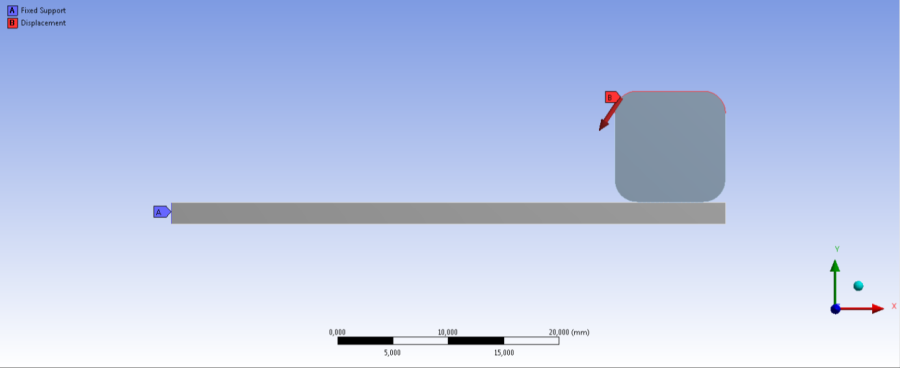
A pontos összehasonlíthatóság miatt a konzol fix megfogása (Fix Support) a rajta lévő testre elmozdulás típusú terhelés kerül (Displacement) . Ezen terhelés nagysága irányonként definiálva: X irányban -2mm és Y irányban -3mm nagyságú. A terhelési modell az alábbi ábrán látható. Az ábrán kék jelzéssel a fix megfogás helye, míg piros jelzéssel az elmozdulás típusú terhelés helye és iránya látható (7.3. ábra).

7.3. ábra - Kontakt feladat, terhelési modell.

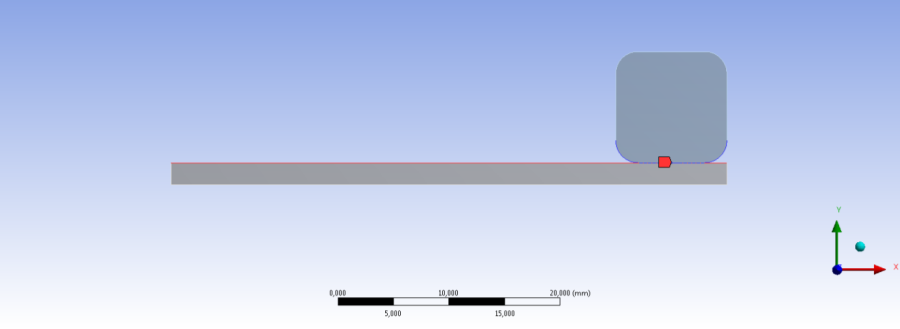
A fenti beállítások után hozzuk létre a két alkatrész megfelelő felületei között lévő kontaktot az Add Manual Contact Region parancs alkalmazásával. Majd válaszuk ki a kapcsolatban résztvevő, a Details panelen jelzett, Contact és Target éleket (7.5. ábra). Az alábbi ábrán kék illetve piros vonallal van jelölve az érintkező felületeket jelentő kontúrvonal (7.4. ábra). Fontos, hogy a lekerekítéseket is vegyük bele a kontakt hatókörébe, mivel azok az alkatrészek deformációjakor érintkezésbe léphetnek a konzol felső élével.

7.4. ábra - Konzolos kontakt feladat geometriája a kijelölt kapcsolódó élekkel.

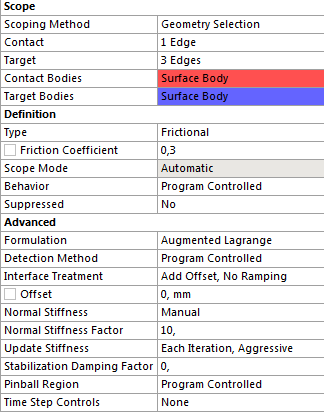
A modellfában megjelenő kontaktot kijelölve, a Details panelen tudjuk átállítani a kontakt típusát (alapértelmezettként Bonded ), és egyéb tulajdonságát (7.5. ábra). A következőkben végezzük el az alábbi beállításokat és futtassuk a szimulációt mindegyik kontakt típussal, majd hasonlítsuk össze az alkatrészek viselkedését.

7.5. ábra - Súrlódásos kapcsolat beállításának részletei.

7.2.1. Súrlódásos kapcsolat (Frictional)

A legáltalánosabban használt kapcsolat típus a súrlódásos kapcsolat (Details/Definition/Type: Frictional) . Mivel ez áll a legközelebb az érintkező felület valós viselkedéséhez, ez a leggyakrabban használt kapcsolat-típus a több alkatrészből álló szerkezetek viselkedésének modellezésénél.

A súrlódási tényezőt (Friction Coefficient) 0,3-ra állítjuk (ez megfelel az acél és a polietilén közötti átlagos súrlódási tényezőnek).

A beállításoknál még fontos a szoftver által használt számítási formula kiválasztása, a pontosabb eredmény érdekében súrlódásos kapcsolatnál célszerű a kiterjesztett Lagrange típusú (Augmented Lagrange) számítási formulát választani, valamint a merevségi mátrix újraszámítását (Update Stiffness) minden iteráció után (Each Iteration, Agressive) . Előfordulhat, hogy a kontaktfelületek elemei közötti rugómerevséget (Normal Stiffness) is definiálni kell. Jelen példánkban ezt a merevségi értéket (Normal Stiffness Facor) 10-re választjuk. Az összes, súrlódásos kapcsolatkor használt beállítást tartalmazza a 7.5. ábra.

7.2.2. Súrlódásmentes kapcsolat (Frictionless)

Súrlódásmentes kapcsolatnál a súrlódási tényező nulla, melyre külön típus van definiálva a kontakt típusok között (Details/Definition/Type: Frictionless) . Az összes többi beállítás megegyezik a súrlódásos kapcsolatnál használt beállításokkal. Végezzük el a beállításokat és futtassuk a szimulációt.

7.2.3. Elválás nélküli kapcsolat (No separation)

Ebben az esetben a két alkatrész kontakt felülete között a súrlódási tényező nulla, azonban a két alkatrész a kontakt felületeinél nem válhat szét. Az összes többi szimulációs beállítás megegyezik az első két típusú kontaktnál használttal. Végezzük el a beállításokat és futtassuk a szimulációt.

7.2.4. Végtelen súrlódású kapcsolat (Rough)

Ebben az esetben a két alkatrész közti kontakt felületek közti súrlódási tényező végtelen, azonban a két alkatrész normál irányban elmozdulhat egymáshoz képest. Ebben a példában az előzőekhez képest annyi a különbség, hogy kiterjesztett Lagrange formula helyett Normál Lagrange formulát használjunk. Ebben az esetben nem történik meg a két alkatrész között egymásba nyomódás. Végezzük el a beállításokat és futtassuk a szimulációt.

7.2.5. Ragasztott-hegesztett típusú kapcsolat (Bonded)

Ebben az esetben a súrlódási tényező a két alkatrész mereven kapcsolódik egymáshoz. A beállításoknál ebben a példában annyiban tértünk el a súrlódásos kapcsolathoz képest, hogy a két alkatrész közti normál merevséget nem definiálunk. (Mivel itt a két alkatrész nem fog egymáshoz képest elmozdulni, így egyszerűbb ezt a szoftver által konrollált értéken hagyni a számítási idő csökkentése végett.)

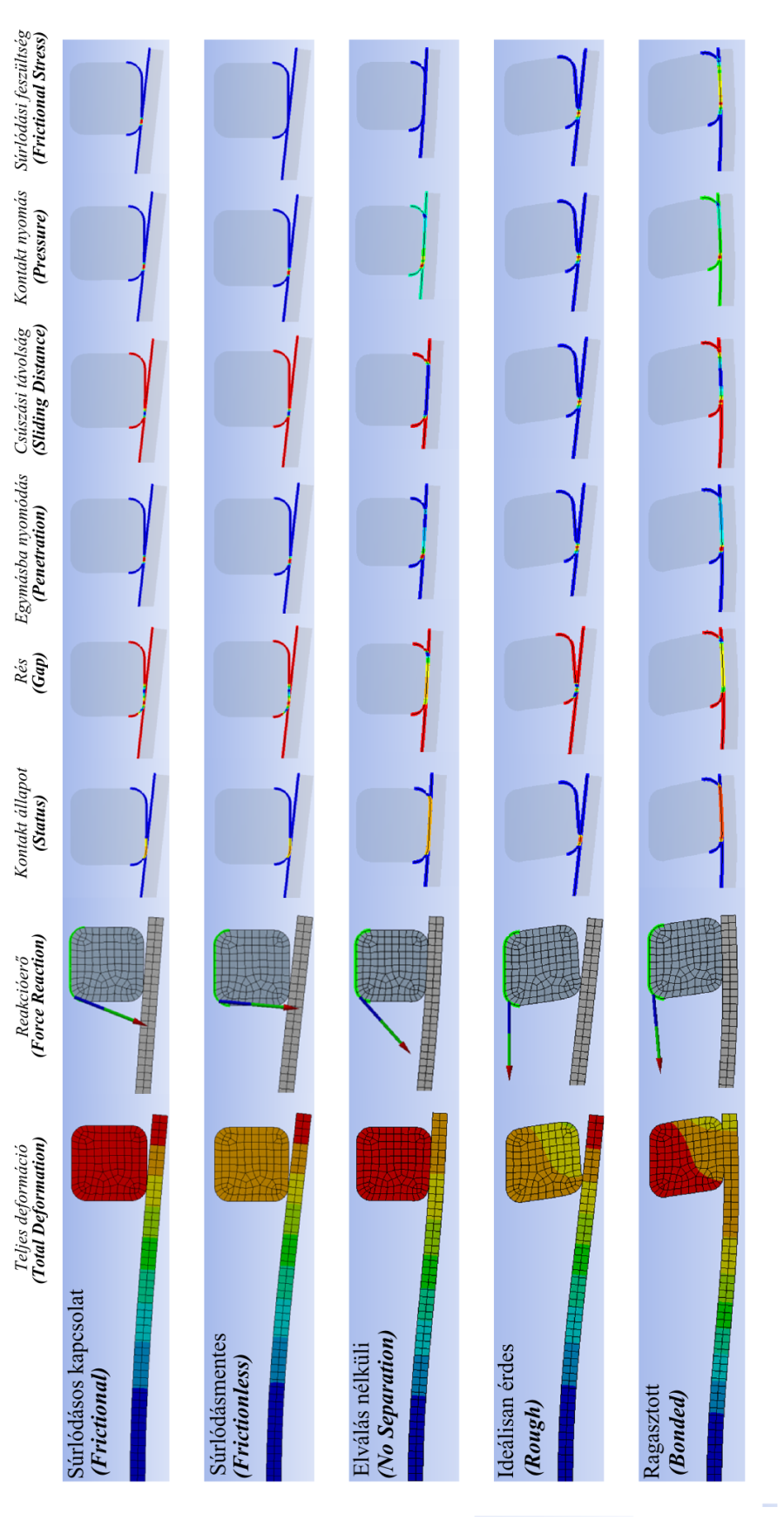
7.2.6. Eredmények

Az ötféle kontakttípus viselkedésének jellegzetességeit, első lépésben vizsgáljuk meg a teljes deformáció (Total Deformation) , és az elmozdulás kényszeren eső reakcióerő (Force Reaction) lekérdezésével. A csúszás folyamatának vizsgálatakor, a felhasználói felület alján lévő Graph fülön grafikusan (és mellette táblázatos formában is) nyomon követhetjük a reakcióerő (Force reaction) komponenseinek változását az elmozdulás (idő) függvényében.

A kontaktfelületeken végbemenő folyamatok vizsgálatára a Contact Tools eszköz szolgál, melynek segítségével az alábbi eredményeket lehet lekérdezni:

Kontakt állapot (Status) – megadja, hogy a két felület milyen kapcsolatban áll egymással:
- távol van (Far), – kék színnel jelölve,
- közel van (Near), – sárga színnel jelölve,
- csúszik (Sliding), – narancs színnel jelölve,
- tapad (Sticking), – piros színnel jelölve.
Rés (Gap) - a két alkatrész közötti rés mértékét adja meg. (A piros részeken nulla a rés mértéke, míg a kék szín felé negatív értelmű rés található.)
Egymásba nyomódás (Penetration) – a két alkatrész kapcsolódó felületének (elemeinek) egymásba hatolását adja meg. (Kék színnel a nulla értékű részek, míg piros szín felé közeledve egyre nagyobb, pozitív értelmű egymásba nyomódás figyelhető meg.)
Csúszási távolság (Sliding Distance) – a két kapcsolódó felület egymáson való tangenciális irányú relatív elmozdulásának, vagyis elcsúsznak mértékét adja meg.
Kontakt nyomás (Pressure) – az érintkezési felületeken eső, a felületekre merőleges irányú normál feszültség, vagyis palástnyomás értékét adja meg.
Súrlódási feszültség (Frictional Stress) – az érintkezési felületeken eső, a felületekkel párhuzamos tangenciális, vagyis csúsztató feszültség értékét adja meg.

Az eredményeket a könnyebb átláthatóság érdekében táblázatos formában összegeztük (7.6. ábra).

7.6. ábra - A kontaktvizsgálat eredményei.

7.3. Példa - Érintkezési feszültség és benyomódás

Az alábbi példában egy acélgolyó és egy alumínium sík lap érintkezésénél fellépő feszültséget és alakváltozást vizsgáljuk meg. A golyót a síkra merőleges irányú F erő nyomja a sík laphoz.

Kiinduló adatok:

A golyó sugara: R = 10 mm,

A terhelőerő: F = 100 N,

A sík felületű test anyaga – acél: Rugalmassági modulus: E₁ = 200 GPa, Poisson tényező: ν₁ = 0,30,

A golyó anyaga – alumínium: Rugalmassági modulus: E₂ = 71 GPa, Poisson tényező: ν₂ = 0,33.

7.3.1. Analitikus megoldás

A két érintkező test érintkezési helyén ébredő feszültséget és deformációt számoljuk ki Hertz módszerével [25.] . Kiindulásnak adva van egy végtelen félsík és a vele érintkező R sugarú gömb melyet a sík felületre merőleges F erő terhel. Feltételezzük, hogy a testek anyaga homogén, izotróp és érvényes rájuk a Hooke törvény, valamint a testek között súrlódásmentes kapcsolatot tételezünk fel.

Határozzuk meg az érintkezés helyén ébredő maximális palástnyomás és a két test közeledésének mértékét.

Gömb és sík érintkezésénél a maximális palástnyomás értéke:

$p_{m a x} = 0,5784 \cdot \sqrt[3]{\frac{F}{η^{2} \cdot R_{1}^{2}}}$

(7.1)

A két test közeledésének mértéke

$δ = 0,8255 \cdot \sqrt[3]{\frac{{(η \cdot F)}^{2}}{R_{1}}}$

(7.2)

A benyomódott, (érintkező) felület sugara

$a = 0,9086 \cdot \sqrt[3]{η \cdot F \cdot R_{1}}$

(7.3)

ahol:

$η = \frac{1 - ν_{1}^{2}}{E_{1}} + \frac{1 - ν_{2}^{2}}{E_{2}}$

(7.4)

ν – az adott anyag Poisson-tényezője,

E – az adott anyag rugalmassági modulusa.

A számolás eredményei:

	Maximális palástnyomás:	p _max =871,4MPa
	A két test közeledése:	δ=0,00548mm
	A érintkező felület sugara:	a=0,23409mm

7.3.2. Numerikus megoldás

A fenti problémát ANSYS Workbench-ben, 2D-s Tengelyszimmetrikus feladatként oldjuk meg, mivel mind a geometria, mind pedig a terhelési és peremfeltételek tengelyszimmetrikusak. Ennek előfeltétele, hogy a projektfelületen (a tulajdonságok panelen) átváltsuk a geometria típusát 2D-re, és a rajzolás során az XY sík +X térfelén dolgozzunk. Készítsük el az ábrán látható geometriát, úgy, hogy a golyónak csak a „jobb” alsó (R=10mm) negyedét rajzoljuk meg. A függőleges felezés a tengelyszimmetria miatt szükséges, a vízszintes tengely menti kettévágást pedig azért tehetjük meg, mert a felső rész már nem fog érdemi hatást gyakorolni az érintkezési pontban ébredő feszültségi állapotra, és alakváltozásokra. Érdemes úgy létrehozni a vázlatot, hogy az érintkezési pont a koordinátarendszer origójába essen. Az alsó síkfelület modellezésére egy 10x10mm-es négyzetet használunk (7.7. ábra).

A geometria megrajzolása után adjuk hozzá az anyagkönyvtárunkhoz (Engineering Data) az alumínium ötvözet (Aluminium Alloy) és a szerkezeti acél (Structural Steel) anyagmodelleket, majd átlépve a szimulációs felületre, rendeljük hozzá őket a megfelelő alkatrészekhez.

A modellfában a geometriát kiválasztva, állítsuk át az analízis típusát tengelyszimmetrikusra (Outline/…/Geometry => Details /Definition/2D Behavior: /Axisymmetric) .

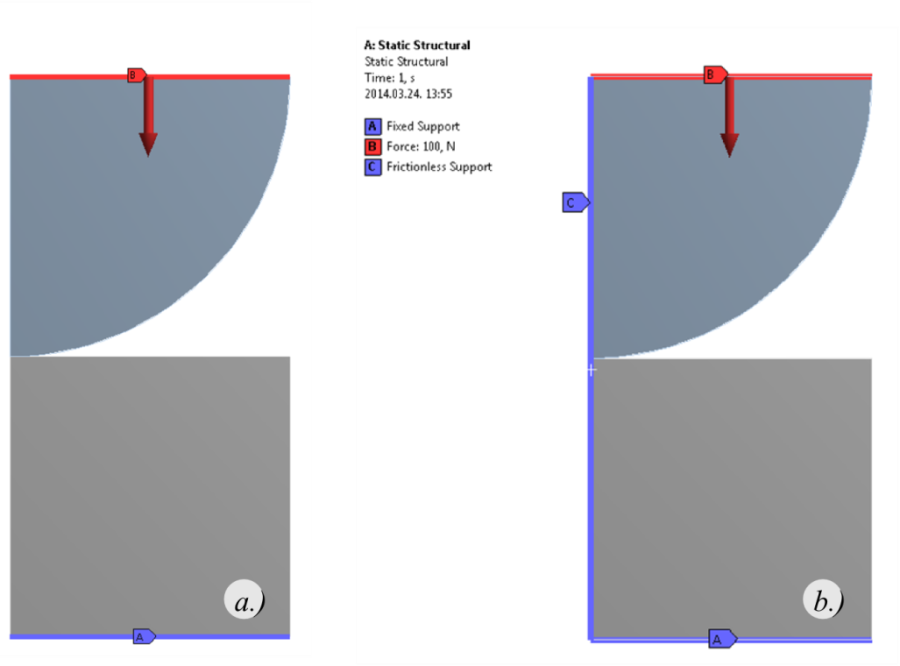
A terhelések és peremfeltételek megadásánál definiáljunk a golyó felső sík felületére egy (lefelé ható), –Y irányú 100N nagyságú erőt a komponenseivel megadva (Loads/Force) . A négyzet alsó élén lévő fix megtámasztás (Fix Support) már kellő mértékben meghatározza a szerkezetünk viselkedését, ugyanis a szimmetriatengelyre ható kényszer automatikusan érvényesül (7.7. ábra, a.). Viszont, mint majd később látni fogjuk, némiképp befolyásolja az eredményeket, ha manuálisan is hozzárendeljük a forgástengely oldalirányú elmozdulását megkötő kényszert (Frictionless Support) , (7.7. ábra, a.).

7.7. ábra - Peremfeltételek és erőterhelés.

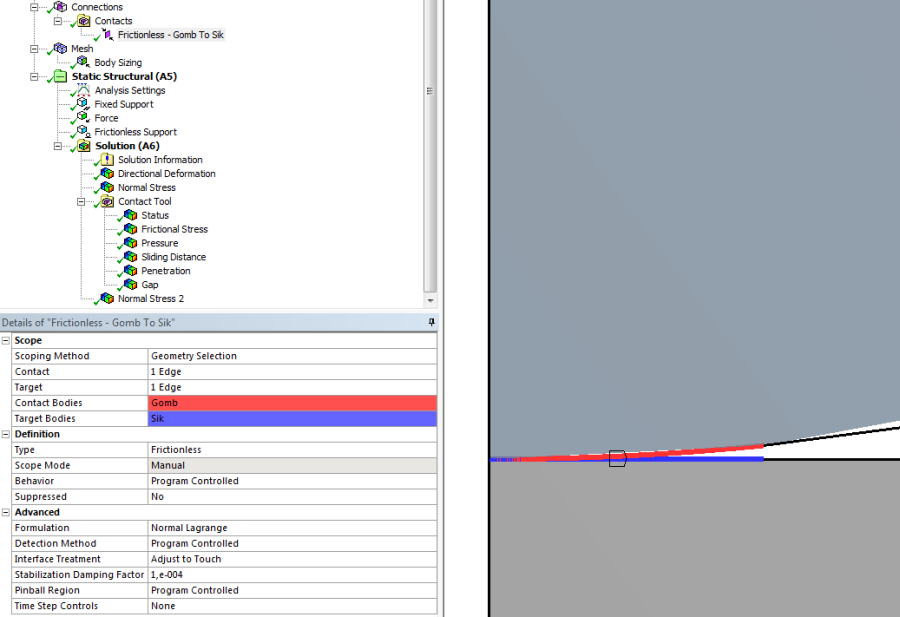
Következő lépésben hozzuk létre a két alkatrész közötti kapcsolatot. Beállítástól függ, hogy a geometria importálásakor automatikusan felismeri-e az egymáshoz közel lévő felületeket/éleket, vagy manuálisan kell megadni azokat. Ha automatikus kontakt definíció történt akkor csak a beállításokat kell megváltoztatni (ugyanis az alapértelmezetten, mindig ragasztott, vagyis Bonded kontaktot rendel hozzá a program). Ha nem jött létre a kontakt automatikusan, akkor az Add Manual Contact Region parancsal megtehetjük. Az érintkező élek kijelölése után állítsuk át a kontakt típusát súrlódásmentesre (Details/Definition/Type:Frictionless) . Az összehasonlíthatóság kedvéért nem használunk súrlódásos kapcsolatot, ugyanis az analitikus összefüggések súrlódásmentes érintkezést feltételeznek. Használjuk a 7.8. ábra beállításait.

Megjegyzés: Ha az érintkező éleket nem egy folytonos vonallal rajzoljuk meg, hanem két folytatólagosan elhelyezett, és a megfelelő kényszerekkel ellátott vonalszakaszból, akkor lehetőség van az él lokális kijelölésére. Így nem vesznek részt a kontaktban olyan területek, amelyek biztosan nem fognak érintkezésbe lépni a szimuláció során (7.8. ábra).

7.8. ábra - Kontaktbeállítások.

Mivel egy nemlineáris kontaktról van szó, a konvergencia elősegítése érdekében, érdemes csökkenteni az időlépéseket (Outline/…/Analisis Settings => Details/Step Controls) . Ezért végezzük el az alábbi beállításokat:

Details/Step Controls:

Auto Time Stepping: On,

Defined By: Substeps,

Initial Substeps: 10,

Minimum Substeps: 10,

Maximum Substeps: 1000.

Details/Solver Control: Large Deflection: On.

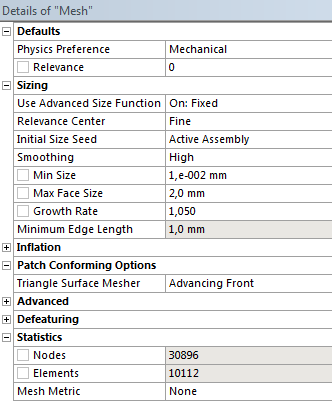
A hálózás globális beállításánál alkalmazzuk a fix méretfunkciót (Details/Sizing/Use Advanced Size Funktion: „On:Fixed”) , amellyel többek között megadhatjuk az elemek minimális (Min size: 0,01mm), maximális (Max Face Size: 2mm) méretét, és a növekmény (Growth Rate: 1,05) értékét (7.9. ábra).

7.9. ábra - Globális hálóbeállítások.

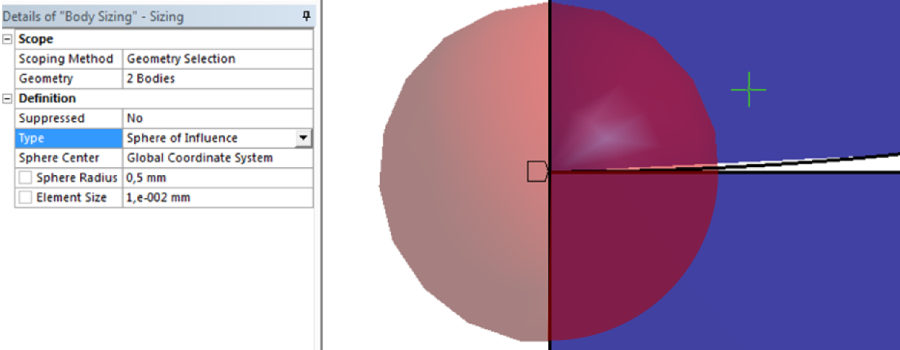
Az érintkezés helyén történő hálósűrítést egy Sizing parancs hozzáadásával érhetünk el, melynek hatókörét a teljes modellre kivetjük (Details/Geometry: 2 Bodies) , típusát Sphere of Influence -re állítjuk, melynek középpontjául a globális koordinátarendszert választjuk. A gömb sugarát (Sphere Radius) 0,5mm-re, a gömbön belül elhelyezkedő elemek méretét (Element Size) pedig 0,01mm-re választjuk (7.10. ábra).

7.10. ábra - Lokális hálósűrítés beállítása az érintkezés helyén.

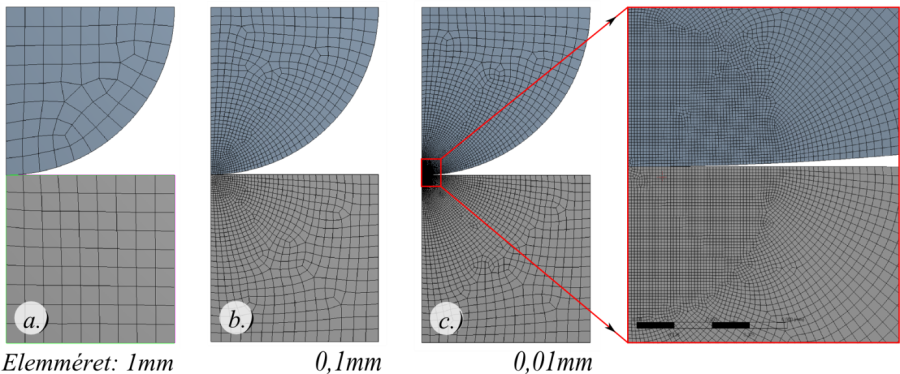
Az analízist elvégezhetjük a lokális hálósűrítés elemméretének változtatásával (7.11. ábra), hogy megfigyeljük az elemméret eredményre gyakorolt hatását (7.15. ábra).

7.11. ábra - Különböző mértékű lokális hálófinomítás.

A háló beállítása után futtassuk a szimulációt, és kérdezzük le az Y irányú deformáció (Directional Deformation) , (7.12. ábra, b.), és normálfeszültség (Normal Stress) , (7.12. ábra, b.) értékét a teljes modellre, valamint az Y tengely mentén futó 2mm hosszú konstrukciós vonalra (Path) , (7.13. ábra).

7.12. ábra - Az analízis eredménye: a.) Y irányú elmozdulás, b.) Y irányú normálfeszültség.

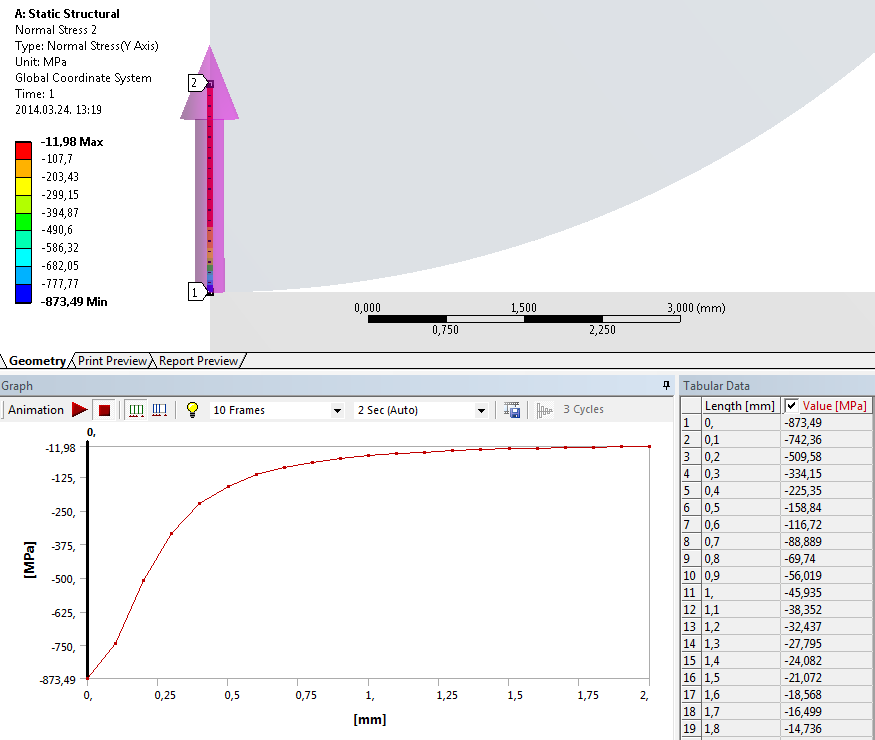
7.13. ábra - Az Y irányú normál feszültség értékének vonal menti lekérdezése.

Megjegyzés: Egy (a tengelyszimmetrikus analízisnél elvileg szükségtelen), a tengelyt oldalirányban megkötő Frictionless kényszer hozzáadásával a Normal Lagrange eljárással számolt kontaktnyomás (Contct Tool/Pressure) értéke 873,42MPa, ami 0,23%-os eltérést eredményezett az elméleti értékhez képest. A tengelyt megkötő Frictionless kényszer nélkül a Normal Lagrange kontaktnyomás (Contct Tool/Pressure) értéke teljesen fals értéket ad, az Augmented Lagrange és a Pure Penalty pedig 849 MPa-t, ami egy nagyságrenddel nagyobb (2,5%-os) hiba az előzőhöz képest, de még így is elfogadhatónak számít.

7.3.3. Összefoglalás

A numerikus analízis és az analitikus számolás eredményeit az alábbi ábrákon foglaljuk össze.

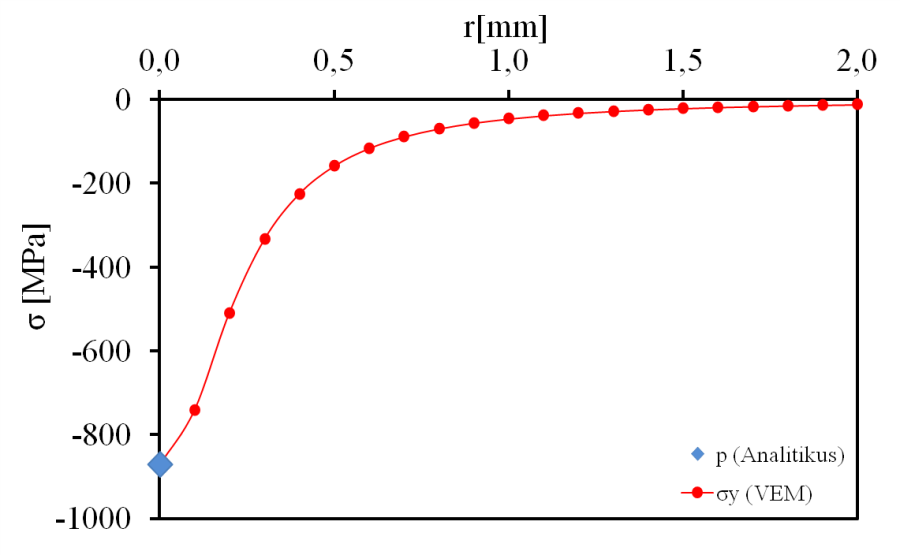
Az Y irányú normál feszültség értéke a kontaktfelülettől való távolság (r) függvényében, és az analitikus számolásból származó kontaktnyomás összehasonlítása.

a.) Az érintkezési pontban lekérdezett Y irányú normál feszültség és a kontaktnyomás értéke. b.) A két test közeledésének (benyomódás) mértéke, és a számítási idő az elemméret függvényében.

7.14. ábra - Az Y irányú normál feszültség értéke a kontaktfelülettől való távolság (r) függvényében, és az analitikus számolásból származó kontaktnyomás összehasonlítása.

Az analízis különböző elemmérettel történő futtatásának eredményeiből látható, hogy megfelelő kontaktbeállítás és hálófinomítás mellett az elméleti és a numerikus eredmény jó egyezést mutatnak.

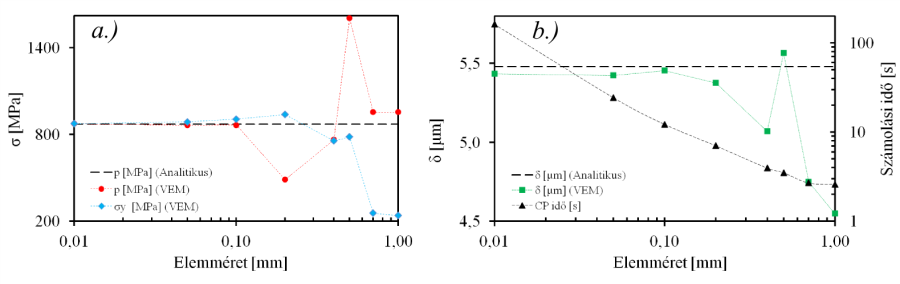
7.15. ábra - Az elemméret hatása az érintkezési feszültségre és benyomódás mértékére.

7.2. táblázat - A végeselemes és az analitikus megoldás eredményeinek összehasonlítása, különböző elemméret mellett.

Elemméret [mm]	δ [μm]	p [MPa]	σ _y [MPa]	CP idő [s]	Elemszám
0,01	5,43	873,4	873,5	160,7	10112
0,05	5,42	863,8	886,0	24,2	2486
0,10	5,45	864,2	905,9	12,2	1490
0,20	5,37	486,0	937,5	7,0	809
0,40	5,07	763,2	755,1	3,9	383
0,50	5,57	1602,9	783,3	3,5	314
0,70	4,75	954,9	254,1	2,7	194
1,00	4,55	954,8	238,8	2,6	151
Analitikus:	5,48	871,4	871,4	-	-

Vissza		Előre
6. fejezet - A geometriai modellek egyszerűsítésének lehetőségei	Főoldal	8. fejezet - Kihajlás vizsgálat