6. fejezet - A geometriai modellek egyszerűsítésének lehetőségei
Vissza		Előre

6. fejezet - A geometriai modellek egyszerűsítésének lehetőségei

Tartalom

Az egyszerűsítések csoportosítása többféleképen történhet, pl. szimmetriák típusa, vagy a mechanikai probléma dimenziója, ill. az alkalmazott elemtípus szerint. Ezekkel illetve az egyszerűsítések okaival, a geometriai, perem és terhelési feltételeket érintő követelményekkel, valamint az alkalmazott elemtípusokkal már foglalkoztunk a 2. fejezet fejezetben. Most nézzünk néhány egyszerű gyakorlati példát ezek alkalmazására. Az alábbiakban olyan modelleket vizsgálunk meg, amelyeken ugyanaz a terhelési eset többféle egyszerűsítéssel vizsgálható, ezért a feladatok sorrendje nem követi a fent említett csoportosítási lehetőségeket.

6.1. Példa szimmetriafeltételek alkalmazására: belső nyomással terhelt cső

Az alábbiakban egy belső nyomással terhelt cső modelljén keresztül mutatjuk be a szimmetria-feltétel alkalmazását 3D-s test, ill. héjmodell esetén és a 2D-s sík alakváltozás, ill. tengelyszimmetrikus modell használatát (6.1. ábra).

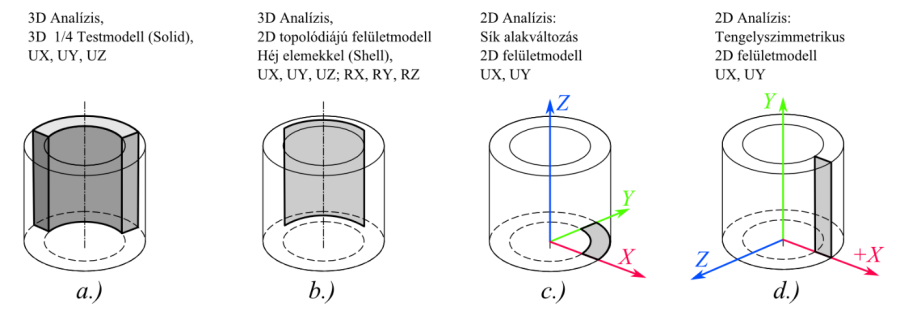
a.) ¼ testmodell, b.) ¼ héjmodell, c.) ¼ sík alakváltozás modellje, d.) tengelyszimmetrikus modell.

6.1. ábra - Csőszakasz modellje különböző megközelítés szerint.

Kiinduló adatok:

Külső átmérő: D=12mm,

Falvastagság: t=2mm,

Magasság: H=10mm,

Anyag : Acél: rugalmassági modulus: E=200GPa, Poisson-tényező: v=0,3,

Belső nyomás: p=100MPa,

Megtámasztás: Szimuláció típusától függően változó. A modellezett eset a tengelyirányú elmozdulásban gátolt cső, vagyis a kiemelt szakasz mindkét végén a tengelyirányú elmozdulást megkötő, a radiális elmozdulást engedő kényszerek szükségesek.

6.1.1. Analitikus megoldás

A fenti feladat analitikus megoldását kétféleképpen végezzük el, vékony és vastag falú csövek számítási módszere szerint [25.] .

Feltételezzük, hogy a cső anyaga lineáris, homogén és izotróp.

Méretei – belső sugár: r_b=4mm, külső sugár: r_k=6mm, a hossza pedig ebben az esetben lényegtelen.

A vastag falú csövek keresztmetszetének feszültségállapotát az alábbi egyenletekkel írhatjuk le.

A radiális irányú feszültségkomponens:

$σ_{r} = B - C \cdot {(\frac{r_{b}}{r})}^{2}$

(6.1)

A tangenciális irányú feszültségkomponens:

$σ_{t} = B + C \cdot {(\frac{r_{b}}{r})}^{2}$

(6.2)

Ahol:

	$B = \frac{p_{b} \cdot r_{b}^{2} - p_{k} \cdot r_{k}^{2}}{r_{k}^{2} - r_{b}^{2}}$	(6.3)
	$C = \frac{r_{k}^{2}}{r_{k}^{2} - r_{b}^{2}} (p_{b} - p_{k})$	(6.4)

r – a cső külső _(k) és belső _(b) sugara,

p – a csövet terhelő nyomás, (esetünkben p _k =0).

A tengelyirányú feszültségkomponenst a peremfeltételektől függően tudjuk számolni. Esetünkben cső mindkét vége rögzítve van axiális irányban, tehát az ilyen irányú alakváltozás nulla.

$ε_{a} = \frac{1}{E} \cdot [σ_{a} - ν \cdot (σ_{r} + σ_{t})] = 0$

(6.5)

Ebből a tengelyirányú feszültség értéke:

$σ_{a} = ν \cdot (σ_{r} + σ_{t})$

(6.6)

Vékonyfalu csövek esetén azzal a feltételezéssel élünk, hogy a cső anyagában csak tangenciális és axiális feszültség ébred, tehát a cső falában ébredő radiális feszültségkomponens 0. Ekkor a belső nyomás és a geometria ismeretében a tangenciális feszültségkomponens:

$σ_{t} = \frac{p \cdot r}{t}$

(6.7)

Ahol:

r – a cső közép sugara,

t – a cső falvastagsága,

Az axiális feszültség a peremfeltételek és az (6.5) egyenlet alapján, az alábbi módon számolható:

$σ_{a} = ν \cdot σ_{t}$

(6.8)

✎ A fenti egyenletek alapján határozzuk meg a rúd keresztmetszete mentén ébredő feszültségkomponenseket és ábrázoljuk az egyenértékű feszültséget.

6.1.2. A feladat megoldása ¼ testmodell segítségével

Hozzuk létre a csőszakasz teljes testmodelljét Design Modellerben , és jelöljük ki a szimmetriasíkokat. Többféle lehetőség is kínálkozik a tükörszimmetria érvényesítésére, egyik az, ha a geometria modellezőben rendeljük hozzá a legördülő menüsor Tools/Symmetry parancsának kiadásával. Első lépésben meg kell határoznunk a szimmetria síkok számát (Details …/Number of Planes) , esetünkben 2, (de akár 3 is lehetne, ha a hossza mentén is kettévágnánk). Ezután a beállítottaknak megfelelő számú kijelölő ablak jelenik meg a panelen. Ha cső tengelyvonala egybeesik a globális koordinátarendszer Y tengelyével, akkor az XY és YZ síkokat kell kiválasztanunk a modellfából (6.2. ábra, b.). Állítsuk be a részleges (Partial) modellt és nyomjuk meg a Generate gombot. A parancs hatására a szimmetriasíkok feldarabolják modellt, és csak egy ¼ modell marad.

Másik lehetőség a szimmetria kényszer definiálására, ha eleve ¼ modellt hozunk létre, és a testmodell megfelelő felületeihez hozzárendeljük a kényszert akár a geometriamodellező, akár a szimulációs felületen. Ha ¼ modellünk van, akkor egyszerű kinematikai kényszerek segítségével is definiálhatjuk a szimmetriát, mégpedig olyan elmozdulás kényszer segítségével, amely csak a felület síkjában történő elmozdulást engedi, és az arra merőleges irányút nem. Ez az ANSYS -ban a Frictionless Support nevet viseli, de akár a Diplacement kényszert is alkalmazhatjuk erre a célra az egyes szabadságfokok megfelelő megkötésével.

Hasonló módon kötjük meg a két véglap axiális elmozdulását a radiális szabadságfokok engedésével. Itt is használhatjuk a Frictionless, vagy a Diplacement kényszert.

A modell belső felületére (6.2. ábra, b. – B felületre) helyezzünk el egy 100MPa nagyságú nyomást (Pressure) .

Ezután végezzük el a modell hálózását, 1mm-es méretű tégla elemeket tartalmazó rendezet struktúrájú hálóval (6.2. ábra, a.), és futtassuk a szimulációt. Az elemméret beállításához kapcsoljuk ki a Details panelen a Use Advanced Size Function -t és az Element Size sorban adjuk meg az elemméretet.

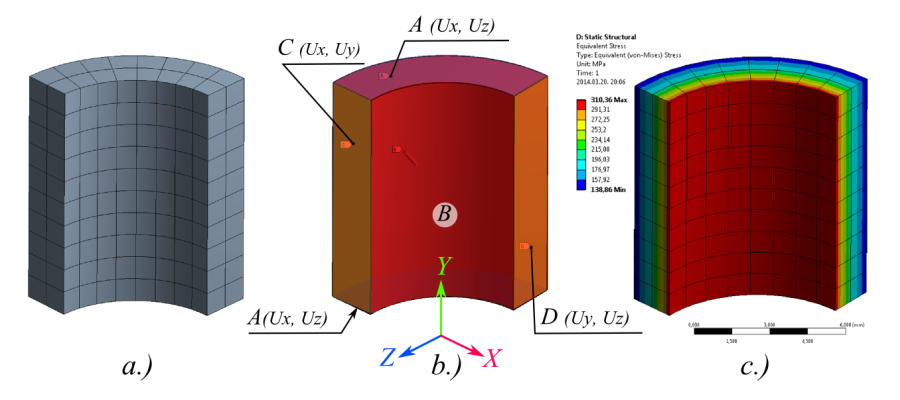
a.) Végeselemháló, b.) Peremfeltételek és terhelés, c.) A cső falában ébredő egyenértékű feszültség

6.2. ábra - ¼ testmodell.

A szimuláció futtatása után kérdezzük le az egyenértékű feszültséget, fajlagos nyúlást és a radiális deformációt. Ez utóbbihoz egy henger koordinátarendszert kell definiálnunk, amit a modellfa koordinátarendszerek sorára jobbgombbal kattintva hozhatunk létre (Outline/Coordinate Systems(JG)/Insert/Coordinate System) . Kijelölve az új elemet a modellfán, a Details panelen állítsuk át a típusát henger koordináta rendszerre (Details/Type/Cylindrical) , és az origó referenciáját a globális koordinátarendszerre (Details/Origin/Defined by/Global Coordinates: 0,0,0) . A tengelyeket forgassuk be a henger állásának megfelelően ( Principal Axis/Axis: X, Defined by: Global Z Axis; Orientation About Principal Axis/Axis: Z, Defined by: Global Y Axis) , (6.3. ábra).

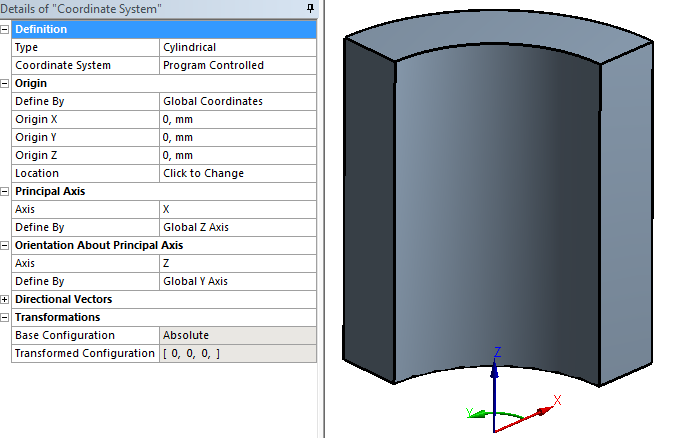
6.3. ábra - Hengerkoordináta-rendszer beállítása a radiális elmozdulások lekérdezéséhez.

Így a deformáció lekérdezését az X tengely menti elmozdulásra átállítva (Type:Directional Deformation/Orientation: X axis) , a radiális elmozdulást kapjuk eredményül.

6.1.3. A feladat megoldása negyed héjmodell segítségével

A feladat héjmodellel történő megoldásának előnye, hogy viszonylag kevés véges elem számot tartalmaz a modell, de mégis mindhárom irányú terheléseket és eredményeket is meg tudunk jeleníteni a segítségével. Szimmetria síkoknak az XY és YZ síkokat választottuk. A henger alakú héj átmérője 10mm, (6.4. ábra).

6.4. ábra - Csőszakasz negyed felületmodellje.

Az analízis típusa ebben az esetben 3D-s, így az alapbeállítások maradhatnak érvényben. A héjmodell vastagságát a szimuláció során definiáljuk (Outline/Geometry/Surface Body => Details/Definition/Thickness: 2mm.) . Héjmodell esetén definiálni kell a felülettől való eltolás irányát is. Annak függvényében, hogy a véges vastagságú héjszerkezetet annak belső, külső, vagy középfelületével modelleztük (a középfelület az alapértelmezett).

A hálózásnál 1mm-es elemméret esetén 80 elemet tartalmazó modell alakul ki (6.5. ábra).

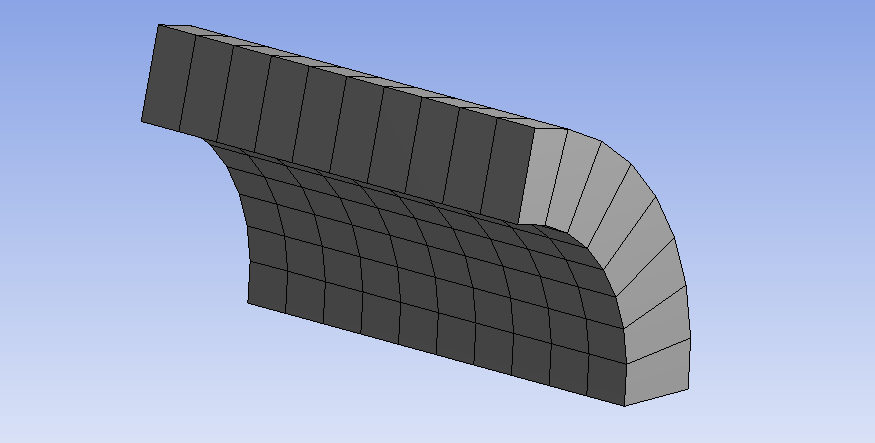
6.5. ábra - Hálózott modell a negyed héj esetén

A cső két végét elmozdulás kényszer segítségével rögzítjük, melynél az axiális (Y) irányú elmozdulást 0 értéken rögzítettük, míg a henger tengelyére merőleges (X és Z) irányokban a test szabadon elmozdulhat. A szimmetriasíkok mentén az adott síkban történő mozgást megengedő és a síkra merőleges irányú elmozdulást gátoló kényszert kell definiálnunk. Ez utóbbi peremfeltétel automatikusan létrejön, ha a geometria létrehozásánál, vagy a szimulációs felületen definiáltuk a szimmetriakényszert (Symmetry) .

A belső nyomást az egész felületre érvényesített -100MPa nagyságú nyomás típusú (Pressure) terheléssel definiáltuk (6.6. ábra). A negatív előjel azért szükséges, mert a felületre ható nyomás iránya a felületi normálissal ellentétes irányú.

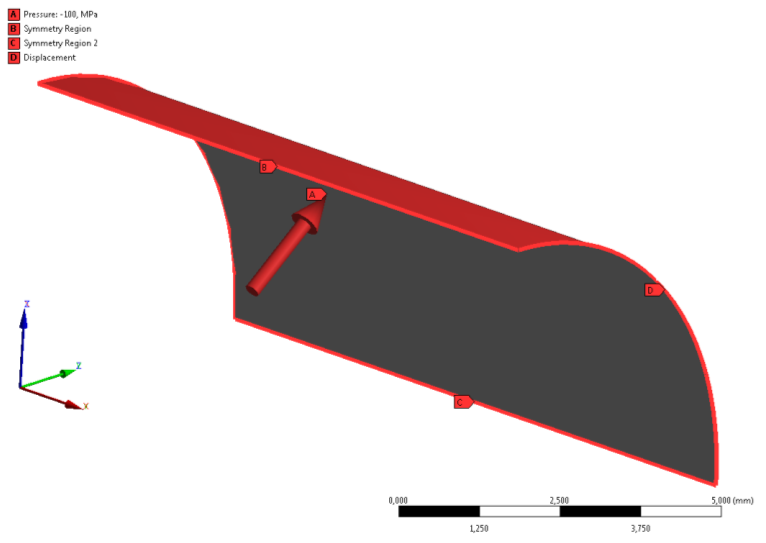
A – nyomás (p=100MPa); Szimmetriakényszerek: B (Ux, Uz), C (Ux, Uy); Kinematikai kényszer: D (Uy, Uz).

6.6. ábra - Terhelés és a permfeltételek a negyed felületmodellel felépített cső esetében.

A szimuláció lefuttatása után, az előző példához hasonlóan kérdezzük le az egyenértékű feszültséget, a fajlagos nyúlást és a radiális deformációt. Az eredményeken látható, hogy az értékek változása a vastagság mentén eltér az előző szimuláció eredményétől. Ennek oka, hogy a héjelemekkel végzett szimuláció (ellentétben a kontinuum elemekkel), nem ad információt a radiális irányú normál feszültségekről.

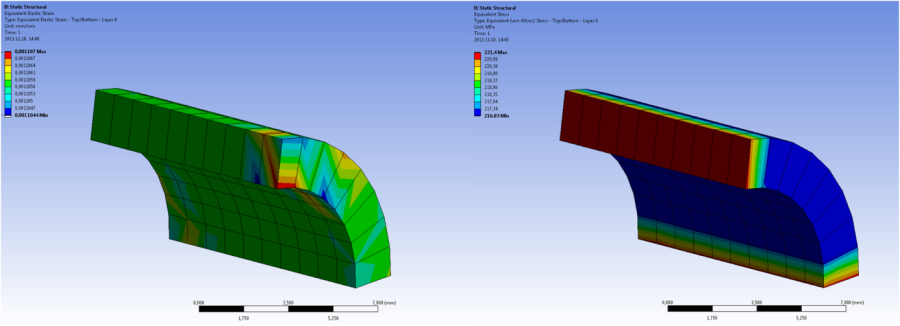
6.7. ábra - A megnyúlás és egyenértékű feszültség a csőmodell negyed héjmodellként való szimulációja során

6.1.4. A feladat megoldása 2D-s sík alakváltozás (Plane Strain) típusú modellként

A feladatot az ANSYS Workbench végeselem szoftverben oldjuk meg. Mivel feltételeztük, hogy a cső keresztmetszetéhez képest hosszú, tehát a tengelyirányú (Z) kiterjedése jelentősen nagyobb, mint a radiális irányú (X és Y) kiterjedése, valamint tengelyirányú terhelés nincs jelen, a feladat megoldható 2D-s sík alakváltozás típusú szimulációval. Emellett a cső geometriája miatt szimmetria feltételeket is alkalmazhatunk; elegendő a negyed geometria felépítése. (Megjegyzés: a nyomás típusú terhelés természetesen egy az egyben definiálható, mivel felülethez kötött, azonban például erőterheléses feladatnál figyelni kell a terhelés arányos osztására.)

A geometria tehát a cső egy negyed szelete, melyet egy sík felületmodellként (Surface Body) definiálunk a koordinátarendszer XY síkján. Az ANSYS Workbench Design Modeler moduljában létrehozott geometriát mutatja a 6.8. ábra. Az egyszerűség kedvéért a fősíkok szolgáltatják a szimmetria síkokat. Természetesen a 2D-s geometria esetén szimmetria tengelyekről beszélünk, melyek így a globális koordinátarendszer X és Y tengelyei.

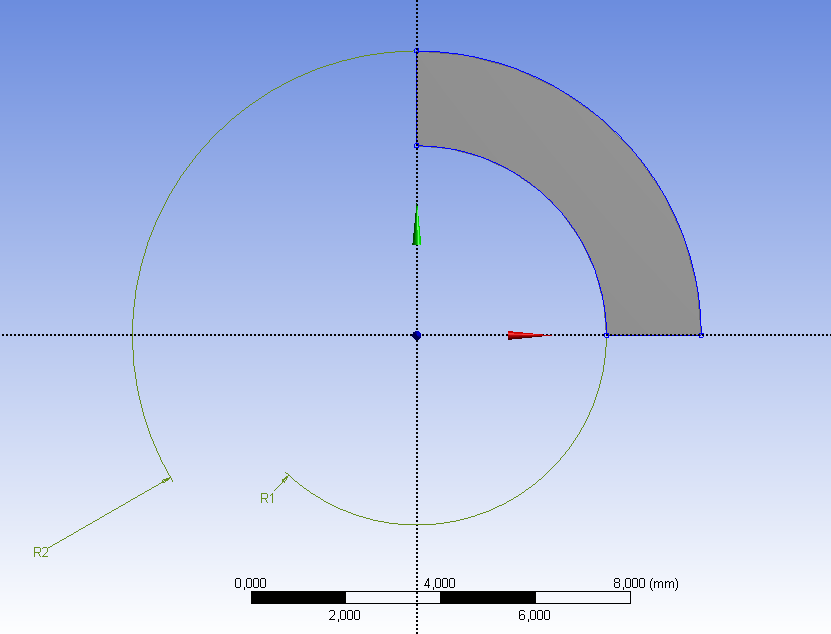
6.8. ábra - Cső modell 2D-s negyed geometriája

Mivel az analízis típusa sík alakváltozás (Plane Strain) , a 2D-s viselkedést a szimulációs környezetbe való belépés előtt be kell állítanunk, mert utólagosan már nincs lehetőség az átjárásra. Célszerű a geometria létrehozása előtt átállítani, a Static Structural/Geometry sorát kijelölve, a projektfelület jobb oldalán megjelenő tulajdonságok panelen (Properties of Schematic … : Geometry/Advanced Geometry Options/Analysis Type: 2D) , (6.10. ábra). Ha a panel nem jelenik meg akkor a statikai analízis paneljének Geometry sorára való jobb gombos kattintással, majd Properties parancs kiadásával előhozható.

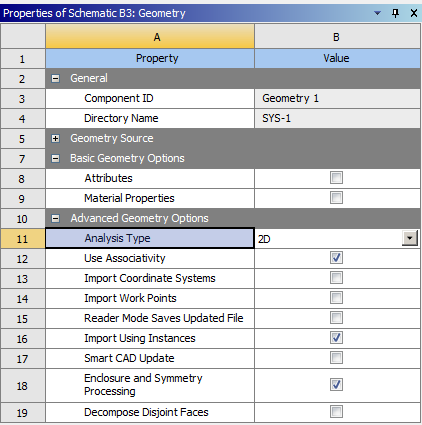
6.9. ábra - Váltás 2 dimenziós geometriára.

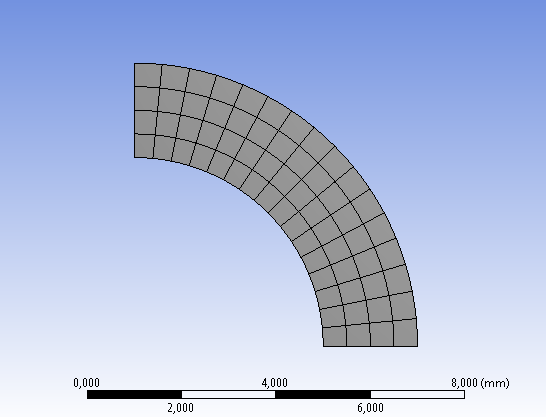
A szimulációs környezetbe való belépés után a modellfában a geometriát kijelölve, a Details panelen tudjuk beállítani a szimuláció típusát sík alakváltozásra (Outline/…/Geometry/ => Details…/Definition: Plane Strain) . A szimuláció során szerkezeti acél anyag került beállításra. A hálózás során strukturált hálót használunk négyszög elemekkel (Mapped Face Meshing) . A véges elemek mérete 0,5mm (6.10. ábra).

A modell így 64 elemet tartalmaz, tehát viszonylag kevés, azonban ez olyan pontos eredményt fog adni, mintha a teljes 3D-s geometriát kb. 5000 elem segítségével szimulálnánk, tehát majdnem 80-szoros sebességgel kapunk eredményt.

6.10. ábra - 2D-s negyed csőmodell hálója

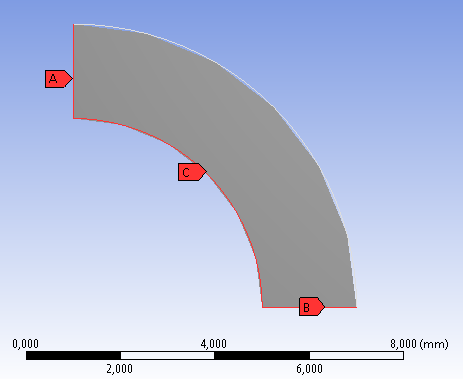
A szimmetriafeltételeknél mindig figyelni kell arra, hogy a megfogások megfeleljenek a valóságnak. Jelen esetben a valós viselkedés modellezése az X és Y tengelyre illeszkedő 2 él adott tengelyre merőleges elmozdulásának megkötése. Ez egy-egy elmozdulás típusú kényszer segítségével oldható meg, melyek az illeszkedő tengely irányába eső elmozdulást szabadon engedik, míg a tengelyre merőlegest gátolják (6.11. ábra. A és B - címkével jelölt geometriai elemek).

A szerkezet terhelése a cső belső falán ébredő 100MPa nagyságú nyomás (6.11. ábra. C - címkével jelölt geometriai elemek).

6.11. ábra - 2D-s negyed csőmodell terhelése és megfogásai

A szimuláció futtatása után kérdezzük le az egyenértékű feszültséget, fajlagos nyúlást és a radiális deformációt. Ez utóbbihoz egy polár koordináta rendszert kell definiálnunk. Az alábbi ábrán láthatjuk az ébredő egyenértékű feszültség eloszlását a cső fala mentén (6.12. ábra). A minimum és a maximum értékek mutatják a cső belső és külső falában ébredő feszültséget.

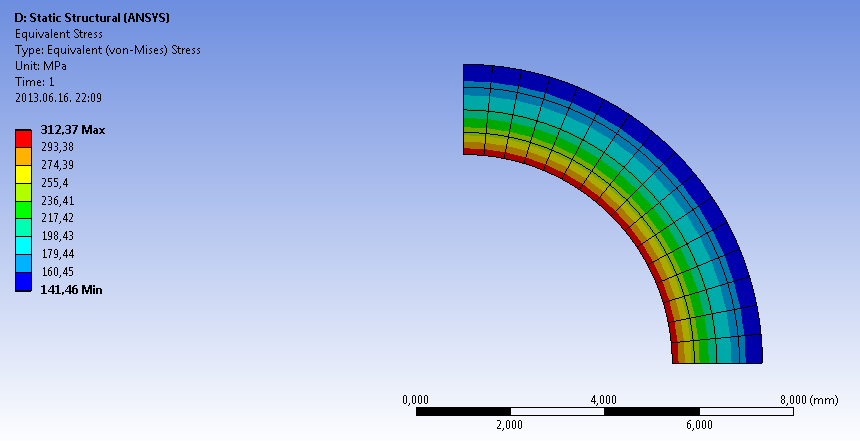
6.12. ábra - 2D-s negyed csőmodell egyen értékű feszültség értékei

6.1.5. A feladat megoldása 2D-s tengelyszimmetrikus (Axisymmetric) típusú modellként

Ugyanezt a feladatot meg lehet oldani 2D-s tengelyszimmetrikus modellként, mivel mind a geometria, mind a terhelés tengelyszimmetrikus. Ebben az esetben a geometria azt a fél hosszmetszetet jelenti, amelyet körbeforgatva megkapjuk a teljes geometriát, tehát a csövet modellező feladatnál ez egy 10mm*2mm-es téglalap a forgatási tengelytől 4mm-es minimális távolságra. Megjegyzés: ANSYS szoftverben a 2D-s tengelyszimmetrikus modelleket úgy kell felépíteni, hogy a forgástengely a globális Y tengely legyen, a geometria pedig az 1. és a 4. sík negyedben (+X) helyezkedjen el (6.13. ábra).

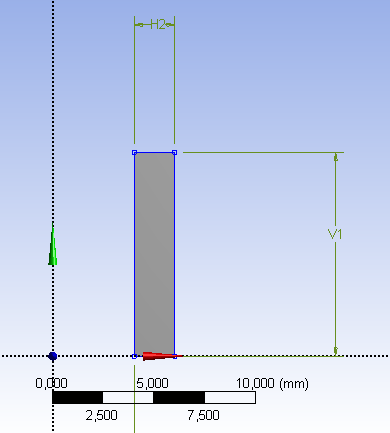
6.13. ábra - 2D-s tengelyszimmetrikus csőmodell geometriája

Mivel az analízis típusa 2D tengelyszimmetrikus, a 2D-s viselkedést, az előző feladathoz hasonlóan, a szimulációs környezetbe való belépés előtt be kell állítanunk (6.10. ábra), (S tatic Structural/Geometry => Properties of Schematic … : Geometry/Advanced Geometry Options/Analysis Type: 2D) ,

Belépve a szimuláció környezetbe, a modellfa geometria sorát kijelölve állítsuk be a szimuláció típusát tengelyszimmetrikusra, (Outline/…/Geometry => Details /Definition/2D Behavior: /Axisymmetric) .

Az anyag hozzárendelés és a szimuláció általános beállításai után készítsük el a végeselemes hálót. A háló, ahogy az előző esetben is 0,5mm nagyságú négyszög elemekből áll. Az így létrehozott háló összesen 80 elemet tartalmaz (6.14. ábra).

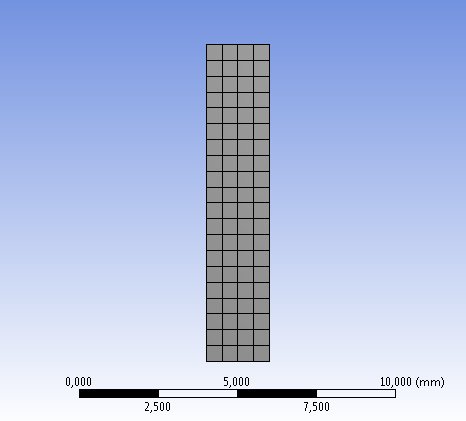
6.14. ábra - 2D-s tengelyszimmetrikus csőmodell véges elemes hálója

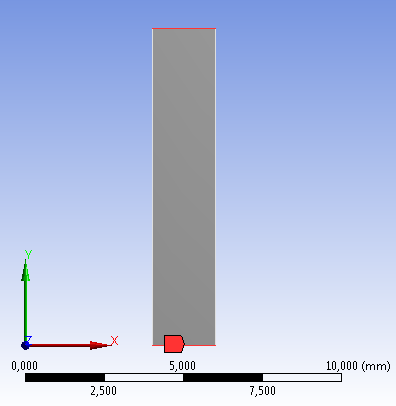
A megfogások definiálása itt is különös figyelmet igényel. A csőmodell két végén olyan elmozdulás típusú kényszert célszerű alkalmazni, amely megengedi a cső tágulását, tehát radiális (X) irányú elmozdulását, de leköti az axiális (Y) irányú elmozdulás lehetőségét. Mivel ebben a modellben a két véglap párhuzamos egymással, elegendő egyetlen megfogást megadni, mert mindkét oldal ugyanolyan irányban mozoghat, illetve van lekötve (6.15. ábra).

6.15. ábra - 2D-s tengelyszimmetrikus csőmodell véglapjainak megfogása (UY=0).

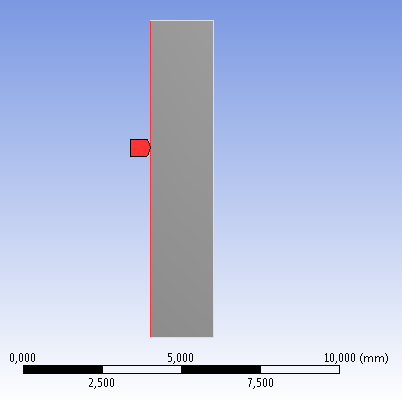
A 100MPa-os belső nyomás a csőfelület belső felületén, tehát itt a tengelyhez közel álló párhuzamos élen van (6.16. ábra).

6.16. ábra - 2D-s tengelyszimmetrikus csőmodell nyomásterhelése

A szimuláció lefuttatása után, az előző példához hasonlóan kérdezzük le az egyenértékű feszültséget, a fajlagos nyúlást és a radiális deformációt. Ez utóbbihoz most nem kell poláris koordináta rendszert definiálnunk, mivel az az X tengely irányába esik. Az alábbi ábrán láthatjuk az ébredő egyenértékű feszültség eloszlását a cső fala mentén (6.17. ábra). A minimum és a maximum értékek mutatják a cső belső és külső falában ébredő feszültséget.

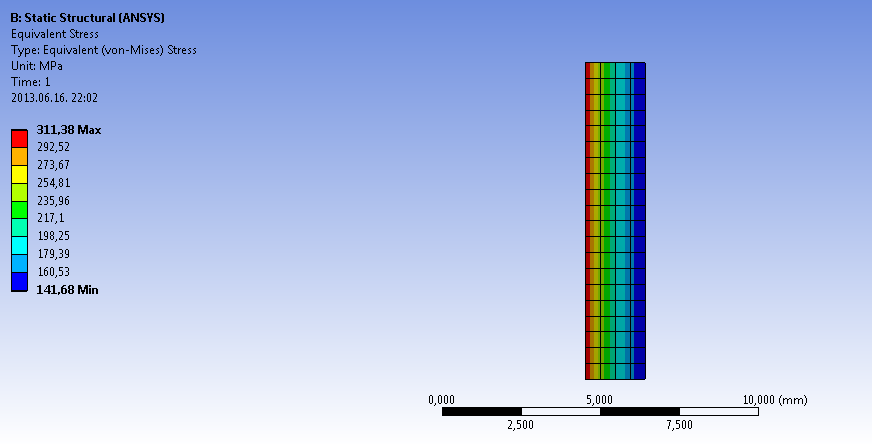
6.17. ábra - 2D-s tengelyszimmetrikus csőmodell egyenértékű feszültség viszonyai

6.1.6. Összefoglalás

Miután négy féle módon elvégeztük a szimulációt, azonos feltételekkel (azonos anyag és geometria, azonos elemméret és szimulációs beállítások) láthatjuk, hogy a héjmodell kivételével az eredmények nagymértékben egyeznek az analitikus számolással, melyet a vastag csövekre alkalmazott formulákkal végeztünk. Ugyanakkor, a vékonyfalú csövekre alkalmazott analitikus számolás eredménye jó egyezést mutat a héjmodellel végzet szimulációval. Ez nem meglepő, hisz mindkét eljárás a kiterjedéséhez (itt átmérő és hossz) mérten kis falvastagságú szerkezetek vizsgálatára szolgál.

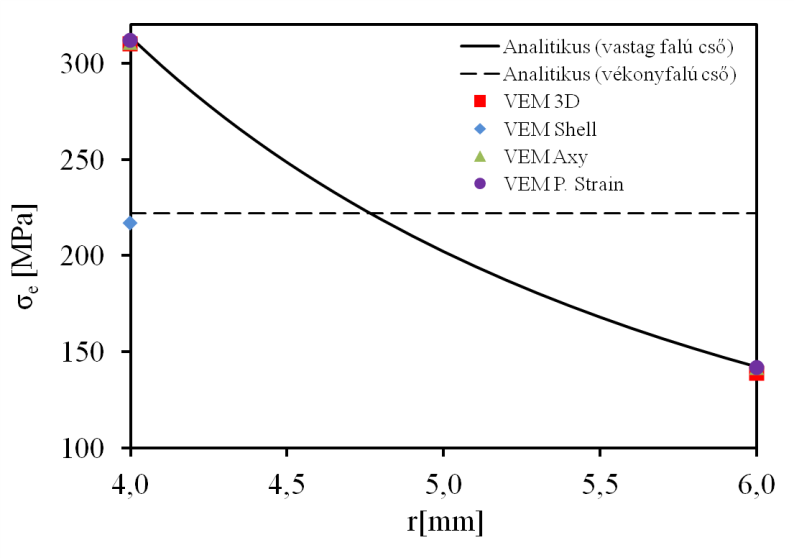
6.18. ábra - A cső falában ébredő (von Mieses féle) egyenértékű feszültség analitikus és végeselemes megoldása.

6.1. táblázat - A négy különböző végeselemes módszer és az analitikus eredmények összehasonlítása.

Egyenértékű feszültség, [MPa]	Analitikus (vastag falú cső)	VEM 3D	VEM Axy	VEM P. Strain	Analitikus (vékonyfalú cső)	VEM Shell
Külső oldalon	313	310	311	312	222	217
Belső oldalon	142	139	142	142

Egyenértékű feszültség, [MPa]

Analitikus

(vastag falú cső)

VEM

Axy

VEM

P. Strain

Analitikus

(vékonyfalú cső)

VEM

Shell

Külső oldalon

313

310

311

312

222

217

Belső oldalon

142

139

142

6.2. Példa egy oldalon befogott, hajlított tartó négyféle megoldására

Az alábbi példában egy egyik oldalon befogott, koncentrált erővel terhelt gerenda statikai analízise által fogjuk bemutatni, hogy a különböző típusú szimulációk összeállításának módját és eredményeit.

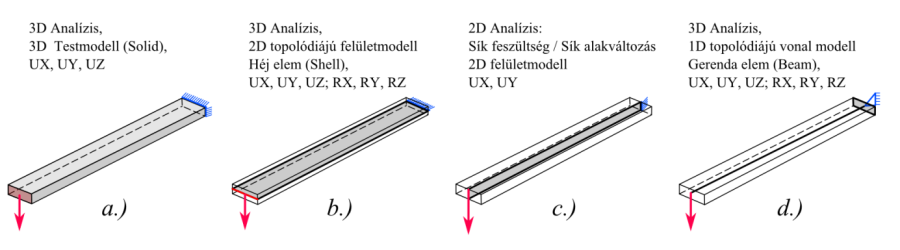
a.) Testmodell, b.) héjmodell, c.) 2D sík alakváltozási, vagy sík feszültségi modell, d.) gerendamodell.

6.19. ábra - Egy oldalon befogott, hajlított tartó négyféle megoldása.

Az alábbi ábrákon látható a geometriai modellt az adott a terhelési és permfeltételekkel a következő módokon fogjuk tudni vizsgálni (6.19. ábra):

3D-s teljes testként (3D body) .
3D-s felületmodellként (Shell body),
2D-s sík alakváltozás és sík feszültség típusú feladatként (2D Plane Strain, Plane Stress) ,
Vonalmodellként (Gerenda elemmel), keresztmetszettel definiálva (Line body, Cross section)

6.20. ábra - A hajlított rúd geometriai méretei [mm]

6.21. ábra - Terhelési modell a hajlított rúd esetében

Minden esetben azonos anyagtulajdonságok lesznek definiálva; az ANSYS Workbench beépített szerkezeti acél (Structural Steel) nevű anyagja. A szimulációk beállításánál a nagy alakváltozások megengedettek (Simulation Settings/Large deflection: On) .

6.2.1. A feladat megoldása 3D-s teljes testmodellel (3D body)

A 3D-s geometria használata általában a leghosszadalmasabb számítási igényű eljárás. Tehát célszerű (amennyiben lehetséges) a további példák során bemutatott egyszerűsített eljárásokat használni. A teljesség kedvéért azonban bemutatjuk a teljes 3D-s geometria szimulációját is ugyanazon a példán. A geometriai modell felépítése történhet a véges elemes szoftverben illetve akármelyik más CAD rendszerben is.

Jelen példában az ANSYS Workbench Design Modeler moduljában építettük fel a hasábot, egyetlen kihúzás (Extrude) segítségével. A vázlatot egy 100x10mm-es téglalap alkotja, a kihúzás mértéke normál irányba 2mm, (6.22. ábra).

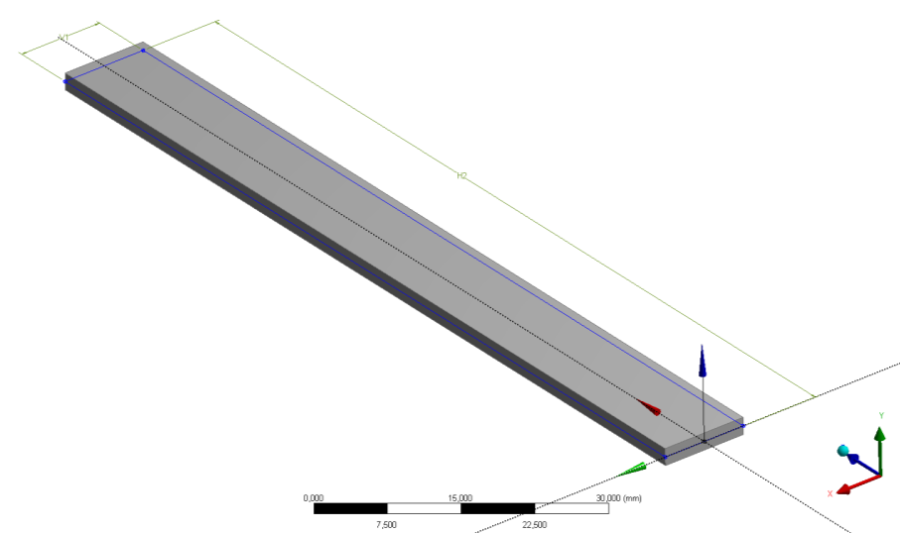
6.22. ábra - Az elkészített 3D-s geometria

Az általános beállítások után (anyag hozzárendelés, nagy elmozdulások engedélyezése stb.) készítsük el a véges elemes hálót téglaelemek felhasználásával (6.23. ábra). Az elemek mérete 1mm, így összesen 2000 elemből áll a modell.

6.23. ábra - A 3D-s modell véges elemes hálója

Az eredmények összehasonlíthatósága miatt definiáljunk azt a konstrukciós geometriát, amely segítségével a vonal menti deformáció lekérdezhető.

Konstrukciós geometrialétrehozás ANSYS Workbenchben :

A konstrukciós görbe (Path) egy olyan térbeli görbét jelent, mely mentén diszkrét pontokban lekérdezhető az eredmény, és az eredmény pontonként táblázatban és diagramon is megtekinthető. A pontokat és értékeket tartalmazó táblázat exportálható abból a célból, hogy más programok segítségével is elemezhető legyen. A diszkrét pontokhoz tartozó eredményeket idő és út függvényében is meg lehet jeleníteni, az út természetesen a vonal kezdő pontjától a végpontja felé haladva jelenik meg.

A konstrukciós vonal definiálását kétféle módon tehetjük meg; a kezdő és végpont megadásával, illetve meg lévő egyenes kijelölésével.

Első lehetőséget kétféle módon lehet megoldani. Közvetlenül a kezdő és végpont megadásával (ilyenkor létező pontok kijelölése szükséges), vagy a vonal megadható a pozitív x tengely és a háló modell metszéseként. (Ebben az esetben a kezdő és végpont helyzetét jelöli ki a háló, és e két pont közti vonal lesz a konstrukciós elemünk.) A konstrukciós pálya lehet egyenes, vagy íves, attól függően, hogy milyen típusú koordináta rendszert használunk. (Descartes-féle koordináta rendszernél egyenes, míg henger koordináta rendszernél íves.) A konstrukciós vonal diszkrét pontjainak száma definiálható, de maximum 200 lehet. (Megjegyzés: a kezdő-és végpont segítségével csak tömör test és felületmodell esetén lehet megadni a konstrukciós egyenest.)

Második lehetőség, amikor egy meglévő él kijelölésével definiáljuk a konstrukciós vonalat. Ebben az esetben a vonal alatt lévő csomópontok jelentik a vonal diszkrét pontjait. Több egyenesből álló vonalláncoknál figyelni kell arra, hogy a vonalak egymással folytonosak legyenek.

ANSYS Workbenchben mielőtt létrehoznánk egy konstrukciós geometriát egy „Path Object”- et létre kell hozni, melyet a konstrukciós eszköztárban (Construction Geometry toolbar) találhatunk meg. Ezután a fenti módszerek bármelyikével létrehozható a kívánt konstrukciós vonal.

A példában szereplő útvonalat a modellfa modell sorának kijelölésével, a felső ikonsorból hozzuk létre (Outline/Model=>Construction Geometry/Path) . Az útvonal típusa legyen élre illeszkedő, melyet a testmodellünk egyik hosszanti élének kijelölésével rendelhetünk hozzá (6.24. ábra).

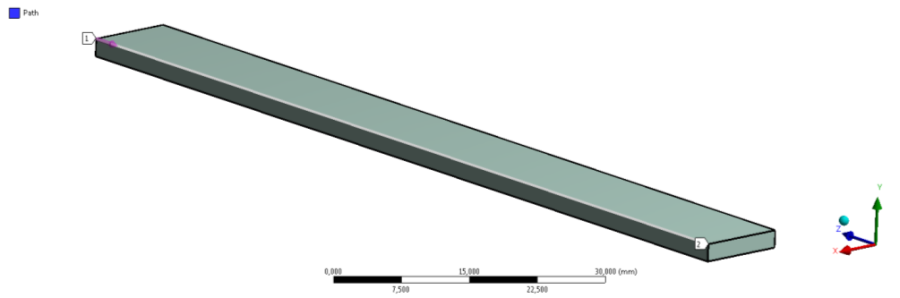
6.24. ábra - A 3D-s modellen létrehozott konstrukciós geometria

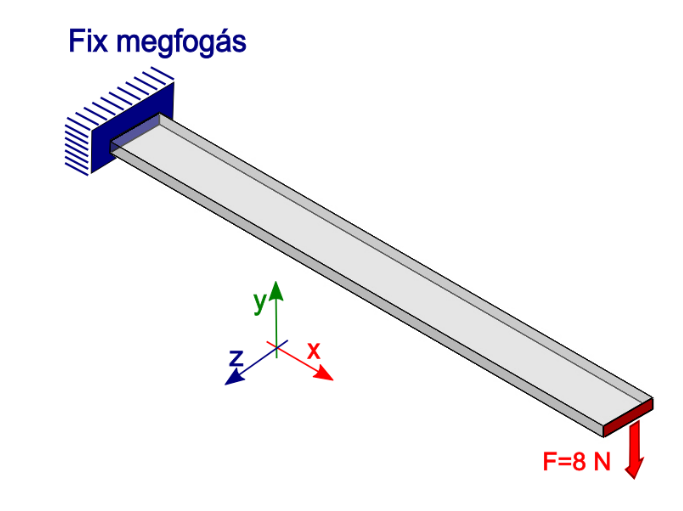
A terhelési és peremfeltételek elkészítésekor összesen két elemet használtunk; egy fix megfogást a rúd egyik véglapján (Supports/Fix support) , mely a véglap csomópontjainak minden szabadságfokát eliminálja és egy erő (Force) jellegű terhelést a rúd másik végén. Az erőt komponensenként megadva –Y irányban 8N nagyságú, míg X és Z irányba 0N nagyságú. A terhelést a 6.24. ábra mutatja, ahol piros B jelű címkével a –Y irányú, 8N nagyságú erőterhelés, és a kék A jelű címkével ellátott fix megfogás van jelölve.

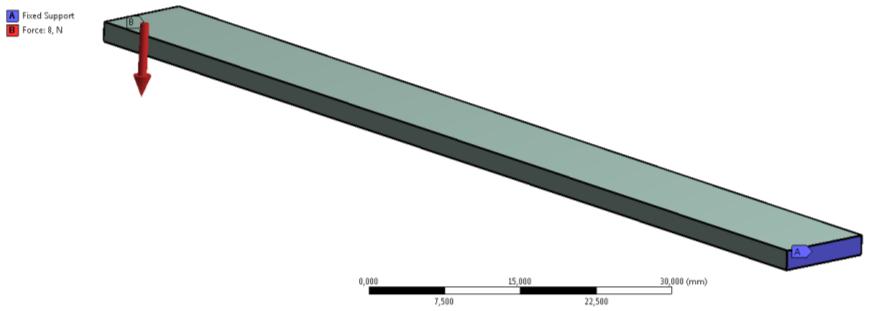
6.25. ábra - 3D-s geometria esetén a terhelési modell megadása

A szimuláció futtatása után kérdezzük le a teljes (6.26. ábra), és az Y irányú lehajlás értékét a létrehozott konstrukciós vonal (Path) mentén (6.27. ábra).

6.26. ábra - 3D-s modell esetén a teljes deformáció eloszlása [mm]

6.27. ábra - 3D-s modell esetén a vonal menti, y irányú deformáció [mm]

6.2.2. A feladat 3D-s megoldása felületmodell (shell) definiálásával

A modellt egy felületi geometriával (Surface) és a hálózáskor hozzárendelt vastagsági paraméterrel definiáljuk, amely héj (Shell) elemekkel való szimulációt jelent. Jelen esetben egy 100x10mm-es síklap és egy ehhez tartozó 2mm-es vastagság határozza meg a testet.

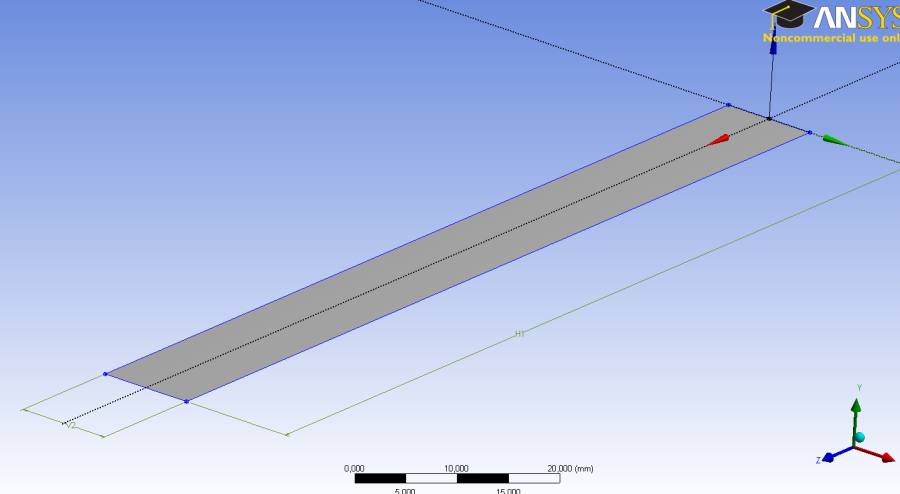
6.28. ábra - A felületi geometria

Az ANSYS Workbench Design Modeler moduljában a vázlatelemek felületté alakítása a Concept menü Surfaces From Sketches menüpontjában végezhető el (6.29. ábra).

6.29. ábra - Felületmodell létrehozása vázlat alapján (menüpont elérése)

A geometria elkészülte után, lépjünk be a szimulációs környezetbe. A modellfában a geometria alatt megjelenő felületmodellt kijelölve állítsuk be a lemez vastagságát (Outline/…/Geometry/Surface Body => Details…/Definition/Thickness: 2mm) , az eltolás típusát hagyjuk „közép”-re állítva ( Offset Type: Middle ). Az anyagot hagyjuk az alapértelmezett szerkezeti acélnak (Strutural steel) .

Ezután végezzük el a hálózást. Ugyanúgy, mint az előző esetben 2mm-es elemméretet használtunk. Látható, hogy ez meglehetősen eltér az előző esettől, mivel a test vastagsága mentén csak egy elemre oszlik a geometria (6.30. ábra).

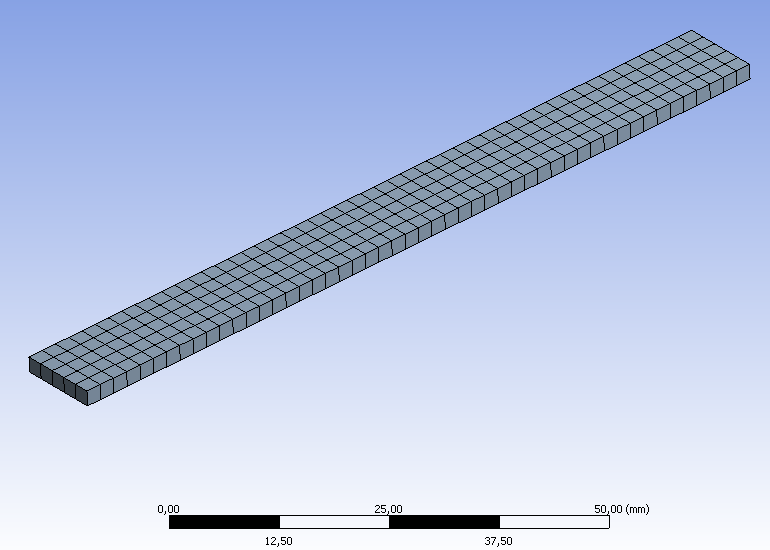
6.30. ábra - Véges elemes háló shell modell esetén

Ahogy az előbbi esetben itt is, hozzunk létre egy konstrukciós geometriát, mely segíti az eredmények értékelését. Jelen esetben az egyik hosszanti él lett a konstrukciós vonal (Path) alapja (6.31. ábra).

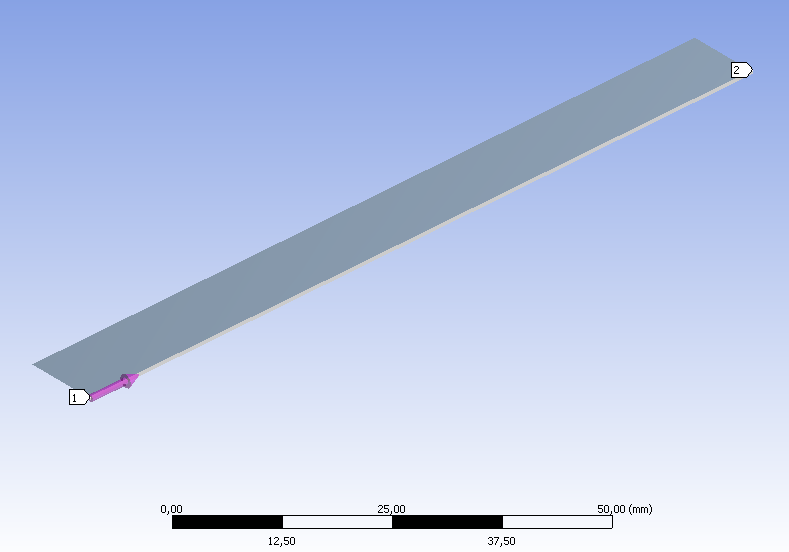
6.31. ábra - Konstrukciós vonal shell modell esetén

A terhelés ugyanaz, mint az előző esetben (Fix megfogás a test egyik véglapján, 8N erőterhelés –Y irányban a másik végén), mivel itt felületmodellről van szó, a véglapok kijelöléséhez a felületet határoló él kijelölése szükséges (6.32. ábra).

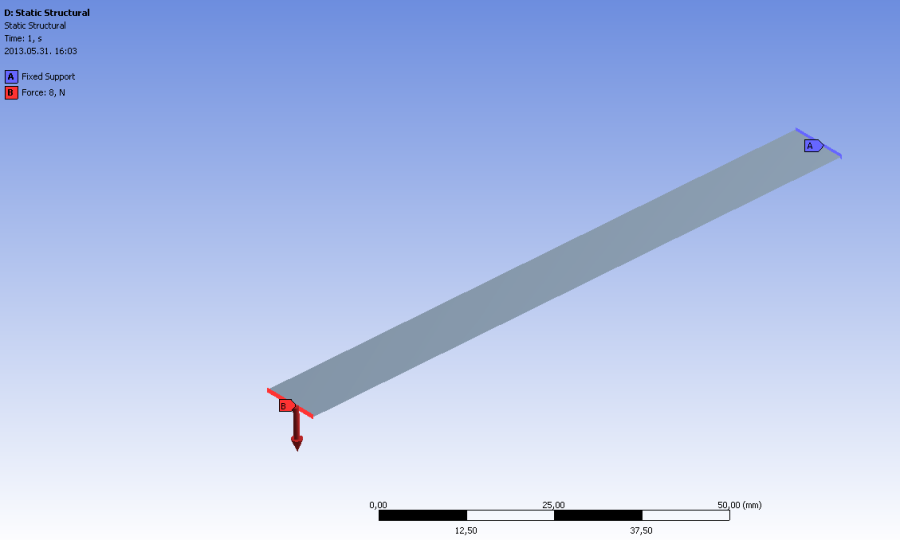
6.32. ábra - Terhelési modell felületi test esetén

A szimuláció futtatása után a kérdezzük le a teljes (6.33. ábra), és a konstrukciós vonal menti Y irányú deformációt (6.34. ábra).

6.33. ábra - Teljes deformáció [mm]

6.34. ábra - Y irányú deformáció [mm] konstrukciós vonal mentén

6.2.3. A probléma megoldása 2D-s feladatként

A fenti probléma megoldására kétféle 2 dimenziós eset áll rendelkezésünkre a sík feszültség (Plane Stress) és a sík alakváltozás (Plane Strain).

A sík feszültség (Plane Stress) analízis esetén a test vizsgált metszetére merőleges (ANSYS-ban: Z tengely) irányában nem ébred feszültség. Ez az állapot vékony (a vizsgált metszetre merőleges kiterjedése kisebb, mint a másik két irányban), és a vizsgált metszet síkjába eső terhelési és megfogásai feltételekkel rendelkező testekre jellemző.

A 2D-s sík alakváltozás (Plane Strain) típusú szimulációk lényege, hogy a test vizsgált keresztmetszetére merőleges (ANSYS-ban: Z tengely) irányában nincs alakváltozás. Ez az állapot hosszú, állandó keresztmetszetű (a vizsgált keresztmetszetre merőleges kiterjedése nagyobb, mint a másik két irányban), és a hossz mentén állandó és a keresztmetszet síkjába eső terhelési és megfogásai feltételekkel rendelkező testekre jellemző. Ennél fogva a feszültségi állapot és a keresztmetszet síkjába eső alakváltozási állapot is azonos a hossz (Z tengely) mentén, tehát elegendő egyetlen keresztmetszet 2D-s vizsgálata. A sík alakváltozásnál végtelen hosszú modellt feltételezünk fajlagos terhelésekkel, míg az általánosított változatánál (Generalized Plane Strain) a vastagságot is megadhatjuk.

Mivel ebben a példában a terhelés és megfogás is egyenletes a Z tengely mentén (és nincs Z tengely irányú komponense), mindkét eset megvalósítható. Viszont, mivel a valós geometria Z irányú mérete lényegesen kisebb, mint az X irányú hossza, és nagyobb mint az Y irányú magassága, ezért egyik eljárás geometriai feltételeit sem teljesíti., vagyis Z irányban sem a feszültség, sem pedig az alakváltozás értéke nem lesz teljesen 0. Viszont mivel elhanyagolható mértékűek a síkbeli komponensekhez képest, ezért jó közelítést jelentenek. Végezzük el az analízist mindkét esetre és vessük össze az eredményeket.

Vázlatkészítésnél a 100x2mm-es téglalp megrajzolását az XY síkon szükséges elvégezni. A 10mm-es vastagságot pedig a szimuláció során tudjuk megadni. A 6.35. ábra mutatja az elkészült vázlatot és a felületet, amelyet a vázlatból definiáltunk (Concept/ Surfaces From Sketches) . A felület létrehozásának menete ugyan az, mint a 3D-s Shell modelles példában, annyi különbséggel, hogy a felületnek mindenképp egy síkban (XY) kell lennie (6.35. ábra), és a szimuláció során 2D-s beállításokat kell alkalmazni az ott használt 3D-s helyett. A 2D-s viselkedést a szimulációs környezetbe való belépés előtt be kell állítanunk, ( Static Structural/Geometry => Properties of Schematic… : Geometry/Advanced Geometry Options/Analysis Type: 2D) .

6.35. ábra - Az elkészült vázlat és felület

A szimulációs környezetbe való belépés után a modellfában a geometriát kijelölve, a Details panelen tudjuk beállítani a szimuláció típusát általánosított sík alakváltozásra (Outline/…/Geometry/ => Details…/Definition: Generalized Plane Strain) . A későbbiekben futtassuk le szimulációt a sík feszültség (Plane Strain) beállítással is.

A geometria elkészítése és a szükséges beállítások (anyagdefiniálás, nagy alakváltozás engedélyezése, vastagság beállítása stb.) után készítsük el a végeselemes hálót, mely elemméretét állítsuk 1mm-re. Mivel itt jóval kevesebb véges elem adódik, mint például a 3D- szimulációk esetén, lehetőség van a sűrűbb háló használatára (6.36. ábra).

6.36. ábra - A véges elemes háló (elemméret 1 [mm])

A terhelés hasonlóan az eddigi esetekhez egy fix megfogást és egy –Y irányú, 8N nagyságú erőterhelést jelent (6.37. ábra).

6.37. ábra - A terhelési modell

Mivel ennél az esetnél is szükség van a vonal menti deformáció értékeire, így definiáljuk a konstrukciós vonalat ( Path ) a rúd felső élén (6.38. ábra).

6.38. ábra - A konstrukciós vonal (path) definiálása

Eredményként, a bevezetésben megfogalmazott problémák ellenére, az eddigiekhez nagyon hasonló értékeket kaptunk. A teljes deformáció eredményét a 6.39. ábra, az Y irányú, vonal menti deformáció eredményét a 6.40. ábra szemlélteti.

6.39. ábra - Teljes deformáció [mm]

6.40. ábra - Vonal menti, y irányú deformáció [mm]

6.2.4. A feladat megoldása vonalmodell keresztmetszet definiálásával (gerenda elemmel)

A vonalelemek két fő csoportja a rúd (Truss) és a gerenda (Beam) elemek, melyeknek alkalmazását a szerint választhatjuk ki, hogy a vizsgált szerkezetben lévő vonal elemek felvesznek-e hajlító igénybevételt (gerenda), vagy csak tengelyirányú terhelést (rúd). Esetünkben egyértelműen a gerendamodellre van szükség mivel a konzol tengelyére merőleges terhelés hajlításra veszi igénybe a tartót. Az ANSYS Workbench használatakor a program a vonal elemeket automatikusan gerenda elemekkel hálózza be.

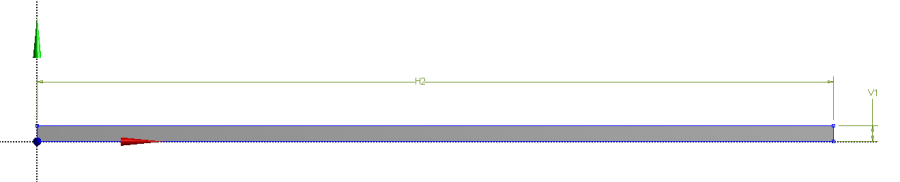
A geometria két részből, a tartó tengelyét képviselő vonalmodellből, és a keresztmetszet definíciójából áll. A vezérgörbe a Z tengely mentén fekvő, 100mm hosszú vonal, a keresztmetszet pedig egy 10x2mm-es téglalap (6.41. ábra).

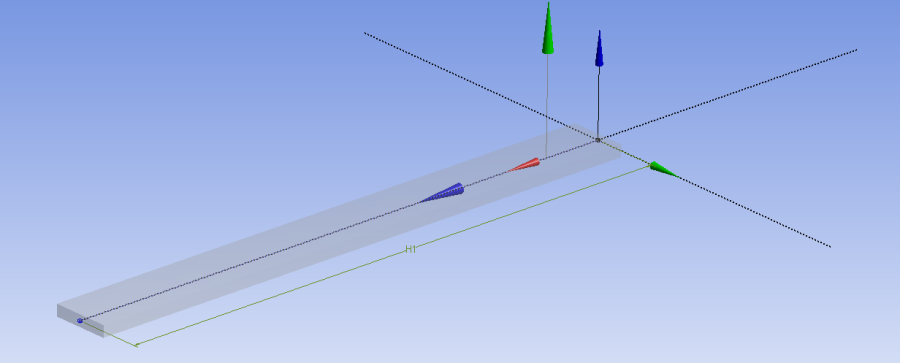
6.41. ábra - A vonal test és keresztmetszet alapján definiált geometria

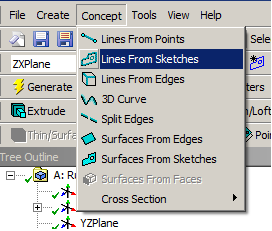
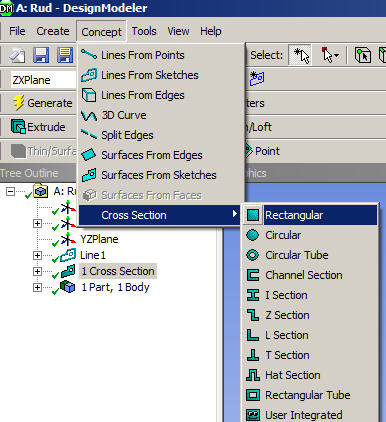
Az ANSYS Workbench Design Modeler moduljában a vonal test a Concept menü Lines From Sketches parancsával hozható létre, a már előzőleg megrajzolt vonal vázlatának kijelölésével (6.42. ábra). A keresztmetszet definiálását a Concept menü Cross Section parancsával lehet elvégezni (6.43. ábra). Lehetőségünk van az előre definiált, jellegzetes keresztmetszetek kiválasztására (ilyenkor csak a méreteket kell megadni), illetve saját vázlat készítésére. Ezután a vonalmodellhez (line body) , a létrehozott keresztmetszetet hozzá kell rendelni. Ehhez a modellfa utolsó (az alkatrészek és a testek számát mutató) sorát le kell gördíteni és a vonalmodell kijelölése után a Details panel Cross Section sora mellett kiválasztani a létrehozott keresztmetszet nevét („Rect1”).

A keresztmetszet definiálásakor figyelni kell a vonalelem orientációjára (a zöld színű koordinátatengely jelöli a +Y irányt). A keresztmetszet a modellen való állásának ellenőrzésére, a View menüben bekapcsolhatjuk a testmodell (Cross Section Solids) és/vagy a vonal koordinátarendszer (Cross Section Alignments) láthatóságát (6.41. ábra).

6.42. ábra - ANSYS WB Design Modeler moduljában a vonal testté alakításhoz használatos menüpont elérése

6.43. ábra - ANSYS WB Design Modeller moduljában a keresztmetszet definiálásához használatos menü elérése

Miután a szimuláció beállításai megtörténtek (pl. anyag hozzárendelés) elkészítjük a véges elemes hálót. A testet 2mm-es elemmérettel hálóztuk be. Ahogy a 6.44. ábra mutatja a vonalmodell mentén mindenhol csak 1 db elem helyezkedik el. Így a véges elemes modellünk 50 elemet tartalmaz.

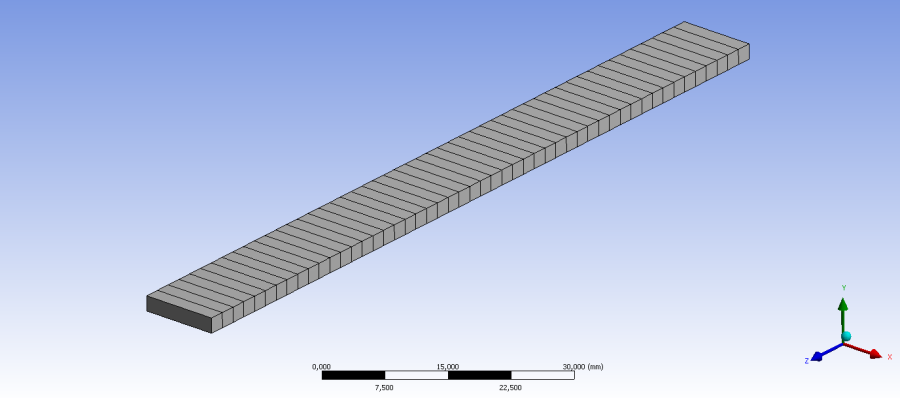
6.44. ábra - A véges elemes háló

Az eredmények lekérdezéséhez definiáljunk egy konstrukciós rajzi elemet (Construction Geometry) , melynek segítségével egy vonal (Path) mentén lekérdezhető a szimuláció eredménye. Jelen feladatban a konstrukciós segédvonalat a test közepén végigfutó vonalmodell kijelölésével definiáljuk (6.45. ábra).

6.45. ábra - Konstrukciós vonal definiálása diszkrét kezdő és végpont segítségével

A megtámasztás (Supports/Fix support) és az erő (Loads/Force) megadásakor a 2 végpontot jelöltük ki. A terhelést a 6.46. ábra mutatja, ahol piros, B jelű címkével a –Y irányú, 8N nagyságú erőterhelés, és a kék, A jelű címkével ellátott fix megfogás van jelölve. Mivel vonalmodell lett definiálva a terhelések és megfogások megadásakor, a vonalak végpontjainak kijelölésével az adott csomópontok mind a 6 szabadságfokát meghatároztuk.

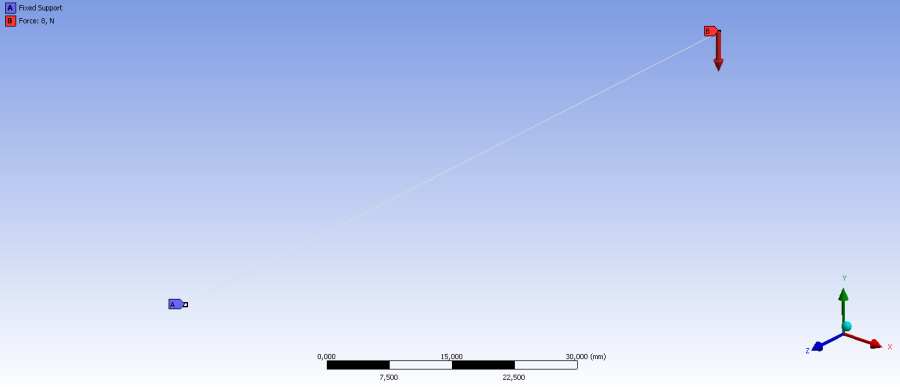
6.46. ábra - A terhelési modell

A szimuláció lefuttatása utána az alábbi eredményeket kérdeztük le:

Y irányú deformáció (Directional Deformation) a konstrukciós vonal mentén (6.47. ábra),
Teljes deformáció (Total Deformation) (6.48. ábra),

6.47. ábra - Y irányú deformáció [mm] a konstrukciós vonal mentén

6.48. ábra - Teljes deformáció [mm] (a minimum és maximum értékek feltüntetésével).

Gerendamodell esetén a Beam Result menüponttal további, specifikusan a gerendák igénybevételére vonatkozó eredmények is lekérdezhetőek (6.49. ábra). Kérdezzük le az alábbi eredményeket:

Teljes hajlító nyomaték (Total Bending Moment) (6.50. ábra),
Teljes nyíróerő (Total Shear Force) (6.51. ábra)

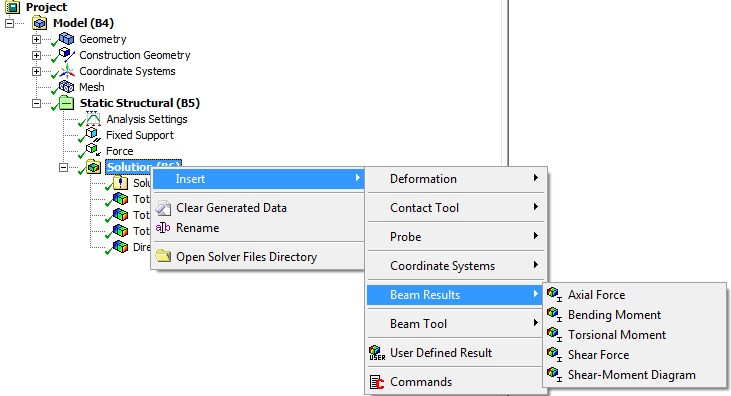
6.49. ábra - Gerendák igénybevételére vonatkozó eredmények is lekérdezhetőek.

6.50. ábra - Teljes hajlító nyomaték [Nmm] eredménye.

6.51. ábra - Teljes nyíróerő [N] eredménye.

Vegyük észre, hogy a folytonos színátmenet ellenére, a nyíróerő értéke az elvártaknak megfelelően, gyakorlatilag állandó a rúd hossza mentén.

6.2.5. Összefoglalás

A fenti példán jól látható, hogy ugyanazon feladat négyféle megoldása nagyon hasonló eredményeket hozott. A rúdvég lehajlásának mértékét a Táblázat 6.2 mutatja, a végeselemes eredmények és az analitikus számolástól való eltéréseik százalékos feltüntetésével.

6.2. táblázat - A különféle geometriai megoldások eredményeinek összehasonlítása az analitikus megoldással.

Modell (Elemtípus)	Szimuláció típusa	Uy [mm]	Eltérés [%]
3D testmodell	3D Térbeli	1,983	0,85
2D héjmodell	3D Térbeli	1,983	0,85
1D vonal elem	3D Térbeli	1,9998	0,01
2D felületmodell	2D sík feszültség	1,999	0,05
2D felületmodell	2D sík alakváltozás	1,935	3,25
	Analitikus megoldás	2,000

6.3. Példa gerenda modell alkalmazására: Hegesztett rácsos szerkezet

Rúdmodell használatát akkor célszerű megfontolni, mikor olyan feladattal állunk szembe, amelyben rácsszerkezetek, zártszelvények, csövek, azonos, vagy váltakozó keresztmetszetű idomelemekből álló szerkezetek mechanikai, vagy egyéb szimulációját kívánjuk elvégezni. Ebben az esetben a szimuláció lefutása lényegesen rövidebb időt vesz igénybe, ahhoz képest, mintha a teljes test vizsgálatát végeznénk. Hátránya azonban, hogy általában nem lehetséges a csomópontok vizsgálata. Amennyiben például egy ilyen szerkezet csomópontjában lévő hegesztett kötés szimulációjára is szükség van, célszerű először rúdmodellként analízist készíteni, majd a csomópont környezetének teljes modelljét vizsgálva a rúdmodell analízisből származó terhelési értékekkel szimulálható a csomópont mechanikai viselkedése. A módszer különösen hasznos például hídszerkezetek, rácsos tartók statikai és dinamikai ellenőrzéséhez.

Rúdmodellt (Trust) használunk abban az esetben, ha a modellezett szerkezetben szereplő, rudak csak tengelyirányú, (vagyis rúdirányú) erőt képesek felvenni. Tehát hajlító nyomaték nem ébred a csatlakozási csomópontokban (csuklóval modellezhető).

Gerendamodellt (Beam) alkalmazunk akkor, ha a csatlakozási pontokban nyomaték is átadódik, tehát a gerendamodellen hajlító igénybevétel is ébredhet. Például vékony, vagy közepesen vékony idomelemekből álló hegesztett rácsszerkezet szimulációjánál alkalmazhatjuk.

A vonalelemek egyik speciális fajtáját, a csőmodelleket (Pipe) vékony falú, vagy közepesen vékony falú főleg kör keresztmetszetű csövek vizsgálatánál alkalmazhatjuk. Ebben az esetben az ANSYS lehetőséget kínál olyan speciális terhelések definiálására, mint például a cső-nyomás.

A gerendamodell (Beam) készítéséhez egy vonalmodellt (Line body) és egy keresztmetszetet (Cross Section) kell definiálni. A vonalmodellek kizárólag egyenes, vagy görbe vonalakból állnak, nincs felületük, vagy térfogatuk, a gerendamodell nyomvonalát határozzák meg. A gerendamodell keresztmetszetének (Cross Section) megadása a felület nagyságának illetve a különböző irányú másodrendű nyomaték értékek számolásához szükséges. A keresztmetszet definiálásakor lehetőség van megadni, hogy a keresztmetszet mely pontján menjen keresztül a vezérgörbe (tehát a vonalmodell). Ez lehet például a keresztmetszet középpontja, súlypontja, nyírási középpontja, vagy egy tetszőlegesen megadott pont.

Az alábbi esetben egy négyszög keresztmetszetű zártszelvényből álló háromszög alakú hegesztett tartókonzol szimulációját vizsgáljuk meg. A feladathoz tartozó geometriát a 6.52. ábra mutatja.

6.52. ábra - A tartókonzol geometriai méretei [mm]

A terhelési model:

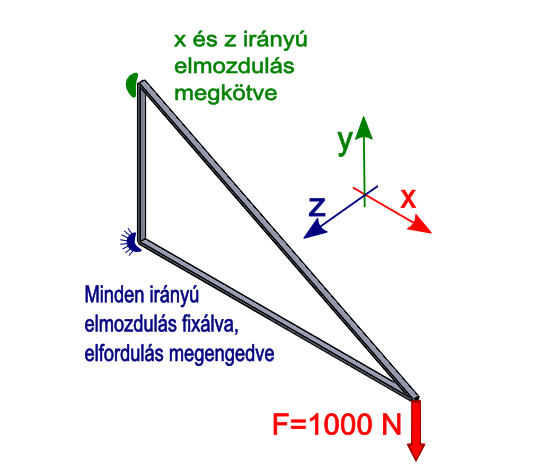
6.53. ábra - A konzol terhelési modellje

A végeselemes szoftverben elegendő a szerkezet körvonaláról vázlatot készíteni, majd ehhez a körvonalhoz hozzárendelni a megrajzolt, vagy kiválasztott keresztmetszetet (6.55. ábra). Csak abban az esetben kell a keresztmetszetet vázlat szintjén elkészíteni, amikor a szokványostól eltérő, egyedi keresztmetszetet használunk.

A keret nyomvonalának megrajzolása után a vázlatot (Sketch) vonalmodellé (line body) kell alakítani a Concept menüpont Lines From Sketches parancsával. A keresztmetszet kiválasztását és a méreteinek megadását a Concept menü Cross Section parancsával lehet elvégezni. A vonalmodell (line body) létrehozása után, a létrehozott keresztmetszetet hozzá kell rendelni. Ehhez a modellfa utolsó (az alkatrészek és a testek számát mutató) sorát le kell gördíteni és a vonalmodell kijelölése után a Details panel Cross Section sora mellett kiválasztani a létrehozott keresztmetszet nevét („Rect1”).

Megjegyzendő, hogy bár a modellen a zártszelvény darabok csatlakozási pontjában úgy látszik, mintha az egyes darabok a belső oldalon egymásba érnének, a külső oldalon meg távol lennének egymástól ez csak a megjelenítési képen ilyen, a szimuláció során itt egy pontban érintkezés valósul meg.

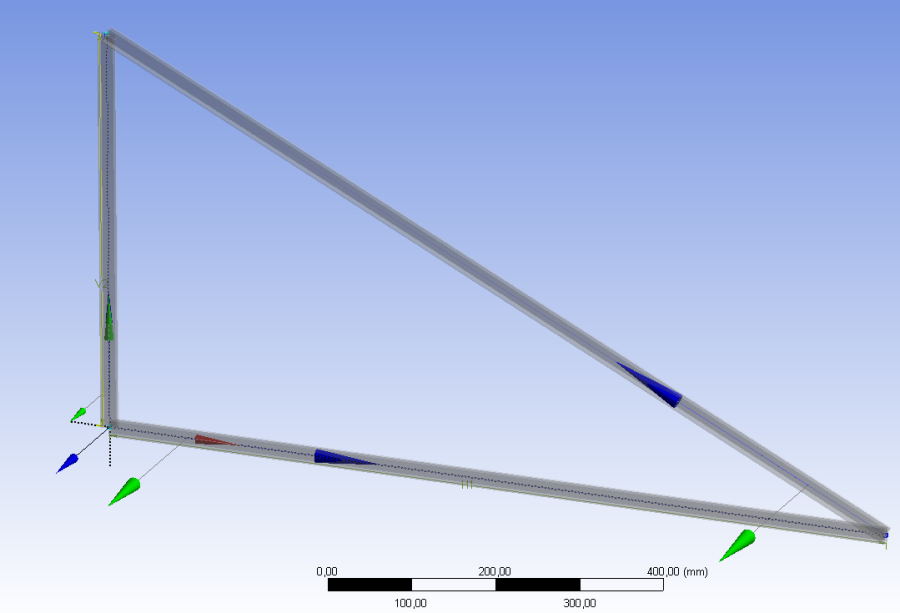
6.54. ábra - Az elkészült geometria (rúdmodell)

Ahogy láthatjuk a modellünk minden egyes vonalszakaszának az Y és Z irányokat jelző koordinátatengelyek jelennek meg. A kék színű (Z) vektor mutatja az adott vonal, vagy görbeszakasz érintő (tangent) irányát, míg a zöld színű (Y) vektor a keresztmetszet +Y irányát jelöli. Amennyiben ezek nem olyan irányban állnak alapértelmezetten, ami a feladatunkhoz megfelelő, akkor módosíthatjuk az állásukat.

6.55. ábra - A rúdmodellhez tartozó keresztmetszet vázlata

Az elkészült geometria anyaga jelen esetben az ANSYS Workbench szerkezeti acél (Structural Steel) nevű anyagja. A végeselemes háló elkészítése során 100 mm-es elemméretet használjunk (6.56. ábra). Látható, hogy a vonalmodell felosztása csak a vonal mentén történt meg, a keresztmetszetben csak egy elem található. Így látható ezzel a módszerrel, kevés elemmel, viszonylag gyors lefutású szimulációk hozhatóak létre (ebben a példában a modell mindössze 27 elemet tartalmaz.)

6.56. ábra - A véges elemes háló (100 mm-es elemméret)

A véges elemes háló elkészítése után a legfontosabb feladat a terhelési modell definiálása. Definiáljuk a következő típusú megfogásokat és terheléseket (6.57. ábra):

Erő terhelés a konzol végén: komponensenként definiált erő (Force) , a globális koordinátarendszer szerinti –Y irányban. A többi irányban az erő komponensei nulla értékűek. (6.57. ábra, piros színű, C jelű címke jelzi.)

Csuklós megtámasztás a konzol alsó részén: elmozdulás ellen biztosított, de elfordulást (minden tengely mentén) megengedő megfogás, mely egy pontra vonatkozik (Simply Supported) . (6.57. ábra, kék színű, A jelű címke jelzi.)

Görgős megtámasztás a konzol felső részén: globális X és Z irányú elmozdulás ellen biztosított, de az Y irányú elmozdulás és az elfordulás (minden tengely mentén) megengedett (Remote displacement) . (6.57. ábra, sárga színű, B jelű címke jelzi.)

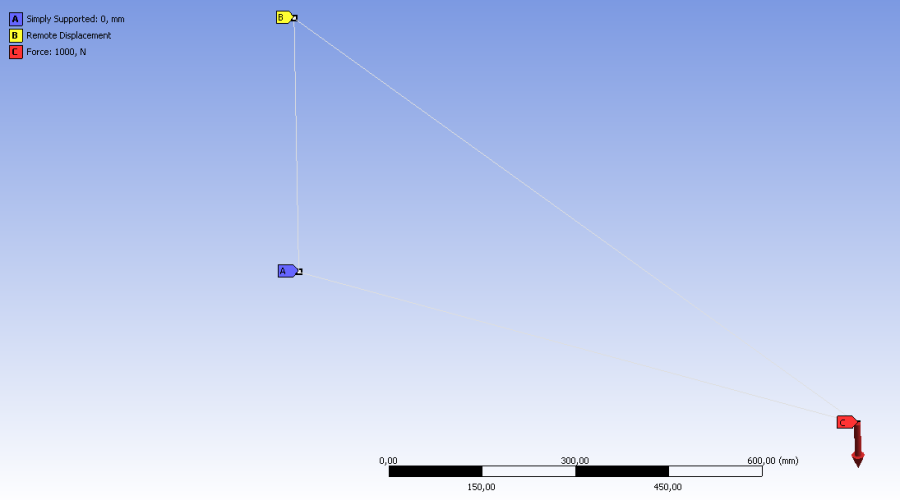
6.57. ábra - A terhelési modell

A szimuláció futtatása után kérdezzük le a számunkra fontos eredményeket. Jelen példánkban a következő jellemzőket célszerű lekérdezni:

Teljes deformáció (Total Deformation) , lásd 6.58. ábra
Teljes hajlító nyomaték (Total Bending Moment) , lásd 6.59. ábra
Axiális irányú erő (Axial Force) , lásd 6.60. ábra
Csavaró nyomaték (Torsional Moment) , lásd 6.61. ábra
Teljes nyíróerő (Total Shear Force) , lásd 6.62. ábra

Az alábbi ábrákon láthatóak az egyes eredmények.

6.58. ábra - Teljes deformáció a konzolon [mm]

6.59. ábra - Hajlító nyomaték a konzolon [Nmm]

6.60. ábra - Tengely irányú erő a konzolon [N]

6.61. ábra - Csavaró nyomaték a konzolon [Nmm]

6.62. ábra - Megoszló erő a konzolon [N]

6.4. Mechatronikai példa: CD fej tartó rugók

Az alábbi példán egy CD-fej tartó rugók analízisét végezzük el gerenda modell (rugó szálak) és testmodell (mozgó fej) alkalmazásával. A valós szerkezetben a fej egy lencserendszert tartalmazó egység, melynek a függőleges (Y) és egyik irányú vízszintes (X) elmordulását elektromágneses tekercsekkel és megfelelően lágy rugórendszerrel kell biztosítani. Ennek egyik szokásos megoldása a fej 4 db. vékony rugószálra való felfüggesztése. A rendszer csillapítását rendszerint a szálak rögzítésénél elhelyezett nagy viszkozitású anyag biztosítja, de a statikai szimuláció szempontjából ez elhagyható. Jelen analízis feladata a rugóelemek erő-elmozdulás karakterisztikájának megállapítása, vagyis, hogy a gerjesztőtekercsek által kifejtett erő hatására mennyi lesz a fej elmozdulása.

A feladat megoldásához, először hozzuk létre a geometriát az ANSYS Design Modellerében . Első lépésben célszerű a fejet jelképező testmodell vázlatát létrehozni egy, a globális koordinátarendszer XY síkjával párhuzamos munkasíkon. Így a későbbiekben a vázlaton szereplő téglalap négy sarokpontját felhasználhatjuk referenciaként a rugószálakat jelentő vonalmodellek létrehozásakor. Ehhez tehát hozzunk létre egy új síkot párhuzamosan a globális koordinátarendszer XY síkjával, és 10mm-el eltolva a +Z irányban (New Plane) . Az újonnan létrehozott síkra rajzoljunk egy az origóra szimmetrikusan elhelyezett téglalapot, 8x4mm-es méretekkel. Majd hajtsuk végre a kihúzást 8mm hosszon (6.63. ábra).

A következő lépésben hozzunk létre konstrukciós pontokat a vonalelemek túlsó végénél, a globális koordináta rendszer XY síkján. A pontok elhelyezésére használjuk a Create/Point parancsot, és a Details panelen adjuk meg a pontok koordinátáit: Point1(4,2,0); Point1(-4,2,0); Point1(-4,-2,0); Point1(4,-2,0).

Ezután páronként kössük össze a konstrukciós pontokat a testmodell a vázlatának négy sarokpontját a Concept/Lines From Points paranccsal.

A már tanult módon hozzuk létre a vonalmodellek 0,1mm átmérőjű kör keresztmetszetét a Concept/Cross Section/Circular paranccsal és rendeljük hozzá az egyes vonalmodellekhez (Line Body) .

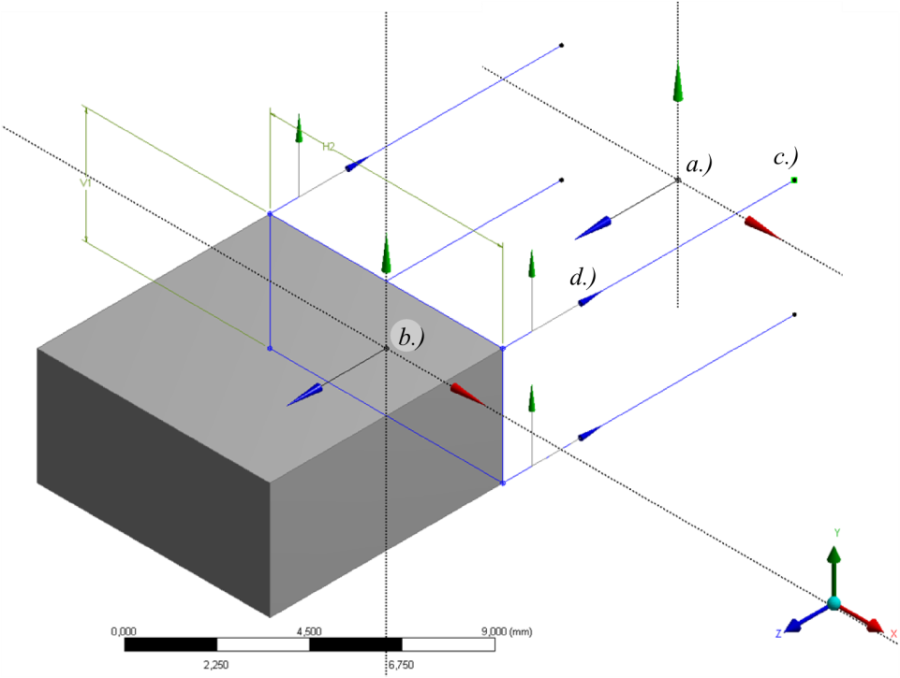
a.) Globális koordináta rendszer, b.) a testmodell vázlatának munkasíkja, d.) a vonalmodellek és a létrehozásukhoz használt c.) konstrukciós pontok

6.63. ábra - A CD-fej egyszerűsített geometriája.

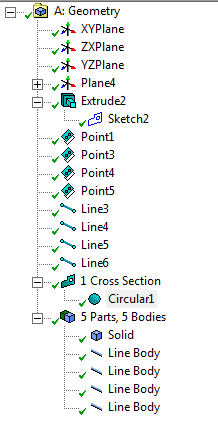
6.64. ábra - A modellfán szereplő elemek.

A fenti lépések elvégzése után a modellfa utolsó sora 5 elemet kell, hogy tartalmazzon, 1 testmodellt (Solid) és 4 vonalmodellt (Line Body), (6.64. ábra). Ha ez így jelenik meg, lépjünk ki a geometria modellezőből és szerkesszük az anyagmodelleket tartalmazó Engineering Data -t. Rendeljünk hozzá a szimulációnkhoz az ANSYS General Materials anyagkönyvtárából (jobb felső könyveket ábrázoló ikon bekapcsolásával), a Polyethylene, és a Cooper Alloy anyagokat. Ezután lépjünk át a szimulációs felületre és rendeljük hozzá az anyagmodelleket az egyes alkatrészekhez, Testmodell: Polyethylene, Vonalmodellek: Cooper Alloy.

Helyezzük el a megtámasztásokat (Fix Support) a vonalelemek szabad végeire és az –Y irányú 0,2N nagyságú erőterhelést (Force) a testmodell teljes térfogatára.

Mivel több testből áll a modellünk létre kell hozni a testmodell és a vonalmodellek közötti kapcsolatot. Ehhez a modellfa Connections pontjára való jobbgombos kattintással adjunk hozzá a modellhez 4 db. ponthegesztés nevű kapcsolatot (Outline/…/Connections(JG)/Insert/Spot Weld) , és mindegyiknél jelöljük ki a Details panelen a megfelelő pontpárokat. Az egymást elfedő elemek kijelölésénél segítséget jelent a modelltér bal alsó sarkában megjelenő lapok, a különböző alkatrészek színével. A lapokra való kattintással választhatjuk ki, hogy egy helyen lévő pontok közül, melyik legyen kijelölve.

Ezután futtassuk a szimulációt és kérdezzük le az alábbi eredményeket (6.65. ábra):

A fej Y irányú deformációja (Directional Deformation) ,
A teljes modell Y irányú deformációja (Directional Deformation) ,
A rúdban ébredő kombinált feszültség maximuma (Maximum Combined Stress) ,
A rúdban ébredő rúdirányú feszültség (Direct Stress) .

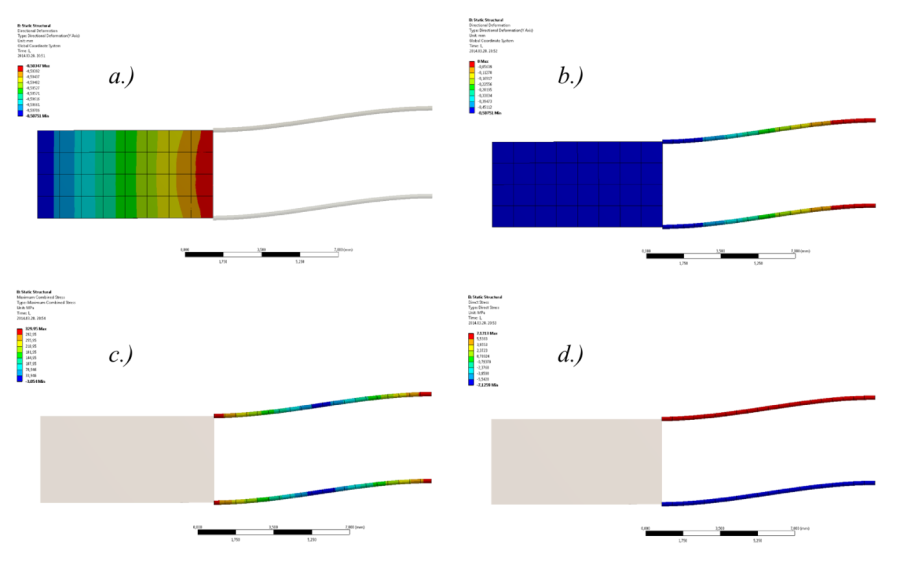
a.) a fej és, b.) a teljes modell Y irányú deformációja, c.) a rúdban ébredő kombinált feszültség maximuma, és d.) a rúdban ébredő rúdirányú feszültség

6.65. ábra - A CD-fej vizsgálatának eredményei.

Vissza		Előre
5. fejezet - Paraméter vizsgálatok, optimalizációs feladatok	Főoldal	7. fejezet - Több alkatrészes, statikai analízis

6. fejezet - A geometriai modellek egyszerűsítésének lehetőségei

6.1. Példa szimmetriafeltételek alkalmazására: belső nyomással terhelt cső

6.1.1. Analitikus megoldás

6.1.2. A feladat megoldása ¼ testmodell segítségével

6.1.3. A feladat megoldása negyed héjmodell segítségével

6.1.4. A feladat megoldása 2D-s sík alakváltozás (Plane Strain) típusú modellként

6.1.5. A feladat megoldása 2D-s tengelyszimmetrikus (Axisymmetric) típusú modellként

6.1.6. Összefoglalás

6.2. Példa egy oldalon befogott, hajlított tartó négyféle megoldására

6.2.1. A feladat megoldása 3D-s teljes testmodellel (3D body)

6.2.2. A feladat 3D-s megoldása felületmodell (shell) definiálásával

6.2.3. A probléma megoldása 2D-s feladatként

6.2.4. A feladat megoldása vonalmodell keresztmetszet definiálásával (gerenda elemmel)

6.2.5. Összefoglalás

6.3. Példa gerenda modell alkalmazására: Hegesztett rácsos szerkezet

6.4. Mechatronikai példa: CD fej tartó rugók

6.5. Ellenőrző feladatok

6.5.1. Feladat

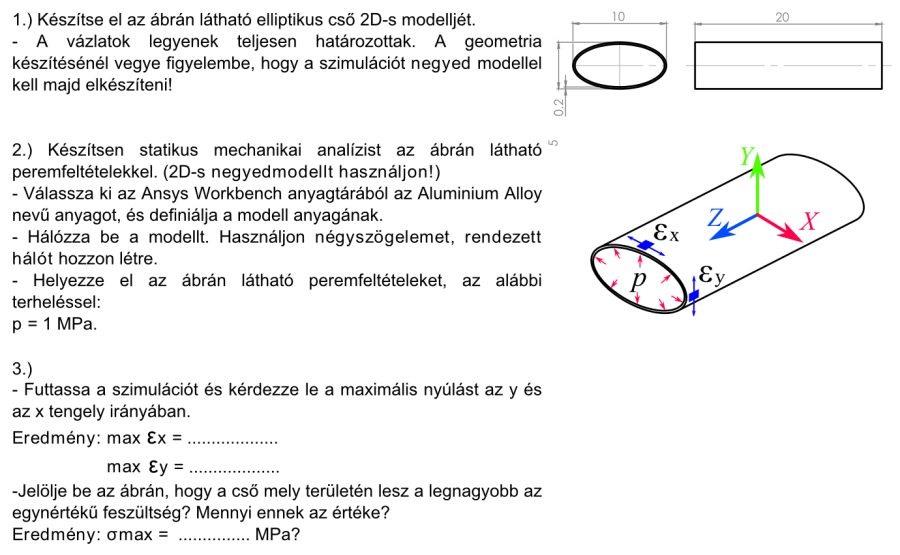
6.5.2. Feladat