5. fejezet - Paraméter vizsgálatok, optimalizációs feladatok

A következő példát ANSYS Workbench -ben oldjuk meg. A feladat egy statikai analízishez kapcsolódó szimuláción keresztül mutatja be a paraméterek beállítását és a geometriai optimalizációt. Mivel a korábbiakban a statikai analízis már bemutatásra került, így itt ezt a részt csak nagyvonalakban mutatjuk be.

Az optimalizáció előtt mindig el kell készíteni az alap analízist, csak utána lehet minden paramétert beállítani.

Elindítunk egy statikai analízist, majd létrehozzuk az új geometriát az ANSYS Worbench beépített Design Modeler moduljában.

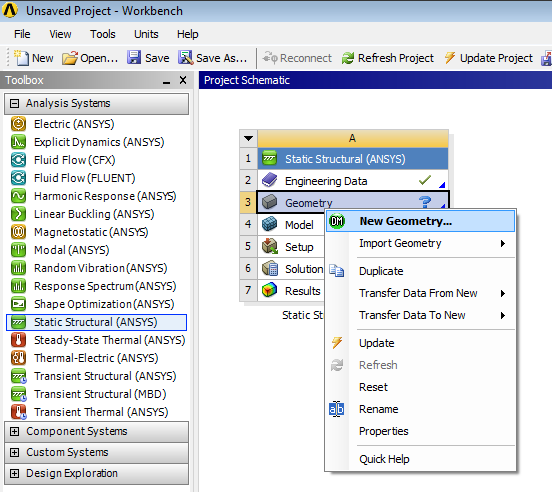
A geometria nagyságrendjének megfelelően, mm-t választunk szimuláció mértékegységeként, így elegendően kis numerikus hiba terheli a szimulációnkat.

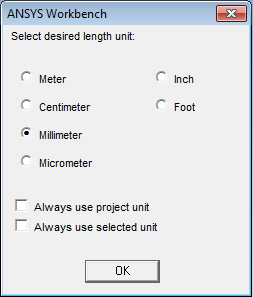
Ezután történik a geometriai modell megalkotása. Jelen esetben 3 dimenziós geometriát használunk. Létrehozzuk az XY síkon az első vázlatunkat, amelyre felrajzoljuk a geometria alapját.

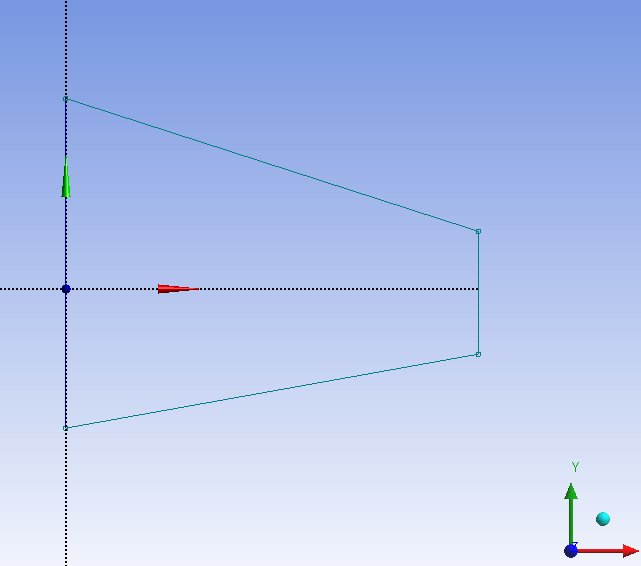
Általában célszerű a tengelyekhez kapcsolódóan elhelyezni a geometriát, mert így az alapsíkokkal dolgozhatunk, kevesebb esetleges plusz síkot, koordinátarendszert kell létrehozni. A vázlatokat célszerű mindig teljesen határozottá tenni. Ennek eléréséhez praktikus, ha minél több kényszert és minél kevesebb méretet használunk. Egy paraméteres modell esetén mindig érdemes előre átgondolni, hogy milyen paraméterekkel kell majd dolgoznunk és annak megfelelően felépíteni a geometriai modellt. Jelen esetben egy szimmetriakényszert definiálunk, a Sketching eszköztár Constrains al-menüjéből Symmetry kiválasztásával. ( ANSYS Workbench használatakor mindig először kell kiválasztani a szimmetria tengelyét, utána pedig a szimmetrikus rajzi elemeket, erre a sorrendre a parancssorban is tájékoztatást kapunk.)

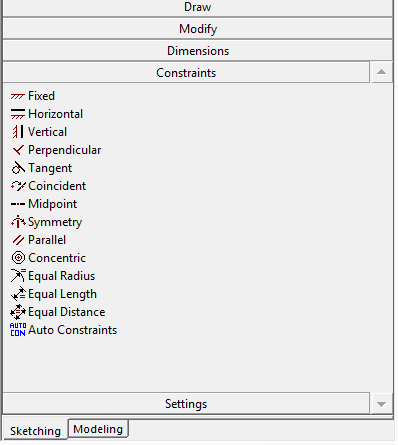
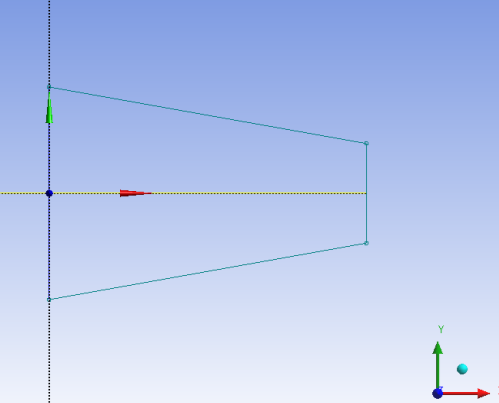
Így kialakul a már kényszerekkel ellátott körvonal. (Szerencsésebb először a geometriai kényszereket megadni és csak utána a méreteket.)

Ezután annyi méret megadása szükséges, amennyi teljesen határozottá teszi a körvonalat.

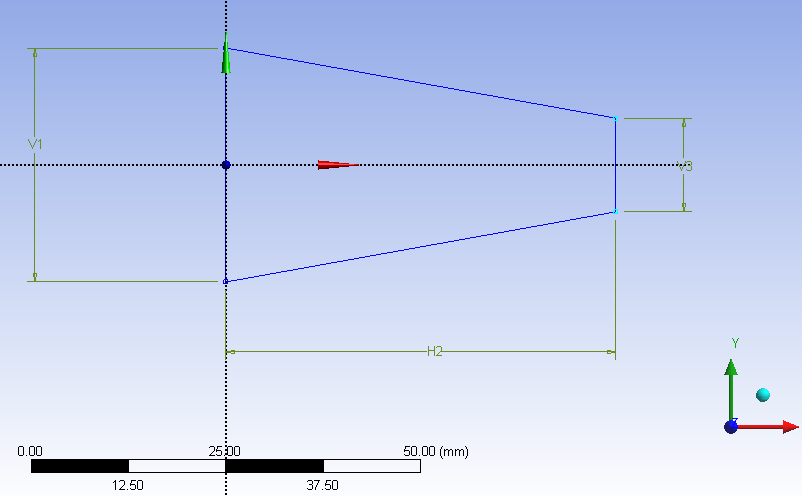
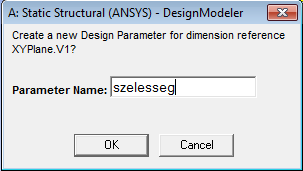
A méretek elhelyezése után következik a méretek beállítása konkrét értékre, majd ezek paraméterré alakítása a Details panelen (5.7. ábra). A méret neve melletti kis fehér négyzetre kattintva (bal gombbal) lehet paraméterré tenni az adott méretet. Ilyenkor egy kék színű D betű kerül az üres négyzetbe. Ekkor megjelenik egy párbeszédablak, amelybe a paraméter nevét kell megadni (mint általában, most is kerüljük az ékezetes karakterek használatát). Amennyiben a későbbiekben szeretnénk a méretet kivenni a paraméter készletből egyszerűen újra rákattintva az immár D betűt tartalmazó négyzetre újra üressé válik és a méret kikerül a paraméterek közül.

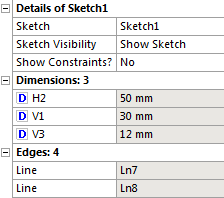
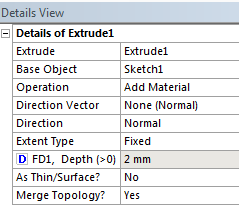
Ezután a vázlatot az kihúzás (Extrude) paranccsal 3 dimenziós testté alakítjuk (korábbi példából már ismert módon). Látható, hogy az alaksajátosságokat létrehozó parancsoknál is megtalálható az üres négyzet a méret (jelen esetben a kihúzás mértéke) előtt, így azt is paraméterként definiálhatjuk (5.9. ábra). Minden teljesen ugyanúgy működik, mint a vázlatban meghatározott paramétereknél.

Az alaptest létrehozása után felrajzoljuk az első furathoz tartozó vázlatot, majd kényszerek és méretek megadásával teljesen határozottá teszünk, majd szintén az kihúzás (Extrude) parancs segítségével kivágjuk a furatot. Ilyenkor a kivágás műveletet kell választani (Details View/Operation/Cut Material) , (5.10. ábra).

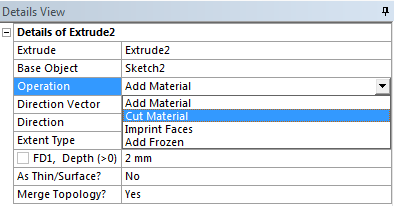
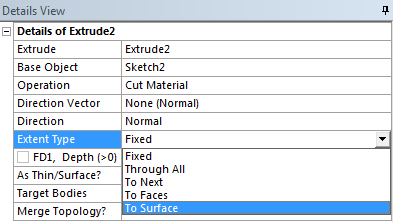
Amennyiben előre tudjuk, hogy a test vastagsága változni fog különösen fontos, hogy a kihúzás mélysége (Extent Type) lehetőségek közül olyat válasszunk, amely a megváltozott vastagság esetén is ugyanolyan alaksajátosságot hoz létre. (Ha itt figyelmetlenségből a 2 mm-es alapértelmezett távolságot nem módosítjuk, akkor a vastagság növekedésével nem átmenő furat alakul ki.) Ezért most ezt átállítjuk a felületig (To Surface) opcióra (5.11. ábra).

Végfelületnek (Target Face) , (5.12. ábra) a test vázlattal ellentétes oldalát határozzuk meg (5.13. ábra).

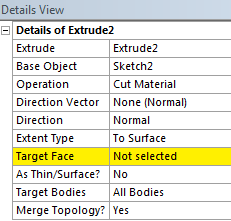
A kiválasztást az elfogadás (Apply) gombbal véglegesítjük. Ha véglegesítésre kerül egy kiválasztott felület, akkor az felveszi a tulajdonságának megfelelő színt a zöld helyett. (Jelen esetben türkiz színűvé válik, 5.13. ábra)

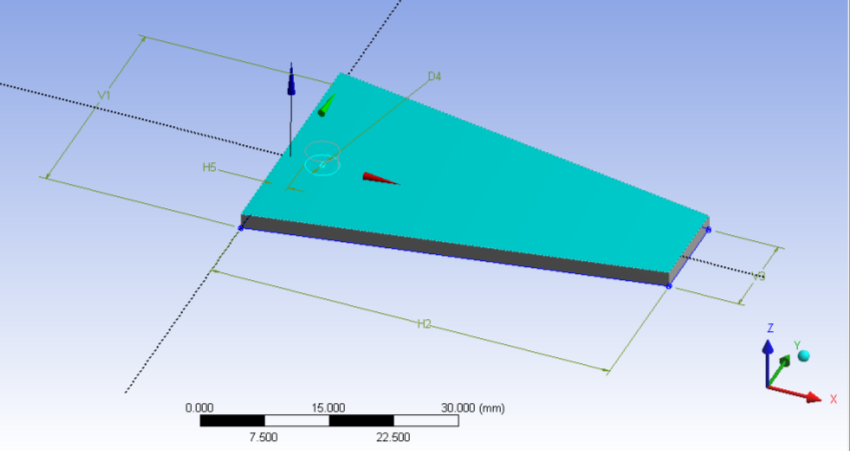
A szokásos létrehoz (Generate) gombbal elvégeztetjük a parancsot. Immár kialakult az egy furattal rendelkező test (5.14. ábra).

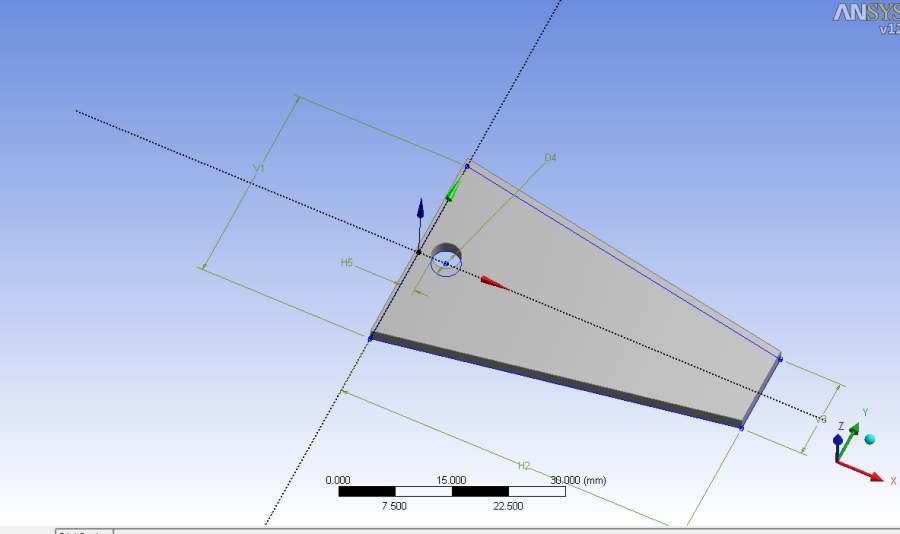
Ezután történik a furatok kiosztása. Optimalizációtól függetlenül is érdemes kiosztással létrehozni az ismétlődő alaksajátosságokat, de ilyenkor különösen is praktikus, mert diszkrét paraméterként beállítható a furatok száma is. (Diszkrét paraméternek nevezzük azokat a változókat, amelyek csak egész számokat vehetnek fel értékként.) Kiosztást a létrehozás (Create) menüpont kiosztás (Pattern) parancsával tudunk készíteni (5.15. ábra). Megvalósítható testek, felületek és akár vonal elemek kiosztása is. Amennyiben például egy furatot szeretnénk kiosztani, akkor a furat belső felületét kell kiválasztani, mint kiosztandó geometria (ebben az esetben, a felső ikonsorban a kiválasztás szűrőjét át kell állítani a felületkijelölés (Face) opcióra).

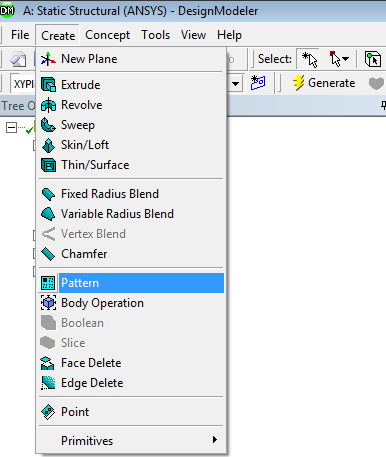
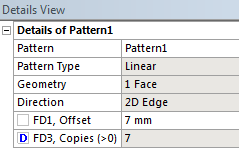
A kiosztás részleteit tartalmazó Details panelen be kell állítani a kiosztás típusát (jelen esetben linear, tehát vonal menti egyenes kiosztásról van szó), az egyes elemek közötti távolságot, és az elemek számát. Mint látjuk akár az elemek száma, akár a köztük lévő távolság paraméternek választható. Fontos tudni, hogy a későbbiekben, az optimalizáció során az ANSYS Workbench -ben át kell állítani az elemszám paramétert diszkrét változóvá, mert alapesetben, ha folyamatos változóként van definiálva az automatikus méretváltozás során akár nem egész értéket is felvehet.

Amennyiben a geometria elkészült, a projekt ablakban megjelenik a paraméter készlet (Parameter Set) . A szövegdobozból kifelé mutató nyíl jelzi, hogy egyelőre csak bemenő paramétereket tartalmaz a véges elemes projektünk (5.17. ábra). Amennyiben a szimulációt lefuttatjuk és kimenő paramétert is meghatározunk, itt megjelenik egy, az eredményekből a paraméter készletbe mutató nyíl is.

Ezután következik a statikai analízis beállítása és az alap szimuláció lefuttatása. (A beállítások csak szükséges mértékben lesznek ismertetve.)

A geometria anyagtulajdonságát jelen esetben nem módosítjuk, szerkezeti acél anyagot használunk.

Az alapértelmezett háló (Mesh) túlságosan nagy elemekből áll, a geometria legkeskenyebb részén csak 1 sor elem található, ezért a hálóméretezés (Sizing) eszközzel beállíthatunk egy sűrűbb, tehát kisebb elemekből álló hálót (5.19. ábra).

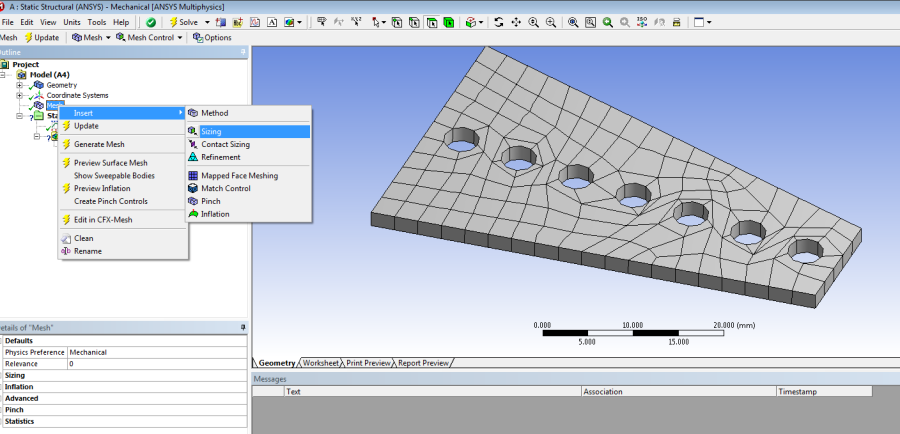
A háló elemméretét 1mm-re állítsuk, így már biztosan több sor elem lesz a legkisebb vastagságnál.

A hálósűrítés felületének a test felső lapját határozzuk meg (5.20. ábra).

Külön lépés helyett a mesh (háló) details ablakában is be lehet állítani a háló elemeinek méretét.

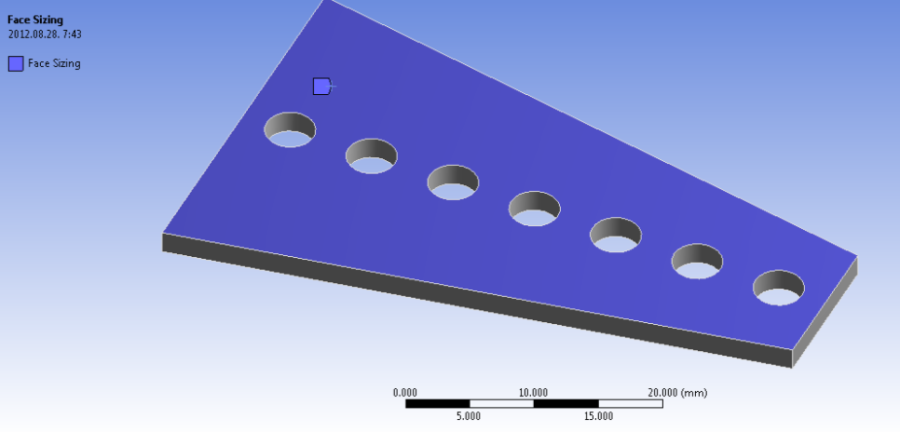
Az 1mm-es háló már elégségesnek mondható, az elemek rendezettek (5.21. ábra).

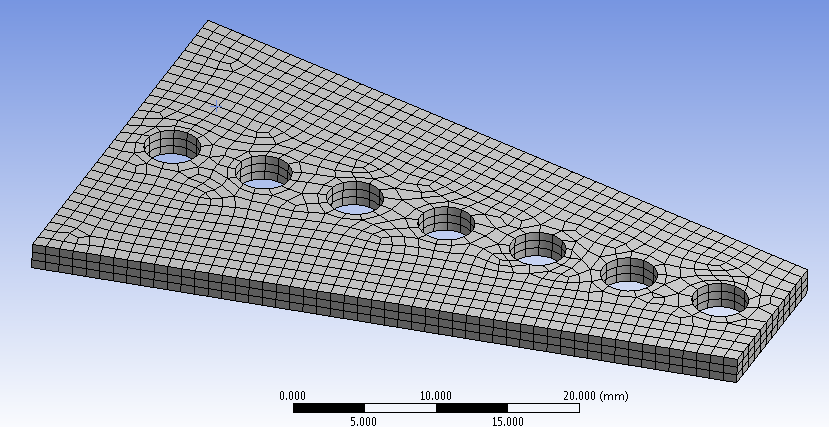
Ha a hálóval elkészültünk beállítjuk a terheléseket és megfogásokat. Jelen esetben fix befogás (Fixed Support) típusú befogást definiálunk a test szélesebb végére (5.22. ábra).

A testre hat egy erőterhelés (Force) a megfogással ellentétes, rövidebb oldalon. Ennek nagysága alap esetben 50N, mely a globális -Z irányba mutat. Amennyiben a globális koordináta rendszer segítségével nem tudjuk megadni az erő hatásvonalát, akkor vektorosan is lehet definiálni, ehhez felhasználható bármilyen más koordináta rendszer tengelye, valamint a geometriához kapcsolódó élek bármelyike, vagy egy külön erre a célra létrehozott vonal elem.

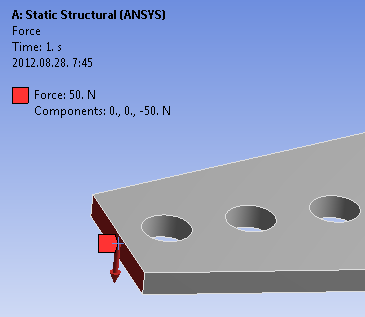
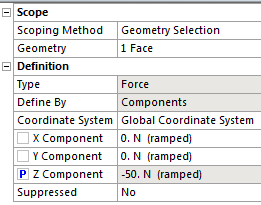
Ahogy itt is látjuk, az erőértékek előtt megjelenik az üres négyzet, amely jelzi, hogy paraméterként definiálhatók. Ezt meg is tesszük, ami változás a geometriai paraméterekkel szemben, hogy itt már nem lehet nevet adni a paraméternek, hanem az előre definiált nevet kapja, amely egyértelműen definiálja az adott terhelés komponenst.

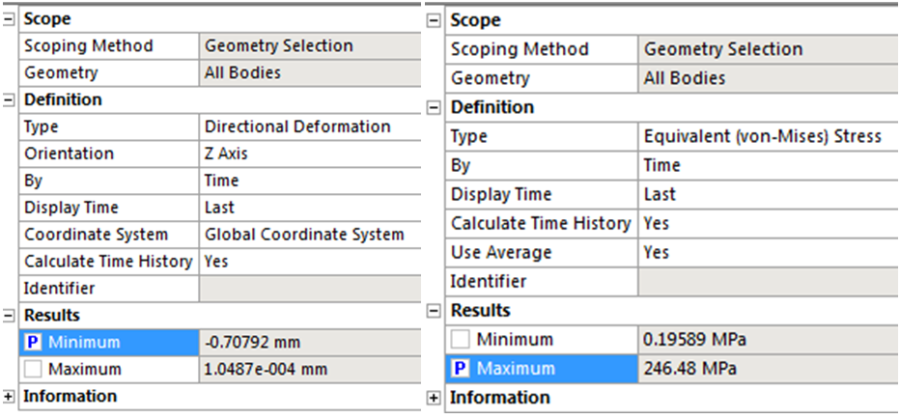
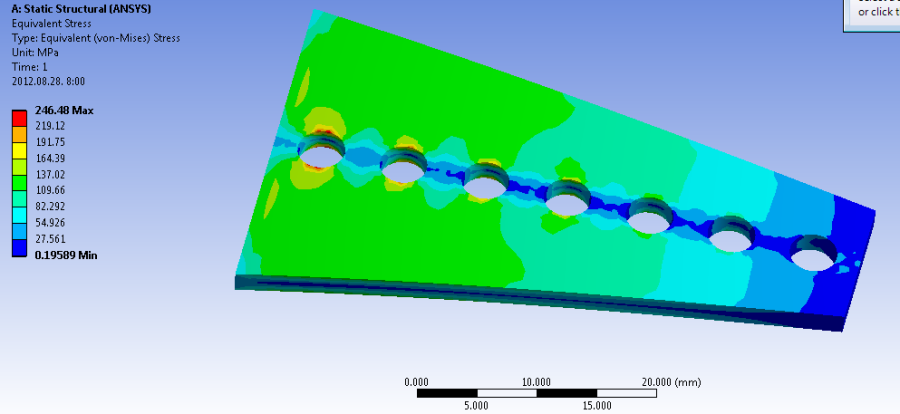
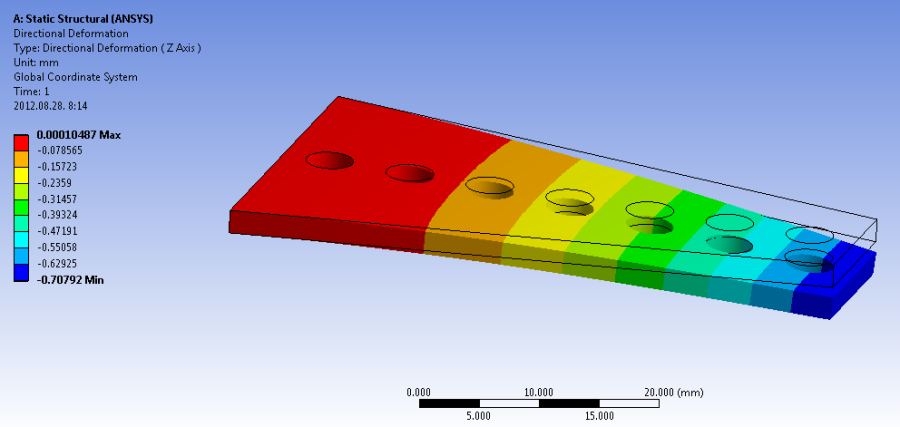
Érdemes előre meghatározni, hogy a rendszernek milyen típusú válaszára, vagyunk kíváncsiak, természetesen itt már érdemes olyan végeredményt is lekérdezni, amire optimalizálni szeretnénk. A modellfa megoldás (Outline/…/Static…/Solution) pontjában kiválasztjuk a teljes deformáció (Total Deformation) , egyenértékű feszültség (Equivalent von Mises Srtess) és az irány menti deformáció (Dierctional Deformation) opciókat. Fontos, hogy az irány menti deformációnál azt az irányt válasszuk ki, amely releváns a szimulációnk szempontjából, jelen esetben a Z irányt (Z axis) válasszuk ki. Már most is láthatjuk a Details ablakban, az eredmények (Results) felületen a paraméterek definiáláshoz szükséges jelölő négyzetet. Akár már most meg lehet adni, hogy mely eredményeket tesszük paraméterré, de ezt a szimuláció után is megtehetjük.

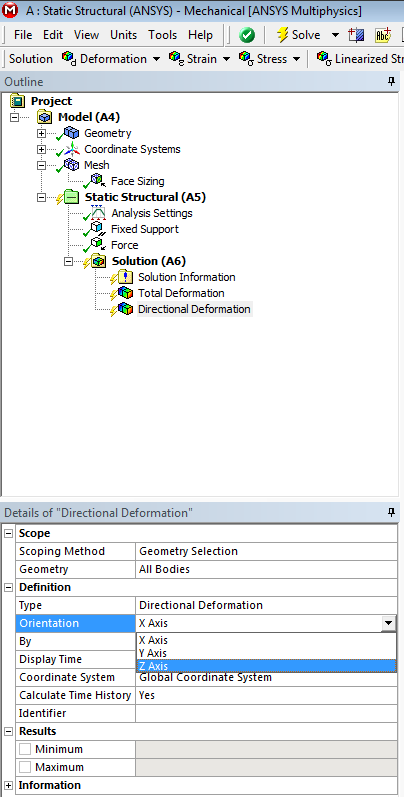
Futtassuk a szimulációt, majd az adott eredményképre kattintva kiválasszuk ki, hogy mely eredménytípusokat definiáljuk paraméternek. Ahogy a terhelésnél is, itt sem lehetséges a paraméter nevének változtatása. Jelen esetben a Z irányú deformáció minimumát és az egyenértékű feszültség maximumát választjuk paraméternek. Előbbinél figyelni kell, hogy mivel a terhelés –Z irányba hat, a tulajdonképpeni maximális deformáció az irány menti deformáció előjeles eredményének minimális értékeként kapjuk.

A futtatás után, nézzük meg az eredményeket, itt még észre lehet venni esetleges hibákat, ha valami nem az előzetes várakozásnak megfelelően viselkedik érdemes ellenőrizni a beállításokat, anyagmodelleket.

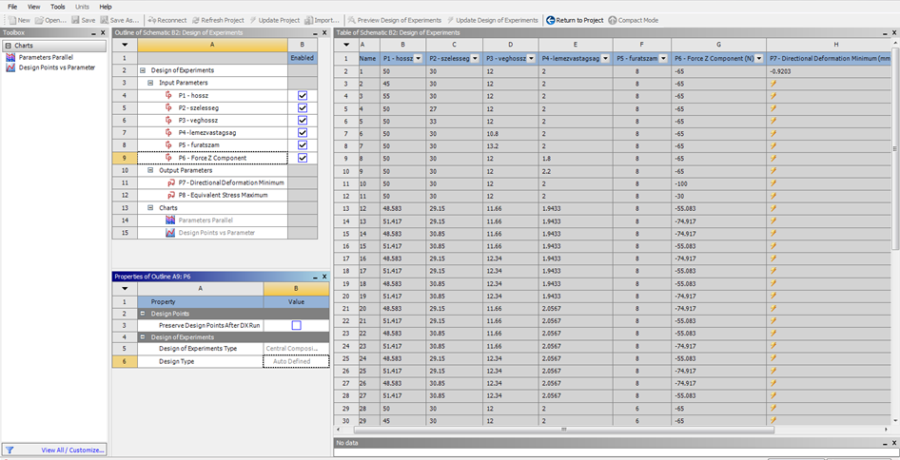
Ha a szimuláció lefutott és a kimenő paraméterek is definiálásra kerültek elkezdődhet a tulajdonképpeni paramétervizsgálat és optimalizáció. A projektablakban a Design Exploration menü alpontjaiból lehet választani a kívánt feladatot, melyet a paraméterkészlet (Parameter Set) alá kell behúzni a projektünkbe. Ebben a példában válasszuk a célértékre optimalizálás (Goal Driven Optimization) lehetőséget (5.29. ábra), amely magában foglalja a válasz felület (Response Surface) menüpontot is, ezeket csak egymás után lehet elvégezni, ahogy látszik is a projektünkben (5.30. ábra).

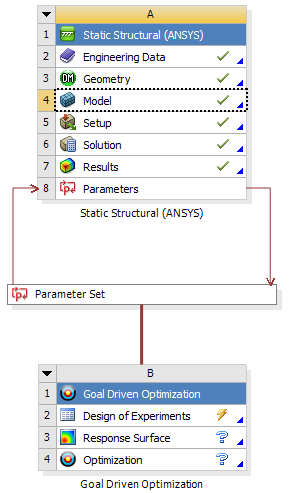
Itt is célszerű felülről lefelé haladni a menüpontok között. Első lépésként a design konfigurációk (Design of Experiments) menüpontban be kell állítani az összes változó típusát és szélső értékeit (azt az értéktartományt, amelyet felvehet a megoldás során).

A szokásos jobb kattintással tudjuk módosítani a paramétereket. Több táblázat segítségével lehet mindent beállítani ezen az egyetlen képernyőn.

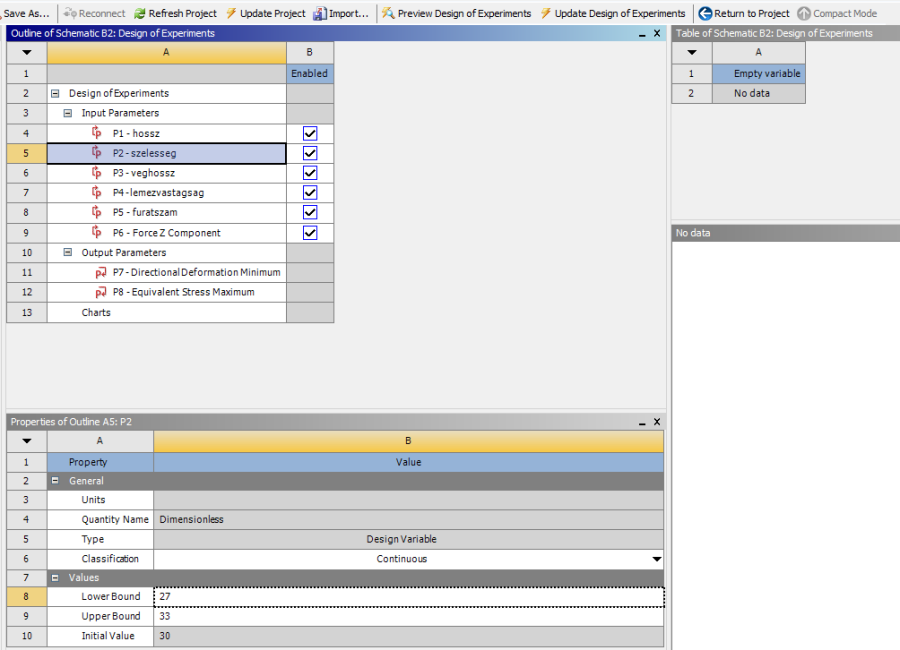
Látjuk, hogy az összes paraméter fel van sorolva a bal felső táblázatban. Ezeknek „P” előtagos sorszámozása van, a sorszám mellett van a paraméter neve. A bemenő paraméterekből nem muszáj mindegyiket használni, az engedélyezett (Enabled) oszlopban a pipák ki illetve bekapcsolásával lehet elhanyagolt, vagy aktív paraméterekké változtatni. Alapesetben minden paraméter aktív. Amennyiben egy paramétert kiveszünk az aktívak köréből, az alapértéken marad, a szimuláció további részében nem változik. A bal felső táblázatban kijelölt paraméter értékeit az alatta lévő táblázatban lehet beállítani. Itt be lehet állítani a paraméter típusát (Classification) és értékét. Alapbeállításként mindegyik folytonos (Continous) típusú változó.

A következő típusokból lehet választani:

Ha folyamatos típusút választunk, akkor meg kell adni a paraméter értéktartományának alsó- és felső határát (Lower és Upper Limit) . Alapbeállításként ez ±10%-os eltérésű az alapértékhez képest, amely tájékoztatásként szerepel a táblázatban, de ennek a mértéke nem módosítható. A határokat tetszőlegesen lehet változtatni (természetesen addig a határig, amíg a geometria fel tud épülni mindegyik paraméter-érték kombinációban.

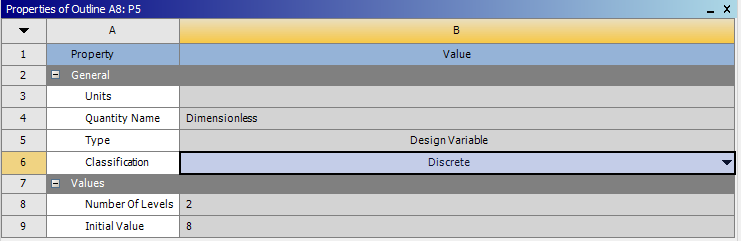
Ha mindegyik paramétert beállítottunk a kívánt típusra és a kívánt értéktartományokra, elkezdődhet az optimalizáció folyamata. Ekkor az Update of Design Experiments gombra kattintva a szoftver a paraméterek változtatásaival elkészíti azokat a design kombinációkat, amelyekre elvégzi az alap szimulációt. Ez táblázatos formában megjelenik a képernyőn és a jobb szélső oszlopba folyamatosan jelennek meg az adott sorhoz tartozó megoldott kimenő paraméterértékek.

Ha lefutott a szimuláció az összes design konfigurációra (Design Points) , akkor a Response Surface -re továbblépve (5.35. ábra), lehet megtekinteni a bemenő paraméterek hatását a kimenő paraméterekre. Ehhez az eredmények frissítése szükséges (amit a projekt ablakban megjelenő jellegzetes két zöld körkörös nyíl ikon jelez), amit az Update Response Surface gomb segítségével érünk el (5.36. ábra). Ekkor megtekinthetővé válnak az előbbi számítások eredményei (5.37. ábra).

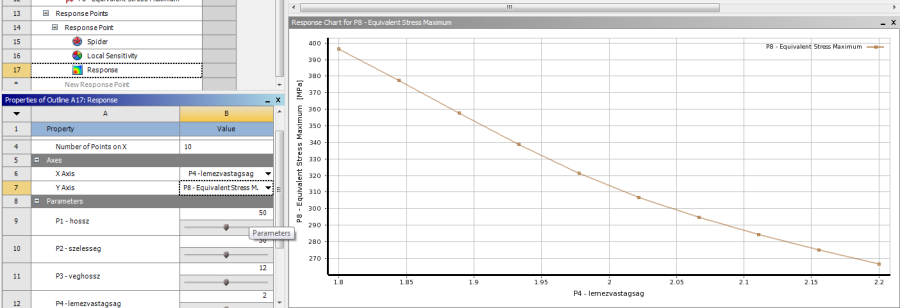
Az eredmények legtipikusabb megjelenítési formája a 2D-s diagram, melyhez ki kell választani a két paramétert, melyek közötti összefüggést meg szeretnénk tudni. Természetesen az egyik bemenő, a másik pedig kimenő paraméter. Ezeket a diagram x és y tengelyére is el lehet helyezni, tetszőleges kombinációban.

A többi paraméter értéke természetesen ebben az esetben konstans, értékét a paraméter melletti csúszkával lehet beállítani. Alapesetben a középértéknél helyezkedik el. Ha a grafikon típusa megkívánja, akkor lehet növelni a grafikonon megjelenő pontok számát (Number of Pionts on X).

Amennyiben egyszerre 3 paraméter közti összefüggést szeretnénk ábrázolni a megjelenítési mód (Mode) menüpontban lehet váltani a 2D-s megjelenítésről 3D-s ábrázolásra.

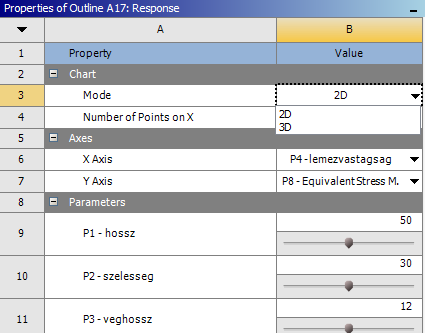
Ebben az esetben az x, y és z tengelyek változói is kiválaszthatóak, értelem szerint legalább egy kimenő és legalább egy bemenő paraméternek kell lennie.

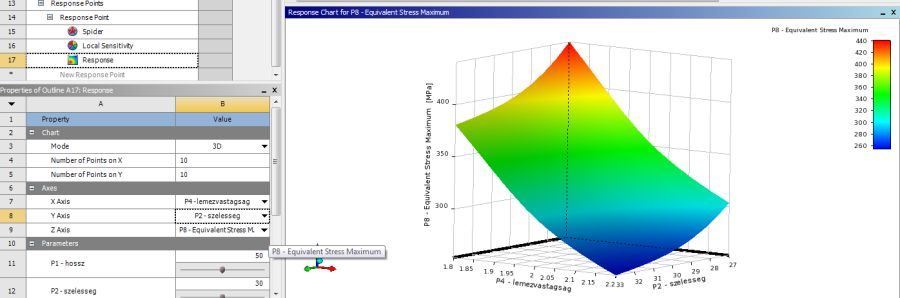
A 3 dimenziós grafikon az egér bal gombját lenyomva tartva forgatható, és az egér görgetőjével közelíthető és távolítható, így a leginformatívabb oldaláról nézhető. Ha kellőképpen áttekintettük a paraméterek közti összefüggéseket, akkor elkezdhetjük a célértékre való optimalizálást. Ehhez az optimalizáció (Optimization) almenüt kell kiválasztani (5.40. ábra).

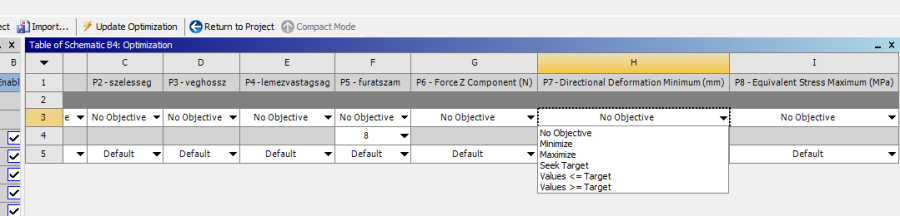
Az ekkor megjelenő táblázatban az egyes paraméterekkel szemben támasztott kívánalmakat állíthatjuk be (5.41. ábra).

A következő lehetőségek közül választhatunk:

Ha olyan célt határozunk meg, amelyhez tartozik célérték, akkor ennek értékét a 4. sorban kell megadni. Természetesen bizonyos szintig lehet súlyozni a célok fontosságát, ezt alapértelmezett (Default) , alacsony fontosságú (Lower) és fontos (higher) lehet. Érdemes egyszerre csak 1-2 paraméterre optimalizálni. Ha a beállítások megtörténtek az Update Optimization gomb megnyomásával lehet a célértéknek megfelelő konfigurációkat keresni. Ilyenkor csak abban a paraméter tartományban keres megoldást a szoftver, amelyet előzetesen beállítottunk a Design of Experiments táblázatban. Amennyiben más tartományban is szeretnénk megoldást keresni, vagy egy-egy paraméter tartományát szeretnénk kibővíteni újra definiálni kell ezeket az értéktartományokat.

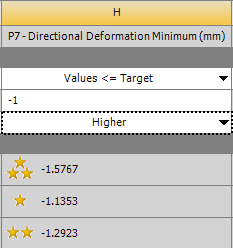
Ha olyan kívánatos célt határoztunk meg, amelyre van megoldás az előzetesen lefutott konfigurációk között, akkor csillagokkal jelölve megjelenik 3 lehetséges verzió, melyek közül a 3 csillagos a leginkább közelíti a célértéket, az 1 csillagos a legkevésbé a felkínáltak közül. Amennyiben nincs olyan megoldás az előzetesen számoltak között, amely megfelelne a kívánt célnak, akkor csillagok helyett piros x-ek jelzik, hogy a talált (a célt leginkább megközelítő) konfigurációk valójában nem felelnek meg az elvárt követelményeknek. Ilyenkor a paraméterek tartományát módosítani kell és újra futtatni a szimulációs folyamatot.