4. fejezet - Nemlineáris statikai analízis
A valós szerkezetek viselkedése általában eltér a lineáristól. Sok esetben a lineáris szimuláció jó közelítést adhat a probléma megoldására, de számos esetben hibás eredményre vezet, mivel az alapjául szolgáló feltételezések már nem helytállóak. A nemlineáris szimuláció megoldása több terhelési lépésben történik. A konvergencia elérése érdekében, az egyes lépéseket a program iterálva oldja meg, ezért a nemlineáris feladatok sokkal idő és számításigényesebbek, mint a lineáris.
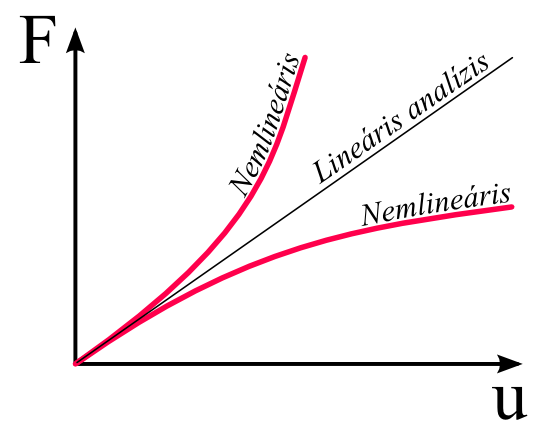
4.1. A nemlinearitás okai
A nemlineáris viselkedést okozhatja az anyagi viselkedés, a nagy deformáció, vagy a nemlineáris terhelési, vagy peremfeltételek, ill. kontaktok.
4.1.1. Anyagi nemlinearitás
A nemlinearitás egyik alapvető oka a nemlineáris anyagi viselkedés. Jellemzője, hogy a feszültség és fajlagos nyúlás közötti kapcsolat nem lineáris, tehát az analízis során az anyag merevsége változik (nem érvényes rá a Hooke törvény). Nemlineáris feszültség-alakváltozás tulajdonsággal rendelkező plasztikus (plastic), multilineáris rugalmas (multilinear elastic), és a nagyrugalmas (hyperelastic) anyagmodellek a szerkezet különböző merevségét eredményezik a különböző terhelési szinteken (és hőmérsékleteken). A kúszás (Creep), viszkoplasztikus (viscoplasticity), és viszkoelasztikus (viscoelasticity) anyagmodellek nemlinearitása lehet idő, sebesség, hőmérséklet-, és a feszültség szerinti.
4.1.2. Geometrriai nemlinearitások, nagy deformációk
A végeselemes analízisekben jelentkező nemlinearitások egyik fő oka az egész szerkezetre jellemző nagy elmozdulások, amelyek egyben a terhelési konfiguráció megváltozását is jelentik, (Például egy vékony, egyik oldalán befogott rúdra ható erő és a rúd tengelye által bezárt szög a rúd nagymértékű lehajlásával jelentősen megváltozik).
Nagy deformációk esetén a terhelés hatására létrejövő merevségváltozás már nem elhanyagolható, (Például egy kábel-szerkezetet terhelő húzóerő a merevség növekedését okozza, míg egy kupola, vagy boltív szerű szerkezet terhelés hatására történő átpattanásakor (snap-through) először lágyítja, aztán merevíti a szerkezetet). A nemlineáris szimuláció során lehetőségünk van nagy alakváltozások (Large Deflections) számolására. Ilyenkor a szoftver újraszámolja a modell merevségi mátrixát minden lépés során.
4.1.3. A terhelési állapot megváltozása, nemlineáris kontaktok
Nemlineáris viselkedést okoz a vizsgált szerkezet státuszának / terhelési állapotának megváltozása a szimuláció alatt. Ennek okai a szerkezet és a terhelés együttes viselkedésében keresendő. Ilyen viselkedést mutat pl. egy megfeszített kötél, amely meglazul; két felület, amelyik egyszer érintkezik máskor nem.
Tehát a nemlineáris viselkedés egyik gyakori forrása a nemlineáris viselkedésű kontaktok. A ragasztott (Bonded) kivételével a kapcsolódó felületek elmozdulhatnak egymáson, ezért az átadódó terhelés lépésenként változó. A nemlineáris szimulációban a program lépésenként frissíti az átadott terhelés mértékét, eloszlását és irányát.
4.2. A nemlineáris feladat megoldása
Newton-Raphson közelítés az alkalmazott terhelés felosztásával és több lépésben történő közelítésével oldja meg a nemlineáris feladatot. Minden megoldás előtt a program megbecsül egy az egyensúlyi helyzetből kitérítő (out-of-balance) terhelési vektort, ami az elemfeszültségeknek megfelelő visszaható (restoring,) terhelés és az alkalmazott terhelés különbsége. Ezután a program futtat egy lineáris megoldást az out-of-balance terhelési vektor felhasználásával és vizsgálja a konvergenciát. Ha nem teljesítette a konvergencia kritériumot, akkor az out-of-balance terhelési vektort újra megbecsüli, a merevségi mátrixot frissíti, és újra futtatja a számolást. Ezen lépéseket addig futtatja, amíg nem konvergál a szimuláció. Különböző eszközök léteznek a konvergencia elősegítése érdekében úgy, mint az él keresés (line search), a terhelések automatikus felosztása (automatic load stepping), kettéosztás (bisection).
Amennyiben a számolás nem konvergál, a terhelési lépések csökkentésével lehet elősegíteni a megoldást.
-
A terhelési lépéseket (load steps) a felhasználó állítja be közvetlenül.
-
Ezek feloszthatóak al-lépésekre (substeps / time steps), mely történhet automatikusan, vagy manuálisan.
-
A konvergencia elérése érdekében, minden al-lépésben számos egyensúlyi iteráció (equilibrium iterations) fut le.
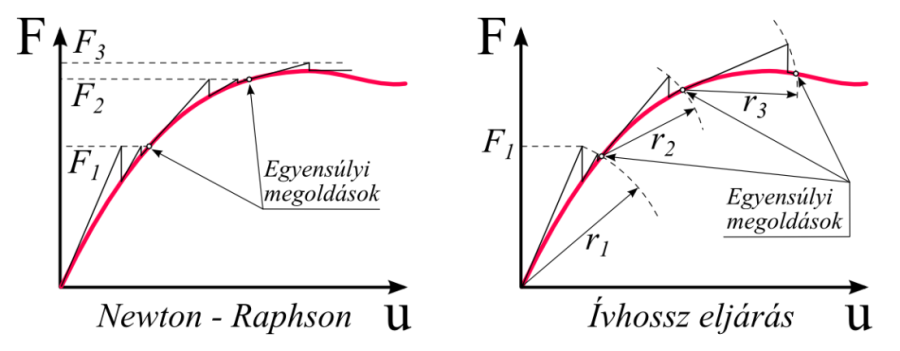
Egyes esetekben a Newton-Raphson egyedüli alkalmazása nem vezet eredményre a szingulárissá váló érintő merevségi mátrix (tangent stiffness matrix) miatt. Olyan esetekben következhet ez be, amikor például a szerkezet instabil lesz és átbillen (snap-through) egy másik egyensúlyi helyzetbe, pl. nemlineáris kihajlás vizsgálatkor. Ilyen esetekben célszerű az Ívhossz (arc-length) eljárás kiegészítő alkalmazása. Az ívhossz eljárás a Newton-Raphson egyensúlyi iteráció konvergenciáját eredményezi egy ív mentén, azáltal, hogy megakadályozza a divergenciát olyan esetekben, amikor a terhelés-deformáció görbe meredeksége nulla illetve negatív értékűvé válik (4.2. ábra) [45.] , [6.] .
4.2.1. Alkalmazható anyagmodellek
A nemlineáris mechanikai anyagmodell merevségét a feszültség-nyúlás karakterisztikájával, vagy a származtatott paramétereivel definiáljuk (pl.: hiperelasztikus anyagállandók, multilineáris karakterisztika, stb.). Időben állandó inerciális terhelések alkalmazása esetén a sűrűség definiálása is szükséges.
A nemlineáris anyagmodellek tartalmazhatnak plaszticitás (plasticity), felkeményedő (stress stiffening), nagy alakváltozás (large deflection / large strain), nagyrugalmas (hyperelasticity), és kúszás (creep), stb. viselkedésű elemeket.
4.2.2. Alkatrész viselkedés
A lineáris statikai analízishez hasonló viselkedésű alkatrészek alkalmazhatóak. Amennyiben a modell nemlinearitásokat tartalmaz, (pl. karcsú szerkezetek nagy lehajlása, instabil viselkedése, vagy hiperelasztikus anyagmodell, stb.) a számolási idő jelentősen megnövekedhet az iteratív procedúrának köszönhetően. Ilyen esetén célszerű egyszerűsítéseket alkalmazni, mint pl. a szimmetria feltételek, 2d-s, vagy héjmodell.
4.2.3. Hálózás
A lineáris statikai analízisnél alkalmazott szempontok, továbbá a nemlineáris viselkedéssel gyakran együtt járó nagy alakváltozások figyelembevétele szükséges a háló elkészítésénél. Nemlineáris vizsgálatok esetén a hálónak követnie kell az adott szimuláció tulajdonságait, megfelelően finom háló szükséges például a nagy plasztikus alakváltozást szenvedő területeken.
4.2.4. A szimuláció beállításai
-
Nagy lehajlások (Large Deflection) bekapcsolása szükséges, ha egy karcsú szerkezet lehajlása meghaladja a vastagsága 10%-át, hiperelasztikus anyagmodell alkalmazásakor, vagy ha instabil viselkedést (pl. kihajlást) várunk. (Kis elmozdulást akkor feltételezhetünk, ha a fajlagos nyúlás elég kicsi ahhoz, hogy az eredő merevség ne változzon jelentősen.) A nagy elmozdulások opció bekapcsolásával a merevség az elemek alakjával és orientációjával változik, ami pontosabb eredményhez vezet. A nagy lehajlások alkalmazásával a számolás iteratívvá válik, ami növelheti a számolási időt.
-
Időlépések – a szimuláció nemlineáris megoldása szükségessé teheti az időlépések alkalmazását, vagyis a terhelés kis lépésenkénti növelését. Több lépésre akkor is szükség lehet, ha lépésenként különböző terhelési állapotot akarunk beállítani, pl. előfeszítés beállítása, elmozdulás kényszer bekapcsolása / kikapcsolása, stb. (Részletesebben lásd a 2. fejezet fejezet ide vonatkozó részét.)
-
A kimenet beállításával (Output Controls) határozhatjuk meg a mentésre szánt lépéseket, mivel egy nemlineáris szimuláció sok olyan lépést tartalmazhat, amelyre nem, vagyunk kíváncsiak és fölöslegesen növelik a tárolandó adatok mennyiségét.
-
Nemlineáris beállítások
-
Nemlineáris kontrollokkal (Nonlinear Controls) módosíthatjuk a konvergencia kritériumokat. Az adott al-lépésekben lefutó egyensúlyi iterációk akkor sikeresek, ha az out-of-balance terhelés egy meghatározott konvergencia kritérium értéke alá csökken.
-
Vonalkeresés (line search) – hatásos, de energiaigényes megoldás a konvergencia elérése érdekében. Alkalmazása erő jellegű terhelések, karcsú szerkezetek alkalmazása, vagy oszcilláló konvergencia minta esetén ajánlott.
-
Stabilizáció (Stabilization) – Kis erők hatására fellépő nagy deformáció instabilitást okozhat, amelyet a csomópontokhoz rendelt mesterséges csillapításokkal tudunk stabilizálni. A csillapítás értékét megadhatjuk a csillapítási fokkal (damping factor), vagy a disszipált energia aránya (energy dissipation ratio, 0-1), melyek lehetnek konstansok (Constant), vagy csökkenő (Reduce, lineárisan 0-ra csökken) értékűek.
-
4.2.5. Peremfeltételek / Peremfeltételek / Eredmények
A lineáris statikai analízisben alkalmazható terhelések és peremfeltételek érvényesek, valamint az eredmények lekérdezésének és kiértékelésének módja is hasonló.
4.3. Mintafeladat instabil terhelési állapotra
Az alábbi példában egy lineáris anyagmodellel definiált alkatrész terhelés hatására létrejövő nemlineáris viselkedését fogjuk bemutatni. A szerkezeti instabilitás egyik gyakran emlegetett esete a boltozatszerű geometriák átpattanása (snap-through). Egy ilyen boltozatos héjszerkezet domború felületét terhelő nyomás hatására bekövetkező átpattanását vizsgáljuk meg.
Kiinduló adatok:
Átmérő: D=20mm,
Magasság: H=3mm,
Vastagság: t=0,1mm,
Anyag: Acél: E=200GPa, v=0,3,
Terhelő nyomás: p=12MPa,
Megtámasztás: Fix megfogás körben a perem mentén.
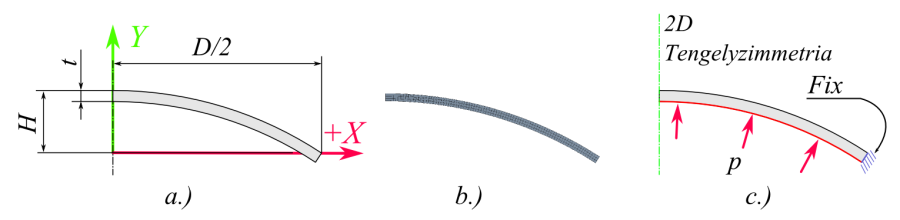
A feladatot az ANSYS Workbench végeselem programban oldjuk meg. A modell létrehozása a Design Modeller -ben az XY síkra rajzolt körív (az alábbi ábrán piros vonallal jelölve), Y tengely (zöld pont-vonal) körüli megforgatásával történik (4.3. ábra, a.). Fontos, hogy csak felületmodellt készítsünk, melynek vastagságát a szimulációs környezetben (Mechanikal modul) adunk. Az így létrejött héjmodell kisebb számolási igénnyel bír, mint ha testmodellel hoznánk létre. A strukturált háló létrehozását elősegítendő, osszuk fel a felületetet az ábrán látható módon (4.3. ábra, b.). A felosztáshoz használjuk a már ismert (Extrude/Inprint Faces) opciót két lépésben. Első lépésben rajzoljuk meg és válasszuk le a központi íves oldalakkal definiált négyszögű régiót (zöld vonal), majd második lépésben ennek sarkaitól kifelé húzott vonalakkal (kék vonalak) válasszuk 4 részre a külső gyűrűszerű felületet. Figyeljünk arra, hogy a két rajz külön vázlaton készüljön el.
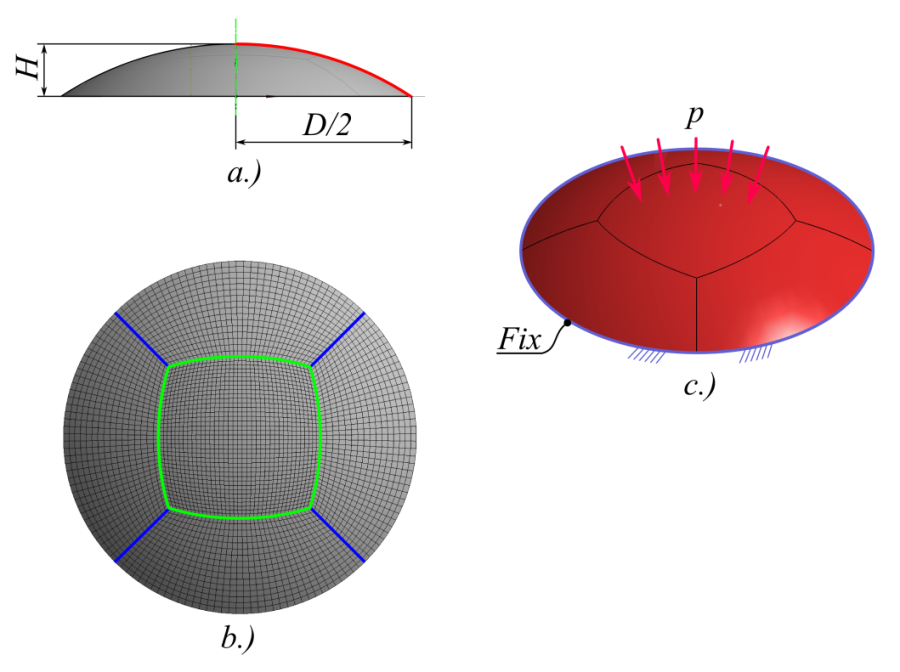
a.) geometriai modellje, b.) hálózása valamint c.) terhelése és megtámasztása
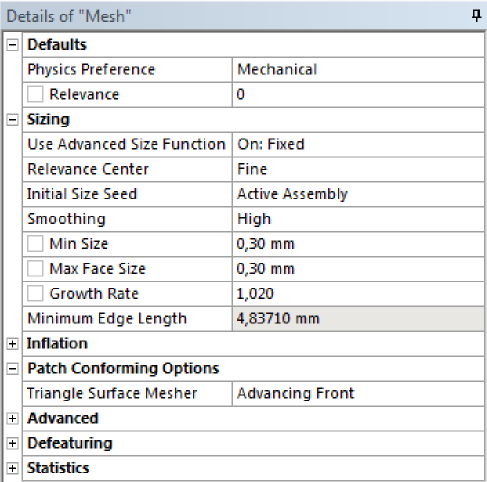
A geometriához alapértelmezettként hozzárendelt szerkezeti acélt hagyjuk érvényben. A hálózásnál használjunk 0,2mm-es elemméretet, négyszögelemekkel. Ehhez a modellfában kijelölt háló (Outline/Mesh) globális elemméretét állítsuk be a Details of „Mesh” panel Sizing részén. Használjuk a Use Advanced Size Function: On: Fixed opciót az ábrán látható elemméret beállításokkal (4.4. ábra). A fenti ábrán lévő rendezett háló elérése érdekében adjuk ki az Outline/Mesh(JG)/Insert/Mapped Face Meshind parancsot és jelöljük ki mind az 5 felületelemet.
Helyezzünk el egy Fix kényszert a modell pereme mentén, (él mentén), majd a nyomást (Pressure) a teljes felületre érvényesítve (4.3. ábra, c.).
A szimulációt az alapbeállításokkal futtatva azt tapasztaljuk, hogy nem fut le. A modellfa Settings sorát kijelölve a Details panelen végezzük el az alábbi ábrán látható beállításokat (4.5. ábra).
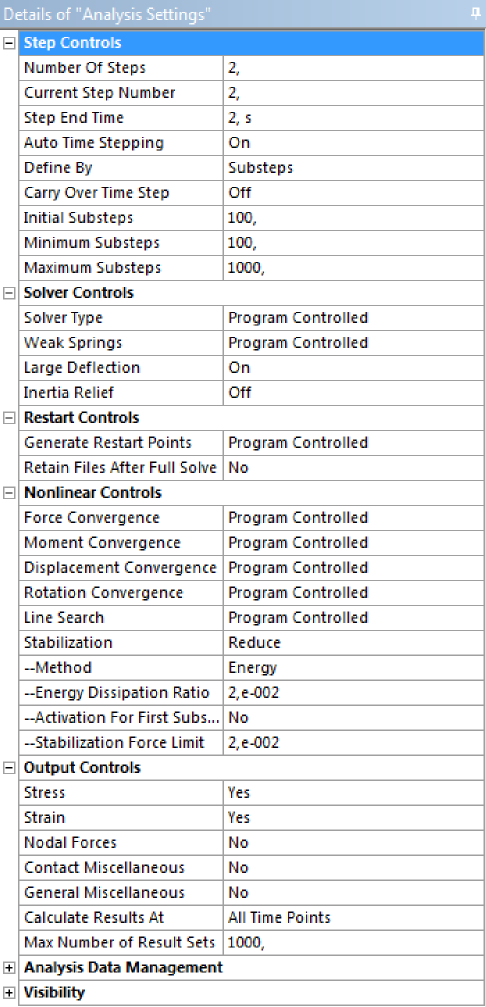
Indítsuk el az analízis számítását. A modellfa megoldási információk (Outline/Solution/Solution Information) elemére kattintva nyomon követhetjük a számolás folyamatát. A Force Convergence opció segítségével információt kaphatunk arról, hogy a számolás konvergál-e, és, hogy az egyes lépések végrehajtódtak-e. Ez főleg a nagy számolási igényű feladatoknál jelent segítséget.
A számolás lefutása után adjunk hozzá egy a deformáció lekérdező parancsot (Outline/Solution(JG)/Insert/Deformation/Total Deformation) , majd a képernyő alján lévő Graph panelen animáljuk az átpattanás folyamatát.
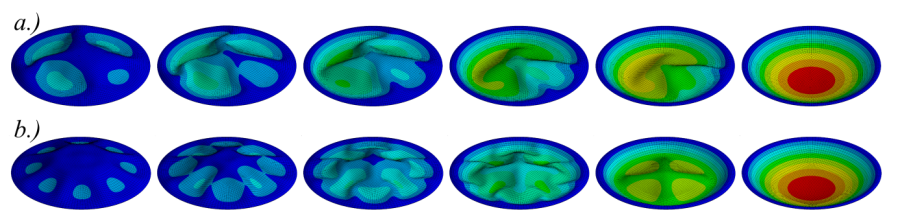
a.) strukturálatlan, és b.) strukturált háló esetén
Futtassuk a szimulációt strukturált és strukturálatlan hálóval, és hasonlítsuk össze az eredményeket. Látható, hogy a 4 szegmensre osztott hálóstruktúrával az eredmény is 4 szegmenses mintázatot mutat (4.6. ábra).
Megjegyzés: Vegyük figyelembe, hogy az analízis során lineáris anyagmodellt alkalmaztunk, ami nem vette figyelembe azt, hogy az átpattanás során helyenként a feszültség igen magas, a valós anyag folyáshatárát és szakítószilárdságát is meghaladó értéket ért el.
4.4. Mintafeladat anyagi és geometriai nemlinearitásra
A következő feladat során szimuláljuk az egyik oldalán nyomással terhelt, elasztomer membrán felfújódását. Az analízis nemlinearitását a nemlineáris anyagi viselkedés és a rendkívül nagy elmozdulások okozzák, ez utóbbi következménye továbbá a terhelési feltételek megváltozása is.
Kiinduló adatok:
A geometria egy forgásszimmetrikus, domború membrán, melynek méretei:
Átmérő: D=50mm,
Magasság: H=7,4mm,
Vastagság: t=1mm,
Anyag: Szilikongumi (paramétereit lásd lentebb),
Terhelő nyomás: p=0,04MPa,
Megtámasztás: Fix megfogás körben a perem mentén,
Az anyagmodell létrehozásához egytengelyű húzó és nyomó, valamint kéttengelyű anyagvizsgálatokból származó adatok állnak rendelkezésre (4.7. ábra, Táblázat 4.1).
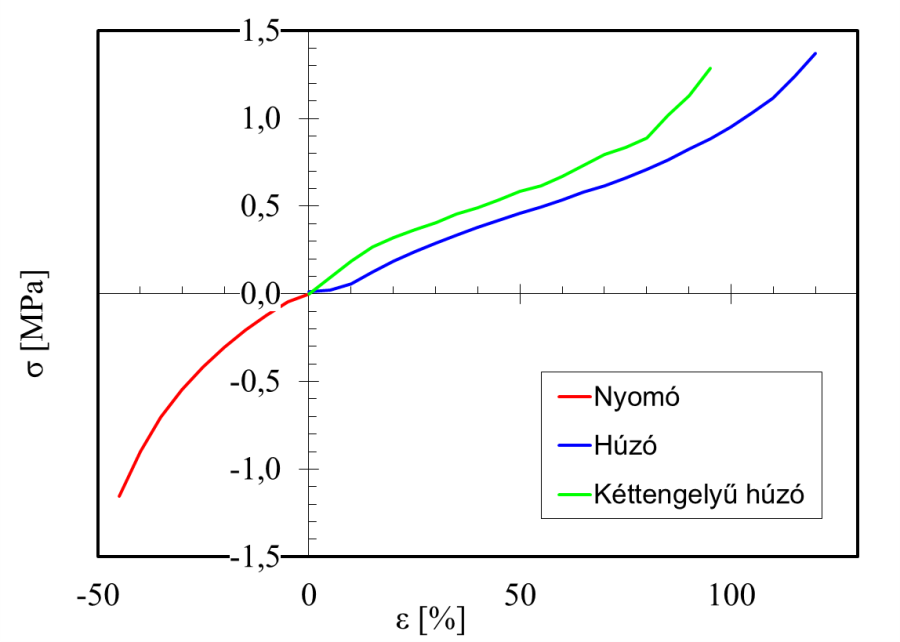
A nyomó és húzóvizsgálatokat egy táblázatba másolva egy adatsorként (Uniaxial Data) lehet bevinni a programba.
|
Egytengelyű |
Kéttengelyű húzó |
||
|---|---|---|---|
|
ε [-] |
σ [Mpa] |
ε [-] |
σ [Mpa] |
|
-0,450 |
-1,157 |
0,000 |
0,000 |
|
-0,400 |
-0,901 |
0,050 |
0,094 |
|
-0,350 |
-0,705 |
0,100 |
0,188 |
|
-0,300 |
-0,547 |
0,150 |
0,268 |
|
-0,250 |
-0,416 |
0,200 |
0,322 |
|
-0,200 |
-0,304 |
0,250 |
0,365 |
|
-0,150 |
-0,207 |
0,300 |
0,405 |
|
-0,100 |
-0,121 |
0,350 |
0,456 |
|
-0,050 |
-0,048 |
0,400 |
0,493 |
|
0,000 |
0,000 |
0,450 |
0,536 |
|
0,050 |
0,020 |
0,500 |
0,584 |
|
0,100 |
0,055 |
0,550 |
0,616 |
|
0,150 |
0,123 |
0,600 |
0,669 |
|
0,200 |
0,186 |
0,650 |
0,732 |
|
0,250 |
0,242 |
0,700 |
0,793 |
|
0,300 |
0,290 |
0,750 |
0,834 |
|
0,350 |
0,334 |
0,800 |
0,886 |
|
0,400 |
0,378 |
0,850 |
1,018 |
|
0,450 |
0,419 |
0,900 |
1,128 |
|
0,500 |
0,457 |
0,950 |
1,286 |
|
0,550 |
0,495 |
|
|
|
0,600 |
0,535 |
|
|
|
0,650 |
0,579 |
|
|
|
0,700 |
0,617 |
|
|
|
0,750 |
0,661 |
|
|
|
0,800 |
0,709 |
|
|
|
0,850 |
0,762 |
|
|
|
0,900 |
0,827 |
|
|
|
0,950 |
0,885 |
|
|
|
1,000 |
0,951 |
|
|
|
1,050 |
1,031 |
|
|
|
1,100 |
1,119 |
|
|
|
1,150 |
1,236 |
|
|
|
1,200 |
1,371 |
|
|
Az anyagmodell definiálásához az ANSYS Workbench projektfelületén helyezzünk el egy Engineering Data panelt, majd duplán kattintva rá, lépjünk be az analízis anyagkönyvtárába. A Structural Steel alatti sorra kattintva, és az új anyag nevét (Szilikongumi) beírva hozzunk létre egy új anyagot. Az ekkor még üres keretbe behúzással, vagy dupla kattintással, helyezzünk el a bal oldali panel Experimental Stress Strain Data részéről egy Uniaxial Test Data és egy Biaxial Test Data elemet. A jegyzet fenti táblázatából a megfelelő adatpárost másoljuk be az anyagmodell megfelelő helyére (a jobb felső, Table of Properties panelen található táblázatokba). Ügyeljünk arra, hogy a táblázat fejlécén a megfelelő mértékegységet válasszuk (mm mm^-1; MPa). Mindkét vizsgálati adat táblázata mellett lévő hőmérséklet (Temperature) cellába írjunk 22°C-ot, ami az adott anyagvizsgálat elvégzésekor mért környezeti hőmérsékletet jelenti. Ezután szintén a bal oldali panel Hyperelastic sora alatti anyagmodellek közül dupla kattintással helyezzünk el egy 5 paraméteres Mooney-Rivlin anyagmodellt. Az anyagmodellünkben megjelenő Mooney-Rivlin sort gördítsük le, majd abszolút hibavizsgálatra (Absolute Error) állítva, jobb gombos kattintással a Curve Fitting sorra, a Solve Curve Fit parancs kiadásával illesszünk görbét a vizsgálati adatokra. Miután ellenőriztük a görbe illeszkedését a jobb oldali grafikonon, jobbgombos menüből másoljuk az illesztett paramétereket az anyagmodellbe ( Curve Fitting(JG)/Copy Calculated Values to Property) . Ez után az Mooney-Rivlin modellben megjelenő paraméterek között írjunk az összenyomhatatlansági (Incompressibility Parameter, D1) paraméter cellájába 0-t, (ez jelenti az elasztomerekre jellemző térfogat-állandóságot), majd ellenőrizzük a modellt alkotó mindhárom görbét. Az anyagmodell létrehozása után térjünk vissza projektfelületre, majd adjunk hozzá egy statikai (Static Structural) analízist, melybe kössük be az Engineering Data panelt.
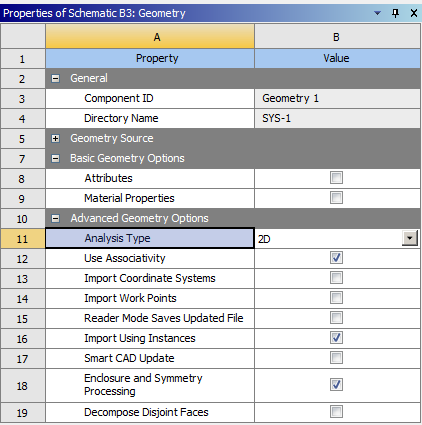
Az analízis típusa 2D tengelyszimmetrikus analízis lesz, amihez a 2D-s viselkedést a szimulációs környezetbe való belépés előtt be kell állítanunk, mert utólagosan már nincs lehetőség az átjárásra. Célszerű a geometria létrehozása előtt átállítani, a Static Structural/Geometry sorát kijelölve, a projektfelület jobb oldalán megjelenő tulajdonságok panelen (Properties of Schematic … : Geometry/Advanced Geometry Options/Analysis Type: 2D) , (4.8. ábra). Ha a panel nem jelenik meg akkor a statikai analízis paneljének Geometry sorára való jobb gombos kattintással, majd Properties parancs kiadásával előhozható.
A szerkezeti analízis Geometry sorára duplán kattintva hozzuk létre a geometriát. A 2D-s tengelyszimmetrikus analízis előfeltétele az ANSYS-ban, hogy a forgástest félmetszetét az XY síkon helyezzük el a +X térfélen, ugyanis az Y tengely lesz a forgásszimmetrikus analízis tengelyvonala. Hozzuk létre a rajzon lévő geometria vázlatát, majd feszítsünk rá sík felületet a Tools/Surfaces From Sketches paranccsal (4.9. ábra, a.). Méretek:
a.) Geometria, b.) hálózás, c.) Peremfeltételek és terhelés
Ezután a Geometry alatti bármelyik sorra való dupla kattintással lépjünk be a Melchanical modulba, vagyis a szimulációs környezetbe. A modellfán a geometriát kijelölve a szimuláció típusát állítsuk tengelyszimmetrikusra (Outline/…/Geometry => Details /Definition/2D Behavior: /Axisymmetric) .
A geometriát legördítve a felületmodellhez rendeljük hozzá az általunk létrehozott „Szilikongumi” nevű anyagmodellt (Outline/…/Geometry/Surface Body => Details/Material/Assigment: Szilikongumi) .
A hálózásnál állítsunk be 0,3mm-es globális elemméretet és rendezett hálót (Mapped Face Meshing) .
Adjuk hozzá az ábrán látható megfogást és terhelést.
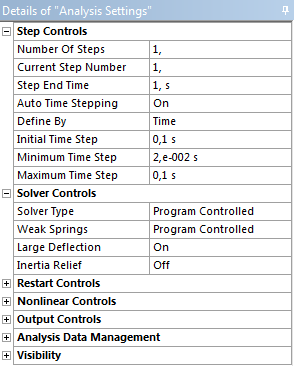
Az analízis beállításainál állítsunk be az időlépéseket az alábbi ábrán látható módon (Outline/…/Static Structural/Analysis Settings => Details/Step Controls) és kapcsoljuk be a nagy elmozdulásokat lehetővé tevő Details/Solver Controls Large Deflection opciót (4.10. ábra).
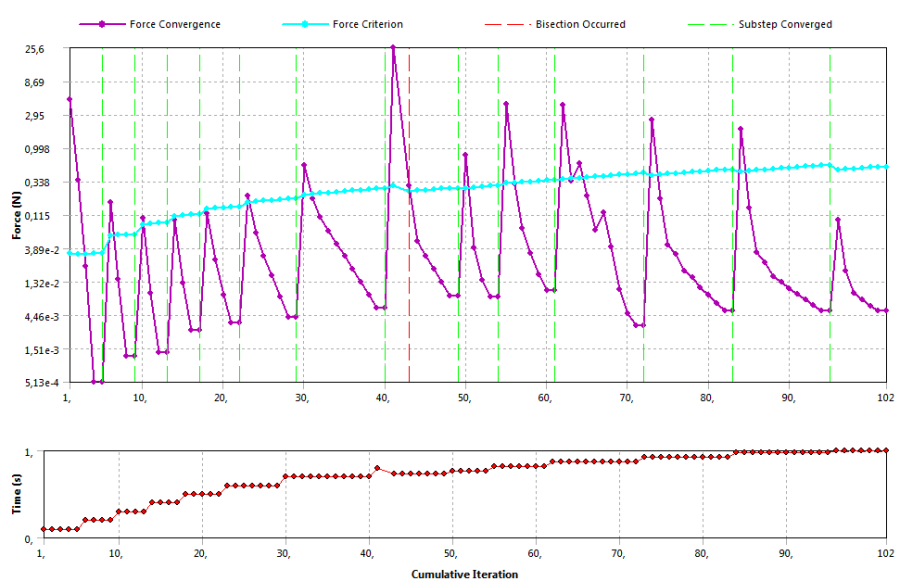
Ezután futtassuk a szimulációt, miközben figyeljük a megoldás konvergenciáját (4.11. ábra), (Outline/…/Solution/Solution Information=> Details/Solution Information/Solution Output/Force Convergence) .
Ha lefutott az analízis, kérdezzük le az 1. főfeszültség (Maximum Principal Stress) és 1. főnyúlás (Maximum Principal Strain) értékét, és a külső kontúr irány menti elmozdulását (Directional Deformation) mind X mind pedig Y irányban.
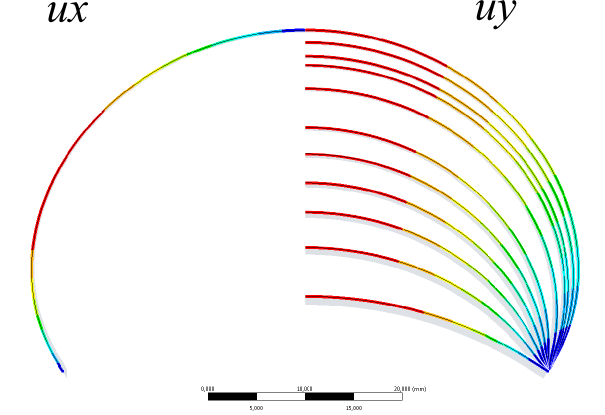
Megjegyzés: A fenti eredmények a felső felületet jelentő él mentén lettek lekérdezve. Az eredményeket a már tanult módon (jobb gombos kattintás a megfelelő lekérdezés során, majd Convert to Path Result ) átalakíthatjuk útvonal menti lekérdezéssé. Így megkaphatjuk az X és Y irányú elmozdulások értékét az útvonal menti elhelyezkedést jelző S[mm] paraméter függvényében (Lásd 3. fejezet 1. példáját). A modellfában az útvonalra jobb gombbal kattintva kiexportálhatjuk a vizsgált pontok kiinduló XY koordinátáit (Outline/Construction Geometry/Path(JG)/Export) , ezzel kiszámolhatjuk és akár diagramon is ábrázolhatjuk a deformált test alakját.