9. fejezet - Jelgenerálás
A tesztelő- vagy mérő-rendszerek nagyon fontos eleme a jelgenerátor .
A következő feladatok mintapéldák a jelgenerátorok alkalmazására:
Jelek szimulálása akkor fontos egy folyamat tesztelése céljából, amikor valós jelek nem állnak rendelkezésre, amikor nem áll rendelkezésünkre mérés-adatgyűjtő berendezés, hogy valós jeleket megmérjük vagy egyáltalán nincsenek valós jelek.
Jelek generálása digitális analóg (D/A) átalakítóval történik.
Ez a fejezet a jelgenerálás alapjait mutatja be.
9.1. Egyszerű vizsgáló jelek
Az egyszerű vizsgáló jelek a következők:
-
szinusz hullám,
-
négyszögjel,
-
háromszögjel,
-
fűrészjel,
-
zavarjelek néhány típusa,
-
több szinusz hullámból álló jeleket.
A hangerősítő rendszerek tesztelésre általánosan használt jel a szinusz hullám. Az egyszerű szinusz hullámot gyakran használják a rendszerből származó harmonikus torzítás meghatározására is. Több szinusz hullámból álló jelet széles körben alkalmaznak az intermodulációs torzítás mérésére, vagy frekvencia válasz meghatározására.
A Táblázat 9.1 táblázat néhány gyakran előforduló mérésnél használt jelet sorol fel.
|
Mérés |
Az alkalmazott bemeneti jel |
|---|---|
|
Szinusz hullám |
|
|
Multitone (két szinusz hullám) |
|
|
Multitone (több szinusz hullám, impulzus, frekvencia-változtatással), szélessávú zaj |
|
|
Intermoduláció |
Sinc |
|
Egységugrás |
|
|
Négyszög jel |
Ezen jelformák számos vizsgálat alapjául szolgálnak egy rendszer egyedi gerjesztésre adott válaszának mérésekor. A (9.1. ábra) és (9.1. ábra) ábrán látható vizsgáló jelek megtalálhatók a jelgenerátorokban.
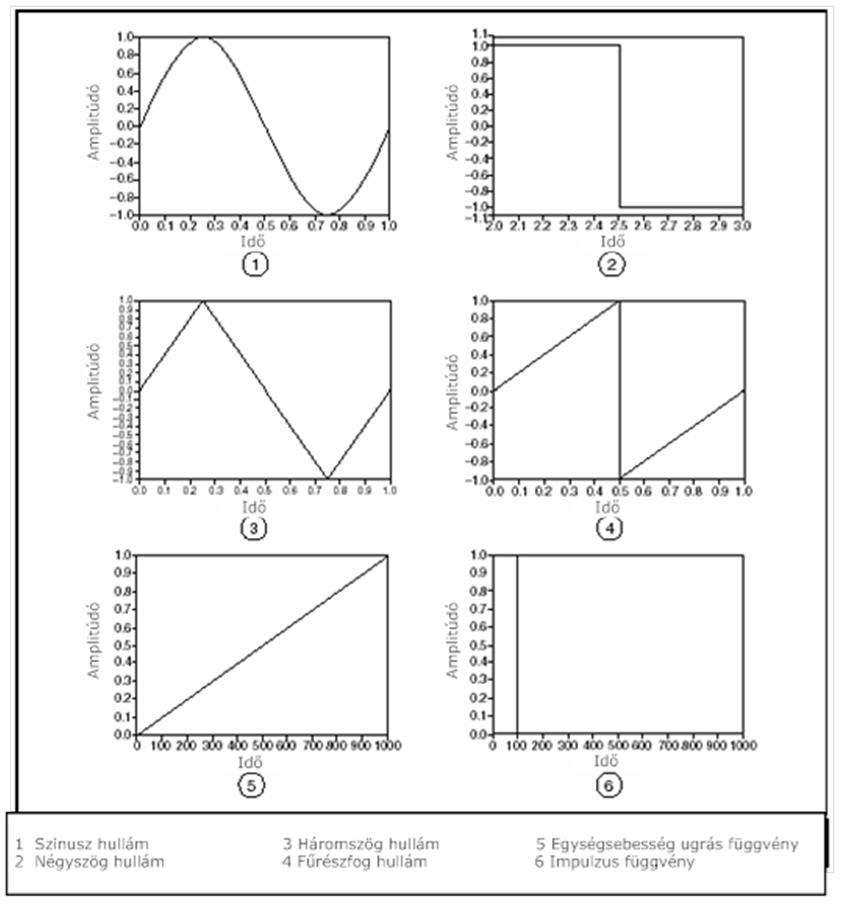
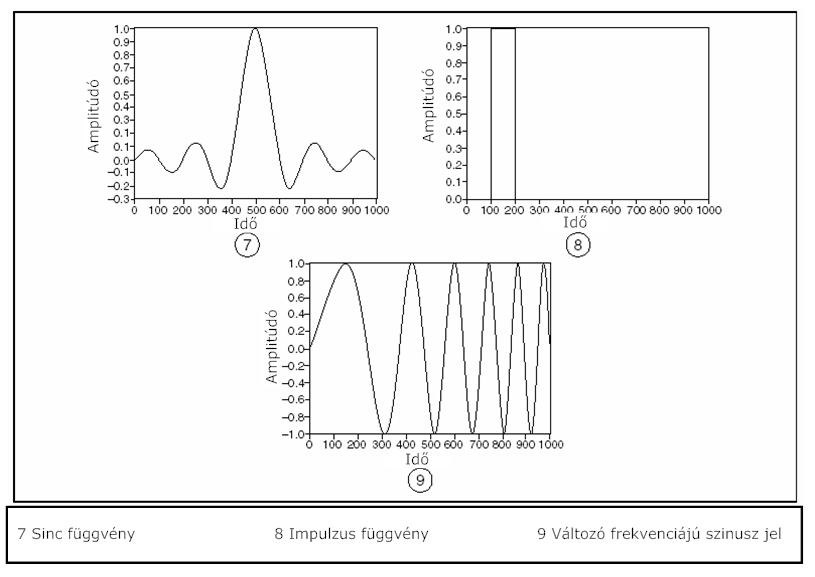
A legfontosabb, hogy az egyszerű vizsgáló jeleket frekvencia összetevőik alapján megismerjük.
A szokásos vizsgáló jelek frekvencia összetevőinek jellemzői:
-
A négyszög hullámok az alapfrekvencia páratlan rendszámú felharmonikusainak szuperpozíciójából keletkezik.
-
A háromszög és fűrész jeleknek olyan felharmonikus komponensei vannak, melyek az alapfrekvencia többszörösei.
-
Egy impulzus jel tartalmazza az összes frekvenciát, amelyeket egy adott mintavételi számmal és gyakorisággal reprezentálni lehet.
-
A változó frekvenciájú szinusz jelnél egy szinusz görbe jelenik meg egy indítási frekvenciától a megállási frekvenciáig, ily módon állít elő energiát egy adott frekvencia tartományban. A frekvencia végigsöprés jelalakjának diszkrét frekvenciái függnek a mintavételi gyakoriságtól, az indítási és megállási frekvenciáktól valamint a mintavételek számától.
9.2. Frekvencia átvitel mérése
Ahhoz, hogy egy frekvenciafüggvény mérést jól végezhessünk el, a mérési frekvenciatartománynak jelentős gerjesztő energiával kell rendelkeznie. Két alapvető jel használatos frekvenciafüggvény mérésekre, a változó frekvenciájú jel, valamint egy széles sávú zavarjel , az úgynevezett fehér zaj . Ebben a fejezetben az Egyszerűvizsgáló jelekről szóló rész ad bővebb információt a frekvencia végigsöpréses jelről. A Zavarjel generálás-ról szóló részben találhatók információk a fehér zajról.
Legjobb, ha nem használunk ablakokat (lásd 7.1.3.4. szakasz fejezetben) a frekvencia átviteli jelek vizsgálatakor. Amennyiben generálunk egy változó frekvenciájú gerjesztő jelet ugyanazzal a gyakorisággal, ahogyan kapjuk a választ, akkor hozzá tudjuk illeszteni az adatgyűjtés keret méretét a frekvencia végigsöpréses hosszához. Általában az ablak nélküli elemzés a legjobb választás szélessávú jelforrásokhoz. Mivel némelyik gerjesztő jel nem folytonos az időjel rögzítésen keresztül, ablak használatával eltompulhatnának a fontos tranziens függvényrészek.
9.3. Többtónusú jelgenerálás
A szinusz hullámon kívül az egyszerű vizsgáló jeleket a spektrális összetételükön túl nem lehet teljesen szabályozni. Például a négyszögjel harmonikus komponensei a frekvenciában, a fázisban és amplitúdóban viszonylag rögzítettek. Azonban létre tudunk hozni többtónusú jeleket külön-külön egyedi frekvencia komponensekkel adott amplitúdóval és fázistolással.
Egy többfrekvenciás jel különféle szinusz hullámok vagy hangfrekvenciás jelek összegzéséből állítható elő, egyenként egy határozott amplitúdóval, fázistolással és frekvenciával. Egy többfrekvenciás jel tipikusan úgy jön létre, hogy az önálló frekvenciájú komponensek meghatározott amplitúdóval szerepelnek a jelben. Ha a bejövő többfrekvenciás jel FFT-jét (Fast Fourier Transformation) meghatározzuk, a frekvencia komponensek mindegyike pontosan beleesik egy egyedi frekvencia sávba, amely nem ad módot színkép szóródására, vagy veszteség megjelenésére. A többfrekvenciájú jelekkel szokták meghatározni egy berendezés frekvencia átviteli-függvényét, és a megfelelő frekvenciák kiválasztásával, szintén mérni lehet olyan mennyiséget, mint az intermodulációs torzítás.
9.3.1. Csúcstényező
A jelet alkotó komponensek egymáshoz viszonyított fázisai határozzák meg az adott amplitúdójú többfrekvenciás jel csúcstényezőjét. A csúcsfaktort a jel RMS értékének ( Root Mean Square = négyzetes középérték ) és maximális kitérésének arányaként definiálják.
Például egy szinusz hullám csúcstényezője 1.414 : 1
Egy nagy csúcstényezőjű többfrekvenciás jel ugyanakkora maximális amplitúdó mellett, kevesebb energiát tartalmaz mint egy kisebb csúcstényezőjű jel.
Más szóval a nagyobb csúcstényező azt jelenti, hogy egy adott szinusz komponens amplitúdója kisebb, mint egy kisebb csúcstényezőjű ugyanolyan szinusz frekvencia egy többfrekvenciás jelben. Egyedi szinusz frekvenciák esetében egy magasabb csúcstényező alacsonyabb jel-zaj viszonyt eredményez. Ezért a fázisok megfelelő kiválasztása kritikus pont, amikor egy használható többfrekvenciás jelet akarunk létrehozni.
Hogy elkerüljük a csúcslevágást, a többtónusú jel legnagyobb értéke nem lépheti túl a jelgeneráló készülék maximális lehetőségét, tehát a jel legnagyobb amplitúdójára vonatkozó határértéket. Létrehozhatunk egy adott amplitúdójú többtónusú jelet az alkotó szinusz tónusok fázisviszonyai és amplitúdói különböző kombinációjának változtatásával. Egy jel generálásához megfelelő közelítésnek úgy kell megválasztani az amplitúdókat és a fázisokat, hogy a csúcstényező minél kisebb legyen.
9.3.2. Fázis jel generálás
A következő leírás szerint szokás a többfrekvenciás jelek frekvenciáinak fázisait előállítani:
A szomszédos frekvenciák közötti fáziskülönbséget 0-tól 360 fokig lineárisan változtatva, a frekvenciák közötti fázisok véletlenszerű változtatásával.
A szomszédos frekvenciák közötti fáziskülönbséget 0-tól 360 fokig lineárisan változtatva elő lehet állítani nagyon alacsony csúcsfaktorú többfrekvenciás jeleket.
Azonban a kapott többfrekvenciás jel a következő nem kívánt jellemzőkkel rendelkezik:
A többfrekvenciás jel fázistorzításra nagyon érzékeny.
Ha a jelgenerálás folyamán a készülékben vagy a vezetékekben nemlineáris fázistorzítás jön létre, akkor a csúcsfaktor jelentősen megváltozhat.
A többfrekvenciás jelnél jelentkezhetnek időtartománybeli ismétlődő jellegzetességek, melyeket a (9.3. ábra) ábrán követhetünk nyomon.
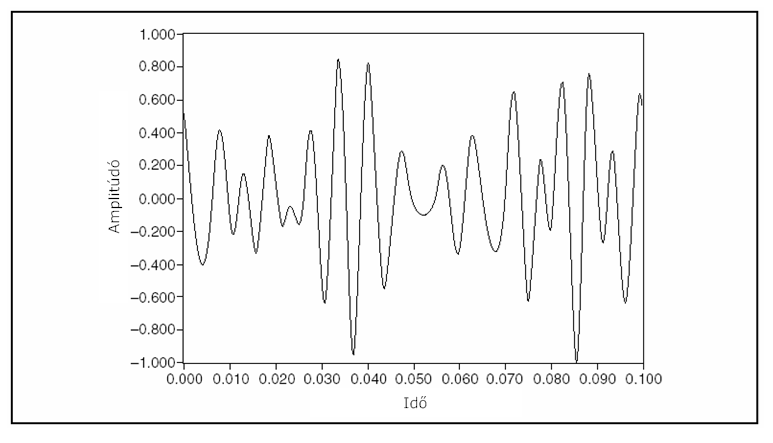
A 9.3. ábra ábra szerinti jel egy olyan frekvencia végigsöpréses jelre hasonlít, amelynek a frekvenciája csökkenni látszik balról jobbra. A látszólagos balról jobbra mutató frekvenciacsökkenés jellemző azokra a többfrekvenciás jelekre, amelyeket a szomszédos frekvenciák fáziskülönbségének lineáris változtatásával hoznak létre. Gyakran kívánatosabb egy olyan jelet használni, ami sokkal zajosabb mint a (9.3. ábra) ábrán lévő.
Véletlenszerűen változtatva a fázisokat, olyan többfrekvenciás jelet kapunk, amelynek amplitúdói majdnem Gauss eloszlást követnek, ahogy a frekvenciák száma növekszik. A 9.4. ábra a frekvencia fázisok véletlenszerű változtatásával létrehozott jelet szemlélteti.
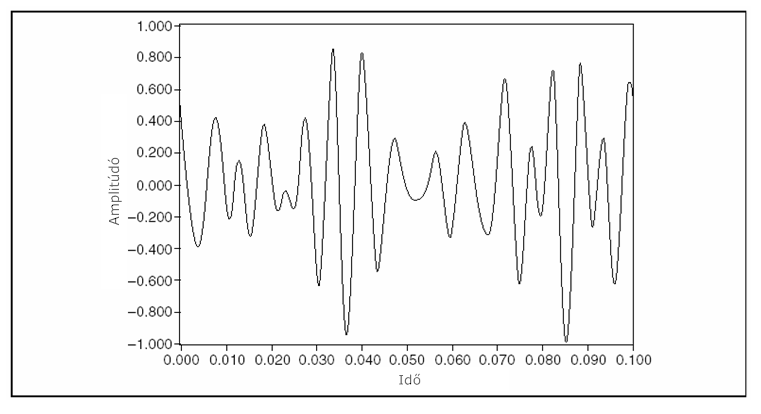
Azon túl, hogy a (9.4. ábra) ábrán látható jel sokkal zajosabb, kevésbé érzékeny a fázistorzításra.
A 9.4. ábra ábra szerinti fázis viszonyú többfrekvenciás jelek általában egy 10 és 11 dB közötti csúcsfaktort érnek el. (Vagyis a csúcsérték az effektív érték három, négyszerese.)
9.3.3. Változó frekvenciájú szinusz jel, illetve többfrekvenciás jel
Ahhoz hogy egy rendszert jellemezhessünk, általában meg kell mérni a rendszer jelátviteli tényezőjét több különböző frekvencián. Ebben segítenek a következőkben felsorolt eljárások.
A változó frekvenciájú szinusz függvény simán és folytonosan változtatja a szinusz hullám frekvenciáját egy megadott frekvencia tartományban.
A léptető szinusz függvény egy állandó frekvenciájú szinusz jelet szolgáltat addig, amíg egy bizonyos gerjesztés tart, aztán növeli a frekvenciát egy diszkrét értékkel. A folyamat addig tart, amíg az összes érdekelt frekvencián végig nem halad.
A többfrekvenciás hullám olyan jelet szolgáltat, amely egyedi szinusz hullámú komponensekből áll.
A többfrekvenciás jeleknek van egy jelentős előnyük a végigsöprő szinusz és a léptető szinusz jelekkel szemben. Egy adott frekvencia tartományra vonatkozóan, a többfrekvenciás megközelítés sokkal gyorsabb lehet, mint az annak megfelelő végigsöprő szinusz mérés, amely főleg a kimenetek véges beállási idejének következménye (lásd 7. fejezet fejezet sávszélesség és analízis idő kapcsolatáról szóló meggondolásait).
Minden szinusz jelnél a léptető szinusz mérésekor várakozni kell a rendszer beállási idejének leteltéig, mielőtt elkezdhetjük a mérést.
Egy végigsöprő szinusz mérés kimeneti beállási ideje még bonyolultabb lehet. Ha a rendszernek vannak kis frekvenciájú pólusai és/vagy zérusai illetve Q-rezonanciái, a rendszer ilyenkor egy viszonylag hosszabb beállási időt vesz igénybe. Egy többfrekvenciás jelnél viszont csak egyszer kell megvárni a beállási időt. A többfrekvenciás jel legkisebb frekvenciájának egy periódusa rendszerint elegendő a beállási idő szempontjából. A többfrekvenciás jelre kapott válasz feldolgozása már nagyon gyors lehet. Használhatunk egy egyszerű gyors Fourier transzformációt számos frekvencia pont, amplitúdó és fázis egyidejű mérésére.
A változó frekvenciájú szinusz közelítés bizonyos helyzetekben alkalmasabb, mint a többfrekvenciás közelítés. Az egyenként megmért frekvenciák a többfrekvenciás jelben érzékenyebbek a zajra, mivel az egyes frekvenciák energiaszintje alacsonyabb, mint egy egyedülálló frekvenciájú jelnek. Például tekintsünk egy 10V-os maximális amplitúdójú önálló szinusz jelet, amelynek 100 Hz a frekvenciája. Egy többfrekvenciás jel 10 frekvenciát tartalmaz, (köztük a 100 Hz-est is), legnagyobb amplitúdója szintén csak 10V lehet. Ezért a 100 Hz-es frekvencia-komponensnek amplitúdója kisebb lesz mint 10V. A 100 Hz-es frekvenciájú összetevő alacsonyabb amplitúdója abból az eljárásból következik, hogy az összes szinusz jel összegződik. Feltéve, hogy a zaj azonos szintű, a 100 Hz-es komponens jel-zaj viszonya (SNR = Signal Noise Rate) kedvezőbb a végigsöprő szinusz közelítés esetén. A többfrekvenciás közelítésben az egyes jelek amplitúdóinak és fázisainak beállításával mérsékelhetjük a redukált jel-zaj viszonyt úgy, hogy ahol szükséges nagyobb energiát használunk, a kevésbé kritikus frekvenciáknál pedig kisebbet.
Amikor egy rendszer többfrekvenciás gerjesztésre adott válaszát vizsgáljuk, az FFT közben elhasznált energia a zajnak, vagy a vizsgálat alatt álló berendezés indukált torzításának tulajdonítható.
Az FFT frekvenciafelbontása a mérési idő miatt korlátozott. Ha meg akarjuk mérni a rendszerünket 1.000 kHz-en és 1.001 kHz-en, a legjobb a közelítést két független szinusz jel alkalmazásával kapunk. Két önálló szinusz jel alkalmazásával el tudjuk végezni a mérést néhány ezredmásodperc alatt, míg ugyanez a többfrekvenciás mérés legalább 1 másodpercig tart.
Némely alkalmazásnál, mint például egy kristály rezonancia frekvenciájának meghatározásánál, kombinálni kell egy durvább többfrekvenciás mérést egy szűk tartományú finomabb méréssel.
9.4. Zavarjel generálás
Zavar jeleket alkalmazhatunk a frekvencia függvény mérésének elvégzéséhez, vagy bizonyos folyamatok szimulálására.
A zajok néhány típusa gyakran használt, amelyek a következők:
-
homogén fehér zaj,
-
Gauss-eloszlású zaj,
-
véletlenszerű periódikus zaj.
A fehér szó a zaj elnevezésében a jellemző frekvencia tartományára utal. Az ideális fehér zaj teljesítménye egyenletes az adott sávszélességben, és egyenletes teljesítmény eloszlást eredményez a megfigyelt frekvencia tartományban. Ilyenformán pl. a 100 Hz-től 110 Hz-ig terjedő frekvenciatartomány teljesítménye egyenlő az 1000 Hz és 1010 Hz közötti intervallum teljesítményével. Gyakorlati mérésekben az egyenletes teljesítmény eloszlás megvalósításához végtelen számú mintavételre volna szükség. Tehát amikor fehér zajjal végzünk méréseket, a teljesítmény spektrum rendszerint átlagolt, minél több átlagértékkel számolunk, annál egyenletesebb teljesítmény spektrumot kapunk.
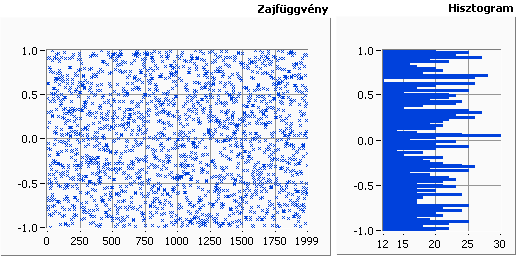
A homogén és a Gauss elnevezések a valószínűségi sűrűség függvényre ( PDF = Probability Density Function ) utalnak, ami a zaj időtartománybeli mintái amplitúdójának függvénye. A homogén fehér zajhoz tartozó valószínűségi sűrűség függvény a megadott maximális és minimális szinteken belül homogén. Más szóval bizonyos határok között valószínűleg minden amplitúdó értéke egyenlő. Az elektronikus elemekben létrejött termikus zaj eloszlásban hasonlít a homogén fehér zajhoz.
A 9.4. ábra ábra a homogén fehér zaj mintáinak eloszlását mutatja.
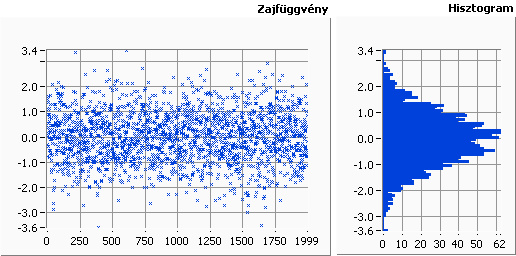
A Gauss-eloszlású zajra vonatkozó valószínűségi sűrűség függvény Gauss-féle függvény (haranggörbe).
Ha a homogén fehér zajt bevezetjük egy lineáris rendszerbe, a kimeneten Gauss-eloszlású zajt kapunk eredményül. A 9.6. ábra ábra a Gauss zaj mintáinak eloszlását mutatja.
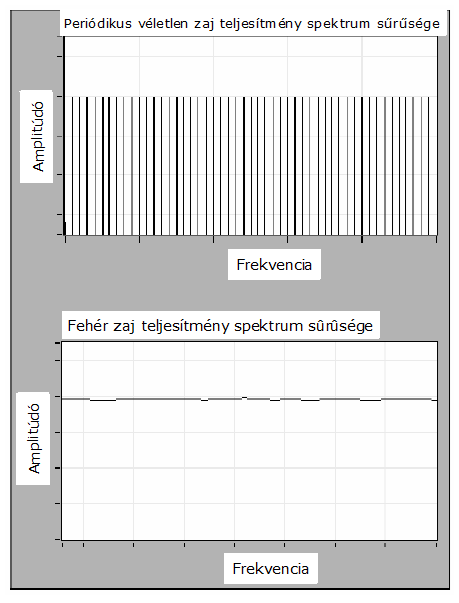
A véletlenszerű periodikus zaj (PRN = Periodic Random Noise) szinuszos jelek összegződése azonos amplitúdókkal, de véletlenszerű fázissal. A véletlenszerű periodikus zaj tartalmazza az összes olyan frekvenciájú szinusz hullámot, amelyeket egész számú periódusokon ábrázolni lehet a szükséges számú mintával. Mivel a véletlenszerű periodikus zaj csak egész periódusú szinusz hullámot tartalmaz, nincs szükségünk véletlenszerű periodikus zaj ablakra, mielőtt elvégezzük a spektrum analízisét. A véletlenszerű periodikus zaj ön-ablakozó ,ezért nincs benne színkép-szóródás.
A véletlenszerű periodikus zajnak nincs minden frekvencián azonos energiája, mint a fehér zajnak, hanem csak diszkrét frekvenciákon, amelyek az alapfrekvencia harmonikus összetevőinek felelnek meg. Az alapfrekvencia egyenlő a mintavételi frekvenciának és a minták számának hányadosával. A zajszint azonban minden egyes diszkrét frekvencián azonos nagyságú.
A véletlenszerű periodikus zajt alkalmazhatjuk egy lineáris rendszer frekvencia függvényének meghatározására egyszeri adatsorral, ahelyett hogy néhány mérés után a frekvenciafüggvényeket átlagolnánk, ahogy azt tennünk kell nem periodikus véletlenszerű források esetében. A 9.6. ábra ábra a véletlenszerű periodikus zaj spektrumát és a fehér zaj átlagolt színképét mutatja.
9.5. Normalizált frekvencia
Az analóg rendszerekben egy jel analóg frekvenciáját Hertzben (Hz) mérik vagy periódus/másodperc-ben. A digitális rendszerekben azonban gyakran egy digitális frekvenciát használnak, amely az analóg frekvencia és a mintavételező frekvencia arányát jelenti, ahogy azt a következő egyenlet bemutatja:
|
|
(9.1) |
periódus/minták száma. Néhány jelgeneráló VI használ egy f frekvencia bemenetet, amelyen periódus/minta mértékegységben kéri a normalizált frekvencia értékét.
A normalizált frekvencia értékkészlete 0.0-tól 1.0-ig tart, amely megfelel a 0-tól f s mintavételező frekvenciáig terjedő valós tartománynak. A normalizált frekvencia burkolja az 1-et, ezért az 1.1-nek a normalizált frekvenciája 0.1. Például ha egy jelet az f s /2 Nyquist frekvenciával mintavételezünk, ez periódusonként szimpla mintavételezést eredményez, azaz 1 minta/periódust. Ez a mintavételi gyakoriság megegyezik a 1 periódus/minta normalizált frekvenciával.
A normalizált frekvencia reciproka 1/f értéke megadja, hogy a jel egy periódusában hányszor mintavételeztük, amely a periódusonkénti minták száma.
Amikor olyan VI-t használunk amelyen van normalizált frekvencia bemenet, át kell váltani a frekvencia mértékegységét normalizált periódus/minta egységre. Ilyen normalizált mértékegységeket kell használnunk a következő jel generáló VI alkalmazásokban:
-
Szinusz hullám
-
Négyszög hullám
-
Fűrészfog hullám
-
Háromszög hullám
-
Tetszőleges hullám
-
Változó frekvenciájú szinusz jel
Ha a periódusok frekvencia mértékegységét használjuk, mindig át kell alakítani a periódusokat a periódusok per mintavételekre, amelyet úgy határozunk meg, hogy a periódusok számát elosztjuk a létrehozott minták számával.
Például 2 periódus frekvenciája osztva 50 mintával, eredmény normalizált frekvenciában f=1/25 periódus/minta. Ez azt jelenti, hogy a szinusz hullám egy periódusában f reciproka, azaz 25 mintát veszünk.
Ha azonban Hertz-et kell használnunk frekvencia mértékegységként. Ha át akarjuk alakítani a Hertz-et periódus/minta egységre, osszuk el a Hz-ben mért értéket a mintavételi gyakorisággal (minta/másodperc), ahogy azt a következő képlet mutatja:
|
|
(9.2) |
Például ha 60 Hz-et elosztunk a mintavételi frekvenciával 1000 Hz-el, a normalizált frekvencia f=0.06 periódus/minta lesz az eredmény. Tehát ez majdnem 17 vagy 1/0.06 , a szinusz hullám az egy periódusra eső minták száma.
A jelgeneráló programok sok általános jelet előállítanak, amelyekre a hálózatok elemzésénél és a szimulációnál van szükség. Használhatja a jelgeneráló alkalmazásokat, és előállíthat analóg gerjesztő jeleket.
Irodalom
[9.1.] LabVIEW Control Design User Manual. 2009.