10. fejezet - Digitális szűrés
Vissza		Előre

10. fejezet - Digitális szűrés

Tartalom

Ez a fejezet bemutatja a digitális jelek szűrését, összehasonlítja a digitális és analóg szűrőket, bemutatja a véges impulzus válasz (FIR = Finite Impulse Response) és a végtelen impulzus válasz (IIR = Infinite Impulse Response) szűrőket, valamint bemutatja, hogyan kell kiválasztani a megfelelő digitális szűrőt egy adott feladathoz.

10.1. Bevezetés a digitális szűrés gyakorlati alkalmazásába

A szűrési eljárás megváltoztatja a jelet alkotó frekvencia komponensek amplitúdóit. Például a mély hangszín szabályzó a sztereo rendszereken megváltoztatja a jel alacsony frekvenciáinak amplitúdóját, a magas hangszín szabályzó pedig a magas frekvenciás komponensek amplitúdóit alakítja át. A mély és magas szabályzók beállításával kiszűrhetjük vagy kiemelhetjük a különböző frekvenciájú hang jeleket. Két általános szűrő alkalmazás csökkenti a zajt és csonkítja a sávszélességet. A csonkítás egy aluláteresztő szűrőt tartalmaz, és csökkenti a mintavétel frekvenciáját.

A szűrési folyamat lehetővé teszi, hogy a jel számunkra lényeges részeit kiválasszuk a nyers (zajos) jelből. Egy klasszikus lineáris szűrő a frekvencia tartományban kiemeli a lényeges részeket az eredeti jelből.

A digitális szűrés előnyei az analóg szűréssel szemben :

Egy analóg szűrő bemenetén analóg jel x(t) jut be és kimenetén szintén analóg jel y(t) jelenik meg. Az x(t) is és y(t) is a t folytonos (idő)változó függvényei, és végtelen sok értéket felvehetnek. Analóg szűrők tervezéséhez komoly matematikai ismeretek szükségesek, és ismerni kell a szűrők rendszerekben kifejtett hatásának bonyolult folyamatát is.

A modern mintavételező és digitális jelfeldolgozó eszközök térhódítása miatt az analóg szűrőket (majdnem mindenütt) helyettesíthetjük digitális szűrőkkel. Olyan alkalmazásokban, amelyek megkövetelik a szűrők programozhatóságát, mint például az hangtechnikában, a híradástechnikában, a geofizikában valamint számos egyéb területen.

A digitális szűrők a következő előnyökkel rendelkeznek az analóg szűrőkkel szemben:

nagyobb pontosság érhető el velük, mint R-L-C áramkörökkel,
olyan szűrők is megvalósíthatók, amelyeknek nem létezik valós, R-L-C elemekből készíthető megfelelőjük,
A digitális szűrők paraméterei programozhatók, így könnyen változtathatók és az eredmény gyorsan tesztelhető.
A digitális szűrők egyszerű számtani műveletekkel dolgoznak, amelyek az összeadás, kivonás, szorzás, osztás.
A digitális szűrők működését nem befolyásolja a hőmérséklet és a páratartalom változása, illetve nem tartalmaznak különleges pontosságot igénylő alkatrészeket.
A digitális szűrőknek különlegesen jó a teljesítmény/költség aránya.
A digitális szűrők tulajdonságai nem függnek a gyártási verzióktól és tulajdonságaik nem "öregszenek".
Készíthetők ún. adaptív, vagyis a feladathoz automatikusan alkalmazkodó szűrők is.

10.2. A Z transzformáció

A Z-transzformáció a Laplace-transzformáció diszkrét idejű megfelelője. Általánosabb a 6.5. szakasz fejezetben tárgyalt diszkrét Fourier-transzformációnál (DFT), mert kevésbbé szigorúak a konvergencia feltételek.

Általánosan egy {f_k} diszkrét számsorozat Z transzformáltja definíció szerint:

$F (z) = Z [{f_{k}}] = \sum_{k = 0}^{\infty} f_{k} \cdot z^{- k}$

(10.1)

ahol:

$f_{k} = f (t_{k}) = f (k \cdot h)$

(10.2)

	t _k =k.h	az k.-ik mintavételezési időpont
	h	a mintavételezési időtartam
	k	pozitív egész szám

Itt is belépő függvény van, amely ugyanolyan szerepű, mint a Laplace transzformációnál volt.

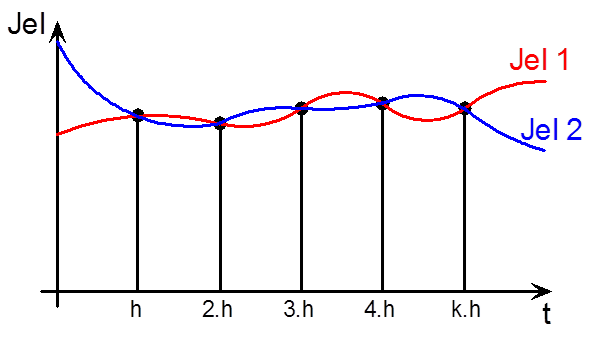
10.1. ábra - Analóg jelek mintavételezése és a mintavétel értéke

A Z transzformációval meghatározott értékek csak a mintavételi időpontokban adnak információt , hogy két mintavétel között mi történik, arra nem.

A jelek Z transzformációjának összefüggései alapján meghatározható függvények táblázatba foglalhatók:

10.1. táblázat - Jelek Z transzformációja

f(t)	f(n.h)	F(z)
$1 (t)$	1	$\frac{z}{z - 1}$
t	$n \cdot h$	$\frac{z \cdot h}{{(z - 1)}^{2}}$
$t^{2}$	${(n \cdot h)}^{2}$	$\frac{z \cdot (z + 1) \cdot h_{}^{2}}{{(z - 1)}^{3}}$
$a^{\frac{t}{h}}$	$a^{n}$	$\frac{z}{z - a}$
$e^{- a t}$	$e^{- a (n \cdot h)}$	$\frac{z}{z - e^{- a \cdot h}}$
$t \cdot e^{- a t}$	$n \cdot h \cdot e^{- a (n \cdot h)}$	$\frac{z \cdot e^{- a \cdot h} h}{{(z - e^{- a \cdot h})}^{2}}$
$\sin (ω t)$	$\sin (ω \cdot n \cdot h)$	$\frac{z \cdot \sin (ω \cdot h)}{z^{2} - 2 \cdot z \cdot \cos (ω \cdot h) + 1}$
$\cos (ω t)$	$\cos (ω \cdot n \cdot h)$	$\frac{z \cdot (z - \cos (ω \cdot h))}{z^{2} - 2 \cdot z \cdot \cos (ω \cdot h) + 1}$
$e^{- a t} \cdot \sin (ω t)$	$e^{- a (n \cdot h)} \cdot \sin (ω \cdot n \cdot h)$	$\frac{z \cdot e^{- a \cdot h} \cdot \sin (ω \cdot h)}{z^{2} - 2 \cdot z \cdot e^{- a \cdot h} \cdot \cos (ω \cdot h) + e^{- 2 n \cdot h}}$

A Z transzformált értékek mindegyike egy $\frac{N (z)}{P (z)}$ alakú polinom.

Ezek csak a legfontosabb transzformációs összefüggések, további kiszámított Z transzformációs összefüggések mintavételes szabályozási kézikönyvekben találhatók.

Mintapélda:

Egységugrás-függvény Z transzformáltja:

$x(t) = {\begin{matrix} 1(t) & 0 \leq t \\ 0 & t < 0 \end{matrix}$

(10.3)

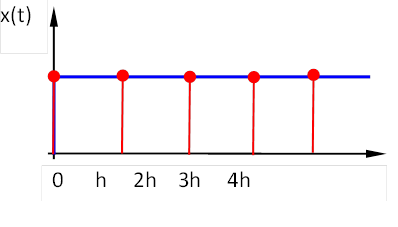
10.2. ábra - Analóg jelek mintavételezése és a mintavétel értéke

$\begin{array}{l} Z {1(t)} = \sum_{k = 0}^{\infty} 1 \cdot z^{- k} = \\ \sum_{k = 0}^{\infty} z^{- k} = 1 + z^{- 1} + z^{- 2} + z^{- 3} + ... = \frac{1}{1 - z^{- 1}} \end{array}$

(10.4)

Magyarázat:

A mértani sor összege:

$S_{n} = a_{1} \cdot \frac{q^{n} - 1}{q^{} - 1}$

(10.5)

amelybe behelyettesítve az a₁= 1 és $q = z^{- 1}$ (q = quotient = kvóciens) értékeket, $n \to \infty$ esetén kapjuk a $Z {1 (t)} = \frac{1}{1 - z^{- 1}}$ összeget:

$\lim_{n - > + I n f} (1 \cdot \frac{z^{- n} - 1}{z^{- 1} - 1}) = \frac{- 1}{z^{- 1} - 1} = \frac{1}{1 - z^{- 1}}$

(10.6)

10.2.1. A Z transzformáció legfontosabb tulajdonságai

Linearitás:

$Z [a \cdot {f_{k}} + b \cdot {g_{k}}] = a \cdot F (z) + b \cdot G (z)$

(10.7)

A Laplace transzformáció és a Z transzformáció kapcsolata:

$e^{- k \cdot (s \cdot h)} = z^{- k}$

(10.8)

Eltolási tételek:

Eltolás az időtengelyen negatív irányban

$Z {f_{k - n}} = z^{- n} \cdot F (z)$

(10.9)

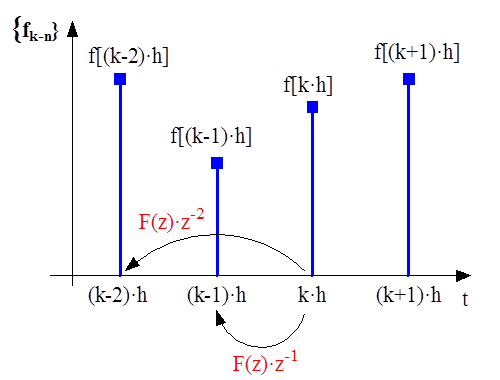
10.3. ábra - Diszkrét jel érték eltolása az időtengelyen negatív irányban

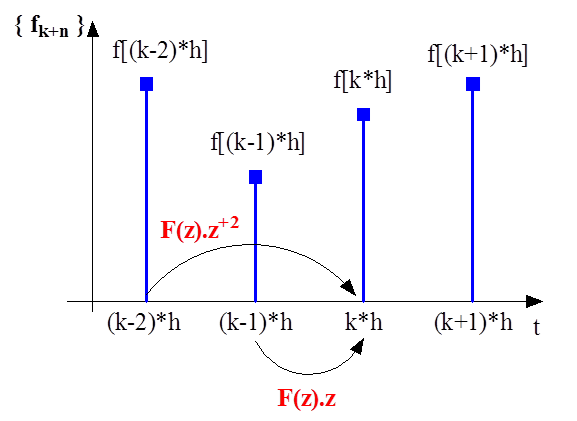
Eltolás az időtengelyen pozitív irányban

$Z {f_{k + n}} = z^{n} \cdot F (z) - (z^{n} \cdot f_{0} + z^{n - 1} \cdot f_{1} + ... + z \cdot f_{n - 1})$

(10.10)

Például n=2 esetén

$Z {f_{k + 2}} = z^{2} \cdot F (z) - (z^{2} \cdot f_{0} + z^{1} \cdot f_{1})$

(10.11)

ahol

	f ₀	a függvény értéke t=0.h időpontban
	f ₁	a függvény értéke t=1.h időpontban

10.4. ábra - Diszkrét jel érték eltolása az időtengelyen pozitív irányban

Végérték tételek:

	$f [0] = \lim_{z \to \infty} F (z)$	(10.12)
	$z = e^{s \cdot h}; s \Rightarrow \infty a k k o r z \Rightarrow \infty$

	$f [\infty] = \lim_{z \to 1} (1 - z^{- 1}) \cdot F (z)$	(10.13)
	$z = e^{s \cdot h}; s \Rightarrow 0 a k k o r z \Rightarrow 1$

az $f_{\infty}$ ilyen módon történő meghatározása akkor igaz, ha az $(1 - z^{- 1}) \cdot F (z)$ -nek nem helyezkedik el egyetlen pólusa sem az egység sugarú körön, illetve azon kívül.

A megoldás módszere hasonló a Laplace transzformációnál megismert módszerhez. A bemenő jelet és az átvitelt leíró függvényt transzformáljuk (Z transzformáció), majd az eredményt visszatranszformáljuk.

10.2.2. Az inverz Z transzformációs módszerek

10.2.2.1. Táblázatból való visszakereséssel

Ilyenkor a Táblázat 10.1 táblázat F(z) oszlopát alkalmazzuk bementként és az f(t) időfüggvényt határozzuk meg a táblázatból.

10.2.2.2. Résztörtekre bontással

A számítások eredményeként általában a kimenő jel z transzformáltját határozzuk meg, amely az Y(z). Ezt bonthatjuk fel a nevező (Y(z)) gyökei szerint felírt résztörtekre.

$Y (z) = A_{1} \frac{z}{z - z_{1}} + A_{2} \frac{z}{z - z_{2}} + ... + A_{N} \frac{z}{z - z_{N}}$

(10.14)

alakra hozzuk, ahol

	$z_{1}, z_{2},........ z_{N}$	a nevező egyszeres gyökei,
	$A_{1}, A_{2},........ A_{N}$	állandók.

A meghatározott $A_{1}, A_{2},........ A_{N}$ együtthatók segítségével a megoldás idő tartományban

	${y_{k}} = A_{1} \cdot {z_{1}^{k}} + A_{2} \cdot {z_{2}^{k}} + ... + A_{N} \cdot {z_{N}^{k}}$	(10.15)
	$y [k] = A_{1} \cdot z_{1}^{k} + A_{2} \cdot z_{2}^{k} + ... + A_{N} \cdot z_{N}^{k}$	(10.16)

alakú lesz.

Egy tag rekurzív formulává történő visszaalakításánál az $y (k \cdot h) = \sum_{i = 1}^{N} [A_{i} \cdot x (k \cdot h) + z_{i} \cdot y ({k - 1} \cdot h)]$ alakú kifejezésben az A_i és z_i értékek a meghatározó paraméterek. N az elemek száma.

A résztörtekre bontás a nevező többszörös gyökei esetén is alkalmazható, ilyenkor a reziduum tétel segítségével határozzuk meg a függvényt.

10.2.2.3. Sorba fejtéssel

Az Y(z) függvényt, amely általában egy számláló (NUM(z)) és egy nevező (DEN(z)) polinomok hányadosaként jelenik meg, z^-1 hatványsorba fejtjük.

$\begin{array}{l} Y (z) = \frac{N U M (z)}{D E N (z)} = y_{0} + y_{1} \cdot z^{- 1} + y_{2} \cdot z^{- 2} + ... + y_{i} \cdot z^{- i} + ... \\ = \sum_{n = 0}^{\infty} y_{n} \cdot z^{- n} \end{array}$

(10.17)

A z^-1 hatványsor együtthatói a diszkrét számsorozat mintavételi időpontokban felvett értékeit fogják megadni. Ha Y(z) racionális törtfüggvény, a sorfejtést a számláló nevezővel való osztásával végezhetjük.

10.2.2.4. Diszkrét konvolúcióval

A diszkrét konvolúciós összeget ugyanúgy alkalmazhatjuk az inverz Z transzformáció meghatározásához a mintavételes rendszereknél, mint a koncolúciós integrált az inverz Laplace transzformációnál a folytonos rendszereknél.

Az inverz Z transzformációhoz alkalmazzuk az Y(z) függvényt, amelyet bontsuk fel két Z transzformált függvény szorzatára, (amelyek egyszerűbbek Y(z)-nél).

$Y (z) = Y_{1} (z) \cdot Y_{2} (z)$

(10.18)

Így Y(z) kifejezhető, mint a szorzatban szereplő Y₁(z) és Y₂(z) függvények z^-1 hatványaival felírt komponenseinek sorozatával.

$\begin{array}{l} Y (z) = [y_{1} [0] + y_{1} [1] \cdot z^{- 1} + y_{1} [2] \cdot z^{- 2} + ....] \cdot \\ \cdot [y_{2} [0] + y_{2} [1] \cdot z^{- 1} + y_{2} [2] \cdot z^{- 2} + ....] \end{array}$

(10.19)

A két függvény sorozat összeszorzásával a következő függvényt kapjuk:

$\begin{array}{l} Y (z) = [y_{1} [0] \cdot y_{2} [0]] \cdot z^{- 0} + \\ + [y_{1} [0] \cdot y_{2} [1] + y_{1} [1] \cdot y_{2} [0]] \cdot z^{- 1} + \\ + [y_{1} [0] \cdot y_{2} [2] + y_{1} [1] \cdot y_{2} [1] + y_{1} [2] \cdot y_{2} [0]] \cdot z^{- 2} + .... \end{array}$

(10.20)

Az y[k] általánosan leírható függvénye időtartományban:

$\begin{array}{l} y [n] = y_{1} [0] \cdot y_{2} [n] + y_{1} [1] \cdot y_{2} [n - 1] + .... + y_{1} [n] \cdot y_{2} [0] = \\ = \sum_{k = 0}^{n} y_{1} [k] \cdot y_{2} [n - k] = \sum_{k = 0}^{n} y_{1} [k - n] \cdot y_{2} [k] \end{array}$

(10.21)

ami nem más mint y₁[k] és y₂[k] diszkrét konvolúció függvénye.

Ezt az inverz Z transzformációs eljárást akkor érdemes alkalmazni, ha az y₁[k] és y₂[k] már eleve idősorozatként áll rendelkezésünkre.

A diszkrét konvolúciót általánosan a következő összefüggéssel határozhatjuk meg:

$y [k] = Z^{- 1} [Y_{1} (z) \cdot Y_{2} (z)] = y_{1} [n] * y_{2} [n]$

(10.22)

A * a konvolúciós szorzat, amelynek definícióját a 10.21 képlettel adtuk meg.

10.3. Egyszerű digitális szűrők

A digitális szűrők következő alaptípusait különböztetjük meg:

Véges impulzus válasz szűrő ( FIR = Finite Impulse Response ), más néven mozgó átlag szűrő ( MA = Moving Average )
Végtelen impulzus válasz szűrő ( IIR = Infinite Impulse Response ), más néven autoregressziós mozgó-átlag szűrő ( ARMA = Autoregressive Moving-Average )
Nemlineáris szűrő

A szűrők csoportosítása általában az impulzus bemeneti jelre adott válaszuk alapján történik.

10.3.1. Impulzusválasz

Az impulzus egy rövid idő alatt 0-tól a maximum értékig felfutó, majd szintén nagyon gyorsan a 0 értékre visszatérő jel. A 10.17. egyenlet matematikai alakban írja le az impulzust.

$\begin{array}{l} x_{0} = 1 \\ x_{i} = 0 h a i \neq 0 \end{array}$

(10.23)

Egy szűrő impulzus válasza a szűrő egy impulzusra adott válasza, és alakja függ a szűrő működési paramétereitől illetve a szűrő típusától. A 10.5. ábra ábra a különböző típusú szűrőket mutatja be.

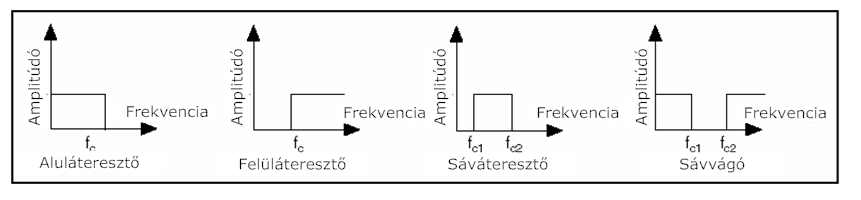
10.5. ábra - A különböző típusú szűrő karakterisztikák

Az impulzus válasz Fourier transzformáltja a szűrő frekvencia válasza.

A szűrő frekvencia válasza információt ad a szűrő frekvencia áteresztő képességéről a különböző frekvenciákon. Más szóval egy szűrő frekvenciaválasza megmutatja a szűrő erősítését különböző frekvenciákon. Egy ideális szűrő erősítése az átviteli sávban 1, a csillapítási sávban pedig 0. Egy ideális szűrő az átviteli sávban lévő összes frekvenciát változatlanul átengedi a kimenetre, illetve a csillapítási sáv frekvenciáit nem engedi a kimenetre.

10.3.2. Szűrők osztályozása impulzusválaszuk alapján

A szűrő impulzusválasza eldönti, hogy egy adott szűrő véges impulzus válaszú szűrő (FIR) vagy végtelen impulzus válaszú szűrő (IIR).

A véges impulzus válasz szűrő (FIR) kimeneti jele csak a jelenlegi és az előző bemeneti értékektől függ.

A végtelen impulzus válasz szűrő (IIR) kimeneti jele függ a jelenlegi és az ezt megelőző bemeneti értékektől, valamint a megelőző kimeneti értékektől is.

Egy pénztárgép példájával jól lehet szemléltetni a véges impulzus válasz szűrők (FIR) és a végtelen impulzus válasz szűrők (IIR) működése közötti különbséget.

A példában a következő feltételek adottak:

	x[k]	az aktuális árucikk ára, amelyet éppen beütöttünk a gépbe
	x[k–1]	eggyel korábban beütött árucikk ára
		1 ≤ k ≤ N
	N	az összes beütött árucikk darabszáma

A következő szabály leírja a pénztárgép működését:

A pénztárgép összeadja minden egyes (eddig) eladott árucikk árát, meghatározva ezzel az úgynevezett futó összeget y[k]-t.

A következő 10.18 egyenlet megadja az y[k]–t a k-dik árucikkig.

$y [k] = x [k] + x [k-1] + x [k-2] + x [k-3] + ... + x [1]$

(10.24)

Tehát N árucikk összege az y[N] lesz.

y[k] egyenlő 1-től a k-adik árucikkig az árak összegével. y[k-1] egyenlő (k-1)-ig bezáróan az árak összegével. Tehát a 10.24 egyenlet felírható a következő alakban is.

$y [k] = y [k-1] + x [k]$

(10.25)

Az összeghez hozzáadva 27.0% adót és leírva újra a 10.24 és 10.25 egyenletet, a következőket kapjuk.

	$\begin{array}{l} y [k] = 1 .27 \cdot x [k] + 1 .27 \cdot x [k- 1] + 1 .27 \cdot x [k- 2] + \\ 1 .27 \cdot x [k- 3] + ...... + 1 .27 \cdot x [1] \end{array}$	(10.26)
	$y [k] = y [k-1] + 1 .27 \cdot x [k]$	(10.27)

A 10.26 és 10.27 egyenletek azonos módon írják le a pénztárgép működését. Azonban a 10.26 egyenlet csak a bementet alkalmazza a működési leírásához, míg a 10.27 egyenlet a bemeneteket és kimeneteket egyaránt alkalmazza a folyamat jellemzéséhez.

A 10.26 egyenlet egy nem rekurzív , vagy FIR műveletet mutat be.

A 10.27 egyenlet egy rekurzív vagy IIR műveletet mutat be.

Azok az egyenletek, amelyek leírják a szűrő működését és olyan alakúak (felépítésűek), mint a 10.24, 10.25, 10.26 és 10.27 egyenletek, differencia-egyenletek .

A szűrők közül a véges impulzus válasz szűrőket (FIR) a legegyszerűbb tervezni. Ha egy egyszerű impulzus jelenik meg a véges impulzus válasz szűrő bemenetén, és az összes későbbi bemenő érték nulla, akkor a véges impulzus válasz szűrő kimenete véges idő múlva szintén nulla értékű lesz. Azt az időtartamot, amely alatt a szűrő kimenete beáll a nulla értékre, a szűrő együtthatóinak darabszáma határozza meg.

További információkat a véges impulzus válasz szűrőkről ezen fejezet FIR szűrők című részéből ismerhetünk meg.

Mivel a végtelen impulzus válasz szűrők (IIR) a jelenlegi és a korábbi bemeneti- valamint a korábbi kimeneti értékek alapján működnek, az ilyen szűrő impulzusválasza sohasem éri el a nulla értéket ezért, ezek végtelen válaszfüggvények. Ezzel az IIR szűrők című fejezet rész foglalkozik bővebben.

10.3.3. Szűrő együtthatók

A 10.24 egyenlet minden egyes tagjának 1.27 volt a szorzótényezője. A 10.25 egyenletben y[k–1] tagnak 1.0, az x[k] tagnak pedig 1.27 az szorzótényezője. Ezek a szorzótényezők a szűrő együtthatói . A végtelen impulzus válasz (IIR) szűrőre vonatkozó bemeneti szorzó tényezői az előreható együtthatók a kimeneti szorzóegyütthatók pedig a visszaható együtthatók .

10.4. Egy ideális szűrő jellemzői

Az ideális szűrőt nem lehet megvalósítani!

Az ideális szűrők lehetővé teszik egy megadott frekvenciasáv teljes (veszteségmentes) áteresztését, míg a nem kívánt frekvenciatartomány jeleit teljes egészében (maximálisan) elnyomják. Következő csoportosításban aszerint osztályozzuk a szűrőket, hogy egy frekvenciatartomány jeleit átengedik vagy elnyomják.

Aluláteresztő szűrők: átengedik az alacsony, és levágják a magas frekvenciájú jeleket
Felüláteresztő szűrők: átengedik a magas, és levágják az alacsony frekvenciájú jeleket
Sáváteresztő szűrők : egy bizonyos frekvenciatartomány jeleit átengedik
Sávvágó szűrők: egy bizonyos frekvencia tartomány jeleit nem engedik át

A 10.6. ábra ábra az egyes szűrő típusok frekvencia válaszait mutatja be. (f_c = f_cut)

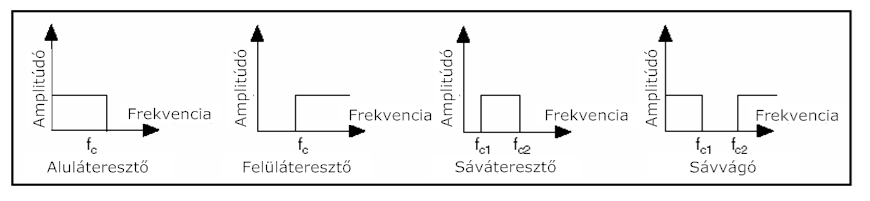
10.6. ábra - Ideális szűrők frekvencia válaszai

A (10.6. ábra) ábrán bemutatott szűrők a következő módon viselkednek:

Az aluláteresztő szűrő f_c alatt minden frekvenciát átenged.
A felüláteresztő szűrő f_c felett minden frekvenciát átenged.
A sáváteresztő szűrő f_c1 és f_c2 között minden frekvenciát átenged.
A sávvágó szűrő f_c1 és f_c2 között minden frekvenciát csillapít (levág).

Az f_c, f_c1, és f_c2 frekvencia pontok kijelölik a különféle szűrők határfrekvenciáit.

A szűrők tervezésénél ezeket a határfrekvenciákat kell megadnunk bemeneti adatként.

A szűrő átviteli sávja az a frekvenciatartomány, amelyet a szűrő átenged. Az ideális szűrő erősítése az átviteli sávban 1 (amely megfelel 0 dB erősítésnek), így a jel amplitúdója sem nem növekszik sem nem csökken.

A szűrő vágási sávja az a frekvenciatartomány, amelyet a szűrő teljes egészében levág. A (10.7. ábra) ábra az átviteli (PB = PassBand) és vágási sávot (SB = StopBand) mutatja az egyes szűrő típusokra.

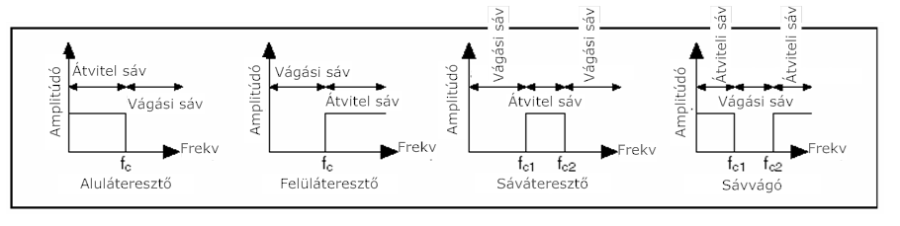
10.7. ábra - Átviteli sáv és vágási sáv

A (10.7. ábra) ábrán látható szűrők átviteli és vágási sávjait a következőképpen jellemezhetjük:

Az alul- és a felül-áteresztő szűrőknek egy átviteli és egy vágási sávjuk van.

A sáváteresztő szűrőnek egy átviteli és két vágási sávja van.

A sávvágó szűrőnek két átviteli és egy vágási sávja van.

10.5. Valóságos (nem ideális) szűrők

Ideális esetben egy szűrőnek egységnyi (0 dB) az erősítése az átviteli sávban, és nulla ( $- \infty$ dB) az erősítése a vágási sávban. A valóságos szűrők nem tudják teljesíteni egy ideális szűrővel szemben támasztott követelményeket. A gyakorlatban mindig van egy véges átmeneti sáv az átviteli és vágási sáv között. Az átmeneti sávban a szűrő erősítése fokozatosan változik egytől (0 dB) nulláig $- \infty$ dB) átviteli sávtól a vágási sávig.

10.5.1. Átmeneti sáv

A 10.8. ábra ábra bemutatja az átviteli, a vágási és az átmeneti sávokat a valós szűrő típusokra.

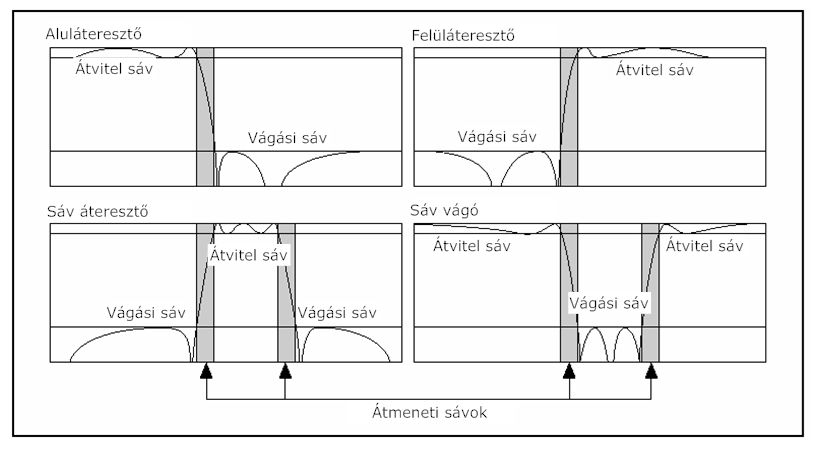
10.8. ábra - Nem ideális szűrők

A (10.8. ábra) ábrán az x-tengelyen ábrázoljuk a frekvenciát, y-tengelyen pedig a jel amplitúdó átvitelének arányát deciBel-ben (dB). Az átviteli sáv tartományában a szűrő erősítése 0 dB-től -3 dB-ig változik.

10.5.2. Átviteli sáv ingadozása és vágási sáv csillapítása (ripple)

Sok alkalmazásban megengedhetjük, hogy az átviteli sáv erősítése kis mértékben eltérjen az egységnyi (1) értéktől. Ez az eltérés az átviteli sáv ingadozása , vagyis a különbség a valóságos és az ideális egységnyi erősítés között. A gyakorlatban nem valósítható meg, hogy a vágási sáv csillapítása végtelen legyen, ezért meg kell állapítani egy megfelelő nagyságú értéket. Az átviteli sáv ingadozását, és a határfrekvencia csillapítását megadhatjuk dB egységben. 10.28 egyenlet szerint.

$d B = 20 \cdot \lg (\frac{A_{0} (f)}{A_{i} (f)})$

(10.28)

Ahol lg a 10-es alapú logaritmust jelenti, $A_{i} (f)$ egy f részfrekvencia amplitúdója szűrés előtt, és $A_{0} (f)$ egy f részfrekvencia amplitúdója szűrés után.

Ha ismerjük az átviteli sáv hullámosságát, vagy a vágási sáv csillapítását, akkor a 10.28 egyenlettel meghatározhatjuk a bemenő és kimenő amplitúdók arányát. Az amplitúdók aránya megmutatja, hogy az átviteli vagy vágási sáv milyen mértékben térnek el az ideálistól.

Például amikor az átviteli sáv ingadozása 0.02 dB, a 10.29 egyenletből a következő összefüggés írható fel.

	$- 0.02 = 20 \cdot \lg (\frac{A_{0} (f)}{A_{i} (f)})$	(10.29)
	$\frac{A_{0} (f)}{A_{i} (f)} = 10^{- 0.001} = 0.9977$	(10.30)

A 10.29 és 10.30 egyenletek megmutatják, hogy a bemenő és kimenő amplitúdók arányának mekkora az eltérése az egytől, amely az átviteli sáv ideális esetben. A gyakorlatban, szűrő tervezésekor megpróbálják megközelíteni a megkívánt ideális intenzitásfüggvényt, bizonyos megszorításokkal korlátozva.

A Táblázat 10.2 táblázat összehasonlítja a valós és az ideális szűrők jellemzőit.

10.2. táblázat - Ideális és valóságos szűrők jellemzői

Jellemző	Ideális szűrő	Valós szűrő
Átviteli sáv	Lapos és állandó	Hullámos lehet
Csillapítási sáv	Lapos és állandó	Hullámos lehet
Átmeneti sáv	Nincs	Van(nak) átmeneti sáv(ok)

A valós szűrők tervezésekor kompromisszumra törekszünk, hogy a kívánt szűrő jellemzőt kiemeljük a kevésbé kívánt jellemzők rovására. Választásunkat két dolog befolyásolja, azaz hogy véges impulzus válasz szűrőről (FIR) vagy végtelen impulzus válasz szűrőről (IIR) van-e szó, illetve, hogy milyen a szűrőalgoritmus felépítése.

10.6. Mintavételi idő

A szűrő sikeres működéshez fontos a megfelelően megválasztott mintavételi idő. A vizsgált jel maximális frekvencia összetevője általában meghatározza a szükséges mintavételi frekvenciát.

Rendszerint a vizsgált jel Fourier transzformáltja legnagyobb frekvenciájú összetevőjének 10-szeresét (általában) már elegendő mintavételi frekvenciának választani!

Ha a határfrekvencia túl közel van a Nyquist frekvenciához, növelni kell a mintavételi frekvenciát. Ha a határfrekvencia túl közel van az egyenfeszültséghez (0 Hertz), akkor csökkenteni kell a mintavételi frekvenciát.

Általában csak akkor változtassunk a mintavételi frekvencián, ha ütközési problémák fordulnak elő.

10.7. Véges impulzus válasz (FIR) szűrők

Véges impulzus válasz szűrők ( FIR szűrők ) olyan digitális szűrők, amelyeknek időben véges hosszúságú impulzusválaszuk van. A véges impulzus válasz szűrők működésükkor csak az aktuális és az előző bemeneti értéket veszik figyelembe a szűrő algoritmusában. Az ilyen típusú szűrőket a legegyszerűbb megtervezni. A véges impulzus válasz szűrők más néven is ismertek, mint nem visszatérő (nem rekurzív), konvolúciós , vagy mozgó átlag (MA) szűrők .

A véges impulzus válasz szűrők a szűrő-együtthatók konvolúcióját végzik a bemenő értékek egy sorozatán, és létrehozzák a kimeneti értékek (azonosan sorszámozott) sorozatát. A 10.25. egyenlet egy véges impulzus válasz szűrő véges konvolúcióját adja meg.

$y [k] = \sum_{i = 0}^{N_{b}} b_{i} \cdot x [k - i]$

(10.31)

ahol

	x[k-i]	a szűrő bemenő jelének értéke az [k-i]-ik időpillanatban,
	y[k]	a szűrt kimenő jel értéke az [k]-ik időpillanatban,
	b _i	a szűrő (FIR szűrő) i-ik együtthatója
	N _b	a szűrő együtthatóinak száma (fokszáma).

A véges impulzus válasz szűrők (FIR szűrők) a következő tulajdonságokkal rendelkeznek:

A FIR szűrők lineáris fázismenetet valósítanak meg, mert a szűrő együtthatói szimmetrikusak.

A FIR szűrők mindig stabil működésűek.

A FIR szűrők a jelek szűrését a konvolúció alkalmazásával teszik lehetővé. Ezért általában a kimenő sorozat mindig tartalmaz késleltetést , amelyet a következő egyenletben láthatunk

A kimenő jel késleltetése mintavételi lépésben = $\frac{N_{b} - 1}{2}$ .

A 10.9. ábra ábra bemutatja egy FIR szűrő tipikus amplitúdó- és fázisfüggvényét, összehasonlítva a normalizált frekvenciával.

10.9. ábra - FIR szűrő amplitúdó és fázis függvénye összehasonlítva a normalizált frekvenciával

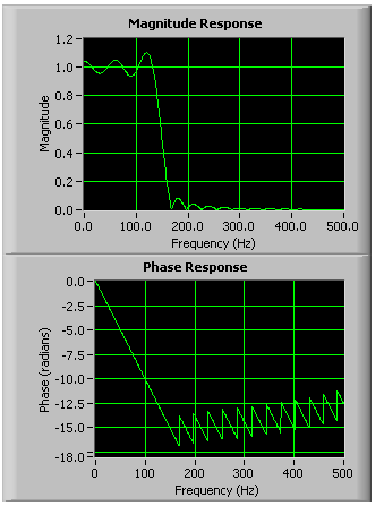
A (10.9. ábra) ábrán, a fázis-függvényben lévő szakadások akkor keletkeznek, amikor az abszolút értéket használjuk az amplitúdó függvény meghatározásához. A fázis jelleggörbe szakadásai PI (π = 3.14) egész számú többszöröseinél vannak, bár a fázisfüggvény teljesen lineáris.

10.7.1. Leágaztatások (Taps)

A leágaztatás kifejezés gyakran feltűnik a véges impulzus válasz szűrők (FIR szűrők) leírásaiban. A 10.10. ábra ábra illusztrálja a leágaztatás műveletét.

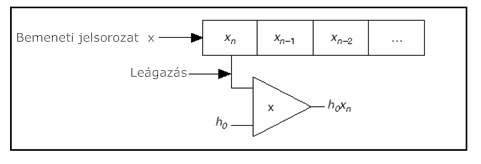
10.10. ábra - Leágaztatás

A 10.10. ábra ábra bemutatja a bemenő mintákat

{ $x [k], x [k - 1], ..., x [k - N_{b}]$ }

(10.32)

tartalmazó N_b-elemű shift regisztert.

A leágaztatás kifejezés a shift regiszter leágaztatásának működéséből ered.

A taps kifejezés általában a FIR szűrő együtthatóinak számára utal.

10.7.2. Véges impulzus válasz szűrők (FIR szűrők) tervezése

Egy diszkrét rendszer előírt frekvenciafüggvényét (legjobban) közelítve tervezünk véges impulzus válasz szűrőket (FIR). A legtöbb általános tervezési módszer jól közelíti a kívánt amplitúdó függvényt, emellett, hogy egy jó lineáris fázis menetet biztosít.

A lineáris fázis menet azt jelenti, hogy a jel terjedési késleltetése azonos minden frekvencián a rendszerben.

A 10.11. ábra ábra egy VI blokkdiagramot mutat be, amely egy egyenletes hullámosságú sáváteresztő véges impulzus válasz szűrő (FIR szűrő) frekvenciafüggvényét adja meg.

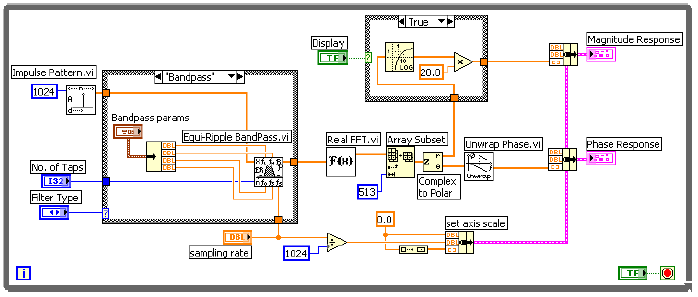
10.11. ábra - Egyenletes hullámosságú sáváteresztő FIR szűrő frekvenciafüggvénye

A (10.11. ábra) ábrán látható VI a következő lépéseket hajtja végre, amikor kiszámítja a szűrő frekvenciafüggvényét:

Egy impulzus jellel gerjesztjük a szűrőt.
A case-struktúra (case = eset) meghatározza a szűrő típusát, hogy az alul- vagy felül-áteresztő, sávvágó vagy sáváteresztő. A case-struktúrából kijövő jel a szűrő impulzusválasza.
A case-struktúrából kijövő impulzusválaszon a FFT.VI diszkrét Fourier-transzformációt végez, és meghatározza a szűrő frekvenciafüggvényét úgy, hogy az impulzusválasz és a frekvenciafüggvény alkotják a Fourier-transzformáltat, h(t) az impulzusválasz. H(w) a frekvenciafüggvény.
Az FFT.VI által kibocsátott adatokat redukálja a Array Subset függvénnyel. A valódi FFT eredményeinek fele ismétlődik, ezért a VI – nek elegendő az FFT.VI által kibocsátott adatok felét feldolgoznia.
A Complex to Polar függvénnyel előállítja az FFT.VI-ből kapott adatok amplitúdó és fázis függvényét. Az FFT.VI komplex kimenetének amplitúdó/fázis alakját egyszerűbb értelmezni, mint az FFT Descartes koordinátájú komponenseit.
A fázis értékeket átalakítja fokokra.
Az amplitúdó értékeket átalakítja deciBel-ekké (dB).

A 10.12. ábra ábra a VI által, a 10.11. ábra ábra szerint megvalósított szűrő amplitúdó-és fázisfüggvénye.

10.12. ábra - Egy egyenletes hullámosságú sáváteresztő FIR szűrő amplitúdó és fázisfüggvénye

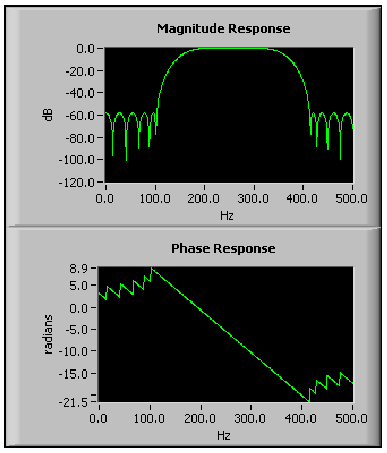
A (10.12. ábra) ábrán, amikor az abszolút értéket alkalmazunk, hogy kiszámítsuk az amplitúdó függvényt, szakadások keletkeznek, ezek okoznak a fázisgörbén is szakadásokat. A fázisgörbe azonban egy lineáris függvény, mivel a rendszerben minden frekvenciának azonos a terjedési késleltetése.

Mivel a véges impulzus válasz szűrők (FIR szűrők) intenzitásgörbéje hullámos, a FIR szűrők tervezésekor a következő feladatokat kell megoldani:

Szűrő tervezése az ideálishoz lehető legközelebb eső amplitúdó függvénnyel;

Szűrő tervezése , amely a hullámosságot előírt módon osztja el;

Például egy aluláteresztő szűrő rendelkezik egy ideális amplitúdó függvény alakkal. Egy valóságos alkalmazás megengedhet egy kis hullámosságot az átviteli sávban, és egy kicsivel többet a vágási sávban. A szűrő konstrukció algoritmusának egyensúlyban kell tartania a viszonylagos hullámosságot és az éles átmeneti sávot.

A leggyakrabban alkalmazott módszerek a véges impulzus válasz szűrők (FIR szűrők) tervezéséhez az ablakozás és a Parks-McClellan algoritmus , amely úgy is ismert, mint a Remez-csere módszer .

10.7.3. Véges impulzus válasz szűrők (FIR szűrők) tervezése ablakozással

A témakör elméletét a 7.1.3.4. szakasz fejezetben már tárgyaltuk, most a gyakorlati alkalmazást tekintjük át.

A legegyszerűbb módszer véges impulzus válasz szűrők (FIR szűrők) tervezésére az ablakozás, mert a megvalósítása kényelmes és egyszerű. A FIR szűrők ablakozással való tervezése az amplitúdó függvény inverz FFT-ját adja és egy simító ablakot alkalmaz.

A simító ablak egy idő dimenziójú ablak.

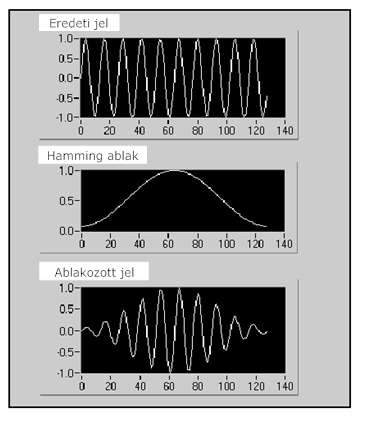
10.13. ábra - Hamming-ablakkal ablakozott jel

Egy FIR szűrő ablakozással történő tervezéséhez a következő lépéseket kell elvégezni:

Meg kell határozni egy ideális frekvenciafüggvényt;

Meg kell határozni az ideális frekvenciafüggvény impulzusválaszát;

Az impulzusválaszt le kell rövidíteni, hogy véges számú együtthatóból álljon;

Szimmetrikus simító ablakot kell alkalmazni.

Az ideális impulzusválasz megcsonkítása a Gibbs-jelenségben nyilvánul meg. A Gibbs-jelenség a határfrekvenciák közelében lengő viselkedésként jelenik meg a FIR szűrő frekvenciafüggvényében. Ezt a jelenséget tudjuk gyengíteni olyan módon, hogy simító ablakot használunk, így ”kisimítjuk” az ideális impulzusválasz frekvencia vágását. A FIR együtthatókat csökkentve a végeken, csökkenthetjük a frekvenciafüggvény oldalsó hurkainak magasságát. Azonban ha csökken a hurkok magassága, akkor kiszélesedik a főhurok, és a határfrekvenciáknál szélesebb lesz az átmeneti sáv.

Egy simító ablak kiválasztásához kompromisszum szükséges a határfrekvenciák közelében lévő oldalhurkok magassága, és az átmeneti sáv szélessége között. Csökkentve az oldalhurkok magasságát, növekszik az átmeneti sáv szélessége. Csökkentve az átmeneti sáv szélességét, növekszik az oldalhurkok magassága a határfrekvenciák közelében.

Az ablakozásos FIR szűrő tervezésnek a következő hátrányai vannak:

Nincs figyelemmel a következőkre

Az ablakozás egyenlőtlen fodrozódás eloszlást okoz.
Az ablakozás szélesebb átviteli sávot eredményez, mint más tervezési módszerek.
Nehézségek jelentkeznek a paraméterek pontos meghatározásban
Az ablakozás nehezíti a határfrekvencia meghatározását, amely egy megadott csillapítással rendelkezik.
A szűrő tervezőjének meg kell határoznia:
- az ideális vágási frekvenciát.
- a mintavételi frekvenciát.
- a leágazások számát.
- az alkalmazott ablak típusát.

A FIR szűrők ablakozással való tervezése nem igényel bonyolult számítási műveleteket. Ezért az ablakozás a leggyorsabb módszer FIR szűrők tervezésénél. Viszont az ablakozás nem a legjobb technika FIR szűrők tervezéséhez.

10.7.4. Optimális FIR szűrők tervezése a Parks-McClellan algoritmussal

A Parks-McClellan algoritmus, vagy a Remez-csere módszer, egy hiba kritériumon alapuló iteráló módszert alkalmaz a FIR szűrő együtthatóinak meghatározására. A Parks-McClellan algoritmust a legkedvezőbb lineáris fázismenetű FIR szűrő együtthatóinak tervezésére alkalmazhatjuk. A Parks-McClellan algoritmussal tervezett szűrők optimálisak lesznek, mert a szűrő aktuális amplitúdó függvénye és a szűrő ideális amplitúdó függvénye között minimálisra csökkennek a hibák.

Az optimális FIR szűrők lecsökkentik az ellentétes hatásokat a határfrekvenciáknál. Az optimális FIR szűrők tervezése nagyobb ellenőrzési lehetőséget kínál közelítési hibák felett, különböző frekvencia sávokban, mint egyéb más FIR szűrő tervező technikák, mint például az ablakozás, amely nem nyújt ellenőrzési lehetőséget a különböző frekvencia sávokban a közelítési hibákra.

Optimális FIR szűrőket a Parks-McClellan algoritmussal tervezhetünk, amelyeknek a következő a jellemzői vannak:

Az amplitúdó függvény súlyozott hullámossága egyenletesen oszlik el az átviteli és a vágási sávokban.
Éles átmeneti sávja van.

Ha a FIR szűrőket a Parks-McClellan algoritmussal tervezzük, egy optimális amplitúdó függvényt kapunk. A tervezés folyamata bonyolultabb és számításigényesebb, mint az ablakozásnál.

10.7.5. Egyenletes hullámosságú FIR szűrők tervezése Parks-McClellan algoritmus alkalmazásával

A Parks-McClellan algoritmust használhatjuk egyenletes hullámosságú FIR szűrők tervezésére. Az egyenletes hullámosságú konstrukció egyenlően osztja el az átviteli és a vágási sáv ingadozását, és lineáris fázismenetű szűrőket hoz létre.

Ahhoz, hogy egy egyenletes hullámosságú szűrőt tervezzünk, meg kell határozni a következő jellemzőket:

Határfrekvencia
Leágazások száma
Szűrő típusa, azaz aluláteresztő, felüláteresztő, sáváteresztő, vagy sávvágó
Átmeneti frekvencia
Vágási frekvencia

Az egyenletes hullámosságú szűrők határfrekvenciája megszabja az átviteli sáv, vagy a vágási sáv élét, vagy mindkettőt. Az egyenletes hullámosságú szűrők vágási és átviteli sávjának ingadozása okozza a következő impulzusválaszokat:

Átviteli sáv - az intenzitásfüggvény nagyobb vagy egyenlő, mint 1

Vágási sáv - az intenzitásfüggvény kisebb vagy egyenlő, mint a vágási sáv csillapítása

Például ha veszünk egy aluláteresztő szűrőt, az átviteli sáv határfrekvenciája a legnagyobb frekvencia, amelyre az átviteli sáv feltételei teljesülnek. Hasonlóképpen a vágási sáv határfrekvenciája a legalacsonyabb frekvencia, amelyre a vágási sáv feltételei teljesülnek

10.7.6. Keskeny sávú FIR szűrők tervezése

A különlegesen szűk sávszélességű FIR szűrők hagyományos módszerekkel történő tervezése nagy elemszámú szűrőt eredményezne. A nagy elemszámú FIR szűrők hosszú tervezési és kivitelezési időt igényelnek, valamint számítási pontatlanságra hajlamosak. Néhány esetben a hagyományos tervezési módszerek, mint a Parks-McClellan algoritmus, sem tudnak elfogadható szűk sávú FIR szűrőt meghatározni.

Az interpolációs véges impulzus válasz (IFIR) típusú szűrőtervezési módszer egy hatékony algoritmust ajánl a keskeny sávú FIR szűrők tervezésére. Az IFIR módszert alkalmazva olyan keskeny sávú szűrőket lehet tervezni, amelyek kevesebb együtthatót, és számítást igényelnek, mint ha a Parks-McClellan algoritmust közvetlenül végrehajtva tervezünk szűrőt. A „FIR keskeny sáv együtthatók.VI” (FIR Narrowband Coefficients.VI) az IFIR módszert alkalmazza a keskeny sávú FIR szűrő együtthatók meghatározására.

A következő paramétereket kell megadnunk, amikor keskeny sávú szűrőt tervezünk:

Szűrő típus: aluláteresztő, felüláteresztő, sáváteresztő, sávvágó
Átviteli sáv ingadozás egy lineáris skálán
Mintavételi frekvencia
Átviteli sáv frekvencia, ami a sáváteresztő és sávvágó szűrők átviteli sávjára vonatkozik
Vágási sáv frekvencia, ami a sáváteresztő és sávvágó szűrők vágási sávjára vonatkozik
Sáváteresztő és sávvágó szűrők középfrekvenciája
Vágási sáv csillapítása dB-ben

A 10.14. ábra ábra annak a VI–nek a blokkdiagramját mutatja, amely egy keskeny sávú sáváteresztő FIR szűrő frekvenciafüggvényének becslését állítja elő, az impulzusválaszt frekvenciatartományba transzformálva.

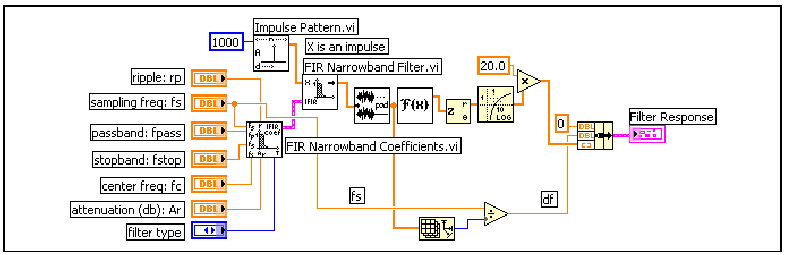
10.14. ábra - Keskeny sávú FIR szűrő frekvenciaválaszának becslése

A 10.15. ábra ábra bemutatja azt a válaszfüggvényt 0-tól a Nyquist frekvenciáig, ami a (10.14. ábra) ábrán lévő VI impulzusgerjesztésre adott eredménye .

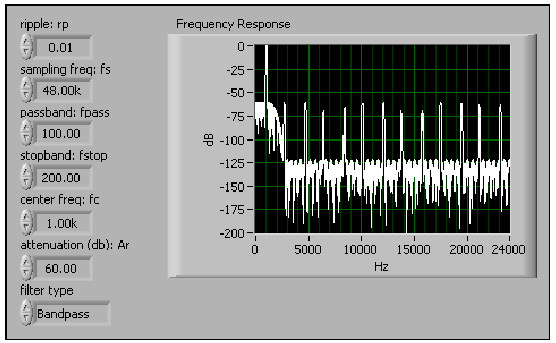
10.15. ábra - Szűk sávú sáváteresztő FIR szűrő, 0-tól a Nyquist frekvenciáig tartó, becsült frekvenciagörbéje

A (10.15. ábra) ábrán a főpanel szabályzóival beállított szűrő válaszfüggvénye az 1 kHz középvonalú keskeny átviteli sáv.

A 10.16. ábra ábra a szűrő válaszfüggvényének részletét mutatja.

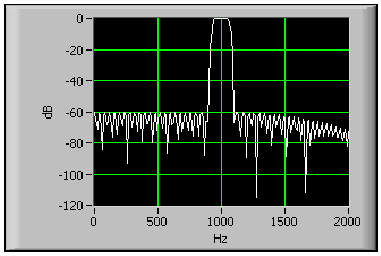
10.16. ábra - Keskeny sávú sáváteresztő FIR szűrő becsült frekvenciamenetének részlete

A (10.16. ábra) ábrán a keskeny átviteli sáv pontosan 1 kHz-re központosítva és a jel csillapítása 60 dB-lel az átviteli sáv alatt van.

10.7.7. Széles sávú FIR szűrők tervezése

Az IFIR technikát alkalmazhatjuk a széles sávú alul-, és felüláteresztő FIR szűrő tervezéséhez is. Egy széles sávú aluláteresztő FIR szűrőnek egy határfrekvenciája van, közel a Nyquist frekvenciához. A szélessávú felüláteresztő FIR szűrőnek egy 0-hoz közeli határfrekvenciája van. Használhatjuk szélessávú alul, -és felüláteresztő FIR szűrők tervezésére a FIR keskeny sávú együtthatók VI–t. A 10.16. ábra ábra bemutatja azt a frekvenciafüggvényt, amelyet a (10.14. ábra) ábrán látható VI hoz létre, amikor arra használjuk, hogy egy szélessávú aluláteresztő FIR szűrő frekvenciafüggvényét meghatározzuk.

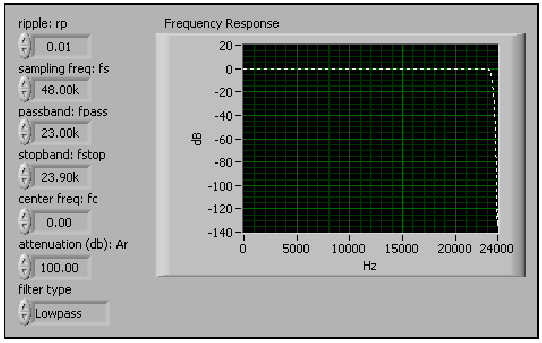
10.17. ábra - Szélessávú aluláteresztő szűrő frekvenciaválasza 0-tól a Nyquist frekvenciáig

A (10.17. ábra) ábrán lévő főpanel szabályzói beállítanak egy szűk sávszélességet a 23.9 kHz-es vágási sáv és a 24 kHz-es Nyquist frekvencia között. Azonban a frekvenciafüggvény 0-tól 23.9 kHz-ig fut, amely miatt a szűrő szélessávúvá válik.

10.8. Végtelen impulzus válasz (IIR) szűrők

A végtelen impulzus válasz szűrők (IIR = Infinite Impulse Response), más néven rekurzív vagy autoregresszív mozgó átlag (ARMA) szűrők az aktuális és a korábbi bementi értékek, valamint a korábbi kimeneti értékek szerint működnek.

Egy IIR szűrő impulzusválasza alatt értjük az általános IIR szűrőnek egy olyan impulzusra adott válaszfüggvényét, amelyet a 10.27. egyenlet definiál. Elméletileg egy IIR szűrő impulzusválasz függvénye soha nem éri el a nulla értéket, ez tehát egy végtelen válaszfüggvény. A következő általános differencia-egyenlet az IIR szűrő működését írja le:

$y [k] = \frac{1}{a_{0}} \cdot (\sum_{j = 0}^{N_{b}} b_{j} \cdot x [k - j] - \sum_{i = 1}^{N_{a}} a_{i} \cdot y [k - i])$

(10.33)

ahol

	b _j	az előreható szűrőegyütthatók halmaza,
	N _b	az előreható szűrőegyütthatók száma,
	a _i	a visszafelé ható szűrőegyütthatók halmaza,
	N _a	pedig a visszaható szűrőegyütthatók száma.

Ezt impulzusátviteli függvény formában felírva:

$H (z) = \frac{Y (z)}{X (z)} = \frac{b_{0} + b_{1} \cdot z^{_{- 1}} + b_{2} \cdot z^{_{- 2}} + ... + b_{N b} \cdot z^{_{- N b}}}{a_{0} + a_{1} \cdot z^{_{- 1}} + a_{2} \cdot z^{_{- 2}} + ... + a_{N a} \cdot z^{_{- N a}}}$

(10.34)

ahol

	$b_{0}, b_{1},........ b_{N b}$ ,
	$a_{0}, a_{1},........ a_{N a}$	állandó együtthatók,
	N _b, N_a	pedig pozitív egészek

Ha a nevezőkkel elvégezzük a beszorzásokat, akkor

$\begin{array}{l} a_{0} \cdot Y (z) + a_{1} \cdot z^{_{- 1}} \cdot Y (z) + a_{2} \cdot z^{_{- 2}} \cdot Y (z) + ... + a_{N a} \cdot z^{_{- N a}} \cdot Y (z) = \\ = b_{0} \cdot X (z) + b_{1} \cdot z^{_{- 1}} \cdot X (z) + b_{2} \cdot z^{_{- 2}} \cdot X (z) + ... + b_{n b} \cdot z^{_{- N b}} \cdot X (z) \end{array}$

(10.35)

Behelyettesítve az

	$Y (z) = \sum_{k = 0}^{\infty} y [k] \cdot z^{- k}$	(10.36)
	$X (z) = \sum_{k = 0}^{\infty} x [k] \cdot z^{- k}$	(10.37)

a következő összefüggést kapjuk:

	$\sum_{i = 0}^{N a} a_{i} \cdot z^{- i} [\sum_{k = 0}^{\infty} y [k] \cdot z^{- k}] = \sum_{j = 0}^{N b} b_{j} \cdot z^{- j} [\sum_{k = 0}^{\infty} x [k] \cdot z^{- k}]$	(10.38)
	$\sum_{i = 0}^{N a} a_{i} \cdot [\sum_{k = 0}^{\infty} y [k] \cdot z^{- k}] \cdot z^{- i} = \sum_{j = 0}^{N b} b_{j} \cdot [\sum_{k = 0}^{\infty} x [k] \cdot z^{- k}] \cdot z^{- j}$	(10.39)

Az eltolási tételt és az inverz Z transzformációt alkalmazva a kifejezés a következő alakú lesz:

$\sum_{i = 0}^{N a} a_{i} \cdot y [k - i] = \sum_{j = 0}^{N b} b_{j} \cdot x [k - j]$

(10.40)

A kifejezést összegzési alakban felírva a következő kifejezést kapjuk:

$\begin{array}{l} a_{0} \cdot y [k] + a_{1} \cdot y [k - 1] + ... + a_{N a} \cdot y [k - N_{a}] = \\ = b_{0} \cdot x [k] + b_{1} \cdot x [k - 1] + ... + b_{N b} \cdot x [k - N_{b}] \end{array}$

(10.41)

Az egyenletben szereplő $y [k], y [k - 1],... y [k - N_{a}]$ a (szabályozó) kimeneti számsorozatának, $x [k], x [k - 1],... x [k - N_{b}]$ , pedig a bemeneti számsorozat pillanatnyi és megelőző értékei.

Ha kifejezzük a kimeneti számsorozat aktuális értékét, akkor ehhez az alábbi rekurzív összefüggést kapjuk:

$\begin{array}{l} y [k] = \frac{b_{0}}{a_{0}} \cdot x [k] + \frac{b_{1}}{a_{0}} \cdot x [k - 1] + ... + \frac{b_{N b}}{a_{0}} \cdot x [k - N_{b}] \\ - (\frac{a_{1}}{a_{0}} \cdot y [k - 1] + \frac{a_{2}}{a_{0}} \cdot y [k - 2] + ... + \frac{a_{N a}}{a_{0}} \cdot y [k - N_{a}]) \end{array}$

(10.42)

Ha tehát H(z) racionális törtfüggvény, akkor H(z)-nek megfelelő számítási egyenlet lineáris differenciaegyenlet.

A z^-1 hatványaival felírt racionális törtfüggvény alakban megadott H(z) átviteli függvény realizálhatóságának feltétele: a₀<>0.

A mintavételes rendszereknél nem szükséges az Nb $\leq$ Na feltétel a megvalósításhoz z^-1 hatványaival felírt racionális törtfüggvény alakban megadott H(z) esetén.

A 10.33. egyenlet egy olyan szűrőt ír le, amelynek elméletileg végtelen hosszúságú az impulzusválasza és értéke nem egyenlők nullával. Azonban a gyakorlati szűrési feladatokban egy stabil IIR szűrő impulzusválasza véges számú mintavétel után gyakorlatilag közel 0 szintre csökken.

A legtöbb IIR szűrő konstrukcióban és az összes LabVIEW IIR szűrőnél az a ₀ együtthatójuk egyenlő 1-el . Az aktuális k indexű kimenő mintaérték, a előreható együtthatókkal megszorzott aktuális bemenetek és korábbi bemeneti értékeket, valamint a kimeneti együtthatókkal megszorzott korábbi kimeneti értékek összegeként adódik, ahogy azt a 10.43. egyenlet is mutatja.

$y [k] = \sum_{j = 0}^{N_{b}} b_{j} \cdot x [k - j] - \sum_{i = 1}^{N_{a}} a_{i} \cdot y [k - i]$

(10.43)

ahol

	x[k]	az aktuális bemeneti érték,
	y[k]	az aktuális kimeneti érték,
	x[k-j]	a korábbi bemeneti értékek,
	y[k-i]	a korábbi kimeneti értékek.

Az IIR szűrőknek ingadozásaik lehetnek az átviteli sávban, a vágási sávban, vagy mindkettőben.

Az IIR szűrőknek nemlineáris fázisfüggvénye van.

10.8.1. Az IIR szűrés kaszkádképlete

A 10.44. egyenlet egy IIR szűrő közvetlen formájú impulzus-átviteli függvénye (a₀=1 esetén).

$H (z) = \frac{Y (z)}{X (z)} = \frac{b_{0} + b_{1} \cdot z^{- 1} + ... + b_{N_{b}} \cdot z^{- N_{b}}}{1 + a_{1} \cdot z^{- 1} + ... + a_{N_{a}} \cdot z^{- N_{a}}}$

(10.44)

A 10.44. egyenletnél a 10.33. differencia-egyenlet alakjából nyert formájú szűrőt nevezzük közvetlen alakú IIR szűrőnek .

Egy közvetlen alakú szűrő érzékeny az együtthatók számából és a számítási pontosság határaiból adódó hibákra. Egy eredetileg stabil konstrukciójú szűrő is instabillá válhat, ha megnöveljük az együtthatók számát. Ahogy a szűrő fokszáma növekszik, a szűrő egyre instabilabbá válik.

Csökkenthetjük egy szűrő hibákra való érzékenységét, ha felírjuk a 10.44. egyenletet, mint a Z transzformált tényezők szorzatát. Így alacsonyabb fokú részekre osztjuk fel a közvetlen alakú átviteli függvényt.

A 10.44. egyenlet tényezőkre bontásával, a szűrő impulzus-átviteli függvénye átalakul másodfokú impulzus-átviteli függvények szorzatává, ahogy a 10.45. egyenletben láthatjuk.

$H (z) = \prod_{n = 1}^{N_{s}} \frac{b_{0 n} + b_{1 n} \cdot z^{- 1} + b_{2 n} \cdot z^{- 2}}{1 + a_{1 n} \cdot z^{- 1} + a_{2 n} \cdot z^{- 2}}$

(10.45)

ahol N_s a másodfokú részfüggvény sorszáma, $N_{s} = ⌊ \frac{N_{a}}{2} ⌋$ a legnagyobb egész szám $\leq \frac{N_{a}}{2}$ , és $N_{a} \geq N_{b}$ .

A 10.39. egyenlet szerint definiált szűrő felépítését úgy ábrázolhatjuk, mint egy olyan szűrőt, amely másodfokú szűrők sorba kapcsolásából áll. A 10.18. ábra ábra a kaszkádszűrést mutatja be.

10.18. ábra - Kaszkád szűrés sorba kapcsolt fokozatai

Az egyes önálló szűrő tagokból a 10.18. ábra ábra alapján felépíthetjük a végtelen impulzusválasz (IIR) közvetlen alakú szűrő struktúrát.

A végtelen impulzusválasz (IIR) közvetlen alakú szűrő struktúrát úgy kell kialakítani, hogy a szűrőben szereplő egyes tagok a következő feltételek szerint működjenek:

A végtelen impulzusválasz (IIR) közvetlen alakú szűrő felépítése minimális számú matematikai műveletet igényel,
Minimális számú késleltető elemre, és belső szűrő állapotra van szüksége.
Minden egyes k-adik tagnak van egy bemenete, egy kimenete, és két előző belső állapota amelyek: $m_{d} [k - 1]$ és $m_{d} [k - 2]$ .

Ha n a minták száma a bementő sorozatban, akkor a szűrés a következő egyenletek szerint zajlik:

$\begin{array}{l} y_{0} [k] = x [k] \\ m_{d} [k] = y_{d - 1} [k - 1] - a_{1 d} \cdot m_{d} [k - 1] - a_{2 d} \cdot m_{d} [k - 2] d = 1,2, \dots, N_{s} \\ y_{d} [k] = b_{0 d} \cdot m_{d} [k] + b_{1 d} \cdot m_{d} [k - 1] + b_{2 d} \cdot m_{d} [k - 2] d = 1,2, \dots, N_{s} \end{array}$

(10.46)

Minden egyes mintára ahol k= 0, 1, 2, … , n–1 .

az egyenletek a következő függvényből erednek:

$H (z) = \frac{Y (z)}{X (z)} = \frac{b_{0} + b_{1} \cdot z^{- 1} + b_{2} \cdot z^{- 2}}{1 + a_{1} \cdot z^{- 1} + a_{2} \cdot z^{- 2}}$

(10.47)

egy új bevezetett változóval M(z)-vel kifejezzük Y(z)-t:

$Y (z) = (b_{0} + b_{1} \cdot z^{- 1} + b_{2} \cdot z^{- 2}) \cdot M (z)$

(10.48)

amely időtartományban

$y [k] = b_{0} \cdot m [k] + b_{1} \cdot m [k - 1] + b_{2} \cdot m [k - 2]$

(10.49)

ahol

	$M (z) = \frac{X (z)}{1 + a_{1} \cdot z^{- 1} + a_{2} \cdot z^{- 2}}$	(10.50)
	$M (z) + a_{1} \cdot z^{- 1} \cdot M (z) + a_{2} \cdot z^{- 2} \cdot M (z) = X (z)$	(10.51)
	$M (z) = X (z) - a_{1} \cdot z^{- 1} \cdot M (z) - a_{2} \cdot z^{- 2} \cdot M (z)$	(10.52)

ami időtartományban

$m [k] = x [k] - a_{1} \cdot m [k - 1] - a_{2} \cdot m [k - 2]$

(10.53)

10.8.2. Másodfokú szűrés

Alul-, és felüláteresztő szűrők helyett, amelyeknek egy határfrekvenciájuk van, tervezhetünk közvetlenül másodfokú szűrő fokozatokat. Az így kapható alul-, és felül áteresztő végtelen impulzusválasz ( IIR ) szűrők sorba kapcsolt másodfokú szűrőkből épülnek fel.

Minden másodfokú szűrő fokozat a következő jellemzőkkel rendelkezik:

d = 1,2, …,N_s, ahol k a másodfokú szűrő fokozat sorszáma,
N_s a fokozatok száma = (N_a+1)/2.
Minden másodfokú szűrő fokozatnak két visszaható együtthatója van, (a_1d, a_2d).
Az összes visszaható együtthatók száma =2·N_s
Minden másodfokú szűrő fokozatnak három előreható együtthatója van, (b_0d, b_1d, b_2d).
Az összes előreható együtthatók száma =3·N_s.

A jelfeldolgozó VI – okban, amelyek előre-, és visszaható együttható paraméterekkel működnek, vektorok tartalmazzák minden egyes másodfokú szűrő fokozat együtthatóit. Például egy IIR szűrőnél, amelynek két szűrő fokozata van, összesen 4 visszaható és 6 előreható együtthatót szükséges megadni, ahogy az alábbi egyenletek is mutatják.

	Visszaható együtthatók száma = 2·N_s =4
	Visszaható együtthatók: {a₁₁, a₁₂, a₂₁, a₂₂ }

	Előreható együtthatók száma = 3·N_s =6
	Előreható együtthatók: {b₀₁, b₁₁, b₂₁, b₀₂, b₁₂, b₂₂ }

10.8.3. Negyedfokú szűrés

A sáváteresztő és sávvágó szűrőknek , amelyeknek két határfrekvenciájuk van, a negyedfokú szűrő konstrukció jobb hatásfokú, mint a másodfokú szűrő fokozatok. A végtelen impulzusválasz ( IIR ) sávvágó, sáváteresztő szűrők a negyedfokú szűrők összekapcsolásával készíthetők, amelyek negyedfokú tagok sorba kapcsolásával jönnek létre.

Minden negyedfokú szűrő tag a következő jellemzőkkel rendelkezik:

d = 1,2, …,N_s, ahol d a negyedfokú szűrő fokozat sorszáma,
N_s a fokozatok száma = (N_a+1)/4.
Minden negyedfokú szűrő fokozatnak négy visszaható együtthatója van, (a_1d, a_2d, a_3d, a_4d).
Az összes visszaható együtthatók száma =4·N_s
Minden negyedfokú szűrő fokozatnak öt előreható együtthatója van, (b_0d, b_1d, b_{2d ,}b_3d, b_4d).
Az összes előreható együtthatók száma =5·N_s.

A sorba kapcsolt fokozatokat összeépítjük egy negyedfokú szűrő struktúrába, olyan módon, ahogyan azt a másodfokú szűrésnél is tettük.

A következő egyenletek mutatják be, hogyan működik a szűrés negyedfokú tagok esetén.

$\begin{array}{l} y_{0} [k] = x [k] \\ m_{d} [k] = y_{d - 1} [k - 1] - a_{1 d} \cdot m_{d} [k - 1] - a_{2 d} \cdot m_{d} [k - 2] - a_{3 d} \cdot m_{d} [k - 3] - a_{4 d} \cdot m_{d} [k - 4] \\ y_{d} [k] = b_{0 d} \cdot m_{d} [k] + b_{1 d} \cdot m_{d} [k - 1] + b_{2 d} \cdot m_{d} [k - 2] + b_{3 d} \cdot m_{d} [k - 3] + b_{4 d} \cdot m_{d} [k - 4] \end{array}$

(10.54)

ahol

d = 1,2, …,N_s.

az egyenletek a következő függvényből erednek:

$H (z) = \frac{Y (z)}{X (z)} = \frac{b_{0} + b_{1} \cdot z^{- 1} + b_{2} \cdot z^{- 2} + b_{3} \cdot z^{- 3} + b_{4} \cdot z^{- 4}}{1 + a_{1} \cdot z^{- 1} + a_{2} \cdot z^{- 2} + a_{3} \cdot z^{- 3} + a_{4} \cdot z^{- 4}}$

(10.55)

egy új bevezetett változóval M(z)-vel kifejezzük Y(z)-t:

$Y (z) = (b_{0} + b_{1} \cdot z^{- 1} + b_{2} \cdot z^{- 2} + b_{3} \cdot z^{- 3} + b_{4} \cdot z^{- 4}) \cdot M (z)$

(10.56)

amely időtartományban

$\begin{array}{l} y [k] = b_{0} \cdot m [k] + b_{1} \cdot m [k - 1] + b_{2} \cdot m [k - 2] + \\ b_{3} \cdot m [k - 3] + b_{4} \cdot m [k - 4] \end{array}$

(10.57)

ahol

	$M (z) = \frac{X (z)}{1 + a_{1} \cdot z^{- 1} + a_{2} \cdot z^{- 2} + a_{3} \cdot z^{- 3} + a_{4} \cdot z^{- 4}}$	(10.58)
	$\begin{array}{l} M (z) + a_{1} \cdot z^{- 1} \cdot M (z) + a_{2} \cdot z^{- 2} \cdot M (z) + \\ a_{3} \cdot z^{- 3} \cdot M (z) + a_{4} \cdot z^{- 4} \cdot M (z) = X (z) \end{array}$	(10.59)
	$\begin{array}{l} M (z) = X (z) - a_{1} \cdot z^{- 1} \cdot M (z) - a_{2} \cdot z^{- 2} \cdot M (z) - \\ a_{3} \cdot z^{- 3} \cdot M (z) - a_{4} \cdot z^{- 4} \cdot M (z) \end{array}$	(10.60)

ami időtartományban

$\begin{array}{l} m [k] = x [k] - a_{1} \cdot m [k - 1] - a_{2} \cdot m [k - 2] - \\ a_{3} \cdot m [k - 3] - a_{4} \cdot m [k - 4] \end{array}$

(10.61)

10.8.4. IIR szűrő konstrukciók

A digitális végtelen impulzus válasz (IIR) szűrő típusok a klasszikus analóg szűrő típusok digitális megfelelői, amelyek a következők:

Butterworth-szűrők
Csebisev-szűrők
Csebisev II-szűrők, Inverz Csebisev vagy II-es típusú Csebisev szűrőként is ismert
Elliptikus-szűrők, más néven Cauer-szűrők
Bessel-szűrők

Az IIR szűrő típusok abban különböznek egymástól, hogy az átviteli sáv és a vágási sáv között milyen éles az átmenet illetve hogy milyen tulajdonságuk van-az átviteli és a vágási sávban.

10.8.5. Csúcshiba minimalizálása

A Csebisev , a Csebisev II , és Elliptikus szűrők minimalizálják a csúcshibát úgy, hogy közben az előírt hibát biztosítják a frekvencia válasz függvényben.

A csúcshiba alatt az ideális és aktuális szűrő frekvenciafüggvénye közötti különbségének abszolút érték maximumát értjük. A szűrő frekvencia függvényében megengedett hullámosság mértéke dB-ben kifejezve, meghatározza a tűréshatáron belüli hibát. Típustól függően a szűrő minimálisra csökkenti a csúcshibát az átviteli, a vágási sávban, vagy mindkettőben.

10.8.6. Butterworth-szűrők

A Butterworth-szűrők a következő jellemzőkkel rendelkeznek:

Csillapított amplitúdó függvény minden frekvencián
Az amplitúdó függvény monoton csökkenő egy adott határfrekvenciától
Maximális laposság, az átviteli sávban a válaszfüggvény egységnyi értékű, a vágási sávban pedig nulla.
Fél-teljesítmény frekvencia vagy 3 dB-s csökkenési frekvencia összefüggés-ben van a vágási frekvenciával.

A Butterworth-szűrők előnyei, a simaságuk és monoton csökkenő frekvencia függvényük. A 10.19. ábra ábra egy aluláteresztő Butterworth-szűrő amplitúdó-frekvencia függvényét mutatja be.

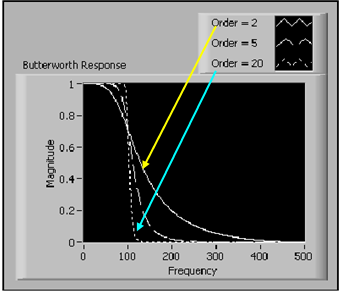
10.19. ábra - Aluláteresztő Butterworth-szűrő amplitúdó-frekvencia függvénye

Ahogy a (10.19. ábra) ábrán látható, mi határozzuk meg a Butterworth-szűrő vágási frekvenciáját, a LabVIEW beállítja az átmenet meredekségét annak arányában, hogy hányad fokú a szűrő. A magasabb fokú Butterworth-szűrő görbéje megközelíti az ideális aluláteresztő szűrő függvényét.

A Butterworth-szűrők nem mindig nyújtanak jó közelítést az ideális szűrő válaszfüggvényhez képest, mert lassú a lecsengésük az átviteli és vágási sáv között.

10.8.7. Csebisev-szűrők

A Csebisev szűrőknek a következő jellemzőik vannak:

Minimális csúcshiba az átviteli sávban
Egyenletes ingadozású amplitúdó függvény az átviteli sávban
Monoton csökkenő amplitúdó függvény a vágási sávban
Élesebb frekvencia levágású, mint a Butterworth-szűrők

A Butterworth-szűrőhöz hasonlítva egy Csebisev-szűrő élesebb frekvencia levágás valósít meg az átviteli és vágási sáv között, alacsonyabb fokú szűrővel. A Csebisev-szűrő éles átmenete kisebb abszolút hibát, gyorsabb végrehajtást eredményez, mint egy Butterworth-szűrőé. A (10.20. ábra) ábra egy aluláteresztő Csebisev-szűrő amplitúdó-frekvencia függvényét mutatja.

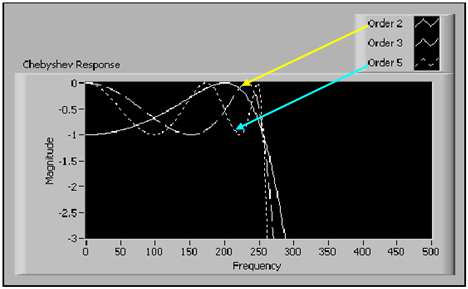
10.20. ábra - Aluláteresztő Csebisev-szűrő amplitúdó-frekvencia függvénye

A (10.20. ábra) ábrán az átviteli sávban a tűréshatár bekorlátozza az ingadozó görbét. az éles frekvencia levágás a vágási sávban jelentkezik.

10.8.8. Csebisev II - szűrők

A Csebisev II szűrőknek a következő jellemzői vannak:

Minimális csúcshiba a vágási sávban
Egyenletes ingadozású amplitúdó függvény a vágási sávban
Monoton csökkenő amplitúdó függvény az átviteli sávban
Élesebb frekvencia levágású, mint a Butterworth-szűrők

A Csebisev II - szűrők hasonlítanak a Csebisev-szűrőkre. A következőkben viszont eltérnek a Csebisev-szűrőktől : - A Csebisev II - szűrők az átviteli sáv helyett a vágási sávban csökkentik a csúcshibát.

A Csebisev-II szűrőknek egyenletes ingadozású amplitúdó függvénye van az átviteli sáv helyett a vágási sávban.

A Csebisev-II szűrőknek monoton csökkenő amplitúdó függvénye van az átviteli sávban a vágási sáv helyett.

A 10.20. ábra ábra egy aluláteresztő Csebisev II – szűrő amplitúdó-frekvencia függvényét mutatja be.

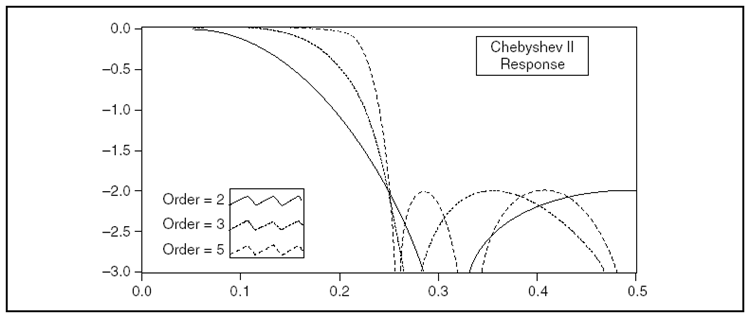
10.21. ábra - Aluláteresztő Csebisev II -szűrő amplitúdó-frekvencia függvényét

A (10.21. ábra) ábrán látható módon a hiba tűréshatára bekorlátozza az ingadozó görbét a vágási sávban. Szintén a vágási sávban látszik a sima, monoton lecsengés.

A Csebisev II –szűrőknek ugyanazok az előnyeik a Butterworth-szűrőkkel szemben, mint a Csebisev-szűrőknek, azaz élesebb átmenetük van egy alacsonyabb fokú szűrővel, kisebb abszolút hiba, gyorsabb működés mellett.

10.8.9. Elliptikus szűrők

Az elliptikus szűrők jellemzői:

Minimális csúcshiba a vágási és átviteli sávban
Egyenletes ingadozású amplitúdó függvény a vágási és átviteli sávban

Összehasonlítva a Butterworth vagy Csebisev-szűrőkkel, az Elliptikus szűrők adják a legélesebb átmenetet az átviteli és vágási sáv között, amely megmagyarázza, hogy miért annyira elterjedtek.

A 10.22. ábra ábra egy aluláteresztő Elliptikus szűrő amplitúdó-frekvencia függvényét mutatja.

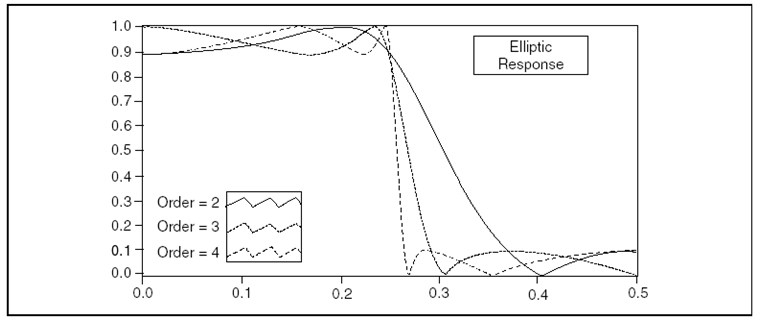
10.22. ábra - Aluláteresztő Elliptikus-szűrő amplitúdó-frekvencia függvénye

A (10.22. ábra) ábrán az azonos maximális elfogadható hiba (csúcshiba) bekorlátozza a hullámosságot a átviteli és a vágási sávban egyaránt. Még az alacsony fokú Elliptikus szűrőknek is meredek átmeneti élük van.

10.8.10. Bessel-szűrők

A Bessel-szűrők a következő tulajdonságokkal rendelkeznek:

Maximálisan lapos amplitúdó- és fázisfüggvény
Közel lineáris fázisfüggvény az átviteli sávban

A Bessel-szűrőket arra használhatjuk, hogy az összes IIR szűrőre jellemző nemlineáris fázistorzítást lecsökkentsük a segítségével. A nagy rendszámú IIR szűrőknek határozott, meredek lefutású nemlineáris fázistorzításuk van, különösen a szűrők átmeneti tartományában. Előállíthatjuk a lineáris fázisfüggvényt FIR szűrőkkel is.

A 10.23. ábra ábra egy aluláteresztő Bessel-szűrő amplitúdó-, és fázisfüggvényét ábrázolja.

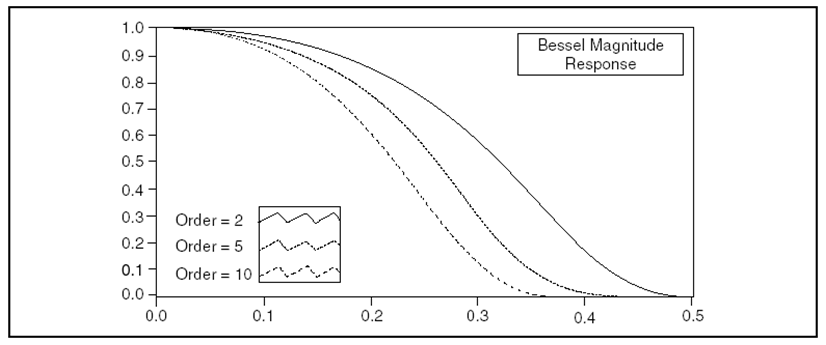
10.23. ábra - Egy aluláteresztő Bessel-szűrő amplitúdó-frekvencia függvénye

A (10.23. ábra) ábrán látható, hogy az amplitúdó görbe sima és monoton csökkenő minden frekvencián.

A 10.24. ábra ábra egy aluláteresztő Bessel-szűrő fázis-frekvencia függvényét mutatja.

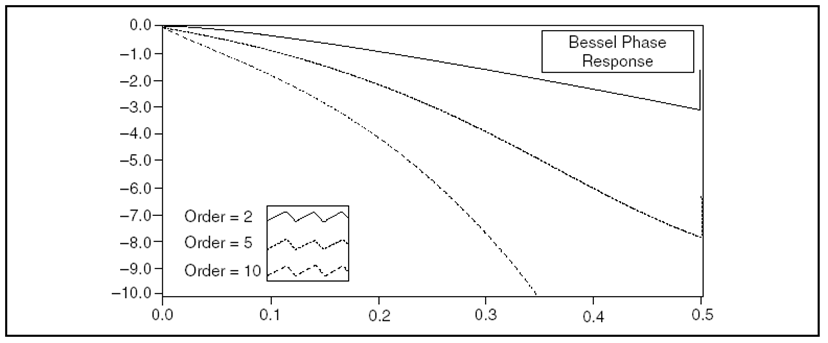
10.24. ábra - Aluláteresztő Bessel-szűrő fázis-frekvencia függvénye

A 10.24. ábra ábra közel lineáris fázismenetet mutat az átviteli sávban. A fázisfüggvény monoton csökkenő minden frekvencián.

A Butterworth-szűrőkhöz hasonlóan a Bessel-szűrőknél is magas fokszámú szűrőre van szükség, hogy lecsökkentsük a csúcshibát, amely korlátozott használatot tesz lehetővé.

10.8.11. IIR szűrők tervezése

Amikor egy feladatra kiválasztunk egy IIR szűrőt , ismernünk kell a szűrő válaszfüggvényét. A 10.25. ábra ábra egy olyan VI blokkdiagramja, amely egy IIR szűrő impulzusra adott válaszfüggvényét határozza meg.

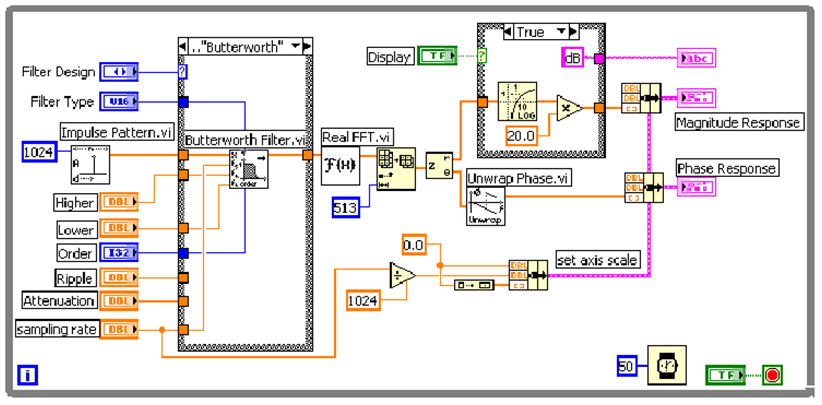
10.25. ábra - IIR szűrő frekvenciaválasza

Azonos matematikai elméleteket alkalmaznak az IIR és FIR szűrők tervezésére, a (10.25. ábra) ábrán látható VI blokkdiagram, amely egy IIR szűrő frekvenciaválaszát határozza meg, és a (10.11. ábra) ábrán látható VI blokkdiagram, amely egy FIR szűrő frekvenciaválaszát adja, közös tervező elemekből épülnek fel. A legfőbb különbség a két VI között az, hogy a 10.25. ábra ábra bal oldalán lévő case struktúrában van, amelyik az IIR szűrő konstrukcióját is megadja a szűrő típusa mellett. A 10.25. ábra ábra szerinti VI kiszámítja az IIR szűrő frekvenciaválaszát, közben ugyanazokat a lépéseket végzi el, amelyeket a FIR szűrők tervezése című fejezetben már bemutattunk.

A 10.26. ábra ábra egy sáváteresztő elliptikus IIR szűrő amplitúdó- és fázisfüggvényét mutatja be.

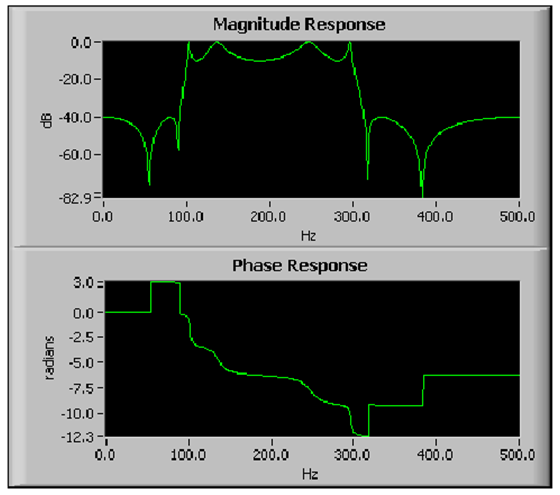
10.26. ábra - Egy sáváteresztő elliptikus IIR szűrő amplitúdó és fázis függvénye

A (10.26. ábra) ábrán látható fázis információ nyilvánvalóan nemlineáris. Amikor eldöntjük, hogy IIR vagy FIR szűrőt alkalmazunk az adatok feldolgozásához, jussanak eszünkbe a nemlineáris fázis információt nyújtó IIR szűrők. Bővebb információval szolgálhat az IIR és FIR közötti választásról ezen fejezet FIR és IIR szűrők összehasonlítása című és a Digitális szűrő típus kiválasztása című részei.

10.8.12. IIR szűrők jellemzői

Az IIR szűrők a következő tulajdonságokkal rendelkeznek:

Az IIR szűrő VI–k az első hívás alkalmával a 10.26. egyenlet szerint a negatív előjelű indexekkel jelölt értékeket nulla értéknek veszik.
Az átmeneti-függvény válasz vagy késleltetés, arányosan a szűrő fokszámával, és lezajlik mielőtt a szűrő eléri az állandósult állapotát. Bővebb információt erről a témáról ezen fejezet „ Átmeneti függvény ” című része ad.
A szűrt jelsorozat elemeinek száma megegyezik a bemenő sorozat elemeinek számával.
A szűrő megtartja a belső állapot értékeit, amikor a szűrési művelet befejeződik.

10.8.13. Átmeneti függvény

Az átmeneti válasz (függvény) azért jelenik meg, mert a szűrő kezdeti állapota nulla, vagy értékek vannak a negatív előjelű indexeknél. Az átmeneti válasz függvény késleltetése függ a szűrő típusától.

Az átmeneti válasz (függvény) késleltetése alul- és felüláteresztő szűrőnél egyenlő a szűrő rendszámával (mintavételi időlépésekben).

Késleltetés _{alul,felül áteresztő szűrő} = a szűrő_rendszáma

(10.62)

Az átmeneti válasz (függvény) késleltetése sáváteresztő és sávvágó szűrőnél egyenlő a szűrő rendszámának kétszeresével (mintavételi időlépésekben).

Késleltetés _{sáváteresztő sávvágó szűrő} = 2·a_szűrő_rendszáma

(10.63)

Eltüntethetjük az átmeneti választ (függvényt) egy IIR szűrő VI sorozatos meghívásával, ha engedélyezzük az állapot memóriát.

Hogy a folyamatos szűrés számára engedélyezzük az állapot memóriát, az IIR szűrő VI init/cont bementére kapcsoljunk egy IGAZ (TRUE) értéket.

A 10.27. ábra ábra bemutat egy átmeneti választ (függvényt) és az IIR szűrő állandósult állapotát.

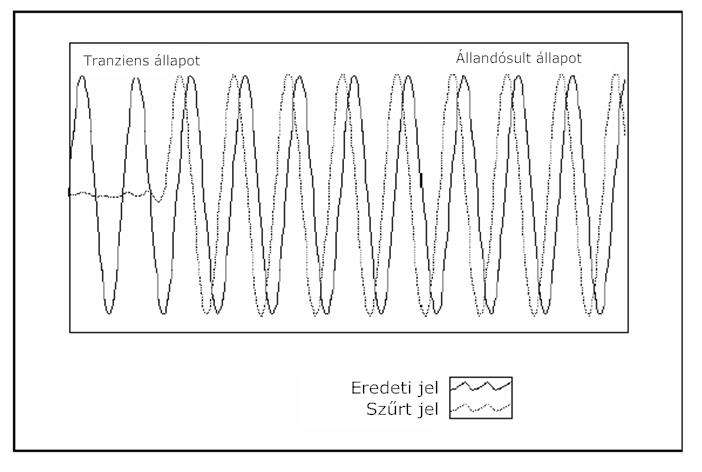
10.27. ábra - Átmeneti (tranziens) válaszfüggvény és egy IIR szűrő állandósult állapota

10.9. A FIR és az IIR szűrők összehasonlítása

Mivel a digitális szűrők tervezésekor kompromisszumokat kell kötnünk, hogy egy számunkra fontos szűrő jellemzőt kiemeljünk a kevésbe fontos jellemzők közül, a FIR és IIR szűrők összehasonlítása segítséget nyújthat egy adott feladat megoldásához szükséges szűrő kiválasztásában.

Az IIR szűrők ugyanolyan mértékű csillapításra képesek, mint a FIR szűrők, de sokkal kevesebb együttható alkalmazásával. Ebből kifolyólag az IIR szűrők sokkal gyorsabban működnek, és hatásosabb szűrő eljárást valósítanak meg, mint egy FIR szűrő.

Lineáris fázisfüggvényhez alkalmazzunk FIR szűrőt. Az IIR szűrők nemlineáris fázisfüggvényt hoznak létre. Lineáris fázisfüggvényt igénylő feladatokhoz tehát FIR szűrőt használjunk!.

A fázis információt nem igénylő feladatokhoz használjunk IIR szűrőt.

Bővebb információval szolgál erről a témáról ezen fejezet Digitális szűrő típus kiválasztása című része.

10.10. Nemlineáris szűrők

A simító ablakok, az IIR szűrők és a FIR szűrők lineárisak, mert eleget tesznek a szuperpozíció és az arányosság elvének, ahogy a 10.64. egyenlet leírja.

L {a·x(t) + b·y(t)} = a·L {x(t)} + b·L {y(t)}

(10.64)

ahol a és b állandók , x(t) és y(t) villamos jelek (időfüggvények) , L{} egy lineáris szűrő művelet, a bemenetek és kimenetek közötti összefüggés műveleteken keresztül valósul meg, ahogy azt a 10.31. és 10.43. egyenlet leírja.

Egy nemlineáris szűrő nem tesz eleget a 10.64. egyenletnek. Ezen kívül nem határozhatjuk meg a nemlineáris szűrő kimenő jeleit konvolúciós művelet segítségével, mert az együtthatók egy összeállítása és a szűrő impulzusválasza között nincs (nem állapítható meg) egyértelmű kapcsolat. A nemlineáris szűrők sajátos szűrőkarakterisztikával rendelkeznek, amelyeken nagyon bonyolult a lineáris számolási eljárások alkalmazása.

A medián szűrő egy olyan nemlineáris szűrő, amely egyesíti magában az aluláteresztő szűrő és egy magas frekvenciájú szűrő jellemzőit. Az aluláteresztő tulajdonságok lehetővé teszik a nagy frekvenciás zaj ”eltűntetését”. A nagyfrekvenciás tulajdonságok lehetővé teszik, hogy a medián szűrő megtartsa az éleket és megkímélje azok információtartalmát.

Példa:

Zajos impulzus szűrése Medián szűrővel

Az “Impulzus paraméter.VI” (Pulse Parameters.VI) elemezi egy impulzus diagram bemenő sorozatát, és előállítja azokat az impulzus paramétereket, amelyek legjobban leírják ezt az impulzust. Miután a VI elvégzi a jelalak elemzését, azért hogy meghatározza az időtengelyt és a bemenő sorozat csúcsát, további információ nélkül a jel és a zaj megkülönböztetése nehézkessé válik. Ezért az impulzus paraméterek pontos meghatározásához a bemenő jelsorozat zajrésze maximális amplitúdójának kisebbnek vagy egyenlőnek kell lennie az impulzus átlagos amplitúdójának 50%-ánál. Számos gyakorlati alkalmazásnál nehéz elérni az 50%-os jel/zaj viszonyt. A szükséges jel/zaj viszony teljesítéséhez még el kell végezni egy sor számítási műveletet, hogy kiemeljük az impulzus lényeges információit.

Ha az impulzus olyan zajjal rendelkezik, amelynek átlagos amplitúdó maximuma meghaladja az impulzus átlagos amplitúdójának 50%-át, akkor aluláteresztő szűrőt használhatunk a nem kívánatos zaj eltávolításra. Azonban a szűrő időben eltolja (késlelteti) a jelet, és eltompítja az impulzus éleit, mivel ”levágja” az átmeneti élek magas frekvenciájú információt. A Medián szűrő hatásosabban tudja az impulzust szűrni, mint egy aluláteresztő szűrő, mert megóvja az élek információtartalmát, miközben eltünteti a magas frekvenciájú zajt.

A 10.28. ábra ábra egy VI blokk diagramját mutatja, amely létrehoz, és analizál egy zajos impulzust.

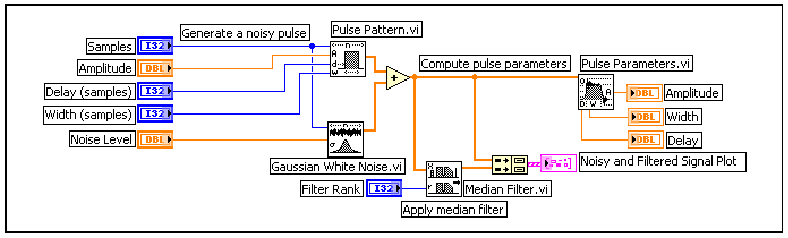
10.28. ábra - A Medián szűrő alkalmazása, hogy meghatározzuk az impulzus információit

A (10.28. ábra) ábrán látható VI létrehoz egy zajos impulzust, amelyben az átlagos zaj csúcs amplitúdó az impulzus amplitúdó 100%-ánál nagyobb. A (10.28. ábra) ábrán lévő VI által generált jel a következő ideális impulzus értékekkel rendelkezik:

5.0 V –os amplitúdó
64 mintavételnyi késleltetés
32 mintavételnyi szélesség

A 10.29. ábra ábra bemutatja a zajos impulzust, a szűrt impulzust, és a (10.28. ábra) ábrán lévő VI-ből visszatérő becsült impulzus paramétereket.

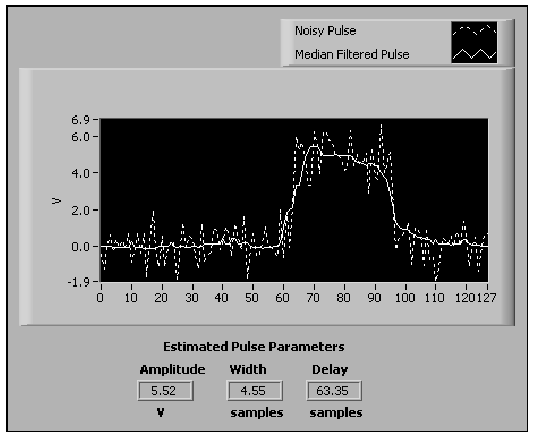
10.29. ábra - Zajos impulzus és Medián szűrővel szűrt impulzus

A (10.29. ábra) ábrán a Medián szűrővel létrehozott impulzus jelet kísérhetjük figyelemmel, úgy hogy a zaj eltorzítja az impulzust.

Az elemzés szabályos elvégzéséhez a Medián szűrő.VI–al eltávolíthatjuk a magas frekvenciájú zajt. Az 50%-os jel/zaj viszony eléréséhez, az „Impulzus paraméter VI”-t alkalmazzuk.

10.11. Digitális szűrő típus kiválasztása

Egy konkrét feladathoz legalkalmasabb szűrő kiválasztásához a következő kérdésekre kell választ adni:

A szűrés eredménye lineáris fázisfüggvényt igényel?

Az elemzés elviseli az amplitúdó függvény ingadozásait?

Szűk frekvencia átviteli sávra van szükség?

Egy gyakorlati feladatban alkalmazhatjuk a 10.30. ábra ábrát segítségként, a megfelelő szűrő típus kiválasztásához.

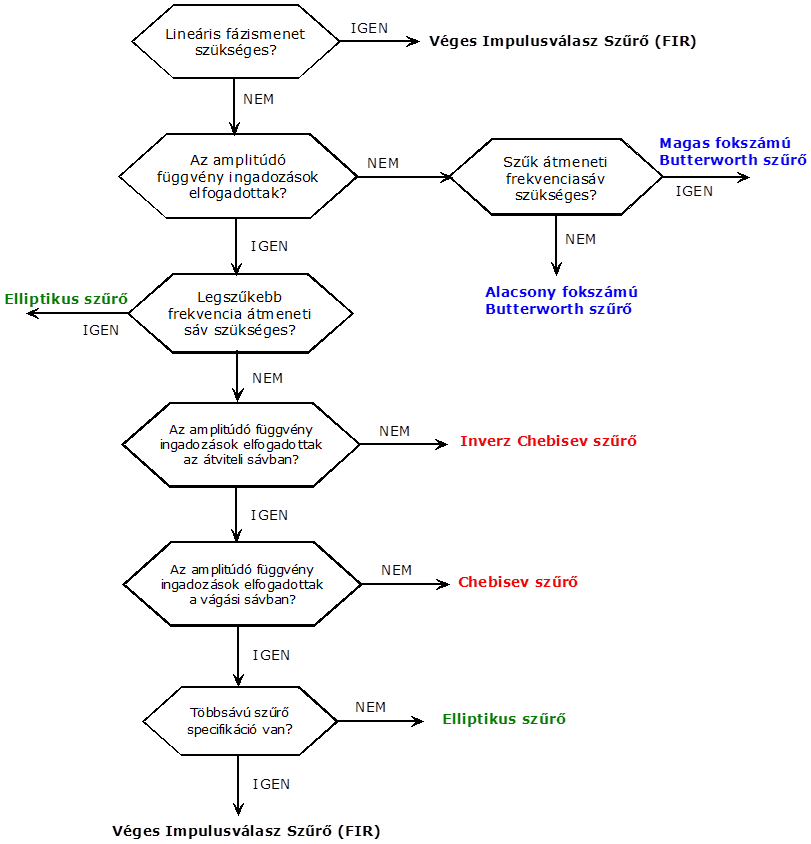
10.30. ábra - A megfelelő szűrő kiválasztásának folyamatábrája

A 10.30. ábra ábra egy kiválasztási módszert mutat be az adott feladathoz legjobban megfelelő szűrő kiválasztására. Általában több szűrő típust is ki kell kipróbálni, hogy közülük megtaláljuk a legalkalmasabbat.

Irodalom

[10.1.] LabVIEW Control Design User Manual. 2009.

Vissza		Előre
9. fejezet - Jelgenerálás	Főoldal	11. fejezet - Diszkrét frekvencia analízis