11. fejezet - Diszkrét frekvencia analízis
- 11.1. A frekvencia és az időtartomány közötti különbségek
- 11.2. Fourier transzformáció, mint a DFT alapja
- 11.3. (Időben) Diszkrét Fourier transzformáció (DFT)
- 11.4. Frekvencia lépés a DFT minták között
- 11.5. Gyors Fourier transzformáció alapjai (FFT= Fast Fourier Transformation)
- 11.6. A frekvencia információ megjelenítése a Fourier transzformáció után
- 11.7. Kétoldalas 0(nulla) frekvencia középpontú FFT transzformáció
- 11.8. Teljesítmény Spektrum SAA(f)
- 11.9. A spektrumokkal végzett számítások
- 11.10. Amplitúdó és fázis spektrumok kiszámítása
- 11.11. Frekvencia válasz függvény
- 11.12. Kereszt teljesítmény spektrum SAB(f) (Cross Power Spectrum)
- 11.13. Frekvencia válasz és hálózat analízis
- 11.14. Ablakozási technika
- 11.15. Átlagolás a mérési eredmények ábrázolásához
- 11.16. Visszhang észlelése
- Irodalom
Ez a fejezet tárgyalja a diszkrét Fourier transzformáció (DFT = Discrete Fourier Transformation) alapjait, a gyors Fourier transzformációt (FFT = Fast Fourier Transform), az alapvető jelanalízis számításokat, a teljesítmény spektrumon végrehajtott számításokat, és azt hogy hogyan kell alkalmazni az FFT-alapú függvényeket hálózatok mérésére. Használjuk az NI = National Instruments Példakeresőt, hogy megtaláljuk azokat a mintapéldákat, amelyek alkalmazzák a digitális jelfeldolgozó VI-ket és a mérés analízis VI-ket, FFT és frekvenciaanalízis elvégzéséhez.
11.1. A frekvencia és az időtartomány közötti különbségek
Az időtartománybeli ábrázolás a mintavételi időpontokban megadja a jel amplitúdóját, amelyet mintavételeztünk. Bár sok esetben inkább a jel frekvencia tartalmát kell ismernünk, mint az egyedi minták amplitúdóit.
A Fourier-tétel kimondja , hogy bármely időtartománybeli hullámalakot le lehet írni sinus és cosinus függvények súlyozott összegeként. Ugyanazt a hullámalakot megjeleníthetjük frekvencia tartományban is, mint az egyes frekvencia összetevők amplitúdóját és fázisát.
Előállíthatunk bármely hullámalakot szinusz hullámok összegeként, ahol az egyes szinuszos tagok önálló amplitúdó és fázis értékkel rendelkeznek. A 11.1. ábra ábra bemutatja az eredeti hullámalakot, és az összetevő tag frekvenciákat. Az alapfrekvencia -lal van jelölve, a második felharmonikus 2· frekvenciájú, a harmadik felharmonikus pedig 3· frekvenciájú.
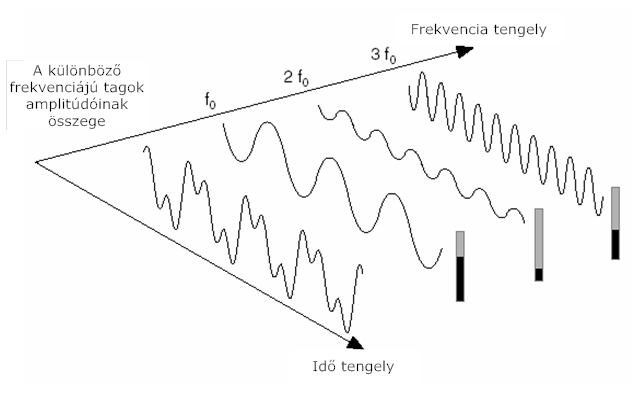
A frekvencia tartományban meghatározhatók azok a szinusz komponens függvények, amelyek létrehozznak egy komplex időtartománybeli hullámalakot.
A 11.1. ábra ábra egy olyan hullámalakot mutat be, amely az időtartományban úgy bontható fel komponensekre, mint a frekvencia tartományban különböző szinuszos komponensekre. Minden frekvencia komponens amplitúdója megegyezik az ehhez a frekvencia komponenshez tartozó időtartománybeli hullámalak amplitúdójával. A jel megjelenítése egyéni frekvencia komponensek segítségével a frekvencia tartománybeli megjelenítés . A frekvencia tartománybeli megjelenítés általában számos lényeges információt ad meg a jelről és arról a rendszerről, amellyel létrehoztuk.
A jelátalakítóból (analóg/digitális átalakítóból) érkező minták időtartományban írják le a jelet. Néhány analízis adat, mint például a harmonikus torzítás értékét nehéz pontosan meghatározni az időtartománybeli hullámalak tanulmányozásával. Amikor ugyanazt a jelet egy FFT analizátor (Dinamikus Jel analizátorként is ismert) műszer segítségével megjelenítjük frekvencia tartományban, könnyen megállapíthatjuk a harmonikus frekvenciákat és az amplitúdókat.
A Parseval tétel
A Parseval-tétel kimondja, hogy az időtartományban meghatározott (kiszámított) összes energiának meg kell egyeznie a frekvenciatartományban kiszámított összes energiával. Ez az energia-megmaradás tétele . A 11.1 egyenlet a Parseval tétel folytonos alakja. A 11.2 egyenlet pedig a Parseval tétel időben diszkrét alakja.
|
|
(11.1) |
|
|
|
(11.2) |
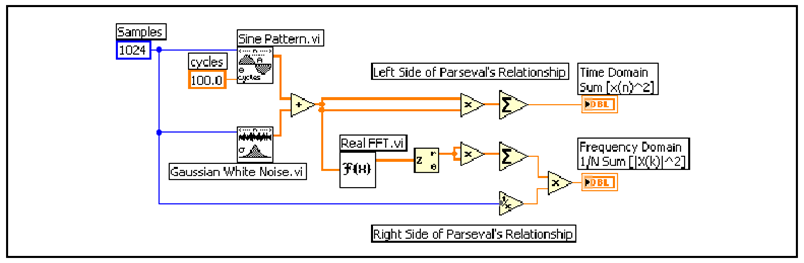
A (11.2. ábra) ábrán látható VI Diagram panel egy valós bemeneti jelsorozaton végzett műveleteket mutat be. A blokkdiagram felső része az időtartománybeli jel energiáját határozza meg a 11.1 egyenlet bal oldalát alkalmazva. A blokk diagram alsó része átkonvertálja az időtartománybeli jelet frekvencia tartományba és meghatározza a frekvenciatartománybeli jel energiáját a 11.1 egyenlet jobb oldalát alkalmazva.
A 11.3. ábra ábra a (11.2. ábra) ábrán bemutatott VI számított eredményeit mutatja be.
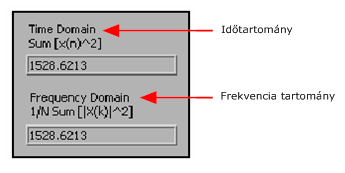
A 11.3. ábra ábra bemutatja, hogy az összes számított energia az időtartományban megegyezik a frekvencia tartományban meghatározott értékkel.
11.2. Fourier transzformáció, mint a DFT alapja
A 6.2. szakasz fejezetben részletesen bemutattuk a Fourier transzformáció kialakulásának történetét és kapcsolatát a Fourier sorral. Jelen fejezetben felhasználva ezeket ez elméleti ismereteket, a mintavételes jelek Fourier transzformációját mutatjuk be.
A Fourier transzformáció egy olyan eljárás, amellyel a jel tulajdonságait és azok kapcsolatait vizsgálhatunk meg frekvencia tartományban. A Fourier transzformáció leggyakoribb alkalmazása a lineáris idő-invariáns rendszerek vizsgálata valamint a spektrum analízis.
A következő egyenlet a kétoldalas Fourier transzformációt definiálja:
|
|
(11.3) |
A következő egyenlet a kétoldalas inverz Fourier transzformációt adja meg:
|
|
(11.4) |
A kétoldalas Fourier transzformáció azt jelenti, hogy a Fourier transzformáció és az Inverz Fourier transzformáció figyelembe veszi az összes negatív és pozitív frekvenciájú és időpontú jelet a transzformációnál. Az egyoldalas transzformáció azt jelenti, hogy a transzformáció matematikai leírása csak a jel pozitív frekvenciáit és időtartománybeli történéseit veszi figyelembe.
A Fourier transzformáció pár tartalmazza a jel reprezentációját mind idő mind pedig frekvencia tartományban. A következő összefüggés általánosan mutatja be a Fourier transzformáció párt.
|
|
(11.5) |
11.3. (Időben) Diszkrét Fourier transzformáció (DFT)
Az algoritmust, amelyet arra használunk, hogy időtartománybeli mintavételezett jel értékeket frekvencia tartományba transzformáljunk (időben) Diszkrét Fourier transzformációnak (DFT) nevezzük (lásd 6.5. szakasz fejezet). A DFT kapcsolatot állít fel az időtartománybeli jel mintavételezett értékei (minta-értékek) és frekvencia tartománybeli reprezentációjuk között. A DFT-t széles körben alkalmazzák a spektrum analízisben, az alkalmazott mechanikában, hang-elemzéseknél, képfeldolgozásoknál, numerikus analízisnél, műszer és telekommunikációs feladatoknál.
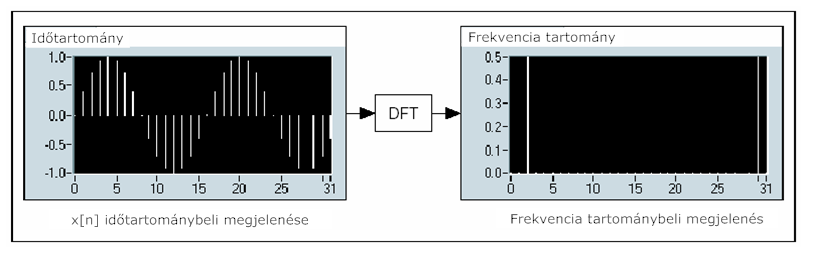
Tételezzük fel, hogy rendelkezésünkre áll egy N mintából álló adatcsomag egy mérésadatgyűjtő berendezésből. Ha alkalmazzuk a diszkrét Fourier transzformációt (DFT) erre az időtartománybeli N mintára , az eredmény szintén N értéket fog tartalmazni és a jel frekvencia tartománybeli tulajdonságait jeleníti meg.
11.3.1. Kapcsolat az N mintát tartalmazó időtartománybeli és frekvenciatartománybeli jel értékek között
Ha a jelből egy megadott mintavételi frekvenciával veszünk mintákat, a 11.6 egyenlet megadja az egyes minták közötti időtartamot, vagy más néven mintavételi időt .
|
|
(11.6) |
ahol
|
h |
a mintavételi időtartam, |
|
|
f s |
pedig a mintavételi frekvencia (minta/másodperc). |
A mintavételi időből lehet meghatározni azt a legkisebb frekvenciát, amelyet a rendszer még meg tud vizsgálni a DFT illetve a hozzá kapcsolódó eljárások segítségével.
A 11.7 egyenlet definiálja a diszkrét Fourier transzformációt . A függvény eredményei az X[k] értékek, amelyek a frekvencia tartományban adják meg a mintavételezett jel Fourier transzformált értékét.
|
k=0, 1, 2,....., N-1 |
(11.7) |
ahol
|
x[i] |
értékek a mintavételezett jel időtartománybeli értékei |
|
|
N |
a minta értékeinek száma. |
Hasonlóan a h időlépéshez, amely az időtartományban adja meg az x mintái közötti időtartamot az X frekvenciatartománybeli megjelenítésében is van egy frekvencia lépés vagy frekvencia felbontás, amely a 11.8 egyenlet ad meg.
|
|
(11.8) |
ahol
|
Δf |
a frekvencia felbontás, |
|
|
f S |
a mintavételi frekvencia, |
|
|
N |
a minták száma, |
|
|
h |
a mintavételi idő, |
|
|
N.h |
pedig a teljes vizsgálati időtartam. |
A frekvencia felbontás növeléséhez, azaz Δf csökkentéséhez, növelni kell a minták számát (N) mialatt a mintavételi frekvenciát (f S ) állandó értéken tartjuk, vagy csökkenteni kell a mintavételi frekvenciát mialatt az N értékét tartjuk állandó értéken. Mindkét megközelítés az N·h vizsgálati időtartam megnövelését jelenti.
11.3.2. Mintapélda a Diszkrét Fourier Transzformáció (DFT) meghatározására
Ez a fejezet egy mintapéldát mutat be, amely alkalmazza a 11.3 diszkrét jelekre érvényes alakját, a 11.7 egyenletet azért, hogy meghatározzuk egy egységugrás jel diszkrét Fourier transzformált értékét. A példában a következő feltételezéseket alkalmazzuk:
-
X[0] a jel átlagértéke vagy 0(nulla) frekvenciájú komponense.
-
A 0(nulla) frekvenciájú komponensnek állandó +1 V amplitúdója van.
-
4 mintavételi értékünk van.
-
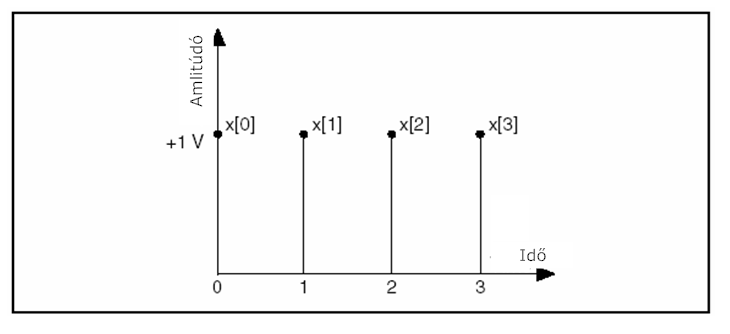
Minden minta értéke +1 V nagyságú, ahogy azt a 11.5. ábra ábra mutatja.
Az eredményként kapott idősort a következő egyenlet adja meg:
|
x[0] = x[1] = x[2] = x[3]= 1 |
(11.9) |
/Mivel ez az idősor véges, ezért a konvergencia feltétel automatikusan teljesül. Ilyen értelemben beszélhetünk itt az egységugrás Fourier transzformáltjáról. Általános értelemben a folyamatosan mintavételezett egységugrásnak csak Z transzformáltja létezik. (lásd Táblázat 11.1 táblázatot)/
A DFT alkalmazza az Euler összefüggést, amelyet a következő egyenlet ad meg:
|
|
(11.10) |
Ha a 11.3 egyenletet alkalmazzuk, hogy meghatározzuk a DFT sorozatot a (11.5. ábra) ábrán bemutatott jelsorozathoz és alkalmazzuk az Euler összefüggést, a következő egyenleteket kapjuk:
|
|
(11.11) |
|
|
|
(11.12) |
|
|
|
|
(11.13) |
|
|
|
(11.14) |
ahol
|
X[0] |
a 0 frekvenciájú komponens amplitúdója, |
|
|
N |
a minták száma. |
Így a 0 frekvenciájú komponenst kivéve minden további érték 0 (nulla) értékű a DFT sorozatban, ahogy azt feltételeztük. Az X[0] értéke a DFT elvégzése után meghatározóan függ N értékétől. Mivel a példánkban N=4 volt, így X[0]=4. Ha N=10 lett volna a transzformáció után X[0]=10 lett volna.
Ez a függőségi viszony X[0] és N között megjelenik az összes további frekvencia komponensnél is. Ezért a DFT után kapott kimeneti értékeket rendszerint elosztjuk N-el, hogy a frekvencia komponensek korrekt amplitúdóit kapjuk meg.
11.3.3. Amplitúdó és fázis információ
A bemeneti időtartománybeli jel N minta értéke N értéket fog meghatározni a Diszkrét Fourier transzformáció segítségével. A 11.3 egyenlet bemutatja, hogy a bemeneti jel x[i] lehet valós vagy komplex érték , az X[k] azonban mindig komplex érték , bár az imaginárius rész lehet nulla értékű is. Más megfogalmazásban minden frekvencia komponensnek van amplitúdója és fázistolása.
Leggyakrabban az amplitúdó spektrumot szoktuk megjeleníteni egy diagramban, amely nem más, mint X[k] valós és képzetes rész négyzetének összegéből vont négyzetgyök (a komplex szám abszolút értéke).
A fázistolás az időrekordok kezdetére vonatkozik vagy egy egyciklusú cosinus hullám kezdetére, amely az időrekordok kezdeténél indul el. Egycsatornás fázistolás mérések csak akkor stabilak, ha bemeneti jel triggerelt jelérték. Kétcsatornás fázis mérésnél meghatározható a fáziseltérés a csatornák jelei között, így ha a csatornákat egyszerre mintavételezzük triggerelés rendszerint nem szükséges.
A fázistolás a képzetes és a valós rész hányadosának arcus tangense, rendszerint π és -π értékek közötti számérték radiánban, vagy 180° és –180° közötti érték fokban.
A valós jel (x[i] valós) Diszkrét Fourier transzformáltja a következő szimmetrikus tulajdonságokkal rendelkezik:
|
|
(11.15) |
|
|
|
(11.16) |
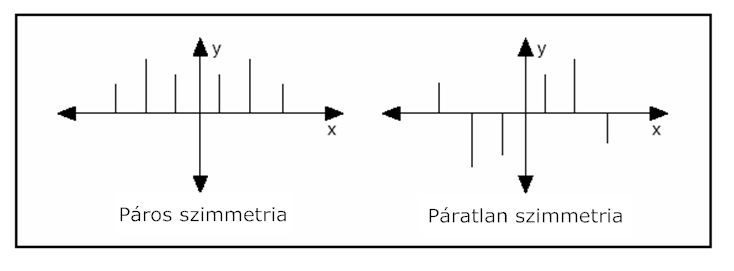
Az amplitudó X[k] páros szimmetriájú , míg a fázis(X[k]) páratlan szimmetriával rendelkezik. A páros szimmetriájú jel szimmetrikus az y tengelyre, míg a páratlan szimmetriájú jel az origóra szimmetrikus.
A 11.6. ábra ábra a páros és páratlan szimmetriát mutatja be.
A szimmetria miatt a Diszkrét Fourier Transzformáció N értéke az információt duplikáltan tartalmazza. Emiatt a DFT értékeinek csak a felét kell kiszámítani, mivel a másik fél értékeinek meghatározásánál felhasználhatjuk a már kiszámított értékeket.
Ha a bemeneti jel ( x[i] ) komplex érték és a DFT aszimmetrikussá válik, ekkor az előbb javasolt számítási eljárás nem alkalmazható.
11.4. Frekvencia lépés a DFT minták között
Ha a mintavételi időintervallum h másodperc és az első mintaadat (k=0) a 0-dik másodpercbeli mérési adat és a (k>0) akkor a k-dik mintavételi adat a k.h másodpercnél mért jel értéke. Hasonlóan, ha a frekvencia felbontás Δf, akkor a DFT k-dik eleme a k×Δf Hz frekvenciájú komponens lesz. Ez a megállapítás a frekvencia komponensek első felére érvényes, a komponensek másik felében a negatív frekvencia komponensek találhatók.
Meg lehet adni egy olyan mintavételi frekvenciát, amellyel a mintavételezett jelben lévő maximális frekvenciát is mindig pontosan elő tudjuk állítani alul-mintavételezés (aliasing) nélkül, ez az úgynevezett Nyquist frekvencia .
A Nyquist frekvencia megegyezik az alkalmazott mintavételi frekvencia felével , amelyet a következő képlettel írhatunk le:
|
|
(11.17) |
ahol a Nyquist frekvencia, a mintavételi frekvencia (sampling frequency) (sample/secundum = minta /másodperc).
Attól függően, hogy az N értéke páros vagy páratlan különböző a DFT k-dik komponense. Például, ha N=8 és p adja meg a Nyquist frekvencia indexét, p = N/2 = 4.
A Táblázat 11.1 táblázat mutatja be a Δf lépéssel a komplex X sorozatot.
|
X[p] |
Δf |
|
X[0] |
0 frekvencia |
|
X[1] |
Δf |
|
X[2] |
2×Δf |
|
X[3] |
3×Δf |
|
X[4] |
4×Δf (Nyquist frekvencia) |
|
X[5] |
-3×Δf |
|
X[6] |
-2×Δf |
|
X[7] |
-Δf |
A negatív értékek a második oszlopban a Nyquist frekvencia felett negatív frekvenciákat jelentenek, ezek azok az elemek, amelyeknek az indexe nagyobb mint p.
Ha N=8, X[1]-nek és X[7]-nek ugyanaz az amplitúdója; X[2]-nek és X[6]-nak ugyancsak azonos az amplitúdója; X[3]-nak és X[5]-nek hasonlóan azonos az amplitúdója. A különbség csupán az, hogy X[1], X[2] és X[3] pozitív frekvenciákhoz tartozik, míg az X[5], X[6] és X[7] negatív frekvenciákhoz. X[4] értéke a Nyquist frekvenciánál mérhető.
A 11.7. ábra ábra a X komplex kimeneti sorozatot mutatja N=8 esetén.
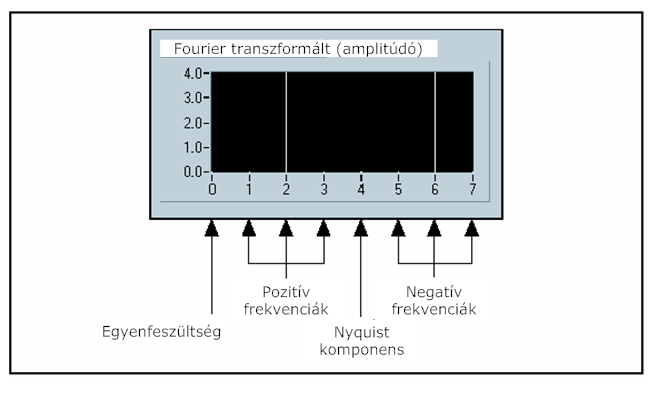
Ez egy reprezentáció, ahol láthatók a kétoldalas transzformáció pozitív és negatív frekvenciái.
Amikor N páratlan, akkor nincs komponens a Nyquist frekvenciánál. A Táblázat 11.2 táblázat bemutatja az X[p] értékeket Δf lépéssel, amikor N=7 és p = (N-1)/2 (7-1)/2= 3.
|
X[p] |
Δf |
|
X[0] |
0 frekvencia (állandó jel érték, egyenfeszültség) |
|
X[1] |
Δf |
|
X[2] |
2×Δf |
|
X[3] |
3×Δf |
|
X[4] |
-3×Δf |
|
X[5] |
-2×Δf |
|
X[6] |
-Δf |
Ez egy reprezentáció, ahol láthatók a kétoldalas transzformáció pozitív és negatív frekvenciái.
Ha N=7, X[1]-nek és X[6]-nek ugyanaz az amplitúdója; X[2]-nek és X[5]-nak ugyancsak azonos az amplitúdója; X[3]-nek és X[4]-nek hasonlóan azonos az amplitúdója. A különbség csupán az, hogy X[1], X[2] és X[3] pozitív frekvenciákhoz tartozik, míg az X[4], X[5] és X[6] negatív frekvenciákhoz. Mivel N értéke páratlan nincs komponens a Nyquist frekvenciánál .
A 11.8. ábra ábra a X komplex kimeneti sorozatot mutatja N=7 esetén.
![X[p] komplex kimeneti sorozat N=7 esetén](images/image_XI_8.png)
Ez egy reprezentáció, ahol láthatók a kétoldalas transzformáció pozitív és negatív frekvenciái.
11.5. Gyors Fourier transzformáció alapjai (FFT= Fast Fourier Transformation)
A Diszkrét Fourier transzformáció közvetlen megvalósításánál N minta esetén közelítőleg N 2 komplex műveletet kell elvégeznünk, amely nagyon időigényes számítási művelet.
A Gyors Fourier transzformáció (FFT) egy olyan (gyors) algoritmus, amellyel kiszámíthatjuk a DFT-at. A következő egyenlet adja meg a DFT transzformációs képleltét:
|
k=0, 1, 2,....., N-1 |
(11.18) |
ahol
|
x[i] |
értékek a mintavételezett jel időtartománybeli értékei |
|
|
N |
a minta értékeinek száma. |
A következő mérések magukba foglalják az FFT alapú jelanalízis alapfüggvényeit:
-
FFT
-
Teljesítmény spektrum
-
Kereszt teljesítmény spektrum
Ezek az alapfüggvények felhasználhatók, hogy segítségükkel létrehozzunk további mérési függvényeket, mint például a frekvencia válaszfüggvényt vagy az impulzus választ illetve a koherencia függvényt valamint az amplitúdó illetve a fázis spektrumot .
Az FFT és a teljesítmény spektrum nagyon hasznos az állandósult és a tranziens jelek frekvencia tartalmának mérésénél. Az FFT egy átlagos frekvencia tartalmat ad meg a teljes mérési tartományban. Ezért az FFT-t akkor célszerű alkalmazni, ha a jel állandósult állapotban van vagy abban az esetben, ha egy átlagos energiatartalomra van szükség mindegyik frekvenciánál.
Egy FFT megegyezik egy olyan párhuzamosan kapcsolt szűrő csoporttal, amelynek a sávszélessége Δf középpontú és minden frekvencia komponense 0 (nulla) frekvenciától növekszik lépésközzel. Ezért a frekvencia komponenseket frekvencia tárolóknak vagy FFT tárolóknak nevezzük.
A Teljesítmény spektrum alfejezet még ebben a fejezetben további információkat közöl a teljesítmény spektrumról.
11.5.1. A frekvencia komponensek kiszámítása
Minden frekvencia komponens egy időtartománybeli jel amplitúdó értékének és egy exponenciális alakban felírt komplex számnak a szorzata, ahogy azt a következő egyenlet megadja:
|
|
(11.19) |
ahol
|
k=0, 1, 2,....., N-1 |
A 0 (k=nulla) frekvenciájú komponens az értékek sorozata különböző n értékeknél.
Az első (k=1) frekvencia komponens az értékek sorozata különböző n értékeknél. Mivel ilyenkor k=1 a függvény egy egyszeres frekvenciájú cosinus jelet, míg a függvény egy egyszeres frekvenciájú sinus jelet fog eredményezni.
Általánosan, a k-ik tároló az x(n) jelek szorzata k ciklusú cosinus függvényekkel, amelyekből az X(k) valós részét, míg a sinus jelek segítségével az X(k) képzetes részét állítjuk elő.
Az FFT alkalmazása frekvencia analízisre további két fontos összefüggéssel rendelkezik .
Az első összefüggés megadja a legmagasabb analizálható frekvencia és a mintavételezési frekvencia közötti kapcsolatot.
|
|
(11.20) |
ahol a legmagasabb frekvencia, amely még analizálható, a mintavételezési frekvencia. Az Ablakozás alfejezet ebben a fejezetben további adatokat ad meg -ról.
A második összefüggés kapcsolatot ad meg a frekvencia felbontás és a teljes mintavételezési idő között, amely kapcsolatban áll a mintavételezési frekvenciával és az FFT blokk méretével a következő egyenlet szerint:
|
|
(11.21) |
ahol a frekvencia felbontás, h (az időtartománybeli) két minta közötti mintavételi idő, a mintavételezési frekvencia és végül N az FFT blokk mérete vagyis a minták száma.
11.5.2. Gyors FFT transzformáció számítási időszükséglete
Amikor a bemeneti jelsorozat mérete kettő egész hatványa N=2 m , aDFT számításai elvégezgetők olyan módon, hogy közelítően csak műveletet végezzünk el, amely az DFT kiszámításának leggyorsabb módja.
A DSP (Digital Signal Processing ) irodalom utal olyan algoritmusokra, amelyek gyorsabbak, mint a gyors FFT számítás. Általánosan a bemeneti jelsorozat mérete, amelyet alkalmaznak mindenütt kettő egész kitevős hatványai, például az 512, a 1024 vagy a 2048 értékek.
A következő ábrákon (11.9. ábra és 11.10. ábra) a DFT konvencionális kiszámítási módjának és a kettő egész hatványa esetén alkalmazható FFT számítás időszükségleteit láthatjuk ugyanolyan méretű mintákon.
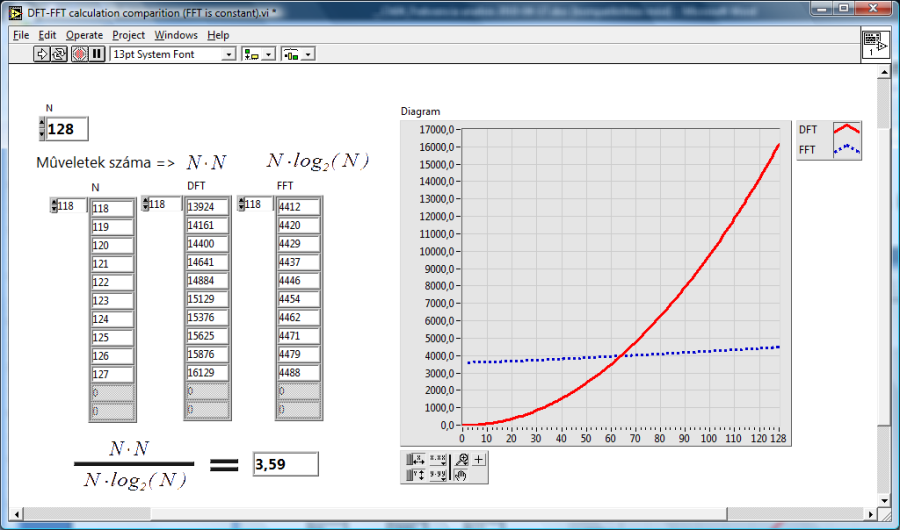
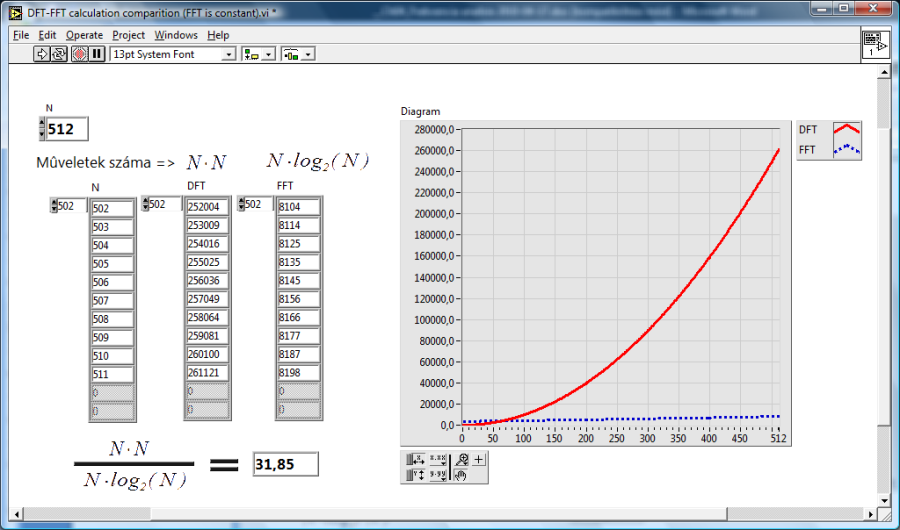
Amikor a bemeneti jelsorozat mérete nem kettő egész kitevős hatványa, de felbontható mint kis prímszámok egész kitevős hatványai, akkor alkalmazhatunk egy olyan speciális algoritmust (Cooley-Tukey algorithm), amely ilyen esetben is a lehető leggyorsabban kiszámítja a bemeneti jelsorozat DFT értékét.
Például a 11.22 egyenlet egy bemeneti jelsorozatot ad meg, amelynek mérete N felbontható kis prímszámok szorzatára.
|
|
(11.22) |
ahol
|
m, j, k = 0,1,2,3,... |
Arra a bemeneti (mért) jelsorozatra, amelyet a 11.22 egyenlettel adtunk meg, az FFT alapú .VI a DFT számításokat közelítőleg olyan sebességgel végzi el, mintha a jelsorozat mérete kettő egész kitevős hatványa volna.
A gyakran használt bementi jelsorozat méretek, amelyek (könnyen) felbonthatók kis prímszámok szorzatára a következők: 480, 640, 1000 és 2000.
11.5.3. Nulla értékekkel történő feltöltés (Zero Padding)
A nulla értékkel történő feltöltés technikáját akkor alkalmazunk, amikor a bemeneti sorozat méretét szeretnénk kettő egész számú hatványának megfelelő méretűvé tenni. A megoldásnál nulla jel értékeket adunk hozzá a bemeneti jelsorozat végéhez, így a teljes jelsorozat hosszúságát kettő következő egész számú kitevőjének megfelelő hosszúságúra növeljük. Például, ha van 10 mintánk a vizsgált jelből 6 nulla értéket hozzáadva a sorozat végéhez 16 minta hosszúságú sorozatot kapjunk, amely 2 negyedik hatványa. A 11.11. ábra ábra bemutatja a 10 mintából álló sorozat kiegészítését 16 minta hosszúságú sorozattá.
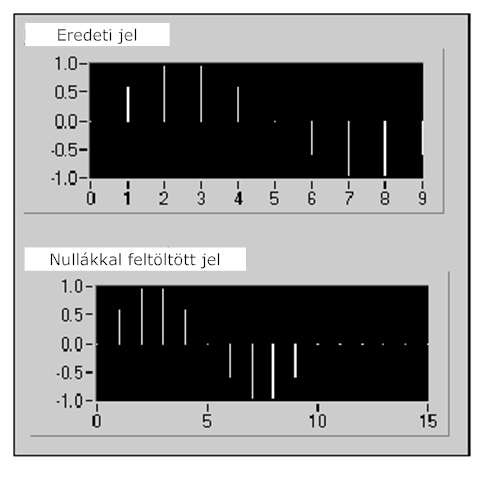
Az időtartománybeli jelsorozat végéhez hozzáadott nulla értékek nem befolyásolják a frekvencia felbontást. A frekvencia felbontás növelésének módja, hogy az időtartománybeli jelnél megnöveljük a mérés időtartamát és így hosszabb mérési rekordokkal dolgozzunk.
A mért értékek számának kettő hatványának megfelelő értékére történő növelése rövidebb számítási időt jelent az FFT számításánál. A nullákkal történő kiegészítés egy interpolációs FFT meghatározását teszi lehetővé, amely nagyobb képernyő felbontást eredményez.
11.5.4. Az FFT VI
A több adattípus fogadására alkalmas FFT VI meghatározza a jel gyors Fourier transzformáltjának(FFT) két típusát, amelyek a következők:
valós FFT (Real FFT) és a
komplex FFT (Complex FFT).
A két típusú FFT között az a különbség, hogy a valós FFT (Real FFT) a valós értékű jel Fourier transzformáltját határozza meg, míg a komplex FFT (Complex FFT) a komplex jel FFT értékét számítja ki.
Az eredmény mind a valós, mind a komplex FFT számítás esetében komplex érték.
A mért jelek legnagyobb része valós értékű jel. Ezért ezekhez a valós FFT számítást kell alkalmazni. Ha a komplex bemeneti jel képzetes részét nullává tesszük, akkor a komplex FFT-t is alkalmazhatjuk a valós FFT számításához. A következőkben egy példát mutatunk be, amelynél alkalmazzuk a komplex FFT-t és a bemeneti jel tartalmaz valós és képzetes részű komponenst. Ilyen jelek gyakran fordulnak elő a telekommunikációban, amikor a bemeneti jelet egy komplex exponenciális értékkel moduláljuk. A modulációs eljárás egy komplex jelet eredményez, amelyet a (11.12. ábra) ábrán láthatunk.
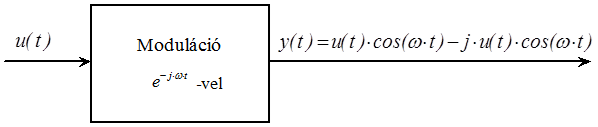
11.6. A frekvencia információ megjelenítése a Fourier transzformáció után
A Fourier transzformáció diszkrét implementációja, a digitális jel Fourier együtthatóinak (vagy harmonikusainak) térképe. Sajnálatos, de sem idő- sem pedig frekvenciainformáció nincs közvetlen kapcsolatban a FFT-vel.
Ezért a mintavételi időt, a h-t a felhasználónak kell megadnia.
Mivel egy bemeneti jel vektorának értékei a jel változását adják meg, azonos mintavételi időlépéssel meghatározható a jellel kapcsolatos frekvencia (sáv) Hertz-ben. A 11.23 egyenlet megadja a frekvencia felbontás Δf értékét a h-hoz viszonyítva.
|
|
(11.23) |
A 11.13. ábra ábra egy blokk diagramot mutat be, amely pontosan adja meg a frekvencia információt és Δf-et egy megadott mintavételi idő ( 1.000 E-3 ) esetén.
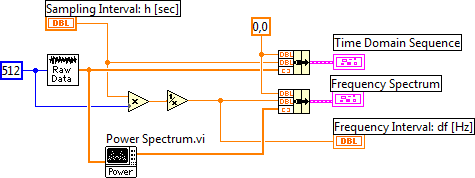
A 11.14. ábra ábra mutatja Δf függvényében azt a képernyőt, amely a (11.13. ábra) ábrán bemutatott VI eredményeként jelenik meg.
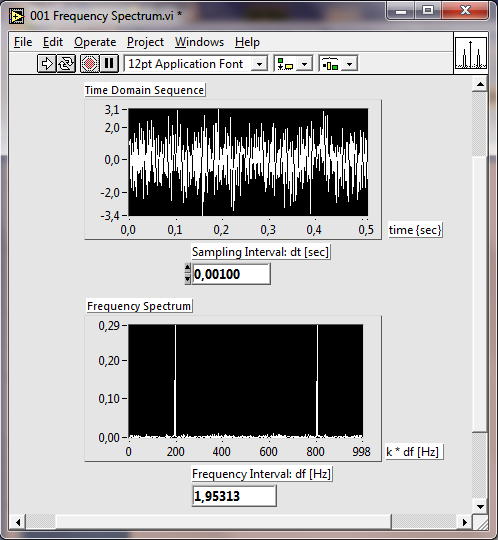
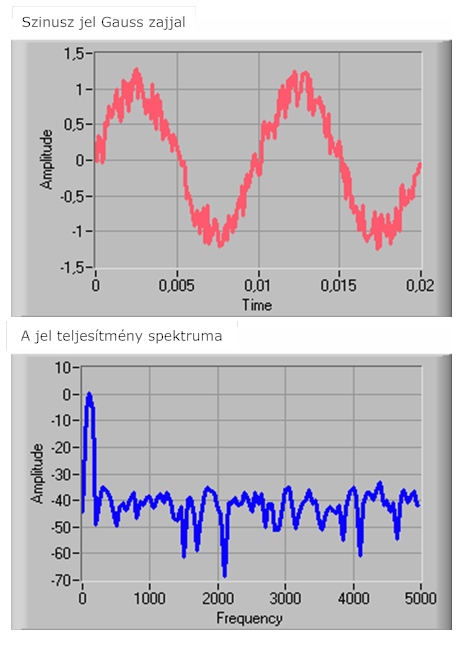
Fontos még az is, hogy milyen bementi adat alapján jött létre a 11.14. ábra ábra ezt a következő ábrán láthatjuk.
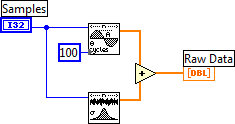
Az ábra egy olyan szinuszos jelet kibocsájtó jelgenerátort mutat be, amely a ”Samples” változóban megadott darabszámú (512) mintát tartalmaz, és amely 100 darab teljes szinuszos ciklust tartalmaz. A második generátor egy Gauss eloszlású zajgenerátor (0 várható értékkel és szigma=1 szórással), amely hasonlóan 512 mintát hoz létre. A két jel összege, amelyet a zajos jelként adunk ki a kimeneten.
Két további általános lehetőség a frekvencia információ megjelenítéséhez a 0 frekvenciás komponens megjelenítése a kétoldalas spektrum közepén.
A továbbiakban a Kétoldalas 0 frekvencia középpontú FFT transzformáció című részben információkat közlünk a 0 frekvenciás komponens megjelenítéséről. A Teljesítmény spektrum fejezetben pedig az egyoldalas spektrum megjelenítésről közlünk adatokat.
11.7. Kétoldalas 0(nulla) frekvencia középpontú FFT transzformáció
A kétoldalas 0 frekvencia középpontú FFT egy olyan eljárást biztosít, amellyel mind a pozitív, mind pedig a negatív frekvenciák megjeleníthetők. A legtöbb transzformációs kézikönyv úgy tárgyalja a Fourier transzformációt és annak tulajdonságait, hogy bemutatja a kétoldalas Fourier transzformáció párokat. Alkalmazhatjuk a Fourier transzformáció frekvencia eltolás (shiftelés) tulajdonságát, hogy meghatározzuk a 0 frekvencia középpontú értékeket. Egy kétoldalas 0 frekvencia középpontú FFT 0 frekvenciás komponense az adatokat tároló puffer közepén helyezkedik el (a puffer maximális indexének felénél).
11.7.1. A kétoldalas 0(nulla) frekvencia középpontú FFT transzformáció matematikai leírása
Ha egy Fourier transzformációs páros, akkor legyen
|
|
(11.24) |
ahol az időfüggvény diszkrét reprezentációjának mintavételi frekvenciája.
Határozzuk meg a -t mint indexet a megfelelő Nyquist komponenshez -hez, ahogy azt következő egyenlet mutatja
|
|
(11.25) |
Az egy beállított index a megfelelő -hez, hogy azt eredményezze, hogy a 0(nulla) frekvenciás komponens a Nyquist komponens helyén jelenjen meg, vagyis egy frekvencia eltolást valósít meg értékkel.
Ha az egy beállított index -hez képest, a diszkrét Fourier transzformáció párosban a következő kapcsolatot valósítja meg.
|
|
(11.26) |
ahol i az elemek száma a diszkrét szekvenciában (sorrendben); az időtartománybeli jelsorozat; pedig reprezentációja frekvencia tartományban.
Ha az exponenciális kifejezést kifejtett alakban írjuk fel, a következő összefüggést kapjuk:
|
|
(11.27) |
A 11.26 egyenlet egy +1 és –1 függvény értékű alternáló sorozat. A 11.26 egyenlet azt mutatja, hogy az eredeti időtartománybeli jelsorozat páratlan elemeit negáljuk és végrehajtunk egy FFT-t az új sorozaton, amelynek 0(nulla) frekvenciás komponense a jelsorozat közepén jelenik meg.
Ezért az eredeti bemeneti jelsorozat, amely a következő:
|
|
(11.28) |
után létrehozott Y jelsorozat
|
|
(11.29) |
létrehoz egy 0(nulla) frekvencia középpontú spektrumot.
11.7.2. A kétoldalas 0(nulla) frekvencia középpontú FFT transzformáció létrehozása
Egy jelet úgy is modulálhatunk a Nyquist frekvenciával, hogy ehhez nem használunk fel semmilyen külső puffert. A 11.16. ábra ábra egy olyan blokk diagramot mutat, amely a 11.26 kifejezéssel bemutatott jelsorozatot hozza létre.
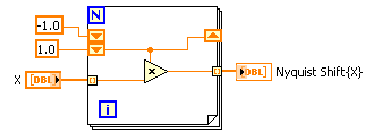
A (11.16. ábra) ábrán a For Loop a bementi szekvencia minden elemét alternálva megszorozza +1.0-el illetve –1.0-el. A műveletet a bemeneti vektor minden elemére elvégzi.
A 11.17. ábra ábra egy VI blokk diagramját mutatja be, amely létrehozza az időtartománybeli jelsorozatot és felhasználja a Nyquist Shift VI és a Power Spectrum VI-okat, hogy létrehozza a 0(nulla) frekvencia középpontú spektrumot.
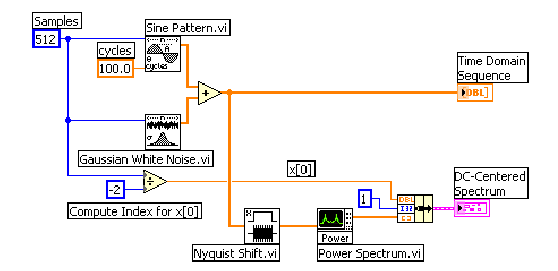
A (11.17. ábra) ábrán Nyquist Shift VI előkészíti az időtartománybeli jelsorozatot, úgy hogy –1.0-el megszoroz minden további elemet a jelsorozatban. A Power Spectrum VI transzformálja az adatokat frekvencia tartományba.
Ahhoz, hogy a frekvencia tengelyt valós frekvencia értékekkel mutathassa a képernyő meg kell adni az értékét, amely az x tengely kezdőfrekvenciájának értéke. A 0(nulla) frekvencia középpontú spektrum számára a következő egyenlet határozza meg értékét.
|
|
(11.30) |
A 11.18. ábra ábra mutatja az időtartománybeli jelsorozatot és a 0(nulla) frekvencia középpontú spektrumot, amely a (11.18. ábra) ábrán bemutatott műveletek végrehajtása után megjelenik a kijelzőkön.
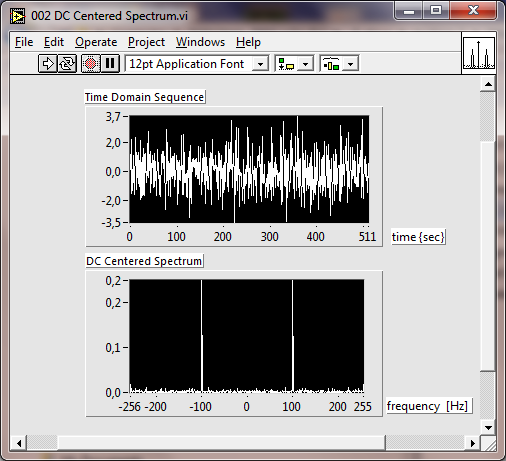
A 0(nulla) frekvencia középpontú frekvenciaspektrum megjelenítésénél, amelyet a 11.18. ábra ábra mutat be a 0(nulla) frekvenciájú komponens, az f=0 a képernyő közepénél jelenik meg.
Létrehozhatunk 0(nulla) frekvencia középpontú frekvenciaspektrumot páros adatmennyiséggel rendelkező bemeneti jelsorozatból ha a páratlan indexű adatokat negáljuk (szorozzuk –1-el).
Nem hozhatunk létre 0(nulla) frekvencia középpontú frekvenciaspektrumot, ha a bemeneti adatok száma páratlan (a páratlan indexű adatokat negálásával), mivel ilyenkor a Nyquist frekvencia két frekvencia tartománybeli FFT érték közé esik. Ilyen esetben rotálnunk kell az FFT tömböt egy olyan index eltolás értékkel, amelyet a következő összefüggés ad meg:
|
|
(11.31) |
A 0(nulla) frekvencia középpontú frekvenciaspektrum megjelenítésénél, páratlan bementi adatszám esetén a következő kifejezés adja meg értékét:
|
|
(11.32) |
11.8. Teljesítmény Spektrum SAA(f)
Ahogyan azt az Amplitúdó és fázis információ fejezetben leírtuk a DFT vagy FFT transzformáció után a valós bemeneti jelből komplex transzformált értéket hozunk létre, amelynek van valós és képzetes része.
A teljesítmény meghatározható az egyes frekvencia komponensekben, amelyet a DFT vagy az FFT reprezentál, ha négyzetre emeljük a frekvencia komponens amplitúdó értékét. Ezek alapján a k. frekvencia komponens teljesítménye – a DFT vagy FFT k. elemével – a következő egyenlettel írható le:
|
|
(11.33) |
ahol a frekvencia komponens amplitúdója.
A 11.3.3. szakasz fejezetben megadtuk, hogy hogyan kell meghatározni egy frekvencia komponens amplitúdójának értékét.
A teljesítmény spektrum egy olyan vektort ad eredményül, amely tartalmazza, az időtartománybeli bementi jel kétoldalas teljesítmény spektrumát a frekvencia tartományban.
A 11.34 egyenlettel meghatározható a kétoldalas teljesítmény spektrum az FFT-ből:
|
|
(11.34) |
ahol FFT*(A) az FFT(A) komplex konjugált értéke.
(Az FFT(A) komplex konjugált értéke az FFT(A) imaginárius részének negálásával és a reális rész megtartásával kapott komplex érték.)
Az elemek értéke a teljesítmény spektrum vektorban minden frekvencia komponensnél arányos az időtartománybeli jel egyes komponenseinek amplitúdó négyzetével.
Mivel egy valós jel DFT vagy az FFT transzformáltja szimmetrikus érték, a teljesítmény a pozitív a frekvenciáknál, és ugyanaz a teljesítmény van a megfelelő negatív frekvenciáknál -nél is, a 0(nulla) frekvenciás és a Nyquist komponenst kizárva.
A kétoldalas teljesítmény spektrum ábrája a negatív és pozitív frekvencia komponenseket mutatja, amelyek magasságát a következő összefüggés adja meg:
|
|
(11.35) |
ahol A k a szinuszos komponens amplitúdója (csúcsértéke) a k. frekvencia komponensnél. A 0(nulla) komponensnek olyan magassága van, mint az értékének az időjelben.
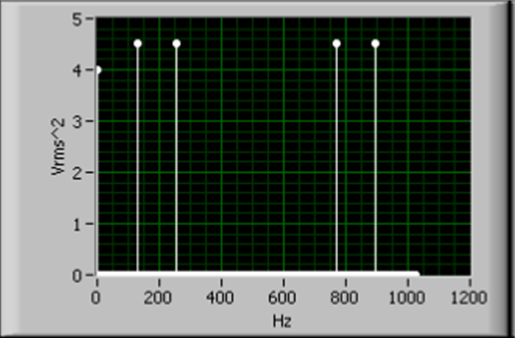
A 11.19. ábra ábra azt a teljesítmény spektrumot mutatja, amelynek az időtartománybeli függvénye 3 Veff szinuszos jelet tartalmaz 128 Hz-nél, 3 Veff szinuszos jelet tartalmaz 256 Hz-nél és egy 2 V-os jelet tartalmaz 0(nulla) Hz-nél. A 3 Veff szinuszos jel megfelel egy 4,2426V amplitúdójú szinuszos jelnek ().
A teljesítmény spektrumot a 11.34 egyenlettel leírt alap FFT függvény segítségével határoztuk meg.
11.8.1. Kétoldalas teljesítmény spektrum konvertálása egyoldalas teljesítmény spektrummá
A legtöbb frekvencia analízist végző berendezés csak a frekvencia spektrum pozitív részét jeleníti megmert a negatív frekvenciákra vonatkozó információ redundáns, mivel a valóságos jelek szimmetrikusak a 0(nulla) frekvenciájú jel körül.
Az analízis függvény kétoldalas eredményei magukba foglalják a pozitív fél spektrumot, amelyet a negatív fél spektrum követ, ahogy azt a 11.19. ábra ábra mutatja.
|
|
(11.36) |
ahol a kétoldalas teljesítmény spektrum, az egyoldalas teljesítmény spektrum, és Na kétoldalas teljesítmény spektrum hosszúsága. Emlékeztetőül a kétoldalas teljesítmény spektrum „eldobott értékei” az N/2-től (N-1) indexekkel jelölt elemekben találhatók.
A nem 0(nulla) frekvenciás értékek az egyoldalas teljesítmény spektrumban az egyes súly értékek a következő összefüggéssel adhatók meg:
|
|
(11.37) |
a 11.37 kifejezés a következő összefüggéssel egyezik meg:
|
|
(11.38) |
ahol a k. frekvenciájú szinuszos komponens négyzetes középértékének (rootmean square = rms) amplitúdója.
A teljesítmény spektrum dimenziója rendszerint a négyzetes középérték négyzetének mennyiségi dimenziója, ahol a mennyiség az időtartománybeli jel dimenziója.
Például egy [V] (Volt) dimenziójú jelalak egyoldalas teljesítmény spektruma a négyzetes középérték (rms) négyzete .
A 11.20. ábra ábra annak a jelnek az egy egyoldalas spektrumát mutatja, amelynek kétoldalas spektruma a 11.19. ábra ábrán látható.
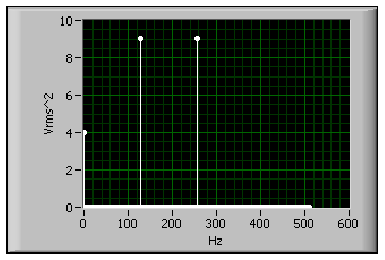
A (11.20. ábra) ábrán a nem nulla frekvenciájú komponensek nagysága kétszerese a (11.19. ábra) ábrán látható nem nulla frekvenciájú komponenseknek. Ugyancsak látható, hogy a (11.20. ábra) ábrán látható spektrum csak a (11.19. ábra) ábrán látható spektrum frekvenciájának feléig tart.
11.8.2. A fázismenet információ elvesztése
Mivel a teljesítményt rendszerint a DFT vagy FFT amplitúdóinak négyzetre emelésével kapjuk, a teljesítmény spektrum rendszerint valós érték. A valós érték (mivel nincs imaginárius és valós értéke külön-külön) nem tartalmaz fázis információt. Ha mégis szükség van a fázis információra, akkor azokat a DFT vagy FFT eljárásokat kell alkalmaznunk, amelyek komplex kimentet adnak.
A teljesítményspektrum információ szabadon felhasználható azokban az alkalmazásokban, amelyekben a fázisinformáció nem játszik szerepet, ilyen például a harmonikus teljesítmény egy jelben. Ha szinuszos jelet adunk egy nemlineáris rendszer bemenő jeleként, meghatározhatjuk az egyes felharmonikus frekvencia komponensek teljesítményét a rendszer kimenetén.
11.9. A spektrumokkal végzett számítások
Ha rendelkezünk az amplitúdó vagy a teljesítmény spektrummal , a bemeneti jel számos hasznos tulajdonságát határozhatjuk meg, mint például a teljesítményt és a frekvenciát , zaj szintet vagy a teljesítmény spektrális sűrűségét.
11.9.1. A teljesítmény és a frekvencia közelítése
Ha egy frekvencia komponens két frekvencia vonal között helyezkedik el, akkor ez a frekvencia komponens úgy jelenik meg. hogy energiája megoszlik a két szomszédos frekvencia komponens energiájának arányosan csökkentett értékével. Az aktuális csúcs a két frekvencia vonal között helyezkedik el.
Az aktuális frekvenciát nagyobb felbontással közelíthetjük a diszkrét frekvencia komponensek segítségével, mint az a frekvencia, amely az FFT eljáráshoz tartozik, ha végrehajtjuk a frekvencia egy súlyozott átlaggal való számítását egy meghatározott csúcsérték környezetében a teljesítmény spektrumban, ahogy azt a következő függvény mutatja:
|
|
(11.39) |
ahol j a látszólagos frekvencia csúcs vektor indexe, amelyre kíváncsiak vagyunk.
A j±3 elfogadható, mivel egy olyan frekvencia kiterjedést reprezentál, amely szélesebb mint a simító ablak legszélesebb sávja a Táblázat 12.3 táblázatban, a Simító ablakok korrekciós tényezői és a legrosszabb esetben fellépő amplitúdó hibák az 12. fejezet fejezetben.
A diszkrét csúcs frekvencia komponensek összegzésével közelíthető a teljesítmény az elemek között a csúcsérték közelében. Más szavakkal, kiszámíthatunk egy területet a csúcsérték alatt. A következő összefüggést felhasználhatjuk, hogy a segítségével közelítsük a diszkrét csúcs frekvencia komponensek teljesítményét.
|
|
(11.40) |
A 11.40 egyenlet csak akkor érvényes, ha a spektrum diszkrét frekvenciájú komponenseket tartalmaz!
Az összefüggés nem érvényes folytonos frekvencia spektrumra!
Ha két vagy több frekvencia csúcs van egymáshoz képest azonosan a hat vonalban, akkor ezek jelentős hatással vannak arra, hogy a teljesítmény és a meredekség az aktuális frekvencián megnövekedjen.
Csökkenthető ez a hatás, ha csökkentjük a frekvenciavonalak számát a 11.40 egyenletben.
Ha a teljesítményt akarjuk meghatározni egy adott frekvencia tartományban, összegezzünk minden tagot a frekvencia tartományban és osszuk el a csillapító ablak zajteljesítményének sávszélességével. A továbbiakban az 12. fejezet fejezetben (Simító ablakok) kapunk részletesebb tájékoztatást a simító ablak zajteljesítményének sávszélességéről.
11.9.2. A zajszint és a teljesítmény spektrum sűrűségének meghatározása
A mérés zajszintje szoros kapcsolatban van a mérés sávszélességével. Amikor egy teljesítmény spektrum alap zajszintjét vizsgáljuk akkor minden keskenysávú zajszintet meg kell vizsgálnunk az összes FFT sávban. Ezért egy adott spektrum zajszintje függ a spektrumhoz tartozó értéktől, amelyet a mintavételi idő és a mérésben szereplő mintavételi pontok száma határoz meg. Más szavakkal a zajszint minden frekvencia vonalnál egyenlő azzal a zajszinttel, amelyet úgy kaphatunk meg, hogy egy Hz-es szűrőt alkalmazunk az adott frekvencia-vonal körül. Ezért, ha egy meghatározott mintavételi idő mellett megduplázzuk a mintavételi adatok számát, csökkenthetjük a zaj teljesítményt 3 dB-el, amely az egyes frekvencia sávokban megjelenik. Elméletileg a diszkrét frekvencia komponenseknek zérus sávszélessége van ezért nem skálázhatók a pontok számával vagy a FFT frekvencia tartományával.
Ahhoz, hogy kiszámolhassuk a jel / zaj viszonyt (SNR = Signal to Noise Ratio) hasonlítsuk össze a vizsgált frekvenciákhoz tartozó teljesítmény csúcsértékeket a szélessávú zaj szintjével. A szélessávú zajszint számítása az összes teljesítmény spektrum sávban történő összegzéssel történik, kivéve a csúcsokat és a 0(nulla) frekvenciájú komponenst, majd osztjuk az összeget az ablak ekvivalens zaj szélességével.
Mivel a zajszint skálázása -el, a zaj spektrumának mérése pedig normalizált formában jelenik meg, ezért a teljesítmény vagy amplitúdó spektrum sűrűségnek nevezzük.
A teljesítmény vagy amplitúdó spektrum sűrűség normalizálja a teljesítmény vagy amplitúdó spektrumot egy olyan spektrumhoz, amelyet egy 1 Hz szélességű négyszög típusú (ideális) szűrő mér, amely egy megállapodás a zajszint mérésekre. A szint minden frekvencia vonalnál megegyezik azzal a szinttel, amelyet úgy kapnánk, ha egy 1 Hz-es szűrőt alkalmaznánk az adott frekvencia vonal körül.
A következő összefüggés a teljesítmény spektrum sűrűséget adja meg:
|
Teljesítmény spektrum sűrűség= |
(11.41) |
A következő összefüggés az amplitúdó spektrum sűrűséget adja meg:
|
Amplitúdó spektrum sűrűség= |
(11.42) |
A spektrális sűrűség formátum alkalmazható véletlen-értékű vagy zajos jelekre egyaránt.
A spektrális sűrűség formátum nem alkalmazható diszkrét frekvencia komponensekre, mivel a diszkrét frekvencia komponenseknek elvileg 0(nulla) sávszélessége van.
11.10. Amplitúdó és fázis spektrumok kiszámítása
A teljesítmény spektrum a teljesítményt úgy mutatja, mint az amplitúdó négyzetes átlag értékét minden frekvencia vonalon, de nem tartalmaz fázis információt. Mivel a teljesítmény spektrum elveszíti a fázis információt, az FFT-t (Fast Fourier Transformation) kell alkalmazni, hogy megnézhessük a jel frekvencia és a fázis információját.
Az a fázis információ, amelyet az FFT biztosít egy relatív fázis információ az időtartománybeli jel kezdetéhez viszonyítva. Ezért ugyanettől a ponttól kell indítani mindent a jelnél, hogy helyes fázismenet értéket kapjunk. Egy szinusz hullám 90 fokos fázistolást mutat a szinuszos hullámú frekvencián. Egy cosinus hullám 0 fokos fázistolást mutat. Az analízis feladatok elsődleges feladata rendszerint meghatározni a relatív fázistolást a komponensek között vagy a fázis eltérést két jel között, amelyeket azonos időpontban mérünk. Két jel közötti fázis eltérést meghatározhatunk valamelyik magas szintű FFT alkalmazásával. Tekintse át a Frekvencia válasz és hálózat analízis fejezetet ebben a könyvben, hogy további információkat kapjon a magas szintű FFT alkalmazásáról.
Az FFT kétoldalas spektrumot hoz létre komplex formátumban valós és képzetes résszel. A kétoldalas spektrum konvertálható polár formátumba, hogy meghatározhassuk a jel amplitúdó és a fázis értékét. A polár formátum frekvencia tengelye megegyezik a kétoldalas spektrum frekvencia tengelyével. Az FFT amplitúdója arányos az időtartománybeli jel pontjainak számával. (Lásd 11.14 képlethez fűzött magyarázatot!) Alkalmazzuk a következő egyenleteket, hogy meghatározzuk az amplitúdó és a fázis értékeket adott frekvencián az FFT elvégzése után.
|
|
(11.43) |
|
|
|
(11.44) |
ahol az arctangens függvény –PI és +PI közötti fázis értékkel tér vissza egy 2·PI radián szélességű értékhatárban.
A következő összefüggés megadja a derékszögű koordinátákból polár koordinátába történő átszámítás függvényét.
|
|
(11.45) |
A derékszögű koordinátákból polár koordinátába történő átszámításhoz alkalmazzuk a 11.43 és 11.44 egyenleteket.
A kétoldalas amplitúdó spektrum az amplitúdó (csúcsérték) felét mutatja a pozitív és negatív frekvenciáknál. Ahhoz, hogy átkonvertáljuk az egyoldalas alakot – kivéve a 0(nulla) frekvenciájú komponenst – kettővel(2-vel) szorzunk és töröljük a vektor második felét. Az egyoldalas amplitúdó spektrum egysége azon amplitúdó érték, amely megadja minden szinuszos amplitúdó komponens csúcsértékét, felhasználva ehhez az időfüggvény értékeit.
Hogy megkapjuk az egyoldalas fázis spektrumot töröljük a kimeneti vektor második felét.
11.10.1. Az amplitúdó meghatározása Vrms-ben valamint a fázis meghatározása fokban
Hogy megnézhessük az amplitúdó spektrumot Vrms-ben (négyzetes középérték [ rms = r oot m ean s quare]) osszuk el a nem egyenfeszültség komponenseket négyzetgyök -vel, majd konvertáljuk a spektrumot egy egy-oldalas formulába. Mivel a nem egyenfeszültségű komponenseket megszoroztuk kettővel, amikor a kétoldalas spektrumot átkonvertáltuk egyoldalas spektrummá, az rms (rms = root mean square => négyzetes középérték) amplitúdó spektrumot közvetlenül meghatározhatjuk a kétoldalas amplitúdó spektrumból úgy, hogy megszorozzuk a nem egyenfeszültségű komponenseket négyzetgyök 2-vel (-vel) és töröljük a vektor második felét. A következő egyenlet bemutatja az alapvető számításokat a kétoldalas FFT-ből egyoldalas amplitúdó spektrumba.
|
|
(11.46) |
|
i =1 ..((N/2)-1) -nél |
|
|
(11.47) |
|
i =0-nál (egyenfeszültségnél) |
ahol
i a frekvencia sor száma; vagy vektor index az A mintavételes jel FFT-jában
A számértékek a Vrms-ben megadják az effektív (rms) feszültség értékért az időfüggvény minden szinuszos komponenséhez.
Az amplitúdó spektrum nagyon hasonlít a teljesítmény spektrumhoz. Az egyoldalas teljesítmény spektrumot kiszámíthatjuk, ha négyzetre emeljük az egyoldalas rms amplitúdó spektrum minden egyes elemét. Következésképpen meghatározhatjuk az amplitúdó spektrumot, ha négyzetgyököt vonunk a teljesítmény spektrum minden egyes eleméből. A teljesítmény spektrum számításáról további részleteket ezen fejezet „Teljesítmény spektrum” alfejezetében talál.
Alkalmazzuk a következő egyenletet, hogy meghatározzuk a spektrum fázistolását szög dimenzióban:
|
|
(11.48) |
11.11. Frekvencia válasz függvény
Amikor két darab, egy időben mintavételezett csatornát elemzünk, rendszerint jobban szeretnénk ismerni a különbségeket a két csatorna között, mint az egyes csatornák tulajdonságait.
Egy tipikus két csatornás analizátor berendezésben, amilyen a (11.21. ábra) ábrán látható, meghatározható a nem-állandósult spektrum, amelyet ablak függvény alkalmazásával számítunk, valamint a két csatorna külön-külön számított FFT függvénye. Az átlagolt FFT spektrum , az auto-teljesítmény (auto-power) spektrum valamint a kereszt-teljesítmény (cross-power) spektrum számított értékek, amelyek segítségével a frekvencia válasz függvény közelítése történik. A koherencia függvényt szintén alkalmazhatjuk, hogy ellenőrizzük segítségével a frekvencia válasz függvény érvényességét.
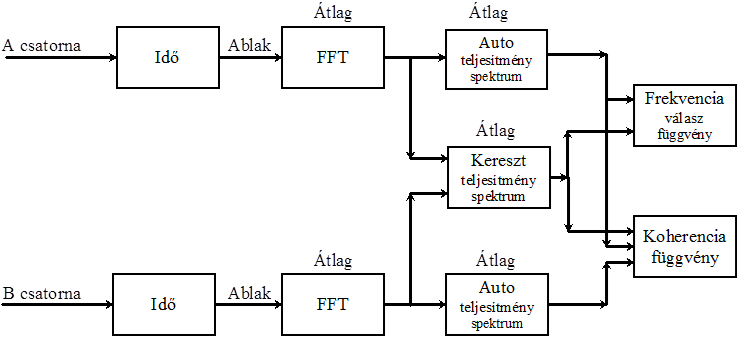
Egy rendszer frekvencia válasz függvényét adott frekvencián a függvény amplitúdójának nagyságával és fázis-szögével írhatjuk le.
A rendszer erősítése a kimeneti jel amplitúdó értéke osztva a bemeneti jel amplitúdó értékével minden frekvencián. A rendszer fázistolása a kimeneti jel és a bemeneti jel fázistolásainak különbsége minden frekvencián.
11.12. Kereszt teljesítmény spektrum SAB(f) (Cross Power Spectrum)
A kereszt teljesítmény spektrumot { SAB(f) } nem alkalmazzuk közvetlenül a mérésekhez, de nagyon hasznos építőelem más mérési típusokhoz.
Alkalmazzuk a következő egyenletet, hogy meghatározzuk a kétoldalas kereszt teljesítmény spektrumot két időfüggvényhez A-hoz és B-hez.
|
|
(11.49) |
A kereszt teljesítmény spektrum egy kétoldalas komplex formula, amelynek van valós és képzetes része. Ahhoz, hogy a kereszt teljesítmény spektrum erősítés és fázistolás információit áttranszformáljuk Descartes koordináta rendszerbe (x,y koordinátákba), alkalmazzuk a polárból derékszögű koordinátákba átalakító szubrutint, amelynek algoritmusát a 11.43 és a 11.44 függvények mutattak be.
Ahhoz, hogy a teljesítmény spektrumot a kétoldalas komplex formátumból átalakítsuk egyoldalas formátumra alkalmazzuk azokat az eljárásokat és függvényeket, amelyeket a „Kétoldalas teljesítmény spektrum átalakítása egy oldalas spektrumba” alfejezet mutat be ebben a fejezetben.
Az egyoldalas kereszt teljesítmény spektrum létrehoz még négyzetes középérték (rms = root mean square) amplitúdókat valamint fázis differenciákat a két jel A és B között. Az egyoldalas kereszt teljesítmény spektrum egysége megegyezik a négyzetes középérték (rms) négyzetével, amely a .
A teljesítmény spektrum megegyezik a kereszt teljesítmény spektrummal, amikor a két jel A és B ugyanaz a jel. Ezért a teljesítmény spektrumra rendszerint úgy hivatkoznak, mint az auto teljesítmény spektrumra vagy auto spektrumra .
11.13. Frekvencia válasz és hálózat analízis
A következő függvényeket alkalmazhatjuk, hogy meghatározzuk egy adott hálózat frekvencia átviteli tulajdonságait:
-
Frekvencia válasz függvény
-
Impulzus válasz függvény
-
Koherencia függvény
11.13.1. Frekvencia válasz függvény H(f)
A 11.22. ábra ábra bemutatja egy hálózat frekvencia válasz függvényének mérési metódusát:

A (11.22. ábra) ábrán egy gerjesztő függvényt alkalmazunk a vizsgált hálózathoz és mérjük a gerjesztést valamint a válasz jelet. A mért gerjesztő jelből és a válasz jelből kiszámítható a frekvencia válasz függvény. A frekvencia válasz függvény egy adott frekvencián megadja a hálózat erősítését és fázistolását.
A 11.50 egyenletet alkalmazzuk a frekvencia válaszfüggvény meghatározásához.
|
|
(11.50) |
ahol H(f) a frekvencia válasz függvény. Az A jel a gerjesztés, B jel pedig a válasz jel, SAB(f) az A és B jel kereszt teljesítmény spektruma, SAA(f) az A jel teljesítmény spektruma.
A frekvencia válasz függvény egy kétoldalas komplex alak, amelynek van valós és képzetes része. Ahhoz, hogy konvertáljuk a frekvencia válasz függvényt erősítéssé és fázistolássá, alkalmazzuk a derékszögű- polár konverziós függvényt a 11.44 egyenlet alapján.
Ahhoz átkonvertáljuk az adatokat egyoldalas formára a válaszfüggvény vektorának második felét el kell hagynunk.
Ha a mérési adatok frekvencia válaszfüggvényeinek átlagértékét szeretnénk meghatározni, a következő lépéseket javasoljuk:
Számítsuk ki az S AB (f) függvény átlagát a következő módon: összegezzük a komplex adatokat és osszuk a mérések számával.
Számítsuk ki az S AA (f) függvény átlagát úgy, hogy összegezzük a komplex adatokat és osszuk a mérések számával.
Határozzuk meg az S AB (f), S AA (f) függvények átlagai segítségével a H(f) frekvencia válasz függvény átlagát az 11.50 egyenlet szerint.
11.13.2. Impulzus válasz függvény FFT1( H(f) )
A hálózat impulzus válasz függvénye a hálózat frekvencia válasz függvényének időtartománybeli reprezentációja.
A hálózat impulzus válasz függvénye egy olyan idő alapú kimeneti jel, amelyet akkor kapunk, ha a hálózatot egy impulzussal gerjesztjük a t=0 időpillanatban.
A hálózat impulzus válaszfüggvényének meghatározásához inverz Fourier transzformálnunk kell a kétoldalas komplex frekvencia válasz függvényt a 11.50 egyenlet alapján.
Az impulzus válaszfüggvény átlagának meghatározásához inverz Fourier transzformálnunk kell a frekvencia válasz függvény átlagát.
11.13.3. Koherencia függvény K(f)
A koherencia függvény arról ad információt, hogy milyen a frekvencia válasz függvény mérésének minősége, valamint, hogy a válasz energiája milyen korrelációban (kapcsolatban) van a gerjesztés energiájával. Ha további jel jelenik meg a válaszban, amely lehet akár egy különlegesen nagy amplitúdójú zaj jel vagy egyéb más jel, akkor a hálózat válaszának mérése nagyon rossz minőségű lesz.
A koherencia függvényt arra használhatjuk, hogy azonosítsuk a különböző zajokat valamint a többi jelforrást, amely hozzájárul a válasz jelhez.
A koherencia függvény a 11.51 egyenlet szerint határozzuk meg:
|
|
(11.51) |
ahol
|
S AB (f) |
a kereszt teljesítmény spektrum, |
|
|
S AA (f) |
az A jel teljesítmény spektruma, |
|
|
S BB (f) |
a B jel teljesítmény spektruma. |
A 11.51 egyenlet egy nulla (0.0) és egy (1.0) közötti értékkel rendelkező koherencia tényezőt is meghatároz a jel frekvenciájának függvényében. A koherencia tényező akkor egy (1.0), ha frekvencia vonal azt mutatja, hogy a válasz energiájának 100%-a megegyezik a gerjesztő jel energiájával és nem lép fel semmiféle zavaró hatás az adott frekvencián.
A koherencia függvény pontos meghatározásához a gerjesztő jelet és az erre adott válasz jelet kettő vagy ennél több esetben célszerű megmérni. Ha csak egy mérés történik, a koherencia függvény minden frekvenciához egységnyi értéket rendel hozzá.
11.14. Ablakozási technika
A gyakorlati alkalmazásokban a vizsgált jel mintavételi értékeiből véges számú értéket tudunk megmérni. Az FFT feltételezi, hogy ez az időfüggvény rekord (felvétel) ismétlődik. Ha a mérési adatok száma egy meghatározott érték az időadatok rekordjában, az ismétlődésnél egy csillapítási hatás lép fel az időtartománybeli jelsorozat határainál.
A gyakorlati alkalmazásokban általában rendelkezünk a mérési adatok ciklusszámának értékével (hozzárendelt értékkel). Ebben az esetben a ciklusok egy nem hozzárendelt értéke, az eredmény rekordok ismétlődésekor egy folytonossági hiányt mutat a mérési adatok határainál. (lásd 12.1. ábra ábrát) Ezek a mesterséges folytonossági hiányok eredetileg nem voltak jelen a mért jelben és ezért egy „energia maszatolást” vagy „energia átszivárgást” jelentenek az aktuális frekvenciából más frekvenciákba.
Ez a jelenség a spektrális energia átszivárgás . Az átszivárgás mennyisége függ a folytonossági hiány amplitúdójának nagyságától, nagyobb amplitúdó nagyobb mennyiségű energia szivárgást eredményez.
Egy periodikus típusú jel időfüggvényének rekordja szinuszos komponensekből áll, ami azt jelenti, hogy rendelkezik egy meghatározott ciklussal az időfüggvény rekordjában. Így egy tökéletesen periodikus jel olyan spektrummal rendelkezik, amely az energiát meghatározott frekvenciájú komponensekben tartalmazza. (11.23. ábra)
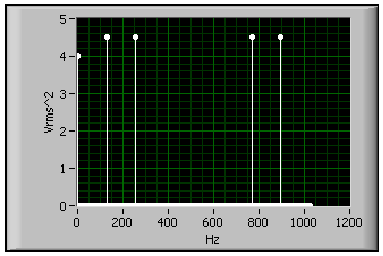
Egy olyan jelnek, amely nem periodikus időfüggvénnyel rendelkezik az energiája eloszlik a különböző frekvenciájú komponensek között. Az FFT spektrum azt az állapotot modellezi, mintha az időfüggvény örökké saját magát ismételné. Ez azt jelenti, hogy az analizált rekordok egy-egy periódus hosszúságú, végtelenül ismétlődő periodikus jel.
Mivel az energia átszivárgás nagysága a folytonossági hiány amplitúdójával arányos a jel határainál, ablakozási technikát alkalmazhatunk , hogy csökkentsük a folytonossági hiányt és ezzel együtt csökkentsük a spektrális energia (át)szivárgást. Az ablakozás az időtartománybeli jelet egy másik időtartománybeli jellel szorozza meg, amelyet ablaknak nevezünk, melynek amplitúdója folyamatosan csökken és csillapított módon viszi (le) 0 értékűre a vizsgált jel éleit. Az eredmény egy olyan ablakozott jel, amelynél nagyon csekély vagy egyáltalán nincs folytonossági hiány a rekordok között, és ezért nagyon kicsiny a spektrális energia (át)szivárgása. Az ablakozás megvalósításához számos ablak típus közül választhatunk. Az ablak kiválasztása függ az alkalmazás jellegétől és valamilyen elsődleges információt arról a jelről, amelyet analizálunk.
A 12. fejezet fejezetben további információkat talál az ablakozásról.
11.15. Átlagolás a mérési eredmények ábrázolásához
A mérési eredmények egymást követő folyamatos átlagolása rendszerint javítja a mérési eredmények pontosságát.
Az átlagolást a mérési eredményeken vagy egy egyéni spektrumon hajtjuk végre, de sohasem egy, hanem több idő rekordon. Választhatunk a következő általános átlagolási módok közül:
Négyzetes (effektív) átlagolás (RMS Average= Root Mean Square Average)
Vektoros átlagolás
Csúcsérték megtartása
11.15.1. Négyzetes (effektív) átlagolás (RMS Averaging)
A négyzetes átlagolás csökkenti a jel ingadozást, de nem csökkenti a zaj alapszintjét. A zaj alapszintje nem csökken, mert a négyzetes átlagolás, átlagolja a jel energiáját vagy a teljesítményét. Az átlagolás eredményeként egy csatornás mérésnél a fázistolás nulla(0) értékű. A négyzetes átlagolás két csatornás mérésnél megőrzi a fontos fázistolási információt.
A négyzetes (effektív) átlagolás metódus szerint történő átlagolásnál a következő egyenleteket alkalmazzuk:
|
FFT spektrum |
|
|
Teljesítmény spektrum |
|
|
Kereszt teljesítmény spektrum |
|
|
Frekvencia válaszfüggvény |
ahol
|
X |
az x gerjesztés komplex Fourier transzformáltja |
|
|
X* |
az X komplex konjugáltja |
|
|
Y |
az y válasz komplex Fourier transzformáltja |
|
|
Y* |
az Y komplex konjugáltja |
|
|
az X átlaga; a valós és a képzetes rész átlag képzése külön-külön történik |
11.15.2. Vektoros átlagolás
A vektoros átlagolás megszünteti a zajt az egyidejű jelekben. A vektoros átlagolás a komplex mennyiségeket direkt módon átlagolja. A valós rész és a képzetes rész átlagolása külön-külön történik. A valós rész és a képzetes rész külön-külön történő átlagolása csökkenti a zaj alapszintet véletlen jeleknél, mivel a véletlen jelek nem fázis koherensek (összefüggők) az egyik idő rekordból a következőbe történő átlépéskor. Ha a valós és képzetes részt külön-külön átlagoljuk, csökkentjük a zaj értékét, de szükségünk van egy indító (trigger) jelre.
|
FFT spektrum |
|
|
Teljesítmény spektrum |
|
|
Kereszt teljesítmény spektrum |
|
|
Frekvencia válaszfüggvény |
ahol
|
X |
az x gerjesztés komplex Fourier transzformáltja |
|
|
X* |
az X komplex konjugáltja |
|
|
Y |
az y válasz komplex Fourier transzformáltja |
|
|
Y* |
az Y komplex konjugáltja |
|
|
az X átlaga; a valós és a képzetes rész átlag képzése külön-külön történik |
11.15.3. A csúcsérték megtartása
A csúcsérték megtartása (rögzítése) az átlagolt értékek csúcsértékével tér vissza. A csúcsérték megtartott átlagolása minden frekvencián (frekvenciavonalon) külön-külön történik, a csúcsérték szintjét megtartja az egyik FFT értékből (rekordból) a következőbe történő átlépéskor.
|
FFT spektrum |
|
|
Teljesítmény spektrum |
ahol
|
X |
az x gerjesztés komplex Fourier transzformáltja |
|
|
X* |
az X komplex konjugáltja |
11.15.4. Súlyozás
Amikor egy négyzetes vagy vektoros átlagolást hajtunk végre minden új spektrális rekordot súlyozunk vagy lineáris vagy exponenciális súlyozással.
A lineáris súlyozás az N darab spektrális rekordot azonos súlyozással látja el. Amikor a megadott számú átlagolás befejeződik, az algoritmus megállítja az átlagolást és megjeleníti az átlagolt eredményt
Az exponenciális súlyozás jobban kiemel egy új spektrális adatot, mint a korábbit és ezeket egy folytonos eljárással minden lépésben újra számolja.
Az exponenciáis súlyozással történő (új) érték meghatározásához a következő formulát alkalmazzuk:
|
|
(11.52) |
ahol
|
X[k] |
a k. rekordból származó bemeneti adat |
|
|
Y[k] |
az átlagolási eljárás eredménye X[1]-től X[k]-ig, |
ahol
|
N = k-val |
lineáris súlyozás esetén; |
|
|
N = konstans |
exponenciális súlyozás esetén |
|
|
( N = 1 ha k = 1 ). |
11.16. Visszhang észlelése
A visszhang észleléséhez általában modulált rendszerek analíziséhez általánosan használt Hilbert transzformációt alkalmazzuk. (lásd 6.4. szakasz fejezetet)
A 7.1.5. szakasz fejezetben pedig látható, hogy a cepstrum analízis milyen módon alkalmazható a visszhang megszüntetésére.
A 11.53 egyenlet az időtartománybeli jelet írja le. Míg a 11.54 egyenlet az időtartománybeli jel Hilbert transzformáltját adja meg.
|
|
(11.53) |
|
|
|
(11.54) |
ahol
|
A |
az amplitúdó |
|
|
a természetes rezonancia frekvencia |
||
|
az idő-csillapítási konstans |
A 11.55 egyenlet az analizált jel amplitúdójának természetes alapú logaritmusát adja meg.
|
|
(11.55) |
A 11.55 egyenlet eredménye egy egyenes egyenlete, amelynek a meredeksége.
Ezért eltávolítható a rendszer idő-konstansa ábrázolásakor.
A 11.25. ábra ábra egy időtartománybeli jelet mutat, amely tartalmaz visszhang jelet.
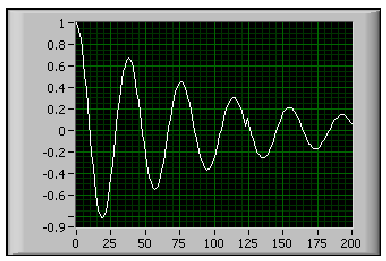
A következő feltételek akadályozzák a visszhang jel felfedezését a (11.25. ábra) ábrán:
Az időkésés a forrás és a visszhang jel között nagyon kis érték és relatív érték a rendszer idő-késleltetési konstans értékéhez képest.
A visszhang amplitúdója kis értékű a forrás amplitúdójához képest.
A visszhang jelet láthatóvá tehetjük, ha az nagyságát logaritmus léptékben ábrázoljuk, mint az a (11.26. ábra) ábrán látható.
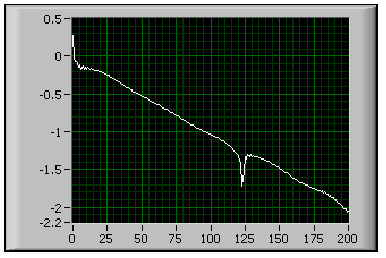
A (11.26. ábra) ábrán a folytonossági hiány világosan látható és kijelöli a visszhang késleltetésének helyét.
A 11.27. ábra ábra bemutatja egy olyan VI blokk diagramját, amely létrehozta a 11.25. ábra és 11.26. ábra ábrákat.
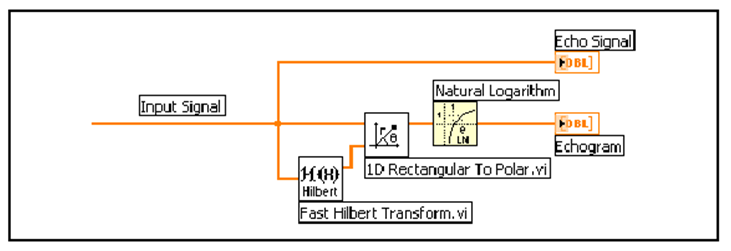
A 11.27. ábra ábra a következő lépéseket tartalmazza a visszhang detektálásához:
Meghatározza a bemeneti jel Gyors Hilbert Transzformáltját, amely az jelet adja eredményül.
Meghatározza az jel amplitúdóját 1D derékszögű-Polár VI segítségével.
Kiszámítja az jel természetes alapú logaritmusát, hogy megállapíthassuk a visszhang létezését.
Irodalom
[11.1.] LabVIEW Control Design User Manual. 2009.