12. fejezet - Simító ablakok
Vissza		Előre

12. fejezet - Simító ablakok

Tartalom

Ez a fejezet bemutatja a spektrális szóródás jelenségét, hogy hogyan kell simító ablakokat használni a spektrális szóródás csökkentésére, a simító ablakok típusait, illetve, hogy hogyan kell a megfelelő típusú simító ablakot kiválasztani, a spektrális analízishez, a szűrő együtthatók tervezéséhez.

Bemutatja a simító ablakok skálázásának fontosságát. (lásd 7.1.3.4. szakasz fejezetet)

Ablakozási vizsgálatokat a következő esetekben alkalmazhatunk:

A megfigyelés időtartamának meghatározása.

A spektrális lebegés csökkentése.

Egy kis amplitúdójú jel elválasztása egy nagy amplitúdójú jeltől, melyek frekvenciái nagyon közel vannak egymáshoz.

FIR szűrő együtthatók tervezése.

A Windows VI-k egyszerű eljárást biztosítanak a mintavételezett jel spektrális karakterisztikájának javítására.

12.1. Spektrális szóródás

A Shannon mintavételezési tétel értelmében, egy időben folytonos jel teljes mértékben rekonstruálható diszkrét, egyenlő időközű mintákból, ha a mintavételezett jel legmagasabb frekvenciájú összetevője kisebb, mint a mintavételi frekvencia fele. A mintavételi frekvencia felét Nyquist frekvenciának nevezzük. A Shannon tétel áthidalja a szakadékot az időben folytonos és a digitális jelek között. A Shannon tétellel kapcsolatos további információk az 8. fejezet fejezetben találhatók.

Gyakorlatilag az időjelet digitalizáló alkalmazások véges számú adatból álló jelsorozatot eredményeznek még akkor is, ha betartjuk a Shannon tételt és gondosan megválasztjuk a mintavételezés körülményeit. Még akkor is, ha az adatok megfelelnek a Nyquist kritériumnak, a véges számú minta energia szóródást okozhat, amit spektrális szóródásnak nevezünk. Emiatt, még megfelelő mintavételezési technikával is előfordulhat, hogy a mérés nem eredményez egy skálázott, egyoldalas spektrumot a spektrum szóródás miatt. Spektrum szóródásnál úgy tűnik, mintha egy adott frekvencia energiája szétszóródna az összes többi frekvencián. A spektrum szóródás az FFT és a DFT algoritmus egyik feltételének az eredménye, annak, hogy az időtartománybeli jelsorozat mindig pontosan ismétlődik (a rekordok többszöri ismétlése miatt). Így a jelek egy időtartománybeli jelsorozatban periodikusan ismétlődnek olyan intervallummal, amely megegyezik az jelsorozat (rekordok) hosszával. Amikor FFT-t vagy DFT-t használunk a jel frekvencia összetevőinek meghatározásához, a transzformáció azt feltételezi, hogy a véges adathalmaz egy periodikus jel egyetlen periódusa. Ezért a jelsorozat végessége (meg)csonkított hullámformát eredményez az eredeti folytonos időfüggvénytől eltérő spektrális karakterisztikával és a végesség éles átmeneti változásokat hozhat létre a mért adatokban. Ezek az éles átmenetek által okozott szakadásokat a 12.1. ábra ábra mutatja be.

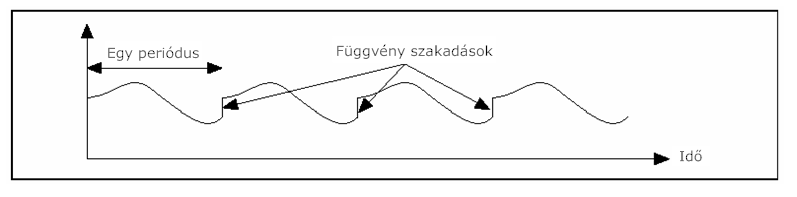
12.1. ábra - Mintavételi periódusból alkotott periodikus hullámforma

A (12.1. ábra) ábrán látható szakadások (folytonossági hiány) a spektrális információk szóródását eredményezik. A spektrális szóródás egy diszkrét idő spektrumot hoz létre, ami az eredeti folytonos idő spektrum „elkenődött” változataként jelenik meg.

12.1.1. Egész számú periódus mintavétele

A spektrális szóródás csak akkor jön létre, ha az adathalmaz (rekord) nem egész számú periódust tartalmaz. A 12.2. ábra ábra egy egész periódusból álló szinusz hullám mintát és Fourier transzformáltját mutatja.

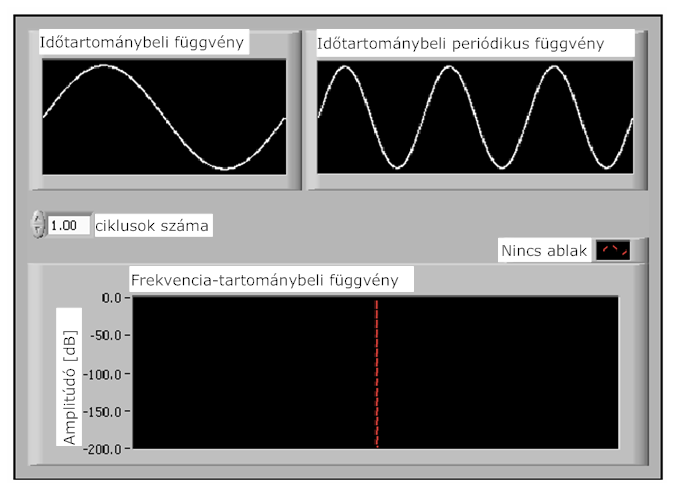
12.2. ábra - Szinusz hullám és Fourier transzformáltja

A 12.2. ábra ábra 1. diagramja a minta időtartománybeli hullámalakját mutatja. A 2. diagramon az 1. diagram szinusz hullámjának periodikusan ismétlődő időfüggvénye látható. A 2. diagramban a hullám periodikusan ismétlődik, ezáltal teljesíti a Fourier transzformáció periodicitásra vonatkozó feltételét. A 3. diagram a jel frekvencia-tartománybeli ábrázolása látható.

Mivel a 2. diagramban a jel periodikus és nincs benne szakadás, a spektruma a 3. diagramban egyetlen vonalként jelenik meg, ami a szinusz hullám frekvenciáját mutatja. A 2. diagram hullámalakjában nincs szakadás, mivel az adatok egész számú periódusból származtak, - esetünkben egyből.

Kizárólag az alábbi eljárások biztosítják, hogy mindig egész számú periódusokat nyerjünk:

A mintavételezésnek szinkronban kell lenni a mért jellel. Így szándékosan egész számú periódus kapható.

A tranziens jelek mérésénél a rögzítés idejének teljesen illeszkedni kell a jelhez.

12.1.2. Nem egész számú periódus mintavételezése

Általában a mérni kívánt ismeretlen jel időben állandó jel. Egy időben állandó jel létezik a mintavétel előtt, alatt és után is. Ebben az esetben nem lehet biztosítani, hogy mintavételezéskor egész számú periódust kapjunk. Ha a minta nem egész számú periódust tartalmaz, spektrum szóródás jön létre, mivel a jel nem egészszámú periódusának frekvencia komponense nem egyezik meg pontosan a spektrum egyetlen frekvenciájával sem. A spektrum szóródás eltorzítja a mérést oly módon, mintha egy adott frekvenciakomponens energiája szétterjedne a szomszédos frekvencia vonalakon vagy sávokon, ami egy “szétkenődött” spektrumot eredményez. Simító ablakok használatával minimalizálni lehet a nem egész számú perióduson végrehajtott FFT miatt kialakuló hatásokat.

A jel periodicitására vonatkozó feltétel miatt mesterséges szakadások jelennek meg az egymást követő periódusok között, amikor a mintavétel nem egész számú periódusból történik. Ezek a szakadások nagyon magas frekvenciájú komponensekként jelennek meg a jel spektrumában. Ezek olyan frekvenciák, amelyeket az eredeti jel nem tartalmaz. A szakadások frekvenciája sokkal nagyobb lehet, mint a Nyquist frekvencia, ezért látszólagos frekvenciaként valahol 0 és f_s/2 között jelenik meg. E miatt lép fel a spektrum szóródás. A DFT-vel vagy FFT-vel kapott spektrum ezért „elkenődött” lesz, nem az eredeti jel valódi spektruma.

A 12.3. ábra ábrán egy szinusz hullám, melynek nem egész számú periódusából történt a mintavétel, valamint a szinusz hullám Fourier transzformáltja látható.

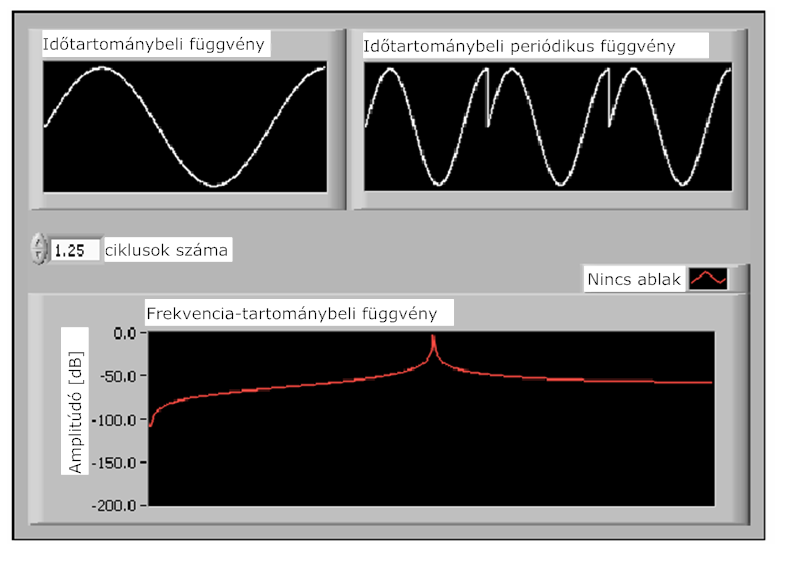
12.3. ábra - Spektrális ábra, amikor a mintavétel nem egész számú periódusból történt

A (12.3. ábra) ábrán az 1. diagram a szinusz hullám 1,25 periódusát tartalmazza. A 2. diagramban a jel periodikusan ismétlődik, a Fourier transzformáció periodicitási feltétele miatt. A 3. diagram mutatja a jel spektrális ábráját. Az energia szétterjed vagy ”szétkenődik” egy széles frekvencia tartományban. Az energia „kiszivárog” az egyetlen frekvencia komponensből és szétterül a többi frekvencián és ezáltal spektrum szóródást okoz.

A spektrum szóródás azért jött létre, mert a bemenő jel rögzítési időtartama véges. A spektrum szóródás legyőzéséhez végtelen mérési időtartamot kellene vennünk –∞-től +∞-ig. Végtelen jelsorozattal az FFT egyetlen vonalat eredményezne, a megfelelő frekvencián. Azonban a gyakorlatban végtelen idejű mérés nem valósítható meg. A véges jelsorozat korlátainak legyőzésére ablakozást használunk a spektrum szóródás csökkentésére.

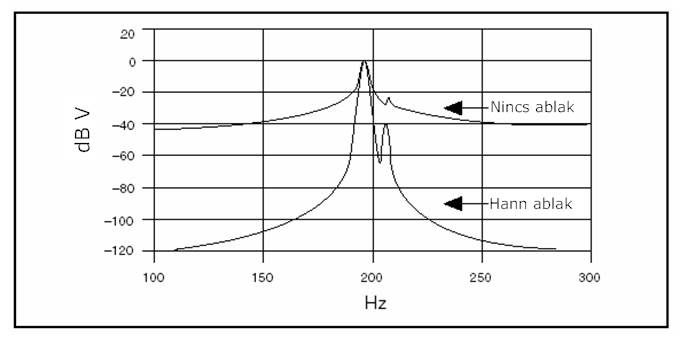
Ezen kívül a spektrum szóródás amplitúdó pontossági hibát is okozva elfedheti a szomszédos frekvencia csúcsokat. A (12.4. ábra) ábrán a spektrum két közeli frekvencia komponense látható simító ablak használata nélkül és Hanning ablak alkalmazásával.

12.4. ábra - A spektrum szóródás elfedi a közeli frekvencia komponenseket

A (12.4. ábra) ábrán a második csúcs sokkal jobban kiemelkedik az ablakozott jelnél, mint amikor nem használunk simító ablakot.

12.2. Ablakozott jelek

A mintavételezett jel spektrális karakterisztikájának javítására általában simító ablakot használunk. Amikor Fourier vagy spektrális analízist hajtunk végre véges hosszúságú (időtartománybeli) adatokon, simító ablakok használatával minimalizálni lehet a csonka hullámforma szakadásait, és ezáltal csökkenteni lehet a spektrum szóródást.

A spektrum szóródás mértéke a szakadás amplitúdójától függ. Ha a szakadás nagyobb lesz, a spektrum szóródás nő, és fordítva. A simító ablak csökkenti a szakadás amplitúdóját minden periódus határán és úgy viselkedik, mint egy előre meghatározott alul-áteresztő szűrő.

Egy jel ablakozásának művelete a véges hosszúságú jelsorozat megszorzását jelenti egy véges hosszúságú simító ablakkal, melynek amplitúdója egyenletesen és fokozatosan nullához tart a széleknél. A simító ablak hossza vagy időintervalluma a minták számával van megadva. Az időtartománybeli szorzás egyenértékű frekvencia tartománybeli konvolúcióval . Emiatt az ablakozott jel spektruma az eredeti jel és a simító ablak spektrumának konvoluciójából adódik. Az ablakozás megváltoztatja a jel alakját az időtartományban, valamint hatással van a spektrumra, amit látunk.

A 12.5. ábra ábra az jel eredeti és egy simítóablak spektrumának konvolúcióját mutatja.

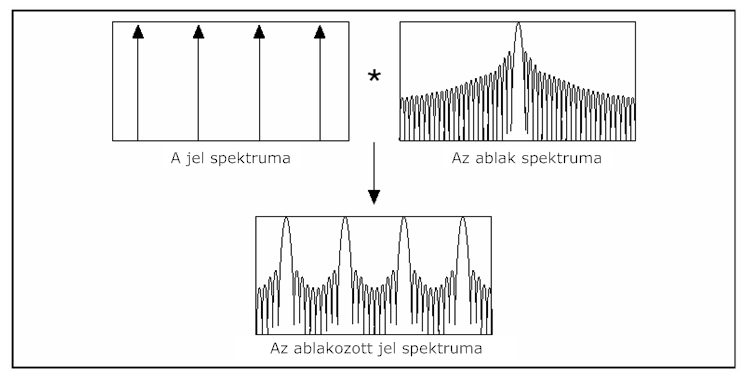
12.5. ábra - Az ablakozott spektrum frekvencia karakterisztikája

Az ablakozás-hatás akkor is fellép, ha nem alkalmazunk simító ablakot. Egy bemenő jel véges jelsorozatának mérése a jel egy állandó ablakkal való megszorzását jelenti az időtartományban. Az állandó ablak alakja négyszögletes és a magassága állandó. A bemenő jel állandó ablakkal való megszorzása az időtartományban megfelel a jel és az állandó ablak spektrumának konvolúciójával a frekvencia tartományban, amelynek sinc függvény karakterisztikája van.

A 12.6. ábra ábra egy Hanning ablak alkalmazásának hatását mutatja egy időfüggvényen

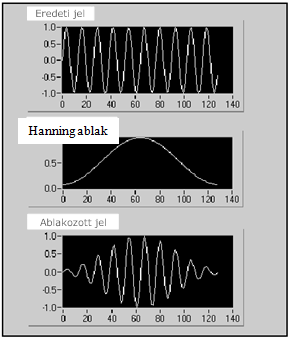
12.6. ábra - Hanning-ablakkal ablakozott jel

A (12.6. ábra) ábrán az ablakozott jel időfüggvénye fokozatosan nullára csökken a végein, mivel a Hanning-ablak minimalizálja a szakadásokat a hullámforma átmeneti végeinél. Simítóablak alkalmazása időtartománybeli adatoknál a frekvenciatartományba való transzformálás előtt minimalizálja a spektrum szóródást.

A 12.7. ábra ábra az alábbi simítóablakok hatásait mutatja:

Ablak nélkül (négyszög ablak)
Hanning ablakkal
„Flat top” ablakkal (Lásd később a 12.3.8. szakasz fejezetben)

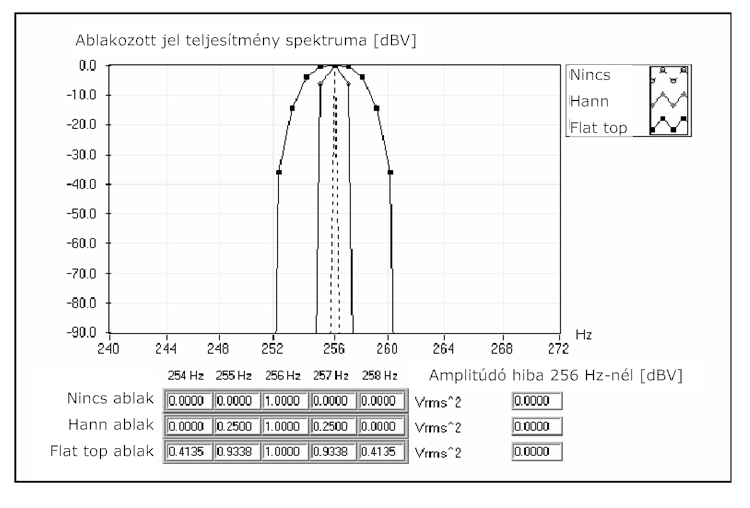
12.7. ábra - Egy 1 V_rms-os 256 Hz-es jel teljesítmény-spektrumaállandó, Hanning és ”Flat top” ablakokkal

A (12.7. ábra) ábrán látható jel adathalmaza egészszámú (256) periódust tartalmaz egy 1024 pontból álló jelsorozatban. Ha az eredeti jel frekvencia összetevő pontosan illenek egy frekvenciavonalra, - ez az az eset, mikor az adathalmaz egészszámú periódust tartalmaz - akkor csak a spektrum fő-szárnya látható.

A simító ablaknak van egy fő-szárnya a vizsgált frekvencia körül. A fő-szárny az ablakok egy frekvenciatartománybeli karakterisztikája. Az állandó ablaknak van a legkeskenyebb fő-szárnya. A Hanning és a „flat top” ablakok némileg szélesebbek. A „flat top” ablaknak van a legszélesebb fő-szárnya az állandó és a Hanning ablakhoz képest. Egészszámú periódus esetén az összes simító ablak ugyanazt a csúcs amplitúdó értéket adja és kitűnő amplitúdó pontosságot biztosít. Az oldal-szárnyak nem jelennek meg, mivel a simítóablak spektruma eléri a nullát Δf intervallumokban a fő-szárny mindkét oldalán.

A 12.7. ábra ábra a 254 Hz és 258 Hz közötti értékeket is mutatja mindegyik simítóablaknál. Az amplitúdó hiba 254 Hz-en mindhárom simítóablak esetén 0 dB. A diagram a spektrum értékeket mutatja 240 és 272 Hz között. Az aktuális értékek mindhárom simító ablakra nézve 254-258 Hz között a diagram alatt láthatók. Δf egyenlő 1Hz.

Ha a jelsorozat nem egész számú periódust tartalmaz , a simítóablak folyamatos spektruma eltolódik a fő-szárny közepétől Δf frekvencia osztással, ami megegyezik frekvencia összetevő és az FFT frekvencia vonal közötti különbséggel. Ez az eltolódás eredményezi az oldal-szárnyakat, amelyek megjelennek a spektrumban. Továbbá amplitúdó hiba lép fel a frekvencia csúcsnál, mivel a fő-szárnya mintavétele kívül esik a középponttól és „elkenődik” a spektrumban. A 12.8. ábra ábra a spektrális szóródás hatását mutatja meg egy olyan jelnél, mely jelsorozata 256,5 periódust tartalmaz.

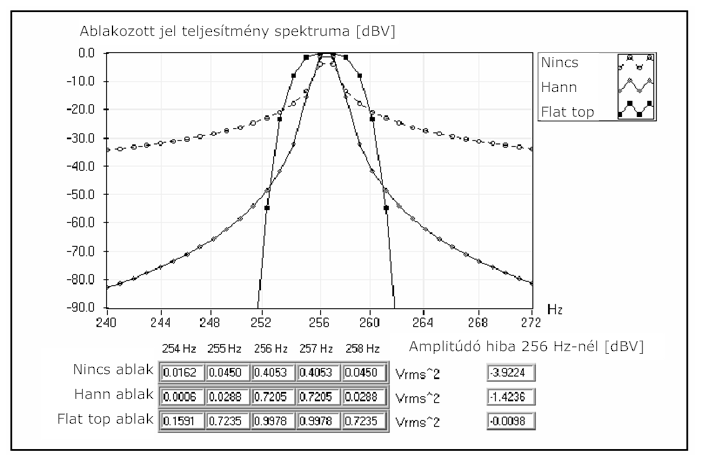
12.8. ábra - Egy 1 V_rms-os 256.5 Hz-es jel teljesítmény-spektruma állandó, Hanning és ”Flat top” ablakokkal

A (12.8. ábra) ábrán nem egész számú periódusoknál a Hanning és a „flat top” ablak sokkal kisebb spektrumszivárgást mutat, mint az állandó ablak. Ezen kívül az amplitúdó hiba is kisebb a Hanning és a „flat top” ablakok esetén. A „flat top” ablak nagyon jó amplitúdó pontosságot mutat, de szélesebb és magasabb oldal lebenyei vannak, mint a Hanning ablaknak.

A (12.9. ábra) ábra egy VI blokkdiagramját mutatja, ami két szinusz jel összegeként kapott jel ablakozott és ablakozás nélküli spektrumát méri.

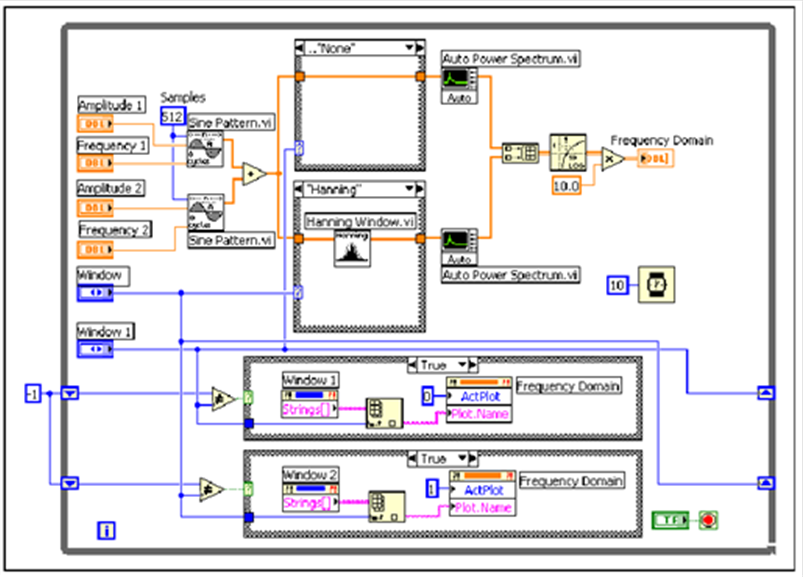
12.9. ábra - Két szinusz jel összegeként kapott jel spektrumának mérése

A 12.10. ábra ábra a két szinusz jel amplitúdóját és frekvenciáját valamint a mérések eredményeit mutatja. A frekvenciák kijelzése a periódusok dimenzióval történik.

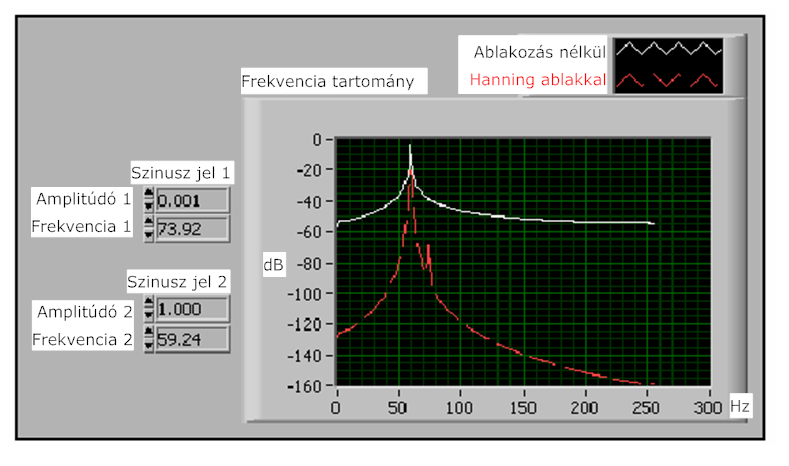
12.10. ábra - Két szinusz jel összegének ablakozott és ablakozás nélküli spektruma

A (12.10. ábra) ábrán az ablakozás nélküli spektrum 20 dB-nél nagyobb spektrális szóródást mutat a kisebb szinusz jel frekvenciájánál. Lehet ennél kifinomultabb technikát is alkalmazni az eredeti időfüggvény frekvencia tartománybeli leírásához. Azonban a legtöbb esetben elegendő simító ablak alkalmazása a frekvenciafüggvény jobb ábrázolásához.

12.3. A különböző simító ablakok tulajdonságai

A simító ablak kiválasztásának egyszerűsítése érdekében szükség van a különböző frekvencia karakterisztikák definiálására, hogy a simító ablakokat egymással össze lehessen hasonlítani. Egy simító ablak aktuális ábrája azt mutatja, hogy a simítóablak frekvencia karakterisztikája egy folyamatos spektrum egy fő és számos oldal szárnnyal. A 12.11. ábra ábra egy tipikus simító ablak spektrumot mutat.

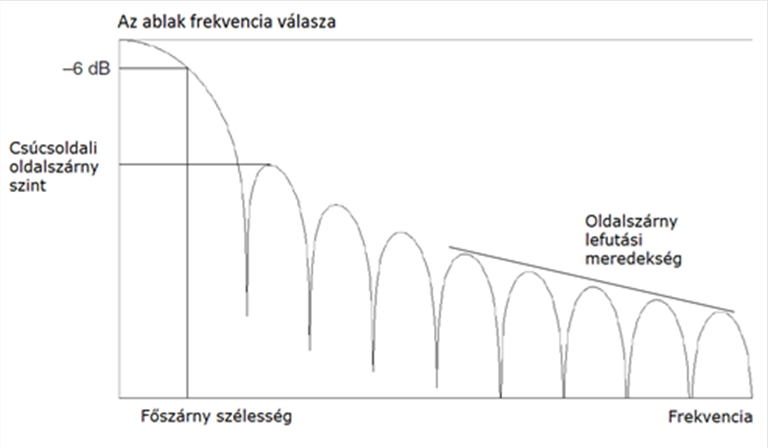
12.11. ábra - Simító ablak frekvencia válasza

12.3.1. Fő szárny

A simító ablak fő szárnyának közepe az időtartománybeli jel minden egyes frekvencia komponensénél megjelenik. Megegyezés szerint, a fő szárny alakjának jellemzése a szélességével történik, ami alatt a csúcshoz képest -3 dB és -6 dB értékekhez tartozó frekvenciák által meghatározott szélességet értjük. A fő szárny szélességének megadása FFT tartományokban vagy frekvencia vonalakban történik.

A simító ablak spektrum fő szárnyának szélessége meghatározza az ablakozott jel frekvencia felbontását. Emiatt, két közeli frekvencia komponens megkülönböztetésének képessége növekszik a fő szárny szélességének csökkentésével. Ahogy a fő szárny keskenyebbé válik és a spektrális felbontóképesség javul, az ablak teljesítménye szétterül az oldal szárnyakba, megnövelve ezáltal a spektrum szóródást és csökkentve az amplitúdó pontosságot. Az amplitúdó pontosság és a spektrális felbontóképesség között kompromisszumot kell találni.

12.3.2. Oldalszárnyak

Oldal szárnyak a fő szárny mindkét oldalán megjelennek és a fő szárnytól f_s/N többszöröseinél elérik a nulla értéket. A simító ablakok oldal szárnyainak karakterisztikái közvetlenül befolyásolják annak a mértékét, hogy a melyik szomszédos frekvenciakomponensek szóródnak a szomszédos frekvencia sávokon. Egy erős szinusz jel oldal szárny frekvenciaválasza elnyomhatja egy szomszédos gyengébb szinusz jel fő szárnyának frekvenciaválaszát!

A maximális oldal szárny szint és az oldal szárnyak csökkenésének mértéke jellemzi a simítóablak oldal szárnyát.

A maximális oldal szárny szint a legnagyobb oldal szárny szintje decibelben a főszárny csúcsához viszonyítva.

Az oldal szárny csökkenésének mértéke az oldal szárny csúcsaira fektetett egyenes meredeksége dB/dekádban megadva.

A Táblázat 12.1 táblázat megadja az egyes simító ablakok jellemzőit

12.1. táblázat - A simító ablakok jellemzői

Simító ablak	-3 dB Főszárny szélesség (sávok)	-6 dB Főszárny szélesség (sávok)	Maximális Oldalszárny szint [dB]	Oldalszárny lefutási meredekség [dB/dekád]
Négyszögletes (ablakozás nélküli)	0.88	1.21	-13	20
Hanning	1.33	2.00	-32	60
Hamming	1.3	1.81	-43	20
Backman-Harris	1.62	2.27	-71	20
Exact Blackman	1.81	2.25	-57	20
Blackman	1.64	2.3	-58	60
Flat Top	2.94	3.56	-44	20

12.3.3. Négyszögletes ablak (ablakozás nélküli állapot)

A négyszögletes ablak értéke 1 az egész hossza mentén. Az alábbi egyenlet írja le a négyszögletes ablakot:

w(n)= 1

(12.1)

ahol

n= 0, 1, 2, .... N-1

Ahol N az ablak hossza és w az ablak értéke

Négyszögletes ablak alkalmazása olyan, mintha nem használnánk egyáltalán ablakot, mivel a négyszög függvény csak véges hosszúságúvá vágja a jelet.

A négyszögletes ablak alkalmazásánál a legnagyobb mértékű a spektrális szóródás.

A 12.12. ábra ábra egy négyszögletes ablakot mutat N=32 értékkel.

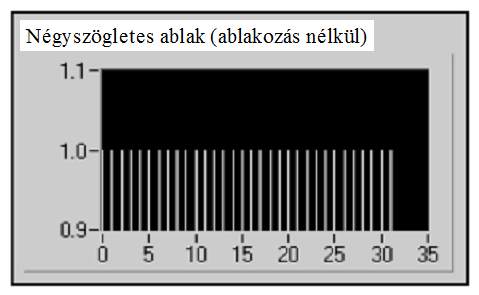
12.12. ábra - Négyszögletes ablak

A négyszögletes ablak olyan tranziens jelek vizsgálatánál hasznos, melyek rövidebb ideig tartanak, mint az ablak. A tranziensek olyan jelek, amelyek rövid ideig állnak fenn. A négyszögletes ablak használatos még sorrendkövetésre, ahol az effektív mintavételi sebesség arányos a forgó gépek tengelyének fordulatszámával. A sorrendkövetésnél a négyszögletes ablak érzékeli a gép rezgésének saját frekvenciáját és a felharmonikusait.

12.3.4. Hanning ablak

A Hanning ablak alakja egy fél koszinusz függvényre hasonlít. Az alábbi egyenlet írja le a Hanning-ablakot:

$w (n) = 0.5 - 0.5 \cdot \cos (\frac{2 \cdot Π \cdot n}{N})$

(12.2)

ahol

n= 0, 1, 2, .... N-1

Ahol N az ablak hossza és w az ablak értéke

A 12.13. ábra ábra egy Hanning ablakot mutat N=32 értékkel.

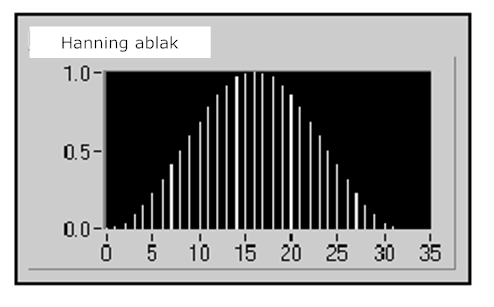
12.13. ábra - Hanning ablak

A Hanning ablak alkalmazása olyan tranziens jelek vizsgálatánál hasznos, melyek az ablak időtartamánál hosszabb ideig fennállnak, valamint általános célú alkalmazásoknál.

12.3.5. Hamming ablak

A Hamming ablak a Hanning ablak egy módosított változata. A Hamming ablak alakja hasonlít egy fél koszinusz hullámra.

Az alábbi egyenlet írja le a Hamming-ablakot:

$w (n) = 0.54 - 0.46 \cdot \cos (\frac{2 \cdot Π \cdot n}{N})$

(12.3)

ahol

n= 0, 1, 2, .... N-1

Ahol N az ablak hossza és w az ablak értéke

A 12.14. ábra ábra egy Hamming ablakot mutat N=32 értékkel.

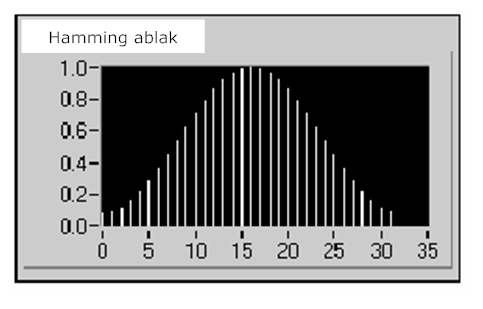
12.14. ábra - Hamming ablak

Amint az a 12.13. ábra és 12.14. ábra ábrán látható, a Hanning és a Hamming ablak hasonlít egymásra. Azonban az időtartományban a Hamming ablak nem közelít annyira nullához a széleknél, mint a Hanning ablak.

12.3.6. Kaiser-Bessel ablak

A Kaiser-Bessel ablak egy rugalmas simító ablak, melynek alakja változtatható a béta tényező értékének változtatásával. Ezért, a feladattól függően az ablak alakja megváltoztatható és így a spektrális szóródás mértéke szabályozható. Az alábbi egyenlet írja le a Kaiser-Bessel ablakot:

Kaiser függvény:

$w [n] = {\begin{matrix} \begin{array}{l} \frac{I_{0} (2 β \sqrt{\frac{n}{L - 1} - {(\frac{n}{L - 1})}^{2}})}{I_{0} (β)} \end{array} & \begin{array}{l} 0 \leq n \leq L - 1 \end{array} \\ 0 & e g y é b k é n t \end{matrix}}$

(12.4)

a képletben I₀(x) Bessel függvény:

$I_{0} (x) = 1 + {\sum_{k = 1}^{\infty} [\frac{{(\frac{x}{2})}^{k}}{k!}]}^{2}$

(12.5)

ahol

n= 0, 1, 2, .... N-1

Ahol N az ablak hossza és w az ablak értéke

A 12.15. ábra ábra a Kaiser-Bessel ablakot mutatja különböző béta értékeknél

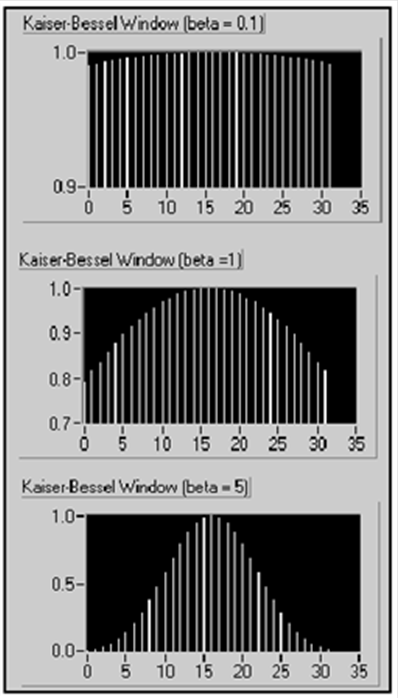
12.15. ábra - Kaiser-Bessel ablak

Kis béta értékeknél a négyszögletes ablakhoz hasonlít. Valójában béta=0-nál négyszögletes ablakot kapunk. Ahogy növeljük béta értékét, az ablak alakja egyre jobban elkeskenyedik mindkét oldalon. A Kaiser-Bessel ablak használható két, közel azonos frekvenciájú, de jelentősen különböző amplitúdójú jel érzékelésére.

12.3.7. Háromszög ablak

Ez az ablak a háromszög alakú. Az alábbi egyenlet írja le a háromszög ablakot:

$w (n) = 1 - | \frac{2 \cdot n - N}{N} |$

(12.6)

ahol

n= 0, 1, 2, .... N-1

Ahol N az ablak hossza, w az ablakfüggvény értéke.

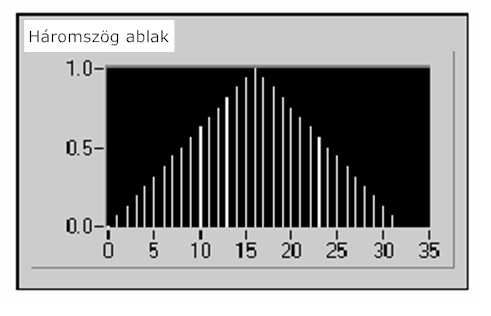
A 12.16. ábra ábra egy háromszög ablakot mutat N=32 értékkel.

12.16. ábra - Háromszög ablak

12.3.8. “Flat Top” ablak

A „flat top” ablaknak van a legnagyobb amplitúdó pontossága a simító ablakok között (±0,02 dB) az olyan jelekre, amelyek tipikusan nem egész periódusokból állnak. Mivel a „flat top” ablaknak széles fő szárnya van, ezért a frekvencia felbontóképessége gyenge. Az alábbi egyenlet írja le a „flat top” ablakot:

$w (n) = \sum_{k = 0}^{4} {(- 1)}^{k} \cdot a_{k} \cdot \cos (k \cdot ω)$

(12.7)

ahol

	$ω = \frac{2 \cdot Π \cdot n}{N}$
és
	a₀= 0.215578948
	a₁= 0.416631580
	a₂= 0.277263158
	a₃= 0.083578947
	a₄= 0.006947368

A 12.17. ábra ábra egy „flat top” ablakot mutat

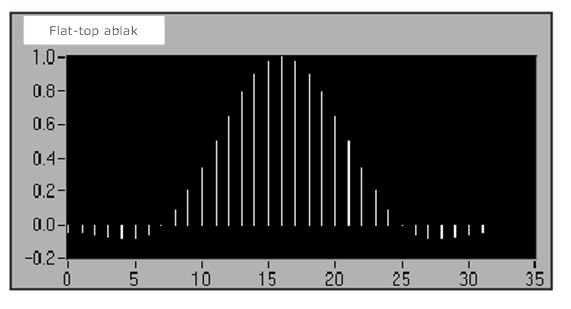
12.17. ábra - Flat Top ablak

A „flat top” ablak a legalkalmasabb egy frekvencia komponens amplitúdójának pontos megmérésére, olyan jeleknél ahol alacsony szomszédos spektrális energia van a jelben.

12.3.9. Exponenciális ablak

Az ablak alakja csökkenő exponenciális függvény szerint változik. Az alábbi egyenlet írja le az exponenciális ablakot:

$w (n) = e^{(\frac{n \cdot \ln (f)}{N - 1})} = f^{(\frac{n}{N - 1})}$

(12.8)

ahol

n = 0, 1, 2, .... N-1

Ahol N az ablak hossza, w az ablak függvény értéke és fa végső érték.

Az ablakfüggvény kezdő értéke 1 és fokozatosan 0-ra csökken. Az exponenciális ablak végső értéke 0 és 1 között beállítható.

A 12.18. ábra ábra az exponenciális ablakot mutatja N=32 értékkel, amikor a végső érték f=0,1.

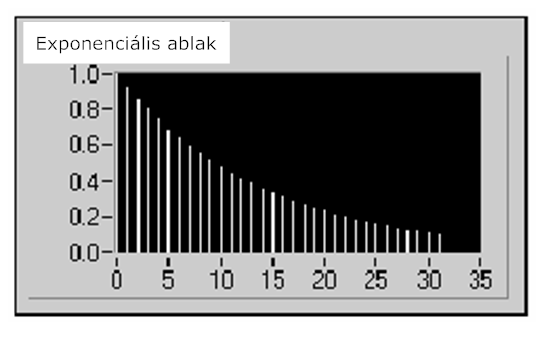
12.18. ábra - Exponenciális ablak

Az exponenciális ablak tranziens válaszfüggvények elemzéséhez használhatók, melyek hossza nem nagyobb, mint az ablak hossza. Az exponenciális ablak csillapítja a jel végét, ezáltal biztosítva, hogy a jel teljesen lecsengjen a minta-blokk végére. Az exponenciális ablak olyan jeleknél is használható, melyek exponenciálisan csökkennek, mint például az alak válasz enyhe csillapítással, amit egy külső hatás, mint például egy kalapácsütés gerjeszt.

12.4. Spektrális elemzéshez használt ablakok összehasonlítása az együttható tervezéshez használt ablakokkal

A spektrális analízis és a szűrők együttható tervezése különböző követelményeket támaszt az ablakokkal szemben. A spektrális analízis DFT-szerű ablakot igényel, míg a szűrő együttható tervezésnél a középpontjára szimmetrikus ablakra van szükség.

12.4.1. Spektrális analízis

A spektrális analízishez tervezett simítóablaknak DFT-szerűnek kell lenni. Egy simító ablak DFT-szerű, ha a skaláris (belső) szorzat a szinuszos jelek egész számú periódusaira azonosan egyenlő nullával. Más szavakkal, egy DFT-szerű szekvencia DFT-jének nincs képzetes összetevője.

A 12.19. ábra és a 12.20. ábra ábra egy Hanning ablakot és egy szinusz hullám periódust mutat 8 mintavételi ponttal.

12.19. ábra - Hanning ablak 8 mintavételi ponttal

12.20. ábra - Szinusz hullám 8 mintavételi ponttal

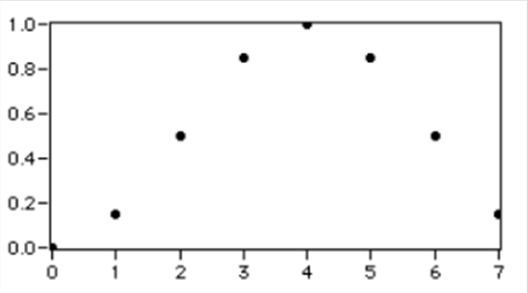
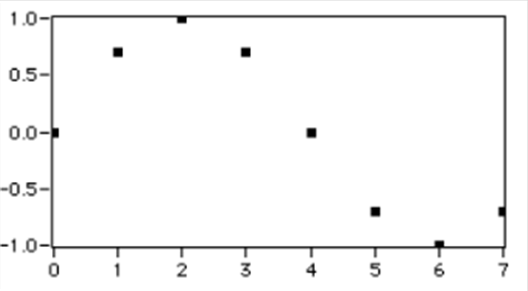
A (12.19. ábra) ábrán látható DFT-szerű Hanning ablak nem szimmetrikus a középpontjára. A ablak függvény utolsó pontja nem egyenlő az első pontjával, hasonlóan a (12.20. ábra) ábrán látható teljes periódusnyi szinusz hullámmal.

A spektrális analízishez használt simító ablakok spektrális ablakok és a következő ablak típusokat foglalja magába:

Skálázott időtartománybeli ablak
Hanning ablak
Hamming ablak
Háromszög ablak
Blackman ablak
Egzakt Blackman ablak
Blackman-Harris ablak
Flat top ablak
Kaiser-Bessel ablak
Általános koszinusz ablak
Elkeskenyedő koszinusz ablak

12.4.2. Ablakok FIR szűrőegyütthatók tervezéshez

FIR szűrőegyütthatók tervezése olyan ablakot igényel, amely szimmetrikus a középpontjára.

A 12.9. és 12.10. egyenletek szemléltetik a különbséget a spektrális ablak és a szűrő együtthatók tervezéshez használt szimmetrikus ablak között.

A 12.9. egyenlet leírja a spektrális analízishez használt Hanning ablakot

$w (i) = 0.5 - 0.5 \cdot \cos (\frac{2 \cdot Π \cdot i}{N})$

(12.9)

Ahol N az ablak hossza, w az ablak függvény értéke és i=0..N-1.

A 12.10. egyenlet leírja a szűrőegyüttható tervezéshez használt szimmetrikus Hanning ablakot

$w (i) = 0.5 - 0.5 \cdot \cos (\frac{2 \cdot Π \cdot i}{N - 1})$

(12.10)

ahol N az ablak hossza, w az ablak függvény értéke és i=0..N-1.

Egy spektrális ablak módosításával, amint azt a 12.10. egyenlet mutatja, meghatározható egy szimmetrikus ablak szűrőegyüttható tervezéséhez. A digitális szűrők tervezésével kapcsolatban további információk a Digitális szűrés című (10. fejezet) fejezetben találhatók.

12.5. A megfelelő simító ablak kiválasztása

Egy simító ablak kiválasztása nem egyszerű feladat. Mindegyik simító ablaknak megvan a saját tulajdonsága, és különböző alkalmazásokhoz való alkalmassága. A simító ablak kiválasztásához meg kell becsülni a jel frekvencia tartalmát. Ha a jel erős egymásra hatással bíró frekvencia komponenseket tartalmaz távol a vizsgált frekvenciától, olyan simító ablakot kell kiválasztani, amelynél nagy az oldal szárnyak csökkenésének mértéke. Ha a jel erős egymásra hatással bíró frekvencia komponenseket tartalmaz a vizsgált frekvenciához közel, olyan simító ablakot kell választani, amelynél az oldal szárny maximális értéke kicsi. Lásd az Táblázat 12.1 táblázatot az oldal szárny csökkenés mértéke és a maximális oldal szárny szint értelmezéséhez a különböző simító ablakok esetén.

Ha a vizsgált frekvencia két vagy több egymáshoz nagyon közeli jelet tartalmaz, a spektrális felbontóképesség a fontos. Ebben az esetben olyan simító ablakot kell választani, amely fő szárnya nagyon keskeny.

Ha egyetlen frekvencia komponens amplitúdó pontossága fontosabb, mint a helyének pontos meghatározása egy adott frekvenciasávban, széles fő szárnyú ablakot kell választani.

Ha a jel spektruma inkább egyenletes vagy szélessávú a frekvencia tartalom tekintetében, négyszögletes ablakot kell választani, vagy nem kell ablakozni a jelet.

Általában a Hanning ablak az esetek 95%-ban megfelelő. Jó a frekvencia felbontóképessége és alacsony a spektrális szóródása. Ha nem ismerjük a jel természetét, de simító ablakot akarunk alkalmazni, Hanning ablakkal kell kezdeni!

A Táblázat 12.2 táblázat felsorolja a különböző típusú jeleket és a hozzájuk használható ablakokat.

12.2. táblázat - Jelek és javasolt ablakok

A jel típusa	Javasolt ablak függvény
Olyan tranziensek, melyek időtartama rövidebb, mint az ablak hossza	Négyszögletes
Olyan tranziensek, melyek időtartama hosszabb, mint az ablak hossza	Exponenciális, Hanning
Általános célú alkalmazások	Hanning
Spektrális analízis (frekvenciaválasz mérések)	Hanning (véletlenszerű gerjesztésre), Négyszögletes (pszeudorandom gerjesztésre)
Két nagyon közeli frekvenciájú, de nagyon különböző amplitúdójú jel szétválasztása	Kaiser-Bessel
Két nagyon közeli frekvenciájú, de majdnem azonos amplitúdójú jel szétválasztása	Négyszögletes
Pontos egy frekvenciájú amplitúdó mérés	Flat top
Szinusz hullám vagy szinusz hullámok kombinációja	Hanning
Szinusz hullám, az amplitúdó pontosság fontos	Flat top
Keskenysávú zavarjel (rezgés adatok)	Hanning
Szélessávú zavarjel (fehérzaj)	Uniform
Közeli térközű szinusz hullámok	Uniform, Hamming
Gerjesztő jelek (kalapács ütés)	Exponenciális
Válasz jelek	Exponenciális
Ismeretlen tartalom	Hanning

Kezdetben lehet, hogy nincs elegendő információ a jelről ahhoz, hogy a legjobb ablakot kiválasszuk. Lehet, hogy különböző simító ablakokkal kell próbálkozni ahhoz, hogy a legjobbat megtaláljuk. Mindig hasonlítsuk össze a különböző ablakok eredményét, hogy megtaláljuk az adott alkalmazáshoz a legmegfelelőbbet.

12.6. A simító ablakok paraméterezése

Amikor simító ablakot alkalmazunk egy időtartománybeli jelhez, az azt jelenti, hogy a jel hossza megtöbbszöröződik a simító ablak hosszára és eltorzul a simító ablak miatt. A simító ablak mindenütt megváltoztatja a jel amplitúdóját. Ha több simító ablakot alkalmazunk ugyanarra a jelre, mindegyik ablak paraméterezése úgy történik, hogy mindegyik csillapító ablakot osztjuk az ablakozott mátrixszal, amelyik az ablak eredmények egy összetartozó erősítése, minden ablakban csökkentve ugyanazt a spektrum amplitúdó eredményt az ablakok korlátozó pontossági feltételeivel. A 12.17. ábra és 12.18. ábra ábrán látható rajzok méretezett simító ablakok alkalmazásának eredményei azonos időtartománybeli jelnél.

Egy FFT egyenértékű egy sorozat párhuzamos szűrő alkalmazásával, ahol mindegyik szűrő sávszélessége egyenlő Δɸ- el. A simító ablak „szétkenő” hatása miatt a simító ablak megnöveli az FFT sáv effektív sávszélességét egy ENBW-nek (equivalent noise-power bandwidth= egyenértékű zaj-energia sávszélesség) nevezett értékkel. Az adott frekvencia csúcsenergiája egyenlő a csúccsal szomszédos frekvencia sávok összegével, megnövelve egy arányossági tényezővel, ami a simítóablak ENBW-jével egyenlő. Az arányossági tényezőt figyelembe kell venni, amikor a teljesítmény spektrumon alapuló számítást hajtunk végre. Lásd a Diszkrét frekvencia analízis című (11. fejezet) fejezetet az energia spektrumon végrehajtott számításokkal kapcsolatban.

A Táblázat 12.3 táblázat felsorolja az arányossági tényezőket, amelyet összetartozó erősítésnek is neveznek, az ENBW-t és a legrosszabb esetben fellépő amplitúdó pontosságot, melyet a középponton kívüli komponenseik okoznak számos simító ablaknál.

12.3. táblázat - Simító ablakok korrekciós tényezői és a legrosszabb esetben fellépő amplitúdó hibák

Ablak	Paraméter (összetartozó erősítés)	ENBW	Legrosszabb esetben fellépő amplitúdó hiba [dB]
Négyszögletes (ablakozás nélküli)	1.00	1.00	3.92
Hanning	0.50	1.50	1.42
Hamming	0.54	1.36	1.75
Blackman-Harris	0.42	1.71	1.13
Pontos Blackman	0.43	1.69	1.15
Blackman	0.42	1.73	1.10
Flat Top	0.22	3.77	<0.01

Irodalom

[12.1.] LabVIEW Control Design User Manual. 2009.

Vissza		Előre
11. fejezet - Diszkrét frekvencia analízis	Főoldal	13. fejezet - Számítógépes mérésadatgyűjtés és beavatkozás