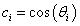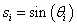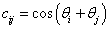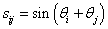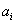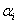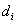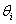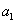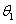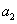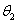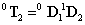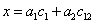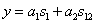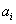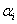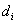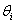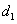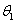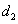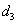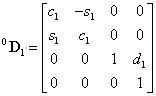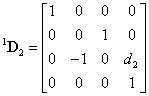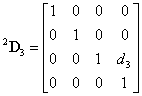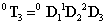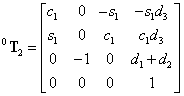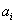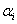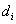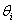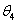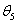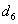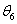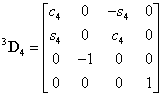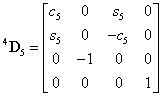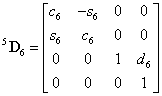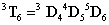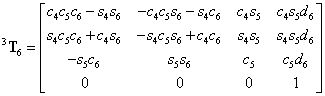4. fejezet - Példák – Tipikus nyíltláncú robotkarok

4. fejezet - Példák – Tipikus nyíltláncú robotkarok
Vissza	3. rész - Melléklet	Előre

Tartalom

4.1. Síkbeli könyök manipulátor
4.2. Hengeres robot
4.3. Gömbi csukló

A Denavit‑Hartenberg konvenció értelmében az egyetlen változó a 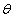szög, a további paraméterek állandók. Továbbá a melléklet folyamán a következő egyszerűsített jelölést alkalmazzuk, amely a robotikai szakkönyvekben általános alkalmazott rövidítés, azaz

, , , és .

4.1. Síkbeli könyök manipulátor

Ahogy az ábrán is látható, a síkbeli könyök manipulátor (angolul: planar elbow manipulator) két kartagból áll.

4.1. ábra - Síkbeli könyök manipulátor [1.]

A csuklók 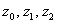tengelyei merőleges a lap síkjára, és kifelé mutatnak belőle. A manipulátor bázisát az 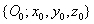koordináta rendszer jelzi. Fontos megjegyeznünk, hogy a koordináta rendszer felvétele során, a Denavit‑Hartenberg konvenciók értelmében a koordináta rendszer origóját, valamint a 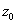tengely irányát tudjuk megválasztani, az 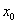tengely iránya tetszőlegesen megválasztható, ezáltal az 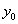tengely iránya kiadódik. 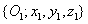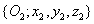A további és koordináta rendszereket a Denavit‑Hartenberg konvenciók értelmében már definiálhatjuk.

A Denavit‑Hartenberg paramétereket az alábbi táblázatba foglaltuk össze

Kar
1	0	0
2	0	0

Az 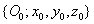koordináta rendszert az 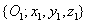koordináta rendszerbe a 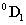transzfomációs mátrixszal vihetjük át, azaz

(4.1)

Az 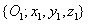koordináta rendszert az 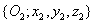koordináta rendszerbe az 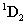transzformációs mátrixszal vihetjük át, azaz

(4.2)

Felhasználva a 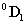és 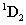transzformációs mátrixokat képezhetjük a 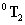transzformációs mátrixot, amely a bázis koordináta rendszert átszámolja a végberendezés koordináta rendszerébe, azaz

(4.3)

kifejtve

(4.4)

Elemezve a 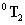transzformációs mátrixot, vegyük észre, hogy a transzformációs mátrix (1,4) illetve a (2,4) eleme reprezentálja az 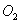origó x és y koordinátáit a bázis koordináta rendszerben leírva, azaz

(4.5)

(4.6)

amelyek továbbá a végberendezés koordinátái a bázis koordináta rendszerben. A 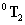transzformációs mátrix forgatási része pedig az 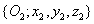koordináta rendszer orientációját mutatja a bázis koordináta rendszerhez képest.

4.2. Hengeres robot

Ahogy az ábrán is látható, a hengeres robot (angolul: cylindrical robot) három kartagból áll.

4.2. ábra - Hengeres robot [1.]

Az 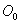origó az 1. csukló, talajhoz rögzített bázis koordinátarendszerének origója. A 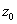tengely az origón fut keresztül és a csuklóból kifelé mutat (ezen tengely körül forog az 1. csukó). Az 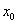tengely irány tetszőlegesen megválasztható, ami választásunk, hogy az 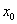tengely merőleges a lap síkjára. Ebben az esetben a 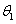paraméter értéke zérus. Ezután az 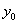tengely iránya már kiadódik.

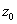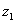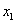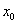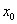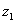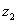A második csukló transzlációt hajt végre. Ez esetben a és tengelyek egymással párhuzamosak és ugyanabba az irányba mutatnak. Ebben az esetben is az tengely iránya tetszőlegesen megválasztható, de célszerű az tengellyel párhuzamosan és az tengellyel azonos irányba felvenni. A Denavit‑Hartenberg konvenciók értelmében és tengelyek merőlegesek egymásra, valamint az 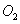origó a tengelyek metszéspontjában helyezkedik el. Az 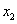tengelyt párhuzamosnak választjuk az 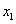tengellyel, tehát ebben az esetben 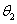paraméter értéke zérus. Végezetül a végberendezéshez rögzített koordináta rendszert alakítjuk ki, amelynek tengelyei párhuzamosak az 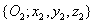koordináta rendszerrel, azonban a koordináta rendszer origója a végberendezés középpontjában található.

A Denavit‑Hartenberg paramétereket az alábbi táblázatba foglaltuk össze

Kar
1	0	0
2	0	-90	0
3	0	0	0

Az 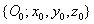koordináta rendszert az 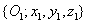koordináta rendszerbe a 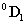transzfomációs mátrixszal vihetjük át, azaz

(4.7)

Az 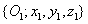koordináta rendszert az 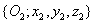koordináta rendszerbe az 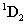transzformációs mátrixszal vihetjük át, azaz

(4.8)

Az 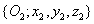koordináta rendszert az 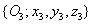koordináta rendszerbe az 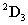transzformációs mátrixszal vihetjük át, azaz

(4.9)

Felhasználva a 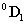, 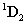és 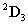transzformációs mátrixokat képezhetjük a 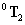transzformációs mátrixot, amely a bázis koordináta rendszert átszámolja a végberendezés koordináta rendszerébe, azaz

(4.10)

kifejtve

(4.11)

4.3. Gömbi csukló

Az alábbi ábrán egy gömbi csukló, vagy Euler csukló látható (angolul: spherical wrist).

4.3. ábra - Euler csukló [1.]

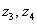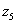A gömbi csukló esetén a és tengelyek egy pontban metszik egymást, a 5. csukló koordinátarendszerének origójában. A Stanford manipulátor egy jó példája az ipari robotoknak, amely gömbi csuklóval rendelkezik. A Stanford manipulátor alapját egy RRP robot, vagy gömbkoordinátás robot képzi.

A Denavit‑Hartenberg paramétereket az alábbi táblázatba foglaltuk össze

Kar
4	0	-90	0
5	0	90	0
6	0	0

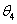
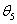
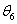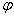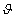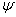A gömbi csukló specialitása, hogy a csuklóváltozók az Euler‑féle szögek, rendre , , és az 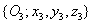koordináta rendszerben kifejezve. A korábbiak értelmében az 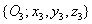koordináta rendszert az 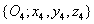koordináta rendszerbe a 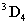transzfomációs mátrixszal vihetjük át, azaz

(4.12)

Az 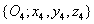koordináta rendszert az 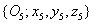koordináta rendszerbe az 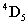transzformációs mátrixszal vihetjük át, azaz

(4.13)

Az 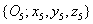koordináta rendszert az 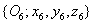koordináta rendszerbe az 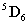transzformációs mátrixszal vihetjük át, azaz

(4.14)

Felhasználva a 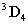, 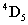és 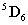transzformációs mátrixokat képezhetjük a 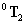transzformációs mátrixot, amely a bázis koordináta rendszert átszámolja a végberendezés koordináta rendszerébe, azaz

(4.15)

kifejtve

(4.16)

Vissza	Fel	Előre
3. fejezet - Példa – A robotvezérlő program használati utasítása	Főoldal	5. fejezet - Példák – robotok csoportosítása